Ionenfallen

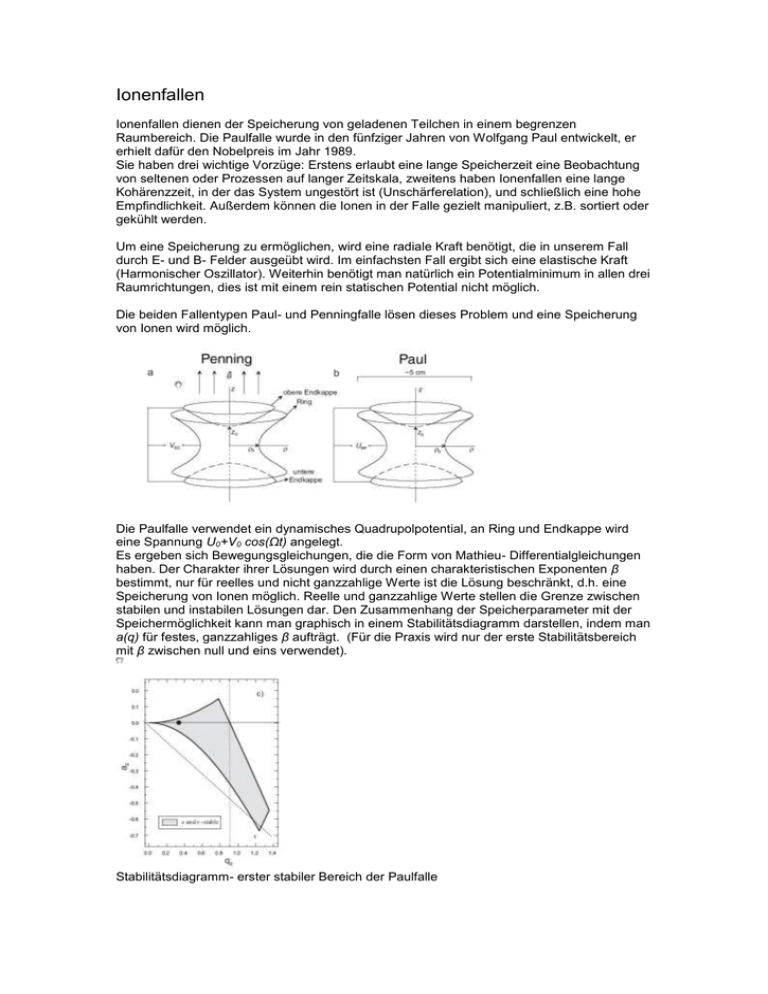
Ionenfallen
Ionenfallen dienen der Speicherung von geladenen Teilchen in einem begrenzen
Raumbereich. Die Paulfalle wurde in den fünfziger Jahren von Wolfgang Paul entwickelt, er
erhielt dafür den Nobelpreis im Jahr 1989.
Sie haben drei wichtige Vorzüge: Erstens erlaubt eine lange Speicherzeit eine Beobachtung
von seltenen oder Prozessen auf langer Zeitskala, zweitens haben Ionenfallen eine lange
Kohärenzzeit, in der das System ungestört ist (Unschärferelation), und schließlich eine hohe
Empfindlichkeit. Außerdem können die Ionen in der Falle gezielt manipuliert, z.B. sortiert oder
gekühlt werden.
Um eine Speicherung zu ermöglichen, wird eine radiale Kraft benötigt, die in unserem Fall
durch E- und B- Felder ausgeübt wird. Im einfachsten Fall ergibt sich eine elastische Kraft
(Harmonischer Oszillator). Weiterhin benötigt man natürlich ein Potentialminimum in allen drei
Raumrichtungen, dies ist mit einem rein statischen Potential nicht möglich.
Die beiden Fallentypen Paul- und Penningfalle lösen dieses Problem und eine Speicherung
von Ionen wird möglich.
Die Paulfalle verwendet ein dynamisches Quadrupolpotential, an Ring und Endkappe wird
eine Spannung U0+V0 cos(Ωt) angelegt.
Es ergeben sich Bewegungsgleichungen, die die Form von Mathieu- Differentialgleichungen
haben. Der Charakter ihrer Lösungen wird durch einen charakteristischen Exponenten β
bestimmt, nur für reelles und nicht ganzzahlige Werte ist die Lösung beschränkt, d.h. eine
Speicherung von Ionen möglich. Reelle und ganzzahlige Werte stellen die Grenze zwischen
stabilen und instabilen Lösungen dar. Den Zusammenhang der Speicherparameter mit der
Speichermöglichkeit kann man graphisch in einem Stabilitätsdiagramm darstellen, indem man
a(q) für festes, ganzzahliges β aufträgt. (Für die Praxis wird nur der erste Stabilitätsbereich
mit β zwischen null und eins verwendet).
Stabilitätsdiagramm- erster stabiler Bereich der Paulfalle
Die Penningfalle hingegen verwendet die Überlagerung eines B- Feldes in z-Richtung und
eines schwachen elektrischen Quadrupolpotentials. Die Lösung der Bewegungsgleichungen
ergibt die Überlagerung von drei Schwingungsbewegungen: Magnetronbewegung
(

c
2

c 2
4

z2
und axiale Bewegung.
2
), modifizierte Zyklotronbewegung (  
c 

c
2

c 2
4

z2
2
)
q
B ist die Zyklotronfrequenz.
m
Nun möchte man in der Falle gespeicherte Ionen auch nachweisen. Grundsätzlich gibt es
zwei verschiedene Möglichkeiten, einmal ein destruktiver und ein nichtdestruktiver Nachweis.
Mögliche Methoden sind z.B. Flugzeitnachweis (TOF), FouriertransformationsIonenzyklotronresonanz (FT-ICR, nicht destruktiv, induzierte Spiegelströme) oder der
Fluoreszenz- Nachweis.
Beim Flugzeitnachweis (destruktiv, in der Pennigfalle) wird die Zyklotronfrequenz als Summe
von ω+ und ω- extern angeregt. Dadurch werden die beiden Bewegungen gekoppelt, was zu
einer Erhöhung der radialen kinetischen Energie und damit des magnetischen Momentes
führt. Dies nutzt man aus, indem man die Ionen nach der Anregung aus der Falle heraus wirft
und in einen Bereich mit inhomogenem B- Feld bringt. In diesem Bereich werden die Ionen
mit dem größten magnetischen Moment am stärksten zum Detektor hin beschleunigt und
haben die kürzeste Flugzeit.
Des Weiteren kann man Ionen in der Falle kühlen. Dadurch reduziert man ihre
Phasenraumfläche (Emmitanz). Es gibt verschiedene Methoden, z.B. Puffergaskühlen,
Laserkühlen, Elektronenkühlen, Widerstandskühlen oder Verdampfungskühlen (letzteres
könnt ihr unter http://www.iap.uni-bonn.de/P2K/ ausprobieren).
Ionenfallen werden heute in zahlreichen Bereichen aktueller Forschung angewendet.
Beispiele sind:













Untersuchung von Antimaterie
g-Faktor (z.B. Proton, hochgeladene Ionen) δm/m=10-9
Test der QED
Präzisionsmassenmessung
Radionuklide δm/m=10-8
Kernstruktur
Astrophysik
Stabile Ionen δm/m=10-10
Neudefinition kg
Fundamentale Konstanten
Laserspektroskopie δm/m=10-9-10-10
Lebensdauermessung
Isotopieverschiebung, Hyperfeinstruktur
Das ISOLTRAP- Experiment am CERN dient der hochpräzisen Massenmessung an
Radionukliden. Herzstück ist eine hyperbolische Penningfalle, in ihr wird die
Zyklotronfrequenz und damit die Masse mittels der Flugzeitmethode bestimmt. Da man
Frequenzen genauer messen kann als Magnetfelder, verwendet man Referenzionen
bekannter Massen. Besondere Vorteile haben hier Kohlenstoff- Cluster, da sie systematische
Unsicherheiten (Refrenzmasse maximal 6u von der unbekannten Masse entfernt) reduzieren,
eine Bestimmung der Genauigkeitsgrenze erlauben und die Unsicherheit in der
Referenzmasse mittels Definition (Grundlage von u) reduzieren. Mit dieser Methode ist es
sogar möglich, angeregte Kernzustände durch ihre zusätzliche Masse vom Grundzustand zu
unterscheiden.
Trennung vom Grundzustand (GS) und angeregtem Zustand (ES) im Flugzeitspektrum.( 68Cu)
Verwendete Literatur:
Klaus Blaum, Script zur Vorlesung Spektroskopie in Ionenfallen
Physik Journal 3 (2004)
Kluge et al. Physica Scripta, T104 (2003)
G. Bollen Traps for Rare Isotopes
A. Kellerbauer et al., Phys. Rev. Lett. 93 (2004)
K. Blaum et al. Europhys. Lett. 67, 585 (2004)