Uebung zu Versuch 6 mit Loesung
Werbung

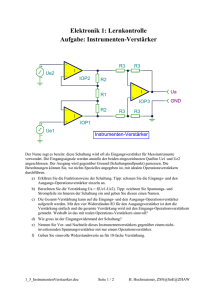
13. Dezember 2012 Übungen zum 6. Versuch Elektronik 1 - UT-Labor 1. Folgende Schaltung zeigt einen einfachen Differenzverstärker. Ub 2 ic1 ic2 Rc Rc ib1 ua1 ib2 ua2 ue2 ue1 Ub 2 ue Re a) Stellen Sie die Maschengleichungen für die Basisemitterspannungen der beiden Transistoren auf. Berücksichtigen Sie dabei die Eingangsspannungen. Lösung: Die Maschen können über die Massen geschlossen werden. Deshalb lassen sich folgende Gleichungen aufstellen: ube1 uobe2 Ub 2 Ub = u e2 − u e + 2 = u e1 − u e + (1) Ähnlich wie bei der Stromgegenkopplung sind die Basisemitterspannungen von der Differenz aus ue1 und ue abhängig. b) Stellen Sie die Maschengleichungen für die Ausgangsspannungen auf. Berücksichtigen Sie dabei die Spannungen an den jeweiligen Kollektorwiderständen. Lösung: Die Maschen können wieder über die Massen geschlossen werden. Deshalb lassen sich folgende Gleichungen aufstellen: ua1 = ua2 = Ub − Rc · ic1 2 Ub − Rc · ic2 2 1 13. Dezember 2012 Elektronik 1 - UT-Labor Übungen zum 6. Versuch 2. Die Vorgänge im Differenzverstärker sollen nun zeitlich verlangsamt betrachtet werden. a) Die Eingangsspannungen ue1 und ue2 werden gleichzeitig erhöht. Vervollständigen Sie die untenstehende zeitliche Abfolge der Veränderungen. ue1,2 Ű ⇒ ube1,2 ib1,2 ic1,2 ue ube1,2 ib1,2 ic1,2 Lösung: Ausgangspunkt ist Gl. 1. Werden beide Eingangsspannungen im gleichen Maße erhöht, vergrößern sich ube1,2 , ib1,2 und ic1,2 ebenfalls im gleichen Maß. Da ue = Re · (ic1 + ic2 ) wird auch die Spannung am Emitterwiderstand größer und kompensiert die Erhöhung der Eingangsspannung. Deshalb: ue1,2 Ű ⇒ ube1,2 Ű ib1,2 Ű ic1,2 Ű ue Ű ube1,2 Ů ib1,2 Ů ic1,2 Ů b) Verändern sich die Kollektorströme? Wie verändern sich die Ausgangsspannungen? Lösung: Die Änderung der Kollektorströme wird bei gleicher Änderung der Eingangsspannung durch den Emitterwiderstand weitestgehend aufgehoben. Die Ausgangsspannungen bleiben deshalb annähernd konstant. c) Wie verändert sich die Spannung an Re ? Warum? Lösung: Die Änderung der Kollektorströme wird bei gleicher Änderung der Eingangsspannung durch den Emitterwiderstand weitestgehend aufgehoben. Die Spannung an Re bleibt ebenfalls annähernd konstant. d) Die Eingangsspannung ue1 wird erhöht. Die Eingangsspannung ue2 wird verringert. Vervollständigen Sie die untenstehende zeitliche Abfolge der Veränderungen. ue1 Ű ⇒ ube1 ib1 ic1 ue ube1 ib1 ic1 ue2 Ů ⇒ ube2 ib2 ic2 ue ube2 ib2 ic2 Lösung: Die Eingangsspannungen ändern sich gegensinnig. Während im linken Zweig der Kollektorstrom größer werden kann, wird der Kollektorstrom im rechten Zweig kleiner. Deren Summe und damit auch die Spannung ue bleibt annähernd konstant. Da sich die Kollektorströme gegensinnig ändern, ist die Stromgegenkopplung durch den Emitterwiderstand unwirksam. Die Spannung ube1 kann weiterhin größer werden, ube2 kleiner. ue1 Ű ⇒ ube1 Ű ib1 Ű ic1 Ű ue ≈ konst. ube1 Ű ib1 Ű ic1 Ű ue2 Ů ⇒ ube2 Ů ib2 Ů ic2 Ů ue ≈ konst. ube2 Ů ib2 Ů ic2 Ů 2 Übungen zum 6. Versuch 13. Dezember 2012 Elektronik 1 - UT-Labor e) Verändern sich die Kollektorströme? Wie verändern sich die Ausgangsspannungen? Lösung: s.o. f) Wie verändert sich die Spannung an Re ? Warum? Lösung: s.o. 3. Von zwei beliebigen Eingangsspannungen können Differenz- und Gleichtaktspannung gebildet werden. uD = ue1 − ue2 ugl = ue1 + ue2 2 Drücken Sie die Eingangsspannungen als Funktion der Gleichtakt- und Differenzspannung aus. Welcher Spannungsanteil wird verstärkt? Lösung: 1 1 · uD ue2 = ugl − · uD 2 2 Beliebige Eingangsspannungen lassen sich also durch ihre Differenz und ihren Gleichtaktanteil ausdrücken. Dabei beschreibt die Differenz uD nur den Spannungsanteil, der aus einer gegensinnigen Änderung der Eingangsspannungen folgt und der Gleichtaktanteil ugl den Anteil der Eingangsspannungen, der aus einer gleichsinngen Änderung folgt. Der Differenzverstärker verstärkt im Idealfall nur den Differenzanteil. ue1 = ugl + 3 13. Dezember 2012 Elektronik 1 - UT-Labor Übungen zum 6. Versuch 4. In der obenstehenden Differenzverstärkerschaltung wurde ein Widerstand Re eingesetzt. Eine bessere Gleichtaktunterdrückung erhält man, wenn stattdessen folgende Schaltung eingesetzt wird. Ub = 40 V Ic Rb Ib Rc ube ZPD1 a) Ermitteln Sie die Kollektorströme für die Lastwiderstände aus der Tabelle. Wie groß ist die Änderung ∆Ic ? Lösung: Hinweis: Die Betriebsspannung sollte bei Ub =40 V liegen. Ib 4 mA 6 mA Kollektorstrom in A für Rc = . . . 33.33 Ω 40.00 Ω 66.67 Ω 100.00 Ω 0.372 0.529 0.372 0.514 0.372 0.457 0.343 0.386 ∆Ic 0.029 0.143 b) Welche Eigenschaft hat die Schaltung? Lösung: Die Änderung des Kollektorstroms ist trotz der Änderung des Kollektorwiderstands sehr klein. Da die Steigung der Kennlinie für Ib =6 mA größer ist, ist auch die Änderung des Kollektorstroms größer. c) Sie wollen die Eigenschaft der Schaltung verbessern, indem Sie den Transistor austauschen. Welcher Parameter des Transistors müßte deutlich besser sein? Lösung: Der differentielle Kollektoremitterwiderstand des Austauschtransistors sollte größer sein. Die Kennliniensteigung ist dann kleiner und damit auch die Änderung im 4 13. Dezember 2012 Übungen zum 6. Versuch Elektronik 1 - UT-Labor u1 (t)/mV Kollektorstrom. 20.0 u1(t) 10.0 0.0 -10.0 -20.0 u2 (t)/mV 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 20.0 u2(t) 10.0 0.0 -10.0 ud (t)/mV -20.0 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 20.0 10.0 0.0 -10.0 ugl (t)/mV -20.0 20.0 10.0 0.0 -10.0 -20.0 t/s 5. An einen Differenzverstärker mit einer Differenzverstärkung von vd =40 und einer Gleichtaktverstärkung vgl = − 40 dB werden die oben gezeigten Signale angeschlossen. a) Bestimmen Sie graphisch den Verlauf der Differenzspannung und der Gleichtaktspannung. 5 Elektronik 1 - UT-Labor 13. Dezember 2012 Übungen zum 6. Versuch b) Welche Größe haben die verstärkten Signalanteile? Lösung: Das Maximum der Differenzspannung sorgt für eine Ausgangsspannung von 400 mV, das Maximum der Gleichtaktspannung für eine Ausgangsspannung von 75 mV. 6