Astronomie mit Gravitationslinsen - Blicke ins junge - Alice
Werbung

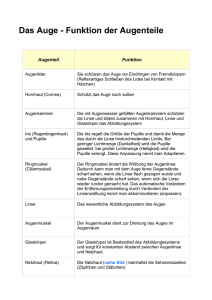
DESY 20. April 2009 Astronomie mit Gravitationslinsen Blicke ins junge Universum ( jung = 700 Mio. Jahre alt ) Dipl.Phys. Albrecht von der Decken Homepage 1609 - - - 2009 Vor 400 Jahren entdeckte Galilei mit seinem Fernrohr 4 Jupitermonde 1609 veröffentlicht Kepler seine ersten beiden Gesetze in Astronomia Nova 1609 (Jan.1610) Der Mond verdeckt die Sonne Bei einer Sonnenfinsternis In der Nacht ohne Ablenkung durch die Sonne Ablenkung von Licht an der Sonne nur 1,75´´ = 0,0005 Grad (1°= 60´ = 3600´´) δ=1,75’’ Mond Zum Nachrechnen für Schüler, die integrieren können: http://www.relativity.li/epstein/pdf-downloads.html dort: G5 und I2 Die Lichtablenkung im Gravitationsfeld der Sonne Negativ von 1919 Eddington vermessen während der totalen Sonnenfinsternis am 21.Sept. 1922 von Campbell ebenso wie Eddington 1919 Negativ von 1919 Eddington ØSonne = 1.400.000 km 1,75‘‘ entsprechen 1.300 km http://www.wissenschaft-schulen.de/sixcms/media.php/767/wis07b%5B1%5D.pdf Ein Astronom staunt, als er 1979 zwei gleich aussehende Quasare im Abstand von 6´´ entdeckt. 1979 Zwillings-Quasar Q0957+561 G-Linse ist die riesige elliptische Galaxie G1 Schwarzes Loch Schwarzes Loch 18 km Umweg auf dem Weg von der Erde zur Venus ( 36 km Raumzeit-Umweg ) Die Sonne hat 1,4 Mio km Durchmesser. Prinzip einer Gravitationslinse Das Objekt mit grosser Masse ist: • ein Stern ….. oder sein Planet (Exoplanet) • ein Schwarzes Loch oder ein Macho • eine ganze Galaxie oder ein Galaxienhaufen Schwarzes Loch Die Strahlungsquelle kann eine Galaxie oder ein Quasar sein. Erde Ablenkwinkel bei der Sonne nur 1,75 Bogensekunden 1°= 60´ = 3600´´ Quellgalaxie und Weg-Pfeile des Lichts von ihr zur Erde sind weiß Quellgalaxie Die Gravitationslinse ist eine weitere Galaxie Erde Beobachter bogenförmige Mehrfachbilder der Quellgalaxie und Abbildungspfeile sind orange Kugelförmige Gravitatinons-Linse ergibt Einstein-Ring Quelle, Linse und Beobachter in einer Linie Längliche Linse ergibt Einstein-Kreuz Galaxie Galaxienhaufen als Linse ergibt bogenförmige Mehrfachbilder einer einzigen Quelle Galaxienhaufen http://www.spacetelescope.org/images/html/heic0404b.html ∆t bis 5 Jahre α Sonne = 1,75´´ Der “Radius“ vom EinsteinRing ist ein Winkel ΘE ΘE 2ΘE http://www.ita.uni-heidelberg.de/~msb/gravLens/index_gr.html Hubble Deep Field Aufnahme mit verschieden langen Bögen Gute Seminararbeit 2007 mit Herleitung der Formeln Massenbestimmung mittels starkem Gravitationslinseneffekt http://pulsar.sternwarte.unierlangen.de/wilms/teach/astrose m07/Gravitationslinsen.pdf Vielfalt der AbbildungsBögen Die Zuordnug der Bögen zu den Quell-Galaxien ist kompliziert. Die beiden roten Bögen mit weißen Markierungen stammen von einer einzigen Quelle Glas-Prisma chromatische Brechung Gravitationslinsen erzeugen eine achromatische Brechung, weil die Raumzeitkrümmung für Licht aller Farben gleich ist. LSS = Large Scale Structure http://www-ik.fzk.de/~drexlin/astro0809/AT09.pdf Beispiel einer Linse M81 Mehrfachbilder einer Quelle Hier 3 bis 5 Bilder http://www.nasa.gov/multimedia/imagegallery/im age_feature_575.html Die Raumzeitkrümmung hat Auswirkung auf alle Wellen, Teilchen und Materie Auf Lichtstrahlen (Photonen) Auf Gravitationswellen Gravitationswellen sind Transversalwellen Auf die kosmische Hintergrundstrahlung CMB Atomkerne vor 13,7 Mrd Jahren Atome vor 13,6 Mrd Jahren vor 13,2 Mrd Jahren vor 11,6 Mrd Jahren http://www.astro.ucla.edu/~wright/CosmoCalc.html z=Rotverschiebung z=8 bis 10 mit und z=5 ohne Gravitations-Linse http://www.iap.fr/col2008/Procee dings/Session%20VI.%20Highz%20Galaxies/Kneib_IAP08.pdf vor 2,5 Mrd Jahren heute Alter=13,7 Mrd Jahre Die am weitesten entfernte Galaxie (13 Mrd.Lichtjahre) wird durch eine Gravitationslinse 25- bis 100-fach verstärkt. Das Licht informiert uns über die Zeit 750 Mio. Jahre nach dem Urknall! http://www.astro.caltech.edu/~joh http://www.astro.ucla.edu/~ wright/cosmolog.htm#News an/cosmic_dawn/z7_pr2.jpg Redshift 10 Galaxies? z=8 LightTravelTime=13MrdLJ z=5 12,5MrdLJ Einstein-Radius + Massenbestimmung Ablenkung des Lichts an der Sonne: Einstein-Radius = ΘE rS = Schwarzschildradius der Sonne = 3 km b = Radius der Sonne = 700 000 km G = γ = Gravitationskonstante Newton M = Masse der Galaxie („Linse“) c = Lichtgeschwindigkeit Dd= Entfernung zur Linse (Deflector) Ds= Entfernung zur Quelle (Source) Dds= Entfernung von der Linse zur Quelle Masse der Linse = M(ΘE) Messung der Hubblekonstanten Ho Schneider S.130 Für β = 0 α(Θ) = Θ = ΘE http://pulsar.sternwarte.unierlangen.de/wilms/teach/astros em07/Gravitationslinsen.pdf Von 1998 bis 2005 wurden 10 Einstein-Ringe entdeckt Doppelter Einstein-Ring und Simulation dazu Es sind 3 Galaxien, die Linse mit 1 Mrd Sonnenmassen im Abstand von 3 LJ, die Quellen bei sechs und elf Mrd LJ. http://de.wikipedia.org/wiki/Einsteinring Original Rekonstruktion http://arxiv.org/PS_cache/arxiv/pdf/0801/0801.1555v1.pdf Restgröße=residual SLACS-Team Uni-Hawaii Sloan Digital Sky Survey http://www.spacetelescope.org/news/science_paper/jackpot_submitted.pdf Entdeckung von 500 Photonen der Ringe in den 500.000 Photonen der Vordergrund-Galaxie Die Masse der Vordergrund-Galaxie L1 und der Galaxie S1=L2 ist für die Einstein-Ringe verantwortlich. Der Anteil der Dunkelmaterie in L1 wurde berechnet. Die Masse der Galaxie S1=L2 ist eine Mrd Sonnenmassen. Erste präzise Messung der Masse einer Zwerggalaxie in dieser Entfernung Gelänge es noch mehr solche doppelten Ringe zu finden, könnte man aus den verschiedenen Radien der Ringe die Krümmung des Raums auf unabhängige Weise berechnen. Etwa 50 Ringpaare werden benötigen, um Dunkle Materie und Dunkle Energie des Universums mit einem Fehler von maximal zehn Prozent zu bestimmen. Noch ist der Fund eines Doppelrings so selten, wie ein Sechser im Lotto. Simulation von Linseneffekten und Einstein-Ring: http://www.tempolimit-lichtgeschwindigkeit.de/isl/isl.html 1. Masse der Linse auswählen 2. Simulation starten mit einem Klick auf das Bild dort wo die Linse sein soll Spiel mit dem Schwarzen Loch 6 Seiten: http://www.tempolimitlichtgeschwindigkeit.d e/isl_d/isl-material.pdf http://www.tempolimitlichtgeschwindigkeit.de Simulation zum Einstein-Ring www.gophy.de/index .php?option=com_do cman&task=docclick &Itemid=57&bid=132 &limitstart=0&limit=5 Abbildung 19 Weinglasfuß mit Einstein-Ring http://www.tempolimit-lichtgeschwindigkeit.de/einsteinring/einsteinring.html Der "richtige" Einstein-Ring Zur Simulation auf das Bild klicken Gravitationslinse aus Glas nachgebaut Querschnitt des LinsenNachbaus aus Glas Licht einer weit entfernen Quelle wird aufgefächert. http://timms.uni-tuebingen.de/List/List01.aspx?rpattern=UT_20040806_001_sommeruni2004_0001 http://idwonline.de/pages/de/ news227261 Gravitationslinsen fächern parallele Lichtstrahlen auf http://www.astronomische-vereinigung-augsburg.de/artikel/physik-und-kosmos/art-test-teil-1/ Das Licht einer weit entfernten Quelle (Hintergrundstern, Galaxie oder Quasar) wird von der Gravitationslinse aufgefächert. Sind Beobachter, Linse und Quelle in einer Linie, so sieht der Beobachter ab einer Mindestentfernung von der Linse einen Einstein-Ring. Die Mindestentfernung ist nur vom Schatten der kompakten Linsenmasse abhängig. Das Licht auf krummen Wegen in der Nähe eines Schwarzen Lochs Schwarzes Loch Stern = Lichtquelle http://www.tempolimit-lichtgeschwindigkeit.de/reiseziel_d/reiseziel-schwarzesloch-material.pdf Neutronenstern mit 10 km Radius und 1,4 Sonnenmassen Aufgrund der gravitativen Ablenkung der Lichtstrahlen kann ein entfernter Beobachter 84 Prozent der Oberfläche einsehen. Eine Lichtquelle, die sich von einem Beobachter aus gesehen hinter einem Neutronenstern befindet, kann sichtbar sein; in diesem Fall ist ein Doppelbild möglich. Ein masseloser Begleitstern umkreist einen Neutronenstern. http://www.tempolimitlichtgeschwindigkeit.de/filme/bbm1/bbm1xd-640x480.mpg http://www.tempolimitlichtgeschwindigkeit.de/ssm/ssm.html Der Film simuliert den Umlauf eines Begleitsterns mit wenig Masse um einen Neutronenstern. Der Beobachter sieht mehr als die Vorderseite des Neutronenstern. Zur Simulation auf das Bild klicken. Funktioniert nur, wenn die ppt-Datei gespeichert und mit PowerPoint geöffnet wurde. Licht auf krummen Wegen Gravitational Lensing from a Spacetime Perspective http://www.emis.de/journals/LRG/Articles/lrr-2004-9/download/lrr-2004-9Color.pdf Seite 53 Bilder einer Hintergrundgalaxie: Vom Einfachbild zum Doppelbild und zum Einstein-Ring Linse Quelle errechnete Einstein-Ringe perfekter Einstein-Ring http://astro.uni-wuppertal.de/~kampert/Kosmologie-Bilder/Gravitationslinse.jpg links die Mehrfachbilder rechts die Quelle mit Kaustik http://www.astro.uni-bonn.de/~peter/Lectures/intro3.pdf Seite 133 links die Mehrfachbilder rechts die Quelle mit Kaustik http://arxiv.org/PS_cache/astro-ph/pdf/9606/9606001v2.pdf http://www.astro.uni-bonn.de/~peter/Lectures/intro3.pdf Seite 133 Simulation: 2 Bögen und Einstein-Ring ohne Grav-Linse mit Grav-Linse http://www-ra.phys.utas.edu.au/~jlovell/simlens/lens.gif Simulation des Gravitationslinseneffekts Ein schwarzes Loch vor einer Galaxie in Seitensicht Weak gravitational Lensing = Schwacher GravitationsLinsen-Effekt (keine Mehrfachbilder) http://en.wikipedia.org/wiki/ Weak_gravitational_lensing Schwacher LinsenEffekt Simulation Wo sind die Linsen? http://people.sissa.it/~bacci/w ork/workshop%20talks/Beyon d%20Einstein,%20Stanford, %20California,%20USA,%20 %20May%202004/Nbody%20Simulations%20and %20Gravitational%20Lensing %20with%20Dark%20Energy .ppt#268,17,Simulating Arcs Die Helligkeitskurve eines Hintergrund-Sterns beim Durchgang eines Sterns mit einem Exoplaneten. Es müssen etwa eine Million Hintergrundsterne gleichzeitig überwacht werden, um Mikrolinsenereignisse zu finden. Lichtkurve für einen Planeten mit Erdmasse, der einen Stern mit 0,3 Sonnenmassen in einer Entfernung von 2 AE umkreist. http://kuffner-sternwarte.at/im_brennp/archiv1998/vks_news_ml_planets.html Exoplanet 1998 Micro-Lensing galaktisch (auch LMC) oder auß ßergalaktisch: BH, Galaxien, Quasare, DM http://arxiv.org/PS_cache/astro-ph/pdf/9606/9606001v2.pdf Bartelmann Micro-Lensing Quelle oder Linse bewegen sich p=0.3 p=0.5 Kennzeichen: achromatisch, symmetrisch und nur eine Variation auf Seite 70, 72 und 74 im Buch in der DESY-Bibliothek + http://www.astro.uni-bonn.de/~peter/Lectures/intro2.pdf Für p = 0.2 p=1 entspricht dem Einstein-Radius Bild 2 Quelle Einstein-Kreis Linse Linse Bild 1 Micro-Lensing Quelle oder Linse bewegen sich p=0.3 p=0.5 Kennzeichen: achromatisch, symmetrisch und nur eine Variation auf Seite 70, 72 und 74 im Buch in der DESY-Bibliothek + http://www.astro.uni-bonn.de/~peter/Lectures/intro2.pdf Es gibt viele Methoden zur Planetensuche: - Radialgeschwindigkeit Dopplereffekt -Transitmethode Helligkeitsbeobachtung CoRoT Kepler USA Start 3/09 CoRoT = Convection, Rotation und planetare Transits http://www.corot.de - Gravitationslinsen-Effekt Micro-Lensing - Fotonachweis mit Stern-Abdeckung ab 2008 http://www.matkit.at/studium/sem_planet/meth.htm Erste Fotos von Exoplaneten 2008 Super Wide Angle Search Bei den Planeten WASP-3b, WASP-4b und WASP-5b handelt es sich jeweils um Planeten, die etwas größer sind als Jupiter und ihren Zentralstern auf extrem engen Umlaufbahnen umkreisen. Es sind also so genannte heiße Jupiter. Dunkle Materie errechnet mit dem schwachen Gravitationslinseneffekt Die Verteilung der Dunklen Materie eit Z ~ ng u ieb h c s r tve o R http://en.wikipedia.org/wiki/ Gravitational_lensing wurde errechnet aus Hubble-Aufnahmen mit dem schwachen Gravitationslinseneffekt Geschichte der Gravitationslinsen Einstein Eddington Chwolson Zwicky Refsdal • Einstein 1912 Notizbuch 1936 Artikel für Herrn Mandl • Eddington 1919 Licht-Beugung an der Sonne 1920 Idee: Mehrfachbilder • Chwolson 1924 Artikel zu fiktiven Doppelsternen: Doppelbild und Einsteinkreis • Zwicky 1937 Idee: Galaxie als Gravitationslinse (Frost Mt.Wilson schon 1923) • Refsdal 1963 Doktor-Arbeit, Professor in Hamburg 1970-2001 • Erste Beobachtung: 1979 Zwillings-Quasar 1985 Einstein-Kreuz 1987 Galaxienhaufen als Linse 1990 schwacher Linseneffekt 1993 Mikrolinseneffekt 1998 Einstein-Ring 2003 Exoplanet (Methode für erdähnliche Exoplaneten) http://www.sciencemag. org/content/vol275/issue 5297/images/large/se49 64527001.jpeg QuellEbene Erde Linse Einsteins Notizbuch 1912 Rechnung zu Gravitationslinsen Chwolson 1924 Artikel mit Doppelbild und Einsteinkreis beugender Stern Quelle Erde Der das Licht der Quelle beugende Stern erscheint zusammen mit dem Abbild der Quelle als fiktiver Doppelstern. Astron.Nachrichten Vol. 221 Seite 329 Sjur Refsdal 1935-2009 http://www.astro.uio.no/ita/nyheter/refsdal_0209 Literatur und Links Galaxien als natürliche Teleskope in Sterne und Weltraum Nov.2008 http://www.astronomie-heute.de/artikel/968641&_z=798889 11 Seiten Gravitationslinsen III: Der schwache Linseneffekt 2 Seiten http://www.astro.uni-bonn.de/~peter/Poster3d.html Gute Seminararbeit 2007 mit Herleitung der Formeln 38 Folien http://pulsar.sternwarte.uni-erlangen.de/wilms/teach/astrosem07/Gravitationslinsen.pdf Der Mikrolinseneffekt - Der starke Linseneffekt - Der schwache Linseneffekt http://www.ita.uni-heidelberg.de/~jmerten/lensing.shtml?lang=de 1 Seite Introduction to Gravitational Lensing - Lecture Scripts 103 Seiten http://www.ita.uni-heidelberg.de/~jmerten/misc/meneghetti_lensing.pdf 4 Microlensing 5.1 Strong lensing 5.2 Weak lensing http://www.ita.uni-heidelberg.de/~jmerten/talks/tonale091208.pdf 21 Folien http://www.ita.uni-heidelberg.de/~jmerten/publications/jm_diploma_thesis.pdf Diplomarbeit http://www.ita.uni-heidelberg.de/~jmerten/talks/imprs170408.pdf 18 Folien Weak and Strong Weak Lensing Micro-Lensing Wambsganss http://www.ita.uni-heidelberg.de/~jmerten/misc/bartelmann_weaklensing.pdf http://arxiv.org/ftp/astro-ph/papers/0604/0604278.pdf Peter Schneider Lehrbuch Einführung in die Extragalaktische Astronomie und Kosmologie 2006 3 Teile zu Gravitationslinsen http://www.amazon.de/gp/reader/3540258329/ref=sib_dp_pt#reader-page http://wwwex.physik.uni-ulm.de/lehre/gk1-2005-2006/node17.html#SECTION00472110000000000000 Gravitationspotential einer homogenen Kugel http://www.physikon.de Φ(r) = - G m / r http://www.spektrum.de/sixcms/media.php/767/potential.doc http://de.wikipedia. org/wiki/Potential Gravitationspotential / Krümmung der Raumzeit Gravitationspotential einer homogenen Kugel Das Licht bewegt sich auf Geodäten und diese zeigen die vollständige ?? Raumzeitkrümmung Γ = Christoffelsymbol http://de.wikipedia.org/wiki/Geod%C3%A4te Äußere Schwarzschildlösung (Flamm'sches Paraboloid) Innere Krümmung der rs = Schwarzschild-Radius Zentralebene zu einem festen Zeitpunkt rs = 2 G M / c² Vollständige Schwarzschildsche Lösung für einen Stern mit homogener Materie rs = Schwarzschild-Radius Innere Krümmung der Zentralebene zu einem festen Zeitpunkt Flamm'sches richtig ?? http://de.wikipedia.org/wiki/Schwarzschild-Metrik Paraboloid PotentialDarstellung von 2 Schwarzen Löchern http://www.geo600.unihannover.de/~aufmuth/Grav itationswellen3_2008.pdf Seite 10 Effektives Potential für Photonen 1.Gravitationspotential 2.Drehimpulspotential 3.Relativistischer Term Seite 176 Effektives Potential nach Newton http://arxiv.org/PS_cache/gr-qc/pdf/9712/9712019v1.pdf Sean M Carroll Spacetime and Geometry: An Introduction to General Relativity Seite 178 ART = Allgemeine Relativitäts-Theorie Für Photonen gilt ε = 0 Für Photonen gilt ε = 0 L = Drehimpuls rs Effektives Potential für Teilchen mit Masse 1.Gravitationspotential 2.Drehimpulspotential 3.Relativistischer Term Seite 176 Effektives Potential nach Newton http://arxiv.org/PS_cache/gr-qc/pdf/9712/9712019v1.pdf Sean M Carroll Spacetime and Geometry: An Introduction to General Relativity Seite 178 ART = Allgemeine Relativitäts-Theorie Für Masseteilchen gilt ε = 1 L = Drehimpuls Für Masseteilchen gilt ε = 1 rs Die Lichtgeschwindigkeit in der Nähe einer großen Masse, die ein ferner feldfreien Beobachter misst wird Koordinaten-Lichtgeschwindigkeit genannt. Die Koordinaten-Lichtgeschwindigkeit für tangentiale Lichtstrahlen ist: für radiale Lichtstrahlen ist: für Lichtstrahlen mit einem Winkel β zwischen dem Lichtstrahl und der Richtung der Masse gilt: Nach Epstein G5 Seite 113: ct(r) c(r,β) β c (r) r rS SchwarzschildRadius Schwarzes Loch β=δ Für rS = 3 km und r = 4 km gilt: radial: cr(r,∞) = 75 000 km tangential: ct(r,∞) = 150 000 km β = 45° c(r, ∞,β) = 118 585 km 2 α = rS = 2 G M / c² http://www.geo600.unihannover.de/~aufmuth/J oeWeber.pdf