I. Löse die Gleichung und führe die Probe durch!

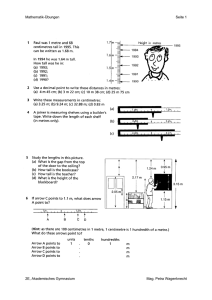
Mathematik-Übungen
Seite 1
Test yourself
2E, Akademisches Gymnasium
Mag. Petra Wagenknecht
Mathematik-Übungen
Seite 2
ÜBUNGEN FÜR DIE 1. SCHULARBEIT:
I.
TEILBARKEIT, TEILER, VIELFACHE
1. Gib die Teilermenge im aufzählenden Verfahren an:
a) T50
b) T45
c) T53
d) T56
e) T104
f) T84
2. Gib alle Ziffern an, die man für * einsetzen kann, sodass eine wahre Aussage
entsteht:
a) 25 x 5634*5
_________
b) 3 x 5*3456 ___________
c) 4 x 22342*
___________
d)
9 x 312*43
___________
3. Ändere in der Zahl 5422 die Ziffer an der Einerstelle so ab, dass die neue Zahl
a) durch 2 b) durch 3 c) durch 4 d) durch 5 e) durch 6 f) durch 9
teilbar ist. Gib alle Möglichkeiten an!
4. Zerlege in Primfaktoren:
a) 74
b) 98
c) 3024
d) 2304
e)
3096
5. Gegeben sind zwei Zahlen:
a) 24 und 32
b) 20 und 35
c) 18 und 48
d) 15 und 27
1) Gib die Teilermenge jeder Zahl an. Gib die Menge der gemeinsamen Teiler an.
2) Zeichne ein Mengendiagramm. Wie lautet der größte gemeinsame Teiler?
6. Ermittle mittels Primfaktorzerlegung den ggT der Zahlen:
a) 24, 40
b) 18, 48
c) 12, 36, 52
7. Ermittle mittels Primfaktorzerlegung das kgV der Zahlen:
a) 6, 10
b) 14, 18
c) 16, 25
d) 12, 16, 20
8. Ermittle durch Kopfrechnen:
a) ggT(12, 30)
c) ggT(36,44)
e) ggT(24, 40)
d)
64,
e)
96,
128
40, 60, 100
b) kgV(6, 9)
d) kgV(10,13)
f) kgV(9, 15)
9. Vom Bahnhof einer Stadt ausgehend verkehren von 6:30 an alle 6 Minuten ein
Autobus der Linie A und alle 10 Minuten ein Autobus der Linie B. Zu welchen
Zeiten zwischen 6:30 und 13 Uhr fahren die Autobusse gleichzeitig vom Bahnhof
ab?
10. Herr Huber und Herr Müller arbeiten in derselben Firma. Herr Huber hat jeden
vierten Arbeitstag Spätdienst, Herr Müller nur jeden sechsten Arbeitstag. Wann
haben sie zum ersten Mal gemeinsam Spätdienst?
II.
GEOMETRIE
1. Zeichne eine Gerade g und nimm auf ihr einen Punkt P an. Konstruiere durch P
die Normale zu g. Zeichne eine Gerade h und nimm einen Punkt Q außerhalb
von h an. Konstruiere durch Q die Normale zu h und miss den Abstand Qh .
Zeichne eine Gerade m und nimm einen Punkt R außerhalb von m an.
Konstruiere durch R eine Parallele zu m. Miss den Abstand Rm .
2E, Akademisches Gymnasium
Mag. Petra Wagenknecht
Mathematik-Übungen
Seite 3
2. Konstruiere eine Gerade m und konstruiere im Abstand d = 3,5 cm die
Parallele n zu m.
3. Konstruiere einen Kreis mit dem Radius r = 3,8 cm und zeichne eine Sekante s,
eine Tangente t und eine Passante p des Kreises.
4. Zeichne einen Kreissektor, Radius r = 6 cm, Sehnenlänge s = 4 cm. Gib die
Größe des Zentriwinkels an.
5. Zeichne ein Kreissegment, wenn der Radius r = 5 cm und die Sehnenlänge s = 5
cm betragen.
6. Gib für das Berechnen von Umfang und Flächeninhalt Formeln an:
b)
7. Ein rechteckiges Grundstück mit einem Flächeninhalt von 27,9 a wird um
186 000 € verkauft.
a) Wie viel € kostet etwa 1 m² dieses Grundstücks?
b) Die eine Seite des rechteckigen Grundstücks ist 31 m lang. Wie lang ist die
zweite Seite und wie groß ist der Umfang des Grundstücks?
8. Berechne jeweils Umfang und Flächeninhalt des dargestellten Häuserblocks!
9. Ein Schwimmbecken fasst 1400 m³ Wasser.
a) Wie oft könnte man Wasser aus vollen 12-Liter-Kübeln hineinschütten?
b) Wie viele Badewannen mit 380 Liter Inhalt ließen sich damit füllen?
10. Rechne in die in Klammern angegebene Einheit um:
a) 324 Liter (hl) b) 4 m³ (hl) c) 2 cm³ (ml) d) 5 hl (m³)
2E, Akademisches Gymnasium
e) 12 dm³ (hl)
Mag. Petra Wagenknecht
Mathematik-Übungen
Seite 4
Übe fleißig für die 2. Schularbeit!
2E, Akademisches Gymnasium
Mag. Petra Wagenknecht
Mathematik-Übungen
Seite 5
I. Geometrie:
1. Der Punkt S(2|3) ist der Scheitel eines Winkels . Der Schenkel a verläuft durch
A(6|0), der Schenkel b durch B(5|6)
a) Miss die Größe des Winkels .
b) Konstruiere zum Winkel einen Parallelwinkel mit dem Scheitel in S1(5|4)
c) Konstruiere zum Winkel einen Normalwinkel mit dem Scheitel in S2(6|6)
2. a) Gib die Größe der einzelnen Winkel an
b) Gib drei supplementäre Parallelwinkelpaare an
c) Gib drei gleich große Parallelwinkelpaare an
3. Der Punkt S(2|2) ist der Scheitel des Winkels
α. Der Schenkel a verläuft durch A(4|1), der
Schenkel b durch B(0|1).
a) Miss die Größe des Winkels α.
b) Konstruiere die Winkelsymmetrale von α.
4. Zeichne den Kreis k mit dem Mittelpunkt M und dem Radius r: k[M(5|4), r=4].
Zeichne die Gerade g, die durch die Punkte P und Q verläuft: g[P(0|1), Q(9|2)].
Gib die Koordinaten der Schnittpunkte an, die die Gerade g mit dem Kreis k hat.
5. Spiegle die Strecke AB an der Geraden g: A(1|2), B(5|0); g[P(6|0),Q(3|6)] und
gib die Koordinaten der gespiegelten Punkte an.
6. Konstruiere das Rechteck ABCD mit a = 4 cm und b = 5 cm.
a) Spiegle das Rechteck an der Geraden g, die zu AC parallel ist und durch den
Eckpunkt B geht.
b) Spiegle das Rechteck an der Geraden g, die zu BD parallel ist und durch X
geht. Der Punkt X liegt dabei auf der Verlängerung der Seite DC und ist 1 cm
von C entfernt.
7. Spiegle den geschlossenen Streckenzug ABCA an der Geraden g und gib die
Koordinaten der Punkte an: A(1|1), B(2|3), C(0|4);
g[P(0|0), Q(5|5)]
8. Teile die Strecke AB mit Hilfe von Streckensymmetralen in 4 gleich große Teile:
A(3|2), B(9|1). Gib die Koordinaten der Halbierungspunkte X, Y und Z an.
9. α = 74°. Teile α in vier gleiche Teile.
10. Konstruiere ohne Winkelmesser durch Halbieren bzw. Addieren geeigneter
Winkel:
a) α = 60°
b) α = 150°
c) α = 15°
II. Brüche:
1. Gib in Liter bzw. in Kilogramm an:
1
4
5
b) 3 hl
c) hl
a) hl
8
5
8
2. Verwandle in eine gemischte Zahl:
87
71
91
a)
b)
c)
8
5
25
3. Schreibe als unechten Bruch:
2E, Akademisches Gymnasium
d) 2
3
t
4
d)
3
e) 1 t
5
89
7
f)
e)
1
t
8
35
12
Mag. Petra Wagenknecht
Mathematik-Übungen
Seite 6
3
3
5
3
1
b) 12
c) 13
d) 2
e) 13
4
5
6
12
4
4. Schreibe die Brüche als Dezimalzahlen:
7
7
5
7
3
a)
b)
c)
d)
e)
11
15
8
12
25
5. Verwandle in einen Bruch:
a) 4,23
b) 0,4
c) 0, 3&
d) 0,2& 3&
e) 2,5& 1&
f) 0,034
6. Gib für die Brüche in 4.einen Näherungswert (auf 2 Dezimalstellen genau) an.
7. Gib als Bruchteil
a) eines Kilogramms an: 5 dag, 12 dag, 50 dag, 2 g, 10 g, 25 g
b) eines Meters an: 2 dm, 6 dm, 50 cm, 25 cm, 5 mm, 14 mm
c) einer Stunde an: 8 min, 48 min, 25 min, 30 min, 15 min, 40 min
8. Berechne den Bruchteil:
a) Eine Schulklasse hat 30 Schüler, 12 Schüler tragen Brillen.
b) Peters Taschengeld beträgt 6 €, 2 € gibt er für Eis aus.
c) Die Kirschenernte betrug 250 kg, 50 kg davon wurden verkauft.
d) Ein Weg hat eine Länge von 45 m, 15 m sind schon asphaltiert.
11. Zutaten für einen Biskuittboden: 2 Eier, 6 dag Zucker, 4 dag Mehl, 2 dag
Stärkemehl. Berechne die Zutatenmenge für die 1 1/2fache Teigmenge.
12. Berechne jeweils die Gesamtgröße: a) 3/5 der Straßenlänge sind 45 km.
b) 5/7 der Erbschaft sind 20000 €.
c)2/3 des Winkels sind 30°.
13. Familie Huber hat ein monatliches Nettoeinkommen von 2500 €. 3/5 von diesem
Betrag benötigt die Familie für die Wohnungskosten und für Nahrungsmittel. Wie
viel € sind das?
14. Frau Reich verdient monatlich netto 1600 €. Für die Miete zahlt sie 480 Euro.
Welcher Bruchteil ihres Nettoeinkommens ist das?
15. Von einer Schule kommen täglich 220 Schüler mit dem Fahrrad zur Schule. Das
sind 5/8 von allen. Wie viele Schüler gibt es?
16. Hanna kauft 75 dag Wurst und bezahlt 5 Euro. Wie viel kostet ein kg Wurst?
17. Die Muskeln machen bei einem Menschen 4/10 der Gesamtmasse aus. Wie viel
kg Muskeln hat ein Mensch, der 85 kg wiegt?
18. Von einem Waldweg von 30 km Länge sind 2/5 der Länge fertiggestellt. Wie lang
ist diese Strecke, welcher Bruchteil des Waldwegs fehlt noch?
a) 2
III. Erweitern, Kürzen, Ordnen von Brüchen
1. Schreibe den fehlenden Nenner bzw. Zähler dazu:
2.n 6.n
3
7
a
a) =
b)
c)
d)
=
=
=
3.n
5 100
11 55
12 96
2. Erweitere so, dass die drei gegebenen Brüche einen möglichst kleinen gleichen
Nenner besitzen:
3 5 1
3 4 7
x 5 y
7 3 x
a) , ,
b) , ,
c) , ,
d) , ,
8 6 4
4 5 10
5 6 15
8 5 20
3. Schreibe den fehlenden Zähler bzw. Nenner an:
5 .y
20 5
12
4
5.x
a)
b)
c)
=
d)
=
=
=
25.y 5
12
27.a
15 3
4. Kürze soweit wie möglich:
90
450
15.8.7
5.6.x
3.z.4
a)
b)
c)
d)
e)
144
300
20.18.14
x.10.9
x.z.2
2E, Akademisches Gymnasium
Mag. Petra Wagenknecht