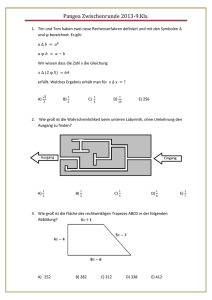
Zwischenrunde 2015 – Klasse 9

FRAGENKATALOG
PANGEA-MATHEMATIKWETTBEWERB
ZWISCHENRUNDE
KLASSE 9
Zwischenrunde 2015
Klasse 9
Antwortbogen
Trage bitte die fehlenden Informationen leserlich in die dafür vorgesehenen
Kästchen ein. Trenne nach der Prüfung den unteren Teil des Antwortbogens
ab. Bewahre diesen bitte gut auf. Darauf sind Deine Benutzerdaten, mit diesen
kannst Du Deine Ergebnisse online einsehen.
Beachte: Antwortbögen ohne Vor- und Nachnamen werden nicht ausgewertet!
Prüfung
1. Zur Beantwortung der 10 Fragen aus 3 Schwierigkeitsstufen hast Du
60 Minuten Zeit.
2. Hilfsmittel (Taschenrechner, Formelsammlung usw.) sind nicht erlaubt.
Leere Blätter für Nebenrechnungen dürfen benutzt werden.
3. Lies Dir die Fragen genau durch. Du solltest nicht an einzelnen Fragen
hängen bleiben, sondern diese vorerst überspringen. Du kannst sie, wenn
Zeit übrig bleibt, zum Schluss immer noch beantworten.
4. Es ist immer nur eine einzige Antwort richtig. Falls dennoch mehrere
Felder gekennzeichnet sind, wird die Aufgabe als falsch gewertet.
5. Bei falscher Antwort wird die Hälfte der jeweils erreichbaren Fragenpunktzahl abgezogen. Also besser keine Antwort, als eine falsche anzukreuzen. Daher nicht raten, sondern rechnen!
6. Wir empfehlen, die Lösungen erst im Fragenkatalog anzukreuzen und
10 Minuten vor Ende auf Deinen Antwortbogen zu übertragen. Schreibe
am besten mit einem gut lesbaren Stift (Füller, Kugelschreiber). Falls
Antworten radiert wurden, bitte darauf achten, dass keine Rückstände
übrig sind. Alle nicht eindeutig angekreuzten Fragen werden als falsch
bewertet. Beachte: Es werden nur die Kreuze auf dem Antwortbogen
gewertet, nicht im Fragenkatalog.
7. Bei der Korrektur einer Antwort auf dem Antwortbogen ist das Kästchen
mit der falschen Antwort komplett auszumalen und die richtige Antwort
normal und gut lesbar anzukreuzen.
1
Zwischenrunde 2015
Klasse 9
8. Der Antwortbogen darf nicht gefaltet oder zerknittert werden.
9. Vermerke außerhalb der auszufüllenden Felder sind nicht erlaubt.
10. Die hell ausgemalten Sterne rechts neben den Aufgaben zeigen dir die
erreichbare Punktzahl.
Auswertung
1. Die Auswertung erfolgt innerhalb weniger Tage und kann unter
http://anmeldung.pangea-wettbewerb.de
im Bereich Schüler-Log-in mit Deinen Benutzerdaten (ID-Nummer und
Passwort) eingesehen werden.
2. Es kommen die jeweils ersten 80 Schülerinnen und Schüler jeder Klassenstufe ins Regionalfinale. Dieses findet am 13.06.2015 an 6 Orten deutschlandweit statt. Falls Du Dich zum Finale qualifiziert hast, erfährst Du dies
sowie den Veranstaltungsort in Deinem Log-in-Bereich. Wir wünschen Dir
viel Erfolg und weiterhin viel Freude an der Mathematik.
2
Zwischenrunde 2015
Klasse 9
Aufgabe 1
⋆⋆⋆⋆⋆
In einem Strumpf sind blaue und rote, aber ansonsten gleiche Kugeln.
Die Wahrscheinlichkeit, blind eine blaue Kugel zu ziehen, beträgt
60 %.
Ersetzt man zwei blaue Kugeln durch zwei rote Kugeln, so beträgt die
Wahrscheinlichkeit, blind eine rote Kugel zu ziehen, 50 %.
Wie viele Kugeln sind in dem Strumpf?
a) 10
b) 12
c) 16
d) 18
Aufgabe 2
e) 20
⋆⋆⋆⋆⋆
Die Zeichnung ist nicht maßstäblich.
Es gilt:
AB ist parallel zu CD, CE = BE
und Winkel BAD = 90°,
AB = 5 cm, AD = 8 cm,
CD = 3 cm.
D
C
E
Wie lang ist AE?
A
a) 1 cm
b) 2 cm
c) 3 cm
B
d) 4 cm
Aufgabe 3
e) 5 cm
⋆⋆⋆⋆⋆
Von sechs Schülern, die 7, 8, 9, 10, 11 und 12 Jahre alt sind, werden
zwei zufällig ausgewählt.
Wie groß ist die Wahrscheinlichkeit, dass der Altersunterschied
der zwei ausgewählten Schüler mindestens drei Jahre ist?
a)
2
5
b)
5
12
c)
3
1
2
d)
3
5
e)
1
3
Zwischenrunde 2015
Klasse 9
Aufgabe 4
⋆⋆⋆⋆⋆
Ein Rechteck mit den Seitenlängen 3 cm und 6 cm wird in drei
gleich große Flächen − zwei Dreiecke und ein Parallelogramm −
zerlegt.
x
Wie lang ist x?
a) 1,1 cm
Die Zeichnung ist nicht maßstäblich.
b) 1,2 cm
c) 1,3 cm
d) 1,4 cm
Aufgabe 5
Berechne:
a)
e) 1,5 cm
⋆⋆⋆⋆⋆
22
32
20152
12
·
·
·
.
.
.
·
12 + 1 22 + 2 32 + 3
20152 + 2015
1
2015
b)
1
2016
c)
1
2014
d)
1
2
e)
1
2 · 3 · . . . · 2015 · 2016
Aufgabe 6
⋆⋆⋆⋆⋆
Verschlüsseltes Rechnen:
Jeder Buchstabe steht für eine Ziffer. Gleicher Buchstabe bedeutet gleiche Ziffer, und gleiche Ziffer bedeutet gleicher Buchstabe.
Es gilt: M = 2 und Y = 7.
Bestimme die Quersumme der
Zahl COY OT E.
a) 14
b) 18
+
c) 24
4
M
D
C
O
O
O
N
N
Y
d) 28
K
K
O
E
E
T
Y
Y
E
e) 34
Zwischenrunde 2015
Klasse 9
Aufgabe 7
⋆⋆⋆⋆⋆
E
Abgebildet sind ein gleichseitiges Dreieck GAH, ein Quadrat
ABCH, ein regelmäßiges Fünfeck
CDEF H und ein weiteres Dreieck GHF .
F
α
b) 41°
H
C
G
Bestimme den Winkel α.
a) 39°
D
A
c) 43°
Aufgabe 8
d) 45°
B
e) 47°
⋆⋆⋆⋆⋆
Es ist
√
√
√
√
a = 1 +√2 · 3, b = 1 + 3 · 2, c = 3 + 2 + 1, d = 3 + 1 · 2,
e = 2 + 3 + 1.
Die aufgeführten fünf Zahlen werden der Größe nach geordnet.
Was ist richtig?
a) a < b < c < d < e
d) d < e < a < b < c
b) e < d < c < b < a
e) e < a < d < c < b
5
c) e < d < a < c < b
e) e < a < d < c < b
Zwischenrunde 2015
Klasse 9
Aufgabe 9
⋆⋆⋆⋆⋆
In den 8 Feldern a, b, c, d, e, f ,
g, h sind Ziffern aus 1, 2, 3, 4,
5, 6, 7, 8, 9 so einzutragen, dass
insgesamt vier dreistellige Zahlen,
eine zweistellige Zahl und eine einstellige Zahl entstehen. Sie haben
folgende Eigenschaften:
a
b
d
e
f
g
c
h
Waagerecht
Senkrecht
1. Zeile: Um 1 verminderte vierte Potenz einer Zahl
2. Zeile: zweistellige Primzahl
3. Zeile: Das Fünffache einer dreistelligen Primzahl
1. Spalte: Drei aufeinanderfolgende
Zahlen
2. Spalte: Dritte Potenz einer einstelligen Zahl
3. Spalte oben: einstellige Quadratzahl
Berechne: a + e + h − c − f
a) −2
b) −1
c) 0
d) 1
Aufgabe 10
e) 2
⋆⋆⋆⋆⋆
Welchen Rest liefert die Division 515 : 6?
a) 1
b) 2
c) 3
6
d) 4
e) 5
Zwischenrunde 2015
Klasse 9
Für Nebenrechnungen
7
Zwischenrunde 2015
Klasse 9
Für Nebenrechnungen
8
Zwischenrunde 2015
Klasse 9
Pangea-Mathematikwettbewerb auf Social-Media-Netzwerken
Folgt uns auch auf unseren Social-Media-Seiten.
Wir informieren euch auf Twitter, Facebook und YouTube über alle Aktionen
und Neuigkeiten rund um den Pangea-Mathematikwettbewerb.
www.facebook.com/pangea.wettbewerb.de
www.twitter.com.pangea mathe
9
Zwischenrunde 2015
Klasse 9
Danke
Für das große Engagement und die nachhaltige Unterstützung unseres Wettbewerbs bedanken wir uns ganz herzlich bei:
Herr Prof. Dr. Wilfried Herget - Universität Halle-Wittenberg - Sachsen-Anhalt
Frau Prof. Dr. Karin Richter - Universität Halle-Wittenberg - Sachsen-Anhalt
Herr Doz. Dr. Gerd Richter - Universität Halle-Wittenberg - Sachsen-Anhalt
Herr Prof. Dr. Albrecht Beutelspacher - Universität Gießen - Hessen
Herr Prof. Dr. Hans-Georg Weigand - Universität Würzburg - Bayern
Herr Prof. Dr. Marcel Erné - Universität Hannover - Niedersachsen
Herr StD. a.D. Dipl.-Math. Michael Löber - Mathematiklehrer - Berlin
Herr Dr. Michael Enzinger - Schulleiter - Bayern
Herr Helge Dietrich - ehem. Vorstand VBE - Berlin
Herr Mustafa Altas - Gremiumsmitglied - Hessen
Herr Dipl.-Math. Salih Ergün - Mathematiklehrer - Berlin
Weiterhin bedanken wir uns auch bei allen namentlich nicht erwähnten, engagierten und ehrenamtlichen Unterstützern.
Copyright © 2015
Die Fragenkataloge sind in allen Teilen urheberrechtlich geschützt. Jegliche
Verwertung ohne Zustimmung von Pangea Wettbewerb e.V., insbesondere Vervielfältigung, Übersetzung und Einspeicherung in elektronische Datensysteme
(z.B. Internet) ist nicht gestattet und wird strafrechtlich verfolgt.
10
ORGANISATION
ORGANISATIONSPARTNER
UNTERSTÜTZER
FINALE UND PREISVERLEIHUNG
S A M S TA G , 1 3 . 0 6 . 2 0 1 5 A N B U N D E S W E I T 6 O R T E N
INFORMATIONEN WERDEN SEPARAT BEKANNTGEGEBEN