Mathcad - Stetig.mcd

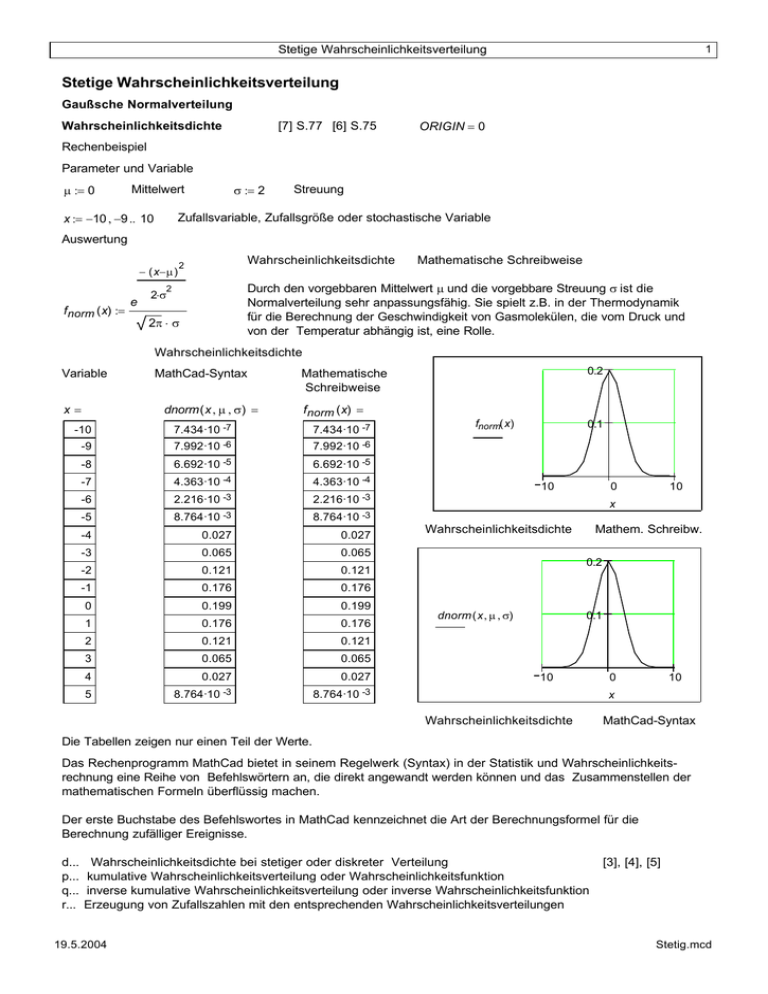
1
Stetige Wahrscheinlichkeitsverteilung
Stetige Wahrscheinlichkeitsverteilung
Gaußsche Normalverteilung
Wahrscheinlichkeitsdichte
[7] S.77 [6] S.75
ORIGIN = 0
Rechenbeispiel
Parameter und Variable
µ := 0
σ := 2
Mittelwert
x := −10 , −9 .. 10
Streuung
Zufallsvariable, Zufallsgröße oder stochastische Variable
Auswertung
− ( x− µ )
Wahrscheinlichkeitsdichte
2
Durch den vorgebbaren Mittelwert µ und die vorgebbare Streuung σ ist die
Normalverteilung sehr anpassungsfähig. Sie spielt z.B. in der Thermodynamik
für die Berechnung der Geschwindigkeit von Gasmolekülen, die vom Druck und
von der Temperatur abhängig ist, eine Rolle.
2
fnorm ( x) :=
e
Mathematische Schreibweise
2⋅σ
2π ⋅ σ
Wahrscheinlichkeitsdichte
Variable
x=
MathCad-Syntax
dnorm ( x , µ , σ) =
0.2
Mathematische
Schreibweise
fnorm ( x) =
-10
7.434·10 -7
7.434·10 -7
-9
7.992·10 -6
7.992·10 -6
-8
6.692·10 -5
6.692·10 -5
-7
4.363·10 -4
4.363·10 -4
-6
2.216·10 -3
2.216·10 -3
-5
8.764·10 -3
8.764·10 -3
-4
0.027
0.027
-3
0.065
0.065
-2
0.121
0.121
-1
0.176
0.176
0
0.199
0.199
1
0.176
0.176
2
0.121
0.121
3
0.065
0.065
4
0.027
0.027
5
8.764·10 -3
8.764·10 -3
fnorm( x)
0.1
10
0
10
x
Wahrscheinlichkeitsdichte
Mathem. Schreibw.
0.2
dnorm ( x , µ , σ)
0.1
10
0
10
x
Wahrscheinlichkeitsdichte
MathCad-Syntax
Die Tabellen zeigen nur einen Teil der Werte.
Das Rechenprogramm MathCad bietet in seinem Regelwerk (Syntax) in der Statistik und Wahrscheinlichkeitsrechnung eine Reihe von Befehlswörtern an, die direkt angewandt werden können und das Zusammenstellen der
mathematischen Formeln überflüssig machen.
Der erste Buchstabe des Befehlswortes in MathCad kennzeichnet die Art der Berechnungsformel für die
Berechnung zufälliger Ereignisse.
d...
p...
q...
r...
Wahrscheinlichkeitsdichte bei stetiger oder diskreter Verteilung
kumulative Wahrscheinlichkeitsverteilung oder Wahrscheinlichkeitsfunktion
inverse kumulative Wahrscheinlichkeitsverteilung oder inverse Wahrscheinlichkeitsfunktion
Erzeugung von Zufallszahlen mit den entsprechenden Wahrscheinlichkeitsverteilungen
19.5.2004
[3], [4], [5]
Stetig.mcd
2
Stetige Wahrscheinlichkeitsverteilung
Wahrscheinlichkeitsfunktion oder kumulative Wahrscheinlichkeitsverteilung
Die Wahrscheinlichkeitsfunktion Fnorm(ξ ) ist die Integralfunktion der Wahrscheinlichkeitsdichte fnorm(x) mit ξ als
oberer Grenze.
Rechenbeispiel
Auswertung
Variable und Parameter
⌠
Fnorm ( ξ) := 
⌡
ξ := −10 , −9 .. 10
variable obere Grenze des Integrationsbereichs
ξ
fnorm ( x) dx
Mathematische Schreibweise
−∞
Wahrscheinlichkeitsfunktion
Variable
MathCad-Syntax
x=
pnorm ( x , µ , σ) =
-10
2.867·10
-9
3.398·10 -6
-8
3.167·10 -5
-7
-4
2.326·10
1
-7
-6
1.35·10 -3
-5
6.21·10 -3
-4
0.023
-3
0.067
-2
0.159
-1
0.309
0
0.5
1
0.691
2
0.841
3
0.933
4
0.977
5
0.994
Fnorm( ξ)
0.5
10
0
10
ξ
Wahrscheinlichkeitsfunktion
Math. Schreibweise
1
pnorm ( x , µ , σ)
0.5
10
0
10
x
Die Tabellen zeigen nur einen Teil der Werte.
Wahrscheinlichkeitsfunktion
MathCad-Syntax
Die Wahrscheinlichkeit Fnorm(a,b) für das Eintreten eines bestimmten Ereignisses beispielsweise im Intervall
zwischen a und b der Zugriffsvariablen
a := 1 und
b := 2
⌠
Fnorm ( ∞ ) := 
⌡
beträgt
⌠
Fnorm ( a , b ) := 
⌡
b
fnorm ( x) dx
Fnorm ( a , b ) = 0.15
.
a
∞
fnorm ( x) dx
Fnorm ( ∞ ) = 1
Das Integral über den gesamten Ereignisraum beträgt 1.
−∞
Bei der stetigen Wahrscheinlichkeitsverteilung ist die Wahrschinlichkeit für das Eintreten eines bestimmten
Ereignisses gleich Null. Es ist immer nur die Wahrscheinlichkeit in einem Bereich der Zufallsvariablen x angebbar.
Inverse kumulative Wahrscheinlichkeitsverteilung
Rechenbeispiel
Die inverse kumulative Wahrscheinlichkeitsverteilung gibt die Zufallsvariable für den vorgegebenen Wert m der
Wahrscheinlichkeit an, bis zu der die Ereignisse möglicherweise schon eingetreten sind. Der Wert dieser
Zufallsvariable ist auch durch die Wahrscheinlichkeitsfunktion gegeben.
Variable und Parameter
m := 0.5
m := 0.159
19.5.2004
Auswertung
qnorm ( m , µ , σ) = 0
qnorm ( m , µ , σ) = −1.997
Stetig.mcd
3
Stetige Wahrscheinlichkeitsverteilung
Mittelwert
Standardabweichung
⌠
µ norm := 
⌡
∞
x ⋅ fnorm ( x) dx
µ norm = 0
σnorm :=
−∞
⌠

⌡
∞
2
( x − µ ) fnorm ( x) dx
σnorm = 2
−∞
Ableitung der Wahrscheinlichkeitsdichte
Mit Hilfe der symbolischen Auswertung läßt sich mit Hilfe von MathCad die Ableitung der
Wahrscheinlichkeitsdichte angeben.
Ableitung der Wahrscheinlichkeitsdichte
d
x=
dx
0.1
fnorm ( x) =
0.05
-10
1.858·10 -6
-9
1.798·10 -5
-8
1.338·10 -4
-7
7.636·10 -4
-6
3.324·10 -3
-5
0.011
-4
0.027
-3
0.049
-2
0.06
-1
0.044
−1
0
0
16
1
-0.044
2
-0.06
3
-0.049
4
-0.027
5
-0.011
d
dx
fnorm( x)
10
0
10
0.05
0.1
x
Ableitung der Wahrscheinlichkeitsfunktion
 −1 ⋅ x2  ⋅ 2 = 0

 8
  1 
⋅ x ⋅ exp 
x= 0
2
π 
An der Nullstelle der Ableitung, hat die
Wahrscheinlichkeitsdichte ein Maximum.
Die Tabellen zeigen nur einen Teil der Werte.
Zufallszahlengenerator auf der Basis der Normalverteilung
Rechenbeispiel
Parameter und Variable
Anzahl der Zufallszahlen
Mittelwert
µ := 10
Zufallszahlen (MathCad-Syntax)
m := 10
Standardabweichung
σ := 2
Auswertung
M := rnorm ( m , µ , σ)
N := sort ( M)
Zufallszahlen (MathCad-Syntax)
sortierte Zufallszahlen (MathCad-Syntax)
Bei jedem Aufruf des Zufallszahlengenerators wird eine
andere Zahlenfolge erzeugt.
19.5.2004
M=
9.122
6.629
8.641
8.097
9.053
8.641
8.097
9.053
6.629
N=
9.122
10.087
9.759
9.759
10.087
11.113
11.113
14.384
11.617
11.617
14.384
Stetig.mcd
4
Stetige Wahrscheinlichkeitsverteilung
15
Mx
15
Nx
10
5
0
5
10
5
10
0
5
x
10
x
Normalverteilte Zufallszahlen
Sortierte, normalverteilte Zufallszahlen
Gleichmäßige Wahrscheinlichkeitsverteilung
Wahrscheinlichkeitsdichte und Wahrscheinlichkeitsfunktion
Rechenbeispiel
Parameter und Variable
a := 0
b := 10
Auswertung
Wahrscheinlichkeitsdichte
Zufallsvariable
MathCad-Syntax
x=
x := 0 .. 10
Grenzen des Intervalls
Zufallsvariable
Kumulative Wahrscheinlichkeitsverteilung
MathCad-Syntax
dunif ( x , a , b ) =
0.1001
punif ( x , a , b ) =
0
0.1
0
1
0.1
0.1
2
0.1
0.2
3
0.1
0.3
4
0.1
0.4
5
0.1
0.5
6
0.1
0.6
7
0.1
0.7
8
0.1
0.8
9
0.1
0.9
10
0.1
1
0.1
dunif ( x , a , b )
0.0999
0.0998
0
5
10
x
Wahrscheinlichkeitsdichte
1
punif ( x , a , b ) 0.5
Mittelwert
⌠
µ uni := 
⌡
10
x ⋅ dunif ( x , a , b ) dx
µ uni = 5
0
Standardabweichung
σuni :=
⌠

⌡
0
5
10
x
Wahrscheinlichkeitsfunktion
10
2
( x − µ ) dunif ( x , a , b ) dx
σuni = 5.774
0
19.5.2004
Stetig.mcd
5
Stetige Wahrscheinlichkeitsverteilung
Inverse kumulative Wahrscheinlichkeitsverteilung
Rechenbeispiel
Auswertung
Parameter und Variable
p := 0.5
qunif ( p , a , b ) = 5
Wahrscheinlichkeit
Zufallsvariable
Zufallszahlengenerator auf der Basis der gleichmäßigen Wahrscheinlichkeitsverteilung
Rechenbeispiel
Parameter und Variable
m := 10
Anzahl der Zufallszahlen
Auswertung
Zufallszahlen
sortierte Zufallszahlen
MathCad-Syntax
MathCad-Syntax
M := runif ( m , a , b )
N := sort ( M)
0.088
0.088
2.759
2.759
5.879
4.58
8.376
4.849
M=
4.849
N=
10
Mx
5.879
7.437
5.99
4.58
7.35
7.444
7.437
5.99
7.444
7.35
8.376
5
0
5
10
x
Zufallszahlen
10
Bei jedem Aufruf des Zufallszahlengenerators erscheint
eine andere Zahlenfolge.
max ( M) = 8.376
Extremwerte
Nx
min ( M) = 0.088
5
0
5
10
x
Sortierte Zufallszahlen
Weibull-Verteilung
[3] S.296 [Differentialgleichungen]
Wahrscheinlichkeitsdichte
Rechenbeispiel
Parameter und Variable
s := 2.5
x := 0 , 0.1 .. 5
Auswertung
fWeib ( x) := dweibull ( x , s )
s− 1
fWeib ( x) := s ⋅ x
19.5.2004
MathCad-Syntax
Wahrscheinlichkeitsfunktion
s
−x
⋅e
Math. Schreibweise
FWeib ( x) := pweibull ( x , s )
MathCad-Syntax
Stetig.mcd
6
Stetige Wahrscheinlichkeitsverteilung
1.5
1
1
fWeib( x)
FWeib( x) 0.5
0.5
0
0
2
4
0
6
0
2
x
6
x
Wahrscheinlichkeitsdichte
⌠

⌡
4
Wahrscheinlichkeitsfunktion
∞
⌠

⌡
fWeib ( x) dx = 1
0
∞
fWeib ( x) dx → 1.
0
Mittelwert
⌠

⌡
∞
⌠
µ Weib := 
⌡
x fWeib ( x) dx = 0.887
0
∞
x fWeib ( x) dx
µ Weib = 0.887
0
Varianz
⌠

⌡
∞
(x − µWeib )
2
⌠
τWeib := 
⌡
⋅ fWeib ( x) dx
0
∞
(x − µWeib )2 ⋅ fWeib ( x) dx
τWeib = 0.144
0
Standardabweichung
σWeib :=
⌠

⌡
∞
(x − µWeib )2 ⋅ fWeib ( x) dx
σWeib = 0.38
0
Cauchy-Verteilung
[5], S.223
Wahrscheinlichkeitsdichte
Rechenbeispiel
Wahrscheinlichkeitsfunktion
Parameter und Variable
x := −2 , −1.8 .. 2
Auswertung
fCau ( x) :=
1
π
[6] S.56
1
⋅
Mathem. Schreibweise
2
1+x
FCau ( x) :=
1
2
+
1
π
atan ( x)
0.4
fCau( x)
1
FCau( x)
0.2
2
0
x
Wahrscheinlichkeitsdichte
19.5.2004
Mathem. Schreibweise
2
0.5
2
0
2
x
Wahrscheinlichkeitsfunktion
Stetig.mcd
7
Stetige Wahrscheinlichkeitsverteilung
Zufallsvariable
Wahrscheinlichkeitsdichte
x=
fCau ( x) =
Wahrscheinlichkeitsfunktion
FCau ( x) =
-2
0.064
0.148
-1.8
0.075
0.161
-1.6
0.089
0.178
-1.4
0.108
0.197
-1.2
0.13
0.221
-1
0.159
0.25
-0.8
0.194
0.285
-0.6
0.234
0.328
-0.4
0.274
0.379
-0.2
0.306
0.437
0
0.318
0.5
0.2
0.306
0.563
0.4
0.274
0.621
0.6
0.234
0.672
0.8
0.194
0.715
1
0.159
0.75
1.2
0.13
0.779
1.4
0.108
0.803
1.6
0.089
0.822
1.8
0.075
0.839
2
0.064
0.852
∞
2
1⋅
⌠

⌡
1
fCau ( x) dx = 0.5
−1
Berechnung mit Hilfe der
Wahrscheinlichkeitsfunktion
FCau ( −1) = 0.25
FCau ( 0) = 0.5
FCau ( 1) − FCau ( −1) = 0.5
FCau ( 1) = 0.75
Mittelwert
⌠
µ := 
⌡
∞
x ⋅ fCau ( x) dx
−∞
Das Integral der Varianz-Funktion von Minus-Unendlich bis
Plus-Unendlich ist unendlich groß, und damit ist auch die
Varianz unendlich groß.
 dx → ∞
2
π
1+x 

x ⋅
−∞
Berechnung mit Hilfe der
Wahrscheinlichkeitsdichte
µ=0
Varianz
⌠



⌡
Wahrscheinlichkeitsfunktion
1
Varianz-Funktion
1⋅
Limes der Varianz-Funktion

2
π
1+x 

2
j ( x) := x ⋅ 
1
lim
j ( x) →
x→ ∞
1
1
π
π
= 0.318
0.4
j( x)
1
0.2
π
2
0
2
x
Varianz-Funktion
19.5.2004
Stetig.mcd
8
Stetige Wahrscheinlichkeitsverteilung
Berechnung der Cauchy-Verteilung mit Hilfe der MathCad-Syntax
Wahrscheinlichkeitsdichte
Parameter und Variable
Wahrscheinlichkeitsfunktion
l := 1
Horizontale Verschiebung
s := 1
Skalenparameter s > 0
x := −2 , −1.8 .. 4
Auswertung
fCau ( x) := dcauchy ( x , l , s )
Fcau ( x) := pcauchy ( x , l , s )
MathCad-Syntax
0.4
fCau( x)
MathCad-Syntax
1
Fcau( x)
0.2
2
Zufallsvariable
0
2
4
0.5
2
x
0
2
4
x
Wahrscheinlichkeitsdichte
Wahrscheinlichkeitsfunktion
Varianz
2
k ( x) := ( x − l) ⋅ dcauchy ( x , l , s )
Varianz-Funktion
0.4
k ( x)
1
Am Verlauf der Varianz-Funktion ist schon erkennbar, dass
auch in diesem Fall die Varianz unendlich groß ist.
0.2
π
In der MathCad-Schreibweise ist die Horizontalverschiebung (Mittelwert) der Wahrscheinlichkeitsdichte in der
Formel schon angebbar.
2
0
2
4
x
Varianz-Funktion
19.5.2004
Stetig.mcd