Gegeben sei das Dreieck ABC: A(0/0), B(14/0), C(9/12)

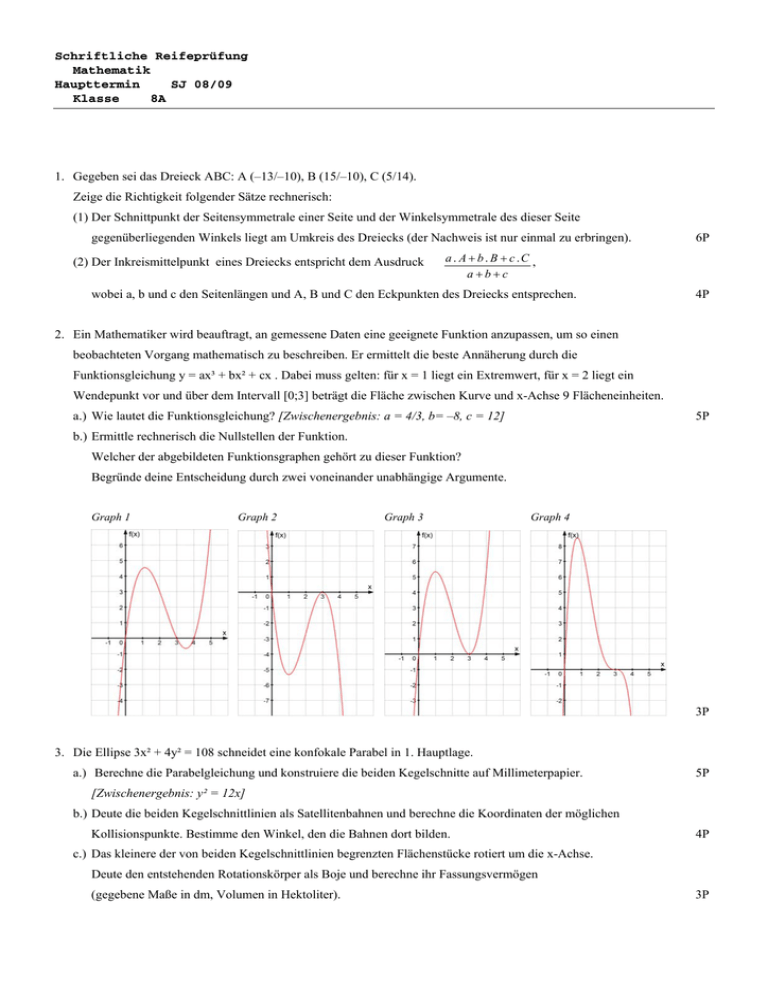
Schriftliche Reifeprüfung
Mathematik
Haupttermin
SJ 08/09
Klasse
8A
1. Gegeben sei das Dreieck ABC: A (–13/–10), B (15/–10), C (5/14).
Zeige die Richtigkeit folgender Sätze rechnerisch:
(1) Der Schnittpunkt der Seitensymmetrale einer Seite und der Winkelsymmetrale des dieser Seite
gegenüberliegenden Winkels liegt am Umkreis des Dreiecks (der Nachweis ist nur einmal zu erbringen).
(2) Der Inkreismittelpunkt eines Dreiecks entspricht dem Ausdruck
6P
a . A + b . B + c .C ,
a+b+c
wobei a, b und c den Seitenlängen und A, B und C den Eckpunkten des Dreiecks entsprechen.
4P
2. Ein Mathematiker wird beauftragt, an gemessene Daten eine geeignete Funktion anzupassen, um so einen
beobachteten Vorgang mathematisch zu beschreiben. Er ermittelt die beste Annäherung durch die
Funktionsgleichung y = ax³ + bx² + cx . Dabei muss gelten: für x = 1 liegt ein Extremwert, für x = 2 liegt ein
Wendepunkt vor und über dem Intervall [0;3] beträgt die Fläche zwischen Kurve und x-Achse 9 Flächeneinheiten.
a.) Wie lautet die Funktionsgleichung? [Zwischenergebnis: a = 4/3, b= –8, c = 12]
5P
b.) Ermittle rechnerisch die Nullstellen der Funktion.
Welcher der abgebildeten Funktionsgraphen gehört zu dieser Funktion?
Begründe deine Entscheidung durch zwei voneinander unabhängige Argumente.
Graph 1
Graph 2
Graph 3
Graph 4
3P
3. Die Ellipse 3x² + 4y² = 108 schneidet eine konfokale Parabel in 1. Hauptlage.
a.) Berechne die Parabelgleichung und konstruiere die beiden Kegelschnitte auf Millimeterpapier.
5P
[Zwischenergebnis: y² = 12x]
b.) Deute die beiden Kegelschnittlinien als Satellitenbahnen und berechne die Koordinaten der möglichen
Kollisionspunkte. Bestimme den Winkel, den die Bahnen dort bilden.
4P
c.) Das kleinere der von beiden Kegelschnittlinien begrenzten Flächenstücke rotiert um die x-Achse.
Deute den entstehenden Rotationskörper als Boje und berechne ihr Fassungsvermögen
(gegebene Maße in dm, Volumen in Hektoliter).
3P
4. a.) (1) Definiere den Begriff Winkelfunktion. Welche Winkelfunktionen sind im
rechtwinkeligen Dreieck definiert? – gib ihre Definitionen in Kurzform an.
(2) In nebenstehender Graphik (Einheitskreis: M(0/0), r = 1e) ist ein spitzer
Winkel α eingezeichnet. Kennzeichne farbig die einzelnen
Winkelfunktionen bezüglich des Winkels α und begründe
α
die Gültigkeit von sin²α + cos²α = 1.
(3) Gehe auf die Tangensfunktion näher ein: Für welche Winkelgrößen ist sie
nicht definiert (Begründung angeben) und wo liegen die Nullstellen?
Weise nach, dass die Tangensfunktion gleich ist dem Quotienten aus
Sinus- und Cosinusfunktion.
5P
b.) Von einem 205m über einem See (Meereshöhe des Sees: 558m) gelegenen Punkt P
sieht man einen Berggipfel unter dem Höhenwinkel 9,17° und sein Spiegelbild im See
unter dem Tiefenwinkel 11,38°. Berechne die Höhe des Berges (auf Meeresniveau bezogen) –
eine Instrumentenhöhe soll unberücksichtigt bleiben.
5P
5. Lotto- und Totospiele sind sehr alt (17. Jahrhundert) und erfreuen sich auch heute noch
weltweit großer Beliebtheit. Sie werden länderspezifisch unterschiedlich angeboten:
Beispielsweise gilt in Österreich beim Lotto „6 aus 45“, in Deutschland hingegen
„6 aus 49“. Verschieden sind auch die Totoscheine: In Österreich sind pro Spielrunde
12 Tipps, in Deutschland hingegen um einer mehr, also 13 Tipps, abzugeben –
unabhängig davon werden noch weitere Spielvarianten angeboten (Zusatzzahl,
Superzahl, …), die aber für folgende Berechnungen unberücksichtigt bleiben sollen:
a.) Berechne die Wahrscheinlichkeit beim Lotto in einem Spiel mindestens 5 Richtige
(1) in Österreich und (2) in Deutschland zu tippen.
Würdest du deinem in Deutschland lebenden Freund einen regelmäßigen
„Grenzverkehr“ nach Österreich anraten, um hier zu spielen und damit die
Gewinnchancen realistisch zu erhöhen? Begründe deine Antwort.
4P
b.) Berechne die Wahrscheinlichkeit für einen Zwölfer im Toto
(1) in Österreich und (2) in Deutschland. Interpretiere deine Ergebnisse.
2P
c.) Die Einschätzung besonders großer und kleiner Zahlen macht oft Schwierigkeiten.
Zur Veranschaulichung werden gerne Vergleiche herangezogen.
Überprüfe daher durch Rechnung folgende Behauptung:
Wenn ein Affe vor einer alten Schreibmaschine (Annahme: 53 Tasten) hockt und
viermal beliebig mit seinem „Zeigefinger“ auf die Tasten tippt, so ist die
Wahrscheinlichkeit, dass er das Wort „Affe“ schreibt annähernd gleich groß
wie die Wahrscheinlichkeit für einen „6er“ im österreichischen Lotto.
2P
→
Ansätze und Rechenschritte sind vollständig und nachvollziehbar anzuschreiben; innerhalb der Rechnungen
sind alle Dezimalstellen zu berücksichtigen – die Ergebnisse sind jeweils sinnvoll gerundet anzugeben.
Notenschlüssel: Sehr gut
Gut
Befriedigend
Genügend
Nicht genügend
48 – 44 Punkte
43 – 38 Punkte
37 – 31 Punkte
30 – 24 Punkte
bei weniger als 24 Punkten.
48P