Universität Konstanz
Werbung

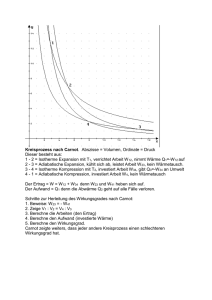
Praktikumsprotokoll: Kritischer Punkt & Heißluftmotor Robin Marzucca, Andreas Liehl 07. und 14. November 2011 Universität Konstanz 1 Inhaltsverzeichnis 1 Einleitung 3 2 Grundlagen 2.1 Ideale und reale Gase . . . . . . . . . . 2.1.1 Van-der-Waals-Gleichung . . 2.1.2 Der kritische Punkt . . . . . . 2.2 Verflüssigung realer Gase . . . . . . . . 2.3 Kreisprozesse . . . . . . . . . . . . . . 2.3.1 Der Carnotsche Kreisprozess 2.3.2 Der Stirlingsche Kreisprozess 2.4 Leistung . . . . . . . . . . . . . . . . . 2.5 Wärmeäquivalente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 3 4 4 6 7 8 10 12 12 3 Der Versuch 3.1 Versuchsteil 1: Kritischer Punkt 3.1.1 Versuchsaufbau . . . . . 3.1.2 Versuchsdurchführung . 3.2 Versuchsteil 2: Heißluftmotor . 3.2.1 Versuchsaufbau . . . . . 3.2.2 Versuchsdurchführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 13 13 13 14 14 14 . . . . . . . . . 15 15 15 17 18 18 20 22 23 25 5 Fragen und Antworten 5.1 Fragen zum Versuchsteil: Kritischer Punkt . . . . . . . . . . . . . . . . . . . . 5.2 Fragen zum Versuchsteil: Heißluftmotor . . . . . . . . . . . . . . . . . . . . . 26 26 27 . . . . . . . . . . . . 4 Auswertung 4.1 Versuchsteil 1: Kritischer Punkt . . 4.1.1 Auswertung der Messwerte 4.1.2 Fehlerdiskussion . . . . . . 4.2 Versuchsteil 2: Heißluftmotor . . . 4.2.1 pV -Diagramme . . . . . . . 4.2.2 Kältemaschine . . . . . . . 4.2.3 Wärmekraftmaschine . . . . 4.2.4 Mechanische und elektrische 4.2.5 Fehlerdiskussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Leistung . . . . . . 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Einleitung In diesen beiden Versuchen sollen wichtige Phänomene der Thermodynamik untersucht werden. Im ersten Teil soll der sog. Kritische Punkt anhand des pV -Diagramms von Schwefelhexafluorid ((SF6 )), sowie dessen Dampfdruckkurve bestimmt werden. Im zweiten Teil betrachten wir thermodynamische Kreisprozesse mit Hilfe eines StirlingMotors. 2 Grundlagen Zunächst werden im Grundlagenteil einige Begrifflichkeiten geklärt und erläutert, die zum Verständnis des Versuchs maßgeblich beitragen. 2.1 Ideale und reale Gase Um den Zustand von Gasen mathematisch zu fassen verwendet man verschiedene Modelle. Eines davon ist die Vorstellung des sog. idealen Gases. Dabei wird angenommen, dass ein Gas aus Atomen bzw. Molekülen besteht, die als Massenpunkte abstrahiert werden und in keinerlei Wechselwirkung miteinander stehen. Lediglich elastische Stöße mit anderen Teilchen (z.B. andere Gasmoleküle oder Festkörper) sind möglich. Den Zustand eines idealen Gases beschreibt die sog. “ideale Gasgleichung“, welche eine Proportionalität zwischen Druck p, Volumen V des Gases, Stoffmenge n und absoluter Temperatur T herstellt: p·V = n·R·T (1) wobei R = 8, 314472 molJ· K die universelle molare Gaskonstante ist. Die Gleichung lässt sich empirisch in Experimenten nachweisen. Da jedoch in der Natur das Modell des idealen Gases nur bedingt realisierbar ist, verwendet man häufig das Modell des realen Gases, welches die Wechselwirkung der Teilchen, zu den größten Teilen Gravitation, untereinander miteinbezieht. Hier verwendet man verschiedene Ansätze, da die Wechselwirkung je nach Zustand des Gases unterschiedlich sein kann. Während in einem Gas mit hohem Druck, also geringen Teilchenabständen, die Abstoßung der Teilchen überwiegt, das Gas ist nur noch schwer zu kompressen, ist bei mittleren Teilchenabständen die Anziehung ein wichtiger Faktor. Bei sehr großen Teilchenabständen verhält sich das Gas quasi ideal. Der einfachste Ansatz, dies zu realisieren ist ein Korrekturfaktor Z in der idealen Gasgleichung (Gleichung (1)), und man erhält die sog Virialgleichung: p·V = Z ·n·R·T (2) 3 2.1.1 Van-der-Waals-Gleichung Da die Virialgleichung (Gleichung (2)) nicht sehr anschaulich ist, wird heute meistens die nach seinem Entdecker benannte Van-der-Waals-Gleichung verwendet. Diese berücksichtigt die Wechselwirkung der Teilchen auf zwei Arten. Zum einen verwendet Van-der-Waals ein verringertes Volumen, indem das Volumen in Gleichung (1) um das Eigenvolumen1 der Teilchen verringert wird und zum anderen wird der Druck nach oben korrigiert, was die Anziehung der Teilchen berücksichtigt. Diese beiden Korrekturen liefern die Van-der-Waals-Gleichung: n 2 p+ · a · (V − n · b) = n · R · T (3) V wobei a und b stoffspezifische und temperaturabhängige Konstanten sind, die sich empirisch 2 bestimmen lassen. Der Term a · Vn wird dabei auch als Binnendruck bezeichnet. Aus dieser Gleichung erhält man die Funktion für den Druck p in Abhängigkeit des Volumens V , welche wir im Versuch untersuchen wollen: p(V ) = a · n2 n·R·T − V − n·b V2 (4) Da die Konstanten a und b Temperaturabhängig sind, erhält man für verschiedene Temperaturen auch verschiedene Kurvenverläufe, die man als Isothermen bezeichnet. Abbildung (1) zeigt einige Isotherme für CO2 . Bei Kompression eines Gases verringern sich die Teilchenabstände, d.h. der Druck erhöht sich und das Volumen verringert sich. In Abbildung (1) erkennt man jedoch einige Isotherme, bei denen für bestimmte Volumina aus einer Erhöhung des Drucks auch eine Vergrößerung des Volumens resultiert. In diesen Bereichen entspricht die Van-der-Waals-Gleichung nicht der Realität. Man korrigiert dies, indem man sog. Maxwell-Geraden einzeichnet, sodass die Funktion im Bereich, in dem die Van-der-Waals-Gleichung nicht stimmt einen konstanten Funktionswert erhält. Die Maxwell-Gerade wird so eingezeichnet, dass das Integral der Differenz von Funktion p(V ) und Maxwell-Gerade im Intervall, in dem die Maxwell-Gerade eingezeichnet wird null ergibt (siehe auch Abbildung (1)). Der Bereich, in der die Funktion durch die Maxwell-Gerade ersetzt wird hat auch physikalisch eine große Bedeutung. In diesem Bereich existieren der Stoff sowohl im flüssigen, als auch im gasförmigen Aggregatzustand. In Punkt A (Abbildung (1)) war der Stoff also noch ausschließlich gasförmig und in Punkt C ist er vollkommen verflüssigt. Man bezeichnet diesen Bereich daher auch als sog. Koexistenzbereich. 2.1.2 Der kritische Punkt Betrachtet man die einzelnen Isothermen, so erkennt man, dass ab einer bestimmten Temperatur die Maxwell-Gerade zu einem einzigen Punkt geschrumpft ist. Diese Temperatur bezeichnet man als die sog. Kritische Temperatur Tk , wo Gas und Fluid des Stoffes die gleiche Dichte aufweisen. 1 Man bezeichnet dieses Volumen auch als Kovolumen: Man abstrahiert die Teilchen als Kugeln, die sich somit nicht näher kommen können aus bis auf den Abstand 2r. Daher gilt für das Kovolumen zweier Teilchen: 2 · b = 43 π(2r)3 = 8 · 34 πr3 = 8 · VT eilchen . 4 Abbildung 1: Einige Isotherme für CO2 [4] Experimentell lässt sich diese Temperatur bestimmen, indem man in einem geschlossenen Behälter ein Fluid erhitzt, wobei in dem Behälter auch das Gas des Stoffes enthalten ist. Durch das Verdampfen des Fluids steigt der Druck im Behälter bzw. die Dichte des Gases und damit auch der Siedepunkt. Andererseits verringert sich die Dichte des Fluids, da es sich aufgrund der steigenden Temperatur ausdehnt. Durch die kontinuierliche Erhöhung des Siedepunkts kann jedoch nicht die ganze Flüssigkeit verdampfen. Als Folge gibt es einen Punkt, wo die Dichte des Gases und die Dichte des Fluids identisch sind und es lässt sich hier die kritische Temperatur bestimmen. Man erkennt den kritischen Punkt daran, dass dort die Phasengrenze zwischen Fluid und Gas verschwindet. Für Temperaturen oberhalb der kritischen Temperatur existiert dann nur noch eine einzige Phase. Man definiert diese Phase als Gas. Da jedoch dieses “Gas“ eine deutlich höhere Dichte hat als ein gewöhnliches Gas, wird es oft auch als überkritisches Fluid bezeichnet. Den dazugehörigen Dampfdruck zur kritischen Temperatur bezeichnet man als kritischen Druck pk und das Volumen an diesem Punkt als kritisches Volumen Vk , wobei meistens das kritische Volumen auf ein Mol gerechnet wird (Vk,m ). Mathematisch lassen sich diese Größen errechnen, indem man die Temperatur ermittelt, in dem die Funktion p(V ) einen Sattelpunkt hat. Es müssen also erste und zweite partielle Ableitung von p nach V null sein. Gleichung (4) liefert die beiden Gleichungen: ∂p ∂V ∂2p ∂V 2 = − T =Tk ,V =Vk,m = T =Tk ,V =Vk,m nRTk 2n2 a ! + =0 3 (Vk,m − nb)2 Vk,m 2nRTk 6n2 a ! − =0 4 (Vk,m − nb)3 Vk,m Lösen des Gleichungssystems liefert: Vk,m = 3b 8a Tk = 27Rb (5) (6) 5 Weiter lässt sich durch Einsetzen der beiden Größen in die Funktion p(V ) (Gleichung (4)) der kritische Druck errechnen. Wir erhalten: a (7) pk = 27b2 2.2 Verflüssigung realer Gase Da im Versuch “kritischer Punkt“ die Verflüssigung von Schwefelhexafluorid (SF6 ) eine wichtige Rolle spielt, soll hier noch kurz auf einige Phänomene zur Verflüssigung von Gasen eingegangen werden. Experimentell lässt sich feststellen, dass sich eine Abkühlung eines Gases allein durch Expansion erreichen lässt. Dieser Effekt wird auch als Joule-Thomson-Effekt bezeichnet. Es ist eine Konsequenz aus dem ersten Hauptsatz der Thermodynamik, welcher direkt aus dem Energieerhaltungssatz abgeleitet ist und besagt, dass die innere Energie eines Systems sich nur in Form von Wärmeaus- bzw. -eintritt oder mechanisch verrichteter Arbeit ändern kann. Für die innere Energie können wir schreiben: U = Ekin + Epot (8) Wir gehen davon aus, dass sowohl keine äußere mechanische Arbeit verrichtet wird, als auch keine Wärmezufuhr von außen stattfindet. Die innere Energie des Systems ist also konstant. Da durch die Expansion des Gases allerdings die potentielle Energie der Teilchen zunimmt, muss die kinetische Energie abnehmen. Als Folge davon sinkt die Temperatur. Es gilt für die Temperatur in einem abgeschlossenen System eine Proportionalität zur kinetischen Energie2 : T = 1 2 1 2 · · · m · v2 = · Ekin R 3 2 3·R wobei hier R die universelle molare Gaskonstante und v 2 die gemittelte Geschwindigkeit der Teilchenbewegung ist. Auflösen nach Ekin liefert hier: Ekin = 3·R ·T 2 (9) Die potentielle Energie ist definiert als die Arbeit, die am Binnendruck verrichtet werden muss, um das Gas vom Unendlichen auf das Volumen V zu komprimieren. Weiter wird die Stoffmenge auf n = 1 mol geeicht. Damit gilt für die potentielle Energie: Z V a a Epot = dV 0 = − (10) 02 V ∞ V Einsetzen von Gleichungen (9) und (10) in Gleichung (8) liefert schließlich die für die innere Energie: U= 3·R a ·T − 2 V (11) Bei genauerer Beobachtung stellt sich heraus, dass der Joule-Thomson-Effekt nur unterhalb einer bestimmten Temperatur auftritt. Diese Temperatur bezeichnet man auch als sog. 2 aus [4] 6 Inversionstemperatur. Um diese zu berechnen betrachten wir zunächst die Enthalpie H des Systems. Diese ist ein Maß für den Wärmeaustausch in einem System und ist definiert durch: H = U + p·V (12) Sie ist also äquivalent zur Wärmeenergie Q. Wir setzen nun p aus Gleichung (4) und U aus Gleichung (11) ein und erhalten: 2·a 3 V − H(V, T ) = R · T · + 2 V −b V Da von außen keine Wärme zugeführt wird, muss auch die Enthalpie konstant bleiben. Daraus resultiert, dass die Ableitung der Enthalpie 0 ergibt. Wir berechnen das totale Differential der Enthalpie durch: ⇔ ⇔ ∂H ∂H ! 0 = dH = dV + dT ∂V ∂T −b 3 2a V 0 = R·T · dV + R · · dT + + (V − b)2 V 2 2 V −b R·T ·b − 2V·2a dT (V −b)2 = dV R · 23 + VV−b ≈ R·T ·b − 2·a 3 2 2 + 1 ·R·V (13) Da der Nenner in Gleichung (13) immer positiv ist, erhalten wir eine negative Temperaturänderung, wenn gilt: 2 · a > R · T · b. Gilt die Gleichheit der beiden Terme, so erhalten wir die Inversionstemperatur: ⇔ 2 · a = R · Tinv · b 2·a Tinv = R·b (14) 2.3 Kreisprozesse Als Kreisprozess bezeichnet man einen thermodynamischen Prozess, in dem ein System verschiedene Zustände durchläuft und irgendwann wieder in den Ausgangszustand zurückkehrt. Dann wiederholt sich der Kreisprozess. Kreisprozesse, die in beide Richtungen durchlaufen werden können, bezeichnet man als reversibel, andere als irreversibel. Reversible Kreisprozesse zeichnen sich dadurch aus, dass die Entropie S sich bei Durchlaufen des Prozesses nicht ändert. Die Entropie ist eine Größe mit der sich, zusammen mit den Größen Temperatur T , Volumen V , Stoffmenge n und Druck p, der Zustand eines Systems beschreiben lässt. Um dies zu erklären, benötigen wir den zweiten Hauptsatz der Thermodynamik, welcher besagt, dass Wärme immer vom wärmeren zum kälteren Körper fließt, aber niemals umgekehrt. Weiter lässt sich feststellen, dass mechanische Arbeit stets komplett in Wärme umgewandelt 7 werden kann. Umgekehrt lässt sich jedoch nicht die gesamte Wärme, die einem System zugeführt wird, in mechanische Arbeit umwandeln. Mit Hilfe der Entropie lässt sich der zweite Hauptsatz auch mathematisch formulieren und für die Entropieänderung gilt: dS = dQ T d.h. als Quotient aus Wärmemenge Q und Temperatur T . Für einen reversiblen Kreisprozess muss also die Entropie konstant sein. 2.3.1 Der Carnotsche Kreisprozess Ein wichtiger Kreisprozess ist der sogenannte Carnotsche Kreisprozess. Dieser lässt sich im pV -Diagramm modellieren (Abbildung (2)). Der Carnotsche Kreisprozess hat vier Zustände, wobei je zwei Zustandsübergänge isotherm, d.h. T = const., und zwei adiabatisch, d.h. dQ = 0, sind. Dabei geht man von einem idealen Gas aus, d.h. der Carnotsche Kreisprozess ist in der Praxis nur bedingt realisierbar. Der Carnotsche Kreisprozess startet in einem Zustand, der durch die Größen (p1 , T1 , V1 ) bestimmt ist. Es folgt ein isothermer Übergang in den zweiten Zustand mit den Größen (p2 , T1 , V2 ). Dieser wird durch Expansion des Gases realisiert. Da nun aber mechanische Arbeit verrichtet wurde, muss sich aufgrund des ersten Hauptsatz der Thermodynamik die Wärmeenergie Q des Systems vergrößern. Hierbei gilt: Z ∆Q1 = −∆W12 V2 p · dV = V1 (1) = = Z V2 1 dV V V1 V2 n · R · T1 · ln V1 n · R · T1 · (15) Abbildung 2: Schematische Darstellung im pV -Diagramm eines Carnotschen Kreisprozesses [4] 8 Anschließend wird das System adiabatisch in den dritten Zustand überführt. Auch hier erhöht sich das Volumen, d.h. auch der zweite Übergang wird durch Expansion realisiert. Das System befindet sich nun im Zustand (p3 , T2 , V3 ) mit T2 < T1 . Da dieser Übergang adiabatisch (dQ = 0) ist, gilt unter Verwendung von Gleichung (12): ∆W23 = dU = −p · dV = U (T2 ) − U (T1 ) (16) Die beiden Zustandsübergänge drei und vier sind fast äquivalent zu den ersten beiden, es handelt sich dieses Mal Allerdings um eine Kompression des Gases anstatt einer Expansion. Damit gilt: − ∆Q2 = ∆W34 ∆W41 V3 = n · R · T2 · ln V4 = U (T1 ) − U (T2 ) (17) (18) Damit lässt sich die gesamte Energie ausrechnen, die im Carnotschen Kreisprozess umgewandelt wird: Wges = ∆W12 + ∆W23 + ∆W34 + ∆W41 V1 V3 = n · R · T1 · ln + U (T2 ) − U (T1 ) + n · R · T2 · ln + U (T1 ) − U (T2 ) V2 V4 V1 V3 = n · R · T1 ln + T2 V2 V4 Weiter gilt für adiabatische Prozesse die Poissonsche Gleichung3 : T · V κ−1 = const. wobei κ der Isentropenexponent ist, auf den hier an dieser Stelle jedoch nicht weiter eingegangen werden soll. Dadurch lässt sich schließlich ableiten: T1 · V2κ−1 = T2 · V3κ−1 T1 · V1κ−1 = T2 · V4κ−1 woraus sich die Identität: V2 V3 = V1 V4 ⇔ − ln V1 V2 = ln V3 V4 herleiten lässt. Damit vereinfacht sich die Formel für die Gesamtenergie zu: V1 Wges = n · R · ln · (T1 − T2 ) V2 (19) Da T1 > T2 und V1 > V2 gilt, hat der Kreisprozess also insgesamt eine positive Energiebilanz. Eine Maschine, die einen Carnotschen Kreisprozess durchläuft, heißt Carnot-Maschine. 3 siehe auch [4] 9 Von solchen Maschinen lässt sich anhand der betrachteten Energiebilanz der Wirkungsgrad η berechnen. Der Wirkungsgrad ist definiert durch den Quotienten aus tatsächlich genutzter Energie und der Maschine zugeführter Energie. Er ist also immer kleiner als 1, da eine Maschine nicht mehr Energie umwandeln kann, als ihr zugeführt wird. Im Falle einer Carnot-Maschine berechnet sich der Wirkungsgrad aus: Wges η = ∆Q1 n · R · ln V1 · (T − T ) 1 2 V2 = n · R · T1 · ln VV12 = T1 − T2 T1 =1− <1 T1 T2 (20) Im Allgemeinen ist es auch möglich, dass der Carnotsche Kreisprozess andersherum durchlaufen wird. In diesem Fall handelt es sich dann statt einer Wärmekraftmaschine um eine Kältemaschine. In diesem Fall muss in das System mechanische Arbeit hineingesteckt werden um den Wärmetransport voranzutreiben. Für eine Kältemaschine erhalten wir den Wirkungsgrad durch: ηK = 1 ηW d.d. wird eine Carnot-Maschine als Kältemaschine betrieben, wird der Wirkungsgrad größer als 1. 2.3.2 Der Stirlingsche Kreisprozess Ein weiterer wichtiger Kreisprozess ist der Stirlingsche Kreisprozess. Die Modellierung eines Stirlingschen Kreisprozesses wird wieder im pV -Diagramm realisiert (Abbildung (3)). Insgesamt verläuft der Stirlingsche Kreisprozess sehr ähnlich wie der Carnotsche Kreisprozess. Zu Beginn befindet sich das System wieder in einem Zustand, der durch die Größen (p1 , T1 , V1 ) bestimmt ist. Der erste Zustandsübergang ist identisch zum Carnotsche Kreisprozess, d.h. hier gilt für ∆W12 Gleichung (15). Das System befindet sich nun im Zustand (p2 , T1 , V2 ). Der nächste Zustandsübergang unterscheidet sich vom Carnotschen Kreisprozess. Er verläuft nicht adiabatisch, sondern isochor (V = const.), d.h. das System befindet sich nun im Zustand (p3 , T2 , V2 ). Dabei gibt das System die Wärmemenge ∆Q2 ab. Die Zustandsübergänge drei und vier sind wieder analog zum Carnotschen Kreisprozess, also quasi die Rückrichtung der ersten beiden Übergänge, nur eben im anderen Temperaturbereich. Entscheidend beim Stirlingschen Kreisprozess ist, dass bei einem isochoren Zustandsübergang keine Arbeit verrichtet wird. Demnach muss gelten: ∆Q2 = −∆Q4 und für die Gesamtenergie gilt damit, wie schon beim Carnotschen Kreisprozess, Gleichung (19). Damit müsste auch der Wirkungsgrad einer Stirling-Maschine der gleiche sein wie bei einer Carnot-Maschine. In der Praxis ist dies jedoch nicht der Fall, wie gleich noch einmal 10 Abbildung 3: Schematische Darstellung eines Stirlingschen Kreisprozesses anhand des pV Diagramms [4] erläutert wird. An dieser Stelle sei nochmals angemerkt, dass auch ein Stirlingscher Kreisprozess andersherum durchlaufen werden kann. Auch hier müsste dann wieder mechanische Arbeit in das System gesteckt werden um den Wärmetransport anzutreiben. Im Versuch findet ein Stirlingscher Kreisprozess auch seine Anwendung. Es wird im zweiten Versuchsteil ein Stirling-Motor, oft auch als Heißluftmotor bezeichnet, verwendet. Daher soll die genaue Funktionsweise eines Stirling-Motors noch einmal erläutert werden. Der Stirling-Motor durchläuft die 4 Zustände des Stirlingschen Kreisprozess. Abbildung (4) zeigt die einzelnen Phasen. Der Stirling-Motor besteht aus einem geschlossenen Zylinder mit zwei Zonen, einer warmen mit Temperatur T1 und einer kalten mit Temperatur T2 . Als Gas wird meistens Luft oder Helium verwendet. Die Verbindung zwischen den Zonen bildet der Verdrängerkolben, der eine Bohrung hat, damit das Gas zwischen den Zonen hin und herströmen kann. In der Bohrung sind Metallspäne, die als Wärmespeicher fungieren. Der Verdrängerkolben ist ebenso wie der Arbeitskolben, der die mechanische Arbeit verrichtet, mit einer Kurbelwelle verbunden, wobei die Kolben eine Phasenverschiebung von ϕ = 90◦ aufweisen. Dies ist notwendig, damit Arbeitskolben und Verdrängerkolben zeitlich versetzt arbeiten können. Die genaue Funktionsweise macht dies deutlich: 1. Bei der isothermen Expansion bewegt sich der Arbeitskolben nach unten, der Verdrängerkolben ist jedoch bereits an seinem tiefsten Punkt und bleibt dort weitestgehend. Dadurch vergrößert sich das Volumen, die Temperatur bleibt jedoch konstant. 2. Bei der isochoren Abkühlung bleibt nun der Arbeitskolben in seiner tiefsten Position und der Verdrängerkolben bewegt sich nach oben. Dadurch bleibt das Gesamtvolumen konstant, die Temperatur sinkt jedoch auf den Wert T2 . 3. Bei der isothermen Kompression bewegt sich nun wieder der Arbeitskolben, diesmal jedoch nach oben was zur Folge hat, dass das Gesamtvolumen abnimmt. Die verrichtete Arbeit wird in Form von thermischer Energie abgegeben. 11 4. Bei der isochoren Erwärmung bewegt sich der Verdrängerkolben nach unten und gibt die im zweiten Zustandsübergang gespeicherte Energie wieder an das Gas ab, wodurch die Temperatur wieder auf den Wert T1 ansteigt. Damit ist das System wieder im ursprünglichen Zustand. Hier wird auch klar, warum der Stirling-Motor einen geringeren Wirkungsgrad als ein Carnotscher Kreisprozess hat, da es technisch nicht möglich ist, die in Punkt 2 abgegebene Wärmeenergie komplett zu speichern und dem System im vierten Takt wieder zuzuführen. Abbildung 4: Die Abbildung zeigt die 4 Phasen des Stirling-Motors. [4] 2.4 Leistung Es soll im zweiten Versuchsteil auch die mechanische und elektrische Leistung des StirlingMotors berechnet werden. Die Leistung berechnet sich als zeitliche Ableitung der Arbeit. Damit gilt für die mechanische Leistung: Pmech = dWmech F · dr = = F ·v = M ·ω = 2·π·M ·ν dt dt (21) wobei hier M das Drehmoment des Motors, ω dessen Kreisfrequenz und ν dessen Frequenz ist. Für die elektrische Leistung gilt unter der Annahme einer konstanten Spannung U und des Ohmschen Gesetzes U = R · I, dass die Proportionalität zwischen Spannung und Stromstärke über einen definierten Widerstand R herstellt: Pel = U · dq U2 dWel = = U ·I = dt dt R (22) 2.5 Wärmeäquivalente Früher wurden Wärmemengen nicht in der heute üblichen SI-Einheit Joule gemessen, sondern in kcal (Kilo-Kalorien), da damals noch nicht bekannt war, dass Wärme auch eine Energieform ist. Eine Kalorie ist definiert als die Wärmemenge, die benötigt wird um 1 kg Wasser von 14,5◦ C auf 15,5◦ C zu erwärmen. 12 Zur Umrechnung zwischen den Einheiten definiert man sog. Wärmeäquivalente. Man unterscheidet dabei zwischen elektrischem und mechanischem Wärmeäquivalent. Die Literaturwerte betragen: W el = W mech = ∆Q[cal] cal = 0, 23885 ∆Wel [W s] Ws ∆Q[cal] cal = 4, 186 ∆Wmech [N m] Nm Das elektrische Wärmeäquivalent lässt sich bestimmen, indem man durch ein elektrisches Gerät (z.B. einen Tauchsieder) Wasser erwärmt. Die elektrische Energie berechnet sich dabei durch die Definition der elektrischen Leistung: Pel = U · I ⇔ ∆Wel = U · I · ∆t wobei hier ∆t die Zeit, die für die Erwärmung um die Temperatur ∆T benötigt wird, ist. Die Wärmemenge ∆Q berechnet sich in solch einem Experiment durch: ∆Q = c · m · ∆T wobei c hier die spezifische Wärmekapazität des erwärmten Stoffes und m dessen Masse ist. Aus dem Quotienten von ∆Q und Pel erhält man schließlich dass elektrische Wärmeäquivalent. Das mechanische Wärmeäquivalent lässt sich bestimmen, indem durch mechanische Arbeit Reibung erzeugt wird. Diese Reibung wiederum erzeugt Wärme. Der Versuch sollte dann so aufgebaut sein, dass der Festkörper, an dem Reibung und damit Wärme erzeugt wird, diese an Wasser abgeben kann. Damit lässt sich wieder die Wärmemenge bestimmen und die mechanische Arbeit lässt sich ebenfalls berechnen. 3 Der Versuch 3.1 Versuchsteil 1: Kritischer Punkt 3.1.1 Versuchsaufbau Der Versuchsaufbau besteht aus einer transparenten volumenkalibrierten Kompressionskapillare gefüllt mit SF6 . Diese befindet sich zur Sicherheit in einem transparentem Kolben mit Wasserfüllung. Weiter ist die Kapillare an ein Temperaturregelungssystem mittels Umwälzpumpe angeschlossen, so dass sich die Temperatur zwischen 0◦ C und 55◦ C regeln lässt. Im unteren Teil der Kapillare ist eine Quecksilbersäule angebracht, durch die das Volumen kontrolliert werden kann. Als Ablesegeräte stehen ein Thermometer und ein Manometer zum Ablesen des Druckes zur Verfügung. 3.1.2 Versuchsdurchführung Es werden insgesamt 10 Isotherme aufgenommen. Dabei wird bis zum Einsetzen der Verflüssigung jeweils in 0.5 ml Volumenabschnitten, danach jeweils in 0.1 ml Volumenabschnitten gemessen. Weiter wird in der Nähe des kritischen Punktes die Phase zwischen Fluid und Gas beobachtet. Der Literaturwert für die kritische Temperatur von Schwefelhexaflourid liegt bei Tk = 45 ◦ C. 13 3.2 Versuchsteil 2: Heißluftmotor 3.2.1 Versuchsaufbau Der Versuchsaufbau im zweiten Versuchsteil besteht aus einem Stirling-Motor (siehe auch Abschnitt 2.3.2) mit pV -Sensorbox, einer Motor/Generator-Einheit und einem Drehmomentmesser. Weiter sind im Kolben des Stirling-Motors zwei Thermometer angebracht um die Temperaturen in Kalt- und Warmzone zu messen. Alle Daten werden mit einem PC mit der Software CASSY Lab aufgezeichnet. 3.2.2 Versuchsdurchführung Der Versuch umfasst zwei Versuchsteile. Im ersten Versuchsteil wird der Stirling-Motor als Kältemaschine (Wärmepumpe) betrieben. Dazu wird die Motor/Generator-Einheit am Stirling-Motor angebracht. Sobald sich an den zwei Temperatur-Messpunkten konstante Temperaturen eingependelt haben, lassen sich die Messungen starten. Es werden zunächst fünf pV -Diagramme aufgezeichnet und gespeichert, aus denen sich später die Daten herauslesen lassen. Weiter wird im ersten Versuchsteil mittels Multimeter die Betriebsspannung U und der elektrische Strom I des Stirling-Motor bestimmt. Im zweiten Versuchsteil wird der Stirling-Motor nun als Wärmekraftmaschine betrieben. Dazu wird die warme Zone am Arbeitskolben mit Hilfe eines Spiritusbrenners erhitzt. Sobald sich wieder konstante Temperaturen eingestellt haben, können wir mit den Messungen starten. Es werden wieder fünf pV -Diagramme aufgezeichnet. Nun belasten wir den Stirling-Motor zusätzlich mit einem Drehmomentmesser. Auch hier werden fünf pV -Diagramme aufgezeichnet. Zusätzlich wird zu jeder Messung das belastende Drehmoment M am Stirling-Motor abgelesen. Hierfür wird eine Skala an den Drehmomentmesser angebracht. Zuletzt wollen wir noch die mechanische und elektrische Leistung des Stirling-Motors messen. Für die mechanische Leistung belasten wir den Stirling-Motor wieder mit einem Drehmomentmesser. Es wurden für 6 verschiedene Frequenzen ν jeweils das Drehmoment abgelesen4 . Für die Messung der elektrischen Leistung verwenden wir die Motor/Generator-Einheit als Generator. Es wird der Stromkreis mit einem elektrischen Widerstand R belastet und die dazugehörige Frequenz ν und die Spannung U gemessen. Hierfür war unser Stirling-Motor jedoch zu Leistungsschwach, weshalb wir einen anderen verwendet haben. Auch dieser war nur in sofern geeignet, dass wir unsere Messung mehrfach unterbrechen mussten und deshalb jeweils drei unabhängige isotherme Messreihen aufzeichneten. Von daher werden später in der Auswertung auch nur die Werte berücksichtigt, die isotherm sind. Da außerdem der Heizwert des Spiritusbrenners bestimmt werden soll, wird noch Masse des verbrannten Brennmittels ∆m, sowie Brenndauer ∆t gemessen. Da für die Auswertung auch der Luftdruck p notwendig ist, wurde dieser ebenfalls noch vermessen. 4 Leider war es uns nicht möglich wie in der Versuchsdurchführung vorgeschlagen 10 Messungen durchzuführen, da mit dem Stirling-Motor nicht ausreichend hohe Drehzahlen erreicht werden konnten und es so leider nicht möglich war, diese ausreichend zu variieren. 14 4 Auswertung 4.1 Versuchsteil 1: Kritischer Punkt 4.1.1 Auswertung der Messwerte Abbildung (5) zeigt die von uns aufgenommenen Isotherme. Es lässt sich hier sehr schön der typische Verlauf der Isotherme für die verschiedenen Temperaturen wie es im Grundlagenteil erläutert wurde erkennen. Vor allem die Tatsache, dass der Druck auf Höhe der MaxwellGeraden, also beim Übergang vom gasförmigen in den flüssigen Zustand, konstant bleibt, lässt sich anhand unserer Messergebnisse bestätigen. Zunächst gilt es anhand der aufgezeichneten Messdaten die Daten des kritischen Punkts zu bestimmen. Da hierfür eine genaue Berechnung schwierig wäre, müssen wir die Temperatur des kritischen Punktes schätzen. Betrachtet man die Kurven, so erkennt man, dass bei den aufgezeichneten Kurven (siehe auch Abb. (5)) die Isotherme für T = 44 ◦ C einen Sattelpunkt aufweist, d.h. wir schätzen die kritische Temperatur auf Tk = 44 ◦ C ± 2 K = (317 ± 2) K. Der Literaturwert für die kritische Temperatur von Schwefelhexafluorid liegt bei Tk,Lit ≈ 45◦ C, was wir durch unser Experiment im Rahmen der Messungenauigkeit also verifizieren können. Die Werte für das kritische Volumen und den kritischen Druck erhalten wir dann ebenfalls aus den Messdaten. Wir schätzen: Vk = (0, 5 ± 0, 1) ml pk = (37, 4 ± 0, 3) · 105 Pa Abbildung 5: Das Diagramm zeigt die aufgezeichneten Isotherme. Da aufgrund der vielen Messwerte Fehlerindikatoren das Diagramm sehr unübersichtlich gemacht hätten, wurde auf diese verzichtet. Bei der Messung mit T = Tk konnten wir im Experiment auch den Übergang erkennen, in dem die Phase zwischen Fluid und Gas verschwindet. 15 Nun wollen wir anhand dieser Daten die Van-der-Waals-Konstanten berechnen. Für a und b ergibt sich nach Lösen des Gleichungssystems, das durch Gleichungen (6) und (7) gegeben ist: a = b = 27 R2 Tk2 · 64 pk 1 RTk · 8 pk Da die Messgrößen für den kritischen Punkt mit einem Fehler behaftet sind, rechnen wir mit einer Fehlerfortpflanzung uns es gilt5 : δa = δb = s 2 27 R2 Tk Tk 2 · · (2 · δTk ) + · δpk 64 pk pk s 2 Tk 1 R · · (δTk )2 + · δpk 8 pk pk Anhand dieser Zusammenhänge erhalten wir: m6 · Pa mol2 cm3 b = (88, 1 ± 0, 6) · 10−5 mol a = (0, 784 ± 0, 012) 6 · Pa Die Literaturwerte für die Van-der-Waals-Konstanten von SF6 liegen bei a = 0, 7857 mmol 2 cm3 6 −5 und b = 87, 9 · 10 mol . Im Rahmen der Ungenauigkeit unserer berechneten Werte, können wir diese also bestätigen. Weiter lässt sich anhand dieser Größen nun die im Gas enthaltene Stoffmenge n bestimmen. Da Vk = n · Vk,m gilt, erhalten wir mit Gleichung (5): n= Vk 3b Da der Wert für b bereits bestimmt ist, lässt sich mit diesem weiterrechnen und wir erhalten als Fehler für die Stoffmenge: s 2 1 Vk 2 · (δVk ) + · δb δn = 3b b Es ergibt sich ein Wert von n = (1, 89 ± 0, 38) mmol. Als nächstes bestimmen wir die Dampfdruckkurve. Diese ergibt sich, indem der Druck auf der Höhe der Maxwell-Geraden in Abhängigkeit der Temperatur bestimmt wird. Tabelle (1) zeigt die von uns abgelesenen Werte für den Druck auf Höhe der Maxwell-Geraden und Abbildung (6) zeigt unsere bestimmte Dampfdruckkurve p(T ) für Schwefelhexafluorid. 5 6 nach [3] aus [5] 16 T [◦ C] 10 20 25 30 35 40 42 44 p [105̂ Pa] 16,6 21,9 24,7 27,6 30,6 34,4 36 37,4 Tabelle 1: Die Tabelle zeigt die bestimmten Werte für den Druck auf Höhe der MaxwellGeraden. Es gilt generell: δT = 0, 3 K und δp = 0, 5 · 105 Pa. Abbildung 6: Die Abbildung zeigt die bestimmte Dampfdruckkurve. Zuletzt wollen wir aus unseren Daten noch die Inversionstemperatur von SF6 nach Gleichung (14) bestimmen. Der Fehler für diese ergibt sich dann nach: r a 2 2 δTinv = · (δa)2 + · δb Rb b Wir erhalten als Wert für die Inversionstemperatur Tinv = 1867 ◦ C ± 35 K = (2140 ± 35) K. Der Literaturwert für die Inversionstemperatur von SF6 lässt sich mit Hilfe von Gleichung (14) berechnen, indem die Literaturwerte für R, a und b eingesetzt werden. Er beträgt Tinv = 2150 K. Damit bestätigt unsere Messung im Rahmen der Messungenauigkeit diesen Wert. 4.1.2 Fehlerdiskussion Im Rahmen der Messungenauigkeit bestätigen unsere gemessenen Werte die Theorie. Allerdings mussten wir dabei generell einen relativ hohen Fehler annehmen. Diesen hätte man reduzieren können, indem wir um den kritischen Punkt herum mehr Isotherme aufgenommen 17 hätten. Allerdings wäre dies mit der Versuchsapparatur nicht ganz einfach gewesen, da die Temperatur generell um ca. ∆T ≈ 0, 5 K schwankte. 4.2 Versuchsteil 2: Heißluftmotor 4.2.1 pV -Diagramme Zunächst wollen wir die am Gasprozess teilnehmende Stoffmenge n berechnen. Dazu verwenden wir das ideale Gasgesetz (Gleichung (1)) und es gilt: n = δn = pV RT s R · T 2 2 (V · δp) + (p · δV ) + pV δT T 2 Dazu wurden aus den aufgezeichneten Diagrammen jeweils die Werte Vmin/max und pmin/max abgelesen7 . Ebenfalls wurden während dem Experiment die Werte für Tmin/max bestimmt. So erhalten wir Gleichungen für das Wertetripel (Tmax , pmax , Vmin ), sowie für das Wertetripel (Tmin , pmin , Vmax ). Da bei der Wärmekraftmaschine die Temperaturen sehr stark schwankten, erschien hier eine Mittelung der Temperaturen eher ungeeignet. Von daher wurden für alle 14 Messungen über die zwei gegebenen Wertetripel jeweils zwei Werte für die Stoffmenge n bestimmt und diese 28 Werte anschließend arithmetisch gemittelt. Die Abweichung ergibt sich schließlich aus der Standardabweichung. Wir erhalten einen Wert von n = (1, 28 ± 0, 19) mmol8 . Weiter betrachten wir nun die aufgezeichneten pV -Diagramme. Abbildungen (7), (8) und (9) zeigen jeweils einen Kreisprozess für den Stirling-Motor als Kältemaschine, unbelastete Wärmekraftmaschine bzw. belastete Wärmekraftmaschine. Weiter wurden in die Diagramme jeweils die Kurven für einen idealen Kreisprozess eingezeichnet. Dazu werden die beiden Isotherme für die maximale und minimale Temperatur berechnet und die Isochore manuell eingezeichnet. Die Berechnung der Isotherme beruht auf dem idealen Gasgesetz (Gleichung (1)). Es ist zu erkennen, dass bei der belasteten Wärmekraftmaschine die Fläche innerhalb des Kreisprozesses leicht größer ist. Dies ist dadurch zu erklären, dass die Wärmekraftmaschine hier mehr Arbeit verrichten muss, als bei der unbelasteten. Weiter ist deutlich zu erkennen, dass bei der Kältemaschine die ideale Kurve deutlich unterhalb der von uns vermessenen und bei der Wärmekraftmaschine die ideale Kurve etwas oberhalb der von uns vermessenen liegt. Dies ist vermutlich aufgrund unserer Messdaten zu erklären. Der Mittelwert für n (s.o.) bildet eine Mittelung aus den Werten für Kältemaschine 7 Da die aufgezeichneten Diagramme ausschließlich Spannungen gegeneinander auftragen, müssen diese generell umgerechnet werden. Die Umrechnung basiert dabei auf Gleichungen (29) und (30), wobei V0 = 32 ml gegeben ist und p0 = 976, 5 hPa der am Versuchstag abgelesene Luftdruck ist. Die beiden Umrechnungs∆U mV faktoren sind ebenfalls gegeben und es gilt: ∆V = 50 mV sowie ∆U = 2 hPa . ml ∆p 8 Im Nachhinein ließ sich sogar feststellen, dass eine Mittelung der Temperaturen auch nur eine minimale Abweichung von unserem berechneten Wert ergeben hätte, jedoch hätte man im Allgemeinen nicht davon ausgehen dürfen. 18 und Wärmekraftmaschine, jedoch lag der Wert bei der Kältemaschine deutlich oberhalb und der Wert für die Wärmekraftmaschine deutlich unterhalb des tatsächlichen Mittelwertes. Entgegen unserer Erwartungen ist bei der Wärmekraftmaschine die Fläche des idealen Prozesses deutlich größer als die des realen Prozesses. In der Realität hat man bei mechanischen Prozessen generell Verluste durch Reibung u.a. Dadurch müsste der reale Prozess eigentlich mehr Arbeit verrichten als der ideale Prozess um den gleichen Effekt zu erzielen. Wir vermuten an dieser Stelle von daher einen systematischen Fehler, der möglicherweise auch mit dem Versuchsaufbau zusammenhängt (siehe auch Abschnitt 4.2.5 “Fehlerdiskussion“). Abbildung 7: Das Diagramm zeigt einen von uns vermessenen Kreisprozess des StirlingMotors als Kältemaschine, sowie deren theoretischen, idealen Verlauf. Abbildung 8: Das Diagramm zeigt einen von uns vermessenen Kreisprozess des StirlingMotors als unbelastete Wärmekraftmaschine, sowie deren theoretischen, idealen Verlauf. 19 Abbildung 9: Das Diagramm zeigt einen von uns vermessenen Kreisprozess des StirlingMotors als belastete Wärmekraftmaschine, sowie deren theoretischen, idealen Verlauf. 4.2.2 Kältemaschine Nun betrachten wir die Kältemaschine. Da eine Auswertung jeder einzelnen Messung hier zu aufwendig wäre, beschränken wir uns auf die Messung, dessen Messdiagramm Abbildung in (7) dargestellt ist. Hier lassen sich basierend auf verschiedenen Betrachtungsweisen verschiedene Werte für Arbeit und Wärme berechnen. Vom Elektromotor aufgewendete Arbeit Wel (22), nach der dann gilt: Wel = Pel · ∆t = Diese berechnet sich nach Gleichung Pel UI = ν ν Mit den von uns gemessenen Werten ergibt sich Wel = (0, 60 ± 0, 06) J9 . Im idealen Stirlingprozess aufgewendete Arbeit W Zur Berechnung dieser Arbeit verwenden wir Gleichung (19) und es gilt: Vmax W = n · R · ∆T · ln (23) Vmin Es ergibt sich ein Wert von W = (0, 060 ± 0, 009) J. Hier sei zu beachten, dass die Werte Vmax und Vmin vom Computer berechnet wurden und von daher als nahezu fehlerfrei anzunehmen sind. Wir setzen daher hier und im Folgenden δVmax = δVmin = 0. 9 Da hier und im Folgenden eine Angabe der Formeln für die Fehlerfortpflanzung eher unübersichtlich wäre und die Leserlichkeit akut beeinflussen würde, wird hier und im Folgenden darauf verzichtet. Generell berechnet sich Fehler für alle berechneten Werte x, deren Formeln fehlerbehaftete Größen xi enthalten rder 2 P ∂x durch: δx = · δx i i ∂xi 20 Im idealen Stirlingprozess der kalten Seite entzogenen Wärme Q Zur Berechnung der entzogenen Wärme auf der kalten Seite des Stirling-Motors verwenden wir Gleichung (17). Es gilt hierbei: Vmax (24) Q = −n · R · Tmax · ln Vmin Einsetzen der Messwerte liefert Q = (−1, 07 ± 0, 16) J. Im realen Prozess aufgewendete Arbeit W ∗ Zur Berechnung der im realen Prozess aufgewendeten Arbeit W, muss die Fläche innerhalb des pV -Diagramms berechnet werden: I W ∗ = − pdV (25) Dies geschieht mittels numerischer Integration und wir erhalten einen Wert von W ∗ = (0, 128 ± 0, 002) J. Da hier das Programm, dass die numerischen Berechnung durchgeführt hat keinen Fehler angegeben hatte, wurde dieser anhand Berechnungen weiterer Zyklen geschätzt, was hier sinnvoll war, da die Werte für die verschiedenen Zyklen kaum voneinander abweichen und der Fehler von daher auch so gering gehalten werden konnte. Im realen Prozess entzogene Wärme Q∗ Auch hier ist wieder numerische Integration notwendig, da für die der kalten Seite entzogenen Wärme Q∗ gilt: Q∗ = − Z Vmax pdV (26) Vmin Entscheidend ist hierbei, dass über den unteren Zweig integriert wird. Ebenfalls muss die Richtung beachtet werden. Auch hier wurde der Fehler wieder geschätzt und es ergab sich ein Wert von Q∗ = (−1, 61 ± 0, 01) J. Wirkungsgrade Zuletzt wollen wir aus den eben berechneten Werten noch die verschiedenen Wirkungsgrade der Kältemaschine berechnen. Wir unterscheiden zwischen idealem, realem und elektrischem Wirkungsgrad. Es ergaben sich folgende Werte: ηideal = ηreal = ηel = Q = 17, 9 ± 3, 8 W Q∗ = 12, 6 ± 0, 2 W∗ ∗ Q = 2, 69 ± 0, 25 Wel Die Werte für den Wirkungsgrad bestätigen die Realität zumindest qualitativ, da der Wirkungsgrad des realen Prozess niedriger ist als der des idealen Prozess. Weiter ist der elektrische Wirkungsgrad am geringsten, was physikalisch dadurch zu erklären ist, dass im Motor noch weitere Energieverluste durch Reibungseffekte zustande kommen. 21 4.2.3 Wärmekraftmaschine Im Folgenden betrachten wir die belastete Wärmekraftmaschine. Da auch hier eine Auswertung jeder einzelnen Messungen zu aufwendig wäre, beschränken wir uns auf eine Messung. Das zugehörige Messdiagramm zeigt Abbildung (9). Mittlere Heizleistung PH des Spiritusbrenners und Heizleistung WH Zunächst wollen wir die mittlere Heizleistung des Spiritusbrenners PH berechnen. Die mittlere Heizleistung des Spiritusbrenners ergibt sich aus dem Quotienten der Masse ∆m = (15, 0 ± 0, 2) g des verbrannten Spiritus und der Zeitspanne ∆t = (4051 ± 10) s 10 , in welcher der Spiritusbrenner in Betrieb war. Es gilt: PH = H · ∆m ∆t wobei H = 27 MJ kg den Heizwert von Spiritus bzw. Äthanol bezeichnet. Es ergab sich für die mittlere Heizleistung: PH = (100, 0 ± 1, 4) W. Daraus lässt sich nun die Heizleistung im von uns aufgezeichneten Kreisprozess berechnen. Für diese gilt: WH = PH · t = PH ν Einsetzen unserer Messwerte liefert WH = (13, 33 ± 0, 35) J. Im idealen Stirlingprozess zugeführte Wärme Q und verrichtete Arbeit W Analog zur Kältemaschine gilt für die zugeführte Wärme Q bzw. verrichtete Arbeit W einer Wärmekraftmaschine wieder Gleichungen (24) bzw. (23). Einsetzen unserer Werte liefert: Q = (−1, 59 ± 0, 29) J W = (0, 51 ± 0, 08) J Im realen Prozess zugeführte Wärme Q∗ und verrichtete Arbeit W ∗ Für die Größen im realen Prozess ist wieder numerische Integration nötig. Dabei gelten analog zur Kältemaschine für die zugeführte Wärme Q∗ Gleichung (26) und für die verrichtete Arbeit W ∗ (25). Es ergaben sich Werte von: Q∗ = (−1, 75 ± 0, 01) J W ∗ = (0, 138 ± 0, 001) J Auch hier wurde der Fehler wieder empirisch abgeschätzt und konnte aufgrund der sehr kleinen Abweichung der einzelnen Zyklen sehr gering gehalten werden. 10 Unsicherheit im Nachhinein abgeschätzt 22 Mechanische Arbeit Wm Nun wollen wir noch die vom Stirling-Motor geleistete mechanische Arbeit Wm berechnen. Die Berechnung basiert auf Gleichung (21) und wir erhalten: Wm = Pm · t = Pm = 2·π·M ν Wir erhalten einen Wert von Wm = (7, 5 ± 3, 1) · 10−3 J. Wirkungsgrade Zuletzt betrachten wir wieder die Wirkungsgrade der Wärmekraftmaschine. Dabei unterscheiden wir wieder zwischen idealem, realem und mechanischem Wirkungsgrad. In diesem Fall lässt sich auch noch der thermische und der Gesamtwirkungsgrad berechnen. Wir erhalten: ηideal = ηreal = ηmech = ηtherm = ηges = W = 0, 32 ± 0, 07 Q W∗ = 0, 079 ± 0, 001 Q∗ Wm = 0, 0043 ± 0, 0018 Q∗ W∗ = 0, 0104 ± 0, 0003 WH Wm = 0, 00057 ± 0, 00024 WH Hier bestätigt sich wieder die Theorie, dass der reale Wirkungsgrad deutlich kleiner ist, als der ideale, was auf vor allem auf Reibungsverluste zurückzuführen ist. Im Allgemeinen sind die Wirkungsgrade sehr klein, was vermutlich mit der Versuchsapparatur zusammenhängt (siehe auch Abschnitt 4.2.5 “Fehlerdiskussion“). 4.2.4 Mechanische und elektrische Leistung Abschließend wollen wir noch die mechanische und elektrische Leistung des Stirling-Motors in Abhängigkeit der Drehzahl bestimmen. Dazu tragen wir die Messwerte graphisch übereinander auf. Tabelle (2) zeigt die gemessenen Werte für Drehmoment M bei Frequenz ν, sowie die berechneten Werte für die mechanische Leistung Pm . Die mechanische Leistung ergibt sich dann über Gleichung (21). Abbildung (10) zeigt die berechneten Werte für mechanische Leistung Pm über der Frequenz ν aufgetragen. Für die Berechnung der elektrischen Leistung verwenden wir Gleichung (22). Tabelle (3) zeigt die gemessenen Werte für Frequenz ν und Spannung U bei angelegtem Widerstand R, sowie die berechneten Werte für Pel . Auch hier tragen wir wieder die elektrische Leistung Pel und Abhängigkeit der Frequenz ν auf. Das Ergebnis zeigt Abbildung (11). Während bei der elektrischen Leistung die Werte noch ansatzweise einem Kurvenverlauf folgen, sind die Werte bei der mechanischen Leistung leider fast vollkommen entartet. Dies hängt in erster Linie mit der Versuchsapparatur zusammen. Zum einen konnten wir lediglich sechs isotherme Werte aufzuzeichnen, wobei auch hierbei der Stirling-Motor nur mit einem geringen Drehmoment belastet werden konnte, ohne dass er stehen blieb. So musste auch der 23 ν[Hz] 8,25 7,30 6,67 6,50 5,83 5,33 M [10−3 N m] 1,7 2,0 2,2 2,5 2,7 3,0 0,088 0,092 0,092 0,102 0,099 0,101 Pm [W ] ± 0,010 ± 0,009 ± 0,008 ± 0,008 ± 0,007 ± 0,007 Tabelle 2: Messwerte für Frequenz ν bei angelegtem Drehmoment M , sowie die daraus berechnete mechanische Leistung Pm . Es gilt generell: δν = 0, 08 Hz und δM = 0, 2 · 10−3 Nm. Abbildung 10: Es ist die mechanische Leistung Pm in Abhängigkeit der Frequenz ν aufgetragen. R[Ω] 150 100 90 80 70 60 50 ν[Hz] 5,83 5,17 4,50 4,17 4,00 3,67 3,33 U [V ] 2,50 2,05 1,80 1,60 1,40 1,30 1,00 0,042 0,042 0,036 0,032 0,028 0,028 0,020 Pel [W ] ± 0,003 ± 0,004 ± 0,004 ± 0,004 ± 0,004 ± 0,004 ± 0,004 Tabelle 3: Messwerte für Frequenz ν und Spannung U bei angelegtem Widerstand R, sowie die daraus berechnete elektrische Leistung Pm . Es gilt generell: δR = 0, δν = 0, 08 Hz und δU = 0, 1 V. 24 Abbildung 11: Es ist die elektrische Leistung Pel in Abhängigkeit der Frequenz ν aufgetragen. Fehler dementsprechend hoch angenommen werden und die Werte repräsentieren nur bedingt die Realität. Für die elektrische Leistung ergibt sich vermutlich eine Kurve mit einem breiten Peak in der Mitte. 4.2.5 Fehlerdiskussion Leider waren die Messungen mit dem Stirling-Motor im Allgemeinen recht schwierig. Wir vermuten, dass der Stirling-Motor generell eine recht niedrige Leistung hatte, weshalb es relativ schwierig war, ihn, als Wärmekraftmaschine betrieben, auf ausreichend hohen Drehzahlen zu betreiben. Für die Messung des Drehmoments waren von daher nur sehr kleine angelegte Drehmomente möglich, da der Motor sonst stehen blieb. Weiter war hier wiederum das Ablesen des Drehmoments recht schwierig, da die Nadel auf der Skala sehr starken Schwankungen unterlag. Von daher musste der Fehler hier ungewöhnlich hoch angenommen werden. Dementsprechend sind auch die Wirkungsgrade aus Abschnitt 4.2.3 mit einem hohen Fehler belastet. Weiter sind dort auch die Wirkungsgrade deutlich niedriger, als normalerweise zu erwarten. Wir gehen davon aus, dass dies ebenfalls darauf zurückzuführen ist, dass der Stirling-Motor nicht in optimalem Zustand war. Da das Gerät jedoch nicht genauer untersucht wurde, lässt sich der Fehler hier nicht näher lokalisieren. Des Weiteren wird vermutlich auch die Heizleistung des Spiritusbrenners (Abschnitt 4.2.1) mit einem höheren Fehler als angenommen belastet sein, da die Größe der Flamme während des Versuchs häufig variiert werden musste, um die Temperatur einigermaßen konstant zu halten. Leider war es hier trotz der regelmäßiger Regulierung der Flamme relativ schwierig die Temperatur konstant zu halten, was allerdings auch auf äußere Umwelteinflüsse zurückzuführen ist. Dieser Sachverhalt verfälscht die Messergebnisse vermutlich ebenfalls noch zusätzlich. 25 Ebenfalls mit Vorsicht zu genießen sind nach wie vor die pV -Diagramme der Wärmekraftmaschine, da da die geleistete Arbeit sichtbar kleiner ist, als die in einem idealen Prozess. Zwar kann dies ebenfalls am vermutlich nicht optimalen Zustand des Stirling-Motors liegen, jedoch lässt sich hier der Fehler nur schwer nachvollziehen. Wir vermuten, wie bereits erwähnt, einen systematischen Fehler, vor allem auch, da sich dieses Phänomen über die anderen aufgenommenen Diagramme fortzieht. Aus diesem Grund soll der Leser darauf hingewiesen werden, dass auch die Werte, die in Abschnitt 4.2.3 auftauchen, mit Vorsicht zu genießen sind. Letztendlich ließen sich jedoch trotz vieler möglicher Fehlerquellen und auch einigen Ergebnissen entgegen den Erwartungen einige Phänomene im Experiment bestätigen. 5 Fragen und Antworten 5.1 Fragen zum Versuchsteil: Kritischer Punkt 1. Leiten Sie aus der Van-der-Waals-Gleichung die folgenden Beziehungen her: 8 a · 27 R · b 1 a = · 27 b2 = 3·b Tk = pk Vk,m Die Beziehungen wurden bereits im Grundlagenteil hergeleitet (Gleichungen (6), (7) und (5)). 2. Berechnen Sie die innere Energie eines Van-der-Waals-Gases in Abhängigkeit von Temperatur und Volumen bei konstanter Teilchenzahl. Zeigen Sie dann, dass insbesondere die isotherme partielle Ableitung der inneren Energie eines Van-der-Waals-Gases nach dem Volumen gleich dem Binnendruck dieses Gases ist: ∂U a (27) = 2 ∂Vm T Vm Die innere Energie U in Abhängigkeit von Temperatur und Volumen wurde bereits im Grundlagenteil (Gleichung (11)) hergeleitet. Differentiation nach V ergibt schließlich: ∂U a = 2 (28) ∂V V 3. Leiten Sie eine Beziehung zwischen den Van-der-Waals-Konstanten a und b und den beiden Inversionstemperaturen des Joule-Thomson-Effektes her. Die Beziehung wurde bereits im Grundlagenteil hergeleitet (Gleichung (14)). 4. Welchem Teil der Van-der-Waals-Kurven entsprechen keine realen Zustände? 26 Erläutern Sie die Bedeutung der Maxwell-Geraden. Diese Fragestellung wurde bereits im Grundlagenteil, Abschnitt 2.1.1, erläutert. 5.2 Fragen zum Versuchsteil: Heißluftmotor 1. Beschreiben Sie anhand der pV -Diagramms die Funktionsweise des “Heißluftmotors“ als a) Wärmepumpe und b) Kältemaschine. Welchen Umlaufsinn hat die durchlaufene Kurve jeweils? Diese Frage wurde bereits ausführlich im Grundlagenteil, Abschnitt 2.3, behandelt. 2. Was versteht man unter einem “perpetuum mobile zweiter Art“? Formulieren Sie den II. Hauptsatz der Wärmelehre unter Verwendung der Begriffe: a) “perpetuum mobile zweiter Art“ b) Entropie. Unter einem “perpetuum mobile zweiter Art“ versteht man eine Maschine, die Wärmeenergie aus der Umgebung in mechanische Arbeit umwandelt, ohne dass dabei die Temperatur der Umgebung sinkt. Dies verletzt zwar nicht den Energieerhaltungssatz, jedoch dem II. Hauptsatz der Thermodynamik, da dieser ja besagt, dass Prozesse, in denen Wärmeenergie zu mechanischer Arbeit umgewandelt wird, irreversibel sind. Mit diesem Hintergrund lässt sich der II. Hauptsatz der Thermodynamik auch einfach formulieren durch: Ein “perpetuum mobile zweiter Art“ ist unmöglich. Mit Entropie lässt sich der II. Hauptsatz der Thermodynamik ebenfalls formulieren. Dies wurde bereits in Abschnitt 2.3 getan. 3. Wie hoch sind die typischen Wirkungsgrade gebräuchlicher Automotoren (OttoMotor, Diesel-Motor)? Vergleichen Sie diese mit dem Wirkungsgrad eines Stirling-Motor. Ein Stirling-Motor hat einen Wirkungsgrad von ca. 0, 10 ≤ νs ≤ 0, 66. Die Wirkungsgrad von Otto-Motor und Diesel-Motor betragen in etwa νO ≈ 0, 37 bzw. νD ≈ 0, 50. Dabei muss jedoch beachtet werden, dass der Wirkungsgrad der meisten Stirling-Motoren deutlich unterhalb von 66% liegt. Von daher lässt sich schließen, dass Otto-Motoren und Diesel-Motoren effektiver arbeiten, jedoch lässt der Wirkungsgrad nicht auf die tatsächliche Leistung des Motors rückschließen. 4. Finden Sie einen Weg, die Integrale aus (2.11.3) bzw. (2.11.1) auf die numerisch 27 berechenbaren Integrale Z Uxmax Uy · dUx Uxmin I Uy · dUx zurückzuführen. Die Funktionen V = p = ∆U ∆V −1 ∆U ∆p −1 · Ux + V0 (29) · Uy + p0 (30) könnten dabei hilfreich sein. I I pdV ∆p = · Uy + p0 dV ∆V I ∆V ∆p · Uy + p0 dUx = ∆V ∆U I I I ∆p · ∆V ∆V = Uy dUx + p0 dUx 2 ∆U ∆U I I ∆p · ∆V Uy dUx = ∆U 2 Da die Integrationsgrenzen bei der Rückführung keine Rolle spielen, verläuft die Rückführung für den Fall des nicht geschlossenen Kurvenintegrals analog. 5. Der Wirkungsgrad des Stirling-Motor kann mit einem technischen Trick maximiert werden. Im Idealfall nimmt er dann den Wirkungsgrad des CarnotProzesses an. Wie könnte der Trick funktionieren? Wie bereits in Abschnitt 2.3.2 erwähnt, müsste man die komplette Wärmeenergie, die im Stirling-Prozess bei der isochoren Abkühlung abgegeben wird speichern, und dem System bei der isochoren Erwärmung wieder zuführen. Mit Hilfe dieses technischen Trick, wäre theoretisch auch der Wirkungsgrad des Stirling-Prozess gleich dem Wirkungsgrad des Carnot-Prozess. Da dies technisch jedoch nur bedingt möglich ist, hat der Wirkungsgrad des Stirling-Prozess in der Realität einen geringeren als der des Carnot-Prozesses. 28 Literatur [1] Runge, Bernd-Uwe: Kritischer Punkt, Versuchsanleitung und Grundlagen, 2011 [2] Runge, Bernd-Uwe: Heißluftmotor, Versuchsanleitung und Grundlagen, 2011 [3] Runge, Bernd-Uwe: C. Fehlerrechnung, Skript zur Fehlerrechnung für das physikalische Praktikum an der Universität Konstanz, 2010 [4] Demtröder, Wolfgang: Experimentalphysik 1: Mechanik und Wärme, 5. Auflage, SpringerVerlag, 2008 [5] Lide, David R: handbook of chemistry and physics, 2002 Abbildungsverzeichnis 1 2 3 4 5 6 7 8 9 10 11 Isotherme am Beispiel CO2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . pV -Diagramm des Carnotschen Kreisprozess . . . . . . . . . . . . . . . . . . pV -Diagramm des Stirlingschen Kreisprozess . . . . . . . . . . . . . . . . . Funktionsweise des Stirling-Motor . . . . . . . . . . . . . . . . . . . . . . . Kurven der aufgezeichneten Isotherme für SF6 . . . . . . . . . . . . . . . . . . aufgezeichnete Dampfdruckkurve für SF6 . . . . . . . . . . . . . . . . . . . . . aufgezeichneter Stirlingscher Kreisprozess als Kältemaschine . . . . . . . . . aufgezeichneter Stirlingscher Kreisprozess als unbelastete Wärmekraftmaschine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . aufgezeichneter Stirlingscher Kreisprozess als belastete Wärmekraftmaschine mechanische Leistung Pmech des Stirling-Motor in Abhängigkeit der Frequenz ν . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . elektrische Leistung Pmech des Stirling-Motor in Abhängigkeit der Frequenz ν 5 8 11 12 15 17 19 19 20 24 25 Tabellenverzeichnis 1 2 3 Dampfdruck des SF6 auf Höhe der Maxwell-Geraden . . . . . . . . . . . . . Messwerte für Frequenz ν bei angelegtem Drehmoment M , sowie die daraus berechnete mechanische Leistung Pm . . . . . . . . . . . . . . . . . . . . . . . Messwerte für Frequenz ν und Spannung U bei angelegtem Widerstand R, sowie die daraus berechnete elektrische Leistung Pm . . . . . . . . . . . . . . 29 17 24 24