Loesung4

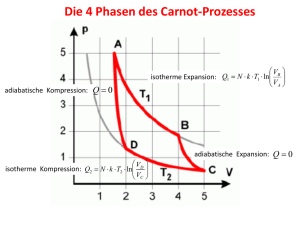
Übungen zur Physik II PHY 121, FS 2017
Abgabe: Dienstag, 28. März 1200
Serie 4
Kreisprozess = cycle
Wirkungsgrad = efficiency
Reversibel = reversible
Reservoir = reservoir
Reversibler Ersatzprozess = equivalent reversible process
Wärmekraftmaschine = (heat) engine
Entropie = entropy
Irreversibel = irreversible
Enthalpie = enthalpy
Allgemeine Fragen
1. Beschreibe den Arbeitsprozess einer Wärmekraftmaschine.
Antwort:
Eine Wärmekraftmaschine ist eine Maschine die Wärme in mechanische Arbeit umwandelt. Dabei durchläuft sie einen Kreisprozess,
welcher ein periodisch ablaufender Prozess ist, der nach einer Reihe
von Zustandsänderung wieder den Ausgangszustand erreicht. Während dieses Prozesses entnimmt eine Arbeitssubstanz Wärme aus
einem heissen Reservoir. Beim Abkühlen und Abgeben der Restwärme an ein kälteres Reservoir wird Arbeit geleistet. Verbrennungsmotoren und Dampfmotoren sind Beispiele für Wärmekraftmaschinen. Das Gegenteil wäre eine Wärmepumpe. Hier läuft der
Kreisprozess entgegen der Richtung der Wärmekraftmaschine. Als
Beispiel für den spezifischen Ablauf eines Arbeitsprozesses siehe
Frage 3. der Carnot-Prozess.
p
T2
1
2
T1
V
2. Nenne einige Beispiele für reversible und irreversible Prozesse. Was ist ein reversibler Ersatzprozess?
Antwort:
Ein Prozess ist reversibel, wenn bei seiner Umkehr der Ausgangszustand wieder erreicht wird, ohne dass
Änderungen in der Umgebung zurückbleiben.
Man kann drei Bedingungen zusammenfassen:
- Es darf keine mechanische Energie aufgrund von Reibung, viskosen Kräften oder anderen dissipativen
Effekten in Wärme umgesetzt werden.
- Wärmeübertragung zwischen Gegenständen darf nur bei einer infinitesimal geringen Temperaturdifferenz auftreten.
- Alle Teilvorgänge des Prozesses müssen reversibel ablaufen, sodass sich das System stets in einem
Gleichgewichtszustand oder in einer infinitesimalen Abweichung davon befindet.
Die Entropie ist für reversible Prozesse konstant (∆S = 0). Ein Beispiel für solch einen Prozess ist der
vollkommen elastische Stoss.
Ein Vorgang ist irreversibel, wenn seine Umkehr zum Ausgangszustand nur unter äusserer Einwirkung
möglich ist, wobei eine Veränderung in der Umgebung zurückbleibt.
Genau betrachtet sind alle Prozesse in der Natur und der Technik irreversible Prozesse (z.B.: ein Glas
das zerbricht, die Reibung oder die Durchmischung von Gasen oder Flüssigkeiten). Einige Prozesse können unter gewissen Einschränkungen und Vereinfachungen jedoch idealisiert und als reversible Prozesse
behandelt werden.
Beispiele für irreversible Prozesse sind:
1
- chemische Reaktionen, die von selbst ablaufen: Wasserstoff verbindet sich mit Sauerstoff zu Wasser. Für
die Zersetzung von Wasser in seine Bestandteile muss jedoch Energie aufgewendet werden.
- Diffusion: Stoffe (Gase) breiten sich aufgrund eines Konzentrationsgefälles so lange aus, bis die Konzentration räumlich konstant ist. Konzentrationsunterschiede dagegen bauen sich nicht von selbst auf.
Die Entropie ist eine Zustandsgrösse, d.h. dass die Entropieänderung ∆S = S2 − S1 bei einem Prozess
zwischen den Zuständen 1 und 2 prozessunabhängig ist. Damit kann man einen beliebigen reversiblen
Prozess, ein sogenannter reversibler Ersatzprozess, statt des ursprünglichen irreversiblen Prozesses zur
Berechnung von ∆S nehmen.
3. Was ist Enthalpie?
Antwort:
Enthalpie ist eine zusammengesetzte (Hilfs-)Zustandsgrösse die sehr oft das Rechnen vereinfacht resp.
erleichtert. Sie setzt sich aus der Summe der innerer Energie und Verdrängungsarbeit zusammen:
H =U +p·V
(0.1)
dH = dU + pdV + V dp
(0.2)
Das totale Differential der Enthalpie lautet:
Für Zustandsänderungen bei konstantem Druck vereinfacht sich der Ausdruck zu:
dH = dU + pdV = dQ = mcp dT.
(0.3)
4. Was ist Entropie?
Antwort:
Entropie ist eine extensive Zustandsgrösse und beschreibt die Unordnung in einem System. Die Entropieänderung kann über die Wärmeänderung definiert werden.
dS =
δQ
T
(0.4)
Für reversible Prozesse ist dS = 0 und für irreversible Prozesse ist dS > 0. Damit ist die Entropie ein
Mass für die Irreversibilität (Nichtumkehrbarkeit) eines Prozesses.
5. Diskutiere den Carnot-Prozess im pV -Diagramm.
Antwort:
Carnot Prozess: Dieser Prozess ist ein Gedankenexperiment, bei dem man ein thermodynamisches System eines idealen Gases durch Expansion und nachfolgende
Kompression zwei isotherme und zwei adiabatische Prozesse durchlaufen lässt. Dabei sind alle Prozesse reversibel und es geht keine Energie durch Reibung, Turbulenzen oder Ähnlichem verloren. Wir betrachten 1 mol
des idealen Gases:
2
- Isotherme Expansion 1→2: Aufnahme von Q12 aus heissem Reservoir mit T1
∆U12 = 0
Z
(0.5)
V2
p · dV = −W12
Q12 =
(0.6)
V1
Q12 = R · T1 · ln
V2
V1
(0.7)
- Adiabatische Expansion 2→3: System ist thermisch isoliert
Q23 = 0 =⇒ ∆U23 = U (T2 ) − U (T1 ) = W23
- Isotherme Kompression 3→4: Abgabe von Q34 an kälteres Reservoir mit T2
V3
= W34
−Q34 = R · T2 · ln
V4
(0.8)
(0.9)
- Adiabatische Kompression 4→1: System ist thermisch isoliert
Q41 = 0 =⇒ ∆U41 = U (T1 ) − U (T2 ) = W41 = −W23
(0.10)
Gesamtbilanz:
Für einen Kreisprozess gilt ∆U = 0. Damit folgt:
∆U = ∆U12 + ∆U23 + ∆U34 + ∆U41 = 0.
(0.11)
Die vom System geleistete Arbeit W23 wird der inneren Energie entnommen (Q23 = 0). Sie ist gleich der
in das System hineingesteckten Arbeit W41 . Somit geben nur die isothermen Prozesse einen Nettobeitrag
Wtot = W12 + W34 .
V1
V3
−(Q12 + Q34 ) = W12 + W34 = R · T1 · ln
+ R · T2 · ln
(0.12)
V2
V4
Die beiden adiabatischen Teilprozesse ergeben:
T1 · V2κ−1 = T2 · V3κ−1
(0.13)
T1 · V1κ−1 = T2 · V4κ−1
(0.14)
und durch Dividieren der beiden Gleichungen folgt damit (achte auf die Indizes):
V3
V3
V1
V2
=
→ ln
= −ln
V1
V4
V4
V2
Benutzt man dies in der Gleichung für die gesamte Arbeitsdifferenz erhält man:
V1
= −WSystem .
Wtot = −Qtot = R · (T1 − T2 ) · ln
V2
(0.15)
(0.16)
Die totale Nutzarbeit ist auch gleich der Fläche, die im Diagramm von dem Kreisprozess aufgespannt
wird. Mit der Definition vom Wirkungsgrad folgt:
ηCarnot =
|Abgegebene Arbeit (Nutzarbeit)|
WSystem
T1 − T2
=
=
.
Zugeführte Wärme
Q12
T1
3
(0.17)
6. Was beschreibt der thermische Wirkungsgrad?
Antwort:
Der Wirkungsgrad ist ein Mass für die Effizienz von Energieumwandlung und Energieübertragung. Es
ist eine dimensionslose Grösse und beschreibt das Verhältnis zwischen nutzbarer Energie und zugeführter
Energie:
Enutzbar
η=
(0.18)
Ezugeführt
Der thermische Wirkungsgrad beschreibt den Anteil der geleisteten Arbeit pro aufgenommener Wärme:
Wärmekraftmaschine: ηW K =
Wärmepumpe: ηW P =
Generell gilt ηW K ≤ ηCarnot < 1 bzw.
1
ηW P
Wout
Qin
(0.19)
Qout
Win
(0.20)
≤ ηCarnot < 1 aufgrund des 2. Hauptsatzes.
Aufgaben
1 p-V-Diagramm [1P]
Die Figur zeigt vier Zustände a, b, c, d im p-V-Diagramm eines idealen
Gases. Die Zustände a und c liegen auf einer Isotherme.
(a) [0.25P] Charakterisieren Sie die gezeichneten Prozesse a-b, b-c,
c-d, d-a sowie a-c.
(b) [0.5P] Stellen Sie den Kreisprozess a-b-c-d-a im p-T- und im T-VDiagramm dar.
(c) [0.25P] In welchem Diagramm lässt sich die geleistete Arbeit gut
ablesen und wie lässt sie sich ablesen?
Lösung
(a) Isobare Zustandsänderung: a-b, c-d,
Isochore Zustandsänderung: b-c, d-a,
Isotherme Zustandsänderung: a-c.
(b)
T
p
a
p2
T3
b
p1
b
a
d
c
T2
c
T1
T1
T2
T3
d
V1
T
V2
V
(c) Im p-V-Diagramm lässt sich die geleistete Arbeit dW = −p dV gut ablesen. Sie entspricht gerade der
Fläche unter der Kurve.
4
2 Kreisprozess [3P]
Gegeben sei der folgende reversible Kreisprozess für ein ideales Gas:
A → B isobar, B → C isochor, C → A isotherm.
(a) [0.5P] Zeichnen Sie den Kreisprozess in einem P-V Diagramm.
(b) [2P] Überlegen Sie welche totale Entropie- und Enthalpieänderung Sie für diesen Kreisprozess erwarten.
Leiten Sie dann die Entropie- und Enthalpieänderung für jeden Schritt des Kreisprozesses her.
(c) [0.5P] Geben Sie die totale Entropie- und Enthalpieänderung an. Entspricht das Ergebnis den Erwartungen?
Lösung
(a)
Abbildung 1: p-V Diagramm des oben beschriebenen Kreisprozesses.
(b) Da der Prozess geschlossen (Kreisprozess) und reversibel und das Gas ideal ist, erwartet man keine Änderung der Entropie und Enthalpie, was wir zeigen wollen. Aus dem Diagramm lesen wir dass gilt pA = pB ,
VB = VC und TC = TA .
- Entropie:
dU − δW
dT
dV
δQ.
rev
=
= cv n
+p
T
T
T
T
dT
dV
= cv n
+ nR
T
V
dT
dp
= cp n
− nR
T
p
dS =
(2.1)
(2.2)
(2.3)
Im letzten Schritt wurde cp = cv + R und die ideale Gasgleichung benutzt.
p · V = nRT
nRT
p
nRdT
nRT
V dT
V dp
dV =
− 2 dp =
−
p
p
T
p
dV
dT
dp
=
−
.
V
T
p
V =
5
(2.4)
(2.5)
(2.6)
(2.7)
- Enthalpie:
dH = dU + d(pV ) = dU + V dp + pdV
= cv ndT + V dp + pdV
dp
dT
= cv ndT + V dp + p −V
+V
p
T
= cp ndT
(2.8)
(2.9)
(2.10)
(2.11)
Wobei wieder die ideale Gasgleichung, dV /V = −dp/p + dT /T und cp = cv + R benutzt wurde.
Somit ergibt sich für die verschiedenen Zustandsänderungen:
Isobar:
∆S = cp · n · ln(TB /TA ) aus (2.3)
∆H = cp · n · (TB − TA ) aus (2.11)
Isochor:
∆S = cv · n · ln(TC /TB ) aus (2.2)
∆H = cp · n · (TC − TB ) aus (2.11)
Isotherm:
∆S = n · R · ln(VA /VC ) aus (2.2)
∆H = 0 aus (2.11)
(c) Wir erhalten, indem wir TC = TA , cp = cv + R und VB = VC nutzen:
∆Stot = nR ln(TB /TA ) + nR ln(VA /VC ) = nR ln(TB /TA ) + nR ln(TA /TB ) = 0
(2.12)
∆Htot = cp n(TC − TA ) = 0.
(2.13)
Die Ergebnisse für die Enthalpie und Entropie sind wie erwartet 0.
3 Stirling [3P]
In der Figur ist ein Kreisprozess an einem idealen 1- oder 2atomigen Gas im p-V dargestellt.
(a) [0.5P] Stellen Sie den gleichen Kreisprozess im p-T- und im
T-V-Diagramm dar.
(b) [0.5P] Bestimmen Sie die Molzahl n und das Volumen V2 .
(c) [2P] Bestimmen Sie für jeden Teilschritt die zu- oder abgeführte Wärme und die Arbeit, sowohl für 1-atomige als auch
für 2-atomige Gase. Wie gross ist der thermische Wirkungsgrad? Vergleichen Sie diesen mit demjenigen eines CarnotKreisprozesses zwischen zwei Reservoirs der Temperatur T1
und T2 .
Gegeben: T1 = 360 K, T2 = 300 K, p1 = 1.2 × 105 Pa, p2 = 0.8 × 105 Pa, V1 = 0.5 m3 .
Lösung
(a)
6
p
T
p1
T1
a
a
b
d
c
d
p2
b
T2
c
T2
T
T1
V1
V2
V
(b) Man benütze zur Bestimmung der Molzahl n die ideale Gasgleichung. Dies ergibt:
n=
p1 · V1
= 20 mol.
R · T1
(3.1)
Zur Bestimmung von V2 verwende man z.B. das Gesetz nach Boyle-Mariotte:
V2 = V1 ·
p1
= 0.75 m3 .
p2
(3.2)
(c) Verwende die Konvention
dU
= δQ + δW
(3.3)
δQ
> 0 Wärme wird dem System zugeführt,
(3.4)
δW
< 0 Gas leistet Arbeit
(3.5)
und betrachte die verschiedenen Prozesse:
a → b: T = T1 = konst., isotherme Expansion
Wa→b
= −nRT1 ln(V2 /V1 ) = −24.3 kJ
(3.6)
Qa→b
= −Wa→b = 24.3 kJ, da ∆U = 0.
(3.7)
Wärme wird zugeführt und System leistet Arbeit.
b → c: V = V2 = konst., isochore Abkühlung
Wb→c
Qb→c
=
0
(3.8)
=
f
∆U = nR(T2 − T1 ) = −15 kJ (1-atomig) oder − 25 kJ (2-atomig)
2
(3.9)
Wärme wird abgeführt und es wird keine Arbeit geleistet.
c → d: T = T2 = konst., isotherme Kompression
Wc→d
=
−nRT2 ln(V1 /V2 ) = +20.2 kJ
(3.10)
Qc→d
=
−Wc→d = −20.2 kJ, da ∆U = 0.
(3.11)
7
Wärme wird abgeführt und es wird Arbeit am System geleistet (Kompression des Gases).
d → a: V = V1 =konst., isochore Erwärmung
Wd→a
Qd→a
=
0
(3.12)
=
f
∆U = nR(T1 − T2 ) = 15 kJ (1-atomig) oder 25 kJ (2-atomig).
2
(3.13)
Wärme wird zugeführt und es wird keine Arbeit geleistet.
Der thermische Wirkungsgrad der Stirling-Maschine berechnet sich zu (Wab ist die Arbeit, die die Maschine ingesamt leistet und entspricht der Fläche im pV-Diagramm, die vom Prozess eingeschlossen ist):
Qzu − |Qab |
Qzu
|Wab |
=
Qzu
|Wa→b + Wc→d |
=
Qa→b + Qd→a
= 0.10 (1-atomig) oder 0.08 (2-atomig).
η=
(3.14)
(3.15)
(3.16)
(3.17)
Ein Carnot-Prozess hätte den Wirkungsgrad η = 1 − T2 /T1 = 0.17.
4 Gay-Lussac: Entropie [2P]
Ein Mol eines idealen Gases der Temperatur T ändere bei einem Gay-Lussac-Überströmungsversuch sein Volumen von Va zu Vb = 2Va . Berechnen Sie die Änderung der Entropie ∆S = Sb − Sa , indem Sie einen geeigneten
reversiblen Ersatzprozess aussuchen.
Lösung
Der reversible Ersatzprozess für den Gay-Lussac Überströmungsversuch ist die isotherme Expansion in infinitesimalen Schritten. Für diesen Prozess gilt:
dU = 0.
(4.1)
Daraus folgt:
dQ = −dW = p · dV
(4.2)
Für die Entropie gilt dann:
dQ
p
dV
= dV = n · R ·
.
T
T
V
Im letzten Schritt wurde die ideale Gasgleichung verwendet. Damit ergibt ∆S = Sb − Sa :
Z b
dV
Vb
J
∆S = Sb − Sa =
n·R·
= n · R · ln
= n · R · ln(2) = 5.76 > 0
V
V
K
a
a
dS =
(4.3)
(4.4)
mit Vb = 2Va .
Für einen reversiblen Prozess gilt ∆S = 0, daher erfährt die Umgebung eine Entropieänderung (beachte das
Vorzeichen) von
∆S = −n · R · ln(2).
(4.5)
8
5 Aluminiumklotz [3P]
Ein Aluminiumklotz (m = 100 g) der Temperatur 80 ◦C wird in 1 Liter Wasser der Temperatur 20 ◦C getaucht.
Das System sei gegen aussen isoliert.
(a) [1P] Wie gross ist die Endtemperatur TE ?
(b) [2P] Berechnen Sie für diesen Temperaturausgleich die Entropieänderung des Aluminiums, des Wassers und des ganze Systems. Dabei sollen Volumenänderungen vernachlässigt werden. Begründen Sie das
Vorzeichen der totalen Entropieänderung in Worten.
Lösung
(a) Zuerst berechnen wir die Gleichgewichtstemperatur TE :
Q%
W
cW mW (TW − TE )
somit
TE =
= Q.
Al
(5.1)
= cAl mAl (TE − TAl ),
(5.2)
cW mW TW + cAl mAl TAl
= 21.3◦ C
cW mW + cAl mAl
(5.3)
mit cW = 4182 J/(kg·K), cAl = 897 J/(kg·K) und ρW = 1.0 g/cm3 .
R E δQ.
(b) Suche nach einem reversiblen Weg, um SE − SA = A Trev zu berechnen: Der Aluminiumklotz wird
sukzessive mit einer Serie von Reservoiren mit jeweils infinitesimalen Temperaturunterschieden dT in
Kontakt gebracht, so dass in jedem Schritt dem Klotz reversibel Wärme entzogen wird. Analog für das
Wasser. Berechne die einzelnen Entropieänderungen:
Z TE
TE
dT
∆SAl =
= cAl mAl ln
cAl mAl
= −16.32 J/K < 0
(5.4)
T
TAl
TAl
Z TE
TE
dT
∆SW =
cW mW
= cW mW ln
= 17.93 J/K > 0
(5.5)
T
TW
TW
⇒∆Stotal = SE − SA = ∆SW + ∆SAl = 1.62 J/K > 0.
(5.6)
Beachte, dass |∆SAl | < |∆SW |, da der Wärmeentzug bei höheren Temperaturen stattfindet als die Wärmezufuhr.
30. März 2017
9