Document

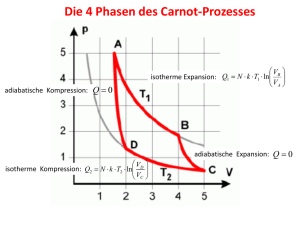
Erster Hauptsatz der Thermodynamik
∆U = ∆Q + ∆W
U : Innere Energie
Beispiel: Ball
Innere Energie: Thermische Bewegungsenergie der Gasteilchen.
Nicht die kinetische Energie, die der Ball besitzt wenn er sich als Ganzes
bewegt und nicht die potentielle Energie aufgrund seiner Lage im
Gravitationsfeld der Erde.
Vorzeichen von ∆Q und ∆W :
positiv für dem System zugeführte Wärmemenge oder Arbeit
negativ für dem System entzogene Wärmemenge oder Arbeit
Erhaltung der Energie:
In einem abgeschlossenen System, in dem sich beliebige
mechanische, optische, thermische, elektrische oder chemische
Vorgänge abspielen, bleibt die Gesamtenergie erhalten.
Zustandsgrößen bzw. Zustandsfunktionen
Ideales Gas: Zustand wird charakterisiert durch die Größen
Temperatur, Druck und Volumen.
Die Vorgeschichte spielt keine Rolle, der Zustand des Gases ist
unabhängig von dem Weg auf dem er erreicht wurde.
Weitere Zustandsgröße: Innere Energie U
Die Arbeit und die Wärmemenge sind keine Zustandsgrößen:
p
A
Weg 1:
Adiabate
Weg 2: ∆Q2 ≠ 0,
∆W2 ≠ 0
∆W2 ≠ ∆W1
∆Q1 = 0,
∆W1 ≠ 0
B
V
Reversible Zustandsänderung:
Vorgang, der durch eine infinitesimale Veränderung einer Variablen
umgekehrt werden kann.
Beispiel:
pa
pa
p a ≈ pi
pi
pi
pa = pi + dp
pi = pa + dp
Gas wird komprimiert
Gas expandiert
Das System (Gas) befindet sich mit seiner Umgebung im Gleichgewicht.
Anwendungen des ersten Hauptsatzes auf ideale Gase
Isobarer Prozess:
Einem Gas wird bei konstantem Druck die Wärmemenge ∆Q zugeführt.
• Erhöhung der inneren Energie ∆U
• Verrichtung von Arbeit durch Volumenvergrößerung gegen den
äußeren Druck ∆W = − p∆V
⇒ ∆Q = ∆U + p∆V
Isochorer Prozess:
Das Volumen ist konstant. Es wird keine Arbeit verrichtet.
⇒ ∆Q = ∆U = CV ⋅ ∆T
Isothermischer Prozess:
Die Temperatur ist konstant, d.h. ∆U = 0.
⇒ ∆Q = −∆W = p∆V
Reversibler adiabatischer Prozess:
Dem Gas wird weder Wärme zugeführt oder entzogen, d.h. ∆Q = 0.
⇒ ∆U = ∆W = − p∆V
ideales Gas ⇒ keine Kräfte zwischen den Gasteilchen
⇒ die innere Energie ist vom Volumen unabhängig (ohne Arbeitsverrichtung)
⇒ ∆U =C V ⋅∆T = − p∆V und mit pV = υRT folgt: CV ∆T = −
υRT
V
∆V
Für beliebig kleine Volumen- und Temperaturänderungen:
T
V
dT
dV
T
V
dT
dV
CV
+ υR
= 0 ⇒ CV ∫
= −υR ∫
⇒ CV ln = −υR ln
T
V
T0
V0
T T
V V
T
V , und mit C p = κ
Mit C p − CV = υR folgt: CV ln
= −(C p − CV )ln
CV
T0
V0
0
0
T
V
V 
T
⇒ ln = (1 − κ ) ln
⇒ ln = ln 
T0
V0
T0
 V0 
κ
Mit T = pV /(υR) folgt: pV = const
(1−κ )
⇒
TV (κ −1) = const
Poisson Gesetz mit dem
Adiabatenexponenten κ
Adiabaten und Isothermen
p
V
Carnotscher Kreisprozess
p
1:
2:
3:
4:
1
4
2
3
V
isotherme Expansion
adiabatische Expansion
isotherme Kompression
adiabatische Kompression
1: Isotherme Ausdehnung des idealen Gases
Ausgangszustand: p1 , TW , V1 , U 1
Das Gas nimmt die Wärmemenge Q1 auf und leistet die Arbeit W1 .
Endzustand: p2 < p1 , TW , V2 > V1 , U 1
mit p = υRTW / V
Geleistete Arbeit: ∆W1 = − p ⋅ ∆V = − ∆Q1
∆V
⇒ ∆W1 = −υRTW
V
⇒ W1 = −υRTW
V2
V2
dV
=
−
υ
RT
ln
= −Q1
∫ V
W
V1
V1
2: Adiabatische
Ausdehnung des idealen Gases
.
Ausgangszustand: p 2 , TW , V2 , U 1
Es findet keine Wärmezufuhr statt, das Gas verrichtet die Arbeit W2 .
Endzustand: p3 < p2 , TK , V3 > V2 , U 2 <U 1
Es gilt: TW V2
κ −1
= TK V3
κ −1
.
Geleistete Arbeit: ∆W2 = ∆U = − p∆V =C V ⋅∆T
Da CV = const gilt: W2 = CV (T K −TW ) = −CV (T W −TK )
3: Isotherme Kompression des idealen Gases
Ausgangszustand: p3 , TK , V3 , U 2
Dem Gas wird die Arbeit W 3 zugeführt und es gibt die Wärmemenge Q2
an das kalte Reservoir ab.
Endzustand: p4 > p3 , TK , V4 < V3 , U 2
Zugeführte Arbeit: W3 = −υRTK
V4
V4
dV
=
−
υ
RT
ln
= −Q2
∫ V
K
V3
V3
4: Adiabatische Kompression des idealen Gases
Ausgangszustand: p 4 , TK , V4 , U 2
Es findet kein Wärmeübertrag statt, dem Gas wird die Arbeit W4 zugeführt.
Endzustand: p1 > p4 , TW , V1 < V4 ,U 1 >U 2
Es gilt: TK V4
κ −1
κ −1
= TW V1
. Zugeführte Arbeit: ∆W4 = ∆U = − p∆V =C V ⋅∆T
Da CV = const gilt: W4 = CV (T W −TK )
Insgesamt geleistete Arbeit: W = W1 + W2 + W3 + W4
V
V2
V
V
− υRTK ln 4 = −υRTW ln 2 + υRTK ln 3
V1
V3
V1
V4
V3 V2
κ −1
κ −1
=
und TK V4
= TW V1
folgt:
V4 V1
mit W2 = −W 4 gilt: W = −υRTW ln
mit TK V3
κ −1
= TW V2
κ −1
und somit W = (TK − TW )υ R ln
V2
V2
W
=
(
T
−
T
)
υ
R
ln
= Q1 − Q2
⇒
W
K
V1
V1
Unter dem Wirkungsgrad η einer Maschine (Kreisprozess) versteht man
den Quotienten aus der gewonnenen mechanischen Arbeit W und der
zugeführten Wärmemenge Q1 :
η=
W Q1 + Q2 Q1 − Q2 TW − TK
T
=
=
=
= 1− K
Q1
Q1
Q1
TW
TW
Beispiel Dampfmaschine:
TW = 673 K (~400 °C)
TK = 323K (~50 °C)
⇒ η ≈ 52%
(maximal möglicher Wirkungsgrad,
wenn die Dampfmaschine eine
reversibel arbeitende CarnotMaschine wäre)
Erfahrungstatsachen:
• Ein hüpfender Ball bleibt irgendwann liegen.
• Eine Pendelschwingung hört irgendwann auf.
• Ein Gas dehnt sich in jedes zur Verfügung stehende Volumen aus.
• Zucker löst sich im Kaffee.
• Ein Ziegel fällt vom Dach.
• Gegenständen kühlen sich in kalter Umgebung ab.
Was bestimmt die Richtung spontaner Vorgänge?
Es würde dem 1. Hauptsatz nicht widersprechen, wenn die Prozesse in
umgekehrter zeitlicher Abfolge stattfinden würden.
Qualitätsminderung von Energie: Die Gesamtenergie wird stärker
ungeordnet verteilt, das Vermögen Arbeit mit der Energie zu leisten nimmt
ab.
Eine weitere Zustandsgröße: Entropie S
Thermodynamische Definition: ∆S =
∆Qrev
T
Die Änderung der Entropie ∆S ist gleich der bei einer reversiblen
Zustandsänderung aufgenommenen Wärmemenge ∆Qrev
dividiert durch die Aufnahmetemperatur T .
Berechnung der Entropie bei einer isothermen Expansion (von V1 nach V2 )
eines idealen Gases:
Der Weg muss reversibel sein!
V2
V2
V2
1
1
1
υRT
V2
∆W = − ∫ pa dV ≈ − ∫ pi dV = − ∫
dV = −υRT ln
V
V1
V
V
V
1. Hauptsatz: ∆U = 0 (isotherme Zustandsänderung) ⇒ ∆W = −∆Qrev
V2
∆Qrev
V2
Entropie: ∆S =
= υR ln
V1
T
V1
Die Entropieänderung ∆S ist positiv. Die Entropie S hat also zugenommen (im
System!). Reversibler Prozess: In der Umgebung hat die Entropie um ∆S
somit ∆Qrev = υRT ln
abgenommen.
Zum Vergleich: Irreversibler Weg
V2
Spontane Expansion ins Vakuum: pi >> pa , p a = 0 ⇒ ∆W = − ∫ p a dV = 0
V1
Ideales Gas: Keine Wechselwirkung zwischen den Teilchen, somit ändert
sich die innere Energie nicht bei der Expansion.
⇒ ∆U = 0 d.h. nach dem 1. Hauptsatz ist auch ∆Qirr
∆Qirr
=0
=0 ⇒
T
Die Entropie ist eine Zustandsgröße!
Entropieänderung ist auch hier: ∆S = υR ln
V2
>0
V1
∆Qirr
Die Entropieänderung darf also nicht über die bei einem irreversiblen
∆S >
Vorgang tatsächlich aufgenommene Wärmemenge berechnet werden!
T
Irreversibler Prozess: In der Umgebung hat die Entropie nicht abgenommen.
Es gibt keine Kompensation, d.h. die Gesamtentropie (System und Umgebung)
hat zugenommen.
2. Hauptsatz: Die Entropie eines isolierten Systems nimmt bei einem spontanen
Vorgang zu, bei einem reversiblen Vorgang bleibt sie konstant.
Der Wirkungsgrad einer Carnot – Maschine (reversibler Kreisprozess)
und die Entropie
η=
⇒
Q1 + Q2 TW − TK
=
Q1
TW
⇒
Q2
T
=− K
Q1
TW
Q1 Q2
+
= 0 = ∆S ges = ∆S1 + ∆S 2
TW TK
maximal zu entziehende Arbeit:
W Q1 − Q2 TW − TK
TK
η=
=
=
= 1−
Q1
Q1
TW
TW
 T
Wmax = Q1 − Q2 = Q1 ⋅ 1 − K
 TW

 = Q1 ⋅η Carnot

2. Hauptsatz (Thomson): Es ist unmöglich, eine zyklisch arbeitende Maschine
zu konstruieren, die keinen anderen Effekt produziert als die Entnahme von
Wärme aus einem Reservoir und die Verrichtung des gleichen Betrages an
Arbeit.
Entropieänderungen in isolierten Systemen: Wärmeübertrag von einem
wärmeren in ein kälteres Reservoir
TW
TK
Q
Spontaner Wärmefluß ist irreversibel. Zur Berechnung der
Entropieänderung muss die Wärmemenge reversibel übertragen werden.
TW
Q
TW
TK
Reversible adiabatische
Expansion des Gases,
die Temperatur sinkt.
Reversible isotherme
Expansion des Gases, die
Temperatur des sehr
großen Reservoirs bleibt
näherungsweise konstant.
Q
TK
Reversible isotherme
Kompression des Gases,
die Temperatur des sehr
großen Reservoirs bleibt
näherungsweise konstant.
Warmer Behälter: ∆SW = −
Q
TW
Entropieänderung beider Behälter:
Kalter Behälter: ∆S K =
Q Q
∆S =
−
TK TW
Q
TK
Die Entropie hat
zugenommen.
Reversibler Prozess: Die Entropie des Gases hat um ∆S abgenommen,
insgesamt ist die Entropie konstant geblieben.
Irreversibler
Wärmeübergang:
TW
Q
TK
Q
Q
−
Entropieänderung der Reservoire ist die Gleiche: ∆S =
, aber die
TK TW
Kompensation fehlt.
Die Entropie des isolierten Systems hat sich durch den spontanen,
irreversiblen Vorgang vermehrt.
Beispiel: Kreisprozesse
Fall 1:
B
Weg 1 und Weg 2 sind reversible Wege
Weg 2
zwischen den Zuständen A und B.
Kreisprozess: A → B → A
Weg 1
Beispiel für ein ideales Gas:
Weg 1: Isotherme, reversible Expansion A → B
Weg 2: Isotherme, reversible Kompression B → A
T
= υR ln
VB und
VA
∆Qrev , n
n =1
Tn
Gesamte Entropieänderung: ∆S = ∑
A
∆Qrev ,1
2
∆Qrev , 2
T
∆S = ∆S A→ B + ∆S B → A = υR ln
= υR ln
VA
V
= −υR ln B
VB
VA
VB
V
− υR ln B = 0
VA
VA
⇒ ∆S ( reversiblerKreisprozess) = 0
Fall 2: Weg 1 ist ein irreversibler und Weg 2 ist ein reversibler Weg
zwischen den Zuständen A und B.
Beispiel für ideales Gas:
Weg 1: freie Expansion ins Vakuum A → B
Weg 2: Isotherme, reversible Kompression B → A
∆Qn ∆Qirr ∆Qrev
V
=
+
= 0 + ∆S B → A = υR ln A < 0
n =1 Tn
T
T
VB
2
∑
VA
υR ln = ∆S B → A = −∆S A→ B < 0 ⇒ ∆S A→ B > 0
VB
Auf dem irreversiblen Weg gibt es keine Kompensation der Entropieänderung in
der Umgebung Irreversible, spontane Vorgänge sind mit einer
Entropiezunahme verbunden!
Clausiussche Ungleichung für einen Kreisprozess: ∑
n
∆ Qn
≤0
Tn
Statistische Definition der Entropie
V1
1
Vn = V1
n
Vn
Im Volumen V1 befinden sich N Gasteilchen. Wie groß ist die Wahrscheinlichkeit P,
1
n
dass sich alle Gasteilchen im Teilvolumen Vn = V1 befinden?
Nur 1 Teilchen ist im Kasten:
bei n = 1 , d.h. V1 = V1
ist P1 = 1
bei n = 2 , d.h. V2 = V1 / 2 ist P1 = 1 / 2
bei n = 3, d.h. V3 = V1 / 3 ist P1 = 1 / 3
1
n
Allgemein: Für Vn = V1
ist P1 =
1
.
n
Für zwei Teilchen im Kasten, die sich im
Teilvolumen befinden sollen gilt:
1
P2 = P1 ⋅ P1 =  
n
2
Für N Teilchen im Kasten, die sich im Teilvolumen befinden sollen gilt:
N
V 
1
PN =   =  n 
n
 V1 
N
Wir betrachten zwei unterschiedliche Zustände A und B:
Zustand A:
1
Alle Teilchen befinden sich im Teilvolumen V3 = V1
3
Zustand B:
1
Alle Teilchen befinden sich im Teilvolumen V2 = V1
2
Wie viel mal wahrscheinlicher ist es, dass alle Teilchen im Zustand B sind als
im Zustand A?
N
 V2 
 
N
 V2 
PB  V1 
=
w=
=  
N
PA  V3 
 V3 
 
 V1 
ln w = N ln
V2
V
R V
= υN A ln 2 = υ ln 2
V3
V3
k V3
⇒ k ln w = υR ln
w : thermodynamisches Wahrscheinlichkeitsverhältnis
V2
= ∆S
V3
Übungen:
1. Kann ein System Wärme aufnehmen, ohne dass sich seine innere Energie
ändert?
2. Ein Gas ändert seinen Zustand
reversibel von A nach C.
Die vom Gas verrichtete Arbeit ist
• am größten für den Weg A B C
• am kleinsten für den Weg A C
• am größten für den Weg A D C
• für alle Wege gleich groß
p
A
B
D
C
V
3. Welches S-T-Diagramm gehört zum Carnotschen Kreisprozess?
S
S
T
S
T
T
1. Hauptsatz (nach Wilhelm Busch)
Hier strotzt die Backe voller Saft,
da hängt die Hand, gefüllt mit Kraft.
Die Kraft, infolge der Erregung,
verwandelt sich in Schwingbewegung.
Bewegung, die in schnellem Blitze
zur Backe eilt, wird hier zur Hitze.
Ohrfeige nennt man diese Handlung,
der Forscher nennt es Kraftverwandlung.