Glossar

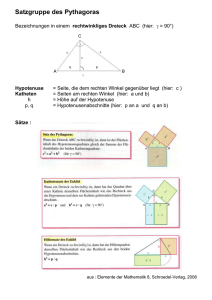
1 Dreiecke - der Satz des Pythagoras
Theorem 1.1.
(a) (Satz von Pythagoras) Sei
ABC
ein
rechtwinkliges Dreieck mit Hypotenuse der
Länge
c
(gegenüber dem rechten Winkel)
a
und Katheten der Länge
c2
a2
und
b.
Dann gilt
b2 .
(b) (Umkehrung des Satzes von Pythagoras) Sei
ABC
ein Dreieck mit "Hypotenu-
c und weiteren Kantenlängen a und b, wobei gilt, dass
b2 , dann ist der der Hypotenuse gegenüberliegende Winkel ein rechter Winkel.
se"(längste Kante) der Länge
c2
a2
Buch I beginnt mit "Denitionen", z.B.
I. Ein Punkt ist etwas, das keine Teile hat.
II. Eine Strecke ist Länge ohne Breite.
III. Die Enden einer Strecke sind Punkte.
X. Wenn
eine
Strecke,
die
auf
einer
ande-
ren Strecke steht, die angrenzenden Winkel gleich macht, heiÿen diese rechte Winkel
und die beiden Strecken heiÿen senkrecht zueinander.
XI. Ein stumpfer Winkel ist ein Winkel, der gröÿer ist als ein rechter Winkel.
XII. Ein spitzer Winkel ist ein Winkel, der kleiner ist als ein rechter Winkel.
Axiome
I. Zwischen zwei Punkten gibt es eine Strecke.
II. Eine Strecke (endlich) ist Teil einer Geraden (unendlich).
III. Zu jeder Wahl von Mittelpunkt und Radius gibt es einen Kreis..
Denition 1.2.
A
wobei
Sei
K
ein Körper. Ein aner Raum über
H eine Menge ist, V
ein
K -Vektorraum
und
K ist
τ : V
pA, V, τ q,
ÝÑ AbbpA, Aq eine
ein Tripel
Abbildung, für die gilt:
@u P V ist τu : τ puq : A Ñ A bijektiv
@p, q P A, D!u P V : τuppq q (V operiert einfach transitiv)
@u, v P V @p P A : τu v ppq τupτv ppqq (τ ist ein Gruppenhomomorphismus)
Formal erlaubt man, um Fallunterscheidungen auszuschlieÿen, auch
Raum.
0
v
v ñ τ0pτv ppqq τv ppq ñ τ0 id
1
A
H, als anen
Die Elemente von A heiÿen Punkte.
Die Dimension von
A
ist deniert als
q bei gewähltem p,Ñq P A erlaubt es, u als
"Verbindungsvektor"von p und q zu betrachten. Bezeichnung pq u. Das heiÿt, es gibt
AAÑV
eine Abbildung
mit folgenden Eigenschaften:
Die Eindeutigkeit von
u
PV
dimA : dimV.
mit
τu ppq
Ñ
pp,qqÞÑpq
Für
p, q, r
drei paarweise verschiedene Punkte gilt:
Ñ
pq
Ñ
qr
Ñ
pr
Ñ
@p P A @u P V D!q P A mit u pq
.
Und
Proposition 1.3.
Dann ist
A
Sei
K
ein Körper,
A
H eine Menge und V
genau dann ein aner Raum, wenn es eine Abbildung
so dass gilt:
Ñ
@p, q, r P A paarweise verschieden: pq
Ñ
@p P A @u P V D!q P A : u pq,
Ñ
qr
K Vektorraum.
AAÑV
ein
Ñ
pp,qqÞÑpq
gibt,
Ñ
pr
u 0 ô p q.
Dritte äquivalente Denition von anem Raum: Es gibt eine Abbildung
V
A Ñ A , so dass gilt:
pu,pqÞÑq:p
u
pu vq pp uq v @p P A, u, v P V .
(A 2) p
0 p @p P A.
(A 3) p
u p für ein p P A ñ u 0.
(A 4) @p, q P A Du P V : q p
u.
Denition 1.4. Ñ
Sei pA, V, τ q ein aner Raum. Eine Teilmenge B € A heiÿt aner Unterraum:ô
Dp0 P A : U : tp0q : q P B u ist ein Untervektroraum von V .
Mit dieser Denition ist B tτu pp0 q : u P U u, d.h. B ist die Bahn von p0 unter der
(A 1)
p
U.
Operation des Unterraums
Denition 1.5.
und
P
(a)
(b)
Ein angeordneter Körper ist ein Paar
eine Teilmenge von
K,
pK, P q, wobei K ein Körper ist
so daÿ gilt:
@a, b P P : a b P P, a b P P .
@a P K : a P P oder a 0 oder a P P , aber nicht zwei dieser Eigenschaften
gleichzeitig
Die Elemente von
Proposition 1.6.
(a)
(b)
1 P P,
K
d.h.
1
P
heiÿen positiv.
Sei
pK, P q ein angeordneter Körper. Dann gilt:
ist positiv.
hat Charakteristik
0,
d.h.
@n P N : n 1 :
2
n-mal
hkkkkkikkkkkj
1 ... 1
0 in K.
(c)
@a P K t0u : a2 P P.
Denition 1.7.
linearform
Sei
, ¡:
V
V
ein reeller Vektorraum. Eine symmetrische nicht-ausgeartete Bi-
V ÑR
pv1 ,v2 qÞÑ v1 ,v2 ¡
heiÿt Skalarprodukt.
pV, , ¡q bestehend aus einem reellen Vektorraum V und einem Skalarprodukt , ¡: V V Ñ R.
Proposition 1.8. Sei pV, , ¡q ein euklidischer Vektorraum. Dann gilt:
|| || : V?Ñ R ist eine Norm, d.h.
(a) Die Abbildung:
Ein euklidischer Vektorraum ist ein Paar
v
(b)
ÞÑ||v||: v,v¡
||λv|| |λ| ||v|| @λ P R, v P V.
||u v|| ¤ ||u|| ||v|| @u, v P V
||v|| 0 ô v 0
V V ÑR
Die Abbildung d :
ist eine Metrik, d.h.
pu,vqÞÑdpu,vq:||uv||
dpu, v q dpv, uq @u, v, P V (Symmetrie)
dpu, v q ¤ dpu, wq dpw, v q @u, v, w P V (Dreiecksungleichung)
dpu, v q 0 ô u v @u, v P V.
Mit dem Skalarprodukt können wir Winkel denieren durch
cosϑ :
u,v¡
||u||||v||
für
u, v
0.
Euklids Proposition I.1: Auf einer gegebenen Strecke soll ein gleichseitiges Dreieck errichtet werden.
Euklids Proposition I.2: Gegeben sind ein Punkt und eine Strecke. Aufgabe: Konstruiere eine Strecke, die den gegebenen Punkt als Endpunkt hat und gleich lang ist wie die
gegebene Strecke.
Zu Pythagoras:
3
2 Axiome und Grundbegrie
Ein Axiom wurde schon zu Euklids Zeiten als problematisch angesehen. Euklids Axiom
I.5 ist das Parallelenaxiom:
Wenn eine gerade Linie j zwei gerade Linien g und h trit, so daÿ die inneren Winkel
α und β
auf derselben Seite weniger sind als
zwei rechte Winkel, dann treen sich die beiden geraden Linien, wenn sie beliebig verlängert werden, auf der Seite der beiden Winkel
α
und
β.
Zwei
Dreiecke
ABC
und
A1 B 1 C 1
heiÿen
ähnlich, wenn sie dieselben Winkel haben.
Das Axiom von Wallis sagt: Gegeben seien ein Dreieck
existiert ein ähnliches Dreieck
A1 B 1 C 1 ,
ABC und eine Strecke DE . Dann
A1 B 1 mindestens so lang ist wie
so daÿ die Seite
DE .
Modernes Parallelaxiom:
Gegeben ist eine Gerade
P
enthält und
g
g
und ein Punkt
P
P g. Dann gibt es genau eine Gerade h, die
nicht schneidet.
Euklids Denition I.23: Parallele Geraden sind zwei Geraden in derselben Ebene, die
einander nicht schneiden.
Euklids Proposition I.27 beginnt: Gegeben
ist eine Gerade
j , die die Geraden g und h so
schneidet, daÿ die entgegengesetzten Winkel
α und β übereinstimmen.
h parallel zueinander.
Dann sind
Euklids Proposition I.16: In einem Dreieck ist der Auÿenwinkel gröÿer als der Innenwinkel und der entgegengesetzte Winkel.
Euklids Proposition I.29: Gegeben sind zwei
g und h und eine Gerade j , die g
h schneidet. Dann sind die Winkel α
β gleich.
Parallelen
und
und
Charakterisierung von Parallelen:
g ||h ô α β
4
g
und
Euklids Proposition I.31: Gegeben ist eine Gerade
eine Parallele
h
zu
g,
die den Punkt
A
g
und ein Punkt
A.
Dann existiert
enthält.
Euklids Proposition I.32:
α
δ
= Auÿenwinkel an
5
In
C
einem
β
und
ABC
Dreieck
α
β
γ
180.
gilt:
3 Hilberts Axiome
Sei E eine Menge und G € P pE q eine Menge von Teilmengen von E .
pE, Gq heiÿt Inzidenzebene, wenn die folgenden Axiome erfüllt sind:
@A, B P E mit A B D!g P G : A, B P g.
@g P G DA, B P g mit A B.
DA, B, C P E @g P G : tA, B, C u ‚ g.
Denition 3.1.
Das Paar
(I 1)
(I 2)
(I 3)
Die Elemente von
E
heiÿen Punkte, die Elemente von
G
heiÿen Geraden.
pP q Playfairs Axiom: Sei g eine Gerade, A ein Punkt mit A R g. Dann gibt es höchstens
eine Gerade h mit A P h und g X h H.
1 1
Zwei Inzidenzebenen pE, Gq und pE , G q sind zueinander isomorph :ô D Bijektion
ϕ : E Ñ E 1 , so dass ϕ eine Bijektion auf der Menge der Geraden induziert, d.h.
@g P G : ϕpgq P G1 und @g1 P G1 Dg P G : ϕpgq g1. ϕ heiÿt dann Isomorphismus.
Ein Automorphismus von pE, Gq ist ein Isomorphismus ϕ : pE, Gq Ñ pE, Gq. Die Automorphismen von pE, Gq bilden eine Gruppe.
Denition 3.2. SeipE, Gq eine Inzidenzebene. Eine Teilmenge Z € E E E heiÿt
Anordnungsrelation genau dann, wenn die folgenden Axiome erfüllt sind, wobei wir
ABC
(Z 1)
(Z 2)
pA, B, C q P Z schreiben oder "B liegt zwischen A und C ".
A B C ñ A, B, C sind drei verschiedene Punkte, die auf einer Geraden liegen,
und es gilt auch C B A.
@A B DC : A B C.
für
(Z 3) Wenn
A, B
C
und
drei verschiedene Punkte auf einer Geraden sind, dann liegt
genau einer der drei Punkte zwischen den anderen beiden.
(Z 4) (Pasch) Seien
A, B und C drei Punkte, die nicht
auf einer Geraden liegen, und g eine Gerade, die
A noch B noch C enthält. Falls g einen
Punkt D enthält, der zwischen A und B liegt,
dann enthält g entweder einen Punkt zwischen
A und C oder einen Punkt zwischen B und C ,
weder
aber nicht beides.
Denition 3.3.
A und B verschiedene Punkte.
AB : tC : A C B u Y tA, B u.
(a) Seien
(b) Seien
A, B
und
C
Die Strecke
ist deniert als
drei verschiedene Punkte, die nicht kollinear sind (d.h. nicht
auf einer Geraden liegen). Das Dreieck
Tripel
AB
ABC
ist deniert als das ungeordnete
pAB, BC, AC q. Die Punkte A, B, C heiÿen Ecken des Dreiecks, die Strecken
AB, BC
und
Theorem 3.4.
Sei
AC
heiÿen die Kanten des Dreiecks.
pE, Gq eine Inzidenzebene mit einer Anordnungsrelation. Sei g P G.
6
(a) Die Menge
E g
lässt sich schreiben als
E g
S1 Y. S2, S1 H, S2 H, so dass
gilt:
AB X g
H.
(a 2) Zwei Punkte
S2 )
in
Wir nennen
A, C
(b) Sei
(b 1)
(b 2)
T1
g
liegen beide in
S1
oder beide in
S2
genau dann, wenn
R g liegen in verschiedenen Teilmengen (einer in S1, der andere
AC X g tPunktu.
genau dann, wenn
S1
S2
und
auf derselben Seite von
Seiten von
R
A, B
(a 1) Zwei Punkte
g . Im Fall (a 1) sagen wir "A und B liegen
g ", im Fall (a 2) sagen wir "A und C liegen auf entgegengesetzten
die beiden Seiten von
g ."
A P g.
Dann ist
g tAu T1
Y. T2, T1 H, T2 H, so dass gilt:
P g tAu liegen beide in T1 oder beide in T2 genau dann, wenn A R BC .
B, D P g tAu liegen in verschiedenen Teilmengen genau dann, wenn A P BD.
B, C
und
T2
heiÿen dann die Seiten von
A
auf
g.
ÝÝÑ
Denition 3.5.
A und B seien zwei verschiedene Punkte. Der Strahl AB ist deniert
ÝÝÑ
als AB : tAu Y tC : C liegt auf der Geraden durch A und B und auf derselben Seite
von A wie B u. Der Punkt A heiÿt der Ursprung des Strahls. Ein Winkel besteht aus zwei
ÝÝÑ ÝÑ
Strahlen AB und AC , die denselben Ursprung haben, aber nicht auf derselben Geraden
liegen. Bezeichnung: ?BAC.
Das Innere eines Winkels
und
B,
C
Sei
D und B
A und C u.
und
durch
?BAC
ist die Menge
tD : D
liegen auf derselben Seite der Geraden durch
A und
liegen auf derselben Seite der Geraden
ABC ein Dreieck. Das Innere
?BAC, ?ABC, ?ACB .
des Dreiecks ist der Durchschnitt des Inneren der
Winkel
Proposition 3.6.
Sei
ABC
Proposition 3.7.
ÝAD
ÝÑ X BCDeinHPunkt
.
ein Dreieck und
im Inneren des Dreiecks. Dann gilt
In einer Inzidenzebene mit Anordnungsrelation gilt:
(a) Seien
A, B, C, D
vier verschiedene Punkte auf einer
Geraden. Dann gilt:
A B C und B C D ñ A B D
A B D und B C D ñ A B C
(b) Auf jeder Geraden liegen unendlich viele verschiedene Punkte.
(c)
@A, B, A B DC : A C B.
7
und
und
A C D.
A C D.
Sei pE, G q eine Inzidenzebene, die die Anordnungsaxiome erfüllt. Sei
€ P pE q die Menge aller Strecken in E . Eine Relation R € S S heiÿt Kongruenz
zwischen Strecken AB und CD , geschrieben AB CD , genau dann, wenn die folgenden
Denition 3.8.
S
drei Axiome erfüllt sind:
(K 1) Gegeben eine Strecke
Ursprung
D
(K 2) Aus
AB
C
AB
und ein Strahl
S,
der
hat. Dann existiert genau ein Punkt
P S, so dass AB CD.
CD und AB EF folgt CD EF. Jede Strecke ist kongruent zu sich
selbst.
(K 3) Gegeben drei Punkte
AB C
A, B, C
auf einer Geraden mit
D, E, F auf einer
Geraden mit D E F . Falls AB DE und BC EF, dann gilt auch AC DF.
und drei weitere Punkte
Denition 3.9.
S
AB
Seien
hat und alle Punkte von
der anderen Seite von
B
CD zwei
AB , der B
und
der Strahl auf der Geraden
AB
Strecken und
als Ursprung
enthält, die von
liegen. Sei
E
A
aus auf
der nach (K 1 )
S , so dass CD BE.
AE die Summe der Strecken AB
AE AB CD.
eindeutig existierende Punkt auf
Dann heiÿt die Strecke
und
CD.
Schreibweise
Denition 3.10. Seien AB und CD Strecken. Wenn es einen Punkt E gibt mit C E D,
CE , dann sagen wir AB ist kleiner als CD. Schreibweise AB CD, und
CD ist gröÿer als AB , Schreibweise CD ¡ AB .
Denition 3.11. Sei pE, G q eine Inzidenzebene, die die Anordnungsaxiome erfüllt. Sei
W die Menge aller Winkel in E . Eine Relation R € W W heiÿt Kongruenz zwischen
Winkeln ?ABC und ?DEF, geschrieben ?ABC ?DEF , genau dann, wenn die
so dass
AB
folgenden Axiome erfüllt sind:
?BAC
ÝDF
ÝÑ.
ÝDE
ÝÑ auf einer gegebenen Seite der Geraden DF , so dass ?BAC (K 4) Gegeben ein Winkel
und ein Strahl
Dann existiert genau ein Strahl
?EDF .
(K 5) Für drei Winkel
α, β
und
γ
folgt aus
αβ
und
α γ,
ist zu sich selbst kongruent.
(K 6)
pSWS q
ABC und DEF
mit AB DE, AC DF und ?BAC ?EDF .
Dann gilt: BC EF, ?ABC ?DEF und
?ACB ?DF E.
Gegeben zwei Dreiecke
In der Situation von (K 6) nennen wir die beiden
Dreiecke
ABC
und
DEF
kongruent.
8
dass
β
γ. Jeder Winkel
Denition 3.12.
?BAC ein Winkel und D ein
AC , aber auf der anderen Seite von A als C . Dann sagen wir, die Winkel ?BAC
und ?BAD ergänzen einander, und ?BAD ist der
Ergänzungswinkel = Komplementwinkel zu ?BAC.
Sei
Punkt auf der Geraden
Proposition 3.13.
?BAC
Seien
?BAD sowie ?B 1 A1 C 1 und ?B 1 A1 D1 zwei Paare
1 1 1
1 1 1
Aus ?BAC ?B A C folgt ?BAD ?B A D .
und
von einander ergänzenden Winkeln.
Proposition 3.14.
?BAC ein Winkel und der Strahl
ÝAD
ÝÑ im Inneren des Sei
1 1 1
Winkels ?BAC. Seien ?D A C ÝÝÑ
?DAC und ?B 1 A1 D1 ?BAD, und die Strahlen A1 B 1
ÝÝÑ
1 1
und A C seien auf entgegengesetzten Seiten der GeraÝÝÑ
ÝÝÑ
1 1
1 1
1 1
den A D . Dann bilden die Strahlen A B und A C einen
Ý
ÝÝ
Ñ
1
1
1
1
1
Winkel, so dass ?B A C ?BAC, und A D liegt im
?B 1 A1 C 1 .
Inneren des Winkels
Denition 3.15.
?BAC
(a) Ein Winkel
?EDF
ÝDG
ÝÑ im
ist gröÿer als
Inneren des Winkels
(b) Ein Winkel
α
heiÿt rechter Winkel
Proposition 3.16.
Denition 3.17.
?EDF , geschrieben ?BAC ?EDF oder
?BAC q genau dann, wenn ein Strahl
?EDF existiert, so dass ?BAC ?GDF.
ist kleiner als
¡ ?BAC p?EDF
Seien
α
und
α1
:ô D
Ergänzungswinkel
rechte Winkel. Dann gilt
β
zu
α
mit
α α1 .
α β.
Eine Inzidenzebene, die die Axiome (I 1) bis (I 3), (Z 1) bis (Z 4) und
(K 1) bis (K 6) erfüllt, heiÿt Hilbert-Ebene.
Die Geometrie der Hilbert-Ebene heiÿt neutrale Geometrie.
Euklid Proposition I.5: In einem gleichschenkligen Dreieck stimmen die Winkel an der Basis überein:
Denition 3.18.
Radius
MA
Seien
α β.
M
und A zwei verschiedene Punkte. Der Kreis Γ um M mit
Γ : tB : B Punkt mit M B M Au. Der Punkt M ist der
M A ist der Radius.
ist deniert als
Mittelpunkt des Kreises,
M und Radius M A, und sei Γ1 ein
1
1
1
1
Kreis mit Mittelpunkt M und Radius M A . Wenn Γ Γ (als Punktmenge), dann ist
1
M M . D.h. der Mittelpunkt eines Kreises ist eindeutig bestimmt.
Lemma 3.19.
Sei
Γ
ein Kreis mit Mittelpunkt
Denition 3.20.
Γ ein Kreis mit Mittelpunkt M und Radius M A. Ein Punkt B liegt im Inneren
Γ (oder innerhalb von Γ), wenn B M oder M B M A gilt. Ein Punkt C
liegt auÿerhalb von Γ, wenn M A M C.
(a) Sei
von
(b) Eine Gerade
ΓXg
g
ist eine Tangente an einen Kreis
Γ
aus genau einem Punkt besteht.
Ein Kreis
1
und Γ
Γ
ist tangential an einem anderen Kreis
genau einen Punkt gemeinsam haben.
9
(oder tangential an
Γ1
(oder berührt
Γ),
Γ1 ),
wenn
wenn
Γ
Proposition 3.21.
(a) Sei
g
h
ein Kreis mit Mittelpunkt
Γ
(c) An jedem Punkt
A
(d) Wenn eine Gerade
Γ
und Radius
M A.
ist
g
eine
und die Punkte von
eine Tangente an
trit sie
M
A, die senkrecht auf M A steht. Dann
g tAu liegen auÿerhalb von Γ.
die Gerade durch den Punkt
Tangente an
(b) Sei
Γ
Sei
Γ
im Punkt
des Kreises
j
Γ
einen Punkt
A.
Dann ist
h
senkrecht zu
M A.
gibt es genau eine Tangente zu
A
von
Γ
Γ.
enthält, aber keine Tangente ist, dann
in genau zwei Punkten.
Proposition 3.22.
1
(a) Seien M, M und
mit Mittelpunkt
A
M
M 1 A.
und Radius
Γ
M1
drei verschiedene kollineare Punkte. Dann gilt: Der Kreis
und Radius
MA
berührt den Kreis
Γ1
mit Mittelpunkt
Γ und Γ1 sich im Punkt A berühren, dann sind ihre Mittelpunkte
kollinear mit A.
(b) Wenn zwei Kreise
M und M 1
(c) Wenn zwei verschiedene Kreise den Punkt
A
gemeinsam haben, aber nicht tan-
gential sind, dann haben sie genau zwei Punkte gemeinsam.
pE q (oderpKKS qq. Seien Γ und Γ1 zwei Kreise, so dass Γ1 mindestens einen Punkt im
Inneren von
Γ
1
sich Γ und Γ .
enthält und mindestens einen Punkt auÿerhalb von
Proposition 3.23.
A
Eine Hilbert-Ebene erfülle
im Inneren eines Kreises
Γ.
Dann schneidet
Γ.
Dann schneiden
pE q. Die Gerade g enthalte einen Punkt
g
den Kreis
Γ.
pE q und pP q erfüllt, heiÿt Euklidische Ebene.
Euklids Proposition X.1: Seien X und Y zwei Gröÿen, X ¡ Y . Wenn man von X mindesDenition 3.24.
Eine Hilbert-Ebene, die
tens die Hälfte abzieht und vom Rest wieder mindestens die Hälfte, und diesen Prozess
wiederholt, erhält man eine Gröÿe, die kleiner ist als
Dedekindsche Schnitte:
Y.
K Y G, K H G, @x P K, y P G : x y, und G hat
.
Q
kein kleinstes Element.
Dedekinds Axiom
kein Punkt in
Punkten in
AP
oder
S
pDq: Sei g
eine Gerade und
zwischen zwei Punkten in
S . Dann gibt es genau einen
B P oder A P B.
T
S Y. T
mit
S
HT
T
@A P S, B P T
liegt und kein Punkt in
Punkt
10
g
P
so, dass
so, dass
zwischen zwei
gilt: Entweder
4 Von synthetischer Geometrie zu Koordinaten
Denition 4.1.
a und b Kongruenzklassen von
Strecken. Dann ist das Produkt a b deniert als die
Kongruenzklasse der Strecke EF in folgender Konstruktion: Sei ABC ein rechtwinkliges Dreieck mit
AB P 1 und BC P a, rechtem Winkel bei B , und
sei α : ?BAC . Sei DEF ein weiteres rechtwinkliges Dreieck mit DE P b, ?EDF α und rechtem
Winkel bei E . Dann ist EF P a b.
Seien
Proposition 4.2. Zu einer Hilbert-Ebene, die pP q erfüllt, existiert ein bis auf Isomorphie
eindeutiger angeordneter Körper
K , dessen Menge P
positiver Elemente genau die Menge
der Kongruenzklassen von Strecken in der Hilbert-Ebene mit den obigen Operationen
,
ist.
Theorem 4.3.
K 2,
Jede Hilbert-Ebene, die
wobei der angeordnete Körper
K
pP q erfüllt, ist isomorph zur Koordinatenebene
durch die Addition und Multiplikation deniert
wird.
Theorem 4.4.
Dann gilt:
Seien
ABC
und
DEF zwei
Dreiecke.
rα α1, β β 1, γ γ 1s
ñ
a
d
eb fc
,
d.h. die beiden Dreiecke sind ähnlich genau dann,
wenn alle entsprechenden Kanten proportionale Länge haben.
Proposition 4.5.
ABC
gilt
( mit
c
11
a2
b2
In einem rechtwinkligen Dreieck
c2
= Hypotenuse).
5 Koordinatenebenen
R2 seien p0, 0q, p1, 0q und n Punkte P1 pa1 , b1 q, . . . , Pn pan , bn q gegeben, sowie ein weiterer Punkt Q pα, β q. Dann
gilt: Der Punkt Q kann mit Zirkel und Lineal aus den Punkten P1 , . . . , Pn genau dann
konstruiert werden, wenn die Zahlen α und β sich aus 0, 1, a1 , . . . , an , b1 , . . . , bn durch
Theorem 5.1 (Descarters).
In der kartesischen Ebene
endlich viele Operationen der folgenden Art ergeben:
Addition, Subtraktion, Multiplikation, Division;
Lösung linearer Gleichungen;
Lösung quadratischer Gleichungen (wobei Quadratwurzeln positiver reeller Zahlen
gezogen werden dürfen.)
Proposition 5.2.
Eine reelle Zahl
αPR
ist mit Zirkel und Lineal konstruierbar genau
dann, wenn es eine Kette von Körpererweiterungen gibt:
Q K0
?
Ki Ki1 p ai q für ein ai P Ki1
ist rQpαq : Qs eine Potenz von 2.
so dass
dann
€ K1 € . . . € Kn „ R
gilt, und
α P Kn .
Wenn
α
konstruierbar ist,
Unlösbare klassische Probleme:
Würfelverdoppelung (Delisches Problem)
Winkeldreiteilung
Quadratur des Kreises
Lemma 5.3.
Mittelpunkt
In einem Kreis vom Radius
O
ein Winkel
?
α
1
sei am
gegeben. Die Strahlen
A und B . Dann hat die Sehne
2 2 cos α.
schneiden den Kreis in
AB
die Länge
d
Theorem 5.4.
Das reguläre
nau dann, wenn
n
n-Eck pn
¥ 3q ist mit Zirkel und Lineal konstruierbar ge-
die folgende Form hat
n 2r p1 . . . ps pr, s ¥ 0q,
wobei die
pi
paarweise verschiedene ungerade Primzahlen sind und jedes
Primzahl ist, d.h.
Proposition 5.5.
mit
Dk : p i 2 2
k
In der Inzidenzebene
AB ||CD, AC ||BD
Proposition 5.6
und
AD||BC
K2
.
(Satz von Pappus)
A, B, C P g
AC 1 ||A1 C und BC 1 ||B 1 C.
eine Fermat-
gibt es vier verschiedene Punkte
genau dann, wenn
2
sischen Ebene K seien Geraden
sowie Punkte
pi
1.
K
In der karte-
g und h gegeben,
A1 , B 1 , C 1 P h, so dass
1 1
Dann gilt auch AB ||A B.
und
12
A, B, C, D
die Charakteristik zwei hat.
K
ist kommutativ genau dann, wenn der Satz von Pappus gilt.
Proposition 5.7.
Sei
K
ein Körper der Charakteristik
Dann existiert eine Konguration wie im Bild:
(Dreieck ABC, D, G P AB, E, H P AC, F P BC,
?
DE ||GH ||BC, DF ||AC, EF ||AB, EG||HB q ô 2 P K.
Proposition 5.8.
relation, die
K ein Körper. Dann gibt es in K 2 genau dann eine
pZ4q erfüllt, wenn K ein angeordneter Körper ist.
Sei
pZ1q bis
(A) Gegeben Strecken
AB . . . AB
loooooooomoooooooon
n
entspricht
(D) Sei
g
AB
und
CD.
Dann existiert
¡ CD.
n P N,
Anordnungs-
so dass
pA1q @ a P P € K D n P N : n ¡ a.
eine Gerade,
zwei Punkten von
T
S Y T, S H, T H, so dass kein Punkt in S zwischen
g
liegt und kein Punkt in
T
zwischen zwei Punkten von
S.
Dann
D! P @ A P S, B P T : A P oder B P oder A P B
1
entspricht: pD q Sei K S Y T so dass @ a P S, b P T : a b. Dann D! c P K so dass
@ a P S, b P T : a ¤ c ¤ b.
Es gibt angeordnete Körper, die nicht-archimedisch sind.
Proposition 5.9.
Sei
K
ein angeordneter Körper, der
(als angeordneter Körper) zu einem Teilkörper von
pD1q genau dann, wenn der Teilkörper ganz R ist.
Proposition 5.10.
pA1q erfüllt. Dann ist K isomorph
R. In diesem Fall erfüllt K
das Axiom
K 2 die zugehörige kartesische
Ebene. Dann gelten die Axiome pK2q bis pK5q. Das Axiom pK1q gilt genau dann, wenn
K die folgende Bedingung erfüllt:
Sei
pq @a P K D b P K : 1
Proposition 5.11.
Sei
K
ein angeordneter Körper und
a2
b2 (K heiÿt dann ein pythagoreischer Körper).
K
ein angeordneter Körper und
K2
die kartesische Ebene. Dann
sind die folgenden Aussagen äquivalent:
(I) In
K2
gilt
pE qp pKKS qq, d.h. @ Kreise Γ, Γ1 so dass Γ1 mindestens einen Punkt
innerhalb von
Γ
und mindestens einen Punkt auÿerhalb von
Γ
enthält:
Γ
und
Γ1
schneiden sich.
(II) In
K2
gilt
pKGS q : @ Γ Kreis, g Gerade, so dass g mindestens einen Punkt im
Inneren von
(III)
K
erfüllt
Γ
enthält:
g
schneidet
Γ.
pq : @ a ¡ 0 D b P K : b2 a.
13
0.
(Dann heiÿt
K
ein euklidischer Körper.)
Der Hilbert-Körper besteht aus den total reellen konstruierbaren Zahlen.
Existenz genügend vieler Kongruenzabbildungen
In
K2
gelten:
pERM q und pK6q.
In Hilbert-Ebenen gilt
pERM q und pK6q.
14
pERM q.
6 Poincarés Modell der nichteuklidischen Geometrie
K
sei ein Körper, der
In
K2
pq aus 5.11 erfüllt.
wählen wir einen Kreis
P Punkte
sind Punkte in
Γ
mit Mittelpunkt
K 2,
0 p0, 0q.
die im Inneren von
Γ
liegen.
P Geraden:
(a)
(b)
tP Punkte auf einer Geraden durch 0u.
tP Punkte auf einem Kreis, der orthogonal
Winkeln schneidetu.
zu
Γ
ist, d.h.
Γ
mit zwei rechten
Denition 6.1.
Sei Γ ein Kreis mit Mittelpunkt 0
r. Die Inversion an Γ ist eine Abbildung
K 2 zt0u Ñ K 2 zt0u, die einen Punkt A 0 nach der
1
folgenden Vorschrift auf A abbildet:
A1 ist der eindeutig bestimmte Punkt auf dem Strahl
und Radius
Ñ
0A, für den gilt: 0A 0A1 r2 .
A1 wird als invers zu A bezeichnet.
Proposition 6.2.
Kreises
0A.
Γ.
Sei
PQ
Sei
A
ein Punkt innerhalb des
die Sehne durch
A
Dann schneiden die Tangenten zu
senkrecht auf
Γ
in
1
die Gerade 0A in A , das invers zu A ist.
Theorem 6.3.
Sei
Γ
ein Kreis mit Mittelpunkt
(a) Eine Gerade durch
(b) Eine Gerade, die
0
0
0.
P
und
Dann gilt für die Inversion an
Q
Γ:
wird auf sich selbst abgebildet .
nicht enthält, wird abgebildet auf einen Kreis, der
(c) Ein Kreis, der in beiden Schnittpunkten senkrecht auf
0
enthält.
Γ steht, wird auf sich selbst
abgebildet.
(d) Sei
γ
γ
ein Kreis, der zwei zueinander inverse Punkte
senkrecht auf
(e) Ein Kreis, der
0
Γ
A
und
A1
enthält. Dann steht
und wird auf sich selbst abgebildet.
nicht enthält, wird auf einen Kreis abgebildet.
Denition 6.4. Seien A, B, P, Q vier verschiedene Punkte in der Ebene. Ihr Doppelverhältnis
ist deniert als
AP BP
AP BQ
pAB, P Qq : AQ
{ BQ AQ
BP
Proposition 6.5. Seien A, B, P, Q vier verschiedene Punkte in der Ebene, alle 0, mit
1 1 1 1
1 1 1 1
Bildern A , B , P , Q unter der Inversion an Γ. Dann gilt: pAB, P Qq pA B , P Q q.
Proposition 6.6.
(a) Das Poincaré-Modell erfüllt die Inzidenzaxiome (I 1), (I 2) und (I 3).
15
pP q gilt im Poincaré-Modell nicht: Es gibt eine P Gerade γ
P Punkt A, so dass mehrere P Geraden existieren, die A enthalten,
γ nicht schneiden (also zu γ parallel sind.)
(b) Das Parallelenaxiom
und einen
aber
Proposition 6.7.
Denition 6.8.
ander
P Anordnungsrelation
Die
erfüllt (Z 1) bis (Z 4).
Mit diesen Bezeichnungen heiÿen die
P kongruent
P Strecken AB
A1 B 1
und
zuein-
genau dann, wenn die folgende Gleichheit von Doppelverhältnissen
gilt:
pAB, P Qq pA1B 1, P 1Q1q
Proposition 6.9.
P Kongruenz
Proposition 6.10.
erfüllt (K 2) - (K 5).
(ERM) für die Poincaré-Ebene: Im Poincaré-Modell gibt es genü-
gend viele Kongruenzabbildungen, d.h.
P Punkte A
(a) Für zwei
und
B
gibt es eine
P Kongruenzabbildung,
die
A
auf
B
abbildet.
P Punkte A, B, C , so dass AB P kongruent zu AC
P Kongruenzabbildung, die A festhält und B auf C abbildet.
(b) Für drei
(c) Für eine
P Gerade γ
gibt es eine
hält und die beiden Seiten von
Korollar 6.11.
Γ
P Kongruenzabbildung,
die
γ
punktweise fest-
vertauscht.
Das Poincaré-Modell erfüllt die Axiome (K 1) und (K 6).
Proposition 6.12.
Innern von
γ
ist, gibt es eine
Die
P
Kreise sind genau die gewöhnlichen Kreise, die ganz im
liegen.
Korollar 6.13.
Lemma 6.14.
In der Poincaré-Ebene gilt (E), d.h. (KKS).
Die Funktion
funktion mit Werten in
K¡0 .
µ : pA, B q
ÞÑ
1
pAB,P Qq
Denition 6.15.
ne
und
A
ein
Punkt
mit
A
R
Grenzparallele (oder Grenzhalbgerade) zu
A)
g
g, B
In irgendeiner Ebene sei
ei-
P
K g. Ein Strahl h, der von A ausgeht, heiÿt
Gerade
g, AB
ist eine multiplikative Abstands-
genau dann, wenn
gXhH
h
(durch
und für alle Strah-
h1 , die (echt) innerhalb des Winkels verlaufen, der
1
von BA und h gebildet wird, gilt: g X h H.
len
Proposition 6.16.
g , ein
Punkt P R g , die Senkrechte P Q zu g mit Q P g
und eine Grenzparallele h durch P , die mit P Q einen
Winkel α bildet. Dann gilt:
Gegeben seien eine Gerade
tan
α
2
µpP,1 Qq
16
Denition 6.17.
Eine hyperbolische Ebene ist eine Hilbert-Ebene, die das folgende
Axiom erfüllt:
(G) Sei
g
eine Gerade und
Geraden
P
P
ein Punkt, der nicht auf
zu
g,
g
liegt. Dann gibt es zwei Grenz-
g senkrechten
P Q liegen. Diese beiden Halbgeraden liegen nicht auf derselben Geraden.
halbgeraden durch
die auf zwei verschiedenen Seiten der zu
Ein Ende ist nach Denition eine Äquivalenzklasse von Grenzparallelen.
Addition:
α und β Enden 8. Sei C P p0, 8q, A gespiegelt aus
C an pα, 8q, B gespiegelt aus C an pβ, 8q. α β :
Endep 8q der Mittelsenkrechten von AB .
Multiplikation:
p0, 8q und nenne sie
α, β ñ α, β deniert,
also
auch
pα, αq, pβ, β q, Schnittpunkte mit
p0, 8q : A und B , sowie 0 für p1, 1q. Sei C auf
p0, 8q so dass 0C 0A 0B (Abstände mit Vorzei-
Wähle
p1, 1q.
eine
Senkrechte
zu
Gegeben Enden
ÝÑ
P 08). Durch C geht die Senkrechte
zu p0, 8q; ihre Enden sind αβ und αβ . Positiv
heiÿt: Auf derselben Seite von p0, 8q wie 1.
chen positiv:
A
Ergebnis:
Die Menge der Enden ist ein angeordneter Körper
Zwei hyperbolische Ebenen sind (als Hilbert-Ebenen) isomorph
K.
ô Die angeordne-
ten Körper sind isomorph.
Eine hyperbolische Ebene ist isomorph zum Poincaré-Modell in
zugeordnete angeordnete Körper ist.
17
K 2,
wenn
K
der