Zufälle in Zahlen
Werbung

Zufälle in Zahlen Ein Comic über Statistik mit einer 95%igen Wahrscheinlichkeit wirklich einer zu sein Zufälle in Zahlen Ein Comic über Statistik mit einer 95%igen Wahrscheinlichkeit wirklich einer zu sein GOVERN DE LES ILLES BALEARS Vicepresidència i Conselleria d’Economia, Comerç i Indústria Direcció General d’Economia CCIX © Edition: Amt für Wirtschaft Projektleitung: Antoni Monserrat I Moll, Generaldirektor der Hauptverwaltung Wirtschaft Koordination: Jose Antonio Pipo Jaldo. Direktor des IBAE. Herausgeber: Balearisches Institut für Statistik (IBAE) Sant Feliu 8-A 07012 - Palma (Mallorca) - SPANIEN Telefon (34) 971 17 67 55 http://[email protected] E-mail: [email protected] Autor: Javier Cubero Management und Herstellung: I n r e v é s S L L Illustration: Alex Fito y Linhart Farben: Pau Genestra Layout: Xisco Alario et Margalida Capó Skript angepasst von: Felipe Hernández Deutsche Übersetzung: T&I Traducción e Interpretación Linguistische Beraterin: Roser Belmonte Juan Koordination: Sebastià Marí und Pere Joan Kollektion: Estadística al carrer. Volum 1 Titel: Zufälle in Zahlen. Ein Comic über Statistik mit einer 95%igen Wahrscheinlichkeit wirklich einer zu sein Nr. IBAE: CCIX Hinterlegung der Pflichtexemplare: 2PM-2463-2002 ISBN: 84-89745-53-6 Druck: Imprenta Latina SL Herausgabedatum: November 2002 © Copyright: Hauptverwaltung Wirtschaft. Amt für Wirtschaft, Handel und Industrie EMPFEHLUNGSSCHREIBEN Das Studium der Mathematik und statistischer Konzepte waren schon immer als schwierige Lernfächer bekannt, die unter den Schülern nie besonders beliebt waren. Daher möchte die Regierung der balearischen Inseln mit der Publikation des Comics Zufälle in Zahlen zur Verbreitung dieser Kenntnisse beitragen. Das gegenwärtige Exemplar, herausgegeben vom Balearischen Institut für Statistik (IBAE) des Amtes für Wirtschaft, Handel und Industrie ist ein wirkungsvolles Instrument, das einerseits den didaktischen Kriterien des ESO (spanische Sekundärstufe) Studienplanes entspricht und andererseits auch der Weiterbildung von Erwachsenen dienen kann. Mit dem Comic wird versucht, all diesen Kenntnisse auf eine einfache und interessante Weise zu vermitteln. Diese Publikation ist Teil des Studienplans, den das IBAE mit der Absicht, der Gesellschaft die von diesem Institut realisierten Studien und Analysen näher zu bringen, in Gang setzte. Sein Ziel ist aber nicht nur die Vermittlung statistischer Daten, welche die sozial-ökonomische Realität der Balearen veranschaulichen, sondern auch der Gesellschaft eine Arbeitsweise näher zu bringen, die für die Planung der Entscheidungen, auf welche die Zukunft unseres Landes aufbaut, wichtig ist. Daher sind Daten, auf die man sich verlassen kann, unumgänglich. Zuletzt möchten wir noch unseren Mitarbeiter unseren Dank aussprechen, die an einer, unserer Meinung nach innovativen Erfahrung, mitgewirkt haben. Zusätzlich möchten wir auch noch die Gruppe von Kreativen und Graphikern erwähnen, die an der Erstellung dieses Comics mitgewirkt haben und den hohen Qualitätsstandard dieses Sektors auf den Balearen beweist. Pere Sampol i Mas Vizepräsident der balearischen Regierung und Minister des Amtes für Wirtschaft, Handel und Industrie VORWORT Aus vielen und sehr verschiedenen Anlässen, ist es für mich eine wirklich große Freude das Vorwort für das Werk, das du in Händen hältst, zu schreiben. Der erste Grund, jedoch nicht der Wichtigste, ist die langjährige Freundschaft, die mich mit dem Autor verbindet, mit dem ich vor nur 35 Jahren den Hörsaal in der Universität teilte. In diesen vergangenen Tagen hätten wir uns nie vorstellen können, dass wir uns nach so langer Zeit wegen unserer gemeinsamen Liebe zur Statistik wiedertreffen würden. Der zweite ist das Werk Zufälle in Zahlen selbst, das ich, wie du als schlauer Leser bestimmt bemerkt hast, nicht als Comic bezeichnen möchte, da ich der Meinung bin, dass es sich dabei um viel mehr als nur um einen Comic handelt. Dies belegt nicht nur die Auswahl der Personennamen, die zweifelsohne nicht zufällig oder willkürlich getroffen wurde, denn jeder Name verbirgt seine kleine oder auch große Geschichte, sondern auch der Geburtstag von 55 am Ende der Geschichte, oder die Rockband Quartil. Ich möchte einige Details, die mir besonders gut gefallen haben, und die dir vielleicht zu denken geben, hervorheben. Anfangen werde ich mit den historischen Pinselstrichen am Beginn jedes Kapitels, fortfahren möchte ich mit den eleganten Erklärungen wie die des Unterschiedes zwischen einer stetigen Variablen (die Spur der Schnecke) und einer Diskreten (die Sprünge des Grashüpfers). Ferner ist noch die Art und Weise zu erwähnen, wie erklärt wird, dass Daten noch viel mehr Information in sich bergen wie man anfangs vielleicht glauben möchte (das Beispiel mit dem Alter der vier Geschwister), und die auch nicht weniger originell ist. Die Art und Weise wie verhindert wurde, Graphiken zu viel zu erörtern, da dies zu augenscheinlichen Fehlern führen kann, hat mich an einen gemeinsamen Professor unseres Mathematikstudiums erinnert. Sehr illustrativ gestaltet sind die Einführungen in die Konzepte der Bevölkerungsdichte und der Bevölkerungspyramide mit ihren Anwendungen in verschiedenen Städten der balearischen Inseln, gemeinsam mit dem Hinweis auf die Autounfälle als Krankheit der Jugendlichen von heute, um die Unregelmäßigkeiten der Pyramide zu erklären. Wahrscheinlich ist es im Kapitel 8, wo das Können des Autors am offensichtlichsten wird: die Symbole um die Indexnummern einzuführen sind ganz einfach genial, einerseits die alten Einheiten (die zugekorkten Falschen ohne Etikett) in Zusammenhang mit den alten Preisen (Notizblock) und andererseits die neuen Einheiten (Milchboxen in Tetra Brik) mit den neuen Preisen (Computerbildschirm). Meine letzten Worte sollen Javier ermuntern das begonnene Werk fortzusetzen, damit wir uns auf diese Weise bald an einem zweiten Teil erfreuen können. Granada, im April 2000 Rafael Herrerias Pleguezuelo Universitätsprofessor angewandter Wirtschaftswissenschaften INHALTSVERZEICHNIS Kapitel 1 - PIERRE DE FERMAT S. 10 Kapitele 2 - THOMAS BAYES S. 15 Kapitel 3 - BLAISE PASCAL S. 22 Kapitel 4 - ADOLPHE QUÉTELET S. 28 Kapitel 5 - JAKOB BERNOUILLI S. 36 Kapitel 6 - CHARLES DODGSON S. 45 Kapitel 7 - WILLIAM SEALEY GOSSET S. 52 Kapitel 8 - LASPEYRES UND PAASCHE S. 61 Kapitel 9 - DE MOIVRE UND GAUSS S. 70 ANLAGEN S. 89 DER SUPERTOLLE Der Supertolle …DIE ALLERWICHTIGSTE PERSON IN DIESEM COMIC: DU! 6 DIE PERSONEN 55 Rätsi Zufälli Binomi Gaußi Graphi 7 KAPITEL 1 PIERRE DE FERMAT Französischer Mathematiker (1601-1665) Seine Kenntnisse brachten ihm den Beinamen „Prinz der Amateure“. Er war einer der Begründer der Wahrscheinlichkeitstheorie. Kapitel 1 - PIERRE DE FERMAT DER GRASHÜPFER WIRD GEWINNEN! WAS FÜR EIN RENNEN! KLAR, DASS DER GRASHÜPFER GEWINNT, ER IST NUN MAL DER SCHNELLSTE. EINS STEHT FEST: DER GRASHÜPFER WIRD GEWINNEN! ICH MÖCHTE EINE HYPOTHESE AUFSTELLEN: WAHRSCHEINLICH WIRD DIE SCHNECKE VERLIEREN. GIB MIR EINEN STIFT UND PAPIER, ICH MÖCHTE DEN VERLAUF DES RENNENS FESTHALTEN. …IN BESTIMMTEN PUNKTEN, WÄHRENDDESSEN DIE SCHNECKE EINE DURCHGEHENDE FÄHRTE HINTER SICH LÄSST. ZUM GLÜCK DER SCHNECKE MACHT DER GRASHÜPFER ZWISCHEN DEN SPRÜNGEN EINE PAUSE. WARTET EINEN MOMENT. DER GRASSHÜPFER SETZT SICH HÜPFEND FORT UND HINTERLÄSST SEINE ABDRÜCKE... AUF DIESE WEISE KÖNNEN WIR DIE SPUREN DER WETTBEWERBER AUFZEICHNEN. 9 Kapitel 1 - PIERRE DE FERMAT SCHON, ABER WIR HABEN EIN PROBLEM. SCHAUT NUR WIE ES SICH DER GRASHÜPFER ÜBERLEGT BEVOR ER HÜPFT... WIR NENNEN IHN „HERRN DISKRET”! HA, HA, HA! DANN NENNEN WIR… SIE NENNT MAN EREIGNISSE, WEIL SIE SICH EREIGNEN, NICHT WEIL SIE ZERSTÖRERISCH SIND, HOLZKOPF! DAS GANZE ERINNERT MICH DARAN, DASS STATISTIKER EREIGNISSE MIT „DISKRETEN“ UND „STETIGEN“ VARIABLEN UNTERSUCHEN. WIR KÖNNTEN EIN LABOR EINRICHTEN UND EXPERIMENTE MACHEN! SUPER! TOLL! …DIE SCHNECKE „FRAU STETIG”. ES KÖNNTE SEIN, DASS DIE STATISTIKER ANFÄNGLICH SPIELE GENAUER UNTERSUCHT HABEN… ICH WEIß NICHT OB DAS DAMIT ZU TUN HAT, ABER ICH HABE EINMAL GEHÖRT, DASS ES SCHWERER IST ZU ERRATEN WAS SICH EINE PERSON WÜNSCHT ALS DAS, WAS EINE MILLION BEGEHRT. DAS BRINGT MICH AUF EINE IDEE! HÖRT ZU. ICH SCHLAGE VOR WIR SPIELEN EIN SPIEL... Experimente: ÜBUNG WIR WERFEN EINE MÜNZE 8 MAL IN DIE LUFT UND SCHREIBEN DIE ERGEBNISSE AUF. DAS GANZE WIEDERHOLEN WIR DREI MAL UND SCHREIBEN AUF WIE OFT KOPF AUFLIEGT. ANSCHLIEßEND WERFEN WIR EINE MÜNZE 50 MAL HINTEREINANDER IN DIE LUFT. ICH WETTE, DASS SICH JETZT DIE ANZAHL DER KÖPFE BESTIMMT MEHR DER ZAHL 25 NÄHERT ALS DIE ANZAHL DER ERSCHIENEN KÖPFE BEI DER VORHERIGEN WURFREIHE DER ZAHL 4 GENÄHERT HAT. DU MEINST ALSO, DASS WIR, JE ÖFTER WIR DAS EXPERIMENT WIEDERHOLEN, UNS DESTO SICHERER SEIN KÖNNEN, DASS KOPF UNGEFÄHR HALB MAL SO OFT OBEN LIEGT. WENN WIR ALSO DIE WÜRFEL 1 MILLION MAL IN DIE LUFT WERFEN, DESTO MEHR WÜRDE SICH DIE ANZAHL DER AUFLIEGENDEN KÖPFE DER HÄLFTE DER WÜRFE ANNÄHERN. UND WENN WIR 10 MILLIONEN MAL WERFEN WÜRDEN, NOCH NÄHER. DESHALB ERHÖHT SICH DIE WAHRSCHEINLICHKEIT, DASS ENTWEDER KOPF ODER ZAHL JE ZUR HÄLFTE DER WÜRFE ERSCHEINT, MIT DER ANZAHL DER GESAMTEN WÜRFE. 10 Kapitel 1 - PIERRE DE FERMAT Experimente: JA GUT, ABER DAS IST LEICHT, WEIL JA EINE MÜNZE NUR 2 SEITEN HAT: KOPF ODER ZAHL, DU GEWINNST ODER VERLIERST. WENN WIR NUN DAS EXPERIMENT MIT EINEM WÜRFEL AUSFÜHREN, SEHEN WIR, DASS NUN 6 MÖGLICHKEITEN ZUR VERFÜGUNG STEHEN. LASS UNS NUN SEHEN WIE OFT DIE ZAHL 5, DIE WIR ALS GEWINN BETRACHTEN, AUFLIEGT. WÜRFELN WIR JETZT 90 MAL UND SCHREIBEN DIE ERGEBNISSE AUF. MAL SEHEN WAS HERAUSKOMMT! WENN WIR ALSO WEDER GEMOGELT HABEN, NOCH DER WÜRFEL MANIPULIERT IST, KÖNNEN WIR MIT BESTIMMTHEIT SAGEN, DASS WIR ETWA 15 MAL GEWONNEN UND 75 MAL VERLOREN HABEN. 1 DAS HEIßT DEMNACH, DASS DIE WAHRSCHEINLICHKEIT, DASS DIE 5 AUFLIEGT, 15 , ALSO 6 , IST, 90 WÄHREND DIE WAHRSCHEINLICHKEIT ZU VERLIEREN, ALSO NICHT 5 ZU WÜRFELN 75 , ALSO 5 , IST. 6 90 SOMIT KÖNNEN WIR AUCH FESTSTELLEN, DASS DIE WAHRSCHEINLICHKEIT ZU VERLIEREN, GLEICH 1 MINUS DER WAHRSCHEINLICHKEIT ZU GEWINNEN, IST. AUF DIESE WEISE IST DIE WAHRSCHEINLICHKEIT, EIN ERGEBNIS EINES FUßBALLSPIELS ZWISCHEN ETWA GLEICH GUTEN TEAMS ZU ERRATEN, 1 (WEIL JA 3 MÖGLICHKEITEN VORLIEGEN KÖNNEN: 3 2 GEWINNEN, VERLIEREN ODER UNENTSCHIEDEN), UND DIE, DAS RESULTAT NICHT ZU ERRATEN, 3 . DAMIT IST BEWIESEN, DASS ES NICHT IMMER LEICHT IST DAS RICHTIGE ZU ERRATEN, GENAUSO WIE ES SCHWER IST IN DER SCHULE DIE GESTELLTEN FRAGEN RICHTIG ZU BEANTWORTEN, AUßER NATÜRLICH ICH GEBE DIE ANTWORT. WIR ERRATEN DAS RICHTIGE ERGEBNIS, WENN WIR SAGEN, DASS DAS ERGEBNIS ENTWEDER „0“, „X“ ODER „2“ SEIN WIRD. AUF DIESE WEISE IST NATÜRLICH DIE WAHRSCHEINLICHKEIT ERFOLG ZU HABEN, GARANTIERT! UND WENN DIE RICHTIGE LÖSUNG IST, EINE 7 ZU WÜRFELN? DANN HABE ICH „0“ WAHRSCHEINLICHKEIT ERFOLG ZU HABEN. IN DIESEM FALL WÜRDE ICH „AUF KEINE 7 WÜRFELN“ SETZEN. Zuerst müssen wir uns darüber einigen, wie wir die Daten festhalten. Lasst uns die Ergebnisse bis zur Zahl 4 mit senkrechten Strichen aufschreiben. Die Fünf halten wir fest, indem wir die bisherigen 4 Striche durchstreichen. Auf diese Weise schreiben wir die Ergebnisse in 5er-Gruppen auf, das uns das Zählen der Ergebnisse erleichtert und wir können so auch die letzte Gruppe von maximal 4 Ergebnissen besser hinzufügen. Schauen wir uns ein Beispiel an: Das wäre eine Zählung von 33. Und dies wäre eine andere Art: 1 10 20 30 11 Kapitel 1 – PIERRE DE FERMAT Experimente: Um die Ergebnisse des Experimentes festzuhalten, damit wir sie auch später verwenden können, füllen wir die untenstehenden Kästchen aus. Diese Spiele sind eine sehr ernste Sache! 8-MALIGER MÜNZENWURF Anzahl Zahlen: _____ Anzahl Köpfe: _____ Köpfe (in rot) Zahlen (in blau) 50-MALIGER MÜNZENWURF Erfolg (in rot) Misserfolg (in schwarz) Anzahl Köpfe: Anzahl Zahlen: 50 – _____ Anzahl Köpfe: _____ WAHRSCHEINLICHKEIT: Münzenwurf: Erfolg = Kopf Misserfolg = Zahl Möglichkeit auf Erfolg mit nur einem Wurf: Gesamtanzahl Möglichkeiten: Würfeln:Erfolg = ”eine FÜNF würfeln“ WAHRSCHEINLICHKEIT= 1 2 Misserfolg = “1 oder 2 oder 3 oder 4 oder 6” Möglichkeit auf Erfolg mit nur einem Wurf: 1 Gesamtanzahl Möglichkeiten (Erfolg + Misserfolg): WAHRSCHEINLICHKEIT= 6 Würfeln: Erfolg = ”eine DREI würfeln“ Misserfolg = “1 oder 2 oder 4 oder 5 oder 6” Möglichkeit auf Erfolg mit nur einem Wurf: 1 Gesamtanzahl Möglichkeiten (Erfolg + Misserfolg): WAHRSCHEINLICHKEIT= 6 Würfeln: Erfolg = ”eine DREI oder eine FÜNF würfeln“ Misserfolg = “1 oder 2 oder 4 oder 6” Möglichkeit auf Erfolg mit nur einem Wurf: Gesamtanzahl Möglichkeiten (Erfolg + Misserfolg): WAHRSCHEINLICHKEIT= 2 6 WAHRSCHEINLICHKEIT EINE DREI ODER EINE FÜNF ZU WÜRFELN Wahrscheinlichkeit eine 3 zu würfeln + Wahrscheinlichkeit eine 5 zu würfeln = 1 + 1 = 2 6 12 6 6 KAPITEL 2 THOMAS BAYES (1702?-1761) Englischer Geistlicher der ersten Hälfte des 18. Jahrhunderts, Vater der Bayes-Statistik. Kapitel 2 - THOMAS BAYES HURRA! WAS FÜR EIN GLÜCK! ICH HABE 3 MÜNZEN GEFUNDEN! GUT, ABER ES SCHEINT KEIN VERMÖGEN ZU SEIN. ES SIND AUßERDEM AUSLÄNDISCHE MÜNZEN... SCHAU, WIE KOMISCH SIE SIND. WAHRSCHEINLICH SIND SIE WERTLOS. SCHON, ABER TROTZDEM GLAUBE ICH NICHT, DASS DIES SO UNGEWÖHNLICH IST. ABER DAS MEINE ICH DOCH NICHT. SCHAU HER, ALLE SIND MIT DEM KOPF NACH OBEN GELANDET! ALSO… WEIL WIR GESEHEN HABEN, DASS DIE WAHRSCHEINLICHKEIT, DASS EINE MÜNZE MIT DEM KOPF NACH OBEN ZUM LIEGEN KOMMT 1 IST, DANN MÜSSTE DIE 2 WAHRSCHEINLICHKEIT, DASS DREI MÜNZEN MIT DEM KOPF NACH OBEN AUFLIEGEN, FOLGENDERMAßEN SEIN: BEWEISEN WIR ES MIT EINEM BEISPIEL. WENN ICH EINE MÜNZE 3 MAL IN DIE LUFT WERFE, MIT WELCHER WAHRSCHEINLICHKEIT LIEGEN 3 MAL KÖPFE AUF? UND MIT WELCHER 2 MAL ZAHL UND EINMAL KOPF? WAHRSCHEINLICHKEIT WAHRSCHEINLICHKEIT K= 1 2 Z= 1 2 GESAMT = 14 1 2 1 + 1 2 + 1 2 = 3 2 UNMÖGLICH! DAS KANN NICHT STIMMEN, DENN DAS GÄBE EINE WAHRSCHEINLICHKEIT 3 VON 2 UND DIE WAHRSCHEINLICHKEIT EINES EREIGNISSES KANN NICHT GRÖßER SEIN ALS 1! ICH WÜRDE VORSCHLAGEN DIES GRAPHISCH DARZUSTELLEN. Kapitel 2 - THOMAS BAYES Experimente: SO. ODER AUF DIESE WEISE. K K Z K K Z K Z K Z K K K K K Z K Z K K Z Z K Z K K Z Z K Z K Z Z K Z Z Z Z 15 Kapitel 2 - THOMAS BAYES Experimente: LASSEN WIR DEN SUPERTOLLEN DAS SCHEMA FÜR 4 WÜRFE ERSTELLEN. 8 Möglichkeiten Anzahl 3 x Köpfe = 1 Wahrscheinlichkeit = 1 8 Anzahl 2 x Köpfe und 1 x Zahl = 3 Wahrscheinlichkeit = 3 8 Anzahl 1 x Kopf und 2 x Zahl = 3 Wahrscheinlichkeit = 3 8 Anzahl 3 x Zahl = 1 Wahrscheinlichkeit = 1 8 Gesamtanzahl: 16 Möglichkeiten Anzahl KKKK = 1 Wahrscheinlichkeit KKKK = 16 4 1 Wahrscheinlichkeit KKKZ = = 16 4 Anzahl KKKZ = 4 Anzahl KKZZ = Wahrscheinlichkeit KKZZ = Anzahl KZZZ = Wahrscheinlichkeit KZZZ = Anzahl ZZZZ= Wahrscheinlichkeit ZZZZ = Kontrolle: + 16 + + + =1 16 = 16 = 8 Kapitel 2 - THOMAS BAYES ALSO, AUS DIESEN EXPERIMENTEN KÖNNEN WIR FOLGENDES ABLEITEN: 1. DIE WAHRSCHEINLICHKEIT EINES SICHEREN EREIGNISSES IST 1. 2. DIE WAHRSCHEINLICHKEIT DES ERFOLGES + WAHRSCHEINLICHKEIT DES MISSERFOLGES IST GLEICH 1. 3. DIE WAHRSCHEINLICHKEIT DES MISSERFOLGES = 1 – WAHRSCHEINLICHKEIT DES ERFOLGES. 4. DIE WAHRSCHEINLICHKEIT EINES EREIGNISSES = 1 – WAHRSCHEINLICHKEIT DES GEGENTEILS. OH! STELLT EUCH VOR, ICH HABE DREI SEHR WERTVOLLE MÜNZEN VERLOREN! ES HANDELT SICH UM ECHTE SAMMLERSTÜCKE, DIE MEIN VATER IN SEINER JACKENTASCHE VERGESSEN HAT. GOTT SEI DANK, SIE SIND’S! VIELEN DANK! IHR HABT MICH GERETTET! GAUßI, MIT WELCHER WAHRSCHEINLICHKEIT SIND DIESE IHRE MÜNZEN? IM SCHNEE UND SO KOMISCH? ICH WÜRDE SAGEN ES HANDELT SICH UM EIN SICHERES EREIGNIS, ALSO 1. LASST UNS ZUR SCHUTZHÜTTE ZURÜCKKEHREN. ES BEGINNT ZU SCHNEIEN UND ICH MÖCHTE AUßERDEM DIE TOTO-ERGEBNISSE SEHEN. 17 Kapitel 2 - THOMAS BAYES IHR MÖCHTET ALSO DIE FUßBALL-TOTO-ERGEBNISSE WISSEN? ES SCHAUT AUS ALS OB DER FERNSEHER KAPUTT SEI... IHR MÜSST EUCH ALSO DAMIT ABFINDEN DIE ERGEBNISSE ZU ERRATEN... JA, ICH HABE EINEN IN DER JACKENTASCHE MEINES VATER GEFUNDEN! DER WÜRFEL HAT ZWAR 6 SEITEN, DOCH ZWEI ZEIGEN EINE “1”, ZWEI EIN “X”, UND ZWEI EINE “2”. FANTASTISCH! DAS IST DIE GELEGENHEIT EIN NEUES EXPERIMENT DURCHZUFÜHREN. HAT JEMAND EINEN TOTO-WÜRFEL? Experimente: Erfahrungen 1 1 X X 2 1 X 2 2 1 X 2 Schätzungen Gemäß des aktuellen Standes 3 wenn sie gewinnen 1 wenn unentschieden 0 wenn sie verlieren 3 1 3 1 0 6 4 3 3 4 0 1 0 3 1 2 1 3 1 0 0 Gemäß unserer Schätzung 1 wenn sie gewinnen 0 wenn unentschieden -1 wenn sie verlieren 1 1 0 -1 2 1 0 SOLL DOCH DER SUPERTOLLE DIE 15 RESULTATE AUSFINDIG MACHEN, OBWOHL ICH GLAUBE ER BRÄUCHTE DAZU SEHR VIEL PAPIER... 18 0 1 1 -1 0 -1 0 -1 HMM… ES MUSS DOCH EINE FORMEL DAZU GEBEN. SIE SOLLTE SCHNELL UND OHNE VIEL ARBEIT ZU LÖSEN SEIN... ICH HOFFE GAUßI FINDET EINE, O.K.? 1 0 -1 0 -1 -2 HE! JETZT SIND WIR DRAN… Kapitel 2 - THOMAS BAYES HURRA! ICH HAB’S! WENN ICH DAS RESULTAT VON NUR EINEM SPIEL ERRATEN MÖCHTE, HABE ICH 3 MÖGLICHKEITEN. ZWEI SPIELE BIETEN INSGESAMT 9 MÖGLICHKEITEN. GRAPHI STELLT 3 SPIELE GRAPHISCH DAR. MAL SEHEN WAS HERAUSKOMMT! BEI DREI SPIELEN KOMMEN WIR AUF 27 MÖGLICHKEITEN. SO KOMME ICH AUF FOLGENDES: FÜR EIN SPIEL: 3 MÖGLICHKEITEN= 31 FÜR 2 SPIELE: 9 MÖGLICHKEITEN= 3 X 3 = 32 FÜR 3 SPIELE: 27 MÖGLICHKEITEN= 3 X 3 X 3 = 33 DEMNACH MÜSSTEN WIR FÜR 15 SPIELE ... 3 X 3 X 3 … (15 MAL) = 315 MÖGLICHKEITEN HABEN. UNSER SUPERTOLLE MÜSSTE ALSO ALLE DIAGRAMME ZEICHNEN, DAMIT WIR WISSEN WIE DIE SPIELE AUSGEHEN, WENN WIR 15 SPIELE FESTSETZEN: 5 FIXE, 6 MIT EINEM DOPPELRESULTAT, UND 4 MIT EINEM DREIFACHEN RESULTAT. DIE LÖSUNG WÄRE DEMNACH: 1 x 1 x 1 x 1 x 1 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 = 15 x 26 x 34 TROTZDEM HAT DER, DER DIE RICHTIGEN ERGEBNISSE ERRÄT, EIN RIESENGLÜCK. WÄHREND IHR ALLE GEPLAUDERT HABT, HABE ICH DIE ANTENNE FREIGESCHAUFELT. SIE WAR VÖLLIG MIT SCHNEE BEDECKT! SCHREIBT LIEBER GLEICH DIE ERGEBNISSE AUF, BEVOR ES WIEDER ZU SCHNEIEN BEGINNT! 19 KAPITEL 3 BLAISE PASCAL Französischer Wissenschaftler (1623-1662) Wahrscheinlich einer der wichtigsten Pioniere der Wahrscheinlichkeitstheorie und der kombinatorischen Formeln. Beeindruckend ist seine wissenschaftlich-briefliche Beziehung mit Fermat. Kapitel 3 - BLAISE PASCAL WIE GEHT’S, BINOMI? EIGENTLICH KÖNNTEN WIR UNSERE EXPERIMENTE MIT DEN WÜRFELN FORTFÜHREN... ICH HABE NOCH IMMER MUSKELKATER VOM WOCHENENDE... DESHALB WERDE ICH IN DER PAUSE NICHT BASKETBALL SPIELEN. HEUTE WIRD OHNEHIN NICHT BASKETBALL GESPIELT, DENN SIE WERDEN DEN PLATZ ZUM KUNSTEISLAUF VERWENDEN. AH, DA KOMMEN AUCH SCHON UNSERE FREUNDE. VIELLEICHT KÖNNEN SIE UNS HELFEN. ICH HABE ZWAR NUR EINEN WÜRFEL, DOCH WIR KÖNNEN’S JA PROBIEREN. Experimente: WÜRFEL NUN ZWEI MAL UND SCHREIB DANN DIE RESULTATE IN ZWEIERGRUPPEN AUF. MAL SEHEN WAS PASSIERT... WISST IHR, DASS MAN DIESES DIAGRAMM „ERGEBNISRAUM” NENNT? VON NUN AN WERDEN WIR ES AUCH SO NENNEN. ES HÖRT SICH VIEL TECHNISCHER AN. 21 Kapitel 3 - BLAISE PASCAL HALLO IHR ALLE! WIE INTERESSANT! WAS WÄRE, WENN WIR DAS GANZE NOCH KOMPLIZIERTER MACHEN? WAS WÄRE WENN WIR NUR DIE SUMME DER AUGENZAHLEN DER BEIDEN WÜRFE GELTEN LASSEN? Experimente: DAS GEFÄLLT MIR GAR NICHT. IRGENDWAS KOMMT MIR KOMISCH VOR. DU HAST RECHT, WENN WIR AUF „AUF 7 SUMMIEREN“ SETZEN UND DEM SUPERTOLLEN LASSEN WIR „AUF 12 SUMMIEREN“, WIRD ER SICH SCHÖN BLAMIEREN! GESAMTANZAHL JA, JA, ES STIMMT, WAHRSCHEINLICHER IST ES, DASS DIE AUGENZAHL BEIDER WÜRFE 7 ERGEBEN ALS 11 ODER 12. BERECHNEN WIR DAS GANZE. UND DAS WIRD UNS LEICHTER FALLEN, WENN WIR DAS DIAGRAMM BETRACHTEN. 22 DER WAHRSCHEINLICHKEIT “ “ “ “ “ “ “ “ “ “ “ “ “ “ “ “ “ “ “ “ MÖGLICHKEITEN: 6 x 6 = 36 DER “ “ “ “ “ “ “ “ “ “ SUMME “2” ........= “3” ........= “4” ........= “5” ........= “6” ........= “7” ........= “8” ........= “9” ........= “10” ........= “11” ........= “12” ........= 1 36 2 36 3 36 4 36 5 36 6 36 5 36 4 36 3 36 2 36 1 36 Kapitel 3 - BLAISE PASCAL MIT RECHT KAM MIR IRGENDWAS KOMISCH VOR. WIR HABEN 6 GELEGENHEITEN ZU GEWINNEN, UNSER SUPERTOLLER NUR 1. GAUßI, KÖNNTEST DU NICHT ETWAS ERFINDEN, DAMIT WIR ALLE SPIELEN KÖNNEN? DASS SICH JEDER EINE BELIEBIGE SUMME AUSSUCHEN KANN UND ES NUR VOM GLÜCK ABHÄNGT, OB MAN GEWINNT ODER NICHT, UND NICHT VON JEDER MENGE MATHEMATISCHER BERECHNUNGEN? ES KANN SEIN. WENN WIR JEDER SUMME EINEN BESTIMMTEN PREIS ZUORDNEN, KÖNNTEN WIR MEINER MEINUNG NACH DAS SPIEL INS GLEICHGEWICHT BRINGEN. ABER ICH WERDE GRAPHIS’ HILFE BENÖTIGEN UM EINIGE PREISTABELLEN DARZUSTELLEN. GRAPHI! KÖNNTEST DU KOMMEN UND UNS HELFEN? ABER KLAR! BIN SCHON UNTERWEGS! Experimente: WIR WISSEN JA BEREITS, DASS DIE WAHRSCHEINLICHKEITEN PROPORTIONAL AUF 1, 2, 3, 4, 5, UND 6 SIND, RICHTIG? SOMIT MÜSSTEN SICH DIE PREISE GENAU GEGENTEILIG VERHALTEN. UNGLAUBLICH! WIE MACHST DU ES BLOß? WO HAST DU DENN NUR DIE TOLLE TABELLE HER? GEFÄLLT SIE DIR? HIER HAST DU SIE... STELLEN WIR DAS GANZE KLAR. WENN ICH DIE SUMME „7“ ALS RESULTAT WÄHLE, HABE ICH 6 MÖGLICHKEITEN MEHR ZU GEWINNEN ALS EINER DER DIE SUMME „12“ WÄHLT. DAMIT MÜSSTE MEIN PREIS UMGEKEHRT PROPORTIONAL SEIN ZU SEINEM. DAS IST NUR RECHT UND BILLIG! GENAU. 23 Kapitel 3 - BLAISE PASCAL Experimente MAL SEHEN, OB ICH ES VERSTANDEN HABE... MIR IST WICHTIG, DASS DAS ERGEBNIS DES SPIELS NUR VOM GLÜCK ABHÄNGT, WIE AUCH MEIN NAME SCHON SAGT.... ALSO WERDE ICH EINE LISTE AUFSTELLEN: DAS STIMMT ABER NICHT MIT DEINER TABELLE ÜBEREIN! HALT, HALT! DIE PREISE SIND: Wahrscheinlichkeit eine “2” zu würfeln = Wahrscheinlichkeit eine “3” zu würfeln = Wahrscheinlichkeit eine “4” zu würfeln = Wahrscheinlichkeit eine “5” zu würfeln = Wahrscheinlichkeit eine “6” zu würfeln = Wahrscheinlichkeit eine “7” zu würfeln = Wahrscheinlichkeit eine “8” zu würfeln = Wahrscheinlichkeit eine “9” zu würfeln = Wahrscheinlichkeit eine “10” zu würfeln = Wahrscheinlichkeit eine “11” zu würfeln = Wahrscheinlichkeit eine “12” zu würfeln = 1 36 2 36 3 36 4 36 5 36 6 36 5 36 4 36 3 36 2 36 1 36 Preis = Preis = Preis = Preis = Preis = Preis = Preis = Preis = Preis = Preis = Preis = 36 1 36 2 36 3 36 4 36 5 36 6 36 5 36 4 36 3 36 2 36 1 ... UND ES IST VOR ALLEM DER WERT 36 … DER ALLES STÖRT! 5 36 36 36 36 36 36 1 , 2 , 3 , 4 , 5 , 6 WÜRDEN DAS SPIEL AUSGLEICHEN. JEDOCH ERSCHEINEN MIR DIE ZAHLEN NICHT UNBEDINGT GEEIGNET, DA ES SICH UM ZAHLEN MIT DEZIMALSTELLEN HANDELT... 24 DESHALB MÜSSEN WIR DIVISIONEN FINDEN, DIE GANZE ZAHLEN ERGEBEN. JETZT HABEN WIR: 36, 18, 12, 9, 36 UND 6. WENN WIR ABER 5 ALLE MIT 5 MULTIPLIZIEREN, DANN ERGEBEN SICH NUR GANZE ZAHLEN: 180, 90, 60, 45, 36 AND 30. DOCH DAS ERGIBT NICHT DAS GLEICHE RESULTAT... Kapitel 3 - BLAISE PASCAL HABT DOCH ETWAS GEDULD.... DAMIT WIR MIT KLEINEREN NUMMERN SPIELEN KÖNNEN, HABE ICH DIE PREISE DURCH 3 DIVIDIERT. WAS HÄLT IHR DAVON? DIE RESULTATE WÄREN DANN: 60, 30, 20, 15, 12 UND 10. WIE IHR SEHT, SIND DIE ZAHLEN KORREKT, SOLANGE WIR DIE PROPORTIONEN EINHALTEN. DER SUPERTOLLE WIRD DIES FÜR UNS NACHPRÜFEN. WIR SPIELEN ALLE EIN PAAR RUNDEN, ZUERST OHNE DIE PREISE AUSZUGLEICHEN. SEHR GUT! MACHEN WIR WEITER! NATÜRLICH! UND DAMIT WIR DIE RESULTATE DES EXPERIMENTS VERGLEICHEN KÖNNEN, SCHLAGE ICH VOR JE 50 MAL, ALSO AUF BEIDE ARTEN, ZU WÜRFELN. ICH WÄHLE DIE SUMME “12”. AUF DIESE WEISE BEWEISE ICH, DASS MAN MIT DIESER ZAHL FAST ALLE SPIELE VERLIERT. SEI NICHT SO UNGEDULDIG, DENN NACHHER SPIELEN WIR DIE AUSGEGLICHENE VERSION MIT DEN PREISEN LAUT DER TABELLE, DIE GAUßI ZUSAMMENGESTELLT HAT. DANN WERDEN WIR JA SEHEN, WER AM MEISTEN GLÜCK HAT! WAS HAST DU DENN VOR? NICHT SO HOCH! 25 KAPITEL 4 ADOLPHE QUÉTELET Belgischer Statistiker und Astronom (1796 – 1874). Aufgrund seiner Entdeckung der Normalverteilung ist er besonders erwähnenswert. Kapitel 4 - ADOLPHE QUÉTELET HÖRT MAL HER! ICH HABE MIR VIER INTERESSANTE AUFGABEN ÜBERLEGT, DIE FÜR UNSERE UNTERSUCHUNGEN NÜTZLICH SEIN KÖNNTEN. ANTWORTET MIR. WAS IST GRÖßER? EIN HALBER METER ZUM QUADRAT ODER DIE HÄLFTE EINES METERS ZUM QUADRAT? WIR MÜSSEN DIE KONZEPTE AUFMERKSAM DURCHDENKEN, UM UNS NICHT FURCHTBAR ZU IRREN. SIE SIND GLEICH GROß. DAS BEZWEIFLE ICH. ZEICHNEN WIR BEIDE AUF, DENN SO WERDEN WIR ES BESSER SEHEN. Die Hälfte von m2 UFF! JETZT WEIL ICH ES SEHE, GLAUBE ICH ES AUCH. DIE HÄLFTE EINES METERS ZUM QUADRAT IST DAS DOPPELTE EINES HALBEN METERS ZUM QUADRAT. 1 2 m zum Quadrat JA, ES IST WAHR, WIR MÜSSEN UNS DIE ANGABEN WIRKLICH AUFMERKSAM ANSEHEN... WEIL WIR ES JA MIT VERSCHIEDENEN FRAGESTELLUNGEN ZU TUN HABEN... …VORGESTERN, ALS ICH DIE STRAßE ENTLANG GING, WURDE MIR FOLGENDE AUFGABE GESTELLT: DAS PRODUKT DER JAHRE VON 4 GESCHWISTERN IST 36, UND DIE SUMME IST EINE NUMMER DER ANDEREN STRAßENSEITE. WIE ALT SIND DIE GESCHWISTER? HMM! ES FEHLT EINE INFORMATION. HM! FAST VERGESSE ICH’S! SIE SAGTEN MIR AUCH NOCH, DASS DIE ÄLTERE SCHWESTER IHRE GRUNDSCHULJAHRE SEHR GUT ABSCHLIEßT. 27 Kapitel 4 - ADOLPHE QUÉTELET WIR WERDEN GLEICH WIE IN DEN VORIGEN SPIELEN VORGEHEN. WIR MÜSSEN DIE PROBLEMSTELLUNGEN GENAU DEFINIEREN, DENN ANSONSTEN KÖNNTEN WIR UNS SEHR LEICHT IRREN! SO IST’S BESSER. HABT IHR GESEHEN WIE WICHTIG ES IST, DIE DATEN GENAU ZU BESTIMMEN, UM AUF DIESE WEISE EIN PROBLEM ZU LÖSEN? STELLEN WIR UNS ZUM BEISPIEL DIE KLASSIFIKATIONEN DER FUßBALLTEAMS VOR. WIR WISSEN ALLE, DASS EIN GEWONNENES SPIEL 3 PUNKTE ERGIBT, EIN UNENTSCHIEDEN 1 PUNKT, UND EIN VERLORENES SPIEL 0 PUNKTE MACHT. Experimente: LASST UNS ALSO EINE ÄHNLICHE AUFSTELLUNG MIT DER GLEICHEN ANZAHL GEWONNENER, UNENTSCHIEDENER UND VERLORENER SPIELE ERSTELLEN. NUR DASS DIE GEWONNENEN SPIELE JETZT 1 PUNKT ERHALTEN, DIE UNENTSCHIEDENEN 0 UND DIE VERLORENEN –1. DAS WÜRDE DANN SO AUSSEHEN: J G E P GF GC P 23 13 4 6 42 30 43 13 -6 7 2.Saragossa 23 10 9 4 40 24 39 10 -4 6 3.Barcelona 23 11 5 7 43 29 38 11 -7 5 4.Celta 23 11 5 10 31 29 35 11 -10 1 5.Alabés 23 10 5 8 26 25 35 10 -8 2 6.Ath.Bilbao 23 9 8 6 34 34 35 9 -6 3 7.València 23 9 6 8 32 25 33 9 -8 1 8.Reial Madrid 22 8 9 5 38 37 33 8 -5 3 9.Rayo Vallecano 23 10 3 10 32 32 33 10 -10 0 1.Deprtivo 10.REIAL MALLORCA 23 9 5 9 31 31 32 9 -9 0 11.Numància 23 8 7 8 32 36 31 8 -8 0 12.Màlaga 23 7 8 8 33 32 29 7 -8 -1 13.At.Madrid 23 8 5 10 36 37 29 8 -10 -2 14.Espanyol 23 7 7 9 33 34 28 7 -9 -2 15.Valladolid 22 7 7 8 22 25 28 7 -8 -1 16.Betis 23 8 3 12 21 37 27 8 -12 -4 17.Racing 23 6 8 9 35 34 26 6 -9 -3 18.Reial Societat 23 5 10 8 25 29 25 5 -8 -3 19.Reial Oviedo 23 6 7 10 24 38 25 6 -10 -4 20.Sevilla 23 4 8 11 24 36 20 4 -11 -7 AKTUELLE KLASSIFIKATION 28 G P GESAMT VORSCHLAG Kapitel 4 - ADOLPHE QUÉTELET DAS GANZE VERÄNDERT SICH GANZ SCHÖN, OBWOHL WIR DIE GLEICHEN DATEN VERWENDEN... WIR SEHEN ALSO, DASS SICH DIE RANGORDNUNG MIT DEM NEUEN PUNKTSYSTEM GRUNDLEGEND VERÄNDERT HAT! NICHT’S LEICHTER ALS DAS! DIE GLEICHEN RESULTATE ORDNEN WIR DURCH EINE AUSLOSUNG. SODANN WÜRDEN WIR DIE TEAMS MIT DER GLEICHEN PUNKTEANZAHL MIT EINER FORTLAUFENDEN ZAHL VERSEHEN. ANSCHLIEßEND GÄBEN WIR NUMMERIERTE KUGELN, SO VIELE WIE NÖTIG SIND NATÜRLICH, IN EINE TROMMEL UND WÜRDEN MIT DER AUSLOSUNG BEGINNEN. ÜBER UNSER SCHEMA KANN MAN DISKUTIEREN, ABER ES WÄRE GÜLTIG, WENN WIR EINIGE PROBLEMCHEN WIE DIE ANORDNUNG DER GLEICHEN ERGEBNISSE LÖSEN WÜRDEN... EINVERSTANDEN, OBWOHL ICH GLAUBE, DASS DIES NICHT GERADE BEGEISTERN WIRD. ABER ES WÄRE EINE KORREKTE MATHEMATISCHE LÖSUNG. ES HANDELT SICH UM EINE BESTIMMTE ORDNUNGSART MIT NUR EINER MÖGLICHEN INTERPRETATION. HM! ICH GLAUBE WIR BEGINNEN EINE TABELLE MIT ZUFALLSVARIABLEN ZU ERFINDEN. HEY! UNSER SUPERTOLLER HAT BEREITS DIE AUFGABE MIT DEN GESCHWISTERN GELÖST UND KOMMT AUF DAS GLEICHE ERGEBNIS WIE ICH... WIR WERDEN ES DEM SUPERTOLLEN ÜBERLASSEN DAS GANZE MIT DEN ERGEBNISSEN DER KLASSIFIKATION DER LETZTEN WOCHE ZU ÜBERPRÜFEN. IN SACHEN STATISTIK MÜSSTEN WIR BEACHTEN, DASS, JE NACHDEM WELCHE REGELN WIR AUFSTELLEN, DIE RESULTATE SEHR ABWEICHEND AUSFALLEN KÖNNEN, OBWOHL MAN DIE GLEICHEN AUSGANGSDATEN VERWENDET. 29 Kapitel 4 - ADOLPHE QUÉTELET WIE LAUTET DIE LÖSUNG? DIE GESCHWISTER SIND 9, 2, 2 UND 1 JAHR ALT. UND WIE BIST DU DARAUF GEKOMMEN? ES GAB ALSO DOCH JEDE MENGE ANGABEN. UND ICH DACHTE, DASS VIELE INFORMATIONEN NICHTS MIT DER AUFGABE ZU TUN HÄTTEN! LASS UNS ALLE MÖGLICHKEITEN ANSCHAUEN UND WENDEN WIR DANN DIE BEDINGUNGEN AN. (IST EUCH BURSCHEN AUFGEFALLEN WELCH „WICHTIGE WÖRTER“ ICH VERWENDE?) ICH GLAUBE ICH HABE DAS PROBLEM RECHT GUT GELÖST. WAS FÜR EINE GROßE KLEINE ERFINDUNG IST DAS PAPIER IN VERBINDUNG MIT DER KAPAZITÄT DES NACHDENKENS, DEN EIFER EINE LÖSUNG ZU FINDEN UND DAS AUFMERKSAME UND AUSFÜHRLICHE STUDIUM! DAS PRODUKT MUSS 36 ERGEBEN. DIE SUMME MUSS EINE GERADE ZAHL SEIN, WEIL SIE DIR DIE AUFGABE AUF DEM GEHSTEIG MIT DEN UNGERADEN HAUSNUMMERN GESTELLT HABEN. ES GIBT EINE ÄLTERE SCHWESTER, DIE ENTWEDER 8, 9, 10 ODER 11 JAHRE ALT IST, DENN SIE IST IN DER GRUNDSCHULE UND HAT BEREITS MEHRERE SCHULJAHRE ERFOLGREICH ABGESCHLOSSEN. Alter der Geschwister Mehrere gerade Grundschuljahre Summe 36 1 1 1 18 2 1 1 12 3 1 1 9 4 1 1 x 9 2 2 1 x x 6 6 1 1 6 3 2 1 4 3 3 1 3 3 2 2 UND NUN EIN ANDERES RIESENPROBLEM: „EINE FAMILIE HAT 4 KINDER: PRAXEDES, 10 JAHRE ALT, AMOR, 8 JAHRE ALT, MONSERRAT, 5 JAHRE ALT, UND REYES, 2 JAHRE ALT. WELCHE DER KINDER SIND MÄDCHEN, UND WELCHE JUNGS? DAS HABE ICH ZUERST AUCH GEGLAUBT. DANN HAT SICH JEDOCH HERAUSGESTELLT, DASS ALLE VIER NAMEN FÜR BURSCHEN ALS AUCH FÜR MÄDCHEN VERWENDET WERDEN. 30 ANSCHEINEND ENTSCHEIDEN SICH DIE ELTERN FÜR EINEN NEUTRALEN NAMEN UND SCHAUEN SICH ERST SPÄTER DAS ULTRASCHALLBILD AN. AUF DIESE WEISE WÄHLEN SIE NAMEN, DIE GLEICHERMAßEN FÜR MÄDCHEN UND FÜR KNABEN PASSEN. ABER DAS IST DOCH GANZ EINFACH. WIR MÜSSEN NUR SCHAUEN OB DIE NAMEN MÄNNLICH ODER WEIBLICH SIND... DANN KÖNNEN WIR DIE ANTWORT NUR DURCH WAHRSCHEINLICHKEITEN FINDEN. Kapitel 4 - ADOLPHE QUÉTELET DAS WITZIGE DER GANZEN GESCHICHTE IST, DASS, ALS ICH DEM MATHEMATIKLEHRER DIE AUFGABE STELLE, DIESER ANTWORTET, DASS ER IN KLASSE GERADE DAS THEMA ERKLÄRT, NÄMLICH DIE BINOMPOTENZEN, DIE ZUR LÖSUNG DIESES PROBLEMS NÖTIG SIND. Experimente: VERSUCHEN WIR DIE AUFGABE GENAU WIE DIE ANDEREN EXPERIMENTE ZU LÖSEN, ANSCHLIEßEND SCHAUEN WIR UNS DIE BINOMPOTENZEN GENAUER AN. HOFFENTLICH ERHÄLT 55 GUTE NOTEN IN DER SCHULE, DAMIT SIE ÖFTER MIT UNS ZUSAMMEN SEIN KANN. NUR WENN SIE LUST HAT, NATÜRLICH. MANCHMAL IST ES JA BEREITS SCHWER BINOMI ALLEIN ZU ERTRAGEN, ICH MAG GAR NICHT DARAN DENKEN, WIE ES SEIN WIRD IN HOCH DREI AUSZUHALTEN! DAS HEIßT KUBIK. LASST UNS EINE TABELLE ERSTELLEN. IN SACHEN STATISTIK SIND TABELLEN DAS TÄGLICHE BROT. MÖGLICHE FÄLLE PRAXEDES AMOR MONSERRAT REYES 10 8 5 2 ? ? ? ? WIE WEIßT DU DENN, DASS ES 16 MÖGLICHKEITEN GIBT? M M M M M M M M WWW WW WW M M M MWWWW M M M M W WW M M WWM M WW M M W W M WW M WM WMW M W MW M WW M W DAS WEIß ICH DESHALB, WEIL DAS ERSTE KIND 2 MÖGLICHKEITEN HAT. DIESE 2 SIND MIT DEN 2 OPTIONEN DES ZWEITEN ZU KOMBINIEREN, DAS ERGIBT BEREITS 4. DIESE 4 MÖGLICHKEITEN SIND MIT DEN 2 DES DRITTEN ZU KOMBINIEREN, ALSO SIND ES 8. UND DIESE WIEDERUM SIND MIT DEN 2 OPTIONEN DES VIERTEN ZU KOMBINIEREN, DAS ERGIBT SODANN 16 MÖGLICHKEITEN. 2 X 2 X 2 X 2 = 24 = 16 ERINNERE DICH AN UNSERE ERFAHRUNGEN MIT DEN KÖPFEN UND ZAHLEN DER MÜNZEN! 31 Kapitel 4 - ADOLPHE QUÉTELET Experimente: WENN WIR DIE TABELLE ANSEHEN, SCHAUT DAS GANZE SO AUS: A. 1 MÖGLICHKEIT UNTER 16 B. 4 MÖGLICHKEITEN UNTER 16 C. 6 MÖGLICHKEITEN UNTER 16 D. 4 MÖGLICHKEITEN UNTER 16 E. 1 MÖGLICHKEIT UNTER 16 4 KNABEN 3 KNABEN UND 1 MÄDCHEN 2 KNABEN UND 2 MÄDCHEN 1 KNABE UND 3 MÄDCHEN 4 MÄDCHEN WIR MACHEN DAS GLEICHE WIE IN UNSEREN ANDEREN SPIELEN. WIR MÜSSEN DIE AUFGABEN GUT DEFINIEREN, DENN ANSONSTEN KÖNNTEN WIR UNS LEICHT IRREN. ALSO ICH WÜRDE SAGEN, ES SIND ZWEI BURSCHEN UND ZWEI MÄDCHEN, DENN AUF DIESE WEISE HABE ICH MEHR MÖGLICHKEITEN ZU GEWINNEN. ICH BIN GERADE AM ÜBERLEGEN, ICH GLAUBE DAS GÄBE SEHR INTERESSANTE DIAGRAMME... 6 / 16 5 / 16 4 / 16 3 / 16 2 / 16 1 / 16 32 ZU SEIN ZU SEIN ZU SEIN ZU SEIN ZU SEIN Kapitel 4 - ADOLPHE QUÉTELET HUI! DIESES DIAGRAMM ERINNERT MICH AN EIN ANDERES, DAS ICH IN EINEM BUCH GESEHEN HABE: ES NENNT SICH „BINOMINALVERTEILUNGSDIAGRAMM“. ICH GLAUBE ICH BIN AUF DEN AUSGANGSPUNKT DER SACHE MIT DEN BINOMPOTENZEN, DIE VORHIN 55 ERWÄHNT HAT, GESTOßEN! ICH WERDE MICH DAMIT ETWAS NÄHER BESCHÄFTIGEN, OBWOHL ICH AUCH DER MEINUNG BIN, DASS WIR SPÄTER AUCH NOCH UNSERE ERFAHRUNGEN MIT DIAGRAMMEN VERTIEFEN SOLLTEN! WO GEHST DU DENN HIN? UND ICH WEIß AUCH SCHON, WER ZU DIESEM THEMA BIS ZUM UMFALLEN ARBEITEN MUSS. DA ICH MICH MORGEN AUSSCHLAFEN KANN, WERDE ICH MICH WOHL HEUTE NACHT MIT BINOMPOTENZEN UND SEINER BEZIEHUNG ZU DEN WAHRSCHEINLICHKEITSAUFGABEN RUMSCHLAGEN. HE! WARTE DOCH AUF UNS! 33 KAPITEL 5 JAKOB BERNOUILLI Französischer Mathematiker (1601-1665) Stammt einer Familie großer Wissenschaftler ab (Jakob, Daniel, Nicolas) Einiger seiner wichtigsten Werke sind Die Kunst der Vorhersage (hinterlassen) und Das Gesetz der großen Zahlen. Kapitel 5 - JAKOB BERNOIULLI WAS FÜR EIN KOMISCHES LAND FÜR EINEN KLASSENAUSFLUG! EINS STEHT FEST: WIR SIND NICHT IN HANOI IN ASIEN! HANOI! ENDLICH! WER HAT ES DENN IN KLASSE VORGESCHLAGEN? HATTEN WIR NICHT DAVON GEREDET IN EINEN VERGNÜGUNGSPARK ZU GEHEN? WAS IST DENN DAS FÜR EIN LAND? NEIN, IN HANOI DER PROVINZ TARTAGLIA IM LAND DES MITTELWERTS. ES IST DAS LAND DER WAHRSCHEINLICHKEITEN. UND WAS SCHAUEN WIR UNS HIER AN? KENNT IHR DEN TURM VON HANOI? WIE AUFREGEND! GEHEN WIR HIN! ES HANDELT SICH ALSO UM EINEN VERGNÜGUNGSPARK? JA, UM ETWAS ÄHNLICHES. ICH GLAUBE WIR HABEN IHN GENAU VOR UNS. 35 Kapitel 5 - JAKOB BERNOUILLI NOCH DAZU HANDELT ES SICH NICHT NUR UM EINE MATHEMATISCHE KONSTRUKTION, SONDERN AUCH UM EIN SPIEL. UND WIE SPIELT MAN ES? ALSO GUT. WIR SPIELTEN ES LETZTES JAHR. WIR STELLTEN 3 STÄBE AUF, IN DIE WIR VERSCHIEDEN GROßE SCHEIBEN MIT EINEM LOCH IN DER MITTE AUFSPIEßTEN. DAS SPIEL BESTEHT NUN DARIN, ALLE SCHEIBEN EINES STABES AUF EINEN DER ZWEI ANDEREN ZU WERFEN, UND ZWAR UNTER FOLGENDEN BEDINGUNGEN: 1. ES DARF NUR JEWEILS EINE SCHEIBE GEWORFEN WERDEN. 2. EINE GROßE SCHEIBE DARF NIE AUF EINER KLEINEN ZU LIEGEN KOMMEN. AUF DIESE WEISE KÖNNEN WIR FESTSTELLEN, DASS MAN MIT 3 SCHEIBEN 7 BEWEGUNGEN AUSFÜHREN MUSS. DAS HEIßT ALSO DANN, 23 - 1 = 8 - 1 = 7 MIT 5 BEWEGUNGEN WÄREN NÖTIG: 25 - 1 = 32 - 1 = 31 MIT 6 BEWEGUNGEN WÄREN NÖTIG: 26 - 1 = 64 - 1 = 63 JA, JA, IST SCHON GUT. MIT „N” SCHEIBEN, SIND 2n - 1 BEWEGUNGEN NOTWENDIG. MENSCH GAUßI! ICH WETTE DU WEIßT INZWISCHEN SCHON ALLES ÜBER BINOME. 36 LASST UNS EIN SPIEL AUFBAUEN UND BEGINNEN WIR MIT NUR WENIGEN SCHEIBEN. WENN WIR NÄMLICH MIT ZU VIELEN SCHEIBEN SPIELEN, WERDEN WIR ALT DABEI. EIN BISSCHEN ETWAS, JA, GLAUBE ICH… WIE WIR ALLE WISSEN, IST EIN BINOM DIE ALGEBRAISCHE SUMME ZWEIER MONOME. DA WÄREN WIR SCHON WIEDER… Kapitel 5 - JAKOB BERNOUILLI Experimente: ANDERS AUSGEDRÜCKT: ES IST DIE SUMME ZWEIER ZAHLEN. DER EINFACHSTE FALL WÄRE (A + B). DA WIR ES JA JETZT MIT BINOMPOTENZEN ZU TUN HABEN, MÜSSEN WIR WIE FOLGT RECHNEN: (a + b) X (a + b) = (a + b)2 (a + b) X (a + b) X (a + b) = (a + b)3 ABER WIE MAN MULTIPLIZIERT, DAS HABEN WIR JA BEREITS IN KLASSE GESEHEN. WIR KÖNNTEN JEDOCH EINIGE SKIZZEN VORBEREITEN, UM UNS DAS GANZE BESSER VORSTELLEN ZU KÖNNEN. WEIßT DU WIE MAN DAS AM BESTEN DARSTELLT, GRAPHI? (a + b)2 b ab a a 2 a b b 2 ab b a a b b b a a a a b b IM ERSTEN FALL HABE ICH EIN QUADRAT MIT DER SEITENLÄNGE (A + B) GENOMMEN. AUF DIESE WEISE WIRD EINE SEITE ZUM QUADRAT ERHOBEN, DAS IST = (a + b)2. MAN SIEHT, DASS DAS ERGEBNIS FOLGENDES IST: a2 + a X b + a X b + b2 = a2 + 2ab + b2 UM DIE SEITE HOCH DREI ZU NEHMEN, HABEN WIR EINEN HEXAEDER ODER SECHSFLÄCHNER GEZEICHNET... WIE BITTE? EINEN WÜRFEL MIT DER SEITENLÄNGE A + B, DER AUFGEGLIEDERT FOLGENDERMAßEN AUSSCHAUT: 2 WÜRFEL a3 UND b3, PARALLELEPIPEDONS A X A X B, UND ANDERE 3 SCHIEFE QUADER A X B X B. WEIL JEDOCH 3 DIMENSIONEN SCHWERER ZU ZEICHNEN SIND, HABE ICH DAS GANZE AUCH IN ZWEI DIMENSIONEN DARGESTELLT: ICH HABE EIN RECHTECK GENOMMEN, EINE SEITE IST A + B, UND DIE ANDERE (a + b)2, AUF DAS ERGEBNIS SIND WIR VORHIN GEKOMMEN... LANGSAM, LANGSAM, ICH BIN NOCH IMMER BEIM „PARALLELEPIPEDON“… 37 Kapitel 5 - JAKOB BERNOUILLI Experimente: (a + b)3 = a3 + 3a2b + 3a2b + b3 (a + b)2 = a2 + 2ab + b2 b a ab a b 2 2 ab 2 2ab 3 2a b a a a 2 a 2 b b b axb 2ab 2 2 ab b 2 3 ICH ZEICHNE EUCH DIE GLEICHEN DARSTELLUNGEN AUF KARIERTEM PAPIER MIT FOLGENDEN GRÖßEN: (a+b) = (3+2) = 5. AUF DIESE WEISE KÖNNEN WIR EINHEIT PRO EINHEIT ZÄHLEN. 2 a a b a 9 6 a=3 a b 6 4 b=2 ab a2 = 9 2ab= 12 b2 = 4 (2 + 3)2 = 52 = 5 x 5 = 25 AH, ICH VERSTEHE. DAS SCHAUT SCHON GANZ ANDERS AUS. 38 =9 3 2 2ab=12 2 2a b 2ab 2 b =4 2 ab 2 a3 = 3a2b = 3ab2 = b3 = (2 + 3)3 = 53 = 5 x 5 x 5 = b 3 27 54 36 8 125 DANN LASST UNS GLEICH (a + b)4, ZEICHNEN. DAS WÄRE ALSO EIN QUADRAT MIT DER SEITENLÄNGE (a + b)2. Kapitel 5 - JAKOB BERNOUILLI Experimente: 2 2ab 4 2a b ab 3 4a b 2 2ab a 2 3 a a 2ab 2a b b 2 2 2 a4 + 4a3b + 6a2b2 + 4ab3 + b4 b 2 2 ab 2 2ab 2 3 b 3 4 ICH GLAUBE ICH HABE EINE NEUE ENTDECKUNG GEMACHT... LASS MICH MAL SEHEN... NACH DEINER LETZTEN ZEICHNUNG, ERGIBT (a + b)4 = (a4 + 4a3b + 6 a2b3 + b4), DAS MAN AUCH AUF DIESE WEISE SCHREIBEN KANN: (aaaa + 4aaab + 6aabb + 4abbb + bbbb) GUT, UND WAS JETZT? SEI NICHT SO UNGEDULDIG, DU WIRST ES GLEICH SEHEN. WENN WIR UNS DAS ERGEBNIS DER 4 JUNGS ODER MÄDCHEN IN ERINNERUNG RUFEN, HATTEN WIR: 1 MÖGLICHKEIT FÜR DEN FALL MMMM (4 KNABEN) 4 MÖGLICHKEITEN FÜR DEN FALL MMMW (3 KNABEN UND 1 MÄDCHEN) 6 MÖGLICHKEITEN FÜR DEN FALL MMWW (2 KNABEN UND 2 MÄDCHEN) 4 MÖGLICHKEITEN FÜR DEN FALL MWWW (1 JUNGE UND 3 MÄDCHEN) 1 MÖGLICHKEIT FÜR DEN FALL WWWW (4 MÄDCHEN) EKA! DIE KOEFFIZIENTEN STIMMEN ÜBEREIN! UND DAS ERGEBNIS ZEIGT MIR DIE VERTEILUNG AUF JUNGE/MÄDCHEN, KOPF/ZAHL, ERFOLG/MISSERFOLG... HEUR 39 Kapitel 5 - JAKOB BERNOUILLI ABER WAS IST, WENN ICH DIE WAHRSCHEINLICHKEIT, DASS IN EINER CLIQUE VON 9 FREUNDEN, 5 JUNGEN UND 4 MÄDCHEN SIND, WISSEN MÖCHTE? MUSS ICH DANN EINE TABELLE MIT ALL DEN MÖGLICHKEITEN ERSTELLEN? DAZU BRÄUCHTE ICH JA EINE EWIGKEIT! ODER MUSS ICH EIN KOMPLIZIERTES DIAGRAMM ERSTELLEN UM DIE ANTWORT AUF (a + b)9 ZU FINDEN? ICH HABE SCHON ERWARTET, DASS DU MIR DAS SAGEN WÜRDEST. UND BIS WIR EINE ALLGEMEINE FORMEL FÜR DIE BINOMPOTENZEN LERNEN, HABE ICH EINE NUMERISCHE PYRAMIDE GEFUNDEN, DIE LEICHT ZU ERSTELLEN IST UND UNSERE AUFGABE LÖSEN WIRD. 1 1 1 1 2 1 1 1 1 1 1 6 10 15 21 28 36 3 1 6 5 7 8 9 3 4 1 1 4 10 20 35 56 1 5 15 35 70 1 6 21 56 1 7 1 28 84 126 126 84 8 36 1 9 1 ICH BIN MIR SICHER, DASS IHR ES BEREITS ENTDECKT HABT! JEDE ZAHL, AUßER DEN EINSERN AM RAND DER PYRAMIDE, DIE IMMER GESCHRIEBEN WERDEN, ERHÄLT MAN DURCH ADDITION DER BEIDEN KOEFFIZIENTEN, DIE ÜBER IHR LIEGEN. KOEFFIZIENTEN SIND DIE ZIFFERN, DIE BETRÄGE. GAUßI, ICH GLAUBE ICH KANN EIN PAAR NÜTZLICHE SCHLUSSFOLGERUNGEN ZIEHEN: DIE AUFGABE BESTEHT DARIN, IN EINER GRUPPE VON 9 PERSONEN, DIE WAHRSCHEINLICHKEIT VON MMMMMWWWW ZU BERECHNEN. 40 Kapitel 5 - JAKOB BERNOUILLI UM DIE MÖGLICHKEITEN ZU BERECHNEN, WERDE ICH ES MIT DEM VERGLEICHEN, WAS WIR FÜR DIE GRUPPE VON 4 GESCHWISTERN GEMACHT HABEN. ICH BIN DARAUFGEKOMMEN, DASS FÜR NULL FRAUEN DER ERSTE KOEFFIZIENT GÜLTIG IST; FÜR EINE FRAU, DIE ZWEITE ZAHL. WIR HABEN AUCH GESEHEN, DASS DIE GRUPPE VON 4 PERSONEN IN DER REIHE ZU SUCHEN WAR, DEREN ZWEITE NUMMER 4 IST (ALLE ERSTEN ZIFFERN SIND EINE EINS). DA DIE JETZIGE GRUPPE AUS 9 PERSONEN BESTEHT, IST DAS ERGEBNIS IN DER REIHE ZU SUCHEN, DEREN ZWEITE ZAHL EINE 9 IST. 1 9 36 84 126 126 84 36 9 1 UND DA ICH NUN 4 FRAUEN HABE, MUSS ICH DIE FÜNFTE ZAHL SUCHEN, DAS HEIßT WIR HABEN 126 MÖGLICHKEITEN. UM DIE GESAMTZAHL DER FÄLLE ZU BERECHNEN, WENDE ICH DEINE REGEL AN... UFF! FÜR 2 WÜRFE WAREN ES 22, FÜR 3 WAREN ES 23, FÜR 4 WAREN ES 24, ALSO 16. DEMNACH SIND ES FÜR 9 29… 55, ES SCHEINT ALS OB DU AUCH ZUR FAMILIE DER BERNOUILLI GEHÖREN WÜRDEST. DU HAST BEINAHE DAS INDUKTIONSPRINZIP BESCHRIEBEN, DOCH DARÜBER WERDEN WIR UNS AN EINEM ANDEREN TAG UNTERHALTEN. LASST MICH MIT MEINEM RECHNER DIE SUMME BERECHNEN.... 512! DAS BEDEUTET, DASS DIE WAHRSCHEINLICHKEIT 126 IST. 512 ICH MUSS EUCH NOCH SAGEN, DASS MAN AUCH DIE SUMME DER REIHE, MIT DER MAN ARBEITET, ADDIEREN KANN, UM AUF DIESE WEISE DIE GESAMTZAHL DER FÄLLE ZU BERECHNEN. 1 + 9 + 36 + 84 + 126 + 126 + 84 + 36 + 9 + 1= 512 WIR LASSEN DEM SUPERTOLLEN FOLGENDE AUFGABE LÖSEN: GEFRAGT IST DIE WAHRSCHEINLICHKEIT, DASS IN EINER KLASSE VON 12 SCHÜLERN, 3 JUNGEN UND DER REST DER SCHÜLER MÄDCHEN SIND. VORAUSSETZUNG IST NATÜRLICH, DASS DIE MÖGLICHKEITEN IN DER GLEICHEN KLASSE ZU SEIN FÜR MÄDCHEN UND FÜR JUNGEN GLEICH IST. 41 Kapitel 5 - JAKOB BERNOUILLI WIR HABEN DIE WAHRSCHEINLICHKEIT FÜR MMMMMWWWW GESUCHT. UNSERE FORMEL WÜRDE ALSO FOLGENDERMAßEN AUSSEHEN: (a5 + b4) 126 a5 b4 OBWOHL WIR IN UNSEREM FALL VORAUSGESETZT HABEN, DASS DIE WAHRSCHEINLICHKEIT FÜR MÄDCHEN UND FÜR BURSCHEN GLEICH IST, WIRD ES FÄLLE GEBEN, IN DENEN DAS NICHT SO IST. DESHALB WERDEN WIR UNS EINE ALLGEMEINE METHODE ANSEHEN, UM EINE DERARTIGE AUFGABE ZU LÖSEN. WIR MACHEN FOLGENDES: 126 X ( 1 5 ) 2 X ( 1 4 126 ) = 512 2 DAS ERGEBNIS. NUN WERDE ICH EIN BEISPIEL MACHEN, IN DEM DIE WAHRSCHEINLICHKEITEN NICHT DIE GLEICHEN SIND. ICH WERDE ES DIR DIKTIEREN, UND ZWAR MIT EINER DUNKLEN, BEEINDRUCKENDEN STIMME: „GEFRAGT IST DIE WAHRSCHEINLICHKEIT, MIT DER MAN, WENN MAN INSGESAMT 9 MAL WÜRFELT, 5 MAL EINE 3 WÜRFELT UND IN DEN RESTLICHEN WÜRFEN EINE ANDERE BELIEBIGE ZAHL.“ 1 5 6 6 ALSO… DIE WAHRSCHEINLICHKEIT EINE 3 ZU WÜRFELN IST DIE WAHRSCHEINLICHKEIT KEINE 3 ZU WÜRFELN IST ERGEBNIS: 26 X ( 1 )5 6 X ( 5 )4 UND SO KOMME ICH ZUM ENDGÜLTIGEN RESULTAT: 126 X ( 1 5 ) 6 X ( 5 4 1 ) = 126 X ( ) 6 7771 78750 = 0, 0078 10077696 X 6 ICH WÜRDE NIE IM LEBEN EINE DERARTIGE WETTE ABSCHLIEßEN! DAMIT HABEN WIR WIEDER EIN GROßES EXPERIMENT BEENDET. JETZT IST EUCH HOFFENTLICH AUCH KLAR WARUM WIR DIESES LAND DER TÜRME UND PYRAMIDEN BESUCHT HABEN. 42 ALLES RECHT UND SCHÖN, ABER LASST UNS INS HOTEL ZURÜCKKEHREN. ICH FREUE MICH SCHON AUF EINEN ERFRISCHENDEN SPRUNG IN DEN POOL! ( 625 )= 1296 KAPITEL 6 CHARLES DODGSON Von seinen Anhängern als LEWIS CARROLL bekannt. Englischer Mathematiker (1832-1898), Autor von „Alice im Wunderland” und „Alice hinter den Spiegeln”. Seine Erzählungen haben mit der Spieltheorie zu tun, und in einigen Fällen können seine Geschichten als Grundlage für statistische Anwendungen betrachtet werden. Kapitel 6 - CHARLES DODGSON ES IST ES WERT EINE WANDERUNG ZU MACHEN. WAS FÜR EINE TOLLE AUSSICHT! NOCH DAZU HATTEN WIR GLÜCK MIT DEM WETTER! ES IST SO EIN KLARER TAG HEUTE, WIR KÖNNEN FAST DIE GANZE INSEL SEHEN, DIE KÜSTE, DIE STÄDTE, DIE DÖRFER UND DIE WÄLDER. BINOMI, HAST DU EINE LANDKARTE MITGEBRACHT, DAMIT WIE WISSEN WELCHE STÄDTE ODER DÖRFER WIR SEHEN? NATÜRLICH, GERADE GESTERN HABEN SIE UNS EINE KARTE DER BALEAREN GEGEBEN, DER DIE AUSDEHNUNGEN DER STÄDTE UND DÖRFER IN KM2 UND DEREN EINWOHNERZAHL ANGIBT. UNSER LEHRER HAT UNS AUFGEGEBEN, DIE BEVÖLKERUNGSDICHTE DER INSELN AUSFINDIG ZU MACHEN. SEHR INTERESSANT. DU HAST ALSO DIE DATEN DER AUSDEHNUNG UND DER EINWOHNER. ICH GLAUBE DIE ANTWORT IST EINFACH: IM SOMMER UND AN DER KÜSTE GIBT ES SEHR VIELE LEUTE, DOCH IM WINTER NUR SEHR WENIGE. DAS IST JA KEIN SCHLECHTER ANFANG! DIE ANGELEGENHEIT GEHT MEHR ODER WENIGER IN DIESE RICHTUNG... APROPOS, DAZU FÄLLT MIR EIN BEISPIEL EIN… DAS DIR, RÄTSI, BESONDERS GEFALLEN WIRD, DENN ES HAT MIT MUSIK ZU TUN. HÖR ZU, KÜRZLICH HABE ICH MIT FREUNDEN VON MIR GESPROCHEN. SIE SIND ROCKER UND HABEN GEMEINSAM EINE BAND MIT DEM NAMEN „QUARTIL“ GEGRÜNDET. SIE HABEN SICH EIN LOKAL GEMIETET, UM DORT ZU ÜBEN. DOCH SIE BESCHWERTEN SICH, DASS DAS LOKAL ZU KLEIN SEI, DENN ES HATTE 12 m2, WÄHREND EINE ANDERE BAND EIN LOKAL MIT 25 m2 HATTE. 44 Kapitel 6 - CHARLES DODGSON UND DA HABEN SIE DOCH AUCH RECHT... ICH BIN MIR NICHT SICHER, DENN ES FEHLEN MIR EINIGE ANGABEN. DAS IST RICHTIG. DIE ANDERE MUSIKGRUPPE NENNT SICH „DEZIL“, UND BESTEHT NATÜRLICH AUS 10 MUSIKERN. JETZT IST DIE SACHE SCHON ETWAS KLARER. DIE ROCKER DER GRUPPE „QUARTIL“ SIND IM IRRTUM, DENN PRO MITGLIED ENTSPRICHT IHNEN 12 = 3 M2, WÄHREND JEDEM 25 4 MUSIKER DER GRUPPE „DEZIL“ EIN ANTEIL VON = 2,5 M2 ENTSPRICHT. 10 AUSGEZEICHNET! SO IST ES. SOMIT KÖNNEN WIR UNS SCHON MIT DER BEVÖLKERUNGSDICHTE BESCHÄFTIGEN. DIESE ERHÄLT MAN, WENN MAN DIE EINWOHNERZAHL EINER STADT DURCH SEINE AUSDEHNUNG, ALSO DURCH DIE ANZAHL DER km2, DIVIDIERT. JA, ES IST BESSER DIE AUSDEHNUNGEN IN km2, ZU BERECHNEN, WEIL m2 WÜRDE EINE ZU KLEINE MESSEINHEIT FÜR EINE GANZE STADT SEIN. MAL SEHEN OB ICH’S VERSTANDEN HABE. WENN WIR DIE GANZE SACHE ANSCHAULICH DARSTELLEN MÖCHTEN, MÜSSTEN WIR EIN GEMEINDEGEBIET AUSSUCHEN UND DESSEN AUSDEHNUNG IN EINEM RELATIV GROßEN MAßSTAB ZEICHNEN. ANSCHLIEßEND MÜSSTEN WIR DAS GEBIET IN QUADRATISCHE PARZELLEN MIT EINER SEITENLÄNGE VON 1 km2 AUFTEILEN UND DANN DIE PERSONEN NACH UND NACH AUF DIE PARZELLEN AUFTEILEN, DAMIT SICH AUF JEDER PARZELLE LETZTENDLICH GLEICH VIELE PERSONEN BEFINDEN. DANN KÖNNTE ES ABER PASSIEREN, DASS WIR DEZIMALSTELLEN ERHALTEN, DAS HEIßT GANZE PERSONEN UND NOCH ETWAS... 45 Kapitel 6 - CHARLES DODGSON JA, JA, ABER WIR SPRECHEN JA VON EINEM MATHEMATISCHEN MITTELWERT, EINER QUOTE, EINEM QUOTIENTEN, EINER VERHÄLTNISZAHL, UND NICHT VON EINER MESSEINHEIT EINES TISCHLERS... ICH WILL DAMIT SAGEN, DASS WIR NIEMANDEN AUSEINANDERSCHNEIDEN MÜSSEN... HEY, MEN! WAS FÜR „ÜBERWICHTIGE WÖRTER“ IHR DOCH VERWENDET! DU BRAUCHST DIR ABER WIRKLICH KEINE SORGEN MACHEN, DENN ALL DIESE WÖRTER BEDEUTEN DAS GLEICHE! SIE SIND SEHR NÜTZLICH, WENN DU DICH NICHT WIEDERHOLEN WILLST. IN ANDEREN WORTEN, WIR NEHMEN DIE EINWOHNERZAHL MEINES DORFES (DEN GANZEN GEMEINDEBEZIRK) UND DIVIDIEREN SIE DURCH SEINE AUSDEHNUNG. ICH BIN GERADE AM ÜBERLEGEN... GOTT SEI DANK MÜSSEN WIR DIE BEVÖLKERUNGSDICHTE DER BALEAREN BERECHNEN, UND NICHT DIE VON HONG KONG. DORT SIND ES JA NUR WENIGE km2 UND WIR MÜSSTEN DESHALB DIE PERSONEN WIE PYRAMIDEN ÜBEREINANDER STAPELN, DAMIT SIE ALLE PLATZ HÄTTEN. . HMM…. GUT…. 46 UND ES WIRD NOCH BESSER, RÄTSI! Kapitel 6 - CHARLES DODGSON AUF, AUF, LASST UNS GEHEN. WIR HABEN DIE KARTE UND WIR MÜSSEN DEN ENTSPRECHENDEN AUFKLEBER AUF JEDE STADT KLEBEN. BEGINNEN WIR ZU RECHNEN: DIE BEVÖLKERUNGSDICHTE DER BALEAREN: 796.483 = 158,896 5.012,6 Personen/km2 DIE BEVÖLKERUNGSDICHTE VON FORMENTERA: 5.859 83,20 = ............... DIE BEVÖLKERUNGSDICHTE VON IBIZA: 8.444 572,6 = ............... DIE BEVÖLKERUNGSDICHTE VON MALLORCA: ............. = ............... 3.640 DIE BEVÖLKERUNGSDICHTE VON MENORCA: ............. ............ = 96,466 Personen/km2 47 Kapitel 6 - CHARLES DODGSON STADT Illes Balears Einwohner Ausdehnung Bevölkerungsdichte 796483 5012,60 158,896 Pers./km2 Alaró 3834 45,70 Pers./km2 Alcúdia 10581 60,00 Pers./km2 Algaida 3542 89,80 Pers./km2 Andratx 8333 81,50 Pers./km2 Artà 5936 139,80 Pers./km2 503 18,10 Pers./km2 5019 29,80 Pers./km2 951 8,30 Pers./km2 4338 84,70 Pers./km2 32587 145,00 Pers./km2 Campanet 2277 34,70 Pers./km2 Campos 6944 149,70 Pers./km2 Capdepera 6752 54,90 Pers./km2 Consell 2210 13,70 Pers./km2 Costitx 849 15,40 Pers./km2 Deià 625 15,20 Pers./km2 Escorca 275 139,40 Pers./km2 Esporles 3811 35,30 Pers./km2 Estellencs 338 13,40 Pers./km2 14600 169,80 Pers./km2 580 19,50 Pers./km2 21103 58,30 Pers./km2 837 17,40 Pers./km2 Lloseta 4529 12,10 Pers./km2 Llubí 1893 34,90 Pers./km2 Llucmajor 21771 327,30 Pers./km2 Manacor 30177 260,30 Pers./km2 Mancor de la Vall 936 19,90 Pers./km2 Maria de la Salut 1733 30,50 Pers./km2 Marratxí 18084 54,20 Pers./km2 Montuïri 2235 41,10 Pers./km2 Muro 6028 58,60 Pers./km2 Palma 319181 208,60 Pers./km2 Petra 2571 69,90 Pers./km2 Pollença 13450 151,70 Pers./km2 Porreres 4226 86,90 Pers./km2 sa Pobla 10064 48,60 Pers./km2 1163 42,30 Pers./km2 Banyalbufar Binissalem Búger Bunyola Calvià Felanitx Fornalutx Inca Lloret de Vistalegre Puigpunyent Kapitel 6 - CHARLES DODGSON Sencelles 1969 52,90 Pers./km2 Sant Joan 1662 38,50 Pers./km2 Sant Llorenç 5594 82,10 Pers./km2 1114 20,30 Pers./km2 Santa Margalida 7107 86,50 Pers./km2 Santa Maria del Camí 4558 37,60 Pers./km2 Santanyí 7974 124,90 Pers./km2 Selva 2918 48,70 Pers./km2 ses Salines 3240 39,10 Pers./km2 Sineu 2616 47,70 Pers./km2 Sóller 11207 42,80 Pers./km2 Son Servera 8065 42,60 Pers./km2 Valldemossa 1599 42,90 Pers./km2 Vilafranca de Bonany 2249 24,00 Pers./km2 772 23,90 Pers./km2 637510 3640,80 Pers./km2 7046 109,90 Pers./km2 Ciutadella 21785 186,30 Pers./km2 Ferreries 3921 66,10 Pers./km2 22358 117,20 Pers./km2 es Mercadal 2723 158,00 Pers./km2 Sant Lluís 4106 34,80 Pers./km2 es Castell 6005 11,70 Pers./km2 1126 32,00 Pers./km2 69070 716,00 96,466 Pers./km2 5859 83,20 Pers./km2 Eivissa 31582 11,10 Pers./km2 S. Antoni de Portmany 14849 126,80 Pers./km2 Sant Josep 13364 159,40 Pers./km2 3943 121,70 Pers./km2 Santa Eulàlia des Riu 20306 153,60 Pers./km2 EIVISSA 84044 572,60 Pers./km2 Santa Eugènia Ariany MALLORCA Alaior Maó es Migjorn Gran MENORCA Formentera S. Joan de Labritja KAPITEL 7 WILLIAM SEALEY GOSSET Britischer Statistiker (1876-1937) Er war Chemiker der Guinness Fabrik und beeindruckte vor allem mit seinen hervorragenden statistischen Werken über kleine Stichproben. Bekannt ist er nicht mit seinem Namen, sondern mit seinem Pseudonym „Student“. Aus diesem Grund nennt sich seine Errungenschaft Student-t-Verteilung. Kapitel 7 - WILLIAM SEALEY GOSSET HEUTE BESUCHEN WIR DAS STATISTISCHE INSTITUT DER BALEAREN. ICH HABE GEFRAGT, OB WIR UNS HIER TREFFEN KÖNNEN, DENN HIER STEHEN UNS JEDE MENGE DATEN ZUR VERFÜGUNG. WIE DIE DINGE HIER FUNKTIONIEREN, INTERESSIERT MICH AUßERORDENTLICH. DIE STATISTIK FÄNGT AN MIR ZU GEFALLEN UND ES WÄRE WICHTIG, DASS SIE MICH HIER KENNEN LERNEN, DENN EINES TAGES, WENN ICH BEREITS ALLES WEIß, KÖNNTEN SIE MICH JA UNTER UMSTÄNDEN ZU IHREM DIREKTER ERNENNEN. LASST EUCH NICHT ZUVIEL SEHEN, WENN IHR NICHT WOLLT, DASS SIE UNS MIT EINER STUDIE BEAUFTRAGEN. JETZT HABEN WIR WIRKLICH JEDE MENGE DATEN FÜR UNSERE EXPERIMENTE. SCHAUT EUCH DIESES DIAGRAMM AN! ES ZEIGT DIE WAHRSCHEINLICHKEITEN MEHRERER MÜNZWÜRFE, ODER DIESES HIER DIE WAHRSCHEINLICHKEITEN MEHRERER SPIELE MIT ERFOLG-MISSERFOLG MIT DER WAHRSCHEINLICHKEIT 1 . 2 51 Kapitel 7 - WILLIAM SEALEY GOSSET Experimente: 1 1/2 1/4 1/8 1/4 3/4 3/8 3/8 4 16 1 16 1/2 6 16 1/8 4 16 1 16 WIR KÖNNEN SIE ABZEICHNEN UND SIE MIT MEINER GRAPHIK VERGLEICHEN. Z K KK KKZ KKK KKKK 52 KKKZ ZZ KZ ZZZ KZZ KKZZ KZZZ ZZZZ Kapitel 7 - WILLIAM SEALEY GOSSET Experimente: DAS WIRD JA IMMER INTERESSANTER. SCHAUT EUCH DIESES DIAGRAMM AN. ES MUSS MIT DEM, WAS WIR GESEHEN HABEN, ZU TUN HABEN, WEIL SIE ES BEVÖLKERUNGSPYRAMIDE NENNEN. 100 - .... 95 - 99 90 - 94 85 - 89 80 - 84 75 - 79 70 - 74 65 - 69 60 - 64 55 - 59 50 - 54 45 - 49 40 - 44 35 - 39 30 - 34 25 - 29 20 - 24 15 - 19 10 - 14 5 -9 0 - 4 40.000 30.000 20.000 10.000 10.000 20.000 30.000 40.000 50.000 53 Kapitel 7 - WILLIAM SEALEY GOSSET JA, ES IST EIN THEMA, DAS UNSERE VORIGE STUDIE ÜBER DIE BEVÖLKERUNG VON EINWOHNERN… ICH HÄTTE AUCH BEVÖLKERUNG VON PERSONEN SAGEN KÖNNEN, ABER WIE IHR VIELLEICHT WISST, IN STATISTIK MEINT MAN MIT BEVÖLKERUNG DIE GESAMTHEIT VON STUDIENOBJEKTEN, SEIEN DIES PERSONEN, PFLANZEN, PREISE, AUSGABEN, ETC... WARUM SAGST DU BEVÖLKERUNG VON EINWOHNERN? MENSCH, GAUßI, KOMM ZUR SACHE! WAS IST DENN EINE BEVÖLKERUNGSPYRAMIDE? EIGENTLICH SIND DIES DIAGRAMME, DIE AUF ZWEI SEITEN LEBENDE MENSCHEN NACH IHREM ALTER DARSTELLEN: AUF DER EINEN SEITE DIE MÄNNER, AUF DER ANDEREN DIE FRAUEN. SIE IST GANZ LEICHT ZU VERSTEHEN. SAG JA NICHT EINFACH. ES IST SCHON EHER GANZ SCHWIERIG, ABER WEIL WIR JA SCHON SOWEIT FORTGESCHRITTEN SIND, KÖNNEN WIR SIE VERSTEHEN. UND WARUM DAS? 54 SCHAU HER. JEDER BALKEN ZEIGT DIE ANZAHL DER LEBENDEN MENSCHEN IN DER ALTERSGRUPPE, DIE IN DER MITTE ANGEFÜHRT WIRD: AUF EINER SEITE DIE BURSCHEN, AUF DER ANDEREN DIE MÄDCHEN. DIESE GRAFIK NENNT MAN PYRAMIDE, WEIL, JE HÖHER, ALSO JE ÄLTER DIE BEVÖLKERUNG, DESTO MEHR NIMMT DEREN ZAHL AB. ICH HABE EINE ANDERE GEZEICHNET. DIE JUNGS MÜSSEN AUF SICH AUFPASSEN, ...UND DIE MÄDCHEN AUCH. Kapitel 7 - WILLIAM SEALEY GOSSET SCHAUT EUCH DEN ALTERSABSCHNITT VON 15 BIS 25 JAHRE AN! DORT NÄMLICH NIMMT DIE PYRAMIDE MEHR AB ALS SIE SOLLTE. IHR SEHT ALSO, DASS MAN VON RICHTIGEN DATEN VIELE SCHLUSSFOLGERUNGEN ZIEHEN KANN, UND NOCH DAZU ZUVERLÄSSIGE! DAS IST AUF DIE MOTORRÄDER UND AUTOS ZURÜCKZUFÜHREN. ICH MEINE DIE KRANKHEIT VON HEUTE: DIE UNFÄLLE. WIR SOLLTEN UNS IM LEBEN AMÜSIEREN, ABER MIT DER BEDINGUNG, DASS WIR NOCH MIT 90 JAHREN STATISTIKEN ERSTELLEN KÖNNEN, WENN WIR MÖCHTEN. JA, DENN MIT ETWAS GLÜCK MÜSST IHR ALLE KOMMEN, WENN SIE MIR DEN NOBELPREIS VERLEIHEN. 55 Kapitel 7 - WILLIAM SEALEY GOSSET BBRRRRUMM... !!! HA, HA, HA! HA, HA, HA! RUHE IM SAAL! ICH MUSS EUCH AUF EINE TATSACHE AUFMERKSAM MACHEN, UND ICH WERDE MICH BEMÜHEN, DIES SO „SYMPATISCH“ WIE MÖGLICH ZU TUN. MAN MUSS DIE GRAPHIKEN IMMER UNTER DIE LUPE NEHMEN: SICH DIE VERWENDETEN MAßSTÄBE UND ALLE DETAILS GENAU ANSEHEN. UM AUF DIESE WEISE DIE NUMERISCHEN DATEN ZU BEWEISEN. WARUM SAGST DU DENN DAS? Experimente: ICH WERDE EUCH EIN BEISPIEL ZEIGEN, DAS IN BÜCHERN ÜBER OPTISCHE TÄUSCHUNGEN VORKOMMT. VERGLEICHT DIE ZWEI GRAPHIKEN.. 56 Kapitel 7 - WILLIAM SEALEY GOSSET Experimente: SIE BESTEHEN AUS DEN GLEICHEN FORMEN, SIE SIND NUR AUF VERSCHIEDENE WEISE ANGEORDNET: ZWEI DREIECKE AUS 16 X 6 RASTER. ZWEI RECHTECKIGE TRAPEZE MIT EINER GRUNDFLÄCHE VON 6 UND 10, UND EINER HÖHE VON 10. AUS DIESEM GRUND MÜSSEN DIE FLÄCHEN DES QUADRATS UND DES RECHTECKS GLEICH GROß SEIN. NÄMLICH: QUADRAT: 16 X 16 = 256 RECHTECK: 26 X 10 = 260 SIE MÜSSTEN DOCH DIE GLEICHE GRUNDFLÄCHE HABEN. NICHT SCHON WIEDER! HAT ES NICHT DEN ANSCHEIN, DASS STRICH A KÜRZER IST ALS STRICH B? BEVOR ICH ES EUCH ERKLÄRE, ZEICHNEN WIR: ICH VERSPRECHE, DASS DIE ZWEI GLEICH LANG SIND, UND IHR KÖNNT EUCH GERNE ÜBERZEUGEN. DAS GLEICHE GILT FÜR DIE VORIGE GRAPHIK: WENN WIR SIE MIT DÜNNEREN STRICHEN ZEICHNEN, SEHEN WIR, DASS DIE FIGUREN NICHT ÜBEREINSTIMMEN. 57 Kapitel 7 - WILLIAM SEALEY GOSSET Experimente: IN ROT S IND D IE 4 FEH LENDE N RASTE R ANGE ZEIGT . DER SUPERTOLLE SOLL DIE FIGUREN ZEICHNEN UND DIE FORMEN AUSSCHNEIDEN. DANN WERDEN WIR SEHEN, DASS SIE NICHT ÜBEREINSTIMMEN. DESHALB MÜSSEN WIR DIE GRAPHIKEN IMMER IN ZUSAMMENHANG MIT DEN NUMERISCHEN DATEN BETRACHTEN. UND WAS MACHEN WIR JETZT? WIR KÖNNTEN DOCH EIN VOLLEYBALLMATCH SPIELEN? IN ORDNUNG, ABER ICH BIN NICHT SCHIEDSRICHTER. 58 LASST UNS ALSO GEHEN! KAPITEL 8 ETIENNE L. LASPEYRES UND HERMANN PAASCHE Erfinder des Preisindexes für die Lebenshaltungskosten, die auch heute noch verwendet werden. Kapitel 8 - LASPEYRES UND PAASCHE HE! HIER IST EIN BUCH, IN DEM WIR VORKOMMEN! WIR WERDEN DOCH NICHT SCHON BERÜHMT SEIN! LASS MAL SEHEN... AH DU HAST RECHT, ES HANDELT SICH UM EINE STATISTIK ÜBER SCHULAUSBILDUNG. BESTIMMT SIND WIR IN DIESEN ZAHLEN ENTHALTEN. Ausbildungsstatistik Jahrgang 88-89 89-90 90-91 91-92 92-93 93-94 94-95 95-96 96-97 97-98 98-99 Balearische Inseln: Kindergarten Index Grundschule Index 19.957 19.958 19.220 19.313 19.706 20.123 20.719 22.063 23.169 23.982 24.449 1 1,0001 0,9631 0,9677 0,9874 1,0083 1,0382 1,1055 1,1609 1,2017 1,2251 96.772 95.596 92.481 89.024 85.944 83.197 80.008 77.419 64.165 55.294 55.600 1,1260 1,1123 1,0761 1,0358 1 0,9680 0,9309 0,9008 0,7466 0,6434 0,6469 UFF! ICH HABE MIR SCHON ALL DEN JOURNALISTENRUMMEL VORGESTELLT! BESTIMMT SIND WIR SCHLIMMEREM ENTGANGEN! 60 Sekundärschule ESO Index 4.432 8.683 10.742 13.609 28.975 38.872 39.821 1 1,9592 2,4237 3,0706 6,5377 8,7708 8,9849 Kapitel 8 - LASPEYRES UND PAASCHE HMMM! MIR IST DIE ANZAHL DER KINDER, DIE IM KINDERGARTEN SIND, DIE SCHÜLER, WELCHE DIE GRUNDSCHULE BESUCHEN UND DIEJENIGEN, DIE WIE WIR IN DER SEKUNDÄRSCHULE SIND, KLAR, DOCH ICH WEIß NICHT WAS DAS MIT DEN INDEXEN BEDEUTEN SOLL! NEIN, DAS BESTIMMT NICHT. ES MUSS SICH UM EIN STATISTISCHES KONZEPT HANDELN. ES WIRD WAHRSCHEINLICH DIE SEITE SEIN, AUF DER WIR SIND. ABER NATÜRLICH. IN STATISTIK, EIN INDEX IST EIN PROZENTANTEIL, DEN MAN VON EINER ZAHL BERECHNET, DIE MAN ALS BASIS VERWENDET. ICH STELLE EINIGE BERECHNUNGEN DER ZAHLEN AN, DIE AUF DER SEITE, DIE WIR VORHIN GEFUNDEN HABEN, STEHEN. DABEI BIN ICH DRAUFGEKOMMEN, DASS SICH DER INDEX DER SPALTE DES KINDERGARTENS, AUS DER DIVISION DER SCHÜLER EINES SCHULJAHRES DURCH DIE ANZAHL DER SCHÜLER EINES ANDERES JAHRES, NÄMLICH DIE DES SCHULJAHRES 89/90 ERGIBT. 19.958 = 1,0001 19.957 10.220 = 0,9631 19.957 23.169 = 1,1609 19.957 DU MEINST ALSO DIE DIVISION DER ANZAHL DER SCHÜLER EINES SCHULJAHRES DURCH EINE ANDERE, DIE WIR ALS AUSGANGSZAHL VERWENDEN. WAS WIR BIS JETZT ENTDECKT HABEN, IST SCHON SEHR GUT. IHR SEHT ALSO, DASS DER INDEX DER SPALTE KINDERGARTEN DIE UNTERSCHIEDE ZWISCHEN GRUPPEN, ÄH... DAS HEIßT ZWISCHEN SCHULJAHREN MISST. ABER ICH HABE JA BEREITS GESAGT, DASS MAN DURCH EINE ZAHL TEILEN MUSS, DIE MAN ALS BASIS NIMMT. ABER DAS GILT NICHT FÜR DIE SPALTE DER GRUNDSCHULE, UND ICH KOMME NICHT DRAUF WIE DORT DER INDEX BERECHNET WURDE. AHA! JETZT HAB ICH’S! IN DER SPALTE GRUNDSCHULE VERWENDET MAN DAS SCHULJAHR 92/93 ALS BASIS... JA, DAS WAR WIRKLICH EIN BEDEUTENDES JAHR, DENN DAMALS ÄNDERTEN SICH UNSERE CHANCEN. DU HAST RECHT, IN DIESEM JAHR TRAT DIE NEUE SCHULREFORM LOGSE, UND DAMIT DIE NEUE SEKUNDÄRSCHULE ESO, IN KRAFT. 61 Kapitel 8 - LASPEYRES UND PAASCHE DEMNACH LÄSST SICH AUS DER TABELLE ABLESEN, DASS IN DEN SCHULJAHREN 90/91, 91/92, 92/93 WENIGER KINDER DEN KINDERGARTEN BESUCHTEN, WÄHREND MAN IM SCHULJAHR 98/99, VERGLICHEN MIT DEN JAHREN 88/89, EINEN ZUWACHS VON 22% VERZEICHNETE. UND AUCH DIE SPALTE DER SEKUNDÄRSTUFE NIMMT DASSELBE JAHR ALS REFERENZ. MEHR NOCH, WENN WIR DIE INDEXE FÜR DIE SEKUNDÄRSCHULE BEOBACHTEN, SEHEN WIR, DASS WIR NICHT NUR UM 22% MEHR SIND, SONDERN DASS WIR UNS IM VERGLEICH ZU DEN SCHÜLERN, DIE IM JAHR 1992 BEGONNEN HABEN, SOGAR VERNEUNFACHT HABEN. JETZT IST ES MIR KLAR! TEILWEISE AUF DIESEN ANSTIEG, ABER AUCH AUF DIE EINFÜHRUNG DES ERSTEN ABSCHNITTES DER NEUEN SEKUNDÄRSCHULE ZURÜCKZUFÜHREN, HAT SICH EIN RÜCKGANG DER SCHÜLERANZAHL IN DER GRUNDSCHULE ERGEBEN, WEIL ES JA DAS 7. UND 8. SCHULJAHR DER GRUNDAUSBILDUNG NICHT MEHR GIBT. DAS HEIßT ALSO, DASS WIR MIT HILFE VON INDEXEN SCHNELLER UND VIEL LEICHTER SCHLUSSFOLGERUNGEN ZIEHEN KÖNNEN, WEIL DIE NUMMERN IMMER MIT DER EINHEIT 1 VERGLICHEN WERDEN. 62 PERFEKT. DAS WIRD JA IMMER BESSER. ES FING MIT DER ERKLÄRUNG VON BINOMI AN, DER ZWISCHEN DEM 22%IGEN ZUWACHS UND DER VERNEUNFACHUNG DER SCHÜLER ZU UNTERSCHEIDEN WUSSTE... UND DA WIR DIESEN INDEX VERSTANDEN HABEN, KÖNNEN WIR AUCH DEN DES EINKAUFSKORBES, DES BRUTTOSOZIALPRODUKTES UND, JA EIGENTLICH ALLE, INTERPRETIEREN. Kapitel 8 - LASPEYRES UND PAASCHE ALLERDINGS SIND DIESE SCHON ETWAS KOMPLIZIERTER. ABER DENKT IHR NUR WEITER DARÜBER NACH WELCHE DATEN WIR FÜR UNSER EXPERIMENT BENÖTIGEN, WÄHREND ICH MICH ERKUNDIGEN GEHE. SCHAUT HER WAS ICH HIER HABE! ES SCHEINT ALS OB DU ’S BEREITS WÜSSTEST. ALSO, PASST MAL GENAU AUF, DENN ES GIBT VERSCHIEDENE ARTEN VON INDEXES: DIE EINFACHEN, WIE DER, DEN WIR SOEBEN ENTDECKT HABEN, UND ANDERE, DIE ETWAS SCHWIERIGER SIND, WIE ZUM BEISPIEL DER VPI (VERBRAUCHERPREISINDEX). AUF ALLE FÄLLE HABEN SIE MIR EIN DIAGRAMM GEZEICHNET, UND WENN UNS DIE SACHE ETWAS KLARER IST, KÖNNEN WIR JA KOMMEN, DAMIT SIE UNS ZEIGEN, WIE MAN SIE UND DIE DAZUGEHÖRENDEN STATISTIKEN ERSTELLT. GIB MIR EIN BISSCHEN ZEIT, ICH MÖCHTE DEINE AUFZEICHNUNGEN ETWAS ÜBERSICHTLICHER DARSTELLEN… WÄHREND IHR DIE GRAPHIKEN VORBEREITET, WERDE ICH EUCH EINE AUFGABE STELLEN. ICH HABE ICH GELESEN, DASS DER FRANZÖSISCHE KÖNIG LUDWIG XV ÜBER EIN JÄHRLICHES EINKOMMEN VON 100 MILLIONEN VERFÜGTE. 63 Kapitel 8 - LASPEYRES UND PAASCHE !!! ¡¡¡ ABER ZWEIHUNDERT JAHRE VORHER, LUDWIG XII HATTE EINKÜNFTE VON 8 MILLIONEN. WER GLAUBT IHR HAT MEHR VERDIENT? ¡¡¡ ! ¡¡ ¡ !! !!! ¡¡¡ !!! DAS IST WIE DIE FRAGE NACH DER FARBE DES WEIßEN SCHIMMELS... EBEN NICHT! UND WEIL EIN WISSENSCHAFTLER DES 12. JAHRHUNDERTS SICH WIE WIR DAMIT BESCHÄFTIGT HATTE, EXPERIMENTE ZU MACHEN, UND AUCH BERECHNUNGEN MIT EINER ART VON EINKAUFSKORB (DEN WIR HEUTE VERBRAUCHSGÜTERINDEX NENNEN WÜRDEN) ANSTELLTE, KONNTE ER NACHWEISEN, DASS SICH DIE WÄHRUNG SEIT DEN ZEITEN LUDWIGS XII BIS ZUM KÖNIG LUDWIG XV 1 UM DEN INDEX VON ABGEWERTET 22 HATTE. RECHNET’S EUCH AUS UND IHR WERDET SEHEN, DASS LUDWIG XII MEHR VERDIENTE. MÜNZEN, SCHMUCK, ETC… MÜNZEN, SCHMUCK, ETC… LUDWIG XII LUDWIG XV Euro 0,5 DM 0,05 Euro 1,25 DM 1,75 Euro 1 DM 1,- 64 ANTIKE LEBENSMITTEL (PREISE IN DEUTSCHE MARK) MODERNE LEBENSMITTEL (PREISE IN EURO) Kapitel 8 - LASPEYRES UND PAASCHE WENN MAN NICHT GENAU SCHAUT UND NICHT BEMERKT, DASS DIE PREISE IN EURO ANGEGEBEN SIND, MEINT MAN, DASS DIE PREISE IN DEN LETZTEN 60 JAHREN NICHT GESTIEGEN SIND. DARUM MUSS MAN DEN WERT DER WÄHRUNG IMMER BERÜCKSICHTIGEN, WIE IM FALL DER BEIDEN KÖNIGE... ICH HABE DIE GESCHICHTE GEHÖRT UND SIE SCHEINT MIR, FÜR DAS, WOMIT WIR UNS BESCHÄFTIGEN, SEHR PASSEND. LASPEYRES-INDEX ALTE EINHEITEN ALTE EINHEITEN IL= NEUE PREISE ALTE PREISE ALTE EINHEITEN X NEUE PREISE ALTE EINHEITEN X ALTE PREISE 65 Kapitel 8 - LASPEYRES UND PAASCHE PAASCHE-INDEX NEUE NEUE EINHEITEN PREISE NEUE EINHEITEN ALTE PREISE IP= NEUE EINHEITEN X NEUE PREISE NEUE EINHEITEN X ALTE PREISE IHR SEHT ALSO, DASS NEBEN DEN EINFACHEN INDEXEN, DIE WIR ENTDECKT HABEN, AUCH NOCH VIELE ANDERE EXISTIEREN. EINIGE ERHÄLT MAN DURCH DIE BERECHNUNG DES MITTELWERTS VON ANDEREN... = MITTELWERT... DAS WORT KOMMT MIR BEKANNT VOR, DOCH ICH WEIß NICHT MEHR WAS ES BEDEUTET... 66 Kapitel 8 - LASPEYRES UND PAASCHE ICH WERDE ES FÜR DAS NÄCHSTE EXPERIMENT AUFSCHREIBEN. UM FORTZUFAHREN... DIESE DARSTELLUNGEN WERDEN UNS WEITERHELFEN. AN EINEM ANDEREN TAG KOMMEN WIR WIEDER INS INSTITUT, DAMIT SIE UNS DIE RESTLICHEN DATEN GEBEN. ICH MÖCHTE EUCH DARAN ERINNERN, DASS WIR NÄCHSTE WOCHE EINE GEBURTSTAGSFEIER HABEN. BRINGT BITTE MORGEN DAS GELD FÜR DAS GESCHENK MIT, ALLE BIS AUF 55 NATÜRLICH, UND AUCH DAS GELD FÜR DIE GEBURTSTAGSFEIER. JEDER GIBT WAS ER KANN, UND WENN JEMAND NICHTS BEISTEUERN KANN, GIBT ER DAS NÄCHSTE MAL MEHR. ABER ES WERDEN AUCH NOCH ANDERE FREUNDE KOMMEN. IN ORDNUNG. UND BRINGT ES IN ZWEI GESCHLOSSENEN KUVERTS, DENN WIR KÖNNEN DAS GANZE DAZU VERWENDEN VON MITTELWERTEN, MEDIANEN UND VON DEN WAHRSCHEINLICHSTEN WERTEN ZU SPRECHEN. WAS FÜHRT IHR DENN IM SCHILDE? SAG IHNEN SIE SOLLEN DASSELBE TUN. SCHHHHH, ES KOMMT 55. OH NICHTS! IMMER SO SCHARFSINNIG... 67 KAPITEL 9 ABRAHAM DE-MOIVRE UND CARL FRIEDRICH GAUß De Moivre (1667-1754). Wichtiger Wissenschaftler mit verschiedenen Fachgebieten der Mathematik. Mit dem Schritt von der Binomial- zur Normalverteilung trug er erheblich zur Weiterentwicklung der Statistik bei. Eines seiner wichtigsten Werke „Über das Maß des Zufalls“ oder auch „Über die Wahrscheinlichkeit in Glücksspielen“ genannt, wendet er die Berechnung von Wahrscheinlichkeiten an. Gauß, ein deutscher Mathematiker und Statistiker (1777-1855), ist vor allem für seine Werke bekannt, welche Themen wie die Normalverteilung, die Streuung, das Fehlerfortpflanzungsgesetz, die Summe der kleinsten Fehlerquadrate,... behandeln. Kapitel 9 - DE MOIVRE UND GAUSS MACHT SCHNELL, 55 WIRD GLEICH KOMMEN! WÄHREND IHR DEN GARTEN SCHMÜCKT, GEHE ICH DAS ESSEN UND DIE GETRÄNKE FÜR DIE FEIER KAUFEN. HABT IHR ALLE DIE UMSCHLÄGE MIT EUREM BEITRAG DABEI? JA, WIR HABEN 15 KUVERTS FÜR DAS GESCHENK, WIR WERDEN SIE „G“ -UMSCHLÄGE NENNEN, UND 16 UMSCHLÄGE FÜR DAS FEST. WAS? 16 KUVERTS? WEIßT DU, ES WAR NÄMLICH SO: ICH HABE 55 UND ZUFÄLLI GETROFFEN. DA ZUFÄLLI MIR DIE UMSCHLÄGE GEGEBEN HAT, WOLLTE MIR 55 AUCH EINEN GEBEN. ABER SEID BERUHIGT, SIE HAT NATÜRLICH KEINE AHNUNG, DASS DIE GEBURTSTAGSFEIER UND DAS GESCHENK FÜR SIE SIND. LASST UNS ALSO DEN INHALT DER UMSCHLÄGE ZÄHLEN UND SIE AUF ZWEI STÖßE AUFTEILEN, EINEN STOß „G“ UND EINEN STOß „F“. BEEILT EUCH, DENN BALD WERDEN SIE KOMMEN! 69 Kapitel 9 - DE MOIVRE UND GAUSS Experimente: G... F.... 100 300 350 400 425 475 500 100 200 250 300 400 G... F.... 1 UMSCHLAG MIT 100 5 UMSCHLÄGE MIT 300 3 UMSCHLÄGE MIT 350 2 UMSCHLÄGE MIT 400 1 UMSCHLAG MIT 425 2 UMSCHLÄGE MIT 475 1 UMSCHLAG MIT 500 KOMMT ALLE, SIE NÄHERN SICH SCHON. 70 1 UMSCHLAG MIT 100 5 UMSCHLÄGE MIT 200 4 UMSCHLÄGE MIT 250 5 UMSCHLÄGE MIT 300 1 UMSCHLAG MIT 400 WIE ICH SEHE HABT IHR DAS EXPERIMENT OHNE UNS BEGONNEN. Kapitel 9 - DE MOIVRE UND GAUSS NEIN, ÄH, EIGENTLICH NICHT. WIR HABEN NUR ZWEI TABELLEN MIT DEN DATEN, DIE UNS ZUR VERFÜGUNG STANDEN, ERSTELLT. UND GAUßI HAT NUR NOCH DARAUF GEWARTET BIS IHR KOMMT. WIR MACHEN EIN SCHULABSCHLUSSFEST? ÄH! WIE IHR ALLE WISST, SOLLEN WIR HEUTE DEN MITTELWERT, DEN MEDIAN UND DEN MODUS BERECHNEN. DAZU HABEN WIR BEREITS ZWEI TABELLEN ERSTELLT: DIE ERSTE IST EINE GEHEIME LISTE, UND DIE ZWEITE BEINHALTET DIE AUFSTELLUNG DER BEITRÄGE FÜR EIN FEST. JEDER HAT EINEN BELIEBIGEN BETRAG, JEDER SO VIEL ER BEITRAGEN KONNTE, BEIGESTEUERT. UND AUFGRUND DIESER DATEN WERDEN WIR DIE FOLGENDEN MITTELWERT-KENNGRÖßEN BERECHNEN. WER WEIß? ÄH, WOLLEN WIR ALSO BEGINNEN. ICH HABE FOLGENDE GRAPHIK GEZEICHNET. SIE KÖNNTE UNS ALS GRUNDLAGE DIENEN. DARSTELLUNG LASST UNS MIT DEM MITTELWERT BEGINNEN. WIR WERDEN ZUERST EINMAL DEN ARITHMETISCHEN MITTELWERT BERECHNEN. DAZU DIENT UNS FOLGENDES BEISPIEL: ALSO, WIR GEHEN DAVON AUS, DASS WIR EINE EINHEITLICHE GRUPPE SIND. JEDER TRUG BEI, SO VIEL ER KONNTE. NEHMEN WIR AN, DASS UNS GLEICHE TEILE ENTSPRECHEN MÜSSTEN. DAS HEIßT ALSO, DAS WIR DEN GESAMTBETRAG AUF ALLE AUFTEILEN MÜSSEN, DAMIT JEDER GLEICH VIEL BEKOMMT. DAZU ADDIEREN WIR ALLE BETRÄGE UND DIVIDIEREN DIE GESAMTZAHL DURCH DIE ANZAHL DER TEILNEHMER. DA HÖRT SICH JA GANZ LEICHT AN. 71 Kapitel 9 - DE MOIVRE UND GAUSS LASST MICH DIE BETRÄGE DER REIHE „G“ ADDIEREN: 100 + 300 + 300 + 300 + 300 + 300 + 350 + 350 + 350 + 400 + 400 + 425 + 475 + 475 + 500. UFF! GEBT MIR EINEN TASCHENRECHNER! WARTE EINEN MOMENT. 55 HAT RICHTIG GERECHNET, DOCH ES GEHT AUCH ANDERS, UND ZWAR: 100 X 1 + 300 X 5 + 350 X 3 + 400 X 2 + 425 X 1 + 475 X 2 + 500 X 1, UND DANN DIVIDIEREN WIR DURCH 15. ICH HABE MEINEN COMPUTER DABEI UND GLAUBE, DASS MAN DIES GANZ EINFACH MIT EINER EXCEL-TABELLE AUSRECHNEN KANN. Modus Median Mittelwert GESAMT: Mittelwert JA DAS STIMMT. LASS MICH DIE REIHE „F“ MIT DEM COMPUTER BERECHNEN. 72 WARTE NOCH EIN BISSCHEN. ICH WERDE VERSUCHEN MIT DEM COMPUTER EINE GRAPHIK ZU ERSTELLEN. Kapitel 9 - DE MOIVRE UND GAUSS GRAPHIK Gesamt: Mittelwert SUPER! ES HAT GEKLAPPT! DANN WÄRE DIE REIHE „F” ALSO FOLGENDERMAßEN: GRAPHIK Gesamt: Mittelwert 73 Kapitel 9 - DE MOIVRE UND GAUSS DAS WÄRE SO: GRAPHIK DER ARITHMETISCHE MITTELWERT IST DIE AM HÄUFIGSTEN VERWENDETE MITTELWERT-MESSGRÖßE UND IST GLEICHZEITIG AUCH DIE, WELCHE SICH AM BESTEN FÜR BERECHNUNGEN EIGNET. DOCH IN EINIGEN FÄLLEN SIND ANDERE KENNGRÖßEN EMPFEHLENSWERTER, DA SIE MEHR ÜBERBLICK VERSCHAFFEN, ODER WEIL ES GANZ EINFACH UNMÖGLICH IST, DEN MITTELWERT ZU BERECHNEN. EIN BEISPIEL WÄRE DAS FOLGENDE: WIR HABEN: 30 MIT 100 50 MIT 200 20 MIT 500 10 MIT MEHR ALS 1000 IN DIESEM FALL VERKOMPLIZIERT SICH DIE BERECHNUNG, DA WIR JA NICHT WISSEN MIT WELCHER ZAHL WIR 10 MULTIPLIZIEREN SOLLEN, MAL TAUSEND, MAL ZWEITAUSEND ODER MAL... 74 Kapitel 9 - DE MOIVRE UND GAUSS ICH HABE MICH ALSO ZU FRÜH GEFREUT... RUHIG BLUT. IN DIESEM FALL BERECHNEN WIR DEN MEDIAN, AUCH ZENTRALWERT GENANNT. ÜBER IHM LIEGEN 50 % DER BETRÄGE UND UNTER IHM DIE RESTLICHEN 50 %. IN DEM FALL DER VORIGEN SEITE IST DER MEDIAN 200. DEUTLICH SIEHT MAN’S AUF DEN GRAPHIKEN VON „G“ UND „F“. Median Mittelwert Median Mittelwert IM ZWEITEN FALL STIMMEN MITTELWERT UND MEDIAN ÜBEREIN, NATÜRLICH DESHALB, WEIL DIE BETRÄGE SYMMETRISCH ANGEORDNET SIND. DAS HEIßT ALSO, DASS, WENN WIR BEIDE WERTE BERECHNEN, WISSEN WIR MEHR ÜBER DIE VERTEILUNG DER WERTE. GENAU SO IST’S, RÄTSI. UND WIR WERDEN AUCH NOCH EINE WEITERE MITTELWERT-MESSGRÖßE EINFÜHREN. WIR NENNEN SIE MODUS ODER HÄUFIGSTER WERT, UND ES HANDELT SICH DABEI, WIE SCHON SEIN NAME SAGT, UM DEN WERT, DER AM HÄUFIGSTEN VORKOMMT. 75 Kapitel 9 - DE MOIVRE UND GAUSS ES KÖNNTE ALSO MEHRERE MODI GEBEN... GENAU. ES KANN ZWAR IMMER NUR EINEN MITTELWERT UND EINEN MEDIAN GEBEN, DOCH IM FALLE DES MODUS, HÄNGT DIE ANZAHL VON DEN UMSTÄNDEN AB. SCHAUEN WIR UNS NOCH EINMAL DIE GRAPHIKEN AN. Median MODUS Mittelwert Median Mittelwert MODUS ICH HATTE ALSO RECHT. IN DER VERTEILUNG „F“ GIBT ES ZWEI MODI. 76 MODUS JA, DIE WINTER -UND SOMMER MODE. IN DIESEM BEISPIEL FALLEN DER MITTELWERT UND DER MEDIAN IN DEN FRÜHLING. Kapitel 9 - DE MOIVRE UND GAUSS IN ANDEREN WORTEN, WIR WISSEN JETZT, DASS WIR FÜR DAS MUTMAßLICHE FEST DURCHSCHNITTLICH 250 PESETEN BEIGESTEUERT HABEN, UND DASS AM HÄUFIGSTEN ENTWEDER 2,5 DM ODER 3 DM GEGEBEN WURDEN. DAS IST NATÜRLICH EINFACH, WENN ES SICH UM KLEINE GRUPPEN WIE UNSERER HANDELT. DOCH ES WÄRE GANZ ETWAS ANDERES, WENN WIR EIN FEST FÜR 3000 JUNGS UND 5000 MÄDCHEN ORGANISIEREN WÜRDEN. ABER KLAR. ES KÖNNTE SICH GENAU SO GUT UM EIN SCHULABSCHLUSSFEST ALS AUCH UM EINE EHRUNG ODER SOGAR UM EIN GEBURTSTAGSFEST HANDELN. UND WANN FINDET ES STATT? JA, WIR WISSEN ZWAR SCHON VIEL, DOCH ES GIBT NOCH VIELE DINGE ZU LERNEN. WAS IST DENN DER ANLASS DES FESTES? OBWOHL, WENN ICH’S MIR RECHT ÜBERLEGE – UND ES MIR DIE STATISTIK ERLAUBT – FÜR EIN FEST IST JEDER GRUND MIT DER WAHRSCHEINLICHKEIT 1 EIN GUTER. DAS SPIELT DOCH KEINE ROLLE. ES HANDELT SICH JA NUR UM EIN MUTMAßLICHES FEST, DAS SICH IN ERSTER LINIE SEHR GUT FÜR UNSERE EXPERIMENTE EIGNET. ABER STELL DIR VOR HEUTE SEI MITTWOCH. NATÜRLICH. JETZT MÖCHTE ICH NOCH ZWEI WEITERE AUFGABEN BESPRECHEN UND ENDLICH DAS FEST VERGESSEN. WAS ICH EUCH NOCH SAGEN WOLLTE, DENN OBGLEICH DER MITTELWERT DIE NÜTZLICHSTE MESSGRÖßE IST, HABEN WIR GESEHEN, DASS DIESER IN MANCHEN FÄLLEN NICHT ZU BERECHNEN IST, UND AUßERDEM HAT ER NOCH EINEN NACHTEIL: ER REAGIERT EMPFINDLICH AUF EXTREME WERTE . WAS? WIE? WO? 77 Kapitel 9 - DE MOIVRE UND GAUSS LASST EUCH DIESES BEISPIEL DURCH DEN KOPF GEHEN. Median = 11 33 =11 3 MODUS: keinen Mittelwert = Gesamt: konzentriert Median = 11 33 =11 3 MODUS: keinen Mittelwert = Gesamt: gestreut Median Mittelwert Alle wären Modi, weil jeder Betrag einmal vorkommt. In diesem Fall würden wir sagen, dass es keinen Modus gibt. Median Mittelwert konzentriert G E S T R WIE IHR AN DIESEM FALL SEHT, IST ES DER PARAMETER ODER KENNGRÖßE DER AUFTEILUNG, DER DIE KONZENTRATION ODER STREUUNG DER WERTE MISST, UND DER EINE LISTE VON DER ANDEREN UNTERSCHEIDET. 78 E U T Kapitel 9 - DE MOIVRE UND GAUSS UND NOCH EIN BEISPIEL: Modus Median Mittelwert Mittelwert Modus Median Mittelwert Mittelwert Modus Median Mittelwert Mittelwert AUS DIESEM BEISPIEL KÖNNEN WIR ABLEITEN, DASS, WENN MAN EINEN AUSREIßER, DAS HEIßT EINEN WERT, DER SEHR WEIT VON DEN ANDEREN ENTFERNT IST (GROßE STREUUNG WIE DIE NUMMER 48 IN UNSEREM FALL) DURCH EINEN KONZENTRIERTEREN WERT, IN UNSEREM BEISPIEL DIE NUMMER 9, AUSTAUSCHT, DIE MITTELWERTE DER BEIDEN FÄLLE SEHR VONEINANDER ABWEICHEN, WÄHREND SICH DER MEDIAN UND DER MODUS NICHT VERÄNDERN. IM GEGENSATZ DAZU, WENN WIR WERTE IM MITTELFELD MODIFIZIEREN (WIE IN DEN LETZTEREN), ÄNDERT SICH DER MITTELWERT NUR WENIG, DER MEDIAN UND DER MODUS BLEIBEN WIEDER GLEICH (OBWOHL SIE SICH IN ANDEREN FÄLLEN VERÄNDERN KÖNNTEN). DAS IST AUCH DER GRUND, WARUM WIR MESSGRÖßEN SUCHEN, DIE UNS ANZEIGEN, OB DIE VERTEILUNG DER WERTE MEHR ODER WENIGER GESTREUT SIND. DAS AM HÄUFIGSTEN VERWENDETE MAß FÜR DIE STREUUNG IST DIE TYPISCHE ODER STANDARDABWEICHUNG, DIE WIR IN DEN BEISPIELEN, DIE WIR VORBEREITEN, SEHEN WERDEN. WIR WERDEN ALSO EIN KLEINES EXPERIMENT DER STANDARDABWEICHUNG MIT DEM SO OFT VERWENDETEN BEISPIEL DER ZWEI SCHINKEN, OFT AUCH MIT HÄHNCHEN, DURCHFÜHREN. 79 Kapitel 9 - DE MOIVRE UND GAUSS WIR HABEN ZWEI PERSONEN, DIE ZUM ESSEN KOMMEN, UND ZWEI SCHINKEN. JA. EINER DER BEIDEN ISST ZWEI SCHINKEN, DER ANDERE KEINEN. DER MITTELWERT ERGIBT EINEN, DAS HEIßT ALSO, DASS, IN STATISTISCHER HINSICHT, JEDER EINEN SCHINKEN GEGESSEN HAT. WIR HATTEN EINMAL ZWEI SCHINKEN... NEIN. WENN WIR AUCH DIE STANDARDABWEICHUNG BERÜCKSICHTIGEN, UND NICHT NUR DEN MITTELWERT, SCHAUT DIE SACHE GANZ ANDERS AUS: Σ Summen Mittelwert Standardabweichung = DIE STANDARD- ODER TYPISCHE ABWEICHUNG WIRD FOLGENDERMAßEN BERECHNET: 1. WIR BERECHNEN DEN UNTERSCHIED ZWISCHEN JEDEM ELEMENT UND DEM MITTELWERT. 2. WIR NEHMEN DIESEN ZUM QUADRAT (AUF DIESE WEISE VERSCHWINDEN DIE NEGATIVBETRÄGE). 3. DANN MULTIPLIZIEREN WIR IHN MIT DER HÄUFIGKEIT (IN UNSEREM BEISPIEL IST DAS GANZ LEICHT, DEN DIE ESSER SELBST SIND DIE HÄUFIGKEIT, ALSO: EINER UND NOCH EINER). 4. ANSCHLIEßEND DIVIDIEREN WIR DURCH DIE GESAMTANZAHL DER HÄUFIGKEIT (IN UNSEREM FALL, 2 ESSER). 5. ZULETZT ZIEHEN WIR DIE QUADRATWURZEL. 80 Kapitel 9 - DE MOIVRE UND GAUSS GANZ SCHÖN KOMPLIZIERT... DU HAST MICH MIT DER HAND IM SCHLAMMASSEL ERWISCHT, GAUßI. SAG MIR DAS NICHT, DENN ICH BIN ÜBERZEUGT, DASS DU ALLE RECHENGÄNGE MIT DEM COMPUTER DURCHGEFÜHRT HAST. Wir multiplizieren jede Reihe: Und ziehen den Mittelwert ab Mittelwert Erheben zum Quadrat Multiplizieren mit f Dividieren Und ziehen die Quadratwurzel Standardabweichung = 1 ICH WERDE DAS BEISPIEL MIT ANDEREN DATEN BERECHNEN. ICH NEHME AN EINER ISST 12 UND DER ANDERE 1 1 . 2 81 Kapitel 9 - DE MOIVRE UND GAUSS SCHINKEN ESSER Σ Summe Mittelwert Standardabweichung = UND ICH NEHME AN, DASS JEDER EINEN SCHINKEN ISST: SCHINKEN ESSER Σ Summe Mittelwert Standardabweichung = UNSER SUPERTOLLER WIRD SICH MITHILFE DER STANDARDABWEICHUNG DER UNTERSCHIEDE ZWISCHEN DEN DREI FÄLLEN BEWUSST WERDEN. ALLE DREI BEISPIELE HABEN ZWAR DEN GLEICHEN MITTELWERT 1, DIE AUFTEILUNG JE EINES SCHINKENS AUF EINEN ESSER ERGIBT EINE ABWEICHUNG „0“, WÄHREND, WENN SICH DER FRESSSACK DEN BAUCH VOLL SCHLÄGT UND DEM, DER NUR NOCH HAUT UND KNOCHEN IST, NICHTS ÜBRIG LÄSST, SICH EINE ABWEICHUNG „1“ ERGIBT, EXTREM HOCH IN DIESEM FALL. 82 Kapitel 9 - DE MOIVRE UND GAUSS IN SACHEN ERNÄHRUNG SOLLTE EIN MITTELMAß GEGESSEN WERDEN UND SICH DIE STANDARDABWEICHUNG DER 0 NÄHERN. DER MAGERSUCHT UND DER FRESSSUCHT SOLLTE DER KAMPF ANGESAGT WERDEN. JETZT DA DU VON MITTELWERTEN UND STREUUNG SPRICHST,... ZUFÄLLI UND ICH HABEN AUF EIGENE FAUST ERMITTLUNGEN ANGESTELLT UND SIND AUF FOLGENDES GESTOßEN: EINE AUFTEILUNG, DIE EINDEUTIG VOM MITTELWERT UND DER STREUUNG BESTIMMT IST, WIRD HÄUFIG IN EXPERIMENTEN VERWENDET, DIE GROßE DATENMENGEN ÜBER ALTER, GEWICHT, GRÖßE VON PERSONEN, ETC. BERECHNEN. SCHON GUT, ABER LASS AUCH WAS FÜR SPÄTER... JA, ABER DAS INTERESSANTE KOMMT NOCH: DIESE AUFTEILUNG, DIE SICH „NORMAL“ NENNT, HAT DIE FORM EINER GLOCKE. Standardabweichung 2 Standardabweichung 0,5 Standardabweichung 1 83 Kapitel 9 - DE MOIVRE UND GAUSS UND SIE HEIßT... MM!!! M BU M U B M U R A B BUMM GAUßKURVE ODER -GLOCKE!!! DIE GAUßKURVE IST ANSCHEINEND „NORMAL”, ABER UNSER GAUßI, NAJA, SO RICHTIG NORMAL, IM WAHRSTEN SINN DES WORTES... IST ER NICHT. ER IST VOR ALLEM EIN GUTER UND FLEIßIGER MENSCH. 84 IHR WERDET SCHON NOCH SEHEN, WENN ER AN DER UNIVERSITÄT UNTERRICHTET UND NEUE THEORIEN ENTDECKT. Kapitel 9 - DE MOIVRE UND GAUSS 2 1 2X 1 X UND WENN ZUFÄLLI EIN FORSCHUNGSZENTRUM FÜR WAHRSCHEINLICHKEITSRECHNUNGEN UND EINEN LOTO TOTO CLUB FÜHRT. UND STELLT EUCH RÄTSI VOR, WENN ER BEI DEN STATISTISCHEN BERECHNUNGEN FÜR EIN FORSCHUNGSPROJEKT EINER NEUEN IMPFUNG MITHILFT, UND 55 MIT IHREN DETAILLIERTEN SOZIOLOGISCHEN STUDIEN... UND WENN GRAPHI IHRE MARKTSTUDIEN DEM VORSTAND EINER GROßEN FIRMA PRÄSENTIERT, UND BINOMI MIT NEUEN MATHEMATISCHEN FORMELN FORTSCHRITTE IN DER STATISTIK MACHT. JETZT ABER GENUG DAMIT. DENN ICH, WEIL WIR IN DER SCHULE SOKRATES DURCHGENOMMEN HABEN, WEIß, DASS ICH NICHTS WEIß. ABER ICH VERSTEHE MEHR DINGE, UND DIE AUCH BESSER. WAS ICH EUCH SAGEN KANN - ICH MEINE IN BEZUG AUF DIE STATISTIK DASS ICH EINE WAHRSCHEINLICHKEIT VON 0,3 HABE MICH ZU IRREN. 85 Kapitel 9 - DE MOIVRE UND GAUSS OKAY, OKAY. JETZT IST ALLES KLAR. ES FEHLT NUR EINE SACHE, EINE DER WICHTIGSTEN, DIE WIR NICHT VERGESSEN HABEN. LASST UNS FÜR EINEN MOMENT IN DEN GARTEN GEHEN. ABER WAS IST DENN DAS? EIN FEST? DU HÄTTEST ES ABER NICHT VERGESSEN, ODER? WIR AUF ALLE FÄLLE NICHT! WIE KÖNNTEN WIR AUCH DEINEN GEBURTSTAG VERGESSEN? ALLES GUTE ZUM GEBURTSTAG! ENDE 86 ANLAGEN ANLAGE 1 MÜNZENWURF 8 ANZAHL KÖPFE: _____ Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) Köpfe (in rot) 88 MAL ANZAHL ZAHL: _____ Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) Zahlen (in blau) ANLAGE 2 MÜNZENWURF 50 MAL Erfolge (in rot) Misserfolge (in schwarz) Erfolge (in rot) Misserfolge (in schwarz) Erfolge (in rot) Misserfolge (in schwarz) Erfolge (in rot) Misserfolge (in schwarz) Erfolge (in rot) Misserfolge (in schwarz) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 ZIEHST DU EINE SCHLUSSFOLGERUNG AUS DEN FARBEN? 89 ANLAGE 3 WAHRSCHEINLICHKEITSRECHNER WAHRSCHEINLICHKEIT AUFBAU 2 3 Erfolg 1 Versuch Misserfolg 1 3 1 Versuch Quadrat (a+b) 2 Versuche (a+b)2 = (a+b) 3 Versuche (a+b)3 = (a+b)2 x (a+b) 4 Versuche (a+b)4 = (a+b)2 x (a+b)2 5 Versuche (a+b)5 = (a+b)4 x (a+b) = (a+b)3 x (a+b)2 a x (a+b) b Es ist die Anzahl der Quadrate 1 Versuch des entsprechenden Monoms durch die Gesamtzahl der Quadrate zu dividieren. a b a a2 ab a a2 a3 a2b b ab b2 ab a2b b a2 ab a2 a4 a3b a3b a2b2 ab2 ab a3b a2b2 a2b2 ab3 ab a2b ab2 ab a3b a2b2 a2b2 ab3 b2 ab2 b3 b a2b2 ab3 ab3 b4 2 Versuche 3 Versuche ab b 4 Versuche a3 a2b a2b a2b ab2 ab2 ab2 b3 a2 a5 a4b a4b a4b a3b2 a3b2 a3b2 ab a4b a3b2 a3b2 a3b2 a2b3 a2b3 a2b3 ab a4b a3b2 a3b2 a3b2 a2b3 a2b3 a2b3 ab4 b2 a3b2 a2b3 a2b3 a2b3 ab4 ab4 ab4 b5 a2b3 ab4 5 Versuche QUADRATE QUADRATE VON a4 GESAMTZAHL QUADRATE QUADRATE a x a x a x a = a4 1 x 16 = 16 81= 0,1975 Wahrscheinlichkeit von 3 Erfolgen und 1 Misserfolg in 4 Versuchen a x a x a x b = a3b 4 x 8 = 32 81= 0,3950 Wahrscheinlichkeit von 2 Erfolgen und 2 Misserfolgen in 4 Versuchen a x a x b x b = a2b2 6 x 4 = 24 81= 0,2962 Wahrscheinlichkeit von 1 Erfolg und 3 Misserfolgen in 4 Versuche a x b x b x b = ab3 4x2=8 81= 0,0098 Wahrscheinlichkeit von 4 Misserfolgen in 4 Versuchen b x b x b x b = b4 1x1=1 81= 0,0123 BEISPIEL:Wahrscheinlichkeit von 4 Erfolgen in 4 Versuchen GESAMT=1 90 ANLAGE 4 WAHRSCHEINLICHKEIT 2 3 Erfolg 1 Versuch Misserfolg a b 1 2 3 4 5 6 1 3 a b 1 2 3 4 5 6 a2 ab ab b2 2 Versuche a2 ab ab b2 a2 a4 a3 b a 3b a2b2 ab a3b a2b2 a2b2 ab3 ab a3b a2b2 a2b2 ab3 b2 a2b2 ab3 ab3 b4 4 Versuche 91 ANLAGE 5 WAHRSCHEINLICHKEIT Erfolg 1 Versuch Misserfolg 5 6 a b 1 2 3 4 5 6 1 6 a b 1 2 3 4 5 6 a2 ab ab b2 2 Versuche a2 ab ab a2 a4 a3b a 3b ab a3b a2b2 a2b2 ab a3b a2b2 a2b2 b2 a2b2 ab3 ab3 4 Versuche 92 b2 a2b2 ab3 ab3 b4 ANLAGE 6 WAHRSCHEINLICHKEIT Erfolg 1 3 Misserfolg 2 3 1 Versuch e f e e f e f 1 Versuch ee ef ef ff ee ef e f 2 Versuche ef ff ee ef ef 3 Versuche ff 4 Versuche ee ef ef ff eee eef eef eef eff eff eff fff eee eef eef eef eff eff eff fff 5 Versuche 6 Versuche 93 ANLAGE 7/1 WAHRSCHEINLICHKEIT Erfolg 1 2 Misserfolg 1 2 1 Versuch PLATZ FÜR STICHPROBEN KOPF (Erfolg) 1,2,3,4,5,6,7,8 94 VON UND ZAHL (Misserfolg) 9 VERSUCHEN ANLAGE 7/2 95 ANLAGE 8 Balearische Inseln Schüler Schuljahr Kindergarten Index Grundschule Index Sekundärschule Index 88-89 89-90 90-91 91-92 92-93 93-94 94-95 95-96 96-97 97-98 98-99 19957 19958 19220 19313 19706 20123 20719 22063 23169 23982 24449 1,012737237 1,012787983 0,975337461 0,980056835 1 1,021161068 1,051405663 1,119608241 1,175733279 1,216990 1,240688115 96772 95596 92481 89024 85944 83197 80008 77419 64165 55294 55600 1,125989016 1,112305687 1,076061156 1,035837289 1 0,968037327 0,93093177 0,900807503 0,746590803 0,643372429 0,646932887 4432 8683 10742 13609 28975 38872 39821 1 1,95916065 2,423736462 3,070622744 6,537680505 8,770758123 8,984882671 Balearische Inseln Schuljahr BUP-COU 88-89 89-90 90-91 91-92 92-93 93-94 94-95 95-96 96-97 97-98 98-99 21209 21982 22185 22590 21038 19926 18513 15571 11772 8901 4946 Schüler Bach-Logse 921 2646 3911 5019 5551 7100 9083 Balearische Inseln Bach-Exper. Gesamt Index 813 1240 2664 4922 2567 237 22022 23222 24849 27512 24526 22809 22424 20590 17323 16001 14029 1 0,929992661 0,914295034 0,839517247 0,706311669 0,652410 0,572005219 Schüler Schuljahr FP1 Index FP2 Index CFGM Index CFGS Index 88-89 89-90 90-91 91-92 92-93 93-94 94-95 95-96 96-97 97-98 98-99 7108 7049 6360 5114 3919 2662 2318 1789 1360 686 184 1,1176 1,1083 1 0,8041 0,6162 0,4186 0,3645 0,2813 0,2138 0,1079 0,0289 4056 4172 4613 4996 5062 4697 3826 2588 1738 1016 480 0,8793 0,9044 1 1,0830 1,0973 1,0182 0,8294 0,5610 0,3768 0,2202 0,1041 75 180 553 813 1050 1225 1763 2466 2903 1 2,4000 7,3733 10,8400 14,0000 16,3333 23,5067 32,8800 38,7067 76 243 226 300 394 698 993 1481 1774 1 3,1974 2,9737 3,9474 5,1842 9,1842 13,0658 19,4868 23,3421 96 ANLAGE 9 Bevölkerung per Altersgruppe und Geschlecht Gesamt Männer Frauen Gesamt Bevölkerung per Altersgruppe und Geschlecht Frauen Männer Männer Bevölkerung Frauen Männer Frauen 97 ANLAGE 10 STADT GESAMT MÄNNER FRAUEN Balearische Inseln 796483 392835 403648 Alaró 3834 1834 2000 Alcúdia 10581 5345 5236 Algaida 3542 1766 1776 Andratx 8333 4164 4169 Artà 5936 2963 2973 503 264 239 5019 2424 2595 951 470 481 4338 2144 2194 32587 16293 16294 Campanet 2277 1115 1162 Campos 6944 3478 3466 Capdepera 6752 3374 3378 Consell 2210 1090 1120 Costitx 849 415 434 Deià 625 311 314 Escorca 275 148 127 Esporles 3811 1900 1911 Estellencs 338 176 162 14600 7268 7332 580 290 290 21103 10425 10678 837 415 422 Lloseta 4529 2231 2298 Llubí 1893 926 967 Llucmajor 21771 10804 10967 Manacor 30177 14988 15189 Mancor de la Vall 936 453 483 Maria de la Salut 1733 861 872 Marratxí 18084 9101 8983 Montuïri 2235 1105 1130 Muro 6028 2979 3049 Palma 319181 154748 164433 Petra 2571 1244 1327 Pollença 13450 6713 6737 Porreres 4226 2102 2124 Banyalbufar Binissalem Búger Bunyola Calvià Felanitx Fornalutx Inca Lloret de Vistalegre ANLAGE 11 sa Pobla 10064 5169 4895 Puigpunyent 1163 576 587 Sencelles 1969 1009 960 Sant Joan 1662 826 836 Sant Llorenç 5594 2793 2801 1114 548 566 Santa Margalida 7107 3532 3575 Santa Maria del Camí 4558 2243 2315 Santanyí 7974 4026 3948 Selva 2918 1425 1493 ses Salines 3240 1642 1598 Sineu 2616 1278 1338 Sóller 11207 5565 5642 Son Servera 8065 4061 4004 Valldemossa 1599 779 820 Vilafranca de Bonany 2249 1101 1148 772 379 393 637510 313279 324231 7046 3490 3556 Ciutadella 21785 10853 10932 Ferreries 3921 2050 1871 22358 10878 11480 es Mercadal 2723 1353 1370 Sant Lluís 4106 2058 2048 es Castell 6005 3017 2988 1126 576 550 69070 34275 34795 5859 2966 2893 Eivissa 31582 15728 15854 Sant Antoni 14849 7507 7342 Sant Josep 13364 6815 6549 Sant Joan 3943 1991 1952 Santa Eulàlia 20306 10274 10032 EIVISSA 84044 42315 41729 Santa Eugènia Ariany MALLORCA Alaior Maó es Migjorn Gran MENORCA Formentera ANLAGE 12 Tabelle der Größen in cm von 40 Grundschülern: 145 160 149 144 169 148 162 151 147 149 152 167 155 141 151 167 171 172 150 152 170 170 167 140 163 132 148 163 152 164 120 168 151 161 170 139 175 142 170 142 18 17 16 Tabelle in aufsteigender Reihenfolge 120 1 145 9 151 17 162 25 169 33 132 2 147 10 151 18 163 26 170 34 139 3 148 11 152 19 163 27 170 35 Median : 152 140 4 148 12 152 20 164 28 170 36 141 5 149 13 152 21 167 29 170 37 ( 20 Zehner Zehner Zehner Zehner Zehner Zehner 100 142 6 149 14 155 22 167 30 171 38 142 7 150 15 160 23 167 31 172 39 20 von von von von von von 120 130 140 150 160 170 15 144 8 151 16 161 24 168 32 175 40 14 13 12 Diagramm „Stämme und Blätter” ) cm cm cm cm cm cm 12: 13: 14: 15: 16: 17: 0 2 0 0 0 0 9 1 1 1 0 2 1 2 0 2 1 3 0 4 2 3 1 5 2 4 2 7 8 8 9 9 2 5 7 7 7 8 9 5 ANLAGE 13 x 50% Median 50% Modus=170 Mittelwert = f xf 120 132 139 140 141 142 144 145 147 148 149 150 151 152 155 160 161 162 163 164 167 168 169 170 171 172 175 1 1 1 1 1 2 1 1 1 2 2 1 3 3 1 1 1 1 2 1 3 1 1 4 1 2 1 120 132 139 140 141 284 144 145 147 296 298 150 453 456 155 160 161 162 326 164 501 168 169 680 171 172 175 Summe 40 6209 6209 40 Standardabweichung = = 155,225 x-x -35,225 -23,225 -16,225 -15,225 -14,225 -13,225 -11,225 -10,225 -8,225 -7,225 -6,225 -5,225 -4,225 -3,225 -0,225 4,775 5,775 6,775 7,775 8,775 11,775 12,775 13,775 14,775 15,775 16,775 19,775 (x-x)2 1240,801 539,401 231,801 202,351 202,351 174,901 126,001 104,551 67,651 52,201 38,751 27,301 17,851 10,401 0,051 22,801 33,351 45,901 60,451 77,001 138,651 163,201 189,751 218,301 248,851 281,401 391,051 (x-x)2f 1240,801 539,401 231,801 202,351 202,351 349,801 126,001 104,551 67,651 104,401 77,501 27,301 53,552 31,202 0,051 22,801 33,351 45,901 120,901 77,001 415,952 163,201 189,751 873,203 248,851 281,401 391,051 6282,975 Varianz = 6282’975 = 40 157,074 Varianz = 12,533 101 Gedruckt auf recyceltem Papier Zufälle in Zahlen




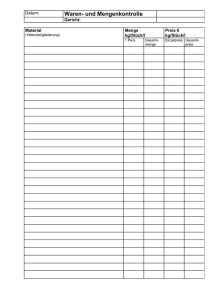

![001_Geologische_Tabelle_Faktoren_3_Endla[...]](http://s1.studylibde.com/store/data/002317598_1-5316e8c22586a8aa95c7fe9ab279021b-300x300.png)




