Mathematik 2 Sekundarstufe I
Werbung

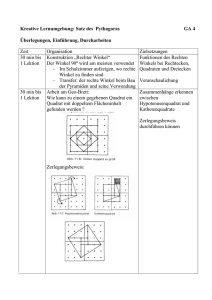
1 2 3 4 5 6 7 8 9 Ergänzungsbeweis Aufgabenstellung 1 a) Blende die grossen Quadrate ein. b) Bewege den Punkt C und beobachte, wie sich die Figur verändert. 2 Angenommen, die beiden grossen Quadrate seien gleich gross. Wie kannst du daraus den Satz von Pythagoras herleiten? 3 Begründe, weshalb ... a) alle acht Seiten der beiden grossen Quadrate gleich lang sind. b) alle acht Winkel der beiden grossen Quadrate rechte Winkel sind. c) bei jedem der beiden grossen Quadraten die vier Winkel, zum Beispiel beim Punkt B, zusammen 180° ergeben. Antworten 1. a) – b) – 2. Mögliche Erklärung: Wenn das rote und das blaue Quadrat gleich gross sind, dann müssen auch die vier roten und die vier blauen Dreiecke gleich gross sein. Die Fläche des blauen Quadrates minus die Flächen der vier blauen Dreiecke ist gleich a2 + b2. Die Fläche des roten Quadrates minus die Flächen der vier roten Dreiecke ist gleich c2. Somit gilt im rechtwinkligen Dreieck: a2 + b2 = c2. 3. a) Mögliche Begründung: Die acht Dreiecke sind kongruent. Sie sind rechtwinklig mit den Seiten a, b und c. Die Seitenlänge des blauen und des roten Quadrates ist immer gleich a + b. b) Mögliche Begründung: Beim roten Quadrat bilden die rechten Winkel der Dreiecke die Winkel des Quadrates. Beim blauen Quadrat werden zwei Winkel von den Kathetenquadraten und zwei Winkel von den rechtwinkligen Dreiecken gebildet. c) Mögliche Begründung: Beim blauen Quadrat wird der Winkel bei B von einem 90°-Winkel und von den Winkeln und gebildet. Die Summe von und beträgt im rechtwinkligen Dreieck 90°. Somit ist der Winkel bei B gleich 180°. Der Winkel beim roten Quadrat setzt sich zusammen aus: 2 + 2 = 2( + ) = 2 · 90° = 180°. © Lehrmittelverlag Zürich Mathematik 2, Kapitel 2b, Themenbuch, Aufgabe 1 1 2 3 4 5 6 7 8 9 Bewegungsbeweis Aufgabenstellung 1. Der Flächeninhalt des wandernden Vierecks ändert sich nicht. Begründe bei jedem der drei Schritte, warum das so ist. 2. Protokolliere den Ablauf und deine Überlegungen auf dem Arbeitsblatt «2 Filmbilder». 3. Wie verscheibt sich der Flächeninhalt des linken Kathetenquadrates in das Hypotenusenquadrat? Zeichne diesen Ablauf ebenfalls auf dem Arbeitsblatt ein. 4. Begründe, warum die beiden Bewegungen zusammen den Satz von Pythagoras beweisen. Antworten 1. Mögliche Begründung: 1. Schritt: Das Quadrat wird zum Parallelenviereck. Die Grundseite und die zugehörige Höhe ändern sich jedoch nicht. 2. Schritt: Das Parallelenviereck wird in unveränderter Form entlang der Höhe des Dreiecks ins Hypotenusenquadrat verschoben. 3. Schritt: Das Parallelenviereck wird zum Rechteck. Die Grundseite und die zugehörige Höhe ändern sich jedoch nicht. 2. – 3. – 4. Mögliche Begründung: Jede der beiden Bewegungen verwandelt ein Kathetenquadrat in ein Rechteck. Die beiden Rechtecke bedecken zusammen die gleiche Fläche wie das Hypotenusenquadrat. Somit ist im rechtwinkligen Dreieck die Summe der Kathenquadrate gleich dem Hypotenusenquadrat. © Lehrmittelverlag Zürich Mathematik 2, Kapitel 2b, Themenbuch, Aufgabe 2