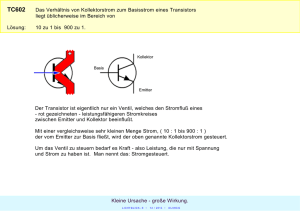
Vorbereitung zum Versuch ” Transistorschaltungen“

Vorbereitung zum Versuch
Transistorschaltungen“
”
Armin Burgmeier (1347488)
Gruppe 15
9. Dezember 2007
0
0.1
Grundlagen
Halbleiter
Halbleiter bestehen aus Silizium- oder Germanium-Gittern und haben im allgemeinen eine schlechte Leitfähigkeit. Durch Ersetzen einiger Gitteratome (Dotieren) mit fünfwertigen Atomen (Phosphor, Arsen) kann sie jedoch erheblich
gesteigert werden. Die überschüssigen Elektronen fungieren dann als Ladungsträger, daher nennt man sie auch n-Halbleiter.
Dotiert man mit dreiwertigen Atomen (Bor, Indium) vergrößert sich die
Leitfähigkeit ebenfalls. Elektrone anderer Atome können in die Elektronenlücke
(Löcher) der dreiwertigen Atome eintreten. Dieses Wandern der Löcher kann
man sich als freibewegliche positive Ladungsträger vorstellen (p-Halbleiter).
0.2
Halbleiterdiode
Grenzt ein n-Halbleiter an einen p-Halbleiter an, so findet ein Diffundierungsprozess statt. Freie Elektronen aus dem n-Halbleiter geraten in den p-Halbleiter
und Löcher in den n-Halbleiter. Da die festen Ladungsträger ortsfest sind baut
sich so eine Spannung auf, die ab einer bestimmten Größe die Diffusion kompensiert.
Legt man eine äußere Spannung mit dem Pluspol am n-Halbleiter an, so ist
die Diode in Sperrrichtung geschaltet. Es werden weitere freie Elektronen vom
n-Bereich in den p-Bereich übergehen und dort weitere Löcher kompensieren.
Es fließt praktisch kein Strom.
Legt man die äußere Spannung aber anders herum an, so werden die Elektronen durch die Grenzschicht beschleunigt und es fließt ein Strom, dessen Stärke
von der angelegten Spannung abhängt.
0.3
Transistor
Da im Versuch nur der npn-Transistor zum Einsatz kommt, wird hier auch
nur dieser beschrieben. Er besteht aus jeweils einer Schicht aus n-, p- und nHalbleiter, also zwei Grenzflächen. Liegt eine externe Spannung an den beiden
1
n-Schichten an, so ist einer der beiden Grenzflächen leitend und die andere nicht.
Folglich wird also auch kein Strom fließen.
Legt man jedoch einen Strom an der Basis (p-Schicht) an, so fließt dieser
wegen der leitenden Grenzfläche zwischen Basis und Kollektor. Da die p-Schicht
sehr dünn ist diffundieren einige der Elektronen aus denen dieser Strom besteht
aber in die Sperrschicht. Da nun Ladungsträger in der Sperrschicht vorhanden
sind kann zwischen den n-Schichten plötzlich wegen der externen Spannung ein
Strom fließen, der im allgemeinen sehr viel größer ist als der Basisstrom.
Auf diese Art und Weise können durch kleine Ströme an der Basis sehr viel
größere zwischen Kollektor und Emitter gesteuert werden.
1
1.1
Kennlinien
Eingangskennlinie
In der nach Schaltung 13 in der Vorbereitungshilfe aufgebauten Schaltung messen wir verschiedene Wertepaare für den Basisstrom IB und für die Spannung
zwischen Basis und Emitter UBE . Die sich ergebende Eingangskennlinie (U über
I) wird in den dritten Quadranten eines Vier-Quadranten-Kennlinienfeldes eingetragen.
Das Spannungsmessgerät sollte möglichst hochohmig sein, da eine spannungsrichtige Messung vorgenommen wird und der gemessene Strom daher nicht
stark von dem echten“Basisstrom abweichen soll.
”
1.2
Ausgangskennlinien
Die Ausgangskennlinie stellen wir an einem Oszilloskop im X/Y-Betrieb dar.
Dazu wird die Schaltung wie in Bild 14 der Vorbereitungshilfe aufgebaut. Als
Maß für die Stromstärke am Kollektor wird die abfallende Spannung UY an
einem konstanten Widerstand R = 2Ω verwendet.
Aus technischen Gründen kann als X-Ablenkung nicht die Spannung UCE
zwischen Kollektor und Emitter verwendet werden, sondern es wird UCE + UY
gemessen. Da der Widerstand R jedoch sehr klein ist, wird aber UY klein und
somit vernachlässigbar gegenüber UCE sein. Vor dem Experiment kann dies
auch nochmal nachgemessen werden.
Da die Ausgangskennlinien abhängig vom Basisstrom sind, sollen mehrere
Kennlinien bei unterschiedlichen Basisströmen aufgenommen werden. Der Basisstrom ist durch einen regelbaren Widerstand bestimmbar und wird so eingestellt, dass der Kollektorstrom IC Werte von 10mA bis 50mA erreicht, in
10mA-Schritten. Die Kennlinien werden in den ersten Quadranten eingetragen.
1.3
Steuerkennlinie
Wir tragen IC über IB in den zweiten Quadranten des Kennlinienfeldes auf. Die
nötigen Messwerte wurden bereits ermittelt.
2
2
Überlagerungstheorem
Das Überlagerungstheorem besagt dass in einer Schaltung mit mehreren Spannungsquellen die Spannung über zwei beliebigen Punkten die gleiche ist wie die
Summe der Spannungen an diesen Punkten wenn jeweils nur eine der Spannungsquellen aktiviert ist. Dabei ist jeweils der Innenwiderstand nicht aktiver
Spannungsquellen zu berücksichtigen.
In diesem Teil des Versuchs wollen wir das Überlagerungstheorem experimentell überprüfen. Dazu verwenden wir Schaltung 15 aus der Vorbereitungshilfe
und messen die Spannung U3 über R3 = 330Ω mit einer, der anderen und zwei
aktiven Spannungsquellen. Für die Spannung U3Gl , bei der nur die Gleichstromquelle aktiv ist, erwarten wir folgenden Wert:
Der Widerstand im gesamten Stromkreis ergibt sich aus einer Reihenschaltung von R2 und einer Parallelschaltung von R3 und R10 . Zu Beachten ist, dass
zu dem Widerstand R1 noch der Innenwiderstand Ri der deaktivierten Spannungsquelle hinzukommt: R10 = R1 + Ri .
Gl
Rges
=
1
1
R1 +Ri
+
1
R3
+ R2
(1)
Die verschiedenen Widerstandswerte sind gegeben.
Der Gesamtstrom im Stromkreis, welcher dem Strom durch den Widerstand
R2 entspricht, ergibt sich dann nach dem ohmschen Gesetz zu
I=
UGl
Gl
Rges
(2)
wobei U die an der Gleichstromquelle angelegte Spannung ist. Den Teil dieser
Spannung, der am Widerstand R2 abfällt lässt sich ebenfalls nach dem ohmschen
Gesetz ermitteln
UR2 = IR2 =
UGl
R2
Gl
Rges
(3)
und nach der Maschenregel findet man damit leicht die gesuchte, am Widerstand
R3 abfallende Spannung
URGl3 = UGl − UR2 = UGl −
UGl
R2
Gl
Rges
(4)
Nach dem gleichen Verfahren kann man die Spannung an R3 für den umgekehrten Fall ermitteln, das heißt wenn die Gleichspannungsquelle abgeschaltet
und die Rechteckspannung angelegt ist. Es ergibt sich
URRe3 = URe −
mit
3
URe
R1
Re
Rges
(5)
Re
Rges
=
1
R2
1
+
1
R3
+ R1
(6)
Sind beide Spannungsquellen aktiviert müsste sich laut dem Überlagerungstheorem
also ein Wert von U3 = URRe3 + URGl3 ergeben. Setzt man die gegebenen Zahlenwerte und berücksichtigt, dass URe eine Rechtecksspannung, also sowohl negativ
als auch positiv sein kann, so erhalten wir:
U3 = 1, 72V ± 1, 70V
3
3.1
3.1.1
Transistorschaltungen
Transistor als Schalter
Beschreibung des Transistors als Schalter
Will man den Transistor als Schalter benutzen, so nutzt man aus, dass er bei
kleinen Basisströmen einen großen Kollektor/Emitter-Strom durchschaltet und
bei gar keinem Basisstrom sperrt. Trägt man die sogenannte Arbeitsgerade
UCE = U − IC RC
(7)
mit der Betriebsspannung U und dem Verbraucherwiderstand RC in das Ausgangskennlinienfeld ein, so sind die Schnittpunkte mit den Kennlinien die Arbeitspunkte. Abbildung 3.1.1 zeigt für U = 12V und RC = 25Ω die Arbeitsgerade und zwei exemplarische Kennlinien für hohen und niedrigen Basisstrom.
Es ist deutlich zu sehen dass der Arbeitspunkt bei niedrigen Basisströmen
nahe bei IC = 0A liegt, es fließt also nur sehr wenig Strom. Bei einem (relativ)
hohen Basisstrom hingegen liegt er bei IC ≈ RUC .
Die Maximalleistung des Transistors beträgt 0, 8W, die elektrische Leistung
am Transistor ist UCE IC . Auch diese Kurve ist im oben erwähnten Diagramm
aufgetragen. Im Normalfall sollte die Arbeitsgerade die so enstehende Hyperbel nicht schneiden, da sonst bei ungünstig gewählten Arbeitspunkten eine
größere elektrische Leistung ensteht als der Transistor verkraftet, was zu dessen Zerstörung führen kann. Da wir aber nur Arbeitspunkte nahe IC = 0 und
UCE = 0 wählen geraten wir nicht oder nur sehr kurz in diesen kritischen Bereich.
3.1.2
Schaltung und Verlustleistung
Eine Spannungsquelle wird über einen Widerstand RV an Kollektor und Basis
des Transistors angeschlossen und bestimmt den Basisstrom. Der Verbraucher
(eine Glühbirne) wird an eine zweite Spannungsquelle U und den Kollektor des
Transistors in Reihe geschaltet (Schaltung 1 im Anhang).
Aus den gemessenen Werten von Strom IC und Spannung UCE können wir
bei verschiedenen Basisvorwiderständen RV die Verlustleistung des Transistors
berechnen.
4
Arbeitsgerade
0.5
0.4
Arbeitsgerade
Leistungshyperbel
Kennlinie mit hohem Basisstrom
Kennlinie mit niedrigem Basisstrom
[IC in A]
0.3
0.2
0.1
0
0
2
4
6
[UCE in V]
8
10
12
Abbildung 1: Arbeitsgerade und Leistungshyperbel
3.2
3.2.1
Verstärker in Emitterschaltung
Arbeitspunkt
Die Schaltung wird nach Bild 2 in der Vorbereitungshilfe aufgebaut. Durch
Verändern des Basisvorwiderstands RV kann der Arbeitspunkt verändert werden. Er soll so eingestellt werden, dass die Hälfte der Betriebsspannung U = 6V
am Transistor und die andere Hälfte am Kollektorwiderstand abfällt.
3.2.2
Arbeitsgerade und Transistorkenngrößen
Die Arbeitsgerade UCE = U − IC RC (bei einem Verbraucher mit Widerstand
RC ) kann durch zwei bekannte Punkte (wie zum Beispiel bei IC = 0 und
UCE = 0) direkt ins Kennlinienfeld eingetragen werden. Der Arbeitspunkt liegt
bei UCE = 6V auf der Geraden. Die geforderten Transistorkenngrößen lassen
sich wie folgt aus dem Kennlinienfeld am Arbeitspunkt entnehmen:
• Stromverstärkungsfaktor β
∆IC
Der Stromverstärkungsfaktor β = ∆I
wird dem zweiten Quadranten des
B
Vier-Quadranten-Kennlinienfeldes entnommen.
• dynamischer Basis-Emitter-Widerstand rB
BE
Der dynamische Basis-Emitter-Widerstand rB = ∆U
entspricht der
∆IB
Steigung der Eingangskennlinie im dritten Quadranten.
5
• dynamischer Kollektor-Emitter-Widerstand rC
CE
Der dynamische Kollektor-Emitter-Widerstand rC = ∆U
∆IC entspricht der
Steigung der Ausgangskennlinie im ersten Quadranten.
3.2.3
Berechnen der Schaltungskenngrößen
Die dynamischen Schaltungskenngrößen Spannunngsverstärkung v, Eingangsimpedanz Ze und Ausgangsimpedanz Za ergeben sich direkt aus den Transistorkenngrößen und können durch Betrachtung von Ersatzschaltbildern wie in der
Vorbereitungshilfe beschrieben ermittelt werden:
v
=
Ze
Za
=
=
Ua
Za
= −β
Ue
Ze
RB + rB
rC + RC
(8)
(9)
(10)
Die Werte sollen für zwei verschiede Basisvorwiderstände RB 1 = 0Ω und
RB 2 = 680Ω ermittelt werden. rC und β sind nahezu konstant; aus demselben
Grund aus dem wir auch nur eine Kennlinie dieser Größen aufgenommen haben:
Sie sind vom Betriebszustand des Transistors unabhängig. rB hängt allerdings
stark vom Basisstrom ab. Daraus folgt direkt, dass die Änderung von rB + rb
der Änderung der Spannungsverstärkung v entspricht.
3.2.4
Messen der Schaltungskenngrößen
In der Emitterschaltung werden Ue und Ua an ein Oszilloskop angeschlossen. Im
a
X/Y-Betrieb kann die Spannungsverstärkung v = U
Ue dann direkt als Steigung
abgelesen werden.
Um die Eingangsimpedanz zu bestimmen, messen wir die Spannung über
einem regelbaren Widerstand R vor dem Verstärkereingang und stellen diesen
anschließend so ein, dass genau die Hälfte der Ausgangsspannung daran abfällt.
Dann muss die andere Hälfte am Eingang des Verstärkers abfallen und es gilt
Ze = R.
Die Ausgangsimpedanz kann man nach dem gleichen Verfahren bestimmen
wobei der Widerstand aber an den Ausgang des Verstärkers angeschlossen ist.
3.2.5
Dachabfall am Koppelkondensator
Die Spannung am Kondensator beträgt
t
U (t) = U0 e− RC
(11)
und darf nach einer halben Periode des Rechtecksignals nicht unter 2% gesunken
sein. Daraus ergibt sich die Bedingung
1
0, 98U0 = U0 e− 2f RC
6
(12)
und daraus
C=−
1
log (0, 98) 2f R
(13)
wobei f = 1000Hz gegeben ist. R entspricht der Eingangsimpedanz und mit
RB = 0 (wie vorgegeben) gilt R = RB = 680Ω.
3.3
RC-Oszillator mit Transistorverstärkung in Emitterschaltung
Die Schaltung wird wie in Bild 12 der Vorbereitungshilfe aufgebaut. Am Oszilloskop lässt sich die Frequenz dann aus der Periodenlänge T bestimmen.
Wie in der Vorbereitungshilfe beschrieben erwarten wir einen Wert von etwa
f ≈ 950Hz.
7