Determianten, Flächen und Volumen

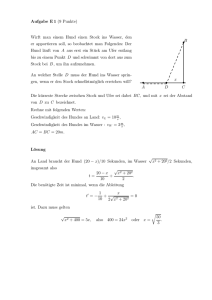
Kapitel 11
Determianten, Flächen und Volumen
In der Schule lernt man, dass man die Fläche eines Dreiecks am Besten als
“Grundseite mal Höhe durch zwei” berechnet. Das ist zwar ganz nützlich,
setzt aber voraus, dass man sowohl auf die Grundseite, als auch auf die Höhe
direkten Zugri↵ hat. Bei der Grundseite mag das unter praktischen Gesichtspunkten ja noch vergleichsweise einfach sein (Zollstock anlegen und Messen).
Bei der Höhe ist dies meinst schon nicht mehr so selbstverständlich. Um sie
bei einer ebenen Figur auszumessen, muss man zunächst einmal einen rechten Winkel anlegen. Liegt das Dreieck im Raum, so kann es sogar notwendig
werden, das man den Satz des Pythagoras bemühen muss (Man denke an
die Giebelseite eines schrägen Walmdachs). In Schulaufgaben hat man nicht
selten Rechenkästchen, die es vergleichsweise einfach machen, den Inhalt zu
bestimmen . . . zumindest so lange eine Seite Achsenparallel ist . . . ansonsten
muss wieder Pythagoras herhalten. Dabei wäre es doch so schön, wenn man
die Fläche direkt aus den Koordinaten der Ecken berechnen könnte, oder in
anderen Fällen aus den Längen der Kanten, denn die kann man ja messen.
An dieser Stelle kommen die Determinanten ins Spiel. Mit ihnen lassen
sich verblü↵end elegante Formeln für Flächeninhalte und Volumina herstellen. Oftmals sind diese nicht nur elegant, sondern lassen auch noch spannende und überraschende Verallgemeinerungen zu. In der Tat haben auch historisch Volumenberechnungen bei der Begründung des Determinantenbegri↵s
ein große Rolle gespielt.
Bevor Sie weiterlesen, überlegen Sie bitte, wie Sie mit Schulmitteln, den
Flächeninhalt des Nebenstehenden Dreicks berechnen würden (ein Kästchen
ist eine Einheit), ohne dabei jemals eine Wurzel zu ziehen, oder mit dem
Geodreieck herum zu hantieren.
Voraussetzungen: Definition von Determinanten, 2 ⇥ 2 und 3 ⇥ 3 Determinanten berechnen können, Multilinearität, Matrizenmultiplikation, die Formel det(A · B) = det(A) · det(B)
163
164
11 Determianten, Flächen und Volumen
1 Prolog
“Papa, gib mir Mathe-Vorhilfe. . .” so fing vor ungefähr neun Jahren ein Gespräch mit meiner Tochter an, die damals in der zweiten Klasse war. Nachhilfe
wollte sie nicht, aber ein wenig Smalltalk über Mathematik konnte sicherlich
nicht schaden. Da sie gerade das kleine Einmaleins lernte und ich Geometrieprofessor bin, einigten wir uns darauf, über die Zusammenhänge von Rechnen
und Geometrie zu reden.
Es ergab sich darauf hin ein Dialog, bei dem wir schrittweise immer komplexere Formen der Flächenberechnung entwickelten. Wir begannen mit einem einfachen Rechteck, bei dem zwei Seitenlängen in Kästcheneinheiten
gegeben waren und bestimmten den Flächeninhalt, also die Anzahl der eingeschlossenen Kästchen. Meine Tochter fing zunächst an, die einzelnen Kästchen
zu zählen, nachdem das aber begann, mühsam und fehleranfällig zu werden,
konnten wir uns schnell darauf einigen, dass genau dies eine hübsche Anwendung für das kleine Einmaleins ist. Ist der Zusammenhang von Multiplikation
und Rechtecken erst einmal verstanden, so kann man nicht viel mehr lernen
wenn man jetzt zwanzig Aufgaben vom selben Typus berechnet. Stattdessen
fingen wir an, die Aufgabenstellung zu variieren: Was passiert mit Rechtecken bei denen ein kleines Rechteck weggenommen wurde? Was passiert mit
beliebig geformten (achsenparallel begrenzten) Flächen? Dies ist eine Fragestellung, bei der man sehr gut eine mathematische Grundstrategie lernen
kann. Komplexe Probleme werden derart in viele kleine Einzelprobleme zerlegt, dass man aus deren Lösung einfach die Gesamtlösung rekonstruieren
kann (diese Strategie sollte man such merken, die werden wir später noch
oft anwenden). Sodann machten wir einen qualitativen Sprung und begannen uns schräg begrenzten Flächen zuzuwenden. Das Grundprinzip ist schnell
verstanden: Wird ein Rechteck entlang einer Diagonalen zerschnitten, so entstehen zwei Teile, die beide gleich groß sind somit jeweils halb so groß wie das
Rechteck. Erstaunlicherweise reicht diese Beobachtung bereits aus, um damit
recht einfach den Flächeninhalt von beliebig geformten Dreiecken zu bestimmen, so lange die Eckpunkte nur auf dem Gitter liegen. Man umschließt das
Dreieck einfach mit einem Rechteck (dessen Inhalt kann man ja einfach ausrechen) und zieht den Inhalt der an den Ecken verbleibenden überstehenden
Dreiecke wieder ab (diese sind halbierte achsenparallele Rechtecke und deswegen auch einfach auszurechen).
In der Tat ist es von diesen Überlegungen sogar nur noch ein kleiner Schritt
bis hin zum Satz des Pythagoras, wie das neben stehende letzte Bild andeutungsweise erkennen lässt. Es treten rechtwinklige Dreiecke mit Kathetenlängen von 3 und 4 Einheiten auf, und man kann berechnen, dass der
Inhalt des mittleren Quadrates 25 Einheiten beträgt. Also muss dessen Seitenlänge, die Hypotenuse, genau 5 Einheiten lang sein. Meine Tochter und
ich haben uns an diesem Nachmittag richtig gut gefühlt.
2 Von Koordinaten zu Flächen
165
2 Von Koordinaten zu Flächen
Was hat das Ganze nun mit Determinanten zu tun? In der Vorlesung
Lineare Algebra lernt man, dass Determinanten dazu verwendet werden
können, um aus den Koordinaten von Eckpunkten Flächeninhalte zu berechnen. Die Überlegungen im letzten Abschnitt, leisten genau das gleiche. Da
der Flächeninhalt eine eindeutige Größe ist, müssen wir im Prinzip bei den
Überlegungen des letzen Kapitels Determinanten ausgerechnet haben (und
das letztlich mit Mitteln der Grundschulmathematik). Wir wollen zunächst
analysieren, was die Betrachtungen des letzten Abschnittes algebraisch leisten.
2.1 Dreiecksinhalt
Zunächst einmal ist es klar, dass der Inhalt eines achsenparallelen Rechtecks,
dessen linke untere Ecke (0, 0) und dessen rechte obere Ecke (x, y) ist, genau
den Flächeninhalt x · y hat. Das Dreieck dass durch halbieren dieses Rechtecks entlang einer Diagonalen entsteht hat den Flächeninhalt x·y
2 . Betrachten
wir nun das an der Seite abgebildete Dreieck, dessen eine Ecke auf den Nullvektor einer Koordinatensystems fällt. Das umschließende Rechteck hat den
Flächeninhalt x1 · y2 . Die beiden orangenen Dreiecke, die an den Nullvektor
grenzen, haben Inhalte x12·y1 und x22·y2 . Für das blaue Dreieck müssen wir
zunächst die Seitenlängen über die Di↵erenzen (y1 y2 ) und (x2 x1 ) be2 x1 )
stimmen: der Flächeninhalt des blauen Dreiecks ergibt sich zu (y1 y2 )·(x
.
2
Alles in Allem erhalten wir für den Flächeninhalt F des weißen Dreiecks:
F = x 1 y2
= x 1 y2
=
x 1 y2
2
= (x1 y2
x 1 y1
2
x 1 y1
2
y1 x 2
2
x 2 y2
2
x 2 y2
2
(y1 y2 )·(x2 x1 )
2
y1 x 2
y1 x 1
y2 x 2
2 + 2 + 2
y2 x 1
2
y1 x2 )/2
Das ist genau die Hälfte der Determinante einer 2 ⇥ 2 Matrix mit den beiden
Spaltenvektoren (x1 , y1 ) und (x2 , y2 ). Somit ergibt sich eine Formel die man
wohl in der Linearen Algebra gelernt hat.
✓
◆
1
x x
F = det 1 2
y1 y 2
2
Es soll hier nicht behauptet werden, dass diese Herleitung besonders einfach ist (mit Mitteln der Linearen Algebra geht das schneller), aber sie ist
besonders elementar. Letztlich haben wir fast nur Flächenberchung achsenparalleler Rechtecke, Ausklammern, Terme zusammenfassen und ein wenig
gesunden Menschenverstand verwendet.
166
11 Determianten, Flächen und Volumen
Gehirngymnastik: Die Formel (x1 y2 y1 x2 )/2 berechnet letztlich die Di↵erenz zweier halbierter Rechtecksinhalte. Frage 1: Welche Rechtecke sind das?
Frage 2: können sie “sehen” wie sich aus der entsprechenden Di↵erenz die
Größe F ergibt?
2.2 Wie allgemein ist das?
Unsere gefundene Formel für den Flächeninhalt ist verblü↵end einfach:
✓
◆
1
x x
F = det 1 2 = (x1 y2 y1 x2 )/2.
y 1 y2
2
Bei genauer Betrachtung des letzten Kapitels wird man allerdings festgestellen, dass wir uns an einer Stelle das Leben ein wenig einfach gemacht haben.
Beim Überragen der Zeichnung des Dreiecks in das Koordinatensystem haben wir die Vektoren so gewählt, dass das Vorzeichen des umschließenden
Rechtecks positiv war, ebenso wie die Vorzeichen der subtrahierten Dreiecke.
Dies lag daran, dass alle Koordinaten der Punkte positiv waren, und (x2 , y2 )
gegen den Uhrzeigersinn gegenüber (x1 , y1 ) gedreht lag. In anderen Situationen werden die in unserer Formel von oben berechneten Summanden, die
den Rechtecks- und Dreiecksflächen entsprechen, eventuell andere Vorzeichen
haben. Funktioniert unsere gefundene Formel dann immer noch? Man kann
sich an dieser Stelle sehr schnell in eine lange Fallunterscheidung verstricken
und versuchen, jeden möglichen Fall für Vorzeichen der Summanden, die sich
durch Lage der Vektoren ergeben können, auszuprobieren. Es gibt aber auch
einen eleganten argumentativen Weg zu verstehen, was die Formel genau leistet. Bevor wir uns dieser zuwenden, müssen wir uns aber über einen wichtigen
Aspekt der Flächenberechnung Gedanken machen, nämlich das Vorzeichen
einer Fläche.
2.3 Orientierte Dreiecke
In der Schule betrachtet man üblicherweise den Flächeninhalt eines Dreiecks
als eine positive Größe. Das ist auch durchaus vernünftig, denn für den Bauer
in einer klassischen Textaufgabe ist ein negatives Stück Acker wenig sinnvoll.
Dennoch ist es in der Mathematik oftmals sinnvoll, sich von Formeln, die bei
einer Berechnung herauskommen, ein wenig, inspirieren zu lassen insbesondere, wenn diese einfach und elegant sind. Im vorliegenden Fall können bei
der Determinante auch negative Werte herauskommen und wer die im letzen
Kapitel angesprochene Mühe auf sich nimmt die Situation für verschiedene möglichen Lagen der Punkte durchzurechnen, stellt fest, dass in ziemlich
genau der Hälfte der Fälle der berechneter Dreiecksinhalt genau gleich der
2 Von Koordinaten zu Flächen
167
positiven Determinante in der anderen Hälfte genau gleich der negativen Determinante sein wird.
Wären wir ausschließlich an positiven Größen für Flächeninhalte interessiert, so müssten wir in unserer obigen Formel streng genommen folgendermaßen schreiben:
✓
◆
1
x x
F =
det 1 2 .
y1 y 2
2
Durch die Betragsstriche werfen wir gewissermaßen Information fort (das Vorzeichen), die vorher in der Determinante noch vorhanden war. Wir wollen nun
untersuchen, was es genau mit dem Vorzeichen auf sich hat, um dann später
festzustellen, dass es mathematisch durchaus sinnvoll und nützlich sein kann
auch negative Flächeninhalte zuzulassen (ganz ähnlich zur Situation bei den
natürlichen Zahlen, bei denen es ja auch nützlich und sinnvoll ist, negative
Zahlen einzuführen). Wir wollen uns also das Vorzeichen der Determinante
✓
◆
x x
det 1 2
y1 y2
ein wenig genauer ansehen. Hierzu halten wir zunächst den einen der beiden Vektoren fest und betrachten die Determinante als✓Funktion
◆ des anderen
x x
Vektors. Sei also v := (x1 , y1 )T und es sei f (v) := det 1 2 . Wir halten
y 1 y2
also den zweiten Spaltenvektor fest und betrachten die Determinante als eine
Funktion des ersten Spaltenvektors. Wie man in der Linearen Algebra lernt,
ist die Determinante eine multilineare Funktion der Spalten der Matrix; also
insbesondere linear in der ersten Spalte. Also ist f (v) eine lineare Funktion
und damit insbesondere stetig in v. Als stetige Funktion kann sie natürlich
wenn man v in der Ebene bewegt nicht plötzlich sprunghaft das Vorzeichen
wechseln, sondern gleitet quasi sanft vom Positiven ins Negative über. Bei diesem Übergang muss sie notwendig zumindest einmal den Wert 0 annehmen,
also schauen wir uns als Nächstes an, für welche Werte f (v) = x1 y2 y1 x2
den Wert 0 annehmen kann. In solch einem Fall gilt x1 y2 = y1 x2 . Anders
ausgedrückt ist dies genau dann der Fall wenn einer der Spaltenvektoren ein
Vielfaches des anderen ist. Für unsere Funktion f (v) bedeutet dies, dass sie
genau dann gleich 0 wird, wenn der Vektor v auf der Geraden liegt, die von
w := (x2 , y2 )T und dem Nullpunkt aufgespannt wird.
Dies passt sehr gut zu zwei Dingen die wir kennen.Der Flächeninhalt unseres Dreiecks wird natürlich zu Null, wenn der Nullpunkt und die beiden
Vektoren auf einer Geraden liegen. Weiterhin kennt man aus der Linearen
Algebra den Satz, dass die Determinante verschwindet, wenn die Spalten linear abhängig sind. Beides ist im Prinzip die gleiche Tatsache, einmal in der
Sprache der Geometrie, einmal in der Sprache der Algebra ausgedrückt. Die
von (0, 0)T und dem Vektor w aufgespannte Gerade teilt also unsere Fläche
in zwei Teile. Auf der einen Seite ist f (v) positiv, auf der anderen Seite ist
f (v) negativ. Der positive Wert ergibt sich wenn – wie in unserem Beispiel
168
11 Determianten, Flächen und Volumen
– die Richtung des Vektors (x2 , y2 ) sich durch eine Drehung von mehr als 0
und weniger als 180 gegen den Uhrzeigersinn aus der Richtung von (x1 , y1 )
ergibt. Muss man im Uhrzeigersinn drehen, wird die Determinante negativ.
Beträgt der Winkel genau 0 oder 180 , so sind die Vektoren mit dem Nullvektor kollinear, und die Determinante verschwindet. In den nebenstehenden
Abbildungen wird einerseits diese Gebietsaufteilung dargestellt, andererseits
sieht man den Wert der Determinante dargestellt als Funktion f : R2 ! R in
Abhängigkeit von v. Da die Determinante eine lineare Funktion in v ist, ist
dieser Funktionsgraph nichts anderes als eine Ebene, die an genau der durch
(0, 0) und (x2 , y2 ) aufgespannten Gerade die Nullline durchstößt. (TODO
Bilder machen).
Definition 11.1. Ist v = (x1 , y1 )T , w = (x2 , y2 )T und 0 = (0, 0)T , so nennt
man die Funktion
✓
◆
1
x1 x2
F(0,v,w) := det
y1 y2
2
den orientierten Flächeninhalt des Dreieckes
= (0, v, w).
2.4 Stimmt unsere Formel?
Wir haben bisher immer noch nicht geklärt, ob die in dieser Definition angegebene Definition auch wirklich mit dem tatsächlichen orientierten
Flächeninhalt des Dreiecks übereinstimmt. Nach unserer Vorarbeit ist das
aber verhältnismäßig einfach: Betrachten wir hierzu doch einmal die klassische Schulformel, dass sich die Dreiecksfläche als Grundseite mal Höhe durch
zwei ergibt. Das einzige was wir von dieser Formel brauchen, ist die Tatsache
dass sie linear in der Höhe des Dreiecks ist. Halten wir wieder den Vektor w
fest, betrachten die Strecke G = 0, w als Grundseite des Dreiecks, so ergibt
sich die Höhe des Dreiecks aus der Position von v gerade so, dass Orte gleicher
Höhe des Dreiecks Parallelen zu G sind. Um nun orientierte Dreiecksflächen
zu betrachten, müssen wir die Höhe auf der einen Seite von G positiv und
auf deren andern Seite negativ werten. Zeichnet man den Funktionsgraph
der sich so ergebenden tatsächlichen Dreiecksfläche, so ergibt sich genau das
gleich Bild wie bei der Determinanten. Die Höhe und somit die Dreichecksfläche verschwindet, wenn das Dreieck ausartet (also v auf der Trägergeraden
der Grundseite G liegt). Also stimmt die Funktion der tatsächlichen gemessenen orientierten Dreiecksfläche mit unserer definierten Funktion F(0,v,w)
sowohl an den Stellen überein, wo sie null werden (die Trägergerade von G,
bzw der von w aufgespannte Unterraum), als auch an einem weiteren Punkt,
wie wir im Abschnitt 1.2.1 gesehen haben. Als lineare Funktionen müssen sie
daher miteinander überein zu stimmen. Wir können somit guten Gewissens
3 Allgemeinere Flächen
169
F(0,v,w) als orientierten Flächeninhalt betrachten. Zwei Dinge sind an dieser
Stelle noch erwähnenswert, die später noch relevant werden sollen.
Bemerkung 1 Für die Linearität des tatsächlichen Flächeninhalts ist es
essentiell wichtig, den orientierten Flächeninhalt zu betrachten. Der Absolutwert des Flächeninhalts f (v) würde sich zwar links und rechts der Gerade
durch G wie eine Lineare Funktion verhalten hätte aber an dieser Stelle einen
Knick, analog zur Betragsfunktion x 7! |x|.
Bemerkung 2 Wir haben argumentiert, dass zwei lineare Funktionen f (v)
und g(v) gleich sind, wenn sie die gleichen Nullstellen haben und in einem
weiteren Punkt übereinstimmen. Wir werden im folgenden noch öfter argumentieren müssen, dass zwei Funktionen identisch sind. Wir werden uns hierzu einen Satz aus der Analysis entlehnen, der dazu dass vielleicht allgemeinste Werkzeug darstellt. Sind zwei Funktionen f (x) und g(x) analytisch und
stimmen sie auf einer volldimensionalen Umgebung (egal wie klein die sein
mag) eines Punktes ihres Definitionsbereiches überein, so sind beide Funktionen identisch. Insbesondere sind lineare Funktionen, affine Funktionen oder
noch allgemeiner Polynome alles analytische Funktionen.
3 Allgemeinere Flächen
Bisher haben wir uns sehr ausführlich mit einem einzigen Dreieck beschäftigt,
dessen eine Ecke sogar noch im Ursprung des Koordinatensystems lag. Das ist
wirklich sehr speziell! Wir wollen uns nun allgemeineren Flächen und deren
Inhaltsbestimmung zuwenden. Wir fangen zunächst mit Dreiecken in beliebiger Lage an. Schaut man sich die Argumentationskette im Abschnitt 1.2.1
an, so wurde beim Bestimmen des Flächeninhalts lediglich auf das darunter
liegende Koordinatenraster, nicht jedoch auf die Position des Nullpunktes
Bezug genommen. Dieser spielte erst eine Rolle, als wir zu konkreten Berechnungen übergegangen sind. Wir könnten nun eine ähnliche Rechnung für
Dreiecke in allgemeinen Positionen anstellen. Statt dessen wollen wir im folgenden einige Aussagen aus der Linearen Algebra verwenden, die uns hier das
Leben ein wenig leichter machen werden. Determinanten haben zwei wichtige
Eigenschaften
1. Determinanten sind multilinear in jeder Spalte
2. Determinanten sind antisymmetrisch in jeder Spalte.
Wir werden diese Eigenschaften im Folgenden sowohl für 2⇥2 Determinanten
als auch für 3 ⇥ 3 Determinanten verwenden.
170
11 Determianten, Flächen und Volumen
3.1 Dreiecke
Wir betrachten nun ein Dreieck mit Eckpunkten u, v, w 2 R2 und bestimmen
den orientierten Flächeninhalt F(u,v,w) . Verschieben wir dieses Dreieck so,
dass die erste Ecke mit dem Nullpunkt zusammen fällt, so ändert sich der
Flächeninhalt nicht. Diese Verschiebung kann man durch Subtraktion des
Vektors u auf allen Ecken erreichen. Es gilt also
F(u,v,w) = F(u
u,v u,w u)
= F(0,v
u,w u)
Wenden wir nun unsere vorherige Formel und die Eigenschaften der Determinante an, so erhalten wir:
F(u,v,w) = F(0,v
=
=
=
=
u,w u)
1
u, w u)
2 det(v
1
u) det(u, w u))
2 (det(v, w
1
det(v, u) det(u, w) +
2 (det(v, w)
1
2 (det(u, v) + det(v, w) + det(w, u))
det(u, u))
= F(0,u,v) + F(0,v,w) + F(0,w,u)
Die letzte Formel hat eine faszinierende geometrische Interpretation: Um
den (orientierten) Inhalt eines Dreiecks
zu erhalten, muss man lediglich
die (orientierten) Inhalte der Dreiecke aufaddieren, die aus den Kanten von
und dem Nullpunkt gebildet werden. Die Kanten werden dabei zyklisch
gegen den Uhrzeigersinn durchlaufen. Dies ist sofort einsichtig, wenn sich der
Nullpunkt im Inneren des Dreiecks befindet. Dann zerfällt das Dreieck in drei
kleinere Dreiecke deren Flächeninhalte allesamt positiv gewertet werden (hier
verbirgt sich wieder das Zerlegungsprinzip, dass wir im Abschnitt 1.1 kennen
gelernt haben).
Überraschenderweise funktioniert das Ganze aber vollkommen unabhängig
davon, wo der Ursprung liegt. Die Vorzeichen sorgen automatisch für die
richtige Buchführung der Flächeninhalte. Dies erscheint zunächst ein wenig
überraschend, ist aber genau das, was unsere gerade hergeleitete Formel besagt. Wir wollen uns dies dennoch an einem konkreten Beispiel verdeutlichen.
Betrachten wir, wie in der untenstehenden Abbildung, ein Dreieck (u, v, w),
3 Allgemeinere Flächen
171
das den Nullpunkt nicht umschließt. So wie die Punkte in diesem Fall liegen,
überschätzt der erste Summand F(0,u,v) die Dreiecksfläche gewaltig. Das was
zu viel berechnet wurde, wird allerdings von den anderen beiden Summanden
F(0,v,w) + F(0,w,u) perfekt kompensiert, da deren orientierter Flächeninhalt
negativ ist.
Bemerkung 3 Auch hier hätten wir argumentieren können, dass der orientierte Flächeninhalt eine analytische Funktion in den Koordinaten der Eckpunkte ist. Damit reicht es nämlich vollkommen aus, dass die Behauptung
für Dreiecke, die den Ursprung umschließen, gilt.
3.2 Vierecke
Betrachten wir als nächstes ein Viereck (t, u, v, w) und dessen Flächeninhalt
F(t,u,v,w) . Das Viereck kann man einfach in zwei Dreiecke (t, u, v) und (v, w, t)
zerlegen. Die Fläche des Vierecks ergibt sich als Summe der beiden Dreiecksflächen wir erhalten also:
F(t,u,v,w) = F(t,u,v) + F(v,w,t)
Berechnen wir den Inhalt der beiden Dreiecke nach unserer Formel, so
ergibt sich:
F(t,u,v,w) = F(t,u,v) + F(v,w,t)
= F(0,t,u) + F(0,u,v) + F(0,v,t) + F(0,v,w) + F(0,w,t) + F(0,t,v)
= F(0,t,u) + F(0,u,v) + F(0,v,w) + F(0,w,t)
Die innere Kante v, t wird hierbei von den beiden Dreiecken in entgegengesetzter Richtung durchlaufen, die entsprechenden Terme fallen somit aus der
Summe heraus.
172
11 Determianten, Flächen und Volumen
Wieder ergibt sich, dass wir zur Berechnung des (orientierten) Flächeninhalts
den Rand des Vierecks einfach nur gegen den Uhrzeigersinn ablaufen müssen,
und für jede Kante vi , vi+1 den Flächeninhalt F(0,vi ,vi+1 ) aufaddieren. Wieder
ist das Ganze vollkommen unabhängig von der genauen Position des Nullpunktes.
An dieser Stelle erweisen sich unsere orienterten(!) Flächeninhalte ein weiteres Mal als richtig nützlich. Sie übernehmen nicht nur die Buchführung
bei unterschiedlichen Positionen des Nullpunktes, sie sorgen auch dafür, dass
nicht-konvexe Vierecke automatisch korrekt berechnet werden. Ein bildhaftes
Beispiel soll zur Veranschaulichung dieses Sachverhaltes genügen:
Das Dreieck (t, u, v) überschätzt zunächst den Flächeninhalt des konkaven
Viereckes (t, u, v, w). Das zweite Dreieck (v, w, t) wird aber im Uhrzeigersinn
durchlaufen, seine Fläche ist somit negativ zu werten und sorgt genau dafür,
dass die einspringende Ecke wieder abgezogen wird.
Die eben gemachte Überlegung, mit der negativ orientierten einspringenden Ecke ist übrigens für die Begründung, dass man um den Flächeninhalt
durch Umlaufen, des Randes und Aufsummieren der Determinanten berechnen kann nicht die einzige Beweisstrategie. Auch ein konkaves Viereck lässt
sich nämlich in zwei Dreiecke zerlegen, die beide nun mit jeweils positiver
Fläche addiert werden. (in unserem Beispiel sind das (u, v, w) und (u, w, t).
Wie zuvor heben werden Kanten aneinander grenzender Dreiecke in unterschiedlichen Richtungen durchlaufen. Die zugehörigen Determinanten heben
sich dabei wieder weg.
3 Allgemeinere Flächen
173
3.3 Beliebige n-Ecke
Hat man einmal das Prinzip verstanden, dass man jede Fläche in Dreiecke zerlegen kann, so kann man damit den Flächeninhalt eines belieben
n-Ecks berechnen. Das Erstaunliche ist, dass man für die Berechnung des
Flächeninhaltes die Dreieckszerlegung letztlich gar nicht benötigt, da alle inneren Kanten an zwei Dreiecke grenzen, von denen sie in entgegengesetzter
Richtung durchlaufen werden. Die entsprechenden Terme in der Berechnung
heben sich dann automatisch weg. Das folgende Bild verdeutlicht an einem
recht willkürlich gewählten Zehneck (v0 , v1 , . . . , v9 ) was passiert:
Wir zerlegen zunächst das Zehneck gedanklich in eine Ansammlung von
Dreiecken (so etwas geht immer, soll aber hier nicht bewiesen werden). Welche Zerlegung wir dabei genau nehmen, ist im Prinzip egal, wie wir gleich
sehen werden. Im obigen Beispiel wurde die Zerlegung sogar so gewählt, dass
im Inneren neue Punkte verwendet werden, die gar nicht als ursprüngliche
Eckpunkte auftauchen. Es gibt sogar Dreiecke (z.B. (a, c, b)) die vollständig
im Inneren liegen. Um nun den Flächeninhalt zu bestimmen, summieren wir
die orientieren Fläche all dieser Dreiecke. In unserem Fall sind das 16 Stück.
Bei jedem der Dreiecke achten wir darauf, dass wir es gegen den Uhrzeigersinn
durchlaufen und wenden unsere Determinantenformel an. Somit liefert jede
Kante einen Summanden (das macht in unserem Fall 48 Summanden). Nun
passiert etwas Wunderbares: Alle inneren Kanten fallen aus der Rechnung
vollständig heraus. (Jede solche innere Kante hat zwei Nachbardreiecke und
beide durchlaufen die Kante in unterschiedlicher Richtung, was dazu führt,
dass sich die Werte der zwei zugehörigen Kanten sich kompensieren.) Übrig
bleiben alle Kanten am Rand des ursprünglichen Zehnecks. Denn das sind
die, die jeweils genau nur einmal auftreten. Die Fläche ergibt sich somit zu
F(0,v0 ,v1 ) + F(0,v1 ,v2 ) + · · · + F(0,v8 ,v9 ) + F(0,v9 ,v0 ) =
9
X
i=0
F(0,vi ,vi+1 ) .
174
11 Determianten, Flächen und Volumen
In der Summe werden dabei hier Indizes modulo 10 gerechnet. Das folgende
Bild erklärt diese Formel nochmals von einer anderen Perspektive. Die in
der Formel aufsummierten Dreiecksflächen beziehen sich ja auf einen beliebig
zu positionierenden Nullpunkt 0 des Koordinatensystems. Nach Wahl dieses dieses Nullpunktes tragen die Kanten, die von 0 aus gesehen gegen den
Uhrzeigersinn verlaufen, eine positive Fläche zur Summe bei. Die, die im Uhrzeigersinn verlaufen, tragen eine negative Fläche bei. Im Bild unten sind auf
der rechten Seite der Gleichung positive Flächen grün und negative Flächen
rot dargestellt. Wieder kompensieren die roten Flächen genau den Bereich,
der in der grünen Fläche des ersten Summanden zu viel angenommen wurde.
Gehirngymnastik: Stellen sie sich für das obige Diagramm einen Film vor,
in dem der angenommene Nullpunkt langsam um das Polygon wandert? Wie
müssen sich während des Filmes dabei rote und grüne Flächen verändern?
3.4 Selbstüberschneidung und Windungszahlen
Wir haben an den Betrachtungen und Beispielen der letzen Abschnitte gesehen, dass wir für ein beliebiges n-Eck (v0 , v1 , . . . , vn ) dessen Flächeninhalt
über die Formel
n
X
F(v0 ,v1 ,...,vn ) =
F(0,vi ,vi+1 )
i=0
berechnen können (Indizes modulo n). Der Begri↵ des Flächeninhalts ist
natürlich nur so lange sinnvoll, wie sich der Kantenzug (v0 , v1 , . . . , vn , v0 )
nicht selbst überschneidet. Tut er das dennoch, gibt es zumindest im klassischen Sinn keinen wohldefinierten Flächeninhalt. Unsere Formel hat sich
jedoch bisher in vielen Aspekten als so elegant und nützlich erwiesen, dass
man diese in vielen mathematischen Situation direkt als Definition des
Flächeninhaltes sich selbst überschneidender n-Ecke hernimmt. Sie ist die
direkte und auch mathematisch sinnvolle Verallgemeinerung des klassischen
3 Allgemeinere Flächen
175
Flächeninhalts auf sich selbst überschneidende Polygone. Wir wollen uns hier
kurz klar machen, was dabei genau gemessen wird. Wir betrachten dazu
zunächst den nebenstehend abgebildeten fünfzackigen Stern. Die Pfeile geben
an, in welcher Reihenfolge und Richtung die Ecken durchlaufen werden. Was
kommt heraus, wenn wir mit unserer Formel den Flächeninhalt dieses Sternes berechnen? Wie immer ist für den Flächeninhalt die exakte Position des
Nullpunktes vollkommen gleichgültig, obwohl er in der Rechnung vorkommt.
Wir können ihn also insbesondere so wählen, dass die Berechnung möglichst
übersichtlich wird. Für den Fünfzackstern müssen insgesamt 5 Dreiecke aufsummiert werden. Wählen wir den Nullpunkt im Inneren des kleinen Fünfecks
im Stern so werden tatsächlich alle aufzusummierenden Flächen positiv und
die die Analyse der Rechnung somit besonders einfach. Sie wird im nächsten
Bild veranschaulicht.
Wir betrachten also
F(v0 ,v1 ,...,v5 ) = F(0,v0 ,v1 ) + F(1,v0 ,v2 ) + F(2,v0 ,v3 ) + F(3,v0 ,v4 ) + F(4,v0 ,v0 ) .
Schaut man sich die Summanden genau an, so stellt man fest, dass jeder
solche Punkt, der in einer Spitze des Sterns liegt in genau einem aufsummierten Dreieck liegt. Jeder Punkt, der im Inneren des zentralen Fünfecks
liegt, wird jedoch von genau zwei aufsummierten Dreiecken erfasst. Somit
wird der Inhalt im Inneren doppelt (!) gezählt. Die nebenstehende Abbildung
verdeutlicht die Zählung der jeweiligen Flächenstückchen. Für jeden Punkt,
der nicht auf dem Kantenzug des n-Ecks liegt, nennt man die Zahl, mit der
der zugehörige Flächenbereich gewichtet werden muss, die Windungszahl des
Punktes. Sie ist für jeden solchen Punkt immer ganzzahlig. In unserem Beispiel hat jeder Punkt im Zentrum des Sternes also Windungszahl 2. Jeder
Punkt in einer Zacke des Sterns hat Windungszahl 1 und Punkte die komplett ausserhalb des Sternes liegen haben eine Windungszahl von 0 (sie tragen
also gar nichts zur Fläche bei).
Die Windungszahl hat eine sehr anschauliche Interpretation, der sie letztlich auch ihren Namen verdankt. Stellt man sich den Kantenzug als ein geschlossenes Seil vor, dass noch dazu eine (z.B. mit Pfeilen gekennzeichnete)
Umlaufrichtung hat, so kann man die Windungszahl in einem Punkt folgendermaßen ermitteln: Man nimmt einen Bleistift und setzt dessen Spitze im
fraglichen Punkt auf. Mit der noch freien Hand zieht man am Seil, bis bis es
176
11 Determianten, Flächen und Volumen
überall soweit als möglich selbstüberscheidungsfrei ist und sich nur noch um
den Bleistift windet. Das Seil darf sich dabei nach Belieben selbst durchdringen, wenn dies dem Entwirren zuträglich ist, nur durch den Bleistift darf es
nicht wandern. Wie oft das Seil sich danach um den Bleistift windet, gibt genau die Windungszahl an. Windungen gegen den Uhrzeigersinn werden dabei
positiv und die im Uhrzeigersinn negativ gezählt. Negative Windungszahlen
entsprechen übrigens genau den Regionen, die in unseren Überlegungen negativen Flächeninhalten zugeordnet werden. Nebenstehende Abbildung zeigt
die Situation eines sich selbst überschneidenden 4-Ecks, bei dem ein Teil der
umschlossenen Fläche negativ zu werten ist.
Gehirngymnastik: Geben sie ein 4-Eck an, bei dem keine drei Eckpunkte
auf eine Geraden liegen und dessen Flächeninhalt Null ist.
Bemerkung 4 Windungszahlen spielen übrigens sowohl in der Analysis,
als auch in der Physik eine sehr große Rolle. Insbesondere bei den vielen
Sätzen über den Zusammenhang von Pfad- und Flächenintegralen (z.B. Sätze
von Gauss/Green/Stokes) müssen Flächenstücke oftmals gemäß ihrer Windungszahlen umschließender Pfade gewichtet werden. Eine typische Anwendung solcher Integralsätze ist es z.B. Flächeninhalte kontinuierlich berandeter
Flächen durch Integrieren über den Rand zu bestimmen. Was wir in diesem
Kapitel geleistet haben, ist im Prinzip eine diskrete Version solcher Zusammenhänge bei der kontinuierliche Pfade durch stückweise geradlinige Polygonränder ersetzt wurden.
Gehirngymnastik: Bestimmen sie die Windungszahlen der verschiedenen
Bereiche in nebenstehender Abbildung.
4 Ein-Blick in die nächste Dimension
All unsere Überlegungen der letzten Abschnitte haben direkte Verallgemeinerungen in beliebige höhere Dimensionen. Ohne all zu sehr auf Details einzugehen, wollen wir die allgemeine Philosophie davon hier kurz vermitteln.
Dazu fassen wir zunächst einmal zusammen, was wir auf den letzten Seiten
eigentlich erarbeitet haben.
1. Wir haben den orientierten Flächeninhalt eines Dreiecks mit einer Ecke
im Nullpunkt berechnet.
2. Wir haben n-Ecke mit mit einem konsistenten Umlaufsinn entlang ihres
Randes versehen.
3. Wir haben die Fläche eines n-Ecks dadurch berechnet, dass wir über alle
Randkanten die orientierten Dreiecks-Flächen aufsummiert haben, die die
jeweiligen Randkanten mit dem Nullpunkt bilden.
4 Ein-Blick in die nächste Dimension
177
4. Die Fläche ergab sich somit allein aus der Betrachtung des Randes, die
Position des Nullpunktes war gleichgültig.
5. Wir haben Windungszahlen betrachtet.
Wir wollen nun sehen, wie sich all diese Konzepte in die nächste Dimension,
also in den Raum übertragen.
4.1 Tetraedervolumina
Wir wollen zunächst das Volumen eines dreidimensionalen Tetraeders bestimmen, dessen eine Ecke der Nullpunkt ist. Die anderen Eckpunkte seien
v 1 , v2 , v3 .
Im Zweidimensionalen mussten wir für ein Dreieck mit einer Fläche im
Ursprung lediglich 12 det(v1 , v2 ) berechnen. Im Dreidimensionalen geht das
analog. Das (orientierte) Volumen eines solchen Tetraeders ergibt sich zu
V(0,v1 ,v2 ,v3 ) =
1
det(v1 , v2 , v3 ).
6
1
Hierbei ergibt sich der Vorfaktor 16 als n!
wobei n die Dimension ist. Das Volumen hat wiederum eine Orientierung die sich daraus ergibt, ob die Punkte
v1 , v2 , v3 im oder gegen den Uhrzeigersinn laufen wenn an sie sich vom Nullpunkt aus ansieht. Die Orientierung schlägt sich im Vorzeichen nieder.
Mit zum zweidimensionalen analogen Argumenten kann man nun auch das
Volumen eines beliebigen Tetraeders bestimmen. Dies ergibt sich zu
V(v0 ,v1 ,v2 ,v3 ) =
1
(det(v0 , v1 , v2 )+det(v0 , v2 , v3 )+det(v0 , v3 , v1 )+det(v3 , v2 , v1 ))
6
Hierbei muss man ein klein wenig auf die Reihenfolge der Punkte in den
Determinanten achten, damit die Vorzeichen der Summanden stimmen. Die
Regel ist die folgende. Betrachtet man das Tetraeder mit Ecken (v0 , v1 , v2 , v3 )
von aussen, so trägt jede Seitenfläche einen Summanden bei. Die Reihenfolge
der Punkte im Summanden ergibt sich aus dem von aussen betrachteten Umlaufsinn der Punkte gegen den Uhrzeigersinn. Mit welchem Punkt man dabei
auf einer Fläche anfängt ist egal, da ja det(a, b, c) = det(b, c, a) = det(c, a, b)
gilt. Vertauscht man bei einem so berechneten Tetraeder zwei Punkte, so
ändert sich das Vorzeichen des orientierten Volumens.
4.2 Der konsistente Umlaufsinn
In der Ebene haben wir nun allgemeine Polygone betrachtet und haben ihrem
Rand zunächst einen Umlaufsinn gegeben. Dies haben wir dadurch gemacht,
178
11 Determianten, Flächen und Volumen
dass die Kanten in der Reihenfolge des Umlaufs orientiert wurden. Für eine
Fläche positiven Inhalts musste dabei der Umlaufsinn gegen den Uhrzeigersinn laufen. Anders ausgedrückt haben wir die Kanten so orientiert, dass
wenn man sich dem Polygon von Aussen nähert eine Kante, die man sieht,
immer von links nach rechts läuft. Dies lässt sich analog auf die räumliche
Situation übertragen. Wir betrachten einen räumlichen Körper, dessen Volumen wir bestimmen wollen. Wir stellen uns die Oberfläche zerlegt in Dreiecke
vor. Jedem Dreieck ordnen wir nun einen Umlaufsinn zu. Dies machen wir
so, dass wenn man sich ein Dreieck von ausserhalb des Körpers anschaut,
die drei beteiligten Ecken gegen den Uhrzeigersinn durchlaufen werden. Diese Reihenfolge gibt die Reihenfolge in den Determinanteneinträgen in obiger
Formel an. (TODO Bilder machen)
Der so gewählte Umlaufsinn hat folgenden E↵ekt: Betrachtet man zwei Tetraeder, die entlang einer gemeinsamen inneren Dreiecksfläche verklebt sind,
so wird diese Fläche von einem Tetraeder in einer Richtung, von dem anderen in der umgekehrten Richtung durchlaufen. Summiert man die beiden
nach obiger Formel berechneten Tetraedervolumina, so heben sich wieder
(vollkommen analog zu 2-dimensionalen Fall) die Determinanten der gemeinsam benutzte Dreiecksflächen weg. Das Volumen hängt also wieder nur vom
Rand ab, nicht von den Verhältnissen im Inneren eines Körpers.
4.3 Die Formel
Betrachten wir nun einen beliebigen (aber wenigsten selbstdurchdringungsfreien) Körper K. Dessen Oberfläche soll in viele Dreiecke zerlegt worden
sein. Für jedes Dreieck betrachten wir ein, wie angegeben, zyklisch geordnetes Tripel (u, v, w) von Eckpunkten. All diese Tripel (also für jedes Oberflächendreieck eines) fassen wir in einer Menge
zusammen. Das Volumen
des Körpers lässt sich dann nach folgender Formel bestimmen
X
VK =
det(a, b, c).
(a,b,c)2
Wieder ist die Formel strukturell unglaublich einfach. Es kommt lediglich
darauf an, dass in der Liste
die Dreiecke nach der angegebenen Regel orientiert sind. (Die Begründung der Formel ist denkbar einfach: zerlegt man
den Körper in lauter Tetraeder und summiert über alle Tetraedervolmina, so
heben sich genau die Summenden, die von Dreiecken im Inneren des Körpers
kommen in der Summe wieder weg, da sie zu zwei aneinandergenzenden Tetraedern gehören.) Mit dieser Regel lassen sich nun tatsächlich beliebige Volumina auch von verschlungenen Körpern oder Körpern mit Henkeln und
Löchern berechnen. Betrachten wir zum Beispiel den Torus in der nächsten
Abbildung. Die Oberfläche ist aus insgesamt 600 Dreiecken zusammengesetzt.
Summiert man über die diesen Dreiecken zugeordneten 600 Determinanten,
4 Ein-Blick in die nächste Dimension
179
so erhält man sofort und exakt das Volumen des von dieser Oberfläche eingeschlossenen Torus.
4.4 Eine Anwendung
Seit Erfindung moderner dreidimensionaler Drucktechniken gibt es im Internet Firmen, die professionellen 3D Druck als Serviceleistung anbieten. Als
Nutznießer eine solchen Dienstleistung lädt man über das Internet eine digitale Beschreibung des auszudruckenden Objektes hoch. In den üblichen Beschreibungssprachen macht man dies durch eine Beschreibung dessen Oberfläche, die wiederum als eine Ansammlung von Dreiecken vorliegt. Das Material, aus dem die Drucke hergestellt werden, ist verhältnismäßig teuer und
nicht selten wird der Objektpreis im Wesentlichen aus dem Materialverbrauch
berechnet. Dieser ergibt sich wiederum direkt aus dem Volumen des bestellten
Körpers.
Will die Firma also (bereits vor Druck) dem Benutzer mitteilen, wie teuer
ein bestelltes Modell wird, so muss sie lediglich die hochgeladenen Dreiecksdaten als Eingabe für unsere Formel des letzen Abschnitts verwenden und
erhält sofort das gesuchte Volumen.