Blatt 4

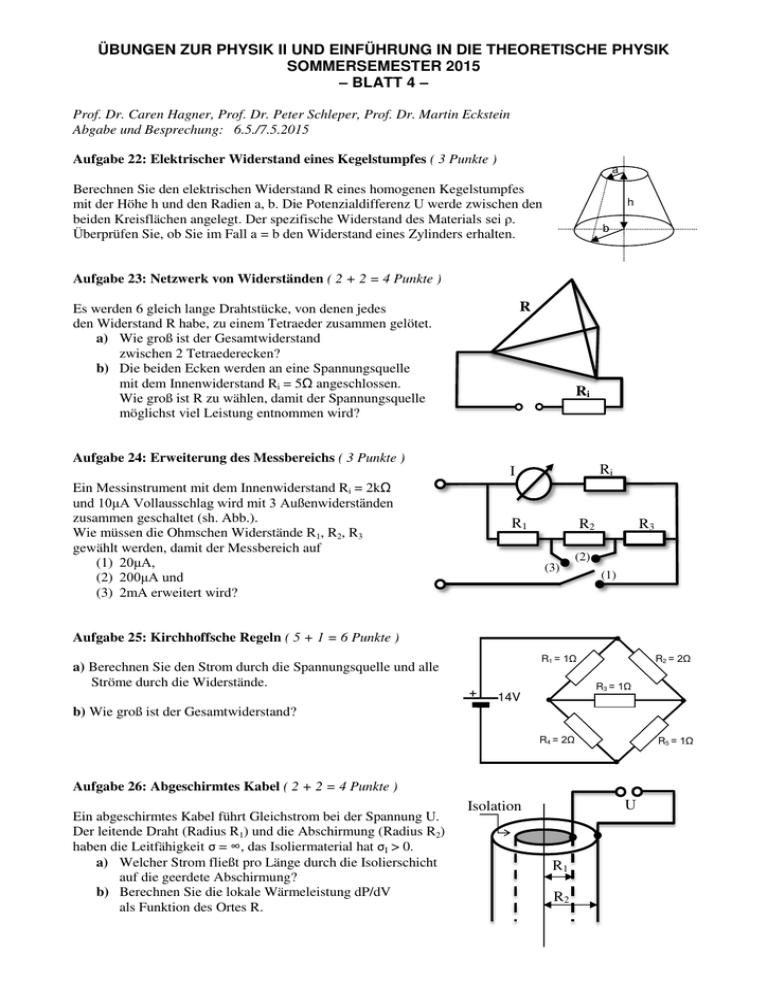
ÜBUNGEN ZUR PHYSIK II UND EINFÜHRUNG IN DIE THEORETISCHE PHYSIK
SOMMERSEMESTER 2015
– BLATT 4 –
Prof. Dr. Caren Hagner, Prof. Dr. Peter Schleper, Prof. Dr. Martin Eckstein
Abgabe und Besprechung: 6.5./7.5.2015
Aufgabe 22: Elektrischer Widerstand eines Kegelstumpfes ( 3 Punkte )
a
Berechnen Sie den elektrischen Widerstand R eines homogenen Kegelstumpfes
mit der Höhe h und den Radien a, b. Die Potenzialdifferenz U werde zwischen den
beiden Kreisflächen angelegt. Der spezifische Widerstand des Materials sei ρ.
Überprüfen Sie, ob Sie im Fall a = b den Widerstand eines Zylinders erhalten.
h
b
Aufgabe 23: Netzwerk von Widerständen ( 2 + 2 = 4 Punkte )
R
Es werden 6 gleich lange Drahtstücke, von denen jedes
den Widerstand R habe, zu einem Tetraeder zusammen gelötet.
a) Wie groß ist der Gesamtwiderstand
zwischen 2 Tetraederecken?
b) Die beiden Ecken werden an eine Spannungsquelle
mit dem Innenwiderstand Ri = 5Ω angeschlossen.
Wie groß ist R zu wählen, damit der Spannungsquelle
möglichst viel Leistung entnommen wird?
Ri
Aufgabe 24: Erweiterung des Messbereichs ( 3 Punkte )
Ri
I
Ein Messinstrument mit dem Innenwiderstand Ri = 2kΩ
und 10μA Vollausschlag wird mit 3 Außenwiderständen
zusammen geschaltet (sh. Abb.).
Wie müssen die Ohmschen Widerstände R1, R2, R3
gewählt werden, damit der Messbereich auf
(1) 20μA,
(2) 200μA und
(3) 2mA erweitert wird?
R1
R2
(3)
R3
(2)
(1)
Aufgabe 25: Kirchhoffsche Regeln ( 5 + 1 = 6 Punkte )
a) Berechnen Sie den Strom durch die Spannungsquelle und alle
Ströme durch die Widerstände.
R2 = 2Ω
R1 = 1Ω
+
R3 = 1Ω
14V
b) Wie groß ist der Gesamtwiderstand?
R4 = 2Ω
R5 = 1Ω
Aufgabe 26: Abgeschirmtes Kabel ( 2 + 2 = 4 Punkte )
Ein abgeschirmtes Kabel führt Gleichstrom bei der Spannung U.
Der leitende Draht (Radius R1) und die Abschirmung (Radius R2)
haben die Leitfähigkeit σ = ∞, das Isoliermaterial hat σI > 0.
a) Welcher Strom fließt pro Länge durch die Isolierschicht
auf die geerdete Abschirmung?
b) Berechnen Sie die lokale Wärmeleistung dP/dV
als Funktion des Ortes R.
U
Isolation
R1
R2
Einführung in die theoretische Physik II
Übung 4 – Abgabe 7. Mai 2015.
Sommersemester 2015
[email protected]
Aufgabe 27: Divergenz in krummlinigen Koordinaten ( 2+1 Punkt)
a. Gegeben sei ein krummliniges Koordinatensyem (u1 , u2 , u3 ) → r(u1 , u2 , u3 ) im R3 , für das die
lokalen Einheitsvektoren
∂r ∂r 1
, i = 1, 2, 3,
êi =
, hi = ∂ui hi
∂ui ein Orthogonalsystem
P bilden (ê1 × ê2 = ê3 , ê2 × ê3 = ê1 , ê3 × ê1 = ê2 ). Zeigen Sie: Für ein
Vektorfeld F (r) = i êi fi (u1 , u2 , u3 ) ist die Divergenz gegeben als
∇ · F (r) =
i
1 h ∂
∂
∂
h2 h3 f 1 +
h1 h3 f 2 +
h1 h2 f 3 .
h1 h2 h3 ∂u1
∂u2
∂u3
Hinweis: Betrachten Sie den Satz von Gauss für ein infinitesimales Volumen V = {r(u1 , u2 , u3 ) :
u0i − ǫ ≤ ui ≤ u0i + ǫ} um r0 = r(u01 , u02 , u03 ). Für ǫ → 0 können Sie zur Berechnung des Oberflächenintegrals auf den sechs Seitenflächen von V das Feld sowie die infinitesimalen Flächenelemente
durch den jeweiligen Wert auf dem Flächenmittelpunkt nähern.
b. Bestimmen Sie unter Verwendung des Resultats aus Aufgabe a die Divergenz eines rotationssymmetrischen Feldes F (r) = êr f (r) (gegeben in Kugelkoordinaten), und vergleichen Sie mit dem Resultat
aus dem letzten Übungsblatt. Berechnen Sie ∆ g(r) = div · grad g(r) für g(r) = rn , n ∈ Z für r 6= 0.
Aufgabe 28: Bildladungen (2+2 Punkte)
a. Gegeben sei eine unendlich ausgedehnte metallische Leiterplatte der Dicke D im Bereich −D < z < 0,
mit positiver Flächenladungsdichte σ auf beiden Flächen. Bestimmen Sie zunächst das Feld ausserhalb der
Platte mit Hilfe des Satzes von Gauss. Betrachten Sie nun eine positive Punktladung Q im Punkt (0, 0, d)
oberhalb der Oberfläche. Berechnen Sie das elektrostatische Potential Φ(r) der Anordnung, sowie die Kraft
auf die Punktladung als Funktion von d.
b. Betrachten Sie eine ungeladene metallische Kugel mit Radius R. Im Abstand d > R vom Kugelmittelpunkt
befinde sich eine Punktladung Q. Bestimmen Sie das elektrostatische Potential Φ(r) der Anordnung, sowie
die Flächenladungsdichte der induzierten Ladung. Wie gross ist die Kraft, mit der die Kugel die Punktladung anzieht? Hinweis: Zeigen Sie zunächst, dass das Potential von zwei Punktladungen Q am Ort (0, 0, d)
und q ′ = QR/d am Ort (0, 0, l) für geeignete Wahl von l < R auf der Kugelschale r 2 = R2 konstant ist.
Aufgabe 29: Die δ-Funktion (2 + 1 Punkt)
a. Berechnen Sie folgende Ausdrücke:
R
a.1. R3 dV δ (3) (r − a)(r 2 − 2r · a + a2 )
R 567
a.2. −22 dx δ(sin(x))
R
a.3. R3 dV δ (3) (r − a)f (r) mit f (r) = r cos(ϑ) (in Kugelkoordinaten) und a = (1, 0, 0) in kartesischen Koordinaten.
b. Zeigen Sie, dass fη (x) =
η
1
π η 2 +x2
für η → 0 die δ-Funktion repräsentiert.