Sphärische Zwei - und Dreiecke - Fakultät für Mathematik, TU

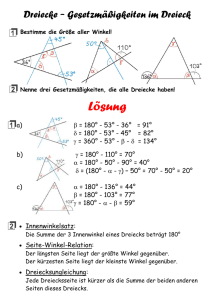
T ECHNISCHE U NIVERSITÄT D ORTMUND
Sphärische Zwei - und Dreiecke
Proseminar
innerhalb des Lehramtsstudiums im Fach
Mathematik
Meryem Öcal
Matrikelnummer 168833
Studiengang LABG 2009
Prüfer: Prof. Dr. Lorenz S CHWACHHÖFER
18. Januar 2017
1
Einleitung
Wie bereits in dem letzten Vortrag erwähnt, befinden wir uns nun in der Sphärischen Geometrie, welche sich in einigen Punkten stark von der ebenen euklidischen Geometrie unterscheidet.
Eines davon ist zum Beispiel die Eigenschaft, dass sich zwei Großkreise immer schneiden
werden, sodass das Parallelenaxiom nicht mehr gilt. Viele aus der euklidischen Geometrie
bekannten Sätze haben auf der Sphäre keine Gültigkeit mehr, wobei man sagen kann, dass es
sie allerdings in abgewandelter Form gibt.
In dieser Ausarbeitung möchten wir uns speziell mit den sphärischen Zwei- und Dreiecken auseinandersetzen, die durch verschiedenen S-Geraden, die durch den Mittelpunkt der
Sphäre verlaufen, erzeugt werden können.
Die Primärliteratur für diese Ausarbeitung beruht auf dem Buch von Andreas Filler, Euklidische und nicht-euklidische Geometrie des Wissenschaftsverlag und setzt für das Verständnis
Kenntnisse der beiden Vorlesungen "Lineare Algebra 1 und 2" voraus.
3
2
Sphärische Zweiecke und ihr Flächeninhalt
Durch zwei voneinander verschiedenen S-Geraden wird die Sphäre in vier Teile zerlegt, die
als spärische Zweiecke bezeichnet werden, wobei die jeweils gegenüberliegenden Zweiecke
zueinander kongruent sind und der Winkel a in der einen Ecke eines sphärischen Zweiecks
dem Winkel a 0 in der anderen Ecke entspricht.
Abbildung 1: Sphärisches Zweieck
Um eine Aussage über den Flächeninhalt sphärischer Zweiecke zu treffen, müssen wir
zunächst klären, was wir unter dem Flächeninhalt einer Figur der Sphäre allgemein
verstehen wollen. Dabei führen wir den Begriff Flächenmaß nicht im Sinne einer
herkömmlichen Definition ein, sondern geben drei Eigenschaften vor, die der Flächeninhalt
besitzen soll.
4
2.1
Axiome des Flächeninhalts von Figuren auf der Sphäre
(i) Kongruente Flächenstücke haben den gleichen Flächeninhalt
(ii) Ist ein Flächenstück f aus zwei Flächenstücken f1 und f2 zusammengesetzt, so ist der
Flächeninhalt F von f gleich der Summe der Flächeninhalte von f1 und f2
(iii) Der Flächeninhalt der Sphäre ist 4 · p · R2
Nehmen wir an, dass die betrachteten Sphären von nun an in dieser Ausarbeitung den
Radius 1 haben und wir alle Winkel im Bogenmaß betrachten.
2.2
Satz
Für den Flächeninhalt F eines sphärischen Zweiecks Z mit einem Winkel a gilt
F = 2·a
(1)
Beweis.
Wir zerlegen das Zweieck Z in n kongruente Zweiecke Zn . Diese haben dann jeweils das
Winkelmaß
an =
a
n
(2)
Fn =
F
n
(3)
und wegen (i) und (ii) den Flächeninhalt
5
Es sei nun kn eine natürliche Zahl derart, dass die folgende Gleichung erfüllt ist:
kn ·an  2p < (kn + 1) ·an
(4)
dh. das k wird so gewählt, dass man die maximale Anzahl von diesen n kongruenten
Zweiecken erreicht, die man um die gesamte Sphäre legen kann, sodass für (k + 1) ·an das
Ganze größer als 2p sein soll.
Dann gilt wegen (ii) auch
kn ·Fn  O <(kn + 1) ·Fn
(5)
wobei O der Flächeninhalt der Sphäre sei und wegen (3) folgt
kn · Fn  O < (kn + 1) · Fn
()
kn
n ·F
O<
(6)
kn +1
n ·F
Setzen wir nun (2) in (4) ein, dann folgt:
kn
n ·a
()
 2p
kn
n
<
kn +1
n ·a
2p
kn + 1
<
a
n

6
(7)
(8)
Es folgt:
kn
n
Dann ist
kn
n
2p
a

2p
kn 1
<
+
a
n n

9
2p >
>
>
a >
>
=
>
>
>
1
kn >
>
;
<
n
n
2p
a
1
kn 2p
<

n
n
a
(9)
(10)
Betrachten wir nun die Grenzwerte dieser Ungleichung, dann folgt aus der Analysis durch
das Sandwichkriterium
kn 2p
=
n!• n
a
lim
(11)
und schließlich aus (6):
()
n!•
()
kn
n

O
kn + 1
<
F
n
(12)
kn
n

O
kn 1
<
+
F
n n
(13)
2p
a

O
2p

+0
F
a
(14)
=)
O 2p
=
F
a
7
(15)
oder wegen (iii) und (15) gilt:
O
4p
2p
=
=
F
F
a
() 4p =
2p
·F
a
() 2a = F
(16)
(17)
(18)
⇤
8
3
Sphärische Dreiecke
Als Sphärische Dreiecke werden Teile der Sphäre bezeichnet, die durch drei sphärische
Strecken begrenzt sind. Der Unterschied zu der euklidischen Geometrie ist, dass man durch
drei Punkte nicht nur ein Dreieck darstellen kann, sondern vier (s. Abbildung 2).
Abbildung 2: Sphärische Dreiecke
Um die Vielfalt dieser Figuren etwas einzuschränken und um drei Punkten der Sphäre
möglichst eindeutig ein Dreieck zuzuordnen, betrachten wir im folgenden nur eine spezielle
Klasse sphärischer Dreiecke, nämlich die Eulerschen Dreiecke.
3.1
Definition
Sphärische Dreiecke, deren sämtliche Seiten und Winkel kleiner als p sind, heißen Eulersche
Dreiecke.
In Abbildung 2 ist dementsprechend nur a) ein Eulersches Dreieck. Für Eulersche Dreiecke
gelten einige Sätze, die wir bereits aus der ebenen Geometrie kennen.
9
3.2
Lemma
Wenn A,B,C 2 Sphäre S ist und keiner liegt einem der anderen gegenüber, dh. A 6=
C,
B 6= C, A 6= B und nicht alle drei auf einem Großkreis. Dann gibt es genau ein Eulersches
Dreieck mit Ecken ABC.
Beweisidee.
Abbildung 3: Sphärische Dreiecke
3.3
Satz
In jedem Eulerschen Dreieck sind die Längen zweier Seiten a und b sowie die Maße der
gegenüberliegenden Winkel entweder paarweise gleich oder der längeren Seite liegt der
größere Winkel gegenüber.
Beweis.
Es sei 4ABC ein Eulersches Dreieck mit den Winkeln a,b ,g sowie den Seiten a, b, c und g
die Mittelsenkrechte von c.
1.Fall: C liegt in g
Liegt der Punkt C auf g, so wird das 4ABC durch eine Spiegelung an g auf sich selbst
10
Abbildung 4: C liegt in g
abgebildet und es gilt daher: a = b sowie a = b .
2.Fall: C liegt in einer der beiden von g begrenzten Halbsphären
Abbildung 5: C liegt in einer der beiden von g begrenzten Halbsphären
Nehmen wir an, der Punkt C liegt in der durch g begrenzten Halbsphäre, zum Beispiel in der,
die auch den Punkt A enthält. Durch die Mittelsenkrechte g wird eine Ebene e festgelegt, die
auf der (euklidischen) Geraden AB senkrecht steht und die (euklidische) Strecke AB halbiert.
Es sei h die Schnittgerade der Ebenen ABC und e, sowie S der Schnittpunkt der
(euklidischen) Geraden h und BC (s. Abbildung 6).
11
Abbildung 6: Schnittfläche von 4ABC
Es gilt
|AS| < |AS| + |SC|
(19)
und da das 4ABC gleichschenklig ist
|AC| < |BS| + |SC|
(20)
(für die euklidische Abstände).
Aufgrund des Zusammenhangs zwischen der Länge von Sehnen und dem Maß der zugehörigen Zentriwinkel folgt daraus b < a und zwar gilt: Je länger die Sehne AB ist, desto größer
ist der Zentriwinkel.
Da B und C auf unterschiedlichen Halbsphären bezüglich g liegen, schneiden sich a und g in
einem Punkt D (s. Abbildung 5) und die sphärische Strecke AB teilt den Winkel a; das liegt
daran, dass D im Inneren von a liegt.
Daher ist ]DAB < a und aufgrund der Eigenschaft, dass 4ABC gleichschenklig ist, gilt
]DAB =b und somit b < a.
12
3.4
Satz
Die Summe der Längen zweier Seiten eines jeden Eulerschen Dreiecks ist stets größer als
die Länge der dritten Seite:
|AB| + |BC| > |AC|
(21)
Abbildung 7: Dreiecksungleichung, Beispiel 1
Beweis.
Um die Dreiecksungleichung zu beweisen müssen wir zwischen zwei Fällen unterscheiden.
1.Fall: |AB| + |BC|
p
Abbildung 8: Dreiecksungleichung, Beispiel 2
13
Falls |AB| + |BC|
p ist, gilt die Behauptung wegen der Definiton des Eulerschen Dreiecks
sofort. Und zwar ist der Grund dafür, dass Eulersche Dreiecke nur durch S-Gerade
aufgespannt werden können, die durch den Mittelpunkt der Sphäre gehen (diese werden
dann als Großkreise bezeichnet) und diese zusammenaddiert größer gleich p sind.
2.Fall: |AB| + |BC| < p
Abbildung 9: Dreiecksungleichung, Beispiel 3
Anderfalls verlängern wir die Seite AB um die zu BC gleichlange Strecke BD.
Nach Satz 6 sind die bei D und C liegenden Winkel des 4BCD kongruent, somit ist das
4ACD dann ebenso ein Eulersches Dreieck, das durch die Strecke BC geteilt wird. Bei C
liegt daher ein größerer Winkel des 4ACD als bei D, demnach gilt
|AD| > |AC|
(22)
() |AB| + |BC| > |AC|
(23)
⇤
Anhand von einigen Beispielen lässt sich leicht verdeutlichen, dass die Sätze 3.3 und 3.4 für
beliebige, d.h. also auch nicht-Eulersche Dreiecke im allgemeinen, nicht gelten (s. z.B.
Abbildung 2)
14
3.5
Satz
Zwei sphärische Dreiecke, die in zwei Seiten und dem von diesen beiden Seiten eingeschlossenen Winkel übereinstimmen, sind kongruent.
Beweis.
Um den Satz zu beweisen, möchten wir eine geeignete sphärische Bewegung konstruieren,
welche das eine Dreieck in das andere überführt.
Abbildung 10: Beweis zu Satz 3.5
1.Schritt Man konstruiere zunächst eine Bewegung, die A0 in A überführt.
2.Schritt Nun erzeuge man eine Drehung um A, so dass der Großkreis AB00 auf Großkreis
AB gedeckt wird.
An dieser Stellen können wir auf zwei Fälle treffen:
p
1.Fall AC00 wird auf AC überführt =)C”’ = C
2.Fall AC00 wird auf "AC
gespiegelt" überführt. Dann muss eine Spiegelung an
p
der S-Geraden AB erfolgen
=)C”’ = C
⇤
15
4
Flächeninhalt, Winkelsumme und Seitensumme Eulerscher Dreiecke; Polardreiecke
Zunächst einmal konstruieren wir eine Sphäre, die durch drei Großkreise, welche durch drei
festgelegten Punkten, die nicht alle unbedingt auf einem Großkreis liegen, in acht Eulersche
Dreiecke zerlegt wird. Diese acht Eulerschen Dreiecke bestehen aus dem Ausgangsdreieck
4ABC, den drei Scheiteldreiecken 4ABd Cd , 4Ad BCd und 4Ad Bd C und den drei
Nebendreiecken 4Ad BC, 4ABd C und 4ABCd , sowie das Gegendreieck 4Ad Bd Cd , wobei
Ad , Bd ,Cd die zu A,B,C diametralen Punkte sind (siehe Abbildung 11)
Abbildung 11: Scheiteldreiecke, Nebendreiecke, Gegendreieck
Als diametral werden zwei Punkte auf einem Kreis oder einer Kugeloberfläche bezeichnet,
welche Antipoden sind, dh. die Verbindungsstrecke beider Punkte beinhaltet den Kreis- bzw.
Kugelmittelpunkt, wobei die Länge dieser Verbindungsstrecke dem Durchmesser entspricht.
Die Eigenschaften diametraler Punkte sind, dass zum einen die beiden Punkte den
größtmöglichen Abstand auf der Kreisoberfläche zueinander haben und zum anderen genau
ein diametraler Punkt Ad zu Punkt A existiert.
16
Wir leiten im folgenden eine Formel für den Flächeninhalt Eulersche Dreiecke her, die vor
allem deshalb interessant ist, weil sie eine fundamentale und überraschende Folgerung
hinsichtlich der Winkelsumme sphärischer Dreiecke ermöglicht.
Das 4ABC und sein Gegendreieck 4Ad Bd Cd gehen durch eine Abbildung auseinander
hervor, die jedem Punkt der Sphäre seinen diametralen Punkt zuordnet. Da eine solche
Abbildung eine Bewegung ist, sind diese beiden Dreiecke kongruent und somit
flächengleich.
Das gleiche gilt für 4Ad BC und 4ABd Cd ,
4ABd C und 4Ad BCd ,
4ABCd und 4Ad Bd C
Wir bezeichnen den Flächeninhalt von 4ABC und 4Ad Bd Cd mit F,
4Ad BC und 4ABd Cd mit F1 ,
4ABd C und 4Ad BCd mit F2
4ABCd und 4Ad Bd C mit F3 .
Da die Dreiecke 4ABC, 4Ad BC, 4Ad Bd C und 4ABd C eine Halbsphäre bedecken, gilt
F + F1 + F2 + F3 = 2 · p
(24)
Die Dreiecke 4ABC und 4Ad BC bilden zusammen ein sphärisches Zweieck mit dem
Winkel a, die 4ABC und 4ABd C ein solches mit dem Winkel b und schließlich 4ABC
und 4ABCd eines mit dem Winkel g.
Abbildung 12: Sphärische Zweiecke aus dem Ausgangsdreieck 4ABC und den Nebendreiecken
17
Dementsprechend gilt nach Satz 2.2:
F + F1 = 2 · a
(25)
F + F2 = 2 · b
(26)
F + F3 = 2 · g
(27)
Man addiere nun die Aussagen (25), (26), (27) zueinander, dann folgt:
(F + F1 ) + (F + F2 ) + (F + F3 )
= 2·a +2·b +2·g
= 2 · (a + b + g)
Daraus folgt dann also die nächste Bezeichnung
3 · F + F1 + F2 + F3 = 2 · (a + b + g),
(28)
und durch Subtraktion der beiden Gleichungen (28), (24) bekommen wir die folgende
Rechnung:
(3 · F + F1 + F2 + F3 )
()
(F + F1 + F2 + F3 ) =
2 · (a + b + g)
a +b +g
()
2·F
2·p = 2·F
(29)
p = F
Somit ist also die letzte Bezeichnung dieses Abschnittes die gesuchte Flächeninhaltsformel
sphärischer Dreiecke, den wir in dem folgenden Satz festhalten:
4.1
Satz
Für den Flächeninhalt F sphärischer Dreiecke 4ABC mit den Winkeln a, b , g gilt:
F = a +b +g
p.
Als wichtige Folgerung aus dieser Formel erhalten wir den nächsten Satz.
18
(30)
4.2
Satz
Die Winkelsumme eines Eulerschen Dreiecks ist stets größer als p.
Anmerkung: Satz 4.2 gilt auch für nicht-Eulersche Dreiecke. Die Begründung mit Hilfe der
Flächeninhaltsformel (30) ist für diesen Fall jedoch nicht möglich, da sich diese auf
Eulersche Dreiecke bezieht. Ein Beweis von Satz 4.2 für nicht-Eulersche Dreiecke kann
mittels Zerlegung in Eulersche Dreiecke geführt werden.
4.3
Definition
Ist 4ABC ein Eulersches Dreieck mit den Innenwinkeln a, b , g, so heißt die Größe
e := a + b + g
p sphärischer Exzeß dieses Dreiecks.
Der sphärische Exzeß eines Dreiecks gibt somit den Überschüss der Winkelsumme über p
an. Die Flächeninhaltsformel (30) kann daher auch in der Form
F =e
(31)
geschrieben werden. Da der Flächeninhalt jedes Eulerschen Dreiecks immer kleiner als der
einer Halbsphäre ist, muss der sphärische Exzeß stets kleiner als 2p sein.
Im folgenden werden wir uns mit dem Polardreieck eines Eulerschen Dreiecks beschäftigen
und zwei Sätze beweisen, mit deren Hilfe wir eine interessante Aussage über die Summe der
Seitenlängen in einem sphärischen Dreieck treffen können und die wir auch für die
Herleitung der Grundformeln der sphärischen Trigonometrie benötigen.
19
4.4
Definition
Als Polardreieck eines Eulerschen Dreiecks 4ABC wird das Eulersche Dreieck A0 B0C0
bezeichnet, dessen Eckpunkte polar zu den Großkreisen sind, auf denen die Seiten des
Ausgangsdreiecks 4ABC liegen und sich jeweils in der dem Dreieck 4ABC
gegenüberliegenden Halbsphäre befinden.
Die Konstruktion dieser Polarpunkte A0 , B0 ,C0 geht wie folgt:
Möchte man den Polarpunkt A0 zu A erzeugen, betrachtet man vorab die Ebene AB und geht
dann zum Mittelpunkt senkrecht dazu hoch bzw. runter. Man nehme nämlich genau den
Punkt, der durch den Schnitt dieser Senkrechten und der Sphäre erzeugt wird, der auf der
anderen Halbsphäre als A liegt. Dieser Schnitt ist dann genau der gesuchte Polarpunkt A0 .
Abbildung 13: Konstruktion Polarpunkte im Beispiel von A
Genauso verfahre man mit den anderen beiden Ebenen AC und BC um die Polarpunkte B0 ,
und C0 rauszubekommen.
20
Der Neigungswinkel der Ebenen OAB und OAC in Abbildung 14 hat dasselbe Maß, wie der
Winkel a des sphärischen Dreiecks 4ABC.
Diesen Neigungswinkel bestimmen wir so, indem wir eine Gerade in der Ebene E1 nehmen,
die senkrecht auf der Schnittgeraden AO der Ebenen E1 und E2 steht und wiederholen diesen
Vorgang mit einer Geraden aus der Ebene E2 . Der Winkel zwischen diesen beiden Geraden
ist der Neigungswinkel a.
Abbildung 14: Neigungswinkel, Polardreieck 4A0 B0C0
Dieses Verfahren wenden wir nun in zwei Punkten an, nämlich einmal im Punkt A des
Dreiecks 4ABC und einmal im Punkt O, also im Mittelpunkt der Sphäre S. Wir bekommen
nun an beiden Punkten 2 Vektoren raus: im Punkt A sind das die beiden Vektoren v1 2 E1 und
v2 2 E2 und im Punkt O die beiden Vektoren w1 und w2 . Dabei ist w1 parallel zu v1 und w2
parallel zu v2 . Demnach ist der Winkel zwischen w1 und w2 ebenfalls der Neigungswinkel a.
Nehmen wir jetzt eine dritte Ebene E3 , die senkrecht zu AO steht und durch den Ursprung
geht, sehen wir, dass w1 und w2 2 E3 ist.
21
Verlängern wir daraufhin die Vektoren w1 und w2 so, dass sie den Großkreis in E3 an den
Punkten B1 und C1 schneiden, wobei w1 der Vektor zu B1 und w2 der Vektor zu C1 wird,
erkennen wir, dass die Punkte B0 ,C0 , B1 ,C1 genau auf diesem Großkreis in E3 liegen, da die
Gerade OB0 auf der Ebene OAC senkrecht steht, muss sie nämlich auch auf OC1 senkrecht
stehen, analog stehen OC0 und OB1 aufeinander senkrecht, wie in Abbildung 15 gezeigt
wird.
Abbildung 15: Großkreis durch B’,C’, B1 ,C1
Betrachten wir nun die Winkel in diesem Großkreis. Aufgrund dessen, dass ein Kreis die
Bogenlänge 2p hat, und OB0 zu OC1 und OB1 zu OC0 senkrecht stehen, also jeweils die
Länge
p
2
haben, ergibt sich die folgende Rechnung:
p
2
+ p2 + a + a0 = 2p
()
a0 = 2p
()
a0 = p
p
a
(32)
a
und auf analoge Weise ließe sich herleiten
b0 = p
b
(33)
c0 = p
g
(34)
22
Wird zu dem Dreieck 4A0 B0C0 das Polardreieck gesucht, so ergibt sich gerade wieder das
ursprüngliche Ausgangsdreieck 4ABC, denn wir verfahren genauso wie oben beschrieben,
betrachten nur andere Ebenen, nämlich die Ebenen OA0 B0 , OB0C0 und OA0C0 .
Damit gelten die Beziehungen (32)- (34) auch für die Seiten des Ausgangsdreiecks und die
Winkel des Polardreiecks.
Wir fassen die Ergebnisse dieser Herleitung in zwei Sätzen zusammen.
4.5
Satz
Jedes Eulersche Dreieck ist das Polardreieck seines Polardreiecks.
4.6
Satz
Die Seiten (Winkel) eines Eulerschen Dreiecks ergänzen sich mit den entsprechenden Winkeln
(Seiten) seines Polardreiecks zu p.
Unmittelbar aus diesem Satz und Satz 4.2 ergibt sich die folgende Aussage über die
Seitensumme Eulerscher Dreiecke.
23
4.7
Satz
Die Seitensumme eines jeden Eulerschen Dreiecks ist kleiner als
2 · p.
Beweis.
Sei 4ABC ein eulersches Dreieck mit den Seiten a, b, c und den Winkeln a, b , g, wobei das
Dreieck 4A0 B0C0 das Polardreieck mit den Seiten a0 , b0 , c0 und den Winkeln a 0 , b 0 , g 0 zu
diesem ist. Alle Winkel seien auch hier im Bogenmaß gemessen.
Dann kann man die Bezeichnungen (32)-(34) mit Hilfe von Satz 4.6 umschreiben in
a=p
a0
(35)
b=p
b0
(36)
c=p
g0
(37)
addiert man nun diese Gleichungen zueinander folgt
(a 0 + b 0 + g 0 ),
a + b + c = 3p
(38)
wobei a 0 + b 0 + g 0 die Winkelsumme des Polardreiecks 4A0 B0C0 ist. Nach Satz 4.2 ist diese
Winkelsumme größer als p und somit die Gleichung (38) insgesamt kleiner 2p.
24
⇤