Definition Bemerkungen

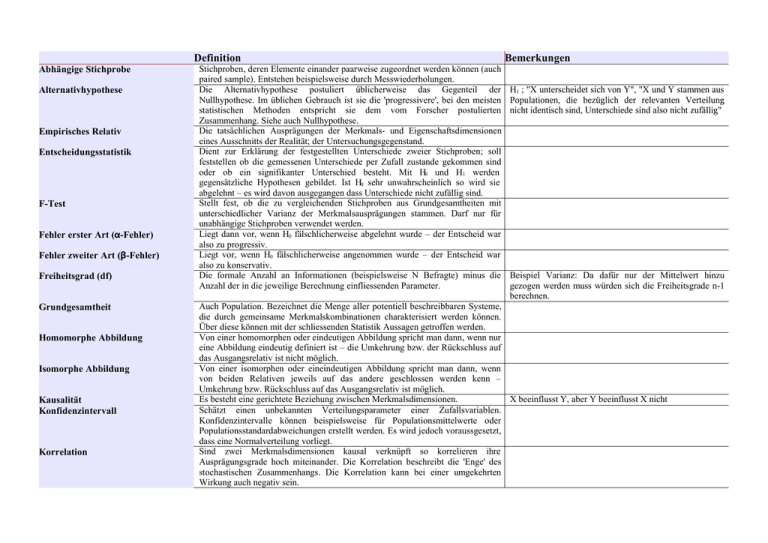
Definition
Abhängige Stichprobe
Alternativhypothese
Empirisches Relativ
Entscheidungsstatistik
F-Test
Fehler erster Art (α-Fehler)
Fehler zweiter Art (β-Fehler)
Freiheitsgrad (df)
Grundgesamtheit
Homomorphe Abbildung
Isomorphe Abbildung
Kausalität
Konfidenzintervall
Korrelation
Stichproben, deren Elemente einander paarweise zugeordnet werden können (auch
paired sample). Entstehen beispielsweise durch Messwiederholungen.
Die Alternativhypothese postuliert üblicherweise das Gegenteil der
Nullhypothese. Im üblichen Gebrauch ist sie die 'progressivere', bei den meisten
statistischen Methoden entspricht sie dem vom Forscher postulierten
Zusammenhang. Siehe auch Nullhypothese.
Die tatsächlichen Ausprägungen der Merkmals- und Eigenschaftsdimensionen
eines Ausschnitts der Realität; der Untersuchungsgegenstand.
Dient zur Erklärung der festgestellten Unterschiede zweier Stichproben; soll
feststellen ob die gemessenen Unterschiede per Zufall zustande gekommen sind
oder ob ein signifikanter Unterschied besteht. Mit H0 und H1 werden
gegensätzliche Hypothesen gebildet. Ist H0 sehr unwahrscheinlich so wird sie
abgelehnt – es wird davon ausgegangen dass Unterschiede nicht zufällig sind.
Stellt fest, ob die zu vergleichenden Stichproben aus Grundgesamtheiten mit
unterschiedlicher Varianz der Merkmalsausprägungen stammen. Darf nur für
unabhängige Stichproben verwendet werden.
Liegt dann vor, wenn H0 fälschlicherweise abgelehnt wurde – der Entscheid war
also zu progressiv.
Liegt vor, wenn H0 fälschlicherweise angenommen wurde – der Entscheid war
also zu konservativ.
Die formale Anzahl an Informationen (beispielsweise N Befragte) minus die
Anzahl der in die jeweilige Berechnung einfliessenden Parameter.
Bemerkungen
H1 ; "X unterscheidet sich von Y", "X und Y stammen aus
Populationen, die bezüglich der relevanten Verteilung
nicht identisch sind, Unterschiede sind also nicht zufällig"
Beispiel Varianz: Da dafür nur der Mittelwert hinzu
gezogen werden muss würden sich die Freiheitsgrade n-1
berechnen.
Auch Population. Bezeichnet die Menge aller potentiell beschreibbaren Systeme,
die durch gemeinsame Merkmalskombinationen charakterisiert werden können.
Über diese können mit der schliessenden Statistik Aussagen getroffen werden.
Von einer homomorphen oder eindeutigen Abbildung spricht man dann, wenn nur
eine Abbildung eindeutig definiert ist – die Umkehrung bzw. der Rückschluss auf
das Ausgangsrelativ ist nicht möglich.
Von einer isomorphen oder eineindeutigen Abbildung spricht man dann, wenn
von beiden Relativen jeweils auf das andere geschlossen werden kenn –
Umkehrung bzw. Rückschluss auf das Ausgangsrelativ ist möglich.
Es besteht eine gerichtete Beziehung zwischen Merkmalsdimensionen.
X beeinflusst Y, aber Y beeinflusst X nicht
Schätzt einen unbekannten Verteilungsparameter einer Zufallsvariablen.
Konfidenzintervalle können beispielsweise für Populationsmittelwerte oder
Populationsstandardabweichungen erstellt werden. Es wird jedoch voraussgesetzt,
dass eine Normalverteilung vorliegt.
Sind zwei Merkmalsdimensionen kausal verknüpft so korrelieren ihre
Ausprägungsgrade hoch miteinander. Die Korrelation beschreibt die 'Enge' des
stochastischen Zusammenhangs. Die Korrelation kann bei einer umgekehrten
Wirkung auch negativ sein.
Korrelationskoeffizient (correlation
coefficient)
Kovarianz (covariance)
Medien (median)
Mittelwert (mean)
Der Korrelationskoeffizient ist eine Masszahl für die Kovarianz zwischen zwei
cov  x , y
r=
; −1r1
Variablen und bewegt sich zwischen -1 und +1, wobei ein Wert von 0 bedeutet
s x⋅s y 
dass keine Korrelation nachgewiesen werden kann. Wie bei der Kovarianz deutet
ein negatives Vorzeichen auf eine gegensinnige Korrelation hin.
Der Korrelationskoeffizient wird auch als Produkt-Moment-Korrelation oder
Pearson-Bravis-Korrelation bezeichnet. Die über die Normierung der Kovarianz
definierte Korrelatoin ist identisch mit der Kovarianz der z-transformierten
Merkmalsausprägungen.
Voraussetzung für de Bestimmung eines Korrelationskoeffizienten ist eine lineare
Beziehung zwischen den betroffenen Variablen.
Beschreibt die 'Enge' des stochastischen Zusammenhangs zwischen zwei cov(x,y) bzw. cov(V1,V2)
Variablen. Ein 'enger' Zusammenhang ist dann gegeben, wenn für geringe
Ausprägungen von V1 auch geringe Ausprägungen von V2 resutlieren. Möglich ist
auch eine 'gegensinnige' Kovarianz – für geringe Ausprägungen von V1 resultieren
hohe Ausrpägungen von V2. Dem Vorzeichen der Kovarianz kann entnommen
werden, ob V1 und V2 gleich- oder gegensinnig variieren.
Der Median einer Verteilung entspricht demjenigen Ausprägungsgrad der Md
Merkmalsdimension, der die in eine Rangreihe geordneten Ausprägungs-grade so
in zwei Hälften teilt, dass je die Hälfte der Beobachtungen einen grösseren bzw.
Einen kleineren Ausprägungsgrad aufweisen als der Median angibt.
'Durchschnitt' der erhobenen Werte.
 x 1 x2... xn
x ,
n
Modalwert (mode)
Normalverteilung
Nullhypothese
Numerisches Relativ
Signifikanz-Niveau
Der Modalwert einer Verteilung ist derjenige Ausprägungsgrad der
Merkmalsdimension, der in den erhobenen Daten am häufigsten auftritt. Nur
sinnvoll bei nominal oder ordinal skalierten Werten.
Die Normalverteilung ist eine Wahrscheinlichkeits-Dichte-Funktion mit folgenden
zentralen Eigenschaften: 1. ist sie glockenförmig und symmetrisch. 2. nähert sie
sich der x-Achse asymptotisch, die Wahrscheinlichkeit wird für x=∞ und
x=−∞ gleich Null. Die normalverteilung wird durch die
Verteilungsparameter μ und σ komplett definiert. Unterschiedliche
Verteilungsparameter haben unterschiedliche Normalverteilungen zur Folge.
Die Nullhypothese ist üblicherweise 'konservativ' und postuliert entsprechend,
dass der vermutete Zusammenhang nicht existiert. Sie steht somit im Gegensatz
zur Alternativhypothese.
In Form von Zahlen und Namen dargestelltes Abbild eines Ausschnitts der
Realität;
die
erhobenen
Daten.
Tatsächliche
Merkmalsund
Eigenschaftsdimensionen werden numerisch repräsentiert.
Entspricht der Irrtumswahrscheinlichkeit p und gibt die Wahrscheinlichkeit an,
mit der eine Annahme falsch ist. Mit anderen Worten: Man irrt sich bei der
Annahme einer Alternativhypothese in p % der Fälle. Je geringer desto besser.
Mo
H0 ; "X unterscheidet sich nicht von Y", "X und Y
stammen aus Populationen, die bezüglich der relevanten
Verteilungen identisch sind, Unterschiede sind also
zufällig"
Standard-Normalverteilung
Standardabweichung (standard
deviation)
Standardfehler der
Standardabweichung σs
Standardfehler des Mittelwerts σ x
Stichprobe
Stichprobenkennwertverteilung
Stochastischer Zusammenhang
t-Test, abhängige Stichproben
t-Test, unabhängige Stichproben
Variabilität (range)
Varianz (variance)
Die Standardnormalverteilung ist eine Normalverteilung mit den zi = (xi – μ) / σ
Verteilungsparametern μ = 0 (Mittelwert) und σ = 1 (Standardabweichung). Sie
wird auch z-Verteilung genannt. Sie wird üblicherweise mit einer linearen
Transformation (z-Transformation) aus der Normalverteilung abgeleitet (siehe
Bemerkungen). Die Fläche unter der Kurve repräsentiert die Wahrscheinlichkeit
für ein Auftreten eines Wertes auf dem entsprechenden x-Achsen-Abschnitt.
Die Standardabweichung s ist die Wurzel der Varianz.
s. Für normalverteilte Daten liegen zwischen den Grenzen
von ( 
x - s) und ( x + s) 68.3% aller
Beobachtungen. Zwischen ( 
x - 2s) und ( x + 2s)
liegen 95.5% aller Beobachtungen)
Aus der Stichprobenkennwertverteilung bestimmte Standardabweichung des
Mittelwerts σs. Aus dem Standardfehler der Standardabweichung und des
Mittelwerts kann nun abgeleitet werden, wie exakt die Stichprobenkennwerte die
Populationsparameter zu schätzen vermögen.
Aus der Stichprobenkennwertverteilung bestimmte Standardabweichung des
Mittelwerts σ x . Aus dem Standardfehler der Standardabweichung und des
Mittelwerts kann nun abgeleitet werden, wie exakt die Stichprobenkennwerte die
Populationsparameter zu schätzen vermögen. Je geringer die Streuung (je kleiner
der Standardfehler), desto genauer repräsentiert ein Stichprobenmittelwert xj
den Populationswert μ.
Jede Teilmenge der Population/Grundgesamtheit, in der die Definitionsmerkmale
der Population möglichst gut (repräsentativ) vertreten sind.
Aus der Grundgesamtheit werden n (undendlich viele) gleich grosse
Zufallsstichproben gezogen und die Verteilung des interessierenden Merkmals
und die zugehörigen Verkeilungskennwerte xi und s i bestimmt. Werden
diese wiederum in Verteilungsdiagrammen dargestellt so erhält man die
Stichprobenkennwertverteilungen.
Zusammenhang zwischen zwei Faktoren, der unterschiedlich 'eng' sein kann und
somit unterschiedlich exakte Aussagen erlaubt.
Zwei Faktoren sind wichtig: Die 'Art' des Zusammenhangs (das
Regressionsmodell) und die Enge (Kovarianz und Korrelation)
Stellt fest, ob für zwei abhängige Stichproben die Arbeitshypothese H0 gilt.
Stellt fest, ob für zwei unabhängige Stichproben die Arbeitshypothese H0 gilt.
V wird durch die Extremwerte der Verteilung bestimmt. Variabilität bezeichnet V. V = (maximaler Ausprägungsgrad) – (minimaler
die 'Breite' der Streuung der gefundenen Werte.
Ausprägungsgrad)
Die Definition der Varianz beruht auf der Ermittlung der mittleren Abweichungen s2
der Merkmalsausprägungen vom Mittelwert 
x der Stichprobe. Da diese
Abweichungen sowohl positive wie negative Vorzeichen aufweisen können sie
nicht einfach aufaddiert werden – ihre Summe wäre 0. Also werden die
Abweichungen quadriert und erst danach aufsummiert. Somit ist die Varianz
definiert als Mittelwert der quadrierten Abweichungen vom Mittelwert der
Stichprobe.
z-Transformation
Zentrales Grenzwerttheorem
Methode mit der eine Normalverteilung in die Standardnormalverteilung überführt
wird.
Besagt, dass die Verteilung der Mittelwerte der Merkmälsausprägungen aus gleich
grossen Stichproben von 'genügendem' Umfang aus der selben Grundgesamtheit
von der Verteilung des Merkmals in der Grundgesamtheit unabhängig und
normalverteilt ist. In den Sozialwissenschaften wird davon ausgegangen, dass dies
für Stichprobengrössen ab 30 gilt.
μ x =μ
Anmerkung:
• Diese Auflistung ist noch in Arbeit!
• Dies ist kein offizielles Dokument des IPMZ und wird es wohl auch nie sein! Ich kann deshalb keinerlei Garantien für die Richtigkeit der Angaben
übernehmen.
• Für Fragen, Kritik, Verbesserungs- oder Änderungsvorschläge bin immer offen! Erreichbar bin ich über [email protected]
Quellen:
• Hirsig, René: Statistische Methoden in den Sozialwissenschaften. Eine Einführung im Hinblick auf computergestützte Datanenanalysen mit SPSS für
Windows, Band I. 3. erweiterte Auflage. Seismo, Zürich 2001.
• http://www.wikipedia.org