Teil 1: Spektroskopie
Werbung

Gliederung (1) (2) (3) (4) Spektroskopie (Galla) Elektrochemie, Membranbiophysik (Adam-Läuger-Stark) BPC2-Praktikum (MPIbp) Formeln-Zusammenfassung Teil 1: Spektroskopie Für die Spektroskopie an biologischen Molekülen können Wellenlängen von 1 nm (Röntgenstrahlung) bis zu 1 m (Radiowellen für NMR) verwendet werden. Lipid-Membranen Zusammensetzung • • • • Proteingehalt: 20% (Myelin-Membran der Nerven) bis 80% (innere Mitochondrienmembran) der Membrantrockenmasse. Phospholipide nehmen den größten Teil der Membranlipide ein. Dann kommen Glykolipide und Cholesterol 20% der Gesamtmasse ist Wasser, das fest gebunden für die Aufrechterhaltung der Membranstruktur erforderlich ist. Membran hat ca. 4nm Dicke, dynamisch: laterale Bewegelichkeit, Rotation um eigene Achse. Modell-Membranen Lyotropie: Eigenschaft von Materialien, die flüssig-kristalline Phasen ausbilden, wenn ein Lösungsmittel hinzugefügt wird. Lyotroper Polymorphismus: Die makroskopische Struktur der Lipid-Doppelschicht ist von der Art der Phospholipide und vom Wassergehalt der Lipid-Dispersion abhängig. • • • Phosphatidylcholine bilden bis zu einem Wassergehalt von 30% (Massenanteil) eine lamellare Phase aus parallelen, übereinandergestapelten Doppelschichten. Bei höherem Wassergehalt entsteht eine heterogene Dispersion aus geschlossenen, multilamellaren Strukturen. Bei sehr hohem Wasserüberschuss (>95%) bilden sich Liposomen/Vesikel, konzentrisch angeordnete Doppelschichten. Durch Behandlung mit Ultraschall entstehen dadurch unilamellare (eine Doppelschicht) Vesikel mit 20-50nm Durchmesser. Thermotrope Phasenumwandlungen: abhängig vom Lipid. Häufig auftretende thermotrope Phasen sind Lα, Pβ und Lβ. Das Phasendiagramm zeigt ihre Existenzbereiche. • • • • • Die Lβ-Phase ist kristallin mit 1D-lamellarer Anordnung. Die CH-Ketten liegen gestreckt in trans-Konformation nebeneinander und sind um 30° gegen die Membrannormale geneigt. Die Neigung ist abhängig vom Flächen-Bedarf der Kopfgruppe (0,5 nm² für DPPC) und der gesättigten CH-Ketten (0,4 nm²). So wird die Hohe laterale Packungsdichte der Ketten erreicht. Es handelt sich um eine langreichweitige 2D-Ordnung aus einem verzerrten quasihexagonalen Gitter. Die Pβ Phase ist ebenso kristallin, besitzt aber im Vergleich zur Lβ Phase eine periodische Wellung als Überstruktur (Ripple-Struktur). Neigung: 30°-50°, reguläres hexagonales Gitter. Die Lα Phase zeigt wegen der großen Zahl an gauche-Isomeren eine hohe Beweglichkeit der CH-Ketten fluide oder flüssigkristalline Phase. Die lamellare Struktur bleibt erhalten, die Lipid-Moleküle sind jedoch entkoppelt. Die Dicke der Lipiddoppelschicht ist geringer als in der Lβ Phase. Phasen-Übergänge sind endotherm und verlaufen kooperativ. Lβ Lα ist die Hauptumwandlung; Lβ Pβ die Vorumwandlung von Lipid-Membranen Die Übergangstemperaturen sind abhängig von der Struktur der Kopfgruppe, der Länge und dem Sättigungsgrad der CH-Kette und bei geladenen Lipiden von dem pH-Wert und der Ionensträke der Dispersion. Molekulare Dynamik in Lipid-Membranen Der Anstieg der Lipid-Beweglichkeit bei der Hauptumwandlung ist auf die thermisch induzierte Bildung von Rotationsisomeren der CH-Ketten zurückzuführen. Die gauche-trans-gauche- (gtg-) Kinke entsteht aus der gestreckten CH-Kette in all-trans Konformation durch Rotation um 120° um eine C-C-Bindung und einer simultanen Rotation um -120° um eine übernächste C-C-Bindung. Eine einzelne gauche-Konformation ist aus sterischen Gründen in der Membran unwahrscheinlich. Die Kinke bewirkt eine laterale Versetzung in der CH-Kette. Dadurch entsteht ein freies Volumen in der Membran, in das Fremd-Moleküle eingebaut werden können. Die Gesamtlänge der CH-Kette wird durch eine gtg-Kinke um 0,127 nm verkürzt (Abnahme der Membran-Dicke). In der kristallinen Phase liegen 7% der CH2-Segmente in gauche-Konformation vor, während es in der fluiden Phase 40% sind. Absorptionsspektroskopie im UV- und VIS-Bereich Wellenlänge-Frequenz-Beziehung Energie eines Lichtquants mit ℎ = 6,63 ∙ 10−34 𝐽𝐽𝐽𝐽 Resonanzbedingung für die Absorption! 1𝑒𝑒𝑒𝑒 = 1,602 ∙ 10−19 𝐽𝐽 1𝑚𝑚𝑚𝑚𝑚𝑚 = 6,02 ∙ 1023 = 1𝐸𝐸 (Einstein) Die Induktionsflussdichte B [Tesla=1vs/m²] ist proportional zur magnetischen Feldstärke H [A/m]; 𝜇𝜇 ist relative Permeabilität, 𝜇𝜇0 ist Induktionskonstante Zeitliche Änderung des elektrischen Feldstärkevektors, 𝐸𝐸𝑥𝑥 ist Amplitude. Ladungsverteilung im Grundzustand Dipolmoment im Grundzustand bzw. angeregten Zustand Übergangsdipolmoment Dipolstärke ist das Quadrat des Betrags des Übergangsdipolmoments. Dipolstärke kann auch aus der Fläche unter dem Frequenz-abhängigen Absorptionssignal erhalten werden. Multiplizität 𝜆𝜆 ∙ 𝜈𝜈 = 𝑐𝑐 = 2,998 ∙ 108 𝑚𝑚/𝑠𝑠 𝐸𝐸 = ℎ ∙ 𝜈𝜈 𝐵𝐵 = 𝜇𝜇 ∙ 𝜇𝜇0 ∙ 𝐻𝐻 𝐸𝐸𝑥𝑥 = 𝐸𝐸𝑥𝑥0 ∙ cos 2𝜋𝜋𝜋𝜋𝜋𝜋 𝜓𝜓0 𝜇𝜇0 bzw. 𝜇𝜇1 𝜇𝜇01 𝐷𝐷01 = |𝜇𝜇01 |2 = 1,63 ∙ 10−38 ∙ 𝜀𝜀𝑚𝑚𝑚𝑚𝑚𝑚 ∙ 𝑀𝑀 = 2𝑆𝑆 + 1 ∆𝜆𝜆 𝜆𝜆 Der UV-VIS-Bereich umfasst Wellenlängen von 180 bis 800 nm. Absorption setzt die Wechselwirkung zwischen Licht und Materie voraus, wobei das Photon seine Energie an die Moleküle abgibt. Licht ist eine transversale Welle, die in Raum und Zeit oszilliert. Die oszillierenden Vektoren des elektrischen und magnetischen Feldes stehen senkrecht aufeinander. Für die UV/VIS-Absorption ist lediglich der elektrische Feldvektor relevant. Bei Molekülen, die klein gegenüber der Lichtwellenlänge sind, kann die Oszillation im Raum vernachlässigt werden. Es muss nur die zeitabhängige Änderung des elektrischen Feldstärkevektors 𝟐𝟐 betrachtet werden: 𝐸𝐸𝑥𝑥 = 𝐸𝐸𝑥𝑥0 ∙ cos 2𝜋𝜋𝜋𝜋𝜋𝜋. Die Intensität des Lichtes ist proportional zu �𝑬𝑬𝟎𝟎𝒙𝒙 � . Der lichtabsorbierende Teil eines Moleküls (Chromophor), besitzt eine bestimmte räumliche Verteilung 𝜓𝜓 der elektrischen Ladung (quantenmechanisch definiert man spezifische Wellenfunktionen). Elektronegativitäts-Unterschiede zwischen den Atomen im Molekül sind Ursache für ein Dipol-Moment 𝜇𝜇. Bei der Absorption von Licht wird die Ladungsverteilung durch das oszillierende Strahlungsfeld verändert, sodass 𝝍𝝍𝟎𝟎 → 𝝍𝝍𝟏𝟏 und 𝝁𝝁𝟎𝟎 → 𝝁𝝁𝟏𝟏 . Die Differenz zwischen dem Dipolmoment des Grundzustandes und dem Dipolmoment des angeregten Zustandes bezeichnet man als Übergangsdipolmoment 𝝁𝝁𝟎𝟎𝟎𝟎 . Die Orientierung von 𝜇𝜇01 definiert die Polarisationsebene der Absorption. Licht geeigneter Frequenz kann optimal absorbiert werden, wenn die Schwingungsrichtung des elektrischen Feldstärkevektors der elektromagnetischen Welle mit der Richtung des Übergangsdipolmomentes übereinstimmt. Ist die Dipolstärke null, so kann auch bei erfüllter Resonanzbedingung kein Übergang erfolgen (Übergangsdipolmoment hat keine Länge). Liegen die Werte von 𝐷𝐷01 nahe null, spricht man von einem verbotenen Übergang, liegen die Werte nahe eins, spricht man von einem erlaubten Übergang. Elektronische Übergänge und Struktur des Spektrums Die Absorption im UV/VIS-Bereich induziert Übergänge zwischen elektronischen Energieniveaus, von einem energetisch niedrigen, in ein energetisch höheres Orbital. Die elektronischen Niveaus sind in Schwingungsniveaus unterteilt (Die weitere Unterteilung in Rotationsniveaus ist für die Absorptionsspektroskopie in Lösungen nicht relevant). Das Verhalten eines Moleküls wird durch das Modell eines zweiatomigen anharmonischen Oszillators wiedergegeben. Quantenmechanisch ergibt sich, dass die Aufenthaltswahrscheinlichkeit der Elektronen der einzelnen Schwingungsniveaus am Rande der Potentialkurve am größten ist. Ausnahme: Grundzustand, wo sich das Elektron am wahrscheinlichsten in der Nähe der Ruhelage 𝒓𝒓𝟎𝟎 der Kerne befindet. Nach der Boltzmann-Statistik befinden sich bei Raumtemperatur fast alle Moleküle im Schwingungsgrundzustand des elektronischen Grundzustandes. Von dort aus erfolgt die Lichtabsorption. Da die Absorption mit 1 fs schneller ist als eine Molekülschwingung mit 100 fs, erfolgt der Absorptionsübergang bei fester Kernlage, also vertikal (Franck-Condon Prinzip). Überlappen die Wellenfunktionen, ist die Übergangswahrscheinlichkeit in dieses Schwingungsniveau groß, sodass mehrere Schwingungsniveaus erreicht werden können, je nach Lage der beiden Potentialkurven. Das Absorptionsspektrum ist die Auftragung der Absorptionswahrscheinlichkeit gegen die Wellenlänge. Die Molekül-abhängige Strukturierung ergibt sich aus den Schwingungsniveaus (00, 01, 02 Übergänge). Ist die 00 Bande am intensivsten liegt ein symmetrisches Spektrum vor. Das Jablonski-Termschema zeigt Übergänge zwischen horizontalen Linien. Die elektronischen Übergänge lassen sich nach den beteiligten Molekülorbitalen klassifizieren. Im Grundzustand kommen bindende σ-Orbitale (bilden Einfachbindungen), π-Orbitale (bilden Mehrfachbindungen) und bei Heteroatomen wie N oder O nichtbindende n-Orbitale vor, die von einsamen Elektronenpaaren besetzt werden. Von diesen Orbitalen kann ein Elektron in die antibindenden Orbitale des angeregten Zustandes angehoben werden, nämlich in das σ*-Orbital oder in das π*-Orbital. Beide zeigen in der Elektronendichteverteilung einen Knotenpunkt auf der Bindungsachse. Der energetisch hoch liegende Übergang σ σ* und der Übergang n σ* sind für die Spektroskopie von Biomolekülen nicht von Interesse. Relevant sind die π π* und die energetisch niedrigen n π* Übergänge. Absorptionsübergänge können auch über ihre Spinanordnung klassifiziert werden. Elektronen in bindenden Orbitalen haben antiparallele Spinorientierung. Die Multiplizität für S=0 ist M=2S+1=1. Dieser Singulettzustand ist meist der Grundzustand (S0-Zustand) des Moleküls, Ausnahme: Sauerstoff (T0-Zustand). Beim Übergang in ein antibindendes Orbital kann der antiparallele Spinzustand erhalten bleiben (S1, S2,… -Zustände) oder es findet beim Absorptionsprozess eine Spinumkehr statt, sodass M=3, also ein Triplettzustand erhalten wird. T1 liegt energetisch unter S1. • • Der S0S1-Übergang gehört zu den erlaubten Übergängen und hat eine hohe Übergangswahrscheinlichkeit. Der S0T1-Übergang ist Spin-verboten. Eine Auswahlregel (Ableitung aus dem Drehimpulserhaltungssatz) besagt, dass sich der Gesamtspin bei einem Übergang nicht ändern darf. Dies bedeutet, dass auch bei erfüllter Resonanzbedingung die Intensität der Absorptionsbanden S0T1 sehr klein ist. Quantifizierung der Lichtabsorption Die Absorptionswahrscheinlichkeit bei gegebener Wellenlänge wird durch den molaren Extinktionskoeffizienten bestimmt. Die Extinktion ist in einer mehrkomponentigen Lösung eine additive Größe. Treten bei hohen Konzentrationen Molekülassoziationen auf, sind positive und negative Abweichungen vom Lambert-Beer Gesetz möglich. Streulichteffekte (z.B. bei Dispersion) erhöhen die Extinktion künstlich, da das Streulicht in der Bilanz des transmittierten Lichtes fehlt. Exponentieller Abfall der Intensität 𝐼𝐼0 in einer transparenten Substanz der Dicke d [cm]. α ist für die Substanz charakteristisch. wenn Substanz der Konzentration c absorbiert und Lömi nicht absorbiert => Lambert-Beersches Gesetz: 𝛼𝛼 = 2,303 ∙ 𝜀𝜀 ∙ 𝑐𝑐, [1000𝑐𝑐𝑐𝑐²/𝑚𝑚𝑚𝑚𝑚𝑚] ∙ [𝑚𝑚𝑚𝑚𝑚𝑚/𝑙𝑙] % Transmission ist Anteil des nicht absorbierten Lichtes 𝐼𝐼 = 𝐼𝐼0 ∙ 𝑒𝑒 −𝛼𝛼𝛼𝛼 𝐼𝐼 = 𝐼𝐼0 ∙ 10−𝜀𝜀𝜀𝜀𝑑𝑑 𝐼𝐼0 lg = 𝜀𝜀𝜀𝜀𝑑𝑑 = 𝐴𝐴 = 𝐸𝐸 𝐼𝐼 𝑇𝑇% = 𝐼𝐼/𝐼𝐼0 ∙ 100 Absorption=Extinktion Für d=1cm: OD 𝑂𝑂𝑂𝑂 = 1 → 𝑇𝑇% = 10 Lösungsmitteleinflüsse Das Lösungsmittel hat einen Einfluss auf den Energieunterschied zwischen Grund- und Anregungszustand, wodurch es zur Verschiebung des Absorptionsmaximums kommt. Bei Wechsel von apolarem zu polarem Lömi (Polaritätserhöhung), kann sich das Absorptionsmaximimum für die π π* und die n π* Übergänge auf verschiedene Weisen verschieben. größere Wellenlänge (Bathochromie, Rotverschiebung => größere Wellenlänge) beobachtet man bei π π*-Übergängen. Die Polarisierbarkeit des Lösungsmittels wird durch die dielektrische Konstante definiert und stabilisiert den Zustand mit dem größten Dipolmoment (in jedem Fall der angeregte Zustand). Das heißt, dass der π*-Zustand im polaren Medium energetisch stärker abgesenkt wird, als der π-Zustand. Dadurch hat der π π*-Übergang in polarem Medium einen geringeren Energieunterschied, wodurch die Absorption rotverschoben ist. kleinere Wellenlänge (Hypsochromie, Blauverschiebung => kleinere Wellenlänge) beobachtet man bei n π* Übergängen. Die Moleküle des Lösungsmittels besitzen aber auch ein permanentes Dipolmoment. Die besetzten nicht-bindenden Orbitale können dadurch eine starke Wechselwirkung mit dem Lömi eingehen und z.B. als Akzeptoren für H-Brücken fungieren. Dadurch ist die energetische Absenkung des n-Zustandes stärker als die des π*-Zustandes. Der Energieunterschied des n π*-Übergangs wird im polaren Medium größer, wodurch die Absorption blauverschoben ist. Anwendungsbeispiele Chromophore Viele Proteine enthalten Chromophore als prosthetische Gruppe: • • • • Porphyrine in Hämoglobin, Cytochromen oder Chlorophyll. Coenzyme wie NADH oder der IsoalloxazinRest im FADH2 haben hohen Extinktionskoeffizienten. Die cis-trans Isomerisierung von Retinal in Rhodopsinen kann Apsorptionsspektrometrisch verfolgt werden. Aminosäuren (W, Y, F) und Basen der Nukleinsäuren weisen intensive Absorption auf. Aminosäuren und Peptide Peptidbindung • π π*-Übergang: 190nm, ε~7000 • n π*-Übergang: 220nm, ε~100 (Symmetrie-verboten) Der Grundzustandsdipol der Peptid-Bindung liegt nahezu entlang der C=O Bindungsachse. Die Absorption ist damit von der Konformation eines Polypeptids abhängig. Extinktionskoeffizient und Absorptionsmaximum 𝜆𝜆𝑚𝑚𝑚𝑚𝑚𝑚 unterscheiden sich daher bei α-Helices und β-Faltblättern. Die Absorption bei 210-220nm (n π*-Übergang), kann nicht zur Quantifizierung des Proteingehalts herangezogen werden, da sie sich mit der Absorption von Seitenketten wie Asp, Asn, Glu, Gln und Arg überlagert. Warum eginet sich denn nicht der π π*-Übergang? Eigene Überlegung: Die π-Bindung würde zerstört, es würde freie Drehbarkeit um die Peptidbindung resultieren => Denaturierung! Daher verwendet man die Absorption der aromatischen Aminosäuren W, Y, F, die zwischen 260 und 280 nm ihre Absorptionsmaxima haben. Da W sehr selten in Proteinen vorkommt, wird oft die Y-Absorption gemessen. Liegt Trp in einem Protein vor, so lässt es sich als natürliche Sonde verwenden, um die Polarisationsänderung bei Konformationsänderungen oder bei Wechselwirkung mit hydrophoben Membranen zu verfolgen. Warum besitzen unterschiedliche Konformere unterschiedliche Absorptionsspektren? Jede AS besitzt ein Übergangsdipolmoment. Diese sind im Raum zueinander angeordnet und wechselwirken miteinander. Es kommt zur Aufhebung der Entartung. Lineardichroismus Dichroitisches Verhältnis: Steht das Übergangsdipolmoment parallel zur Orientierungsachse der Moleküle (𝜀𝜀∥ ≫ 𝜀𝜀⊥ ) ist d>0, stehen sie orthogonal zueinander ist d<0. 𝑑𝑑 = 𝜀𝜀∥ − 𝜀𝜀⊥ 𝜀𝜀∥ + 𝜀𝜀⊥ n π*-Übergang und π π*-Übergang haben unterschiedlich orientierte Übergangsdipolmomente. Voraussetzung ist eine feste, ein-achsige Orientierung der Moleküle, sodass die Übergangsdipolmomente ausgerichtet sind. Jedes Dipolmoment besitzt zwei Komponenten senkrecht zur Ausbreitungsrichtung des Lichts (x-Richtung), die für die Absorption verantwortlich sind: 𝜇𝜇∥ (xz-Ebene) und 𝜇𝜇⊥ (xy-Ebene). Nun folgt die Messung des Absorptionsspektrums mit parallelem und senkrecht linear polarisiertem Licht. Zur Unterscheidung verschiedener Übergänge wird die Extinktion parallel 𝜀𝜀∥ und senkrecht 𝜀𝜀⊥ zur Orientierungsachse des Moleküls notiert und das dichrotische Verhältnis bestimmt. Wenn 𝝁𝝁𝝅𝝅𝝅𝝅∗ nicht parallel zu 𝝁𝝁𝒏𝒏𝒏𝒏∗ steht, sind die Übergänge unterscheidbar (siehe Abbildung von Poly-LGlutamin: Pfeile deuten die Richtungen der Übergangsdipolmomente an). Sind die Lage des Übergangsdipolmomentes sowie die Struktur bekannt, kann man aus dem Dichroismus die Orientierung der Chromophore im Makromolekül bestimmen. An einer orientierten Lösung von DNAMolekülen in der B-Form resultierte d<0. Da das Übergangsdipolmoment in der Ebene der Basen liegt, müssen die Basenpaare senkrecht zur Moleküllängsachse orientiert sein. Lineardichroitsches Spektrum und Absorptionsspektrum (Poly-L-Lysin). Die einzelnen Absorptionsbanden sind im Lineardichrotischen Spektrum (max/min/max) viel besser unterscheidbar: Im Absorptionsspektrum ist die Überlagerung der n π* und π π*-Übergänge zu erkennen. Mithilfe des Lineardichroismus kann die Anisotropie der Absorptionsbande demonstriert werden. Hypochromie und Hyperchromie Höher organisierte, geordnetere Zustände, also Konformationen mit intensiver Wechselwirkung zwischen den Chromophoren zeigen eine Abnahme der Absorption. • • • α-Helix hat geringere Extinktion im Vergleich zum Zufallsknäuel. Poly-Adenosin hat geringere Extinktion im Vergleich zu monomerem AMP. Native DNA hat geringe Extinktion bei 260 nm als thermisch denaturierte oder enzymatisch gespaltene. Die Hypochromie von Nukleinsäuren kann ausgenutzt werden, um das Temperatur-abhängige Schmelzen des Doppelstranges zu verfolgen. Dimer aus miteinander interagierenden Monomeren 1 und 2. Diese sind ungeladen (reine DipolDipol-WW). Die Wechselwirkung zwischen den Monomeren kann eine Absenkung (bei negativer Wechselwirkungsenergie V12 => anziehende WW) oder Anhebung (bei positiver WE V12 => abstoßende WW) der Energie des Übergangs Ea bewirken. Betrachtung verschiedener Orientierungen des Übergangsdipolmomentes. Da dieses fest mit der Molekülachse verbunden ist: Betrachtung verschiedener Molekülorientierungen. Bei einer Stapelanordnung der Monomere, sind parallele von antiparalleler Orientierung zu unterscheiden. Es resultiert eine Netto-Blauverschiebung des Spektrums. (1) Parallel => klassische Abstoßung zweier Dipole, der die Energie Ea um den Betrag V12 erhöht. => Blauverschiebung. (2) Antiparallel => klassische Anziehung, wodurch Ea um V12 erniedrigt wird. Hier erhält man jedoch durch Addition der Übergangsdipolmomente den Wert Null (Dipolstärke ist null), weshalb hier kein Übergang beobachtet wird. => Rotverschiebung tritt also nicht auf. Bei einer Hintereinander-Anordnung der Dipole sind Kopf-Schwanz-Anordnung von Kopf-KopfAnordnung zu unterscheiden. Es resultiert eine Netto-Rotverschiebung des Spektrums. (1) Kopf-Schwanz-Anordnung => Anziehung (negatives V12) => Rotverschiebung. (2) Kopf-Kopf-Anordnung => Abstoßung (positives V12). Die Dipole heben sich auf => Blauverschobener Übergang wird nicht beobachtet. Sind die Dipole unter einem bestimmten Winkel angeordnet, so sind beide Übergänge möglich. Es resultiert eine Aufspaltung in zwei Absorptionslinien. Die Intensitätsverteilung ist vom Winkel zwischen den Dipolen abhängig. Dieser Effekt wird als Exciton-Aufspaltung (analog zur kollektiven Anregung von Phononen in Festkörpern) oder als Davydov-Aufspaltung (Entdecker) bezeichnet. Die Folge der Anregungsdelokalisation ist die Hypo- bzw. Hyperchromie. • • Bei einer Stapelanordnung (Blauverschiebung) nimmt die spektrale Intensität am niederenergetischen Ende der Absorptionsbande ab (Hypochromie). Bei einer Hintereinander-Anordnung (Rotverschiebung) nimmt die spektrale Intensität am niederenergetischen Ende des Spektrums zu (Hyperchromie). Nach der Kuhn-Thomas-Regel ist jedoch die Summe aller Intensitäten konstant. Wenn also bei 260 nm die Intensität von Nukleinsäuren im Polymer kleiner ist als bei gleicher Zahl von Monomeren, muss sie in einem anderen Bereich des Spektrums zugenommen haben. Bei polymeren Nukleinsäuren tritt die Hyperchromie bei kleinen Wellenlängen außerhalb des UV/VIS-Bereichs auf. Hypochromie bei einer Wellenlänge ist immer an Hyperchromie bei einer anderen Wellenlänge gekoppelt. Optische Rotationsdispersion und Circulardichroismus ORD und CD sind spezielle Arten der Absorptionsspektroskopie im UV- oder VIS-Bereich. Grundlage beider Methoden ist die Wechselwirkung linear polarisierten Lichts mit optisch aktiven Substanzen: • • ORD: Die linear polarisierte Welle wird beim Durchlaufen des Mediums Wellenlängenabhängig in ihrer Polarisationsrichtung gedreht. CD: Die beiden zirkular polarisierten Komponenten, aus denen eine linear polarisierte Welle zusammengesetzt ist, werden zusätzlich verschieden stark absorbiert. Physikalische Grundlagen Bei einer natürlichen Lichtquelle sind die Vektoren des elektrischen und magnetischen Feldes isotrop im Raum verteilt. Bei linear polarisiertem Licht schwingt der E-Feldvektor nur in einer Ebene senkrecht zur Ausbreitungsrichtung. Die Richtung des E-Feldvektors entspricht der Polarisationsrichtung. Polarisationszustände des Lichts Eine linear polarisierte Welle lässt sich in zwei zirkular polarisierte Komponenten zerlegen, bei denen die E-Feldvektoren um die Ausbreitungsrichtung rotieren. Dem Umlaufsinn entsprechend werden diese als links- bzw. rechts-zirkular polarisiert bezeichnet (Blickrichtung: dem Strahl entgegengerichtet). Die Summe ergibt zu jeder Zeit den E-Feldvektor des linear polarisierten Lichts. Sind die Amplituden der zwei zirkular polarisierten Wellen verschieden, entsteht elliptisch polarisiertes Licht. Linear polarisiertes Licht kann durch einen Polarisationsfilter erzeugt werden. Sie bestehen meist aus Kunststofffolien, in die submikroskopische, dichroitische Kristalle parallel zueinander eingelagert sind. Diese absorbieren Licht, das parallel orientiert ist und lassen den senkrecht orientierten Anteil mit geringer Schwächung passieren. Dagegen basieren klassische Polarisatoren auf Doppelbrechung, Streuung oder Reflexion (z.B. Nicol-Prisma). Zur Erzeugung zirkular polarisierten Lichtes benötigt man zwei linear polarisierte Wellen, die senkrecht aufeinander stehen und deren Phasen um eine viertel Wellenlänge (90°) gegeneinander verschoben sind. Der resultierende Summenvektor umläuft dann die Ausbreitungsrichtung auf einer Spiralbahn. In der Projektion umläuft der Vektor eine Kreisbahn. Der Gangunterschied von 90° wird durch ein λ/4-Plättchen erzeugt, einer Platte aus doppelbrechendem Material (Doppelbrechung: Lichtbündel wird in zwei senkrecht zueinander polarisierte Teilbündel aufgespalten), das parallel zur optischen Achse geschnitten ist. Für natürliches Licht wird in Durchstrahlrichtung keine Doppelbrechung erhalten. Fällt linear polarisiertes Licht auf die doppelbrechende Platte, wobei die Polarisationsebene genau zwischen der schnellen und der langsamen Achse liegt, wird es in zwei linear polarisierte Komponenten gleicher Intensität aufgespalten: • • Der ordentliche Strahl steht senkrecht zur optischen Achse des Kristalls (langsame Achse) Der außerordentliche Strahl steht parallel zur optischen Achse des Kristalls (schnelle Achse) Beide Strahlen stehen also senkrecht aufeinander. Wegen der unterschiedlichen Lichtgeschwindigkeiten, haben die beiden Strahlen bei Austritt aus dem λ/4-Plättchen einen Gangunterschied, der bei geeigneter Plattendicke gerade 90° ist. Dabei läuft der außerordentliche Strahl dem ordentlichen voraus. • • Hat das eingestrahlte Licht einen Winkel von 45° zur optischen Achse des Kristalls, so wird rechts-zirkular polarisiertes Licht erhalten. Hat das eingestrahlte Licht einen Winkel von -45° (315°) zur optischen Achse des Kristalls, so sind langsame und schnelle Achsen vertauscht, sodass links-zirkular polarisiertes Licht erhalten wird. In elliptisch polarisiertem Licht sind Amplitude und Phase frei wählbar. Zirkular und linear polarisiertes Licht ist ein Spezielfall des elliptisch polarisierten Lichtes: • • Bei zirkular polarisiertem Licht bleibt die Amplitude der Orthogonalstrahlen unbeeinflusst, während die Phase um 90° verschoben ist. Bei linear polarisiertem Licht sind sowohl Amplitude, als auch Phase der Orthogonalstrahlen identisch. Optische Rotationsdispersion Die Brechzahl 𝒏𝒏 = 𝒄𝒄𝟎𝟎 /𝒄𝒄 ist das Verhältnis zwischen Lichtgeschwindigkeit im Vakuum und in der Materie. U Durchläuft linear polarisiertes Licht ein optisch aktives Medium, so wird die Polarisationsebene um einen Winkel α gedreht. Der Drehwinkel ist der Schichtdicke und in Lösungen der Konzentration des optisch aktiven Substrats proportional. Dispersion bezeichnet die Wellenlängen-Abhängigkeit des Rotationsvermögens. Die Lichtgeschwindigkeiten für links- bzw. rechts-zirkular polarisiertes Licht sind in einer optisch aktiven Substanz unterschiedlich. So erfahren die zwei Komponenten beim Durchlaufen einer Materieschicht eine unterschiedliche Zeitverzögerung (Gangunterschied). Dieser hat direkte Auswirkung auf die Polarisationsrichtung des linear polarisierten Lichtes nach Austritt aus der Materieschicht. Durch Kombination der beiden zirkular polarisierenden Wellen wird linear polarisiertes Licht erhalten, dass um den Winkel α im Vergleich zum auf die Materieschicht eingefallenen linear polarisierten Licht gedreht ist. Für jede Substanz mit einer solchen asymmetrischen Wechselwirkung gilt für den Drehwinkel in Abhängigkeit von der Wellenlänge: 𝛼𝛼(𝜆𝜆) = 180° ∙ 𝑑𝑑 ∙ (𝑛𝑛𝐿𝐿 − 𝑛𝑛𝑅𝑅 ) 𝜆𝜆 𝑛𝑛𝐿𝐿/𝑅𝑅 ist der Brechungsindex für links/rechts-zirkular polarisiertes Licht. 𝛼𝛼 ist einheitslos. Als Stoffkonstante wird durch Normierung auf c und d die spezifische Drehung angegeben. Einheit: [Grad*cm²/g], wenn c in [g/cm³]. [𝛼𝛼]𝜆𝜆 = 𝛼𝛼(𝜆𝜆) 𝑐𝑐 ∙ 𝑑𝑑 Molare Rotation bezieht sich auf relative Molekülmasse M in [g/mol]. Einheit: [Grad*cm²/mol] [𝑀𝑀]𝜆𝜆 = 𝛼𝛼(𝜆𝜆) ∙ 𝑀𝑀 10 ∙ 𝑐𝑐 ∙ 𝑑𝑑 Bei polymeren Substanzen wie Peptiden bezieht man sich auf die mittlere Molekülmasse der monomeren Einheiten. Typische molare Drehungen von Aminosäuren liegen im Bereich von 105 grad*cm²/mol; d.h. eine 10−4 molare Lösung einer optisch aktiven Substanz bewirkt bei d=1cm eine Drehung der Polarisationsebene um 1°. Dies entspricht ∆𝑛𝑛 = 1,6 ∙ 10−6 . Die optische Rotation kann positiv (rechts-drehend) oder negativ (links-drehend) sein. Richtung und Größe sind Wellenlängen-abhängig. • • Ein Chromophor mit positivem Cotton-Effekt ist mit steigender Frequenz zunächst rechts- (+) und dann links-drehend (-). Ein Chromophor mit negativem Cotton-Effekt geht mit steigender Frequenz von einer links- in eine Rechts-Drehung über. Circulardichroismus Beim Durchgang des linear polarisierten Lichts durch eine optisch aktive Substanz können nicht nur die Lichtgeschwindigkeiten der beiden zirkular polarisierten Komponenten, sondern auch die Extinktionskoeffizienzen 𝜺𝜺𝑳𝑳 und 𝜺𝜺𝑹𝑹 unterschiedlich sein. Eine stärkere Absorption des links-zirkular polarisierten Lichts führt zur Verkürzung des Vektors der links-zirkular polarisierten Komponente. Der Unterschied ∆𝜺𝜺 = 𝜺𝜺𝑳𝑳 − 𝜺𝜺𝑹𝑹 ist die eigentliche Messgröße, wobei in der CD-Spektroskopie die Elliptizität angegeben wird: 𝜃𝜃(𝜆𝜆) = ln 10 ∙ [𝜀𝜀] = 𝑐𝑐𝑐𝑐²/𝑔𝑔, [𝑐𝑐] = 𝑔𝑔/𝑐𝑐𝑐𝑐³ 180 ∙ (𝜀𝜀𝐿𝐿′ − 𝜀𝜀𝑅𝑅′ ) ∙ 𝑐𝑐 ∙ 𝑑𝑑 ≈ 33 ∙ (𝜀𝜀𝐿𝐿′ − 𝜀𝜀𝑅𝑅′ ) ∙ 𝑐𝑐 ∙ 𝑑𝑑 2𝜋𝜋 Analog zur ORD kann man eine molare Elliptizität definieren: [𝜃𝜃]𝜆𝜆 = 𝑀𝑀∙𝜃𝜃(𝜆𝜆) 10∙𝑐𝑐∙𝑑𝑑 = 3,3𝑀𝑀 ∙ ∆𝜀𝜀 (im Galla ist M=1000, warum?) Die Wellenlängen-Abhängigkeit der Elliptizität zeigt das CD-Spektrum. Auch hier wird positiver (rechts-zirkular polarisiertes Licht wird stärker absorbiert) und negativer (links-zirkular polarisiertes Licht wird stärker absorbiert) Cotton-Effekt unterschieden. Konzept des optisch aktiven Chromophors Konfigurationsisomere (D- oder L-Konfiguration) drehen polarisiertes Licht mit gleichem Betrag jeweils nach links oder nach rechts. Enantiomere besitzen weder eine Spiegelebene noch eine Drehspiegelachse. Optische Aktivität tritt nur bei vorhandener Chiralität auf. Diese ist notwendig und hinreichend für das Auftreten von Enantiomerie. • • • • Ein asymmetrisches C-Atom ist häufig Ursache der Chiralität. Bei Quarz z.B. liegt eine chirale Kristallstruktur vor, die die optische Aktivität verursacht. Substituierte Allene sind durch die senkrechte Anordnung ihrer Liganden chiral. Hexahelicen besitzt durch die sterische Behinderung der endständigen H-Atome eine spiralförmige Struktur und ist daher chiral. Für die Spektroskopie ist nicht primär die räumliche Anordnung des Moleküls von Interesse, sondern die daraus resultierende Asymmetrie der Elektronenverteilung. Bedingung für das Auftreten von optischer Aktivität ist die Tatsache, dass einfallendes Licht eine helikale Ladungsverschiebung erzeugen kann. Daher wird die zirkular polarisierte Welle bevorzugt absorbiert, die einen der helikalen Ladungsverschiebung entsprechenden Drehsinn besitzt. Chromophore mit lokaler Symmetrie besitzen keine optische Aktivität. So ist Cyclohexanon optisch inaktiv (zwei Spiegelebenen). Über induzierte Asymmetrie kann optische Aktivität erzeugt werden. Dies geschieht hier über Einführung einer Methylgruppe: Methylcyclohexanon ist optisch aktiv. Bei Proteinen ist die C=O Gruppe der Peptidbindung das Chromophor. Diese ist isoliert betrachtet nicht optisch aktiv, was sich innerhalb eines Proteins aus zwei Gründen ändert: (1) Aufgrund des benachbarten asymmetrischen C-Atoms tritt eine induzierte Asymmetrie auf, die den Chromophor optisch aktiv werden lässt. (2) Neben diesem statischen Einfluss, ist bei Proteinen die Kopplung mit anderen Chromophoren wichtig: So erzeugt eine asymmetrische Sekundärstruktur (z.B. α-Helix) optisch aktive Chromophore durch Bildung gekoppelter Oszillatoren ohne Symmetriezentrum oder -ebene. Chiralität kann also auch durch die Struktur eines Makromoleküls resultieren, weshalb über die CD-Spektroskopie auch die Konformation von Proteinen bestimmt werden kann. Messtechnik Ein Monochromator lässt nur eine bestimmte Wellenlänge durch. Das monochromatische Licht fällt auf einen Polarisator, der linear polarisiertes Licht erzeugt. Ein zweiter Polarisator hinter der Probenkammer wird als Analysator verwendet. • • Ist die Probe optisch inaktiv, resultiert maximale Intensität am Photomultiplier bei paralleler Orientierung von Polarisator und Analysator. Bei einer optisch aktiven Probe wird die Polarisationsebene des Lichts gedreht, sodass der Analysator um den entsprechenden Winkel nachgeführt werden muss, um maximale Intensität zu erhalten. Die Wellenlänge wird automatisch variiert und der jeweilige Drehwinkel gemessen. Es wird ein ORD-Spektrum erhalten. Zur Aufnahme eines CD-Spektrums muss die Absorption von links- bzw. rechts-zirkular polarisiertem Licht gemessen werden. Dazu wird wie bei der ORD zunächst linear polarisiertes Licht eingestrahlt (Lampe, Monochromator und Polarisator) und nach Durchstrahlen der Küvette das nun elliptisch polarisierte Licht nacheinander für jede Wellenlänge in rechts- und links-zirkulierende Teile separiert (CD-Modulator), verstärkt (Photomultiplier) und detektiert. Dies ist theoretisch durch ein λ/4-Plättchen möglich. Das λ/4-Plättchen wird dabei stetig um 90° gedreht, um abwechselnd links- und rechts-zirkular polarisiertes Licht jeder Wellenlänge zu erzeugen. So kann abwechselnd der Intensitätsverlust von rechts- und linkszirkular polarisiertem Licht nach Durchgang durch die Probe gemessen werden. Nach Lambert-Beer können aus der Absorption die Extinktionskoeffizienten 𝜺𝜺𝑳𝑳 und 𝜺𝜺𝑹𝑹 und damit auch die Elliptizität 𝜽𝜽~∆𝜺𝜺 bestimmt werden. In der Praxis legt man ein elektrisches Wechselfeld an, anstatt das λ/4-Plättchen zu drehen. Im Takt des Wechselfeldes wird damit unter Ausnutzung des piezoelektrischen Effekts die Molekülorientierung im λ/4-Plättchen variiert (entspricht einer Drehung). Ein Photomultiplier misst zeitabhängig im Takt dieses CD-Modulatros nach Durchstrahlen der Probe die Lichtintensität 𝐼𝐼𝐿𝐿 und 𝐼𝐼𝑅𝑅 . Die Elliptizität wird dann berechnet und als Funktion der Wellenlänge (CD-Spektrum) ausgegeben. Anwendungsbeispiele Anhand des Cotton-Effekts ist es möglich durch Vergleich mit Standardsubstanzen Konformationen von Makromolekülen zu bestimmen. Hierzu wird die CD-Spektroskopie als schnelle Methode zur Sekundärstrukturanalyse von Proteinen und Polynukleotiden verwendet. Analyse der Sekundärstruktur von Proteinen Die Abbildung stellt am Beispiel von α-helikalem Poly-Alanin das Apsorptionsspektrum dem CD-Spektrum gegenüber – es sind außerdem die Peaks der einzelnen elektronischen Übergänge einzeln hervorgehoben. Die unterschiedlichen elektronischen Übergänge, die im Absorptionsspektrum überlappen, können wie gezeigt auch mit dem Lineardichroismus dargestellt werden (siehe Beispiel Poly-Lysin). Insgesamt drei aufgelöste Übergänge führen zur beobachteten Spektrenform (bei 190 nm und 204 nm die ππ*-Übergänge und bei 220 nm der nπ*-Übergang). Die einzelnen Banden des CDSpektrums sind deutlich besser aufgelöst. Das Spektrum ist typisch für ein α-helikales Protein. Die Form des CDSpektrums ändert sich charakteristisch mit der Konformation eines Peptids. Der Bereich um 190 nm und zwischen 210 und 220 nm ist sehr gut geeignet, um Konformationsänderungen in Proteinen zu verfolgen (z.B. bei thermischer Denaturierung). Durch Computer-gestützte Spektren-Addition kann eine Konformationsanalyse natürlicher Proteine durchgeführt werden. Dazu werden die CD-Spektren der drei Grundformen so oft anteilig überlagert, bis eine Übereinstimmung mit dem experimentellen Spektrum erreicht ist. Dabei wird ein Prozentsatz immer konstant gewählt (z.B. 20% Zufallsknäuel) und die anderen Prozentsätze ( α-Helix und β-Faltblatt) variiert. Für die Analyse von Protein-Spektren benötigt man Verlgeichsspektren! Die CD-Spektroskopie an Proteinen ist nicht auf die Peptid-Bindung beschränkt. Prosthetische Gruppen mit häufig typischen Absorptionsspektren im sichtbaren Bereich wurden intensiv mittels CD-Spektroskopie untersucht. Polynukleotide und Nukleinsäuren Die optisch aktiven Gruppen in Nukleotiden sind die Purin- und Pyrimidin-Basen, wobei die N-glykosidische Bindung sowie die helikale Anordnung im Polymer ursächlich sind. Damit sind die CD-Spektren von der Basenstapelung abhängig, sodass Konformationsänderungen und LigandBindung analysiert werden können. Ribose und Phosphorester-Bindungen absorbieren nicht im UV/VIS-Bereich. • • Bei der Polymerisierung von AMP ändert sich das Vorzeichen des Cottoneffekts (AMP: negativ, polyA: positiv) Temperatur-Abhängigkeit des CD-Spektrums von Adenosin-5‘-mononicotinat. Bei tiefen Temperaturen sind Basen gestapelt (hohe Peaks), bei hohen Temperaturen dissoziiert. Infrarot-Spektroskopie Die Infrarot-Spektroskopie ist eine Absorptionsmethode im Wellenlängenbereich 2,5-250µm. Er schließt sich direkt an das langwellige Ende des sichtbaren Bereichs an. Durch diese im Vergleich zum UV-VIS-Licht energiearme Strahlung (Wärmestrahlung) können keine elektronischen Übergänge mit Energieunterschieden von etwa 400 kJ/mol angeregt werden, sondern nur noch Molekülschwingungen (40kJ/mol) und Molekülrotationen (4kJ/mol). Die im IR beobachteten Banden sind also auch im UV/VIS-Spektrum vorhanden, aber nicht ausreichend aufgelöst. Abgesehen vom Energieunterschied sind die physikalischen Prinzipien der Vibrations-Absorptions-Spektroskopie die gleichen wie für elektronische Spektren (Lambert-Beer, Übergangsdipolmomente, Dichroismus). Das IR-Spektrum Die Darstellung des IR-Spektrums unterscheidet sich von der des UV/VIS-Spektrums. • • Die Ordinate zeigt nicht den molaren Extinktionskoeffizienten, sondern die prozentuale Transmission %𝑇𝑇 = 𝐼𝐼/𝐼𝐼0 ∙ 100 oder zum Teil die prozentuale Absorption %𝐴𝐴 = 100 − %𝑇𝑇. Eine starke Absorptionsbande zeigt also im ersteren Fall nach unten. Auf der Abszisse ist nicht die Wellenlänge, sondern von rechts nach links steigend der reziproke Wert, die Wellenzahl 𝑣𝑣�[𝑐𝑐𝑚𝑚−1 ] = 104 /𝜆𝜆[µ𝑚𝑚] aufgetragen. Sie gibt an wieviele Wellenlängen einen cm ergeben. Vorteil: Die Wellenzahl ist der Frequenz und damit dem 𝑐𝑐 𝜆𝜆 Energieunterschied proportional: 𝑣𝑣 = = 𝑐𝑐 ∙ 𝑣𝑣� → 𝐸𝐸 = ℎ𝑣𝑣 = ℎ𝑐𝑐𝑣𝑣�. Oszillator-Modelle für zweiatomige Moleküle Die Absorptionsbanden werden sowohl von intramolekularen Schwingungen der Atomkerne in Richtung Kernverbindungsachse als auch von intermolekularen Schwingungen der Moleküle erzeugt. Die Eigenschwingungen eines mehratomigen Moleküls mit einer definierten Frequenz lassen sich anhand eines zweiatomigen Oszillators klassisch mechanisch erklären. Zwei kovalent verknüpfte Atome befinden sich in einem mittleren Abstand zueinander (Gleichgewichtsabstand => Bindungslänge, z.B. C-H=0,107nm). Es herrscht ein Kräftegleichgewicht zwischen Abstoßung der positiven Kerne und negativen Elektronenwolken sowie Anziehung zwischen Kernen und Elektronen der jeweiligen Partner-Atome. Man betrachtet Atome als Punktmassen m1 und m2, die über eine elastische Feder F (rücktreibende Kraft) verbunden sind. Harmonischer Oszillator k=Kraftkonstante Das Hookesche Gesetz 𝐹𝐹 = −𝑘𝑘(𝑟𝑟 − 𝑟𝑟0 ) r=Abstand der Massenpunkte bei Auslenkung, beschreibt die Rückstellkraft r_0=Gleichgewichtsabstand, negatives Vorzeichen, da die Kraft F der Auslenkung rder Feder, nach Kompression r0 entgegengerichtet ist. oder Extension der Feder. 1 Potentielle Energie des schwingenden Systems 𝐸𝐸 = 2 𝑘𝑘 ∙ (𝑟𝑟 − 𝑟𝑟0 )2 Vibrationsfrequenz 1 𝑘𝑘 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 = 2𝜋𝜋 ∙ �µ Reduzierte Masse des Systems Wellenzahl erlaubte Energieniveaus Resonanzbedingung (Energiedifferenz zwischen 2 benachbarten Niveaus) Der Grundzustand besitzt quantenmechanisch die Nullpunktsenergie 𝑚𝑚 1 𝑚𝑚 2 1 +𝑚𝑚 2 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 𝑐𝑐 µ = 𝑚𝑚 𝑣𝑣� = 1 2 𝐸𝐸𝑣𝑣 = �𝑣𝑣 + � ℎ ∙ 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 𝐸𝐸𝑣𝑣 = 𝐸𝐸𝑣𝑣+1 − 𝐸𝐸𝑣𝑣 = ℎ𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 1 𝐸𝐸0 = 2 ℎ𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 Die potentielle Energie steigt symmetrisch auf einer parabolischen Kurve an. Der Scheitelpunkt der Parabel liegt bei r0. Die Schwingungsfrequenz ist nur von der Kraftkonstante (Bindungsstärke) und den schwingenden Massen abhängig, aber unabhängig von der Auslenkung. Die auftretenden Schwingungsniveaus müssen quantenmechanisch erklärt werden: Alle molekularen Energien sind diskret, weshalb die erlaubten Energieniveaus äquidistant sind. Die Quantenzahl v kann die Werte 0,1,2,3… annehmen. Die Absorption findet nur bei erfüllter Resonanzbedingung statt (Frequenz der Schwingung muss mit Frequenz der Strahlung übereinstimmen). Voraussetzung für ein beobachtbares Spektrum ist, dass sich das Dipolmoment des Moleküls ändert. Das heißt, dass eine Schwingung nur in heteronuklearen, zweiatomigen Molekülen IR-aktiv sein kann. Ein homonukleares zweiatomiges Molekül hat kein Dipolmoment, sodass es auch nicht geändert werden kann. In einem symmetrischen mehratomigen Molekül kann nur eine Schwingung, die unsymmetrisch zum Symmetriezentrum erfolgt, IR-aktiv sein. Aufgrund der Nullpunktenergie ist festgelegt, dass ein Molekül immer Schwingungen aufweist. Nur klassisch ist ein ruhendes Atom möglich. Anharmonischer Oszillator Das h.O.-Modell kann für reale Moleküle nicht verwendet werden. Bindungen sind nur in einem kleinen Bereich um ihre Gleichgewichtslänge elastisch und können bei großen Schwingungsamplituden brechen. Statt der harmonischen Parabel gilt das Morse-Potential (LennardJones-Potential, wie bei Van-der-Waals Wechselwirkung). Die Abstände sind nicht mehr äquidistant und das Molekül dissoziiert beim Überschreiten eines bestimmten Energiebetrages ∆𝐸𝐸𝐷𝐷 . Nach den Auswahlregeln sind Übergänge mit ∆𝒗𝒗 = ±𝟏𝟏, ±𝟐𝟐, ±𝟑𝟑 … möglich, wobei die Übergangswahrscheinlichkeit immer niedriger wird. Aus dem Energieunterschied zwischen E0 und E1 lassen sich über die Boltzmann-Verteilung die Besetzungszahlen der beiden Niveaus berechnen. Bei Raumtemperatur liegt die Besetzungszahl von E1 bei etwa 1% der Besetzungszahl des Grundzustandes E0. Auch bei der IR-Spektroskopie gehen demnach praktisch alle Übergänge von v=0 aus. IR-aktive Schwingungen eines mehratomigen Moleküls Die Lage eines Moleküls mit N Atomen ist durch 3N Koordinaten (x,y,z für jedes Atom) eindeutig bestimmt. Ein Molekül hat damit 3N Freiheitsgrade. Die Translation des Gesamtmoleküls benötigt 3 Freiheitsgrade. Die Rotation eines nicht-linearen Moleküls benötigt ebenso 3 Freiheitsgrade. So bleiben für die Vibration 3N-6 (nichtlineares Molekül) bzw. 3N-5 (lineares Molekül) Freiheitsgrade. Bei einem linearen Molekül entfällt ein Rotationsfreiheitsgrad, wegen des geringen Trägheitsmoments der Drehung um die Längsachse. Damit ergeben sich für ein drei-atomiges nichtlineares Molekül wie H2O 3 FG und für ein lineares Molekül wie CO2 4 FG der Vibration. So berechnete Schwingungen heißen Normalschwingungen. Man unterscheidet aufgrund der Schwingungsform Valenzschwingungen und Deformationsschwingungen voneinander. Bei Valenzschwingungen/Streckschwingungen ändert sich die Bindungslänge. Es werden symmetrische (𝒗𝒗𝒔𝒔 ) und asymmetrische (𝒗𝒗𝒂𝒂𝒂𝒂 ) Streckschwingungen unterschieden, je nachdem ob eine vorhandene Molekülsymmetrie erhalten bleibt oder nicht. Bei Deformationsschwingungen/Beugschwingungen ändert sich der Bindungswinkel. Es können symmetrische (𝜹𝜹𝒔𝒔 ) und asymmetrische (𝜹𝜹𝒂𝒂𝒂𝒂 ) Beugschwingungen unterschieden werden. Deformationsschwingungen sind in der Papierebene (in plane) oder senkrecht dazu (out of plane) möglich. Die Abbildung zeigt typische Schwingungen von CH2-Gruppen in CH-Ketten z.B. von Lipiden. Auch Kopplungen zwischen Schwingungen benachbarter Gruppen haben Einfluss auf das IR-Spektrum. Schwingungen, die charakteristisch für das Gesamtmolekül sind heißen Gerüstschwingungen. Sie kommen nicht mehr durch einzelne funktionelle Gruppen (lokalisierte Schwingungen), sondern durch das Molekül als Ganzes zustande. Durch die Überlagerung der Normalschwingungen mit den Gerüstschwingungen ist die Zuordnung der lokalisierten Schwingungen stark erschwert. Dies gilt für den Fingerprint-Bereich ab etwa 1500 cm-1, der für Reinsubstanzen anhand von Vergleichszwecken eine eindeutige Identifizierung ermöglicht. Gerüstschwingungen sind umso ausgeprägter, je größer das Molekül. Nicht jede Schwingung ist IR-aktiv. Bei erfüllter Resonanzbedingung, muss also nicht zwingend Absorption auftreten. Eine Schwingung ist nur dann IR-aktiv, wenn sich das Dipolmoment des Moleküls im Verlauf der Schwingung ändert. Beim CO2 ändert sich bei 𝑣𝑣𝑠𝑠 das Dipolmoment nicht, wodurch sie nicht im IR-Spektrum sichtbar ist, trotz Eigenfrequenz bei 1330𝑐𝑐𝑚𝑚−1 . Bei Wasser ändert sich der Dipol für alle drei Schwingungsmodi. Da die meisten funktionellen Gruppen von Biomolekülen kein Symmetriezentrum besitzen, kann die IR-Spektroskopie zur Strukturbestimmung eingesetzt werden. Einbeziehung der Rotation Jedes Schwingungsniveau ist in mehrere Rotationsniveaus unterteilt. Analog zur Strukturierung des UV-VIS-Absorptionsspektrums durch die Vibrationsniveaus führen hier die Rotationsniveaus zur Strukturierung der IR-Banden. Rotationsspektren können aber nur bei Molekülen in der Gasphase beobachtet werden. Bei fester oder gelöster Form ist dieser niederenergetische Übergang nicht von Interesse. Messtechnik • • • • • Selber Aufbau wie für UV-VIS, nur andere Materialien, da anderer Wellenlängen-Bereich. Lichtquelle: geheizter Festkörper aus Oxiden von Siliciumcarbid. Nernst-Stift aus Zirkonoxid wird vorgeheizt, damit er elektrisch leitend wird (1500K). Er wird über Strom auf dieser Temperatur gehalten. Für Gitter oder Prismen in den Monochromatoren sowie für Linsen, Spiegel und Probengefäße müssen spezielle Materialien verwendet werden, da Glas IR-Strahlung absorbiert. Es werden daher Mineralsalze NaCl, KBr oder NaF verwendet. Als Detektoren für IR-Strahlung werden Halbleiterdioden verwendet. Spezielle IR-Techniken Abgeschwächte Totalreflexion Die Anwesenheit von Wasser schränkt die Möglichkeiten zur Strukturuntersuchung biologischer Systeme mit IR-Spektroskopie stark ein, da die für Biomoleküle interessanten Resonanzen (C=N, C=O, NH, OH) durch die starke IR-Absorption des Wassers um 1600 und 3400 𝒄𝒄𝒎𝒎−𝟏𝟏 überdeckt werden. Messungen sind daher nur bei geringer Schichtdicke und hoher Konzentration möglich, was im Gegensatz zur häufig geringen Löslichkeit oder zur Assoziations-Tendenz von Makromolekülen bei hohen Konzentrationen steht. IR-Messungen an trockenem biologischem Material führen zu einem Verlust der biologischen Relevanz. Einen Ausweg bietet die ATR-Methode. Das Probenmaterial wird als Schicht auf eine Platte mit einer großen Brechzahl aufgetragen. Geeignete Materialien für die ATR-Platte, die für IR-Strahlung transparent sein muss, sind Silberchloride, Thalliumhalogenide oder Germanium. Der Lichtstrahl wird an der polierten Grenzfläche einer Trapez-förmigen Platte unter einem definierten Winkel eingestrahlt. Da die Brechzahl der Platte n1 groß gegenüber der Brechzahl der aufgetragenen Probe n2 ist, tritt beim Überschreiten eines kritischen Einstrahlwinkels θ Totalreflexion auf. Der Strahl wird durch die Platte geleitet. Im Gegensatz zur Reflexion an einer verspiegelten Oberfläche, dringt die elektrische Feldstärke hier bei jeder Reflexion ein wenig in das optisch dünnere Medium ein. Die Eindringtiefe E der so genannten evanezenten Welle ist abhängig vom Einfallswinkel und der Wellenlänge und variiert zwischen <1 und 10 µm. Liegt das Probenmaterial dicht auf der Oberfläche, so wird Licht absorbiert, wodurch der reflektierte Strahl abgeschwächt wird. Verlässt das Licht die ATR-Platte am anderen Ende, so enthält es Informationen über die Absorption der Probe. Diese Methode ist bei 100 Reflexionen hochempfindlich und besonders für Schichten-bildende Materialien (Lipide, Proteine) und stark streuende Proben (fibrilläre Proteine) geeignet. Streuende Proben können nicht in Transmission gemessen werden, weshalb die ATR-IR Methode besser geeignet ist. Das aufgetragene Material kann entsprechend seinem natürlichen Milieu hydratisiert sein, da aufgrund der geringen Eindringtiefe eine wässrige Umgebung auf der Platte nicht erkannt wird (Grund: Die untere Schicht enthält nur die Probe, Wasser befindet sich weiter weg vom Kristallboden). • • • Durch Variation des Einfallwinkels können sogar unterschiedliche Tiefen im Material untersucht werden. Durch Verwendung von polarisiertem Licht kann an orientierten Schichten das dichroitische Verhältnis bestimmt werden. Aus der Lage der Übergangsdipolmomente lassen sich Orientierung und Flexibilität von Molekülsegmenten ermitteln. Fourier-Transform-IR-Spektroskopie Die FT-Technik bietet höhere Aufnahmegeschwindigkeiten bei hoher spektraler Auflösung. Ein Computer ermöglicht eine Korrektur der Lösungsmittel-Absorptionen und eine automatische Spektrenauswertung. Zwei sich überlagernde Wellen unterschiedlicher Frequenz addieren sich zu jeder Zeit. Die durch Interferenz resultierende Welle ist oft eine Schwebung. Die Frequenz der Einhüllenden (Schwebungsfrequenz) entspricht der Differenz der Frequenzen der einzelnen Wellen. Durch die zeitabhängige Aufnahme der Amplitudenänderung einer solchen Welle mithilfe eines Detektors kann die Frequenz der Schwebung und damit der Frequenzunterschied der sich überlagernden Wellen ermittelt werden. Dies gilt auch für eine komplizierte Überlagerung mehrerer Wellen, wobei jede einzelne durch Frequenz und Amplitude definiert ist. Zur Analyse des überlagerten Spektrums muss zunächst am Rechner die zeitabhängige Änderung des Signals gespeichert werden. Typische Zeitintervalle liegen bei 1 ms, wobei für 1k-2k aufeinanderfolgende Intervalle die gemessenen Intensitäten gespeichert werden. Die Gesamtzeit zur Aufnahme des Spektrums in der Zeitdomäne (Interferogramm) beträgt damit 1s. Mithilfe der Fourier-Transformation kann eine komplexe Wellenform in die einzelnen Sinusfunktionen zerlegt werden. Damit können die Frequenzen der beteiligten Schwingungen ermittelt werden. So wird das Frequenzspektrum erhalten. Bei der FT-IR wird die Probe mit dem insgesamt von der Lichtquelle zur Verfügung gestellten Frequenz-Spektrum bestrahlt. Die Strahlung der Lichtquelle enthält ein breites Frequenz-Band im IRBereich. Das Interferometer besteht aus einem Strahlteiler ST und zwei Spiegeln S1 und S2. Der Strahlteiler ist ein halbdurchlässiger Spiegel, der die eine Hälfte des Lichts auf S1 fallen lässt und die zweite Hälfte auf S2 reflektiert. Die zurücklaufenden Wellen interferieren dann am Strahlteiler. Ist die Weglänge S1-ST gleich der Weglänge S2-ST, resultiert konstruktive Interferenz. Ein heller Strahl verlässt den Strahlenteiler. Das gleiche gilt für Wegunterschiede, die ein ganzzahliges Vielfaches der Wellenlänge ausmachen. Bei halbzahligen Vielfachen kommt es zur destruktiven Interferenz. Beim Michelson-Interferometer ist der Spiegel S2 beweglich. In 1s kann er ca. 1 cm in Strahlrichtung ausgelenkt werden. Der Vorteil liegt darin, dass nicht mehr der ganze Wellenlängenbereich Wellenlänge für Wellenlänge vermessen werden muss, sondern das gesamte Spektrum simultan aufgenommen werden kann. So verkürzt sich die Aufnahmezeit von 10-15 Minuten auf unter eine Minute. Ein weiterer Vorteil der FT-Technik liegt darin, dass optische Bauteile wie Monochromator und Spalte zur Abbildung der Lichtquelle nicht benötigt werden. Diese würden das Auflösungsvermögen des Spektrometers begrenzen. Eine gute Auflösung (kleiner Spalt) bedeutet ein Intensitätsverlust (hohes Signal/Rauschen Verhältnis). Die bessere Signalintensität des FT-Spektrometers kann weiter über Spektrenakkumulation verbessert werden. Anwendungsbeispiele Für ein Makromolekül wird aufgrund der 3N-6 Schwingungen ein sehr komplexes Spektrum erwartet. Die vollständige Auswertung des Spektrums ist daher nicht möglich. Anhand charakteristischer Übergänge lässt sich jedoch eine Aussage über die strukturelle Organisation und über die Wechselwirkungen verschiedener Gruppen gewinnen. Schwingungen von Atomen, die an der Ausbildung von H-Brücken beteiligt sind, unterliegen besonders starken Veränderungen. Konformationen und Wechselwirkungen von Proteinen In Peptiden und Proteinen sind drei Absorptionsbanden wichtig: • • • • • Die Amid-A-Bande um 𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝒎𝒎−𝟏𝟏 = N-H Streckschwingung Die Amid-B-Bande um 3100𝑐𝑐𝑚𝑚−1 = erste Oberschwingung der Amid-II-Schwingung; verstärkt durch Fermi-Resonanz mit N-H-Streckschwingung Die Amid-I-Bande bei 𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝒎𝒎−𝟏𝟏 = C=O Streckschwingung Die Amid-II-Bande bei 𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝒎𝒎−𝟏𝟏 = N-H Beugschwingung + C-N Streckschwingung Amid-III bis Amid-VII sind weitere Banden Alle drei Schwingungen gehören zum Grundgerüst des Polypeptids und sind daher besonders intensiv. Die Schwingungen benachbarter Peptid-Gruppen im Rückgrat des Proteins sind aber nicht voneinander unabhängig. Da C=O und N-H Gruppen über HBrücken miteinander interagieren, stellt das ProteinRückgrat eine Reihe schwach gekoppelter Oszillatoren dar. Über H-Brücken ändert sich die Masse der schwingenden Kerne, was sich auf die Schwingungsfrequenz auswirkt (𝝎𝝎𝒗𝒗𝒗𝒗𝒗𝒗 = �𝒌𝒌/𝝁𝝁). Die Kopplung und damit die Frequenzlage, Linienbreite und Intensität sind von der Konformation des Proteins abhängig. Unterscheidung zwischen Zufallsknäuel und geordneten Strukturen (α-Helix und β-Faltblatt) ist anhand der Amid-A-Bande möglich. β-Faltblatt und α-Helix lassen sich über die Amid-I-Bande unterscheiden. Die Amid-I-Bande liegt im Fall von Poly-Lysin (siehe Abbildung) bei einer freien C=O-Schwingung bei 1700𝑐𝑐𝑚𝑚−1 , bei einem Zufallsknäuel aber bei 1655 𝑐𝑐𝑚𝑚−1 und bei einer α-Helix bei 1650 𝑐𝑐𝑚𝑚−1 . Beim Übergang in ein β-Faltblatt erfolgt eine Aufspaltung in eine schwache Bande bei 1690 𝑐𝑐𝑚𝑚−1 und eine starke Bande bei 1620 𝑐𝑐𝑚𝑚−1 . In natürlichen Proteinen findet man dieselbe Tendenz: Mit steigendem β-Faltblatt-Anteil eines Proteins wandert die Amid-I-Bande von 1650 𝑐𝑐𝑚𝑚−1 (z.B. Cytochrom c, 0% Faltblatt) zu 1636 𝑐𝑐𝑚𝑚−1 (z.B. Ribonuklease, 36% Faltblatt). Durch Ausbildung von Wasserstoff-Brücken im Rückgrad der Proteine verschiebt sich die Amid-A-Bande im Vergleich zu nicht-H-Brücken-gebundener monomerer Amide hin zu niedrigeren Wellenzahlen. Diese Verschiebung ist allerdings nicht sehr stark. Zwischen polaren Seitengruppen bilden sich häufig sehr starke H-Brücken, die die Banden des IR-Spektrums zu einem Kontinuum verbreitern können. • • N-H-…N-Brücken verbreitern bei Poly-L-Histidin den Bereich um 3000 𝑐𝑐𝑚𝑚−1 . Brückenbildung zwischen Glutamat und Glutaminsäure –O….H-O würden den Bereich um 1600 𝑐𝑐𝑚𝑚−1 stark verbreitern. Konformationen und Wechselwirkungen bei Nukleinsäuren Bei Nukleinsäuren kann die Ausbildung von H-Brücken bei der Basenpaarung über die Verschiebung der entsprechenden Schwingungen hin zu kleineren Wellenzahlen beobachtet werden. • • Die Modellsubstanz 9-Ethyladenin liefert zwei Banden für die N-H-Valenzschwingung bei 3416 𝑐𝑐𝑚𝑚−1 und 3482 𝑐𝑐𝑚𝑚−1 . Cyclohexylbromuracil zeigt die entsprechende Bande bei 3380 𝑐𝑐𝑚𝑚−1 . • Eine Mischung zeigt zusätzliche Assoziatbanden bei wesentlich geringerer Wellenzahl (3210, 3260, 3330 𝑐𝑐𝑚𝑚−1 ). Bei der C=O-Valenzschwingung in einer G-C-Paarung beobachtet man eine Aufspaltung der Bande um 1700 𝑐𝑐𝑚𝑚−1 (Strukturbande). Anhand dieser kann das Aufschmelzen der Doppelhelix und damit der Verlust der Basenpaarung verfolgt werden. Modell- und Biomembranen IR-Messungen an Modellmembranen werden mit der ATR-Technik durchgeführt. Die Lipid-Schichten liegen auf der ATR-Platte in orientierter Form vor, sodass mithilfe von polarisierter IR-Strahlung orientierungsabhängige Spektren aufgenommen werden können. Das Spektrum zeigt DPPC bei 22°C (unterhalb der Phasenumwandlungstemperatur). Das Dublett der asymmetrischen CH2-Streckschwingung bei 2918 𝑐𝑐𝑚𝑚−1 verschiebt sich beim Überschreiten der Phasenumwandlungstemperatur von 41°C um ca. 6 𝑐𝑐𝑚𝑚−1 . Der Grund sind vermehrt auftretende gauche-Konformationen. Diese geringe Frequenzverschiebung des Absorptionsmaximums ist mit der FT-IR-Spektroskopie problemlos nachzuweisen und wird zur Detektion von Lipid-Phasenumwandlungen verwendet. Integrale Proteine erzeugen unterhalb der Phasenumwandlungstemperatur eine starke Zunahme der Wellenzahl des Absorptionsmaximums, also eine Zunahme der gauche-Lagen im hydrophoben Bereich der Lipid-Membran. Schwingungen der Phosphat-Gruppe oder der N(CH3)3-Gruppe im Cholinteil liefern Informationen über Beweglichkeit und Orientierung im Kopfguppenbereich. Es können auch biologische Membranen aufgenommen werden. So wurde anhand der Amid-I-Bande bei 1650 𝑐𝑐𝑚𝑚−1 festgestellt, dass die Proteine des sarkoplasmatischen Retikulums vorwiegend α-helikal oder als Zufallskäuel vorliegen. Fluoreszenz-Spektroskopie Nach der Anregung von Elektronen durch Licht im UV/VIS-Bereich resultiert ein elektronischer Übergang vom Grundzustand in den angeregten Zustand. Das angeregte Molekül kann auf mehrere Arten in den energetischen Grundzustand zurück kehren. Die Emission von Strahlung (Lumineszenz) wird allgemein in Fluoreszenz und Phosphoreszenz unterteilt. Außerdem kann die Energie durch verschiedene nicht-strahlende Prozesse abgegeben werden. Physikalische Grundlagen Fluoreszenz und Phosphoreszenz wird meist bei aromatischen und heterozyklischen Molekülen beobachtet, insbesondere bei zwei oder mehr kondensierten Ringen. Die Anregungszustände niedrigster Energie sind bei diesen Molekülen die des π-Elektronensystems. Bei Absorption wird ein Elektron aus einem bindenden π-Orbital in ein antibindendes π*-Orbital überführt. Absorptions- und Emissionsübergänge Im Grundzustand eines Moleküls mit gerader Elektronenzahl sind die niedrigsten Orbitale paarweise mit Elektronen besetzt. Nach dem Pauli-Prinzip müssen die Spins der beiden Elektronen eines Orbitals antiparallel ausgerichtet sein. Der Gesamtspin S des Moleküls im Grundzustand ist dann null (Singulettzustand). Im angeregten Zustand können die beiden Spins der π- und π*-Orbitale parallel (S1) oder antiparallel (T1) sein. Diese Zustände besitzen aufgrund unterschiedlicher Elektronenwechselwirkung verschiedene Energien. Die Energie des Triplettzustandes ist dabei niedriger als die des entsprechenden Singulettzustandes. Bei RT befinden sich die Moleküle fast ausschließlich im niedrigsten Schwingsungsniveau des elektronischen Grundzustandes S0. Die Absorption eines Lichtquants geeigneter Energie überführt das Molekül von S0 in den ersten angeregten oder in einen höheren Singulettzustand (S1, S2…). Der Absorptionsprozess zu einem Triplettzustand stellt wegen der Spinumkehr einen quantenmechanisch verbotenen Übergang dar. Die Übergangswahrscheinlichkeit ist sehr gering und von niedriger Intensität (spielt hier keine Rolle). Im Anschluss an den Absorptionsprozess im fs-Bereich finden verschiedene Deaktivierungsprozesse im Molekül statt. Deaktivierungsprozesse Innere Umwandlung (interne Konversion, IC): Verteilung der Energie auf innere Schwingungsmoden eines Moleküls oder Austausch von Schwingungsenergie mit benachbarten Molekülen in Lösungen oder Festkörpern. Dadurch gelangt ein Molekül wieder in das thermische GG mit seiner Umgebung. Es gelangt von einem höher angeregten Zustand in das nullte Schwingungsniveau. Strahlungslose Deaktivierung: Die innere Umwandlung ist auch für den Übergang aus S2- oder S3Zuständen in den S1-Zustand verantwortlich. Es ist von diesen Zuständen ausgehend keine Fluoreszenz beobachtbar (Ausnahme: Azulen fluoresziert aus dem S2-Zustand). (1) Die Elektronen-Energie (S2) wird zunächst in Kernschwingungsenergie überführt (Schwingungsterm gleicher Gesamtenergie des S1-Zustandes). (2) Diese relaxiert über Temperaturausgleich mit der Umgebung in den energetisch niedrigsten Schwingungszustand (Schwingungsrelaxation ist mit 100-1000fs schneller als Fluoreszenz und Phosphoreszenz mit >100µs). (3) Die Energiedifferenz zwischen S1 und S0 ist wesentlich größer als zwischen höheren benachbarten, angeregten Singulettniveaus. Daher kann die strahlungslose Umwandlung von S1 nach S0 nur über gleichzeitige Anregung einer Vielzahl von Schwingungsquanten erfolgen. Da dieser Prozess sehr langsam stattfindet, stellt die Fluoreszenz von S1 nach S0 einen effektiv konkurrierenden Relaxationsmechanismus dar. Interkombinationsübergang (intersystem crossing, ISC): quantenmechanisch verbotene Spinumkehr, durch die der Singulettzustand in einen Triplettzustand (oder umgekehrt) überführt wird. Fluoreszenz-Löschung: Energie wird auf Quencher übertragen. Lumineszenz Fluoreszenz erfolgt vom niedrigsten Schwingungsniveau in S1 in ein beliebiges Schwingungsniveau in S0. Die Übergangsrate kf liegt im Bereich 𝟏𝟏𝟏𝟏𝟕𝟕 − 𝟏𝟏𝟏𝟏𝟖𝟖 𝒔𝒔−𝟏𝟏 . Phosphoreszenz erfolgt vom niedrigsten Schwingungsniveau in T1 in ein beliebiges Schwingungsniveau in S0. Die Übergangsrate liegt zwischen < 1 − 𝟏𝟏𝟏𝟏𝟒𝟒 𝒔𝒔−𝟏𝟏 . Innerhalb von S0 findet erneut Schwingungsrelaxation statt, sodass der Schwingungsgrundzustand erreicht wird. Fluoreszenz hat folgende Eigenschaften: • • • Das Emissions-Spektrum ist unabhängig von der Anregungswellenlänge. Das Fluoreszenzspektrum ist gegenüber dem Absorptionsspektrum zu größeren Wellenlängen hin verschoben. Das Absorptionsspektrum ist durch die Schwingungsniveaus des angeregten Zustandes, das Fluoreszenz-Spektrum durch die des Grundzustandes S0 strukturiert. Bei vergleichbaren Schwingungsstrukturen von S0 und S1 verhalten sich Absorptions- und Fluoreszenz-Spektrum spiegelbildlich zueinander. Quantenausbeute Der Fluoreszenzanteil der Deaktivierungsprozesse wird durch die Quantenausbeute Φ angegeben. Die Übergangsraten für die einzelnen Prozesse sind kf (Fluoreszenz), kic (innere Umwandlung), kisc (Interkombinationsübergang) und kQ (Fluoreszenz-Löschung). Die Quantenausbeute ist unabhängig von der Wellenlänge, da alle Prozesse vom niedrigsten Schwingungsniveau des angeregten Zustandes ablaufen. Φ = Anzahl emittierter Photonen / Anzahl absorbierter Photonen < 1 Φ= Fluoreszenzlebensdauer kf 𝑘𝑘𝑓𝑓 + 𝑘𝑘𝑖𝑖𝑖𝑖 + 𝑘𝑘𝑖𝑖𝑖𝑖𝑖𝑖 + 𝑘𝑘𝑄𝑄 Die Fluoreszenz-Lebensdauer ist die Zeit, die ein Molekül im Mittel im angeregten Zustand bleibt, bevor die Emission erfolgt. 𝑁𝑁0 ist die Molekülzahl im angeregten Zustand. Moleküle, die pro Zeiteinheit über Fluoreszenz in den Grundzustand übergehen: − 𝑑𝑑𝑑𝑑 = 𝑘𝑘𝑓𝑓 ∙ 𝑁𝑁0 → 𝑁𝑁(𝑡𝑡) = 𝑁𝑁0 ∙ 𝑒𝑒 −𝑘𝑘 𝑓𝑓 ∙𝑡𝑡 𝑑𝑑𝑑𝑑 Fluoreszenzlebensdauer ist die Zeit 𝑡𝑡 innerhalb der die Zahl angeregter Moleküle 𝑵𝑵(𝒕𝒕) auf 𝑵𝑵𝟎𝟎 /𝒆𝒆 zurückgegangen ist. Damit ergibt sich 𝝉𝝉𝑭𝑭 = 𝟏𝟏/𝒌𝒌𝒇𝒇 . Die Lebensdauer des angeregten Zustands 𝝉𝝉 = 𝝉𝝉𝑭𝑭 ∙ 𝚽𝚽 = 1 𝑘𝑘 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑄𝑄 muss alle anderen Deaktivierungsprozesse mit einbeziehen und ist die experimentell zugängliche Messgröße. Über Messung der Quantenausbeute lässt sich die Fluoreszenzlebensdauer dann berechnen. Lösungsmittel-Einflüsse Wie bei der Absorption treten auch beim Emissionsprozess bei Variation des Lömis spektrale Verschiebungen auf. Dabei kann es sich um Änderungen der Polarität, der Dielektrizitätskonstanten oder der Polarisierbarkeit des Lömis handeln. • • • Polares Lömi: Der angeregte Franck-Condon-Zustand S1 liegt energetisch höher als der Gleichgewichtszustand des angeregten Moleküls S1e, da sich erst in S1e die polaren LömiMoleküle wegen des unterschiedlichen Dipolmoments des angeregten Zustandes umorientiert haben. Apolares Lömi, geringe Polarisierbarkeit: Im apolaren Medium erfolgt keine Umorientierung der Lömi-Molekle, weshalb die Energien in S1 und S1e näherungsweise gleich groß sind. Diese im Vergleich zum polaren Lömi höherenergetische Fluoreszenz ist damit blauverschoben. Apolares Lömi, hohe Polarisierbarkeit: Der angeregte Fluorophor kann Dipolmomente in den Lömi-Molekülen induzieren, was zu einer Orientierung führt. S1e ist gegenüber S1 erniedrigt. Diese Erniedrigung kann größer sein, als die im polaren Lömi, weshalb die im Vergleich zum polaren Lömi niederenergetische Fluoreszenz rotverschoben ist. Die Richtung der spektralen Verschiebung ist anders als bei der Absorption schwer aus der Polarität des Lömis vorherzusagen. Anregungsspektren Die Form des Emissionsspektrums ist immer gleich und unabhängig von der absorbierten Strahlung, da die Emission immer vom niedrigsten Schwingungsniveau aus S1 erfolgt. • • Fluoreszenzintensität vs. Emissionswellenlänge bei konstanter Anregungswellenlänge ergibt ein Fluoreszenz-Emissionsspektrum. Fluoreszenzintensität vs. Anregungswellenlänge bei konstanter Emissionswellenlänge ergibt Fluoreszenz-Anregungsspektrum. Dies entspricht qualitativ einem Absorptionsspektrum. Konzentrationsabhängigkeit der Fluoreszenz Konzentrierte Lösungen zeigen geringere Quantenausbeuten und Veränderungen im Spektrum. Reabsorption emittierter Fluoreszenz-Strahlung: Je höher die Fluorophor-Konzentration, desto größer die Wahrscheinlichkeit der Reabsorption. Die Voraussetzung ist die teilweise Überlappung des Emissions- und Absorptionsspektrums. Reabsorption tritt damit hauptsächlich für den kurzwelligen Anteil der emittierten Strahlung auf. Die Quantenausbeute für n Reabsorptionsprozesse ist Φn mit Φ < 1. Mit steigender Reabsorption geht damit die Quantenausbeute gegen null, wodurch die Fluoreszenz-Intensität im kurzwelligen Teil des Emissionspektrums verschwindet. Dies hat erheblichen Einfluss auf die Form des Spektrums. Dimer-Bildung im Grundzustand: Wenn der Fluorophor im Grundzustand teilweise als Dimer vorliegt, absorbiert auch der Dimer Strahlung. Die Intensität der Monomer-Fluoreszenz ist verringert, weil ihre Konzentration durch Dimer-Bildung niedriger ist. Dimer-Bildung ist häufig mit einer Rotverschiebung im Absorptionsspektrum verbunden, wobei das Fluoreszenz-Spektrum in seiner Form unverändert bleibt, da Grundzustands-Dimere meist nicht fluoreszieren. Angeregte Dimere (Excimere): Excimere existieren nur im angeregten Zustand. Sie entstehen über eine Wechselwirkung zwischen einem angeregten Monomer und einem Monomer im Grundzustand. Das Absorptionsspektrum bleibt dadurch unverändert. Im Fluoreszenzspektrum tritt eine zusätzliche Bande, rotverschoben im Vergleich zur Monomer-Bande auf. Bei niedrigen Konzentrationen überwiegen Anregung und anschließende Fluoreszenz der Monomere. Mit steigender Konzentration nimmt die Wahrscheinlichkeit der Excimeren-Bildung zu. Diese können strahlungslos zerfallen, unter Erhalt des angeregten Zustands dissoziieren oder bei höheren Wellenlängen fluoreszieren. Der Grundzustand eines Excimers (M+M) ist instabil, denn bei Abnahme des Molekülabstands zwischen zwei Monomeren im Grundzustand nimmt die potentielle Energie stetig zu. Ist hingegen einer der beiden Reaktionspartner im elektronisch angeregten Zustand (M*+M), so kommt es zur Bildung eines Potentialminimums, in dem der Excimer stabilisiert wird. Beim Übergang in den Grundzustand resultiert eine breite, unstrukturierte Bande im Fluoreszenz-Spektrum. Ursache sind die unterschiedlichen Energiedifferenzen zwischen angeregtem Zustand und Grundzustand. (Fluoreszenz immer vom Schwingungsgrundzustand; aber auch hier existiert eine Schwingung, die den Kernabstand variiert; Da Grundzustand exponentielle Energiekurve hat, resultiert für eine kleine Änderung im Kernabstand schon eine große Änderung in der Energie des Grundzustandes und damit auch eine große Änderung der Energiedifferenz)! Die Excimeren-Bildung ist eine dynamische Fluoreszenz-Löschung der Monomere. Sie kann mit der M ist maximale Quantenausbeute der Monomere Stern-Volmer-Gleichung beschrieben werden. Φmax bei unendlicher Verdünnung. 𝑘𝑘𝑎𝑎 𝑐𝑐 ist die Excimeren-Bildungsrate (beachte: Konzentrationsabhängigkeit!). 𝜏𝜏0 ist die Lebensdauer der angeregten Monomere. Für die ExcimerenE kann bei sehr hohen FluorophorKomponente ergibt sich eine inverse Beziehung. Φmax Konzentrationen bestimmt werden. M Φmax − 1 = 𝑘𝑘𝑎𝑎 ∙ 𝑐𝑐 ∙ 𝜏𝜏0 ΦM E Φmax 1 −1= E Φ 𝑘𝑘𝑎𝑎 ∙ 𝑐𝑐 ∙ 𝜏𝜏0 Fluoreszenz-Löschung Quencher reduzieren die Quantenausbeute des Fluorophors. Dabei wird die Energie des Anregungszustandes strahlungslos auf die Quencher überführt. Die Effektivität der beiden Prozesse ist von der Quencher-Konzentration abhängig • • Dynamische Fluoreszenz-Löschung: Kollisionsprozesse Statische Fluoreszenz-Löschung: Komplexbildung Dynamische Fluoreszenz-Löschung: Mit Löschermoleküle Ohne Löschermoleküle Verhältnis der Quantenausbeuten: Übergangsrate der Fluoreszenzlöschung ist proportional zur Quencher-Konzentration Φ 𝐼𝐼 Da Φ0 ~ 𝐼𝐼0 = Fluoreszenzintensität mit und ohne Quencher Φ = 𝑘𝑘 Φ0 = Φ0 Φ kf 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑄𝑄 kf 𝑘𝑘 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 kQ = 1 + 𝑘𝑘 𝑘𝑘𝑄𝑄 = 𝐾𝐾𝑐𝑐𝑄𝑄 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 τ0 = 𝑘𝑘 = 1 + 𝑘𝑘𝑄𝑄 τ0 𝑰𝑰𝟎𝟎 − 𝟏𝟏 = 𝑲𝑲𝒄𝒄𝑸𝑸 𝛕𝛕𝟎𝟎 𝑰𝑰 K = Löschkonstante Stern-VolmerGleichung Stern-Volmer Diagramm zur Fluoreszenz-Löschung von Trp durch NaI hat Steigung 𝐾𝐾τ0 . Löschkonstante kann bei bekannter Lebensdauer ermittelt werden. Statische Fluoreszenz-Löschung: 1 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 Quantenausbeute in Abwesenheit von Quencher sei gleich 1 Quantenausbeute mit Quencher Gleiche Anregungswahrscheinlichkeit von Fluorophor und Komplex Φ0 𝐼𝐼0 ~ Φ 𝐼𝐼 [𝑀𝑀𝑀𝑀]∗ [𝑀𝑀 ∗ ] = [𝑀𝑀𝑀𝑀] [𝑀𝑀] = 𝑘𝑘𝑎𝑎 [𝑄𝑄] 𝑰𝑰𝟎𝟎 − 𝟏𝟏 = 𝒌𝒌𝒂𝒂 𝒄𝒄𝑸𝑸 𝑰𝑰 [𝑀𝑀 ∗ ] =1 [𝑀𝑀] [𝑀𝑀 ∗ ] Φ = [𝑀𝑀 ∗ ]+[𝑀𝑀𝑀𝑀]∗ [𝑀𝑀𝑀𝑀]∗ Φ0 = 1 + [𝑀𝑀 ∗ ] Φ [𝑀𝑀𝑀𝑀] 𝑘𝑘𝑎𝑎 = [𝑀𝑀][𝑄𝑄] ist Φ0 = Komplexbildungskonstante Vergleich: Statische und dynamische Fluoreszenz-Löschung ergeben eine lineare Abhängigkeit des Intensitätsverhältnisses von der Konzentration der Löschermoleküle. Die dynamische Löschung ist zusätzlich von der Lebensdauer des angeregten Fluorophors abhängig, da die Wahrscheinlichkeit für eine Kollision zwischen angeregtem Fluorophor und Quencher mit höherer Lebensdauer des angeregten Zustands steigt. Die Komplexbildung beim statischen Quenchen reduziert lediglich die Konzentration an freiem Fluorophor, beeinflusst aber die Lebensdauer der angeregten Moleküle nicht. Die Unterscheidung zwischen statischer und dynamischer Fluoreszenzlöschung wird anhand der Lebensdauer des gebildeten Komplexes MQ getroffen und stellen damit nur Grenzfälle dar. • • Dynamisch: Lebensdauer von MQ ist viel kürzer als von M* Statisch: Lebensdauer von MQ ist viel länger als von M* Energieübertragung: Förster-Transfer Für Fluoreszenz-Löschung ist eine direkte Kopplung zwischen elektronischen Orbitalen von Fluorophor und Löschermolekül erforderlich. Die Energieübertragung kann auch über größere Abstände bis zu 10 nm erfolgen. Ist das Akzeptormolekül ebenso ein Fluorophor, kann die Energieübertragung anhand der Fluoreszenz des Akzeptors (sensibilisierte Fluoreszenz, da keine direkte Anregung des Akzeptors) nachgewiesen werden. Der Mechanismus des Energieübertrags beruht auf einem Resonanzphänomen (daher: Resonanzenergietransfer): Das Elektronensystem des angeregten Donors wird als mechanischer Oszillator betrachtet, dessen Anregungsenergie auf einen zweiten Oszillator übertragen werden kann (gekoppelte Schwingungen). Bedingung ist, dass der elektronische Übergang des Akzeptors mit der Frequenz des Donors erfolgt (Überlappung von Emissions-/Absorptionsspektrum). Für die effiziente Energieübertragung müssen folgende Bedingungen erfüllt sein: • • • • Donormolekül muss ein Fluorophor mit hoher Fluoreszenzlebensdauer sein. Überlappung von Emissionsspektrum des Donors und Absorptionsspektrum des Akzeptors. Übergangsdipolmomente von Donor und Akzeptor müssen geeignete Orientierung zueinander haben. Abstand zwischen Donor und Akzeptor muss < 10 nm liegen. Im Vergleich zur Reabsorption erfolgt der Energieübertrag, bevor eine Emission der Donorfluoreszenz möglich ist. Reabsorption kann durch eine Verringerung der Schichtdicke der Probe verhindert werden, während bei größeren Abständen die Effizienz des Förster-Transfers gleich null ist. In der Tabelle ist nichttrivialer Übergang = Förster Transfer. Die Transfereffizienz ET ist mit kT = Energieübertragungsrate zwischen Donor und Akzeptor: 𝐸𝐸𝑇𝑇 = 𝑘𝑘 𝑇𝑇 + 𝑘𝑘𝑓𝑓𝐷𝐷 𝑘𝑘 𝑇𝑇 𝐷𝐷 𝐷𝐷 + 𝑘𝑘𝑖𝑖𝑖𝑖 + 𝑘𝑘𝑖𝑖𝑖𝑖𝑖𝑖 Für eine experimentelle Untersuchung des Resonanztransfers, müssen Emissionsmaxima von Donor und Akzeptor ausreichend getrennt sein. Außerdem darf die Anregung des Donors nicht zu einer Anregung des Akzeptors führen. Bestimmung von 𝐄𝐄𝐓𝐓 über Messung der Fluoreszenz-Quantenausbeute des Donors in Anwesenheit (𝚽𝚽𝐃𝐃−𝐀𝐀) und in Abwesenheit (𝚽𝚽𝐃𝐃 ) des Akzeptors: Φ𝐷𝐷−𝐴𝐴 = Φ𝐷𝐷 𝑘𝑘𝑓𝑓𝐷𝐷 𝐷𝐷 𝐷𝐷 𝑘𝑘 𝑇𝑇 + 𝑘𝑘𝑓𝑓𝐷𝐷 + 𝑘𝑘𝑖𝑖𝑖𝑖 + 𝑘𝑘𝑖𝑖𝑖𝑖𝑖𝑖 𝑘𝑘𝑓𝑓𝐷𝐷 𝐷𝐷 𝐷𝐷 𝑘𝑘𝑓𝑓𝐷𝐷 + 𝑘𝑘𝑖𝑖𝑖𝑖 + 𝑘𝑘𝑖𝑖𝑖𝑖𝑖𝑖 = 1 − 𝐸𝐸𝑇𝑇 Alternative zur Bestimmung von 𝑬𝑬𝑻𝑻 : Messung der Lebensdauer der angeregten Donormoleküle. Dies hat den Vorteil, dass keine Verfälschung über Reabsorption erfolgt. Die Fluoreszenzlebensdauer wird nur durch den Resonanztransfer verringert (Reabsorptionsprozess hat keinen Einfluss auf Fluoreszenzlebensdauer). 1 𝐷𝐷 𝐷𝐷 + 𝑘𝑘𝑖𝑖𝑖𝑖𝑖𝑖 τ𝐷𝐷−𝐴𝐴 𝑘𝑘 𝑇𝑇 + 𝑘𝑘𝑓𝑓𝐷𝐷 + 𝑘𝑘𝑖𝑖𝑖𝑖 = = 1 − 𝐸𝐸𝑇𝑇 1 τ𝐷𝐷 𝐷𝐷 𝐷𝐷 𝑘𝑘𝑓𝑓𝐷𝐷 + 𝑘𝑘𝑖𝑖𝑖𝑖 + 𝑘𝑘𝑖𝑖𝑖𝑖𝑖𝑖 Über die Abstandsabhängigkeit der Transfereffizienz können Aussagen über die strukturelle Organisation von Chromophoren in Makromolekülen gemacht werden. 𝑅𝑅 ist Abstand zwischen Donor-Akzeptor. 𝑅𝑅0 ist der Abstand des Donor-Akzeptor-Paares, für den die Wahrscheinlichkeit des Resonanztransfers und der innermolekularen Deaktivierung des Donors (durch strahlende und strahlungslose Prozesse) gleich groß sind. Es ist eine für das jeweilige Donor-Akzeptor-Paar spezifische Konstante, mit Werten zwischen 1 und 5nm. 𝟏𝟏 𝑹𝑹 −𝟔𝟔 ∙� � 𝒌𝒌𝑻𝑻 = 𝝉𝝉𝑫𝑫 𝑹𝑹𝟎𝟎 Wechselwirkungsenergie zwischen Donor und Akzeptor entspricht der zweier Dipole (Abnahme mit der dritten Potenz). Die 𝑅𝑅 −6 -Abhängigkeit kommt wegen der Proportionalität der Energieübertragungswahrscheinlichkeit zum Quadrat der Wechselwirkungsenergie. Die Energieeffizienz ist definiert als der Anteil der absorbierten Photonen, der vom Donor auf den Akzeptor transferiert wird: Es ist der Quotient aus Anzahl der vom Donor zum Akzeptor transferierten Photonen 𝑘𝑘 𝑇𝑇 und der Anzahl der vom Donor absorbierten Photonen 𝑘𝑘 𝑇𝑇 + 1/𝜏𝜏𝐷𝐷 . Durch Einsetzen der obigen Gleichung für 𝑘𝑘 𝑇𝑇 erhält man eine Gleichung zur Bestimmung von R: 𝐸𝐸𝑇𝑇 = 𝑘𝑘 𝑇𝑇 𝑅𝑅06 = 6 𝑘𝑘 𝑇𝑇 + 1/𝜏𝜏𝐷𝐷 𝑅𝑅 + 𝑅𝑅06 Die Messung der Energie-Übertragungseffizienz ermöglicht für Abstände nahe R0 eine genaue Bestimmung des Donor-Akzeptor-Abstandes. Orientierungseinflüsse Konzentrationsdepolarisation Der Resonanztransfer kann auch zwischen zwei gleichen Molekülen erfolgen, da sich Absorptionsund Emissionsspektrum eines Moleküls immer überlappen. Dadurch ändert sich jedoch nicht das Fluoreszenzspektrum. Der Nachweis erfolgt über Messungen der Fluoreszenz-Polarisation. Bei erreichen einer kritischen Fluorophor-Konzentration resultiert eine Abnahme im Polarisationsgrad der Fluoreszenz-Strahlung (Konzentrationsdepolarisation). Die Ursache ist der Resonanztransfer zwischen den Fluorophoren: Da die Übergangsdipolmomente der am Transfer beteiligten Moleküle einen Winkel einschließen erfolgt die Emission der Fluoreszenz-Strahlung unter einer geänderten Polarisationsrichtung. Makroskopisch depolarisiert das linear polarisierte Licht mit zunehmender Anzahl an Transferprozessen. Fluoreszenz-Polarisation Analog zum Absorptions-Übergangsdipolmoment 𝜇𝜇𝐴𝐴 existiert ein Emissions-Übergangsdipolmoment 𝜇𝜇𝐸𝐸 für die Fluoreszenz. Absorptions- und Emissions-Übergangsdipolmomente haben eine definierte Orientierung im molekularen Achsensystem. 𝝁𝝁𝑬𝑬 der meisten Fluorophore schließt mit 𝝁𝝁𝑨𝑨 einen Winkel von 10-40° ein. Vereinfacht wird im Folgenden davon ausgegangen, dass sie dieselbe Richtung haben. Die Polarisation der Fluoreszenz-Strahlung einer Probe ist von der Orientierung des EmissionsÜbergangsdipolmoments abhängig. 𝝁𝝁𝑬𝑬 kann aufgrund von Molekülbewegungen (Rotation des Moleküls, Beweglichkeit von Molekülsegmenten) während der Dauer des angeregten Zustands seine Richtung ändern. Damit sind über die Messung der Polarisation der Fluoreszenz-Strahlung Aussagen über die Rotationsbeweglichkeit, die Orientierung und die Viskosität in der Umgebung der betrachteten Moleküle möglich. Licht wird entlang der x-Achse eingestrahlt. Die Polarisationsebene ist die x-z-Ebene. Die fluoreszierende Probe hat hier das Übergangsdipolmoment 𝜇𝜇 für Absorption und Emission. Die Fluoreszenz-Emission wird auf der y-Achse detektiert, wobei die Komponente parallel und die Komponente senkrecht zur einfallenden Strahlung detektiert werden. quantitatives Maß für die Polarisation: Polarisationsgrad P oder Anisotropie A • • • 𝑃𝑃 = 𝐼𝐼∥ − 𝐼𝐼⊥ 𝐼𝐼∥ + 𝐼𝐼⊥ 𝐴𝐴 = unpolarisierte Strahlung: 𝐼𝐼∥ = 𝐼𝐼⊥ ⟹ 𝑃𝑃 → 0 polarisierte Strahlung 𝐼𝐼⊥ = 0 ⟹ 𝑃𝑃 = 1 teilweise polarisiert für 𝑃𝑃 < 1 𝐼𝐼∥ − 𝐼𝐼⊥ 𝐼𝐼∥ − 𝐼𝐼⊥ = 𝐼𝐼∥ + 2𝐼𝐼⊥ 𝐼𝐼𝐺𝐺𝐺𝐺𝐺𝐺 Die Anisotropie ist physikalisch sinnvoller, da sie die Beiträge aller Polarisationsrichtungen der emittierten Strahlung berücksichtigt. 𝑰𝑰⊥ lässt sich nämlich in zwei Komponenten aufteilen: eine ist in x-Richtung, die andere in y-Richtung polarisiert. Beide Komponenten besitzen die gleiche mittlere Intensität, da die Verteilung des Moleküls unabhängig vom Winkel 𝜑𝜑 ist. Quantitative Beschreibung des Absorptionsprozesses E = E-Feldvektor des eingestrahlten Lichts, 𝜃𝜃 = ∡(𝜇𝜇𝐴𝐴 , 𝐸𝐸). Wahrscheinlichkeit der Absorption: 𝑃𝑃(𝜃𝜃, 𝜑𝜑)~(𝜇𝜇𝐴𝐴 ∙ 𝐸𝐸)2 ~ cos2 𝜃𝜃 Die Absorptionswahrscheinlichkeit ist also am größten für Moleküle, deren Übergangsdipolmoment in Richtung des elektrischen Feldstärkevektors orientiert ist. Bevorzugte Anregung für kleine Winkel 𝜃𝜃 wird als Photoselektion bezeichnet. 𝑁𝑁(𝜃𝜃, 𝜑𝜑) = Relative Anzahl an Molekülen, die eine Orientierung zwischen 𝜃𝜃 und 𝜃𝜃 + 𝑑𝑑𝑑𝑑 sowie 𝜑𝜑 und 𝜑𝜑 + 𝑑𝑑𝑑𝑑 aufweisen. Es gilt: 𝑁𝑁(𝜃𝜃, 𝜑𝜑) 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = sin 𝜃𝜃 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 Die Abbildung zeigt die Verteilung der Übergangsdipolmomente einer isotropen Molekül-Probe für verschiedene Winkel 𝜃𝜃. Die Zahl der Übergangsdipolmomente mit einem bestimmten Winkel 𝜃𝜃 zur z-Achse wird durch die Mantelfläche F eines Kegels mit dem Öffnungswinkel 2𝜃𝜃 repräsentiert. Da die Dichte der Dipolmomente auf jeder Fläche gleich groß sein muss (isotrope Verteilung), ist die jeweilige Zahl der Übergangsdipolmomente proportional zur Fläche 𝐹𝐹 = 𝜋𝜋ℎ ∙ sin 𝜃𝜃 . Das heißt, dass die Anzahl an Molekülen mit einer Orientierung senkrecht zu z viel größer ist, als die Anzahl Moleküle mit einer nahezu parallelen Orientierung. Relative Anzahl an angeregten Molekülen im Winkelbereich 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑: 𝑍𝑍(𝜃𝜃, 𝜑𝜑) 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = 𝑁𝑁(𝜃𝜃, 𝜑𝜑)𝑃𝑃(𝜃𝜃, 𝜑𝜑)𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑~ cos2 𝜃𝜃 sin 𝜃𝜃 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 Bezogen auf die Gesamtzahl der angeregten Moleküle N ergibt sich der Anteil der angeregten Moleküle im Winkelbereich zwischen 𝜽𝜽 und 𝜽𝜽 + 𝒅𝒅𝒅𝒅 sowie 𝝋𝝋 und 𝝋𝝋 + 𝒅𝒅𝒅𝒅: 2𝜋𝜋 𝑁𝑁 = � 𝜋𝜋 � 𝜑𝜑=0 𝜃𝜃 =0 𝑊𝑊(𝜃𝜃, 𝜑𝜑) = 𝑍𝑍(𝜃𝜃, 𝜑𝜑)𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 𝑍𝑍(𝜃𝜃, 𝜑𝜑)𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 2 = cos2 𝜃𝜃 sin 𝜃𝜃 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 𝑁𝑁 4𝜋𝜋 Die Einstrahlung von linear polarisiertem Licht führt zu einer anisotropen Verteilung der angeregten Moleküle, die zylindersymmetrisch zur Polarisationsrichtung der einfallenden Strahlung ist. Grund: Absorption erfolgt auch, wenn Übergangsdipolmoment nicht genau parallel zum E-Feldvektor ist, sondern eben eine Abweichung zwischen 𝜃𝜃 und 𝜃𝜃 + 𝑑𝑑𝑑𝑑 zeigt. Da das EmissionsÜbergangsdipolmoment fest mit der Molekülachse verbunden ist, muss aufgrund der anisotoropen Verteilung der angeregten Moleküle auch die Polarisation der emittierten Fluoreszenz-Strahlung anisotrop sein. Schlussfolgerung: bereits der Absorptionsprozess von linear polarisiertem Licht führt zur Depolarisation der Fluoreszenz. Emission der Fluoreszenz Die Fluoreszenz-Depolarisation basiert auf zwei weiteren Beiträgen: • • Relative Orientierung zwischen Absorptions- und Emissions-Übergangsdipolmoment kann für verschiedene Absorptions- und Fluoreszenzübergänge in einem Molekül verschieden sein. Bewegungen des Moleküls innerhalb der Lebensdauer des angeregten Zustands, die zu einer Änderung der Orientierung des Übergangsdipolmomentes führen. Betrachtung einer starren, isotropen Probe, Annahmen: (1) Bei Absorption und Emission tritt derselbe elektronische Übergang auf, sodass die beiden Übergangsdipolmomente parallel orientiert sind. (2) Räumliche Orientierung des Emissions-Übergangsdipolmoments ändert sich während der Fluoreszenz-Lebensdauer nicht. Es ist lediglich die Photoselektion berücksichtigt! Die Wahrscheinlichkeiten für eine Polarisation der emittierten Strahlung in z- bzw. x-Richtung lauten dann (e = Einheitsvektoren der jeweiligen Raumrichtungen): 𝑃𝑃𝑧𝑧 (𝜃𝜃, 𝜑𝜑)~(𝜇𝜇𝑧𝑧 ∙ 𝑒𝑒𝑧𝑧 )2 ~ cos 2 𝜃𝜃 𝑃𝑃𝑋𝑋 (𝜃𝜃, 𝜑𝜑)~(𝜇𝜇𝑥𝑥 ∙ 𝑒𝑒𝑥𝑥 )2 ~(sin 𝜃𝜃 cos 𝜑𝜑)2 Die relativen Intensitäten 𝐼𝐼∥ und 𝐼𝐼⊥ werden über Multiplikation mit dem Anteil angeregter Moleküle und anschließender Integration über die Kugeloberfläche erhalten: 2𝜋𝜋 𝐼𝐼∥ = � 2𝜋𝜋 𝐼𝐼⊥ = � 𝜑𝜑=0 𝜑𝜑=0 𝜋𝜋 𝑑𝑑𝑑𝑑 � 𝜋𝜋 𝑑𝑑𝑑𝑑 � 𝜃𝜃=0 𝜃𝜃=0 cos2 𝜃𝜃 𝑊𝑊(𝜃𝜃, 𝜑𝜑)𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = 3 5 sin2 𝜃𝜃 cos2 𝜑𝜑 𝑊𝑊(𝜃𝜃, 𝜑𝜑)𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = 1 5 Aufgrund der gemachten Annahmen entsprechen diese Werte dem Maximalwert für 𝐼𝐼∥ sowie dem Minimalwert von 𝐼𝐼⊥ . Damit ergibt sich 𝑷𝑷 = 𝟎𝟎, 𝟓𝟓 und 𝑨𝑨 = 𝟎𝟎, 𝟒𝟒 als Maximalwerte für die FluoreszenzPolarisation einer Probe unbeweglicher, isotrop im Raum verteilter Moleküle (Grenzanisotropie). Für einen beliebigen Winkel γ zwischen den Übergangsdipolmomenten, aber weiterhin unter der Annahme, dass die Orientierung der Moleküle innerhalb der Lebensdauer des angeregten Zustands unverändert bleibt, gilt für die Fluoreszenz-Polarisation rechtsstehende Beziehung. Die Fundamentalanisotropie ist eine Stoffeigenschaft. Sie beschreibt die Anisotropie eines Fluorophors ohne depolarisierende Effekte, unter Berücksichtigung der Grenzanisotropie (Photoselektion) und dem Winkel zwischen den Übergangsdipolmomenten. 3 cos2 𝛾𝛾 − 1 cos 2 𝛾𝛾 + 3 𝟑𝟑 𝐜𝐜𝐜𝐜𝐜𝐜 𝟐𝟐 𝜸𝜸 − 𝟏𝟏 𝑨𝑨 = 𝟐𝟐 𝑃𝑃0 = 𝑨𝑨𝟎𝟎 = 𝟎𝟎, 𝟒𝟒 ∙ 𝑨𝑨 𝟑𝟑 𝐜𝐜𝐜𝐜𝐜𝐜 𝟐𝟐 𝜸𝜸 − 𝟏𝟏 𝟓𝟓 Daraus (einsetzen von 0° und 90° für γ) ergibt sich ein mögliches Intervall für die Anisotropie: die limitierende Anisotropie = −0,2 ≤ 𝐴𝐴0 ≤ 0,4 (ohne depolarisierende Effekte) 1 1 1 1 𝜏𝜏𝐹𝐹 Unter Berücksichtigung von 𝜏𝜏𝐹𝐹 = − = � − � �1 + � Bewegungseinflüssen als Fluoreszenzlebensdauer 𝑃𝑃 3 𝑃𝑃0 3 𝜏𝜏𝑐𝑐 einzigen depolarisierenden des Moleküls 𝑨𝑨𝟎𝟎 = Effekt, gilt die PerrinGleichung: Statisch: Diffusionskonstante 𝐷𝐷𝑟𝑟𝑟𝑟𝑟𝑟 für kugelförmige Moleküle: 𝟏𝟏 𝑨𝑨 𝟏𝟏 𝝉𝝉 = 𝑨𝑨 �𝟏𝟏 + 𝝉𝝉𝑭𝑭 � 𝟎𝟎 𝒄𝒄 1 𝜏𝜏𝑐𝑐 = 6𝐷𝐷 𝑟𝑟𝑟𝑟𝑟𝑟 = Rotationskorrelationszeit Dynamisch: 𝑨𝑨(𝒕𝒕) = 𝑨𝑨𝟎𝟎 𝒆𝒆−𝒕𝒕/𝝉𝝉𝒄𝒄 𝑘𝑘𝑘𝑘 k = Boltzmann-Konstante 𝐷𝐷𝑟𝑟𝑟𝑟𝑟𝑟 = T = Absolute Temperatur 𝑉𝑉ℎ 𝜂𝜂 𝜂𝜂 = Viskosität der Probe 𝑉𝑉ℎ = hydratisiertes Molekülvolumen Der Perrin-Gleichung liegen folgende Annahmen zugrunde: • • • • Moleküle haben dieselben Rotationseigenschaften wie kugelförmige Teilchen mit dem Volumen 𝑉𝑉ℎ . Mikroviskosität der Umgebung eines Moleküls ist gleich der Viskosität der gesamten Probe. Rotationsbewegung ist ungehindert und erfolgt statistisch. Depolarisation erfolgt ausschließlich über Orientierungsunterschiede von Absorptions- und Emissions-Übergangsdipolmoment und durch Brownsche Molekularbewegung (FRET, Reabsorption und andere Effekte bleiben unberücksichtigt). Anhand der Perrin-Gleichung können verschiedene Fallunterscheidungen getroffen werden: (1) 𝝉𝝉𝒄𝒄 ≫ 𝝉𝝉𝑭𝑭 : keine Bewegung des Moleküls innerhalb von 𝜏𝜏𝐹𝐹 , d.h. 𝑃𝑃 = 𝑃𝑃0 bzw. 𝐴𝐴 = 𝐴𝐴0 (2) 𝝉𝝉𝒄𝒄 ≪ 𝝉𝝉𝑭𝑭 : angeregten Fluorophore nehmen innerhalb von 𝜏𝜏𝐹𝐹 eine statistische Verteilung ein, d.h. 𝐼𝐼∥ = 𝐼𝐼⊥ und 𝑃𝑃 = 𝐴𝐴 = 0. (3) 𝝉𝝉𝒄𝒄 ≈ 𝝉𝝉𝑭𝑭 : Orientierung der Moleküle ändert sich innerhalb von 𝜏𝜏𝐹𝐹 . Die Verteilung der angeregten Moleküle bleibt jedoch anisotrop, d.h. 0 < 𝑃𝑃 < 𝑃𝑃0 . Bei Kenntnis von 𝑃𝑃0 und 𝜏𝜏𝐹𝐹 lässt sich durch Messung von P die Rotationskorrelationszeit des Fluorophors aus der Perrin-Gleichung bestimmen. Dann sind auch Probenviskosität und das hydratisierte Molekülvolumen rechnerisch zugänglich, wenn einer der beiden Werte bekannt ist. Um Rückschlüsse auf die Beweglichkeit von Makromolekülen machen zu können, sind Fluorophore mit Fluoreszenz-Lebensdauern im Bereich der Rotationskorrelationszeiten erforderlich. Durch Fluoreszenz-Farbstoffe sind Rotationskorrelationszeiten von 1-100ns, mit PhosphoreszenzFarbstoffen im Bereich von ms möglich. Im Perrin-Plot erfolgt die Auftragung 1/𝐴𝐴0 gegen 𝑇𝑇/𝜂𝜂, sodass bei bekanntem Hydratationsradius sowohl Rotationskorrelationszeit als auch Fluoreszenzlebensdauer ermittelt werden können: 1 𝜏𝜏𝐹𝐹 1 1 6𝑘𝑘𝜏𝜏𝐹𝐹 𝑇𝑇 1 = �1 + � → = + 𝜏𝜏𝑐𝑐 𝐴𝐴 𝐴𝐴0 𝑉𝑉ℎ 𝐴𝐴0 𝜂𝜂 𝐴𝐴 𝐴𝐴0 𝜏𝜏 6𝑘𝑘 , 0 𝑉𝑉 ℎ Steigung ist damit 𝐴𝐴𝐹𝐹 erhalten wird. wobei 𝐴𝐴0 aus dem y-Achsenschnittpunkt Statische und zeitaufgelöste Fluoreszenz-Polarisation Die Fluoreszenz-Polarisation kann statisch oder zeitaufgelöst gemessen werden. • • Statische Messung: kontinuierliche Anregung mit konstanter Lichtquelle. Die Messung der Fluoreszenz-Intensität liefert mittlere Intensitätswerte. Daher entsprechen die Werte für A und P auch zeitlichen Mittelwerten. 𝐼𝐼∥ = 1 ∞ ∫ 𝐼𝐼 (𝑡𝑡)𝑑𝑑𝑑𝑑, 𝜏𝜏 𝐹𝐹 0 ∥ 𝐼𝐼⊥ = 1 ∞ ∫ 𝐼𝐼 (𝑡𝑡)𝑑𝑑𝑑𝑑 𝜏𝜏 𝐹𝐹 0 ⊥ Zeitaufgelöste Messung: Anregung mittels kurzem Laser-Puls. Messung des zeitlichen Verlaufs 𝐼𝐼∥ (𝑡𝑡) und 𝐼𝐼⊥ (𝑡𝑡). Beide Fluoreszenz-Intensitäten fallen exponentiell mit der Zeit ab. Direkt nach dem Laser-Puls wird die Fluoreszenz-Polarisation von der Anisotropie der Absorption (Photoselektion) bestimmt. Moleküle, die zu einem späteren Zeitpunkt fluoreszieren haben bereits eine Rotationsbewegung durchgeführt, wodurch die Fluoreszenz-Polarisation von 𝑃𝑃0 bzw. 𝐴𝐴0 auf einen Endwert abnimmt. Der Endwert ist von 𝝉𝝉𝒄𝒄 und 𝝉𝝉𝑭𝑭 abhängig. Für kugelförmige Moleküle erfolgt die zeitliche Abnahme der Polarisation exponentiell. Die Rotationskorrelationszeit entspricht der Zeit, in der der Polarisationsgrad oder die Anisotropie auf 1/e ihres Ausgangswertes abgefallen sind. Sie ist damit direkt aus dem Experiment bestimmbar (Steigung der Geraden ist −1/𝜏𝜏𝑐𝑐 , der Schnittpunkt mit der y-Achse ist ln 𝐴𝐴0 ). Anwendungsbeispiele Fluoreszenz-Sonden Man unterscheidet zwei Arten von Fluorophoren: Natürliche Fluorophore kommen in biologischen Makromolekülen vor, wie z.B. Tryptophan. Fluoreszenz-Sonden sind organischhe Moleküle, die kovalent an Makromoleküle gebunden werden können oder mit ihnen assoziieren oder interkalieren. • • • • • ANS (1-Anilino-8-Naphthalinsulfonat) assoziiert mit Proteinen oder Lipid-Membranen. Es hat in Wasser eine niedrige Quantenausbeute, emitiert aber in apolarer Umgebung intensive, blauverschobene Fluoreszenz. Dansyl-Chlorid kann kovalent an Amino-Gruppen binden und reagiert ebenso wie ANS auf Änderungen in der Sondenumgebung. Fluoreszin wird über eine Isothiocyanat-Gruppe an Thiol- oder Amino-Gruppen in Proteinen gebunden. Ethidiumbromid und Acridinorange interkalieren in dsDNA und werden als Fluoreszenzmarker für Nukleinsäuren verwendet. Diphenylhexatrien oder Anthroyl-Derivate von Fettsäuren sind Fluorophore zur Untersuchung von Membranstrukturen. Pyren-markierte Lipide bilden Excimere und können als Membran-Sonden eingesetzt werden. Bathochrome Verschiebung der Trp-Fluoreszenz von Proteinen Trp in polarer Umgebung zeigt im Vergleich zu apolarer Umgebung eine rotverschobene Fluoreszenz. Dies kann ausgenutzt werden, um die Assoziation eines Proteins mit Membranen zu untersuchten. Durch Titration des Proteins mit Lipiden ist eine stetige Blauverschiebung gegen einen Sättigungswert zu beobachten, die direkt mit der Inkorporation des Proteins in die Lipid-Membran korreliert. Änderung der Quantenausbeute bei WW mit makromolekularen Systemen ANS wird als Fluorophor zur Bestimmung von Lipid-Phasenumwandlungen verwendet, da er nur an Lipide im fluiden, nicht aber an Lipide im kristallinen Zustand bindet und im Membran-gebundenen Zustand eine wesentlich erhöhte Fluoreszenz-Quantenausbeute resultiert. ANS interkaliert dabei zwischen den polaren Kopfgruppen. Genauso können durch ANS hydrophobe Bereiche von Proteinen titriert werden. Excimere: Bestimmung des lateralen Diffusionskoeffizienten Die Bildung von angeregten Dimeren ist diffusionskontrolliert. Aus der Excimeren-Bildungsrate von Pyren-markierten Lipiden kann der Diffusionskoeffizient für laterale Diffusion in Membranen ermittelt werden. Verhältnis der Quantenausbeute für Excimere und Monomere ist dem Verhältnis der Fluoreszenz-Intensitäten proportional: 𝑘𝑘𝑓𝑓𝑓𝑓 𝜙𝜙𝐸𝐸 𝐼𝐼𝐸𝐸 = ∙ 𝑘𝑘𝑎𝑎 𝑐𝑐 ∙ 𝜏𝜏𝐸𝐸 ~ 𝜙𝜙𝑀𝑀 𝑘𝑘𝑓𝑓𝑓𝑓 𝐼𝐼𝑀𝑀 Bei Kenntnis der Fluoreszenz-Übergangsraten beider Populationen sowie der Lebensdauer der Excimeren 𝜏𝜏𝐸𝐸 , kann über eine Messung der Intensitäten 𝐼𝐼𝐸𝐸 und 𝐼𝐼𝑀𝑀 die Excimeren-Bildungsrate 𝒌𝒌𝒂𝒂 ermittelt werden. Dazu müssen Spektren bei unterschiedlichen FluorophorKonzentrationen 𝑐𝑐 gemessen werden (Abbildung: a, b, c). Es folgt eine Auftragung 𝑘𝑘 𝑓𝑓𝑓𝑓 𝑘𝑘 𝑓𝑓𝑓𝑓 𝐼𝐼𝐸𝐸 𝐼𝐼𝑀𝑀 vs. 𝑐𝑐, wobei aus der Steigung ∙ 𝑘𝑘𝑎𝑎 ∙ 𝜏𝜏𝐸𝐸 die Excimeren-Bildungsrate ermittelt werden kann. Der Wert von 𝒌𝒌𝒂𝒂 𝒄𝒄 ist abhängig von der Kollisionswahrscheinlichkeit zwischen M und M*. Er ist daher proportional zum Diffusionskoeffizienten. Für die Diffusion in der Lipid-Membran (= 2D-Gitter) wird ein Hüpfprozess angenommen, bei dem das Molekül pro Zeiteinheit immer um einen Gitterplatz in eine zufällige Richtung weiter springt. Die Assoziationsrate 𝒌𝒌𝒂𝒂 𝒄𝒄 = 𝒗𝒗𝒋𝒋 𝒏𝒏𝒔𝒔 entspricht dem Produkt aus Sprungfrequenz 𝑣𝑣𝑗𝑗 der Sondenmoleküle und der mittleren Zahl an Sprüngen 𝑛𝑛𝑠𝑠 , die ein Monomer bis zur Excimeren-Bildung ausführen muss. Der Diffusionskoeffizient berechnet sich dann mithilfe der Einstein-Gleichung zu 𝟏𝟏 𝟒𝟒 𝑫𝑫 = 𝒗𝒗𝒋𝒋 𝝀𝝀𝟐𝟐 mit der mittleren Sprunglänge 𝜆𝜆. D ermöglicht eine Aussage über die Fluidität der Membran. • • Für die flüssigkristalline L-α-Phase wurde D zu 𝟏𝟏𝟏𝟏−𝟖𝟖 − 𝟏𝟏𝟏𝟏−𝟕𝟕 𝒄𝒄𝒎𝒎𝟐𝟐 /𝒔𝒔 bestimmt. Sie ist langsamer als die Diffusion von Pyren in Wasser mit 10−6 − 10−5 𝑐𝑐𝑚𝑚2 /𝑠𝑠, da sie auf der Diffusion von zwei langen, kovalent über die Kopfgruppe verknüpften CH-Ketten basiert. In der P-β-Phase oberhalb der Phasenumwandlungstemperatur wurde D zu 𝟏𝟏𝟏𝟏−𝟏𝟏𝟏𝟏 − 𝟏𝟏𝟏𝟏−𝟏𝟏𝟏𝟏 𝒄𝒄𝒎𝒎𝟐𝟐 /𝒔𝒔 bestimmt. Diese Werte können nicht mit der Excimeren-Methode bestimmt werden, da die Diffusion zu langsam ist: Die Excimeren-Bildung findet also sehr unwahrscheinlich innerhalb der Fluoreszenz-Lebensdauer der Pyren-Sonden (~100ns) statt. Excimere: Phasentrennungsphänomene in Lipid-Membranen Das Intensitätsverhältnis ist von der Konzentration der Excimeren-bildenden Sonde abhängig ( 𝑘𝑘 𝑓𝑓𝑓𝑓 𝑘𝑘 𝑓𝑓𝑓𝑓 ∙ 𝑘𝑘𝑎𝑎 ∙ 𝑐𝑐 ∙ 𝜏𝜏𝐸𝐸 ~ • • 𝐼𝐼𝐸𝐸 ). 𝐼𝐼𝑀𝑀 Im Falle eines diffusionskontrollierten Prozesses steigt bei statistischer Sondenverteilung 𝐼𝐼𝐸𝐸 /𝐼𝐼𝑀𝑀 linear mit der Konzentration an (siehe Plot oben) Wenn die Sonde bevorzugt in bestimmte Membran-Bereiche einbaut, kommt es zu einer höheren lokalen Konzentration und damit zu einem höheren 𝐼𝐼𝐸𝐸 /𝐼𝐼𝑀𝑀 Wert. Eine Lipid-Mischung aus geladener Phosphatidsäure (PA) und ungeladenem Phosphatidylcholin (PC) trennt sich bei Temperaturen unterhalb des Phasenübergangs (fluide Phase) durch Zugabe von Calcium-Ionen auf. Calcium komplexiert PA, wodurch es in den kristallinen Zustand übergeht und die beiden Lipide nicht mehr mischbar sind. Innerhalb des kristallinen PA/Ca2+ bilden sich fluide PC-Domänen. Mit steigender Calcium-Konzentration beobachtet man dann eine steigende Excimeren-Bildung (steigendes 𝐼𝐼𝐸𝐸 /𝐼𝐼𝑀𝑀 ), da sich die Pyren-Dekansäure bevorzugt in der fluiden Phase aufhält. Die Sonde wird Ca2+-abhängig aus der kristallinen Phase in die fluide gedrängt. Je größer der PA-Anteil, also die potentiell kristallisierende Phase, desto stärker ist die Ca-induzierte Konzentrationserhöhung von Pyren-Dekansäure in der fluiden Phase. Damit verbunden ist ein größeres IE/IM Verhältnis. Excimere: Protein-Assoziation Mithilfe der Excimeren-Bildung konnte nachgewiesen werden, dass die Ca2+-abhängige ATPase im Membran-gebundenen Zustand als Oligomer vorkommt. Es erfolgt die kovalente Markierung des Proteins mit einem Fluorophor und die Beobachtung der Excimeren-Bildung mit steigender Sondenkonzentration (größerer Anteil Proteine, die mit einer Sonde markiert sind). Excimeren-Bildung entspricht direkt der Protein-Assoziation. Excimer-Laser S.74/155 Lokalisation von Fluorophoren in Membranen durch Fluoreszenz-Löschung Die Effizienz der Fluoreszenz-Löschung durch Radikal-Sonden ermöglicht Rückschlüsse auf die Lage von Fluoreszenz-Sonden in Membranen. Besonders geeignet sind Fettsäuren oder Lipide mit Nitroxid-Gruppen, die sich an jeweils verschiedenen Positionen der CH-Ketten befinden. Aus der bekannten Lage der Nitroxid-Gruppen in der Membran lässt sich die Position der Chromophoren Gruppe der Fluoreszenz-Sonde angeben: Sie befindet sich in der Position, für die die Nitroxid-Gruppe die effizienteste Fluoreszenz-Löschung zeigt. Stern-Volmer-Auftragung zeigt, dass für Pyren-Buttersäure die effizienteste FluoreszenzLöschung mit C5-Radikalsonde, für Pyren-Dekansäure mit C12-Radikalsonde vorliegt. So konnte auch die Lage des Porphyrin-Rings in Chlorophyll-Molekülen nahe der Lipid-Kopfgruppen bestimmt werden (C5-Radiklsonde am effizientesten). Abstandsmessung durch Energieübertragung ANS bindet an Serumalbumin und erhöht seine Fluoreszenz-Quantenausbeute. Zusätzlich kann die Bindung durch Messung des Energietransfers beobachtet werden. Serumalbumin besitzt Tryptophane, die mit ANS Donor-Akzeptor-Paare bilden. Bei Anregung der Trp-Fluoreszenz beobachtet man mit steigendem ANS/Protein Verhältnis eine Abnahme der Protein-Fluoreszenz (Bande II) und eine Zunahme der Ligand-Fluoreszenz (Bande I). Die maximale Energieübertragung liegt bei voll besetzten Ligandbindestellen vor, deren Anzahl aus dem Ligand/Protein-Verhältnis bestimmt werden kann. Wegen der Abstands-Abhängigkeit, lässt sich die Entfernung der Fluorophore bestimmen. Dazu muss R0 bekannt sein und im Bereich des zu messenden Abstandes liegen. Die Abstandsmessung zwischen Donor α-Naphthyl und Akzeptor Dansyl an den Enden unterschiedlich langer L-Prolyl-Peptide ergibt eine mit zunehmendem Abstand geringer werdende Energieübertragungseffizienz. Fluoreszenz-Depolarisation: Messung der Phasenumwandlung von Lipid-Membranen Die Membran-Phasen unterscheiden sich durch Anordnung und Beweglichkeit der Lipid-Moleküle. Daher kann die Phasenumwandlungstemperatur über Fluoreszenz-Depolarisation bestimmt werden. In kristalliner Membranphase liegen CH-Ketten dicht gepackt in all-trans Konformation. Dadurch sind die Sondenmoleküle im hydrophoben Membranbereich in ihrer Bewegung stark eingeschränkt (hoher Polarisationsgrad, 𝑃𝑃 ≈ 0,4). Nach der Phasenumwandlung nimmt die Beweglichkeit der CH-Ketten durch Bildung von gauche-Isomeren stark zu. Dies überträgt sich auf die Sondenmoleküle (Depolarisation). Bestimmung der Rotationskorrelationszeiten von Proteinen durch zeitabhängige FluoreszenzDepolarisation Die logarithmische Auftragung des zeitlichen Verlaufs der Fluoreszenz-Anisotropie ist eine Gerade. Die Steigung ist umgekehrt proportional zur Rotationskorrelationszeit. Bei Untersuchung eines Trp-Restes eines globulären Proteins lässt sich die Beweglichkeit des Trp-Restes schlussfolgern. Ist die Rotationskorrelationszeit viel größer, als man für eine Kugel (Protein) erwarten würde, so hat Trp eine hohe Eigen-Beweglichkeit, umgekehrt ist Trp sehr starr am Protein-Gerüst gebunden. Bestimmung von Diffusionskoeffizienten in Membranen über FRAP FRAP (Fluorescence Recovery after Photobleaching) ermöglicht die Messung von Transportprozessen in und durch Membranen. Dazu muss die Lipid-Membran markiert werden (häufig mit der LipidSonde NBD-PE). Ein Laser bestrahlt ein Messfeld von einigen µm Durchmesser, wodurch die Chromophore irreversibel zerstört werden, die Lipide aber unbeschädigt bleiben. Die zerstörte Fluoreszenz im Messfeld nimmt mit der Zeit durch Diffusion von Chromophoren aus der Umgebung zu. Aus der Anstiegszeit lässt sich der Diffusionskoeffizient ermitteln, sodass Koeffizienten von 10−6 − 10−12 𝑐𝑐𝑚𝑚2 /𝑠𝑠 bestimmt werden können (vergleiche Excimer-Methode). Der Diffusionskoeffizient berechnet berechnet sich direkt aus den experimentellen Parametern (𝑎𝑎 ist der Radius des gebleichten Flecks und 𝜏𝜏1/2 ist die Zeit, in der die Hälfte der Ursprungsintensität wieder hergestellt wurde): 𝐷𝐷 = 𝑎𝑎2 4𝜏𝜏1/2 Der Endwert für die Fluoreszenz ist um den Betrag der gebleichten Moleküle niedriger als der zuvor bestimmte Wert. Füllt man eine Zelle mit Farbstoff und bleicht das Innere aus, so kann der Transport von Farbstoff aus dem Außenmedium in das Innere beobachtet werden. Eine Variante des FRAP ist FLIP (Fluorescence loss in photobleaching). Hier wird eine Region kontinuierlich geblichen, sodass das Verhalten des gesamten Fluoreszierenden Pools außerhalb der Bleichungsregion beobachtet werden kann. FLIP liefert Informationen über die Verbindung von zellulären Strukturen. Elektronenspinresonanz (ESR) Spektroskopie ESR ist eine Absorptions-Spektroskopie-Art, wobei Mikrowellen-Strahlung durch paramagnetische Substanzen absorbiert wird und Übergänge zwischen verschiedenen Energieniveaus der Elektronenspins induziert. Die ESR-Spektroskopie kann nur auf Moleküle mit ungepaarten Elektronen angewandt werden: • • • Übergangsmetalle z.B. in Proteinen und Enzymen. Freie Radikale z.B. als Zwischenstufe bei lichtinduzierten Reaktionen der Photosynthese. Spinsonden (stabile organische Radikale, die meist kovalent an Biomoleküle gebunden sind), Spin-Label-Technik. Der Schwerpunkt der Anwendung liegt auf der Untersuchung der Struktur und Dynamik von LipidMembranen. Physikalische Grundlagen Elektronen besitzen eine Gesamtdrehimpulsquantenzahl 𝑱𝑱, die sich additiv aus Bahndrehimpulsquantenzahl 𝑳𝑳 (Kreisbewegung um den Kern) und Eigendrehimpulsquantenzahl 𝑺𝑺 (Spin, Eigenrotation) zusammensetzt. 𝐽𝐽 ist ein dimensionsloser Vektor, der in Einheiten von ℏ angegeben wird. Der Betrag der Vektoren entspricht dem jeweiligen Drehimpuls P. Gesamtdrehimpulsquantenzahl Beträge der Quantenzahlen ergeben Drehimpulse ℏ=ℎ/2𝜋𝜋 ℎ = 6,626 ∙ 10−34 𝐽𝐽𝐽𝐽 𝐽𝐽 = 𝐿𝐿 + 𝑆𝑆 |𝑆𝑆| = ℏ�𝑆𝑆(𝑆𝑆 + 1) = 𝑃𝑃𝑆𝑆 |𝐿𝐿| = ℏ�𝐿𝐿(𝐿𝐿 + 1) = 𝑃𝑃𝐿𝐿 |𝐽𝐽| = ℏ�𝐽𝐽(𝐽𝐽 + 1) = 𝑃𝑃𝐽𝐽 L ist die Nebenquantenzahl, kann Werte von 0,1,2,3… annehmen, welche den s,p,d,f Orbitalen entsprechen. Das magnetische Moment Eine bewegte Ladung erzeugt nach der klassischen Elektrodynamik ein Magnetfeld: Aus dem Kreisstrom wird ein magnetisches Moment 𝝁𝝁 erzeugt, das senkrecht auf der durch den Kreisstrom aufgespannten Ebene steht. Das gesamte magnetische Moment setzt sich wieder additiv aus den magnetischen Momenten für Bahnumlauf und Eigenrotation zusammen. Magnetische Momente setzen sich wie die Quantenzahlen additiv zusammen 𝜇𝜇𝐽𝐽 = 𝜇𝜇𝐿𝐿 + 𝜇𝜇𝑆𝑆 Betrag des magnetischen Moments: (dasselbe gilt auch für die Vektoren) 𝛾𝛾 = gyromagnetisches Verhältnis (Proportionalitätsfaktor zwischen Drehimpuls und magnetischem Moment eines Teilchens) 𝜇𝜇𝐵𝐵 = Bohrsches Magneton 𝑔𝑔 = 2,0023 Proportionalitätsfaktor für freies Elektron (Landé-Faktor); für Bahndrehimpulse beträgt �𝜇𝜇𝐽𝐽 � = 𝛾𝛾 ∙ |𝐽𝐽| = 𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ |𝐽𝐽| der g-Faktor immer 1 (Aussage ist also, um wieviel der Spin größeren Einfluss auf die Energie hat, als der Bahndrehimpuls) Allgemein: Magneton Für Elektron: z=1 => Bohrsches Magneton 𝑞𝑞∙ℏ 𝜇𝜇 = 2𝑚𝑚 𝑒𝑒∙ℏ 𝜇𝜇𝐵𝐵 = 2𝑚𝑚 = 0,92 ∙ 10−23 𝐽𝐽/𝑇𝑇 𝑒𝑒 𝑒𝑒 = 1,672 ∙ 10−27 𝑘𝑘𝑘𝑘 = Elementarladung 𝑧𝑧 = 1 (Ladungszahl) 𝑚𝑚𝑒𝑒 = Masse des Elektrions Landé-Faktor für ein Atom (Näherung, da ohne quantenelektrodynamische Korrektur) Für freie = „bahnlose“ Elektronen gilt: 𝑔𝑔 = 1 + �𝜇𝜇𝐽𝐽 � = |𝜇𝜇𝑆𝑆 | = −𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ |𝑆𝑆| mit 𝑔𝑔 = 2 (klassisch) 𝑔𝑔 = 2,00232 (quantenmech.) 𝑐𝑐 = Lichtgeschwindigkeit 𝐽𝐽 (𝐽𝐽 +1)+𝑆𝑆(𝑆𝑆+1)−𝐿𝐿(𝐿𝐿+1) 2𝐽𝐽 (𝐽𝐽 +1) achte auf negatives Vorzeichen, da magnetisches Moment und Spin entgegengesetzt orientiert sind. Für viele Anwendungen reduzieren sich die Beziehungen auf den Eigendrehimpuls S, da der Bahndrehimpuls L organischer Radikale vernachlässigbar ist (Betrachtung „bahnloser“ Elektronen). L muss aber bei Übergangsmetallionen mitberücksichtigt werden. Der Zeeman-Effekt im B0-Feld Ein Radikal mit einem freien Elektron wird in ein zeitlich konstantes, homogenes Magnetfeld mit der magnetischen Induktionsflussdichte 𝐵𝐵0∗ gebracht. Der Spin-Vektor (magnetischer Dipol) stellt sich in eine Richtung parallel oder antiparallel zur Magnetfeld-Richtung ein. Der Winkel wird durch Gesetze der Quantenmechanik bestimmt. Für die Projektion des Spin-Drehimpulses 𝑃𝑃𝑆𝑆 auf die 𝐵𝐵0 -Achse (z-Achse) gilt 𝑷𝑷𝒛𝒛 = 𝒎𝒎𝒔𝒔 ℏ . 𝑚𝑚𝑠𝑠 ist die magnetische Quantenzahl, die sich aus der Spin-Quantenzahl ableiten lässt: 𝑚𝑚𝑠𝑠 = 𝑆𝑆, 𝑆𝑆 − 1, 𝑆𝑆 − 2, … , −𝑆𝑆 (genauso gilt für die magnetische Quantenzahl des Drehimpulses 𝑚𝑚𝑙𝑙 = 𝐿𝐿, 𝐿𝐿 − 1, 𝐿𝐿 − 2, … , −𝐿𝐿). Es sind damit nur die Werte ±1/2, ±3/2, ±5/2 … erlaubt. • • • S=0,5 ergibt damit 𝑚𝑚𝑠𝑠 = ±0,5 S=1,5 ergibt 𝑚𝑚𝑠𝑠 = ±0,5, ±1,5 Es ergeben sich demnach 𝟐𝟐𝟐𝟐 + 𝟏𝟏 Einstellungsmöglichkeiten im angelegten Magnetfeld. Für die z-Komponente (parallel zu B0) des magnetischen Momentes gilt dann 𝝁𝝁𝒛𝒛 = 𝜸𝜸 ∙ 𝑷𝑷𝒛𝒛 = 𝜸𝜸 ∙ 𝒎𝒎𝒔𝒔 ℏ. Für S=0,5 entspricht die Komponente des magnetischen Moments in Richtung B0 sehr genau dem Bohrschen Magneton: 𝜇𝜇𝑧𝑧 = −𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ 𝑚𝑚𝑠𝑠 = ±1,0012𝜇𝜇𝐵𝐵 . Energie eines magnetischen Dipols in B0 𝐸𝐸 = 𝜇𝜇𝑧𝑧 ∙ 𝐵𝐵0 = 𝜸𝜸𝑷𝑷𝒛𝒛 𝑩𝑩𝟎𝟎 = 𝜸𝜸𝒎𝒎𝒔𝒔 ℏ𝑩𝑩𝟎𝟎 Für 𝑆𝑆 = ±0,5 → 𝑚𝑚𝑠𝑠 = ±0,5 ergeben sich 2 Energieterme Energiedifferenz der 2 Elektronen-Zustände eines ungepaarten Elektrons im Magnetfeld 1 𝐸𝐸+1/2 = + ∙ 𝜸𝜸ℏ𝑩𝑩𝟎𝟎 2 ∆𝑬𝑬 = 𝜸𝜸ℏ𝑩𝑩𝟎𝟎 𝛿𝛿 = Winkel zwischen Magnetfeldrichtung und Richtung des magnetischen Moments cos 𝛿𝛿 = 𝑚𝑚𝑠𝑠 /|𝑆𝑆| 1 𝐸𝐸−1/2 = − ∙ 𝜸𝜸ℏ𝑩𝑩𝟎𝟎 2 ! abhängig von B0 ! Aufspaltung im äußeren Magnetfeld => Zeeman-Effekt Durch Energiezufuhr von 𝒉𝒉𝒉𝒉 = ∆𝑬𝑬 = 𝜸𝜸ℏ𝑩𝑩𝟎𝟎 in Form von elektromagnetischer Strahlung, kann ein Absorptionsprozess stattfinden, der einen Übergang von E- nach E+ bewirkt. Die Elektronen-Spins klappen dabei um. Bei der ESR-Spektroskopie werden dazu Flussdichten um 0,1-1 Tesla durch Mikrowellen mit Wellenlängen im cm-Bereich (10Ghz) verwendet. Bei einer festen Mikrowellen-Frequenz kann über die Variation des Magnetfeldes die Resonanzstelle bestimmt werden, bei der die Absorption der Mikrowellen-Strahlung auftritt. Im Gegensatz zur Licht-Absorption ist dies ein magnetisches Phänomen: Der Übergang wird durch die magnetische Komponente, nicht durch die elektrische des elektromagnetischen Feldes induziert. Larmor-Präzession im B0-Feld Aus dem Elektronenspin resultiert ein magnetisches Moment, das im Magnetfeld eine Orientierung erfährt. Im Magnetfeld B0 herrscht demnach eine Kraft (Drehmoment 𝚪𝚪 = 𝝁𝝁 × 𝑩𝑩𝟎𝟎 ), die den Elementarmagneten ausrichtet. Nach dem Drehimpulssatz der Mechanik verursacht das Drehmoment eine Richtungsänderung des Spins senkrecht zum magnetischen Moment und senkrecht zum angreifenden Drehmoment. Der Elektronen-Spin-Vektor führt demnach eine Kreisbewegung um die Feldachse aus, was zu einer Drehimpuls-Änderung führt. Das magnetische Moment präzidiert um B0 und hat sich nach einer bestimmten Zeit um den Winkel 𝜑𝜑 in eine neue Lage gedreht. Die Zahl der Umläufe pro Sekunde ist die Larmor-Frequenz: ℎ𝑣𝑣𝐿𝐿 = 𝐸𝐸 = 𝛾𝛾ℏ ∙ 𝐵𝐵0 ⟷ 𝑣𝑣𝐿𝐿 = 𝛾𝛾 ∙ 𝐵𝐵0 ↔ 𝝎𝝎𝟎𝟎 = 𝜸𝜸 ∙ 𝑩𝑩𝟎𝟎 2𝜋𝜋 Diese Frequenz ist kernspezifisch und nimmt linear mit der Magnetfeldstärke zu. Radiowellen dieser Frequenz bewirken die Resonanz des Spinsystems. Durch die kontinuierliche Absorption dieser Frequenzen resultiert das Frequenzspektrum. Bei der NMR werden Pulse mit solchen Frequenzen eingestrahlt, um den Winkel α der Präzession so zu verändern, dass der Vektor in der Nähe der xy-Ebene liegt, wo er messbar ist. Auf der z-Achse ist der Kerndrehimpuls nicht zu messen, da das magnetische Moment sehr gering ist und vom viel größeren externen Magnetfeld überlagert wird. Resonanzphänomen Der Resonanzfall tritt ein, wenn die durch das Magnetfeld B0 festgelegte Larmor-Frequenz mit der Frequenz der eingestrahlten Mikrowelle übereinstimmt. Die eingestrahlte Mikrowelle hat wie jede elektromagnetische Welle eine elektrische und eine magnetische Komponente. Die magnetische Komponente kann als zweites magnetisches Feld B1 betrachtet werden, das senkrecht zu B0 mit der Frequenz 𝑣𝑣𝐿𝐿 rotiert. Im rotierenden Bezugssystem sind B1 und 𝜇𝜇𝑆𝑆 zeitlich konstant. Unter Wirkung von B1 beginnt nun das magnetische Moment um die B1-Achse zu rotieren. Da 𝑩𝑩𝟏𝟏 ≪ 𝑩𝑩𝟎𝟎 , präzediert der Spin um B1 viel langsamer als um B0. Durch Überlagerung der Präzessionen um B0 und B1 resultiert eine Spiralbahn, auf der sich die Spins zwischen den Positionen 𝒎𝒎𝒔𝒔 = ±𝟏𝟏/𝟐𝟐 auf und ab bewegen. Die Resonanzbedingung: B1 muss mit der gleichen Frequenz und mit gleichem Umlaufsinn um die B0Achse rotieren wie die Spins selbst. Dies wird durch eine in die x-Richtung orientierte, linear polarisierte elektromagnetische Welle erreicht. Eine linear polarisierte Welle entspricht der Addition zweier zirkular polarisierter Wellen mit entgegengesetztem Umlaufsinn. Die Komponente, die in der xy-Ebene im Gleichsinn zum magnetischen Moment um B1 rotiert, bewirkt den Resonanzübergang. Boltzmann-Verteilung Energetisch gesehen bedeutet eine Ausrichtung des Atomkerns eine Aufspaltung in Energieniveaus (Zeeman Effekt). Es gibt für einen Spin S, der zuvor zufällig im Raum ausgerichtet war, exakt 2S+1 verschiedene Energieniveaus in einem äußeren Magnetfeld B0. Für Elektronen gilt immer S=+1/2 oder S=-1/2, wodurch 2 mögliche Energieniveaus möglich sind (wie auch für Kernspins der Wasserstoffatome mit I=1/2). Der Abstand der Energieniveaus nimmt linear mit der Magnetfeldstärke zu. Für Elektronen gibt es den energetisch niedrigeren Zustand α bzw. -1/2, der parallel zum Magnetfeld ausgerichtet ist und den energiereicheren, antiparallelen Zustand β bzw. + 1 2 . Es herrscht ein thermisches Equilibrium der Absolutmagnetisierung, wenn alle Spins im α oder β Zustand vorliegen, diese Zustände aber untereinander wechseln können. Die magnetischen Dipol-Übergänge zwischen den durch die 𝑚𝑚𝑠𝑠 -Quantenzahl definierten Energietermen können in beiden Richtungen stattfinden (Absorption und Emission sind gleichberechtigt). Die Zahl der Absorptionsprozesse 𝑁𝑁𝐴𝐴 und Emissionsprozesse 𝑁𝑁𝐸𝐸 ist von der Besetzungszahl der Zeeman-Niveaus abhängig. Boltzmann-Verteilung zwischen 𝐸𝐸+ und 𝐸𝐸− liefert Besetzungszahl-Verhältnis 𝑛𝑛+ /𝑛𝑛_ (+ ist oberes, - ist unteres Energieniveau). ∆𝑬𝑬 𝒏𝒏+ = 𝒏𝒏− ∙ 𝒆𝒆−𝒌𝒌∙𝑻𝑻 Im thermischen GG gilt 𝑛𝑛− > 𝑛𝑛+: Absorption ist proportional zur Besetzungsdifferenz. Bei RT und magnetischen Feldern bis 1T gilt ∆𝐸𝐸 1 𝑛𝑛− ~ → = 1,000007 𝑘𝑘 ∙ 𝑇𝑇 200 𝑛𝑛+ Netto wird also eine Absorption der eingestrahlten Energie erhalten, da das untere Energieniveau mehr besetzt ist. Hohe Magnetfeldstärken und niedrige Temperaturen begünstigen die Intensität des ESR-Signals. Relaxationsmechanismen Spin-Gitter-Relaxation: Durch thermischen Kontakt zwischen Spinsystem und seiner Umgebung wird die durch den Absorptionsprozess gestörte Boltzmann-Verteilung wiederhergestellt. Die frei werdende Energie wird von der Umgebung (Gitter) aufgenommen. Die Spin-Gitter-Relaxationszeit T1 beschreibt die benötigte Zeit, um die Boltzmann-Verteilung bis auf 1/e wiederherzustellen (innerhalb von T1 relaxieren ca. 63% der Spins, e=2,718). In Festkörpern ist T1 kürzer als in Flüssigkeiten, Ursache ist bessere Kopplung zwischen Spinsystem und Umgebung. Bei zu langen Relaxationszeiten oder zu hoher Anregungsleistung tritt ein Sättigungsverhalten ein. Dadurch werden die ESR-Linien breiter und verlieren an Intensität. Sättigungsexperimente ergeben jedoch Aussagen über die Umgebung und sind in der NMR-Spektroskopie wichtig. Spin-Spin-Relaxation: Über magnetische Dipol-Dipol-WW können paramagnetische Nachbarmoleküle ihren Spinzustand austauschen (Spin-Spin-Kopplung). Der Spinaustausch beeinflusst die Lebensdauer 𝜏𝜏 eines Spinzustandes, aber nicht das Besetzungsverhältnis. Nach Heißenberg ist ∆𝑬𝑬 ∙ 𝝉𝝉 = 𝒉𝒉 , weshalb eine kurze Lebensdauer eine große Energieunschärfe bewirkt (Die Spins verlieren mit der Zeit an Kohärenz). Die Breite der Resonanzlinie nimmt damit zu. In Lösungen ist die Linienbreite proportional zu 𝟏𝟏/𝑻𝑻𝟐𝟐 , da die Kopplung an die Umgebung gering ist und die Linienbreite kaum beeinflusst. g-Faktor Zwischen den magnetischen Momenten des Eigendrehimpulses und des Bahndrehimpulses treten Wechselwirkungen auf (Spin-Bahn-Kopplung). Damit kann 𝜇𝜇𝐿𝐿 zu einer Verstärkung oder Abschwächung des äußeren Magnetfeldes B0 und somit zur Vergrößerung oder Verringerung der Energiedifferenz ∆𝑬𝑬 führen. Die Absorptionslinien sind dann durch größere oder kleinere g-Werte bestimmt, die vom g-Wert des freien Elektrons ohne Spin-Bahn-Kopplung (g=2,00232) abweichen. Für Übergangsmetall-Ionen gilt 1 < 𝑔𝑔 < 4. Ein ESR-Spektrum kann durch mehrere Absorptionslinien mit verschiedenen g-Werten charakterisiert sein. Hyperfeinstruktur (Hfs) Jede ESR-Linie wird einem bestimmten g-Wert zugeordnet und kann nochmals eine Aufspaltung erfahren (Hyperfeinaufspaltung). Diese resultiert aus der Wechselwirkung der Elektronen mit den magnetischen Momenten der Atomkerne. Die Kerne erzeugen ein lokales Feld 𝐵𝐵𝑙𝑙𝑙𝑙𝑙𝑙 , das sich mit dem externen B0-Feld zu einem effektiven Feld 𝑩𝑩𝒆𝒆𝒆𝒆𝒆𝒆 = 𝑩𝑩𝟎𝟎 + 𝑩𝑩𝒍𝒍𝒍𝒍𝒍𝒍 addiert. Ein Kern kann mit seinem Kernspin 𝐼𝐼 genau 2𝐼𝐼 + 1 Einstellungen im externen Magnetfeld annehmen. Diese definieren die Kernspin-Quantenzahl 𝑚𝑚𝐼𝐼 . Das lokale Feld kann somit auch 𝟐𝟐𝟐𝟐 + 𝟏𝟏 Werte annehmen und spaltet eine ESR-Linie damit in 𝟐𝟐𝟐𝟐 + 𝟏𝟏 Linien auf. Die jeweilige Resonanz wird bei einem Resonanz-Feld beobachtet: 0 − 𝑎𝑎𝑚𝑚𝐼𝐼 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 = 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 0 ist Resonanzstelle ohne Elektron-Kern-WW. Die Hyperfeinkopplungskonstante 𝒂𝒂 gibt den 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 Abstand der Hyperfeinlinien wieder. Allgemein ergibt eine paramagnetische Substanz mit dem Elektronenspin S und dem Kernspin I ein ESR-Spektrum mit 𝟐𝟐𝟐𝟐(𝟐𝟐𝟐𝟐 + 𝟏𝟏) Linien, da die Auswahlregeln ∆𝒎𝒎𝒔𝒔 = 𝟏𝟏 und ∆𝒎𝒎𝑰𝑰 = 𝟎𝟎 gelten. Messtechnik Der Messraum des ESR-Spektrometers befindet sich in einem homogenen Magnetfeld, das durch einen Elektromagneten erzeugt wird. Die Strahlungsquelle (Klystron) erzeugt eine Mikrowelle im ~10 Ghz Bereich (Wellenlänge: ~3 cm). Ein Klystron ist eine Elektronenröhre zur Hochfrequenz-Verstärkung. Die Frequenz der Mikrowelle bleibt im ESR-Experiment konstant. Die Mikrowelle wird über einen Hohlleiter (hohles, innen vergoldetes Vierkant-Rohr mit einer Kantenlänge, die der Wellenlänge entspricht) zum Probenraum gebracht. Der Probenraum ist ein HohlraumResonator (Cavity), in dem sich durch geeignete Ankopplung eine stehende Welle ausbildet. Die Welle ist linear polarisiert (zwei entgegengesetzt umlaufende zirkularpolarisierte Wellen). Der HohlraumResonator sorgt dafür, dass das zur ESRMessung notwendige magnetische Wechselfeld B1 der Mikrowelle am Probenort „fokussiert“ wird. Das homogene äußere Magnetfeld B0 steht senkrecht zu B1 in z-Richtung. Es wird durch seitlich am Hohlraum-Modulator angebrachte Zusatzspulen mit 100 kHz moduliert (Warum siehe unten). Bei einer festen Mikrowellenfrequenz, die durch die Dimension des Klystrons vorgegeben wird, wird B0 im ESR-Experiment variiert. Wenn die Resonanzbedingung erfüllt ist, absorbiert das System Energie aus der Mikrowellenstrahlung (konstantes B1-Wechselfeld). Die Verringerung der Mikrowellen-Amplitude als Funktion von B0 ergibt das ESR-Spektrum. Gemessen wird jedoch oft nicht Transmission sondern Reflektion, d.h. der Teil der Mikrowellenstrahlung, der letztlich aus dem Hohlraumresonator wieder zurück ins magische T gelangt. Mikrowellen-Sender, Probe und Detektionssystem sind über eine Brückenschaltung, häufig dem „magischen T“, verbunden. Der Klystron befindet sich in Arm 1 und emittiert Mikrowellen in die Arme 2 und 3. Die Mikrowellenenergie in Arm 2 wird nahezu vollständig gedämpft. Die in Arm 3 gelangt in den HohlraumResonator. Der Resonator ist mit einer variablen Lochblende (Iris) gekoppelt, sodass alle ankommende Energie gedämpft wird und keine Reflexion auftritt. Bei Erfüllung der Resonanzbedingung und der damit verbundenen Absorption wird die Anpassung gestört, sodass ein Teil der Mikrowelle in Arm 3 reflektiert wird. Über das magische T fällt der reflektierte Anteil auf einen Kristall-Detektor (Gleichrichter) in Arm 4. Die gemessene Gleichspannung liefert das ESR-Signal und wird auf der Ordinate des ESR-Spektrums aufgetragen. Die Abszisse ist das B0-Feld. Für ein besseres Signal/Rauschen-Verhältnis wird das erhaltene Absorptionssignal moduliert, indem das Magnetfeld mit 100kHz moduliert wird. Dadurch wird aus dem Gleichspannungssignal ein Wechselspannungssignal, das rauschärmer zu verstärken ist. Die Modulationsspulen erzeugen am Ort der Probe ein homogenes magnetisches Wechselfeld, das parallel zum B0-Feld liegt. Die Amplitude des Wechselfelds ist wählbar, darf aber nicht die Halbwertsbreite des Absorptionssignals überschreiten. Die resultierende Wechselstromantwort (ia und ib) verstärkt sich proportional zur Steigung der Signalkurve. Die Amplitudenmaxima des resultierenden Detektorstroms als Funtkion von B0 bilden demnach die Steigung der eigentlichen Absorptionskurve. Die Amplitude der Wechselspannung, gemessen an der Diode, entspricht dann der ersten Ableitung des resultierenden Signals. Zusammenfassung: Es existieren damit drei verschiedene magnetische Felder! (1) Ein B0-Feld in z-Richtung. Dieses Feld setzt sich aus einem konstanten Feld und einem Sweep-Feld zusammen. (2) Ein hochfrequentes (10 GhZ) Wechselfeld B1 in y-Richtung. Dieses Feld resultiert am Probenort aus zwei entgegengesetzt zirkular polarisierten Mikrowellen, die sich zu einer linear polarisierten Welle addieren. (3) Ein zusätzliches 100 kHz-Feld Bm in z-Richtung. Dieses Feld wird durch am Resonator befindliche Helmholtz-Spulen erzeugt und dient der Erhöhung der Spektrometerempfindlichkeit durch Modulation der Feldstärke. Aufgrund der Feldmodulation wird generell die erste Ableitung der Linienform bezüglich der Feldstärke df (B0) dB0 aufgezeichnet. Untersuchung von Biomolekülen Voraussetzung der ESR-Spektroskopie sind ungepaarte Elektronen. In biologischen Systemen ist dies oft gegeben: • • • Proteine enthalten paramagnetische Metall-Zentren. Übergangsmetall-Ionen wie Cu2+, Fe3+ oder Mn2+ können leicht detektiert werden. Redox-Reaktionen, bei denen ein Elektron übertragen wird, gehen mit der Bildung von kurzlebigen, radikalischen Intermediaten einher. Elektronen-Übertragungen bei Photosynthese und Atmungskette müssen daher bei niedrigen Temperaturen (77K, N2Siedetemperatur) untersucht werden. Stark delokalisierte Radikale wie Chinone oder Flavine können auch bei RT aufgenommen werden. Bei der Untersuchung von Membranen, liegt kein natürlicher Paramagnetismus vor, sodass Radikal-Sonden verwendet werden müssen (Spin-Sonden-Technik). Untersuchung von Biomolekülen: Spin-Sonden-Technik Nitroxid-Radikalsonden Zur Untersuchung von Membran-Strukturen oder Segmentbeweglichkeiten in Proteinen werden zwei Klassen von Nitroxid-Radikalsonden verwendet. Derivate des Oxazolidins Derivate des Piperidin- bzw. Pyrrolidin-Ringes (durch Oxidation der entsprechenden sekundären Amine) Beispiel, unten: TEMPO (2,2,6,6Tetramethyl-piperidin-1-oxid) Die radikalische Nitroxid-Gruppe ist von stabilisierenden Methyl-Gruppen an quartären C-Atomen flankiert. Diese setzen die Reaktivität des Radikals soweit herab, dass sie auch in Lösung über Tage und Wochen stabil sind. Der Oxazolidin-Ring kann kovalent an ein Biomolekül verknüpft werden (z.B. Cholesterin oder Fettsäuren der Lipide). Der Fünfring hat dabei eine feste Orientierung zum Biomolekül (wichtig für die Untersuchung der Bewegungszustände der Moleküle). Proteine binden über Amino- und Thiolgruppen an verschiedene Spinsonden mit reaktiven Gruppen. Dazu zählen Analoga des Maleinimids, des Iodacetamids und des Isothiocyanats. Alle genannten Spinsonden können durch Ascorbinsäure reduziert werden. Damit kann die Zugänglichkeit einer Spinsonde aus der wässrigen Phase heraus bestimmt werden. Radikal-Sonden in einem isotropen Lömi zeigen ein typisches 3-Linien-Spektrum. Neben der Hyperfein-Kopplung mit dem Stickstoff-Kern (I=1) sind die zwei Hyperfeinlinien aus der Kopplung mit 13C (I=0,5) für jede der drei N-Linien zu erkennen (sehr klein, da natürliches 13C-Vorkommen sehr gering => 13C-Satelliten). Spin-Sonden-Technik: Spektrale Anisotropie Bei den Nitroxid-Radikalen ist das freie Elektron (S=0,5) in einem p-Orbital am Stickstoff (I=1) lokalisiert. Es wird also eine Hyperfeinstruktur mit drei Linien erwartet. Das p-Orbital liegt bei der Fettsäure-Spinsonde parallel zur Moleküllängsachse (hier: zAchse). Spektrale Anisotropie bedeutet, dass der g-Faktor (bestimmt Lage des Gesamtspektrums) und die HyperfeinKopplungskonstante (bestimmt Abstand der Hyperfeinlinien) von der Orientierung des p-Orbitals und damit von der Orientierung der Spinsonde in B0 abhängig sind. B0 kann durch entsprechende Orientierung der Probe (Nachweis: Radikal-Sonde, eingebettet in eine feste, orientierte Matrix) parallel zu einer der Molekülachsen liegen. Die spektrale Anisotropie resultiert in unterschiedlichen g-Faktoren und Hyperfein-Kopplungskonstanten, wenn eine Aufnahme des Spektrums für 𝐵𝐵0 ∥ 𝑥𝑥, 𝐵𝐵0 ∥ 𝑦𝑦 oder 𝐵𝐵0 ∥ 𝑧𝑧 erfolgt. Oft ist das molekulare System achsialsymmetrisch (hier: z-Achse), sodass zwei Komponenten ausreichen, um das ESR-Spektrum zu beschreiben: 𝑔𝑔∥ = 𝑔𝑔𝑧𝑧𝑧𝑧 , 𝑎𝑎∥ = 𝑎𝑎𝑧𝑧𝑧𝑧 , 𝑔𝑔⊥ = 𝑔𝑔𝑥𝑥𝑥𝑥 = 𝑔𝑔𝑦𝑦𝑦𝑦 𝑎𝑎⊥ = 𝑎𝑎𝑥𝑥𝑥𝑥 = 𝑎𝑎𝑦𝑦𝑦𝑦 Für Orientierungen, die zwischen den Hauptachsen liegen, werden Spektren mit entsprechenden mittleren Werten für g und a erhalten. Hyperfein-Kopplungskonstante und g-Faktor sind dann nur vom Winkel 𝜽𝜽 zwischen Magnetfeld und Molekülachsen abhängig: 𝑔𝑔𝜃𝜃 = �𝑔𝑔∥2 cos 2 𝜃𝜃 + 𝑔𝑔⊥2 sin2 𝜃𝜃 𝑎𝑎𝜃𝜃 = �𝑎𝑎∥2 cos 2 𝜃𝜃 + 𝑎𝑎⊥2 sin2 𝜃𝜃 Aus den experimentell bestimmten Werten für 𝑔𝑔𝜃𝜃 und 𝑎𝑎𝜃𝜃 lässt sich die Orientierung des Moleküls ablesen. Normalerweise liegen keine Einkristalle vor, sodass polykristalline Pulverspektren (alle Orientierungen liegen statistisch verteilt vor) erhalten werden. Das Spektrum enthält alle Werte des g-Faktors und der Kopplungskonstanten. Das Absorptionsspektrum enthält also alle möglichen Resonanzlinien (gestrichelt gezeichnet) von 𝑎𝑎𝑧𝑧𝑧𝑧 bis 𝑎𝑎𝑥𝑥𝑥𝑥 , wobei die „Einhüllende“ eine Gerade darstellt und das ESR-Spektrum wiedergibt. Die maximale Kopplungskonstante 𝒂𝒂𝒛𝒛𝒛𝒛 ist auswertbar, wobei die minimale Aufspaltung 𝒂𝒂𝒙𝒙𝒙𝒙 von der Zentrallinie überdeckt wird und nicht aufgelöst ist (𝑎𝑎𝑥𝑥𝑥𝑥 kann anders ermittelt werden). Die Anisotropie des g-Faktors wurde hier vernachlässigt. Pulverspektrum unter Vernachlässigung der g-Anisotropie und die Ableitung des Spektrums (Detektorsignal). Oben: Pulverspektrum mit a- und g-Anisotropie. Unten: isotropes Spektrum mit isotroper HyperfeinKopplungskonstante. Ein zweiter Extremfall (neben polykristalliner Probe) stellt eine nichtviskose Lösung von RadikalSonden dar. In Lösung erfolgt die Rotation der Moleküle. Ist die Rotationskorrelationszeit kleiner als die Zeit für den Absorptionsprozess, mittelt sich die Anisotropie von a und g heraus. Das Spektrum ist dann unabhängig von der Molekül-Orientierung zu B0. Es ergeben sich die isotropen Mittelwerte: 1 𝑎𝑎0 = (𝑎𝑎𝑧𝑧𝑧𝑧 + 𝑎𝑎𝑦𝑦𝑦𝑦 + 𝑎𝑎𝑥𝑥𝑥𝑥 ) 3 1 𝑔𝑔0 = (𝑔𝑔𝑧𝑧𝑧𝑧 + 𝑔𝑔𝑦𝑦𝑦𝑦 + 𝑔𝑔𝑥𝑥𝑥𝑥 ) 3 Spin-Hamilton-Operator Für den Fall der Achsialsymmetrie gilt: 1 𝑎𝑎0 = (𝑎𝑎∥ + 2𝑎𝑎⊥ ) 3 1 𝑔𝑔0 = (𝑔𝑔∥ + 2𝑔𝑔⊥ ) 3 𝑂𝑂�𝑓𝑓 = 𝑐𝑐𝑐𝑐 Allgemeiner OperatorFormalismus 𝑂𝑂� ist Operator f ist Eigenfunktion c ist Eigenwert der Funktion Bei Anwendung des Hamilton-Operators auf eine Wellenfunktion erhält man für die Eigenwerte die verschiedenen Energieniveaus. Der Spin-Hamilton eines einzelnen Elektrons mit isotropem g-Faktor und mit Spin-KernWechselwirkung hat die Form: � = 𝜇𝜇𝐵𝐵 ∙ 𝑆𝑆 ∙ 𝑔𝑔 ∙ 𝐵𝐵0 + 𝑆𝑆 ∙ 𝑎𝑎 ∙ 𝐼𝐼 𝐻𝐻 Hier sind g und a Tensoren, welche die Orientierungsabhängigkeit berücksichtigen. S, I und B haben jeweils drei Vektorkomponenten (x,y,z). Ordnungsgrade in Lipid-Doppelschichten Bisher wurde keine Segmentbeweglichkeit der Spin-Sonde berücksichtigt, wie sie z.B. auftritt, wenn sie an ein Lipid gekoppelt ist und sich innerhalb der Lipid-Doppelschicht befindet. Die Beweglichkeit der Spin-Sonde kann aus der Hyperfein-Aufspaltung abgeleitet werden. Ist das Spin-markierte Molekül fest in ein Membransystem inkorporiert oder an ein Makromolekül gebunden, resultiert wegen der statistischen Orientierung ein Pulverspektrumähnliches anisotropes ESR-Signal. Da ein biologisches System aber immer eine Flexibilität zeigt, unterscheidet sich die Spektren-Form. Die maximalen und minimalen HyperfeinAufspaltungen 𝑎𝑎𝑧𝑧𝑧𝑧 bzw. 𝑎𝑎𝑥𝑥𝑥𝑥 werden nicht mehr erreicht. Die experimentell bestimmbaren Werte 𝒂𝒂∥ < 𝒂𝒂𝒛𝒛𝒛𝒛 und 𝒂𝒂⊥ > 𝒂𝒂𝒙𝒙𝒙𝒙 weichen umso mehr von diesen ab, je stärker die Beweglichkeit der Radikal-Sonden wird. Mit zunehmender Beweglichkeit wird die maximale HyperfeinAnisotropie 𝑎𝑎𝑧𝑧𝑧𝑧 − 𝑎𝑎𝑥𝑥𝑥𝑥 = 2,5 ∙ 10−3 𝑇𝑇 durch eine begrenzte Bewegung der Sonde herausgemittelt (siehe simulierte Spektren von s=0,4 bis s=1,0; oben ist das Intervall 2𝑎𝑎∥ markiert, unten das Intervall 2𝑎𝑎⊥ ; Die Grenzen bei 2𝑎𝑎⊥ bzw. 2𝑎𝑎∥ sind einfach abzulesen, da her maxima bzw. minima liegen). Zur Beschreibung wird der Ordnungsgrad eingeführt (Verhältnis zwischen beobachteter Hyperfein-Anisotropie und maximaler HyperfeinAnisotropie). 𝒂𝒂∥ − 𝒂𝒂⊥ 𝒔𝒔 = 𝒂𝒂𝒛𝒛𝒛𝒛 − 𝒂𝒂𝒙𝒙𝒙𝒙 Der Ordnungsgrad sinkt mit steigender Beweglichkeit, da dann 𝑎𝑎∥ − 𝑎𝑎⊥ → 0. Für unbewegliche Moleküle ist 𝒔𝒔 = 𝟏𝟏, für eine isotrope molekulare Bewegung resultiert 𝒔𝒔 = 𝟎𝟎. In einem mittleren Bereich zwischen 0 und 1 kann S über die Winkelamplitude der anisotropen molekularen Bewegung ausgedrückt werden: 𝟑𝟑⟨𝐜𝐜𝐜𝐜𝐜𝐜 𝟐𝟐 𝜽𝜽⟩ − 𝟏𝟏 𝒔𝒔 = 𝟐𝟐 𝜃𝜃 ist der Winkel zwischen Membran-Normale und Moleküllängsachse. ⟨ ⟩ bezieht sich auf den zeitlichen Mittelwert. Durch Bildung von Rotations-Isomeren können die Fettsäure-Ketten der Lipide in der fluiden Phase Segmentbewegungen durchführen. In einem einfachen Modell nimmt die Lipid-Kopfgruppe eine feste Position ein. Die CH-Ketten führen eine statistische Bewegung durch, begrenzt durch einen Kegelmantel mit dem Öffnungswinkel 2𝛽𝛽 (anisotrope Bewegung mit begrenzter Amplitude). In einer Lipid-Sonde haben die Achsen der Nitroxid-Gruppe immer eine definierte Orientierung im molekularen Achsensystem. Die z-Achse als Richtung von B0 ist die Moleküllängsachse und gibt die Richtung der maximalen Hyperfein-Aufspaltung mit 𝑎𝑎𝑧𝑧𝑧𝑧 = 3,2 ∙ 10−3 𝑇𝑇 an. Das p-Orbital am NitroxidStickstoff ist in z-Richtung orientiert. Die beiden anderen Komponenten der Hyperfein-Aufspaltung liegen senkrecht zur Moleküllängsachse (𝑎𝑎𝑥𝑥𝑥𝑥 = 𝑎𝑎𝑦𝑦𝑦𝑦 = 5,6 ∙ 10−4 𝑇𝑇) In einer Membran orientiert sich die Sonde vorzugsweise parallel zur Membran-Normalen. In planaren Lipidschichten kann 𝒂𝒂𝒛𝒛𝒛𝒛 bei einer Orientierung von B0 parallel zur Membran und 𝒂𝒂𝒙𝒙𝒙𝒙 = 𝒂𝒂𝒚𝒚𝒚𝒚 bei einer Orientierung von B0 senkrecht zur Membran bestimmt werden (siehe Abbildung, rechts). Bei schneller anisotroper Bewegung nimmt die Sonde statistisch Orientierungen ein, die von der Membran-Normalen abweichen (siehe Abbildung, links). Der experimentelle Wert 𝒂𝒂∥ , ist damit kleiner als 𝒂𝒂𝒛𝒛𝒛𝒛 . Genauso ist 𝒂𝒂⊥ größer als 𝒂𝒂𝒙𝒙𝒙𝒙 = 𝒂𝒂𝒚𝒚𝒚𝒚 . In vesikulären Membransystemen sind die Sonden zusätzlich statistisch über eine Kugel-Oberfläche verteilt. Aus dem ESR-Spektrum können direkt 𝒂𝒂⊥ und 𝒂𝒂∥ abgeleitet werden. Daraus berechnet sich der Ordnungsgrad. Mit dieser Methode können auch Temperatur-abhängige Phasenübergänge beobachtet werden. Für die Messung wurde eine FS-Kette mit dem Oxazolidin-Ring am C5-Atom verwendet. Bei 35°C ist mit steigender Temperatur eine Abnahme von 𝑎𝑎∥ zu erkennen. 𝑎𝑎⊥ nimmt weniger stark ausgeprägt entsprechend zu. Dies korreliert mit einem Übergang der Lipid-Membran von einer quasi-kristallinen in eine flüssigkristalline Phase. Lipid-Protein-Wechselwirkung S-Werte ermöglichen die Charakterisierung von Membran-Zuständen: • • Bei S-Werten im Bereich von 0,8 liegt eine immobilisierte Sonde vor. Bei S-Werten kleiner 0,4 ist die Sonde mobil. Membranproteine können mit unterschiedlichen Lipid/Protein-Verhältnissen in Anwesnheit von Fettsäure-Radikal-Sonden rekonstituiert werden. Die Protein-Menge innerhalb der Membran hat große Auswirkungen auf das ESR-Spektrum. • • • Bei geringem Lipid-Gehalt besteht das ESR-Spektrum nur aus einer immobilisierten Komponente. Lipid und Sonde sind fest an das Protein gebunden. Bei höherem Lipid-Gehalt ist eine mobile Komponente zu erkennen, die der immobilen überlagert ist (Abbildung b). Bei hohem Lipid-Gehalt ist das ESR-Spektrum kaum vom Spektrum der reinen LipidMembran mit hoher Sonden-Mobilität zu unterscheiden. Durch Spektrensubtraktion kann der immobile Teil vom mobilen Anteil getrennt werden. Damit ist die Verteilung der Sonde zwischen Proteinassoziierten Sonden und freien Sonden zugänglich. So kann die Anzahl der Lipide, die mit dem Protein assoziieren bestimmt werden. Die Bildung solcher Lipid-Domänen ist jedoch dynamisch: Die Austauschrate zwischen gebundenem und freiem Lipid liegt bei 107 𝑠𝑠 −1 . Aufgrund des Zeitfensters der ESRSpektroskopie von 𝟏𝟏𝟏𝟏−𝟕𝟕 bis 𝟏𝟏𝟏𝟏−𝟗𝟗 𝒔𝒔 sind Lipid-Domänen messbar. Mit NMR geht dies nicht, Zeitfenster hier: 10−4 bis 10−6 𝑠𝑠. Innerhalb des langen Messzeitraums würde nur eine Mittelung über die beiden Zustände und damit ein einheitliches Spektrum gemessen werden. Abbildung: von oben nach unten steigt das Lipid/Protein-Verhältnis Verteilungskoeffizient und Lipidphasen-Umwandlungstemperatur anhand LÖMI-Effekte Die Spin-Sonde TEMPO kann zur Bestimmung der Phasenumwandlungs-Temperatur verwendet werden. Die Hyperfein-Kopplungskonstante 𝑎𝑎 als Maß für die Stärke der Hyperfein-Wechselwirkung ist von der Elektronendichte am Stickstoff-Kern abhängig. Elektronische Struktur in polaren Lömis Elektronische Struktur in apolaren Lömis Abbildung a zeigt das Spektrum in wässrigem Medium. • • In polarer Umgebung ist die Spin-Dichte des ungepaarten Elektrons am Stickstoff größer (𝑎𝑎 ist größer). Damit ist das Spektrum in apolarer Umgebung weniger aufgespalten. (Abbildung c) Der g-Faktor ist in der apolaren Phase größer (𝑔𝑔𝑤𝑤𝑤𝑤𝑤𝑤𝑤𝑤𝑤𝑤𝑤𝑤 = 2,0056, 𝑔𝑔𝐻𝐻𝐻𝐻𝐻𝐻𝐻𝐻𝐻𝐻 = 2,0061). In apolarer Umgebung wird das Spektrum zu kleineren Resonanzfeldstärken verschoben. (Abbildung b) Besteht die Probe aus zwei Phasen mit unterschiedlicher Polarität und verteilt sich die Sonde zwischen den Phasen, kommt es zu einer Überlagerung der beiden Spektren (Abbildung d = (b+c) + a). Nur die Linie bei hohem Feld scheint aufgespalten. Dies ist der Fall, wenn sich die Sonde TEMPO zwischen der wässrigen und der apolaren Lipid-Phase verteilt. Das Linienhöhen-Verhältnis 𝒇𝒇 = 𝑯𝑯𝑳𝑳 /(𝑯𝑯𝑳𝑳 + 𝑯𝑯𝑾𝑾 ) entspricht direkt dem Verteilungskoeffizienten der Sonde zwischen apolarer und polarer Phase. Im Falle eines Lipids steigt dieser Verteilungskoeffizient bei der Phasenumwandlungstemperatur 𝑇𝑇𝑢𝑢 abrupt an. Bei 𝑇𝑇 < 𝑇𝑇𝑢𝑢 ist die Sonde in der kristallinen Lipid-Phase schwer löslich. Bei 𝑇𝑇 > 𝑇𝑇𝑢𝑢 ist die Sonde in der fluiden Lipid-Phase gut löslich. Aus der Bestimmung des Verteilungskoeffizienten als Funktion der Temperatur kann die Lipid-PhasenUmwandlungstemperatur bestimmt werden. Rotationskorrelationszeit In einer isotropen Probe besteht das ESR-Spektrum aus drei schmalen Linien. Zunehmende Immobilisierung führt zu einer charakteristischen Änderung des Spektrums. In Glycerol-Wasser-Mischungen lässt sich die Rotationskorrelationszeit eines Moleküls mit Radius 𝑎𝑎 über das Stokesche Gesetz bestimmen. 𝜏𝜏𝑅𝑅 ist die Zeit, in der 1/e der Moleküle, die sich um einen bestimmten Winkel aus ihrer Ausgangslage gedreht haben, wieder die Ausgangslage erreicht haben. 𝝉𝝉𝑹𝑹 ist damit kleiner, je schneller die Rotation erfolgt. 𝜏𝜏𝑅𝑅 = 4𝜋𝜋𝜋𝜋𝑎𝑎3 3𝑘𝑘𝑘𝑘 Im schwach immobilisierten Bereich ist eine Intensitätsabnahme der Hyperfeinlinie bei hohem Feld zu beobachten. Im stark immobilisierten Bereich kommt es zur Linienverbreiterung des mittleren Peaks. Der Grenzwert dieser Spektren für große 𝜏𝜏𝑅𝑅 (keine Rotation) ist das Pulverspektrum. Solche Spektren werden auch bei Spin-markierten Proteinen erhalten. Die Rotation des Proteins als Ganzes ist zu langsam, um Einfluss auf das Spektrum zu haben. Aus der Linienbreite der mittleren Linie sowie den Intensitäten kann 𝝉𝝉𝑹𝑹 für die Segmentbeweglichkeit bestimmt werden (Spin-Sonde an Lysin oder Cystein gekoppelt). ℎ0 𝜏𝜏𝑅𝑅 = 6,5 ∙ 10−10 ∙ ∆𝐵𝐵0 ∙ � −1 ℎ−1 Verschiedene Protein-Konformationen zeigen verschiedene Segmentbeweglichkeiten, weshalb das ESR-Spektrum Konformationsänderungen anzeigt, die z.B. durch Titration induziert werden. Bei Calmodulin resultiert eine Zunahme von 𝜏𝜏𝑅𝑅 (Abnahme der Segmentbeweglichkeit) infolge der Ca2+-Bindung. Außerdem kann die Tiefe von Bindetaschen bestimmt werden, indem ein Spinmarkiertes Hapten (im Fall von Antikörper-Antigen Bindung) mit unterschiedlichem Abstand zwischen Dinitrobenzyl- und TEMPO-Gruppe eingesetzt wird. Befindet sich TEMPO noch in der Bindetasche, ist die Segmentbeweglichtkeit eingeschränkt. Außerhalb der Bindetasche ist sie hoch (𝜏𝜏𝑅𝑅 fällt bei Kettenlänge = Tiefe der Bindungstasche stark ab). Laterale Diffusion und Lipid-Phasentrennung Laterale Diffusion ist eine Eigenschaft fluider Membranen. Neben der Fluoreszenz-Spektroskopie kann auch die ESR-Spektroskopie Diffusionskoeffizienten bestimmen. Laterale Phasentrennung bezeichnet die in natürlichen Membranen immer vorkommende heterogene Lipid-Verteilung innerhalb einer Lipid-Schicht. Die Methode basiert auf der Bestimmung der Spinaustausch-WW (2 Spins tauschen ihre Orientierung). Diese WW besitzt nur eine kurze Reichweite, sodass sie nur bei van-der-Waals Kontakten stattfinden. Ermöglicht wird der Kontakt über laterale Diffusion. Dem Effekt der Austausch-WW ist immer eine Verbreiterung durch Dipol-Dipol-WW überlagert. • • • • Der Stoffmengenanteil des markierten Lipids muss größer sein als 2%. Niedriger Stoffmengenanteil (2-5%): Kollisionsfrequenz, also Austauschrate niedriger als Hyperfein-WW => Position der 3 Linien unverändert; Linienbreite nimmt zu. Mittlerer Stoffmengenanteil (5-30%): Erhebliche Linien-Verbreiterung. Hoher Stoffmengenanteil: Drei Hyperfeinlinien fallen zu einer einzigen Austauschverschmälerten Linie zusammen. Die Kollisionsfrequenz der Radikalsonden ist über Computer-Simulationen zugänglich, woraus dann die Austauschfrequenz ermittelt wird. Mit Hilfe eines Diffusionsmodells lässt sich dann über Austauschfrequenz 𝑾𝑾𝒆𝒆𝒆𝒆 und Sonden-Konzentration 𝑐𝑐 den Diffusionskoeffizienten bestimmen. Dieser theoretisch bestimmte Wert zeigt eine lineare Abhängigkeit zwischen Konzentration und Austauschfrequenz. Die Konstante 6 ∙ 10−16 beinhaltet geometrische Faktoren. 𝐷𝐷𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = 6 ∙ 10−16 ∙ 𝑊𝑊𝑒𝑒𝑒𝑒 𝑐𝑐 Dem diffusionskontrollierten Spin-Spin-Austausch (homogene Sondenverteilung) wirkt die Phasentrennung entgegen (Sonde bildet mosaikartige Domänen in der Membran). Dadurch kommt es ständig zum Spin-Spin-Austausch. Die Austauschfrequenz ist nicht mehr linear von der SondenKonzentration abhängig, sondern zeigt eine hyperbolische Abhängigkeit: schneller Anstieg schon bei kleinen Konzentrationen, da sich die Sonden in derselben Domäne befinden (z.B. Ca2+komplexierte Phosphatidsäure in PC bildet Domänen). Transversale Diffusion Der Austausch von Lipiden zwischen zwei Lipid-Schichten einer Doppelschicht ist extrem langsam. Diese Art der ESR-Spektroskopie ist nur anwendbar, wenn die Austauschzeiten bei mehreren Stunden liegen, wie in natürlichen Membranen. Eine Lipid-Sonde mit der Radikal-Gruppe im polaren Bereich wird in Membranvesikel eingebaut, sodass beide Mono-Schichten besetzt sind. Bei 0°C können durch Ascorbinsäure alle außen liegenden Sonden reduziert werden. Innenliegende Sonden werden nicht erreicht, da Membranen bei 0°C impermeabel für Ascorbinsäure sind. Nach Entfernung der Ascorbinsäure (Säulenchromatographie) und Inkubation bei einer höheren Temperatur, findet der Lipid-Austausch statt. Nach bestimmten Zeiten wird der Lipid-Austausch gestoppt (Abkühlen auf 0°C) und der nach außen gelangte Sonden-Anteil reduziert. Der Anteil der verbleibenden Spin-Sonden kann aus der Intensität des ESR-Spektrums ermittelt werden. So ist die Transferrate berechenbar. So können auch Membranpermeabilitäten bestimmt werden: das innere Kompartiment des Vesikels wird mit einer permeierenden Sonde gefüllt. Durch die Membran diffundierte Sonden werden reduziert und der Restgehalt zeitabhängig bestimmt. Untersuchung von Biomolekülen: Metall-Ionen in Proteinen Mithilfe der ESR-Spektroskopie können paramagnetische Übergangsmetall-Ionen wie Cu, Fe, Mn, Co, Ni untersucht werden. Die Elektronen mit ungepaartem Spin befinden sich im Wesentlichen in d-Orbitalen. Aufgrund eines starken Beitrags des Bahndrehmoments weichen daher die g-Faktoren stark vom Wert des freien Elektrons (g=2,0033) ab. Sehr kurze Relaxationszeiten verlangen sehr häufig Messungen bei tiefen Temperaturen. Elektronen-Konfiguration von Übergangsmetall-Ionen Übergangsmetall-Ionen können ein oder mehrere ungepaarte Elektronen besitzen. Die 5 d-Orbitale können mit je zwei entgegengesetzt orientierten Spins besetzt werden, woraus sich zehn mögliche Elektronen-Konfigurationen ergeben. • • Cu+ ist diamagnetisch und zeigt kein ESR-Signal (S=0, 10 Elektronen gepaart). Cu2+ besitzt ein ungepaartes Elektron (9 Elektronen in 3d) und ist ESR-aktiv. Bei mehr als 1 oder weniger als 9 Elektronen in d Orbitalen ist der Spin-Zustand von der Umgebung (Ligandenfeld) abhängig, sodass high spin und low spin Zustände eingenommen werden können. • • Der high-spin Zustand hat durch maximale Einfachbelegung der d-Orbitale den größtmöglichen Spin. Der low-spin Zustand hat durch maximale Doppelbelegung den kleinstmöglichen Spin. Da die Gesamtzahl der ESR-Linien ohne Hyperfein-Aufspaltung 2S beträgt, hat der high-spin Zustand für Fe3+ (S=5/2) fünf ESR-Linien, während der low-spin Zustand für Fe2+ (S=0) ESR-inaktiv ist. Eine unterschiedliche Besetzung der d-Orbitale beinhaltet auch verschiedene Beiträge des Bahndrehimpulses. Dadurch sind die g-Faktoren stark von den Liganden des Metall-Ions abhängig. • • Fe3+ (high-spin): 1,4 < 𝑔𝑔 < 3,1 Fe2+ (low-spin): 2,0 < 𝑔𝑔 < 9,7 Die Komplexität des Spektrums erhöht sich weiter durch die Orientierungsabhängigkeit von g und a. Titration von Mn2+-Bindestellen in Proteinen Da Ca2+ nicht paramagnetisch ist, kann Mn2+ als Ligand für Ca2+-Bindeproteine verwendet werden. Es liegt in wässriger Lösung im high-spin Zustand vor. Die Relaxationszeiten sind lang genug, sodass das Spektrum bei RT aufgenommen werden kann. • • In Lösung resultiert durch Hyperfein-WW mit dem Kernspin 𝐼𝐼 = 5/2 eine Aufspaltung in sechs Linien (𝑎𝑎 = 9,4 ∙ 10−3 𝑇𝑇). Der g-Faktor ist sehr gering (g=2), sodass die mit fünf ungepaarten Elektronen halbbesetzte Schale eine kugelsymmetrische Elektronendichte-Verteilung haben muss und damit kein Bahnmoment aufweist. Durch Zugabe von Calmodulin wird Mn2+ komplexiert. Durch die entstehende Asymmetrie in der Koordinationsphäre werden die Linien verbreitert und die Intensitäten verringert (siehe Abbildungen a, b). Der Endpunkt der Titration wird durch ein scharfes ESR-Spektrum angezeigt. Über diese Methode können die Anzahl an Mn2+-Bindestellen sowie die Dissioziationskonstante bestimmt werden. Die Dissoziationskonstante wird erhalten, wenn die Intensität der letzten ESR-Linie von freiem Mn2+ (isotropes Lösungsspektrum) als Funktion der Mn2+-Konzentration aufgetragen wird, einmal in Anwesenheit (Kurve II) und einmal in Abwesenheit (Kurve I) von Calmodulin. Die Differenz der Kurven erlaubt die Bestimmung der Dissoziationskonstanten. Cytochrom-c-Oxidase Das Molekül besteht aus Cyt-a und Cyt-a3 und zwei Kupfer-Ionenzentren. Die Aufnahme des Spektrums erfolgt bei 81K, wegen der kurzen Relaxationszeiten. Das Spektrum hat Komponenten der Fe3+-Ionen in der low-spin und der high-spin Konfiguration. Das ESR-Signal des Cu2+-Ions hat einen niedrigen g-Wert (g=2). Die fehlende Hyperfein-Struktur im Cu2+-Spektrum (I=3/2) deutet auf eine starke Delokalisation der Elektronen hin, was der Redox-Funktion entspricht. Biologische freie Radikale Freie Radikale treten als Zwischenprodukte vieler enzymatischer Reaktionen auf. Die ESRSpektroskopie kann die Struktur solcher Radikale identifizieren und dadurch Mechanismus oder Kinetiken von Stoffwechsel-Reaktionen charakterisieren. Da solche Reaktionen sehr schnell ablaufen, existieren die paramagnetischen Spezies nur übergangsweise. Das ungepaarte Elektron ist meist stark delokalisiert und wechselwirkt mit verschiedenen Kernen der Umgebung. Damit verbunden ist eine komplexe Hyperfeinstruktur. Anhand von Linienbreite sowie Werten für a und g kann eine strukturelle Zuordnung geschehen, wobei zu Vergleichszwecken ESR-Spektren von chemisch synthetisierten Modellsubstanzen herangezogen werden. Flavin-Radikale: Die Reduktion von FAD erfolgt durch schrittweise Aufnahme von zwei Elektronen und zwei Protonen, sodass radikalische Zwischenstufen entstehen. Ebenso stehen die oxidierte und die reduzierte Form im Gleichgewicht, wodurch halbreduzierte Formen entstehen. Die ausgeprägte Hyperfeinstruktur von Isoalloxazin-Derivaten resultiert aus der WW zwischen ungepaartem Elektron und verschiedenen N- und H-Kernen. • • • Durch Ersatz des H-Atoms an N3 wurden keine Veränderungen im Spektrum beobachtet. Dies deutet auf eine geringe Spin-Dichte an diesen N-Atomen hin, was eine Beteiligung am Elektronentransfer ausschließt. Durch Ersatz des H-Atoms an N1, N5 und N10 konnte festgestellt werden, dass das Elektron nicht im Pyrimidin-Ring delokalisiert ist (Pyrimidin-Ring ist nicht am Elektronentransfer beteiligt). Hohe Elektronendichten wurden am N5, N10, C6 und C8 gefunden, sodass diese am Elektronentransfer beteiligt sein müssen. Substrat-Radikale bei Enzym-Reaktionen: Bei enzymatischer Reaktion können radikalische Zwischenstufen an Enzyme und/oder Substrat entstehen. Bei Peroxidasen entstehen z.B. SubstratRadikale, da Peroxidasen dem Substrat ein Elektron entziehen. Im Komplex mit H2O2 ist die Peroxidase aktiv (oxidierter Zustand, Compound I). Compound I muss dann nacheinander durch zwei Mol SH2 wieder reduziert werden, wobei als Zwischenstufe Compound II entsteht. Die dabei entstehenden SH-Radikale zerfallen durch Disproportionierung. Die ESR-Spektren der entstehenden anionischen Radikale ermöglichen anhand der Intensität des ESR-Signals die Bestimmung der Steady-State Konzentration des Radikals. Die gut aufgelöste Hyperfein-Struktur zeigt, dass sich die Radikale frei in Lösung befinden, da in einem Enzymgebundenen Zustand durch eingeschärnkte Rotation breite Linien resultieren. Strahlenschäden in DNA-Strängen: UV- oder Röntgen-Strahlung können zum Strangbruch führen, wodurch Radikale entstehen, die über ESR-Spektroskopie nachgewiesen werden können. Ein Spektrum bestrahlter DNA konnte durch Vergleich mit Spektren von bestrahlten Einkristallen der vier Basen dem Radikal des Thymidins zugeordnet werden. Kernmagnetische Resonanz Wie bei der ESR ist auch für die NMR ein Resonanzphänomen mit gleicher physikalischer Grundlage verantwortlich. Im Vergleich zu den Elektronen, hat ein Proton jedoch eine wesentlich größere Masse (Faktor 1836). Das magnetische Moment eines Elektrons ist 660mal größer als das eines Protons. Daher werden in der NMR-Spektroskopie zur Erfüllung der Resonanzbedingung niedrigere Frequenzen (100-900Mhz, Radiowellen-Bereich) und stärkere Magnetfelder als in der ESRSpektroskopie (7-21 Tesla) benötigt. Kern-Eigendrehimpulsquantenzahl 𝑰𝑰 Magnetisches Moment des Kerns Kernmagneton |𝐼𝐼| = ℏ�𝐼𝐼(𝐼𝐼 + 1) = 𝑃𝑃𝐼𝐼 𝜇𝜇𝑁𝑁 Bohrsches Kernmagneton 𝑔𝑔𝑁𝑁 = 5,5855 Proportionalitätsfaktor für ein freies Proton; 𝑔𝑔𝑁𝑁 variiert zwischen den verschiedenen Atomkernen zwischen -6 und 6. 𝑒𝑒 ∙ ℏ 𝑚𝑚𝑝𝑝 = 1836,15𝑚𝑚𝑒𝑒 = 𝜇𝜇𝑁𝑁 = = 5,05 ∙ 10−27 𝐽𝐽/𝑇𝑇 Kernmasse 2𝑚𝑚𝑝𝑝 𝜇𝜇𝐼𝐼 = 𝛾𝛾 ∙ 𝐼𝐼 = 𝑔𝑔𝑁𝑁 ∙ 𝜇𝜇𝑁𝑁 ∙ 𝐼𝐼 Daher ist das Kernmagnetische Moment wesentlich geringer => Energiedifferenz geringer! Für die NMR-Niveaus gilt ∆𝐸𝐸 = 𝛾𝛾𝐵𝐵0 ℏ, wie auch für die ESR-Niveaus. Je größer der Wert für 𝛾𝛾, desto nachweisempfindlicher ist die Substanz in der NMR-Spektroskopie. Kerne mit einem großen 𝛾𝛾 Wert werden daher als NMR empfindlich, solche mit einem kleinen Wert für 𝛾𝛾 als NMR-unempfindlich bezeichnet. Während ein Elektron immer die Spinquantenzahl 1/2 aufweist, können Kernspins ein ganz-zahliges Vielfaches von 1/2 annehmen, da mehrere Protonen vorhanden sind, die jeweils eine Spinquantenzahl von 1/2 aufweisen. 𝐼𝐼 kann Werte von 0 bis 6 annehmen, wobei der Kernspin I=0 NMR Inaktivität bedeutet. ESR vs. NMR Die ESR benötigt höhere Energien (Mikrowellen), als die NMR (Radiowellen), da die Energieniveaus zwischen den Spin-Zuständen der Elektronen weiter auseinander liegen, als die zwischen den SpinZuständen des Kerns. Dadurch ist die Boltzmann-Verteilung bei den Elektronen-Spins (großer Überschuss im Grundzustand) auch günstiger als die für die Kern-Spins (nur geringer Überschuss im Grundzustand). Damit haben die ESR-Spektren von Natur aus eine bessere Auflösung als die NMRSpektren, für die eine Akkumulation mehrerer Spektren notwendig ist. Bei der Aufnahme des ESR-Spektrums wird mit einer konstanten Frequenz eingestrahlt und das Magnetfeld über die Zeit verändert (Mikrowellen können schwer in Frequenz variiert werden, da magisches T in der Anpassung stetig geändert werden müsste). Es tritt Absorption für bestimmte Magnetfeld-Größen auf, die anschließend detektiert wird. Jedem Zeitpunkt ist eine Magnetfeldstärke zuzuordnen, der wiederum eine Absorption zuzuordnen ist. Es wird demnach direkt das Spektrum erhalten (keine FT), wobei die Aufnahmezeit wesentlich größer ist als bei der NMR. Bei der NMR werden bei konstantem Magnetfeld (viel höher als bei ESR, daher schwer zu variieren) verschiedene Frequenzen, allerdings alle gleichzeitig, eingestrahlt. Dies ermöglicht schnellere Aufnahmezeiten, benötigt aber die FT, um das Signal in der Zeitdomäne (überlagerte Wellen) in die Frequenzdomäne umzuwandeln. Die geringere Aufnahmezeit relativiert sich, da aufgrund der niedrigeren Auflösung (Boltzmann-Verteilung ungünstig) die Aufnahme und Akkumulation mehrerer Spektren notwendig ist. Bei der NMR-Theorie liegt der Schwerpunkt auf der Betrachtung der Überschussmagnetisierung, was lediglich mit der Messtechnik zutun hat. Die gemessene NMR-Signalintensität nach einem B1-Puls ist ein zeitabhängiges Signal, die mit der Rotation der Magnetisierung in der xy-Ebene variiert. Bei der ESR geht es lediglich um Absorption, die direkt in Form von fehlenden Frequenzen am Detektor aufgezeichnet wird. Die B1-Einstrahlung erfolgt nicht Pulsweise, sondern kontinuierlich, sodass sich die Vektoren ständig um B0 spiralförmig nach oben und unten bewegen. Die Betrachtung einer Überschussmagnetisierung in der ESR-Theorie spielt keine Rolle, da sie nichts mit dem detektierten Signal zutun haben. Die physikalischen Prinzipien sind jedoch identisch. Kernspins in biologischen Substanzen NMR-aktive Isotope haben alle ein 𝐼𝐼 ≠ 0. Dazu zählen 1H, 13C oder 31P. Andere natürlich vorkommende Kerne wie 12C, 16O oder 32S haben 𝐼𝐼 = 0 und damit kein magnetisches Moment und sind NMR-inaktiv. Der Kernspin wird von Neutronen und Protonen beeinflusst. Eine empirische Regel zur Vorhersage der magnetischen Komponente besagt folgendes • • • Nur Kerne mit gerader Massenzahl und gerader Kernladungszahl (Atomzahl) haben 𝑰𝑰 = 𝟎𝟎. Ungerade Massenzahl und gerade Kernladungszahl ergibt ungerades ganzzahliges Vielfaches von ½. Gerade Massenzahl und ungerade Kernladungszahl ergibt ganzzahligen Kernspin. Die Einsatzmöglichkeiten der verschiedenen Kerne in der NMR-Spektroskopie sind durch drei Parameter bestimmt: • Natürliches Vorkommen. • Relative Empfindlichkeit. Die Amplitude des Absorptionssignals pro Feldeinheit ist proportional zum Quadrat des magnetischen Moments und damit stark von der Kernmasse abhängig (je größer die Kernmasse, desto geringer die Absorption; siehe Kernmagneton). • Linienbreite steigt insbesondere bei Kernen mit 𝑰𝑰 > 1/2 durch das elektrische QuadrupolMoment enorm (daher ist 14N praktisch ohne Bedeutung für die NMR). Das Produkt aus natürlichem Vorkommen und relativer Empfindlichkeit ergibt die relative Signalintensität als Maß für die Verwendbarkeit eines Kerns. Für 13C muss damit eine 104 empfindlichere Messung durchgeführt werden, als für 1H. Physikalisches Bild des NMR-Experiments Bei einer makroskopischen Probe mehrerer Kerne, jeweils mit einem magnetischen Moment 𝜇𝜇, addieren sich alle magnetischen Momente vektoriell zu einer makroskopischen Gesamtmagnetisierung M. Ohne äußeres Magnetfeld sind die Kernspins statistisch verteilt, sodass 𝑴𝑴 = 𝟎𝟎. Wird ein äußeres Magnetfeld B0 in z-Richtung eines festgelegten Achsensystems angelegt, orientieren sich die Kernspins parallel bzw. antiparallel zum B0-Feld. Im thermischen GG ist das energieärmere Niveau (paralleler Zustand) aufgrund der Boltzmann-Verteilung stärker besetzt. Dadurch erhält die makroskopische Magnetisierung in z-Richtung den endlichen Wert 𝑴𝑴𝒛𝒛 . Die einzelnen Spins präzedieren mit der Larmor-Frequenz, haben aber keine Phasenbeziehung (Lage ist statistisch auf Kegelmantel verteilt). So mitteln sich alle Komponenten senkrecht zu B0 heraus, sodass keine Magnetisierung 𝑀𝑀𝑥𝑥 in x-Richtung oder 𝑀𝑀𝑦𝑦 in y-Richtung auftritt. Analog zur ESR wird nun in x-Richtung (Senderspule emitiert Hochfrequenz-Feld) ein linear polarisiertes magnetisches Wechselfeld B1 angelegt (Frequenz des Wechselfeldes wird variiert, B0 ist konstant – ESR umgekehrt!). Die zirkular polarisierte Komponente, welche die xy-Ebene im selben Drehsinn wie die präzedierenden Spins umläuft, zwingt den Spin bei Eintritt der Resonanzbedingung (B1-Feld rotiert mit Larmor-Frequenz) einen phasengleichen Umlauf auf (Bündelung der Spins). Dadurch tritt eine Magnetisierung 𝑴𝑴𝒚𝒚 senkrecht zu B0 auf, die in der xy-Ebene mit der Larmor-Frequenz umläuft. Das NMR-Signal wird auf der y-Achse (Empfängerspule) als die durch den rotierenden Magnetisierungsvektor induzierte Spannung gemessen. Im rotierenden Koordinatensystem ist My fest mit der y‘-Achse verbunden und das B1-Feld zeigt stationär in x‘-Richtung. Das B1-Feld wirkt auf Mz und übt ein Drehmoment 𝑫𝑫 = 𝑴𝑴𝒛𝒛 × 𝑩𝑩𝟏𝟏 aus, sodass Mz-Vektor um einen Winkel 𝝋𝝋 um die x‘-Achse (B1-Feld) rotiert – Der Winkel der Rotation ist von der Dauer des B1-Feld-Pulses abhängig. Die neue Magnetisierung bei einem 90°-Puls steht senkrecht zu B0 und senkrecht zu B1; sie liegt auf der y‘-Achse (transversale Magnetisierung My‘). Netto werden mehr Spins von der parallelen Orientierung in die antiparalle (energiereicher) überführt, sodass eine Absorption der Energie aus dem B1-Feld vorliegt. Dadurch wird die Boltzmann-Verteilung gestört. B1-Feld induziert demnach zwei Prozesse: Bündelung der Spins und Störung der Boltzmannverteilung! Fourrier-Transformation Jedes Proton hat eine unterschiedliche Larmorfrequenz, je nachdem in welcher chemischen Umgebung es sich befindet; Bei einer NMR Messung werden alle Frequenzen gleichzeitig eingestrahlt, weshalb auch alle H Atome angeregt werden, wodurch sich ihre Kerndrehimpulsvektoren mit ihrer Larmorfrequenz (nach einem 90° Puls) innerhalb der xy-Ebene um die z-Achse drehen; jedes einzelne Proton induziert dadurch einen Wechselstrom in der Spule mit seiner Larmofrequenz (unterschiedliche Larmorfrequenzen aufgrund unterschiedlicher chemischer Umgebung, siehe unten), wodurch es im FID (freier Induktionsabfall) zu einer Überlagerung aller Larmorfrequenzen kommt; Daher lassen sich aus dem Zeitdomänen-Signal des FID nicht einfach die Frequenzen ableiten. Beim ESR bleibt die Frequenz konstant. Die Änderung des B0-Feldes bewirkt die Anregung der Spins nacheinander (es werden nicht alle B0-Felder gleichzeitig verwendet xD). Daher ist jedes B0-Feld zu jedem Zeitpunkt einer Larmorfrquenz zuzuordnen – kein FT notwendig. Die Fourier Transformation ist eine mathematische Operation, mit der die Zeitdomänen-Information von 𝐹𝐹(𝑡𝑡) (FID) in die Frequenzdomänen-Information von 𝐹𝐹(𝜔𝜔) (Spektrum) umgewandelt wird. Das FID stellt eine periodische Funktion dar, die sich durch eine Reihe harmonischer Funktionen annähern lässt. 𝐹𝐹(𝑡𝑡) = 𝑎𝑎0 + 𝑎𝑎1 cos 𝑥𝑥 + 𝑎𝑎2 cos 2𝑥𝑥 + 𝑎𝑎3 cos 3𝑥𝑥 + ⋯ + 𝑏𝑏1 sin 𝑥𝑥 + 𝑏𝑏2 sin 2𝑥𝑥 + 𝑏𝑏3 sin 3𝑥𝑥 + ⋯ 2 +∞ 𝐹𝐹(𝜔𝜔) = � −∞ +∞ 𝑓𝑓(𝑡𝑡)𝑒𝑒 𝑖𝑖𝑖𝑖𝑖𝑖 𝑑𝑑𝑑𝑑 = � −∞ 𝑓𝑓(𝑡𝑡) ∙ (cos 𝜔𝜔𝜔𝜔 + 𝑖𝑖 sin 𝜔𝜔𝜔𝜔)𝑑𝑑𝑑𝑑 Es wird nacheinander das Produkt zwischen 𝐹𝐹(𝑡𝑡) und dem Sinus-Teil sowie dem Cosinus-Teil aus 𝐹𝐹(𝜔𝜔) gebildet. Dabei werden alle Frequenzen einmal für den Sinus-Teil (Punktsymmetrisch) und einmal für den Cosinus-Teil (Achsensymmetrisch) durchprobiert. Ist z.B. der Sinus-Teil aus 𝐹𝐹(𝜔𝜔)für eine bestimmte Frequenz gleich der Funktion 𝐹𝐹(𝑡𝑡) , so ergibt das Produkt der beiden Funktionen eine maximale Intensität; es resultiert somit ein Peak im Frequenzspektrum; genauso wird das mit dem Cosinus-Teil gemacht. 𝐹𝐹(𝜔𝜔) ist eine komplexe Größe, weshalb man nach der FT zwei Spektren erhält: einen Realteil (durch den Cosinus-Teil) und einen Imaginärteil (durch den Sinus-Teil). Re�F(ω)� = � +∞ −∞ 𝑓𝑓(𝑡𝑡) ∙ (cos 𝜔𝜔𝜔𝜔)𝑑𝑑𝑑𝑑 , +∞ Im�F(ω)� = � −∞ 𝑓𝑓(𝑡𝑡) ∙ (sin 𝜔𝜔𝜔𝜔)𝑑𝑑𝑑𝑑 Zeitfunktion (links) und Frequenzfunktion (rechts) für zwei um 90° phasenverschobene Signale. Die obere Frequenzfunktion ist das Absorptionsspektrum oder der Realteil, und die untere ist das Dispersionsspektrum oder der Imaginärteil. In der Praxis ergibt die Fouriertransformation zunächst eine Kombination der beiden Frequenzfunktionen (jedes Signal liefert 2 Peaks), aus denen man durch Phasenkorrekturen die reinen Absorptionsund Dispersionsspektren berechnet. Bei der Phasenkorrektur wird aus dem einen Teil das für die Praxis relevante Absorptionsspektrum berechnet (enthält 1 Peak je Signal), während der andere Teil, das Dispersionsspektrum, die um 90° phasenverschobenen Signale enthält. Messtechnik In einem Continious wave (cw) Experiment wird die Absorption bei kontinuierlicher B1-FeldStrahlung über den Induktionsstrom in der Empfängerspule gemessen. Um die Resonanzbedingung zu erreichen, kann die Frequenz bei konstantem B0-Feld oder das B0-Feld bei konstanter Frequenz variiert werden (Erinnerung: ℎ𝑣𝑣 = ∆𝐸𝐸 = 𝛾𝛾ℏ ∙ 𝐵𝐵0 ); üblich: Magnetfeldänderung (wie bei ESR; dies gilt aber nur für das veraltete cw-Experiment, nicht für Puls-Experimente). Probleme bei der NMR-Spektroskopie liegen in der Konstanz, der Stärke und der Homogenität des Magnetfeldes. Die Toleranz liegt bei Abweichungen in der Größenordnung 10−8 . Mit gewöhnlichen Elektromagneten können Felder bis 2,5T erzeugt werden. Darüber müssen supraleitende Spulen unter Kühlung mit flüssigem Helium (Widerstand vernachlässigbar) verwendet werden. Moderne Geräte arbeiten nicht mit der cw-Technik, sondern mit der Fourier-Transform-Technik, die mit Pulsen arbeitet. Struktur des NMR-Spektrums Ein NMR-Spektrum ist primär durch zwei Größen charakterisiert. • • Die chemische Verschiebung (Abschirmung des B-Feldes durch Elektronendichte der Umgebung) bestimmt die Größe des Resonanz-Feldes, also die Lage des Übergangs auf der B0-Achse (entsprechend g-Faktor bei ESR-Spektroskopie). Die Wechselwirkung mit benachbarten Kernspins (Spin-Spin-Kopplung) führt zu einer Multiplettstruktur (entsprechend Hyperfein-WW = Elektronenspin-Kernspin-WW bei ESRSpektroskopie). Der Unterschied zwischen den Kernen ist die unterschiedliche Frequenzlage. Bei 10T liegt z.B. die 1 H-Resonanz bei 425,7 Mhz und die 13C-Resonanz bei 107.1Mhz. Mit einem Experiment kann damit nur eine Kernsorte spektroskopisch untersucht werden. Es werden zwar mehrere Frequenzen pro Experiment eingestrahlt, aber innerhalb eines wesentlich geringeren Frequenzbandes, um lediglich Spins derselben Kernsorte mit aufgrund von CV und Spin-Spin-WW leicht unterschiedlichen Larmor-Frequenzen anzuregen. Die chemische Verschiebung Das B0-Feld erzeugt Kreisströme in der Elektronenwolke. Bewegte Ladungen erzeugen aber ein Magnetfeld 𝑩𝑩𝒊𝒊𝒊𝒊𝒊𝒊, das nach der Lenzschen Regel dem erzeugenden B0-Feld entgegengesetzt gerichtet ist. Am Ort des Kerns herrscht somit ein lokales Feld 𝑩𝑩𝒍𝒍𝒍𝒍𝒍𝒍 = 𝑩𝑩𝟎𝟎 − 𝑩𝑩𝒊𝒊𝒊𝒊𝒊𝒊 . Der Kern ist damit abgeschirmt und zur Resonanz muss ein stärkeres B0-Feld verwendet werden. Das induzierte Feld ist jedoch vom angelegten Feld abhängig: 𝐵𝐵𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜎𝜎𝐵𝐵0 , weshalb 𝐵𝐵𝑙𝑙𝑙𝑙𝑙𝑙 = 𝐵𝐵0 (1 − 𝜎𝜎) gilt. Die Größe der Abschirmkonstante 𝜎𝜎 ist stark von der Elektronendichte abhängig, also von den Nachbaratomen eines Kerns. Ansteigende Elektronendichte verringert damit die Resonanzfrequenz: 𝜔𝜔0 = 𝛾𝛾𝐵𝐵0 (1 − 𝜎𝜎) . So ist die Elektronendichte am Proton in C-H größer als im Proton in O-H, da Sauerstoff eine größere Elektronegativität hat als Kohlenstoff. Damit gilt 𝜎𝜎𝐶𝐶𝐶𝐶 > 𝜎𝜎𝑂𝑂𝑂𝑂 und die Resonanz des Protons in C-H liegt bei höherem Feld. Wenig Elektronegative Nachbargruppen (z.B. CH3) = Hohe Elektronendichte am zu untersuchenden Kern (Hier: 1H) = hohe Abschirmung des Kerns = höheres B0-Feld zur Resonanz erforderlich = Niedrige chem. Verschiebung (ppm). Auch Nachbargruppen können die Abschirmung erhöhen (-CH3, -NH2, COO-) oder erniedrigen (-OH, -COOH, -NH3+, -NO2). Im Benzol erzeugt das B0-Feld einen Ringstrom der π-Elektronen. Das entstehende Magnetfeld im Innern des Ringes ist dem B0-Feld entgegengesetzt gerichtet. Außerhalb des Ringes, im Bereich der Protonen, ist das induzierte Feld dem angelegten gleichgerichtet (Verstärkung von B0). Eine vorhandene Abschirmung wird geschwächt, weshalb die Resonanz der Benzol-Protonen bei relativ kleinem Feld liegt. Die chemische Verschiebung ist damit charakteristisch für einen gegebenen Kern in definierter chemischer Umgebung, wodurch strukturelle Zuordnungen möglich sind. Zur Quantifizierung der chemischen Verschiebung wird eine Referenz benötigt, da die Größe des abschirmenden Feldes sowie die entsprechende Resonanzfrequenz mit der Betriebsfrequenz des Spektrometers variiert und daher eine absolute Angabe keinen Sinn macht. So sind beide Werte bei 500Mhz-Spektrometern fünfmal so groß als bei 100Mhz-Spektrometern. 𝛿𝛿 = 𝑣𝑣𝑅𝑅𝑅𝑅𝑅𝑅 − 𝑣𝑣𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 ∙ 106 𝑝𝑝𝑝𝑝𝑝𝑝 𝑣𝑣𝑅𝑅𝑅𝑅𝑅𝑅 Eine Resonanzstelle in einem 200Mhz-Spektrum, die 200 Hz von der Resonanzstelle der Referenz entfernt ist, zeigt eine chemische Verschiebung von 1 ppm. Dasselbe gilt für ein 500 Mhz-Spektrum, da hier die Entfernung 500 Hz ist. Als Referenz für 1H und 13C wird Tetramethylsilan (TMS) verwendet. Diese Protonen haben sehr hohe Resonanz-Feldstärken (große Abschirmung), da Si mit 1,9 eine niedrige Elektronegativität aufweist (H=2,2; C=2,5; N=3,0; O=3,5). Die CV wird im Spektrum von rechts nach links in ppm-Einheiten aufgetragen. Positive Zahlen kennzeichnen damit die Verschiebung zu niedrigerem Feld. Spin-Spin-Kopplung Spin-Spin-Kopplung mit benachbarten Kernen bwirkt eine Multiplettaufspaltung. Im 1H-Spektrum von Alanin in D2O gehört das Duplett bei 1,21 ppm der CH3-Gruppe und das Quartett bei 3,31 ppm dem CαH, da beide Protonen miteinander wechselwirken (Kopplungskonstante bei 7,2Hz für vicinale Proton-ProtonKopplung). Da die Aufnahme in D2O erfolgte, sind die austauschbaren Protonen der Aminogruppe nicht sichtbar. Die Stärke der WW gibt die Kopplungskonstante J an, die unabhängig von B0 ist. Für Protonen liegt sie bei 0-30Hz (100MhzSpektrometer: 0,2 ppm, 500Mhz-Spektrometer: 1ppm). Äquivalente Protonen haben dieselbe chemische Verschiebung, so auch die in CH3. Das benachbarte CαH kann die Spinzustände 𝑚𝑚𝐼𝐼 = ±0,5 einnehmen. Je nach Spinzustand wird damit das Feld am Ort der CH3-Protonen um einen Betrag BA erhöht oder erniedrigt, weshalb das Signal in ein Duplett aufgespalten wird. Das Quartett in CαH kann genauso erklärt werden: Die CH3-Protonen können zu einem Gesamtspin von 𝑚𝑚𝐼𝐼 = ±0,5, ±1,5 kombinieren. Es resultieren zwei verschiedene Feldverstärkungen und zwei verschiedene Feldabschwächungen am CαH, sodass vier Linien resultieren. Es gilt also für die Kpplungskonstante J analog wie für die Hyperfeinkopplungskonstante 0 der ESR-Spektroskopie: 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 = 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 − 𝐽𝐽𝑚𝑚𝐼𝐼 . Allgemein gilt, dass n äquivalente Kerne mit Spin I=0,5 genau n+1 Multiplett-Komponenten erzeugen. Die Intensitätsverhältnisse der einzelnen Banden sind dem Pascalschen Dreieck zu entnehmen. Ein Multiplett mit Überlagerungen entsteht bei Kopplung mit mehreren Sätzen von Kernen. Allgemein beträgt die Multiplizität des betrachteten Kerns bei n benachbarten Kernen mit Spin I: 𝒛𝒛 = 𝟐𝟐𝟐𝟐 ∙ 𝑰𝑰 + 𝟏𝟏 . Bei i Sätzen äquivalenter Kerne mit verschiedener Kopplungskonstante gilt für die einzelnen Multiplizitäten 𝑧𝑧𝑖𝑖 = 2𝑛𝑛𝑖𝑖 ∙ 𝐼𝐼𝑖𝑖 + 1 und für die Gesamtmultiplizität 𝒛𝒛 = ∏ 𝒛𝒛𝒊𝒊 . Für Lysin ergeben sich demnach: • • Für das Proton am Cβ genau sechs Linien (𝑛𝑛1 = 1 vom C α H und 𝑛𝑛2 = 2 vom C γ H2). Für die Protonen am Cγ genau neun Linien (beide Nachbar-C‘s haben zwei Protonen). Die übernächsten Nachbarn sind zu vernachlässigen. Die vicinale Spin-Spin-Kopplung (3J) erlaubt Rückschlüsse auf die Torsionswinkel (KarplusBeziehung), da die Kopplungskonstante mit dem Winkel variiert. So sind trans-Konformation bei 180° und gauche-Konformation bei 60° genau zu unterscheiden. Damit lassen sich für Proteine Sekundärstrukturen bestimmen. Relaxationsmechanismen Die aufgenommene Energie des Spinsystems wird mit der Zeit auf die Umgebung oder auf andere Spins übertragen (Relaxationsprozess). Die Relaxationszeit beschreibt die Zeit, die nach Abschalten des B1-Feldes vergeht, bis der Anteil 1/e der aufgenommenen Energie disspativ abgegeben wurde. • • T1: Spin-Gitter oder longitudinale Relaxation. T2: Spin-Spin oder transversale Relaxation. Beide Relaxationen tragen zur Breite der NMR-Linien bei, da sie die Lebensdauer eines Spinzustandes verkürzen. Eine lange Lebensdauer (~1s) bedeutet nach Heißenberg eine geringe Energieunschärfe (bei 2,35T scharfe Linie von ~0,1Hz). Eine kurze Lebensdauer (𝟏𝟏𝟏𝟏−𝟒𝟒 𝒔𝒔) ergibt eine sehr breite Linie (~1000Hz). Aus der Linienbreite kann damit die Lebensdauer bestimmt werden (eleganter: FT-NMR). Die Relaxation beruht auf fluktuierenden magnetischen Wechselwirkungen. So ist die Dipol-DipolWechselwirkung abhängig von der Rotationskorrelationszeit der benachbarten Moleküle oder molekularen Gruppen. Relaxationszeiten enthalten damit Informationen über inter- und intramolekulare Interaktionen (Konformation und Assoziation bei Makromolekülen). Spin-Gitter-Relaxation Das B0-Feld erzeugt eine longitudinale Magnetisierung in z-Richtung (Mz). Das B1-Feld stört die Boltzmann-Verteilung und verringert die longitudinale Magnetisierung. Nach Ausschalten von B1, kehrt Mz zu ihrem Gleichgewichtswert M0 zurück. Dies folgt einem exponentiellen Zeitgesetz. Die Überschussenergie wird über thermische Prozesse an die Umgebung (Gitter) abgegeben, weshalb es sich um einen enthalpischen Prozess handelt. Spin-Spin-Relaxation 𝑴𝑴𝒛𝒛 = 𝑴𝑴𝟎𝟎 �𝟏𝟏 − 𝒆𝒆−𝒕𝒕/𝑻𝑻𝟏𝟏 � Im B1-Feld präzedieren die Spins in Phase. Daraus resultiert eine Quermagnetisierung My. Ohne B1-Feld geht die Phasen-Kohärenz verloren, wodurch sich die Spins wieder gleichmäßig auf der Kegelfläche verteilen. Die transversale Magnetisierung fällt auf null ab. Es handelt sich um einen entropischen Prozess. Ursache sind WW zwischen Spins, die temporärer und zufälliger Natur sind und eine Feld-Heterogenität verursachen. Da die Spins nicht alle mit derselben Larmor-Frequenz rotieren folgt eine schnelle Dephasierung. Diese Art der Relaxation wird durch Magnetfeld-Inhomogentitäten beschleunigt (muss bei Bestimmung von T2 rausgemittelt werden). Vergleich der Relaxationszeiten 𝑴𝑴𝒚𝒚 = 𝑴𝑴𝒚𝒚𝒚𝒚 �𝒆𝒆−𝒕𝒕/𝑻𝑻𝟐𝟐 � Bei kleinen Molekülen im gelösten oder flüssigen Zustand ist 𝑇𝑇1 ~𝑇𝑇2 . Im festen Zustand oder bei gelösten Makromolekülen ist 𝑻𝑻𝟏𝟏 > 𝑻𝑻𝟐𝟐 , d.h. die Quermagnetisierung fällt auf null ab, bevor die Boltzmann-Verteilung erreicht ist (FID wird durch T2 bestimmt!). T1 kann niemals kleiner als T2 sein. Die longitudinale Gleichgewichtsmagnetisierung M0 kann nur erreicht werden, wenn die Phasenbeziehung verloren gegangen ist. Bei einem endlichen My ist Mz immer kleiner M0. Effektive Relaxationsprozesse sind wie bei der ESR für die Aufnahme eines NMR-Spektrums essentiell. Im CW-Experiment wird der Effekt von B1 auf die Magnetisierung ständig durch die Relaxationsprozesse korrigiert. Puls-Fourier-Transform-NMR In der CW-Technik werden Spektren bei kontinuierlicher Einstrahlung eines B1-Feldes mit konstanter Frequenz durch Variation des B0-Feldes aufgenommen. Das Spektrum ist durch die chemische Verschiebung und die Spin-Spin-Kopplungskonstante charakterisiert. Mithilfe der Puls-FT-NMR werden Zusatzinformationen durch Messung der beiden Relaxationszeiten erhalten. Nach einem B1-Puls wird das Verhalten des Spinsystems zeitabhängig untersucht. Über FT wird dann das Zeitdomänen-Signal in das typische Frequenz-Spektrum umgewandelt. Der kurze Hochfrequenzpuls ist nicht monochromatisch, sondern enthält alle Frequenzen aus dem Gesamtbereich der möglichen Verschiebung eines Kerns. Ein Spektrum kann damit innerhalb ~1s aufgenommen werden. Über Spektren-Akkumulation werden dann intensivere Spektren erhalten. Der Intensitäts-pro-Zeit-Gewinn ist um einen Faktor 100 besser als der in der cw-Technik. Pulstechnik Ein Hochfrequenzpuls der Dauer tp und der magnetischen Induktion B1 in Richtung x‘-Achse dreht die Magnetisierung Mz in der zy‘-Ebene um einen definierten Winkel 𝜽𝜽 = 𝜸𝜸𝑩𝑩𝟏𝟏 𝒕𝒕𝒑𝒑 . 𝛾𝛾 ist das gyromagnetische Verhältnis, das für jeden Kern charakteristisch ist. B1 muss so groß gewählt werden, dass tp klein gegenüber den Relaxationszeiten ist. Typische Werte sind 1µ𝑠𝑠 < 𝑡𝑡𝑝𝑝 < 50µ𝑠𝑠. Freier Induktionsabfall Das Abklingen der Quermagnetisierung nach einem Hochfrequenzpuls wird als FID (free induction decay) bezeichnet. Nach einem 90°-Puls liegt die Quermagnetisierung mit ihrem Maximalwert in der y‘-Richtung. Der Betrag von My‘ entspricht der Intensität des NMR-Signals. Nach dem Puls verlieren die Spins ihre Phasenkohärenz und My‘ klingt mit der Zeit ab: 𝑑𝑑𝑀𝑀𝑦𝑦′ 𝑀𝑀𝑦𝑦′ =− 𝑑𝑑𝑑𝑑 𝑇𝑇2 Dies gilt jedoch nur in einem ideal homogenen B0-Feld. In der Realität liegen immer geringe Inhomogenitäten vor, sodass T2 durch T2* ersetzt werden muss. T2* beinhaltet den Beitrag der transversalen Relaxation und den Beitrag der Magnetfeld-Inhomogenität. Eine bestimmte Abklingkurve entsteht aber nur, wenn die Impulsfrequenz genau mit der Larmorfrequenz übereinstimmt. Sie ist demnach nur für eine spezifische chemische Verschiebung gültig. Ein Vorteil der FT-NMR ist die gleichzeitige Aufnahme des Gesamtspektrums durch einen Hochfrequenzpuls, der alle Frequenzen abdeckt. Die Impulsfrequenz ist damit nicht immer gleich der Resonanzfrequenz („off resonance“ Fall = Frequenzen des Frequenz-Bands, die für keine Spins der Probe eine Resonanz induzieren). Typische Frequenz-Unterschiede zwischen Larmor- und ImpulsFrequenz liegen bei 50 Hz (die eingestrahlten Frequenzen werden im Intervall von 50 Hz um die erwartete Larmorfrequenz gewählt). Durch Interferenzen entstehen Schwebungen, wobei das Interferogramm die Form einer abklingenden Sinusschwingung hat. Für den resonanten und nichtresonanten Fall kann die Zeitdomänen-Information über FT in die Frequenz-Domäne (Absorptionssignal) umgewandelt werden. Bei Protonen eines Moleküls mit verschiedener CV liegt immer der nichtresonante Fall vor. Das Spektrum in der Zeitdomäne stellt komplexe Schwebungen dar. Nach Akkumulation einer Vielzahl solcher FIDs wird das Frequenzspektrum berechnet. Spin-Echo-Methode zur Messung von T2 T2 ist nur messbar, wenn T2 klein gegenüber dem Beitrag aus der Magnetfeld-Inhomogenität ist, sodass T2 die Relaxationsgeschwindigkeit maßgeblich bestimmt. Ansonsten wird ein T2*-Wert bestimmt, der wesentlich kleiner ist als der reale T2-Wert. Die Spin-Echo Methode ermöglicht die Vernachlässigung der Magnetfeld-Inhomogenität. (a) 90°-Puls in Richtung der x‘-Achse kippt die Magnetisierung aus der z- in die y‘-Richtung. (b) Durch Magnetfeld-Inhomogenitäten präzedieren einige Spins schneller (s) und andere langsamer (l), als der auf y‘ liegende Mittelwert. Mit der Zeit geht die Spin-Kohärenz verloren, wodurch My‘ kleiner wird. (c) Zur Zeit 𝝉𝝉 erfolgt ein 180°-Puls wieder entlang x‘. Dadurch rotiert die Magnetisierung um 180° um die x‘-Achse. (d) Die Magnetisierung präzediert immernoch in x’y‘-Ebene, wobei nun die langsamen Spins dem Mittlerwert vorauseilen und die schnellen hinterher laufen. So wird die PhasenKohärenz mit der Zeit wiederhergestellt und My‘ nimmt zu. (e) Zur Zeit 𝟐𝟐𝟐𝟐 nach dem 90°-Puls fallen alle Spins im Mittelwert zusammen. Die gemessene Magnetisierung (Spin-Echo) ist genauso groß wie direkt nach dem 90° Puls. (f) Bei 𝑡𝑡 > 2𝜏𝜏 geraten die Spins wieder außer Phase. Der Vorgang kann wiederholt werden. Die Folge 90°- 𝝉𝝉-180°- 𝝉𝝉-FID beseitigt damit die unterschiedlichen Präzessionsfrequenzen aufgrund der Magnetfeld-Inhomogenitäten (T2* T2). Die Spin-Spin-Relaxation (T2) führt ebenso zu einem Zerfall der Quermagnetisierung innerhalb der Zeit 2𝜏𝜏. Dieser Effekt kann jedoch nicht durch die Pulssequenz aufgehoben werden, sodass das SpinEcho My‘ nach 2𝜏𝜏 kleiner ist und mit jeder weiteren Pulssequenz exponentiell abnimmt. Aus der logAuftragung der maximalen Echo-Amplitude als Funktion von 𝜏𝜏 kann T2 bestimmt werden. Messung von T1 durch Progressive Sättigung Durch 5-10 direkt hintereinander folgende 90°-Pulse wird ein dynamisches Gleichgewicht zwischen Absorption und Relaxation erreicht. Nach der Zeit 𝝉𝝉 erfolgt nach einem weiteren 90°-Puls die Messung des NMR-Absorptionssignals. Ist in dieser Zeit die longitudinale Magnetisierung noch nicht vollständig wiederhergestellt, wird eine geringere Intensität gemessen. Mit größerem 𝝉𝝉 steigt die Signal-Intensität auf ihren Maximalwert an. Die Auftragung ln (𝐴𝐴∞ − 𝐴𝐴𝑡𝑡 ) als Funktion der Wartezeit liefert eine Gerade mit der Steigung −1/𝑇𝑇1 . Messung von T1 durch die Inversions-Erholungs-Methode Ein 180°-Puls invertiert die Magnetisierung auf die (-z)-Richtung. Nach der Zeit 𝝉𝝉 erfolgt der 90°-Puls. Anschließend wird My‘ über ein FID gemessen. Die FT führt zum Absorptionssignal. Bei sehr kurzen Zeiten zeigt die Magnetisierung Mz nach unten, sodass der 90°-Puls die Magnetisierung auf die negative y‘-Achse klappt und ein negatives Absorptionssignal erhalten wird. Nach längeren Zeiten entsteht ein positives Signal. Dazwischen liegt der Nulldurchgang mit Mz=0 und My‘=0. Zur Messung von T1 muss das NMR-Signal als Funktion der Zeit (bis 100s) aufgenommen werden. Die Intensität steigt von –A bis +A. T1 kann am Nulldurchgang ermittelt werden. 𝐴𝐴 = 𝐴𝐴max �1 − 2e τ − T1 � , Anwendungsbeispiele für Protonen-Resonanz Basen-Stapelung 1 − 2e τ − T1 = 0 → τ = T1 ∙ ln 2 Die Basen haben wegen den π-Elektronen Protonen-Resonanzen bei niedrigem B0-Feld (große chemische Verschiebung). In einer verdünnten Lösung von 6,9-Dimethyl-Adenin liegen die Resonanzstellen der Ring-Protonen bei 8,1 (C2) bzw. 7,95 (C8) und die der CH3-Gruppen bei 3,05-3,75. Bei einer Erhöhung der BasenKonzentration, resultiert eine HochfeldVerschiebung (kleinere ppm-Werte) aller Protonen-Resonanzen. Sie beruht auf der Basen-Stapelung senkrecht zu ihrer Ringebene: Die Nachbarmoleküle schwächen den Ringstrom-Effekt, die chemische Verschiebung nimmt ab. Aus der exakten Berechnung des Abschirm-Effektes lässt sich die Lage der Nukleobasen im Assoziat bestimmen. Hochaufgelöste NMR-Spektren erlauben auch die Lokalisierung von dsRNA-Bereichen in RNA-Molekülen. Analyse von Protein-Spektren Problem der Protonen-Resonanz an Proteinen ist die Auflösung und die Zurodnung einzelner Resonanz-Linien (hohe Frequenzen und 2D-NMR bessere Auflösung). Probleme sind: • • In Peptiden kommt es zu einer Überlagerung der Linien vieler chemisch und magnetisch ähnlicher Gruppen. Typische Protonen-Resonanzen von Aminosäuren liegen bei 1-4,5 ppm für das CαH und aliphatische Reste oder bei 7-9 ppm für aromatische AS. In großen, globulären Proteinen sind die einzelnen Linien wegen langer Rotationskorrelationszeiten (kurze Relaxationszeiten) stark verbreitert. Im nativen Zustand sind die Linien aufgrund der starren Struktur und den daraus resultierenden Dipol-Feldern stark verbreitert. Im denaturierten Zustand wird diese Wechselwirkung aufgehoben, sodass das Spektrum aus gut aufgelösten NMR-Linien besteht, die nahezu der Summe der einzelnen AS-Resonanzen entsprechen. Die Zuordnung eines 1D Spektrums eines Peptids erfolgt über Vergleiche mit den Spektren einzelner AS. Aus der Größe der chemischen Verschiebung und der Spin-Spin-Kopplung kann die Information über Struktur und Dynamik des Peptids erhalten werden. Ab 10 kDa ist eine solche Methode sehr schwierig. Protonen-Spinrelaxation in Proteinen und Lipid-Membranen Relaxationsmessungen liefern grundsätzlich Informationen über oszillierende Bewegungen mit Frequenzen im Bereich der Larmorfrequenz. Bei Protonen liegen die Rotationen des Gesamtmoleküls und auch der Segmentbewegungen in diesem Bereich. Kleine Moleküle mit Rotationskorrelationszeiten 𝝉𝝉𝑹𝑹 < 𝟏𝟏𝟏𝟏−𝟗𝟗 𝒔𝒔 ergeben schmale NMR-Linien. Für die Halbwetsbreite einer Linie gilt: ∆𝑣𝑣1/2 ≥ 1 2𝜋𝜋 ∙ 𝑇𝑇2 Der Zusammenhang zwischen Rotationskorrelationszeit und Relaxationszeiten ist komplex. Im Bereich 10−12 𝑠𝑠 < 𝜏𝜏𝑅𝑅 < 10−8 𝑠𝑠 fallen die Relaxationszeiten (schnellere Relaxation) jedoch mit steigender Rotationskorrelationszeit (geringere Beweglichkeit) ab. Die gemessene Relaxationszeit ist also Maß für die Beweglichkeit. Die Relaxationsprozesse in Proteinen oder Lipid-Membranen werden hauptsächlich durch DipolDipol-WW mit Kernen der Umgebung beeinflusst. Die Relaxationszeit ist also von der Anzahl, der Stärke und dem Abstand benachbarter Dipole sowie dem Frequenz-Spektrum der oszillierenden Dipole abhängig, wobei die Stärke mit der sechsten Potenz des Abstandes abnimmt (Lösungsmitteleinflüsse können durch Verwendung deuterierter Lömis ausgeschlossen werden). Anzahl und Abstand ist bei der Protonen-Resonanz schwer bestimmbar. Aussagen reduzieren sich damit auf relative Beweglichkeitsänderungen. Ferrichrom ist ein zyklisches Hexapeptid aus drei Ornithin-Derivaten und drei Glycin-Molekülen mit Affinität für Fe3+. Durch Metall-Koordination, resultiert eine starre Konformation (Rotationskorrelationszeit basiert auf Rotation des Gesamtmoleküls). Die zeitaufgelösten Spektren der Amid-Protonen nach einem 180°-𝝉𝝉-90° Puls zeigen, dass die Relaxationszeiten der drei Glycylund der drei Ornithyl-Reste verschieden sind (0,15 < 𝑇𝑇1 < 0,3). Da das Molekül eine starre Konformation aufweist, bedeutet dies, dass die Amid-Protonen unterschiedliche Dipolumgebungen in der Raumstruktur haben. Das Metall-freie Molekül besitzt in Lösung eine flexible Struktur. Die Relaxationszeiten für die GlycylReste sind etwa gleich (𝑇𝑇1 = 0,31), die für die Ornithyl-Reste leicht verschieden (𝑇𝑇1 = 0,23; 0,24; 0,18). Theoretisch wären größere Relaxationszeiten aufgrund der höheren Beweglichkeit im Vergleich zum komplexierten Ferrichrom zu erwarten. Die größere Beweglichkeit (größere Relaxationszeiten) kann durch abnehmenden Dipol-Dipol-Abstand (kleinere Relaxationszeiten) kompensiert werden. Genaue Aussagen können jedoch nicht getroffen werden. Der physikalische Zustand einer Membran kann zwar qualitativ beschrieben und Phasenumwandlungen verfolgt werden, quantitative Aussagen (Ordnungsgrad, Molekülorientierungen) sind jedoch nicht möglich. Die Linien verschmälern beim Übergang in die fluide Phase, was eine zunehmende Flexibilität bedeutet. pH-Abhängigkeit der NMR-Spektren von Aminosäuren Die chemische Verschiebung von Protonen ist auch vom Ionisationsgrad abhängig. Mit steigendem pD-Wert verschieben sich die Resonanz-Linien von Alanin zu kleineren CVs (höheres Feld). Es wird eine Titrationskurve erhalten, da bei den pK-Werten die CV sprunghaft abfällt. Bei den CαH Protonen ist dieser Einfluss wegen der direkten Nachbarschaft zu den funktionellen Gruppen größer als bei den Protonen der CH3-Gruppe des Alanins. Grund für dieses Verhalten: Die bei hohem pH dissoziierte COO- Gruppe erzeugt mit ihrem delokalisierten π-Elektronenystem eine höhere Elektronendichte am Cα und auch am Cβ. Daraus resultiert eine bessere Abschirmung der Protonen (kleinere 𝛿𝛿-Werte). Die deprotonoerte NH2-Gruppe besitzt im Gegensatz zum NH3+ ein freies Elektronenpaar, was ebenso eine bessere Abschmirmung ermöglicht. Histidin kommt häufig in aktiven Zentren von Enzymen vor. Die CV der Protonen am Imidazol-Ring liegt pH-abhängig zwischen 7 und 9 ppm. Diese pH-Abhängigkeit erleichtert die Zuordnung von Histidin-Resonanzen. Aus den Titrationskurven kann der pK ermittelt werden. Verschiebungen im pK-Wert ergeben Hinweise auf unterschiedliche chemische Umgebungen, sodass Konformationsänderungen detektiert werden können. Moderne Techniken Spin-Entkopplung Bei einfachen Spektren kann aus der Multiplett-Struktur die Kopplungskonstante abgeleitet werden. Multipletts mit gleichen J-Werten sind miteinander gekoppelt. Besteht ein Spektrum aus verschiedenen Multipletts mit gleicher Kopplungskonstante, müssen miteinander koppelnde Kerne über die Spin-Entkopplung zugeordnet werden. Die Nachbarspins erzeugen am Ort des betrachteten Kerns ein Zusatzfeld. Wenn man also mithilfe eines zweiten Senders den koppelnden Nachbarkern durch Einstrahlen in seine Resonanzfrequenz (Doppelresonanz-Technik) zu dauernden Übergängen zwingt, mittelt sich das Zusatzfeld heraus und die Multiplettstruktur des betrachteten Kerns vereinfacht sich oder verschwindet ganz. Bei gleichen Kernen entsteht ein homonuklear entkoppeltes Spektrum. Strahlt man z.B. bei Lysin mit dem Zusatzfeld in die Resonanz der CαH bei 3,8 ppm ein, so koppelt es nicht mehr mit dem CβH2. Das Multiplett vereinfacht sich von sechs auf drei Linien (Kopplung mit CγH2 bleibt bestehen). Da eine Kopplung nur mit Protonen auftritt, die zwei oder drei Bindungen voneinander entfernt sind, kann durch selektive Entkopplung eine eindeutige Zuordnung benachbarter Kerne erfolgen. Die Entkopplung von Protonen ist für die 13C-Spektroskopie besonders wichtig, um die Multiplettstruktur zu vereinfachen (heteronukleare Entkopplung). Zweidimensionale NMR-Spektroskopie Bei der J-Spektroskopie werden chemische Verschiebung und Kopplungskonstante voneinander getrennt auf zwei Achsen dargestellt. Das entkoppelte Spektrum erhält man durch Projektion der 2D-Intensitäten in Richtung der 𝛿𝛿-Achse. Das gekoppelte Spektrum ist eine Projektion in Richtung J-Achse. Ein 1D NMR Experiment hat eine Frequenzachse und eine Intensitätsachse. Ein 2D NMR Experiment hat 2 Frequenzachsen und die Intensitäten entsprechen der dritten Dimension. Sie werden als 3D Peaks oder Konturlinien dargestellt, wobei die Abstände logarithmisch sind. Bei den 2D-NMR-Spektren unterscheidet man zwischen J-aufgelösten und verschiebungskorrelierten NMR-Spektren: J-aufgelöst: 1. Achse chemische Verschiebung, 2. Achse Kopplungskonstanten (J); Verschiebungskorreliert: beide Achsen chemische Verschiebung. Messung eines verschiebungskorrelierten 2D Spektrums am Beispiel einer Probe, die nur eine Resonanzlinie aufweist (Z.B. Chloroform): Aus dem Besetzungsunterschied resultiert eine geringe Überschussmagnetisierung M0 in z-Richtung 90° Puls bringt diese Überschussmagnetisierung auf die y-Achse Während der Zeit t1 präzidiert der Vektor um das statische Feld B0 in z-Richtung (Bewegung in x,y Ebene). Dadurch erhält die Magnetisierung eine Komponente in x- und eine in y-Richtung. Es wird in diesem Zeitraum der Winkel 2𝜋𝜋𝜋𝜋𝑡𝑡1 zurückgelegt. Die Komponente der Magnetisierung in yRichtung beträgt danach 𝑀𝑀 cos 2𝜋𝜋𝜋𝜋𝑡𝑡1 (in x-Richtung mit sin) Zweiter 90° Puls bringt die y-Achsen Komponente der Magnetisierung auf die z-Achse, wodurch sie nicht mehr detektierbar wird. Die x-Achsen Komponenten bleibt in der x,y Ebene und kann detektiert werden. Während der Zeit t2 erfolgt die Aufnahme des FID und eine anschließende Fourriertransformation Wiederholung des Experiments mit verschiedenen t1 Zeiten (Inkrementierung von t1; schrittweise erhöhung um selben Betrag, beginnend bei 0ms). Nach FT erhält man eine Reihe von Peaks an derselben Stelle. Die Höhe der Peaks variiert mit t1 (oszilliert sinus-förmig mit der Frequenz v) Verbindung der Peak-Enden (Datenpunkte) miteinander führt zu einem Schaubild der Amplitude des ursprünglichen Signals, die mit der Frequenz v oszilliert. Dies ist das zweite FID (Interferrogramm). Nach FT erhält man so ein 2 D Spektrum. Es wurden also 2 Richtungen Fourriertransformiert. 2 Fourriertransformationen: 𝑡𝑡2 ⟶ 𝜈𝜈2 (real time) und 𝑡𝑡1 ⟶ 𝜈𝜈1 (Inkrementierung von 𝑡𝑡1 ) COSY: Achse 1 enthält die normale CV, Achse 2 die Differenz-Frequenz zwischen korrelierten Spins. 3D-Strukturbestimmung eines Proteins über COSY, TOCSY, NOESY Die Strukturbestimmung erfolgt in drei separaten Schritten: 1. Zuordnung der Resonanzen (assignment) d.h. Bestimmung der chemischen Verschiebung der einzelnen Kerne. 2. Gewinnung von Strukturinformation d.h. Interpretation der Spektren bezüglich Abständen, Dihedralwinkeln. 3. Strukturberechnung unter Berücksichtigung der NMR-Daten (Pseudoenergie) und der theoretischen Energie des Moleküls. 2D-NMR-Experimente verlaufen nach dem selben Schema: (1) Präparationszeit: Alle Spins werden in einen einheitlichen Ausgangszustand gebracht (2) Evolutionszeit (t1, variabel): Zeitabhängige Entwicklung der Magnetisierung (chemische Verschiebung in der ersten Dimension) (3) Mischphase (tm, konstant): Magnetisierungstransfer auf andere Kerne (bestimmt Signalintensität) a. COSY: direkte J-Kopplung über 2-3 Bindungen. b. TOCSY: J-Kopplung im gesamten Spinsystem. c. NOESY: Kopplung zwischen Protonen in räumlicher Nähe (<5Å); induzierte Dipole. (4) FID (t2) Information über Struktur: • • aus NOE-Intensitäten: Entfernungen zwischen Protonen aus Kopplungen: erlaubte Bereiche für Dihedralwinkel Verbreitetste Strategie: "simulated annealing". Programm erstellt zahlreiche Startstrukturen, Verletzungen der "erlaubten" Bereiche (Entfernung, Winkel) werden als zusätzliche Pseudo-Energie behandelt. Molekulardynamik mit abnehmender Temperatur, am Schluß Energieminimierung. Die 20-30 Strukturen mit der niedrigsten Energie werden als NMR-Struktur veröffentlicht (zeigt Genauigkeit der lokalen Konformationsbestimmung). 13C-NMR Spektroskopie 13C Kerne haben ebenso wie 1H-Kernen einen Spin von 𝐼𝐼 = 0,5. Der Vorteil der 13C-NMR von Makromolekülen liegt darin, dass direkt das Molekülgerüst und funktionelle Gruppen ohne Protonen spektroskopiert werden können. Nachteil: geringe Empfindlichkeit, geringes natürliches Vorkommen (Signal-Intensität um Faktor 6k niedriger als bei 1H). Über Isotopen-Markierung und den NOE-Effekt wird das Signal verstärkt. Die starke Hyperfeinaufspaltung durch Wechsewlrikung mit Protonen kann durch Spin-Entkopplung aufgehoben werden, was die Komplexität des Spektrums erheblich reduziert. Chemische Verschiebung Im Vergleich zur 1H-NMR sind die Werte der CV bei 13C-Kernen erheblich größer. 𝛿𝛿-Werte liegen im Bereich bis zu 200 ppm, während für 1H-NMR maximal 10 ppm erreicht wurde. Qualitativ ist aber der Einfluss von Nachbargruppen der gleiche. Spin-Spin-Kopplung In natürlich vorkommenden Materialien sind nur die heteronuklearen Kopplungen zu 1H-Kernen von Bedeutung. Die homo- und heteronuklearen Kopplungskonstanten der 13C-Kerne sind mit 130-200Hz erheblich größer als die 1H-1H-Kopplungskonstanten mit Werten bis zu 10 Hz. Durch IsotopenMarkierung liefert auch die 13C-13C-Kopplung wichtige Struktur-Informationen. Isotopen-Markierung Natürliche Proben enthalten ca. 1,1% 13C-Kerne bezogen auf den Gesamt-Kohlenstoff. Die Intensitätssteigerung durch Isotopen-Markierung ist durch die zunehmende 13C-13C-Kopplung beschränkt. Doppelresonanz-Technik und NOE-Effekt Bei der 13C-NMR wird meist die 1H-13C-Entkopplung angewendet. Bei der Breitband-Entkopplung enthält das entkoppelnde Feld die Resonanz-Frequenzen aller vorhandenen Protonen. Eine Begleit-Erscheinung der Entkopplung ist eine Intensitätssteigerung aufgrund des NOE. 13Cund 1H-Kerne bilden ein gemeinsames Spinsystem. Erregt man nun die Protonen-Resonanz, wird das GG (Boltzmann-Verteilung) gestört. Das System stellt die Boltzmann-Verteilung durch vermehrte 13C-Relaxation wieder her, d.h. der Grundzustand der 13C-Kerne wird stärker besetzt und es kann mehr Hochfrequenz-Leistung aufgenommen werden. Die Signal-Intensität kann dadurch bis auf das dreifache gesteigert werden. Bestimmung von Segmentbeweglichkeiten durch T1-Messung Die Messung von T1 ermöglicht die Charakterisierung dynamischer Prozesse in Makromolekülen. Unterschiedliche T1-Zeiten z.B. einer bestimmten Aminosäure in verschiedenen Positionen des Proteins, erlauben über die zu berechnenden Rotationskorrelationszeiten Aussagen über Segmentbeweglichkeiten. Die Relaxationszeiten von 13C-Kernen sind wegen der 𝑟𝑟 −3 -Abhängigkeit der Dipol-Dipol-Wechselwirkung stark von den benachbarten Atomen abhängig. 13C-Kerne mit gebundenem Wasserstoff haben Werte zwischen 1s und 20s, 13C-Kerne ohne Wasserstoff haben Relaxatiosnzeiten um 30s. In größeren Molekülen sind die T1-Zeiten wesentlich kürzer (schnelle Relaxation wegen langsamer Rotation). Die Abbildung zeigt die T1-Zeiten der einzelnen 13C-Kerne eines Lipids innerhalb einer Membran. Die Kopfgruppe ist recht beweglich. In der Nähe des Glycerol-Grundgerüsts ist die Beweglichkeit stark eingeschränkt, nimmt aber zum Kettenende hin drastisch zu. 31P-NMR 31P enthält ebenso einen Spin von 𝐼𝐼 = 0,5. Die chemische Verschiebung wird häufig relativ zur Phosphorsäure gemessen. Kopplungskonstanten liegen bei 10-30Hz. 31P-NMR kann in vivo durchgeführt werden, um z.B. Stoffwechselvorgänge zu verfolgen. Darüber hinaus liefert die 31P-Spektroskopie Aussagen über die räumliche Anordnung der Biomoleküle. Dies ist möglich durch die Anisotropie der chemischen Verschiebung. Die Elektronenverteilung um eine R2PO4-Gruppe z.B. in Phospholipiden ist nicht isotrop. Die CV ist von der Orientierung des Molekülachsen-Systems zum B0-Feld abhängig. • • Mittlere Abbildung: 01/02 = Sauerstoffe der Ester-Bindung , 03/04 = freie Elektronen der Ester-Bindung. Rechte Abbildung: H-entkoppeltes 31P-Spektren für unterschiedliche Winkel zwischen B0 und Membran-Normalen. Entsprechend dem g-Faktor der ESR-Spektroskopie muss die CV dann durch einen Abschirmtensor mit 𝛿𝛿𝑥𝑥𝑥𝑥 , 𝛿𝛿𝑦𝑦𝑦𝑦 , 𝛿𝛿𝑧𝑧𝑧𝑧 beschrieben werden. Das 31P-Spektrum ist dadurch Orientierungs-abhängig. Die Anisotropie liefert mit den 𝛿𝛿∥ - und 𝛿𝛿⊥ -Werten von Sonden einen Ordnungsgrad (dadurch ist eine Zuordnung von Lipid-Phasen möglich). Licht-Streuung Im Gegensatz zur Absorption, die nur bei Molekül-spezifischen Wellenlängen auftritt, tritt Streuung im gesamten sichtbaren Wellenlängenbereich auf. Aus der gestreuten Strahlung lässt sich die relative Molekülmasse sowie die Diffusionskoeffizienten der streuenden Teilchen bestimmen. Außerdem werden Informationen über Moleküldimensionen und WW zwischen Makromolekülen erhalten. Man unterscheidet mechanistisch drei verschiedene Streuprozesse: • • • Elastische Streuung: Einfallende und gestreute Strahlung haben die gleiche Frequenz (Rayleigh-Streuung: 𝑑𝑑 ≪ 𝜆𝜆/2, Mie-Streuung: 𝑑𝑑 ≫ 𝜆𝜆/2). Quasi-elastische Streuung: Frequenz des gestreuten Lichts wird durch Translationsbewegungen der streuenden Teilchen verändert. Frequenzspektrum resultiert aus Doppler-Verbreiterung der gestreuten Strahlung. Inelastische Streuung (Raman-Streuung): Streuprozess regt Molekülschwingungen an. Elastische Lichtstreuung Streuung an einem isolierten, isotropen Molekül Eine monochromatische, polarisierte Lichtwelle (keine Absorptionsfrequenz) trifft auf ein einzelnes Molekül. Für die Streuung ist lediglich der elektrische Feldvektor relevant: 𝑥𝑥 𝐸𝐸 = 𝐸𝐸0 ∙ cos �2𝜋𝜋 ∙ 𝑣𝑣 �𝑡𝑡 − �� 𝑐𝑐 Das streuende Teilchen sei klein gegenüber der Wellenlänge, sodass E am Ort des gesamten Teilchens als konstant angenommen werden kann. Das E-Feld übt eine Kraft auf die elektrische Ladung des Moleküls aus, die zu einer Verschiebung der Elektronen und des Kerns in entgegengesetzter Richtung führt und dadurch ein elektrisches Dipolmoment 𝝁𝝁 = 𝜶𝜶𝜶𝜶 induziert. Die Größe des induzierten Dipolmoments wird durch die Polarisierbarkeit α bestimmt (für isotropes Teilchen richtungsunabhängig, also Skalar). Das E-Feld der Strahlung induziert somit ein oszillierendes Dipolmoment: 𝑥𝑥 𝜇𝜇 = 𝛼𝛼 ∙ 𝐸𝐸0 ∙ cos �2𝜋𝜋 ∙ 𝑣𝑣 �𝑡𝑡 − �� 𝑐𝑐 𝑑𝑑𝑑𝑑 𝑥𝑥 = −𝛼𝛼 ∙ 𝐸𝐸0 ∙ 2𝜋𝜋𝜋𝜋 ∙ sin �2𝜋𝜋 ∙ 𝑣𝑣 �𝑡𝑡 − �� , 𝑑𝑑𝑑𝑑 𝑐𝑐 𝑑𝑑 2 𝜇𝜇 𝑥𝑥 = −𝛼𝛼 ∙ 𝐸𝐸0 ∙ 4𝜋𝜋 2 𝑣𝑣 2 ∙ cos �2𝜋𝜋 ∙ 𝑣𝑣 �𝑡𝑡 − �� 𝑑𝑑𝑡𝑡 2 𝑐𝑐 Oszillierende Dipole senden wiederum selbst EM-Strahlung aus. Die elektrische Feldstärke der Dipolstrahlung ist proportional zu 𝑑𝑑2 𝜇𝜇/𝑑𝑑𝑡𝑡 2 und ist vom Winkel 𝚽𝚽 zwischen Dipolachse und betrachteter Streurichtung abhängig. Die Feldlinien ausgehend von einem oszillierenden Dipol sind charakteristisch verteilt. Die Streuintensität ist maximal senkrecht zur Dipolachse; in Richtung der Dipolachse tritt keine Strahlung aus. Abbildung: Links ist Phase der einfallenden Strahlung am Ort des Dipols gezeigt. Rechts die Feldlinien der emittierten Dipolstrahlung. Das E-Feld der Dipolstrahlung lässt sich klassisch berechnen und zeigt lediglich eine im Vergleich zum Einstrahl-Licht veränderte Amplitude: 𝐸𝐸 = 𝛼𝛼 ∙ 𝐸𝐸0 ∙ 4𝜋𝜋 2 ∙ sin Φ 𝑥𝑥 ∙ cos �2𝜋𝜋 ∙ 𝑣𝑣 �𝑡𝑡 − �� 2 𝑐𝑐 𝑟𝑟 ∙ 𝜆𝜆 Die Intensität der Streustrahlung ist proportional zum Quadrat der Amplitude der elektrischen Feldstärke. Das Verhältnis der Streuintensität 𝐼𝐼𝑆𝑆 zur Intensität des eingestrahlten Lichts 𝐼𝐼0 ist (es kürzt sich quasi nur 𝐸𝐸0 aus der Amplitude raus): 𝐼𝐼0 ~𝐸𝐸02 , 2 4𝜋𝜋 2 ∙ sin Φ 𝐼𝐼𝑆𝑆 ~ �𝛼𝛼 ∙ 𝐸𝐸0 ∙ � , 𝑟𝑟 ∙ 𝜆𝜆2 𝑰𝑰𝑺𝑺 16𝜋𝜋 4 2 = 𝛼𝛼 ∙ 2 4 ∙ sin2 Φ 𝑰𝑰𝟎𝟎 𝑟𝑟 ∙ 𝜆𝜆 Wichtig: Richtungsabhängigkeit (𝐬𝐬𝐬𝐬𝐬𝐬𝟐𝟐 𝚽𝚽) und Wellenlängen-Abhängigkeit (𝝀𝝀−𝟒𝟒 ). Letztere erklärt den hohen Anteil kurzwelligen Lichts in der Streustrahlung des Sonnenlichts in der Atmosphäre und lässt den Himmel blau erscheinen. Bisher wurde linear polarisiertes Licht betrachtet. Bei unpolarisiertem Licht besitzt die relative Streuintensität lediglich eine veränderte Winkelabhängigkeit. Der Winkel 𝛉𝛉 liegt zwischen einfallender Strahlung und Beobachtungsrichtung. Die x-Achse ist die Einfallsrichtung des Lichts. 𝑰𝑰𝑺𝑺 16𝜋𝜋 4 1 = 𝛼𝛼 2 ∙ 2 4 ∙ (1 + cos 2 θ) 𝑰𝑰𝟎𝟎 𝑟𝑟 ∙ 𝜆𝜆 2 Winkelverteilung für polarisiertes Licht. 𝐼𝐼𝑆𝑆 ~ sin2 Φ Winkelverteilung für unpolarisiertes Licht. 𝐼𝐼𝑆𝑆 ~1 + cos 2 θ Streuung an mehreren Molekülen Hier muss die gegenseitige Phasenlage der durch die verschiedenen Moleküle emittierten Streustrahlung berücksichtigt werden. Für die Streuung an gelösten Makromolekülen, die relativ zueinander freie Bewegung ausführen können, ist der zeitliche Mittelwert der Streuintensität durch die Summe der Streuintensitäten der Einzelmoleküle gegeben: Streuung an verdünnten Gasen Die Polarisierbarkeit α ist direkt mit der Brechzahl n über die Clausius-Mosotti-Gleichung verknüpft Taylorentwicklung von n nach c ergibt Polarisierbarkeit Streuintensität der Teilchen (einfach oben α ersetzen!) Beziehung zwischen Molekülmasse (über Experiment berechenbar) und Streuintensität (im Experiment gemessen) 𝐼𝐼𝑆𝑆,𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺 = � 𝐼𝐼𝑆𝑆𝑖𝑖 𝟐𝟐 𝒏𝒏 − 𝟏𝟏 = 𝟒𝟒𝝅𝝅 ∙ 𝑵𝑵 ∙ 𝜶𝜶 𝟏𝟏 𝒅𝒅𝒅𝒅 𝑴𝑴𝒓𝒓 𝜶𝜶 = ∙ ∙ 𝟐𝟐𝟐𝟐 𝒅𝒅𝒅𝒅 𝑵𝑵𝑨𝑨 N = Teilchenzahl pro Volumeneinheit. Für verdünnte Gase liegt die Brechzahl nahe 1. 𝑐𝑐 = 𝑀𝑀𝑟𝑟 𝑁𝑁 𝑁𝑁𝐴𝐴 = Teilchenkonzentration 𝑀𝑀𝑟𝑟 = relative Molekülmasse 𝑰𝑰𝑺𝑺 1 𝑑𝑑𝑑𝑑 2 𝑀𝑀𝑟𝑟2 16𝜋𝜋 4 1 = 2 ∙ � � ∙ 2 ∙ 2 4 ∙ (1 + cos 2 θ) 𝑰𝑰𝟎𝟎 4𝜋𝜋 𝑑𝑑𝑑𝑑 𝑁𝑁𝐴𝐴 𝑟𝑟 ∙ 𝜆𝜆 2 Die Änderung der Brechzahl mit der Konzentration 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 muss in einem separaten Experiment bestimmt werden. Bei einer Streuung am idealen Kristall resultiert für eine im Vergleich zur Lichtwellenlänge genügend kleinen Gitter-Konstanten eine Streuintensität nur in Richtung der einfallenden Lichtwelle. Für alle anderen Beobachtungsrichtungen existiert zu jedem Streuzentrum 𝑖𝑖 ein weiteres Streuzentrum 𝑗𝑗, dessen emittierte Streustrahlung eine Phasenverschiebung von 180° gegenüber 𝑖𝑖 aufweist. Damit löschen sich diese Streustrahlungen aus (destruktive Interferenz). In Richtung der einfallenden Strahlung sind alle Streuwellen in Phase und verstärken sich (konstruktive Interferenz). Streuung an Molekülen in Lösung 𝑛𝑛2 − 𝑛𝑛02 = 4𝜋𝜋 ∙ 𝑁𝑁 ∙ 𝛼𝛼 Für Lösungen muss die Brechzahl n0 des Lösungsmittels in der Clausius-Mosotti-Gleichung berücksichtigt werden. Umformen, erweitern mit c 𝛼𝛼 = 𝑛𝑛+𝑛𝑛 0 4𝜋𝜋 ∙ 𝑛𝑛−𝑛𝑛 0 𝑐𝑐 𝑛𝑛−𝑛𝑛 𝜶𝜶 ist hier die Differenz der Polarisierbarkeit der gelösten Moleküle und der Polarisierbarkeit der Lösungsmittel-Moleküle 𝑛𝑛−𝑛𝑛 0 𝑐𝑐 𝑐𝑐 ist die spezifische Änderung der Brechzahl für die gelösten Moleküle ∙ 𝑁𝑁 𝑑𝑑𝑑𝑑 𝒏𝒏 0 Für lineare Änderung gilt: = 𝑐𝑐 𝑑𝑑𝑑𝑑 Für verdünnte Lösung gilt: 𝑛𝑛 + 𝑛𝑛0 = 2𝑛𝑛0 𝒅𝒅𝒅𝒅 𝑴𝑴 𝜶𝜶 = 𝟐𝟐𝟐𝟐𝟎𝟎 ∙ 𝒅𝒅𝒅𝒅 ∙ 𝑵𝑵 𝒓𝒓 𝑰𝑰𝑺𝑺 𝑰𝑰𝟎𝟎 Streuintensität des gelösten Teilchens: 𝑛𝑛 2 𝑨𝑨 𝑑𝑑𝑑𝑑 2 𝑀𝑀 2 16𝜋𝜋 4 1 = 4𝜋𝜋02 ∙ � 𝑑𝑑𝑑𝑑 � ∙ 𝑁𝑁 𝑟𝑟2 ∙ 𝑟𝑟 2 ∙𝜆𝜆 4 ∙ 2 (1 + cos2 θ) 𝐴𝐴 Besser: Streuintensität 𝑖𝑖𝑠𝑠 pro Volumen des streuenden Mediums. Die streuenden Teilchen sind statistisch verteilt => Gesamtintensität pro Volumeneinheit = Summe der Beiträge einzelner Teilchen. Rayleigh-Verhältnis enthält experimentell gegebene Größen Für ideale Lösungen ergibt sich 𝐾𝐾∙𝑐𝑐 𝑅𝑅𝜃𝜃 Für reale Lösungen muss die Wechselwirkung zwischen gelösten Molekülen durch c-abhängige Korrekturterme berücksichtigt werden 1 = 𝑀𝑀 𝑟𝑟 𝐾𝐾 = 𝑲𝑲𝑲𝑲 𝑹𝑹𝜽𝜽 = 2𝜋𝜋 2 ∙𝑛𝑛 02 𝑁𝑁𝐴𝐴 ∙𝜆𝜆 4 𝟏𝟏 𝑴𝑴𝒓𝒓 𝒊𝒊 𝒓𝒓𝟐𝟐 𝑹𝑹𝜽𝜽 = 𝑰𝑰𝒔𝒔 ∙ 𝟏𝟏+𝐜𝐜𝐜𝐜𝐜𝐜𝟐𝟐 𝜽𝜽 𝑑𝑑𝑑𝑑 2 ∙ � 𝑑𝑑𝑑𝑑 � + 𝟐𝟐𝟐𝟐𝟐𝟐 + ⋯ 𝟎𝟎 Der zweite Viralkoeffizient B ist Maß für Stärke der WW. 𝐾𝐾𝐾𝐾 Die Messung von 𝑅𝑅 in Abhängigkeit von 𝑐𝑐 erfolgt bei 𝜃𝜃 konstantem Streuwinkel 𝜃𝜃. Die Extrapolation der Messkurve für 𝑐𝑐 → 0 liefert aus dem Ordinaten-Schnittpunkt die Molekülmasse der streuenden Teilchen. Die Steigung der Kurve bei kleinen Konzentrationen ergibt den VirialKoeffizienten 𝑩𝑩. Streuung an größeren Molekülen Bei größeren Molekülen ist die elektrische Feldstärke der einfallenden Strahlung nicht mehr im gesamten Molekül konstant. Es kann demnach kein punktförmiger Dipol betrachtet werden, da die Ladungen des Moleküls in verschiedenen Teilen des Moleküls mit unterschiedlicher Phase zur Oszillation angeregt werden. Es resultieren induzierte Dipole innerhalb eines Moleküls, die phasenverschoben oszillieren. Die Streuzentren innerhalb eines Moleküls sind in ihrer Anordnung weitgehend fixiert und daher keine unabhängigen Streuer. Die Streustrahlungen des Moleküls interferieren und löschen sich je nach Molekülgeometrie und Streurichtung mehr oder weniger aus. Das unterschiedliche Streuverhalten aufgrund von Interferenzeffekten zwischen Streuzentren kann durch die 𝑃𝑃(𝜃𝜃) ≤ 1 Funktion beschrieben werden. Sie entspricht dem Verhältnis zwischen der Streuintensität des realen Makromoleküls und des punktförmig angenommenen Makromoleküls für einen gegebenen Winkel 𝜃𝜃. 𝑅𝑅𝐺𝐺 ist der Gyrationsradius der streuenden Moleküle (mittlerer Abstand der einzelnen Massenpunkte vom Massenschwerpunkt des Moleküls). 𝑃𝑃(𝜃𝜃) = 1 − 16𝜋𝜋 2 ∙ 𝑅𝑅𝐺𝐺2 𝜃𝜃 ∙ sin2 2 3𝜆𝜆 2 Damit ergibt sich für die Lichtstreuung an realen Lösungen: 𝐾𝐾𝑐𝑐 1 1 = ∙ � + 2𝐵𝐵𝐵𝐵� 𝑅𝑅𝜃𝜃 𝑃𝑃(𝜃𝜃) 𝑀𝑀𝑟𝑟 Die Streuintensität ist hier abhängig vom Winkel 𝜽𝜽, unter dem die Streustrahlung gemessen wird. • • Grenzfall: Rayleigh Streuung für 𝑷𝑷(𝜽𝜽) ≈ 𝟏𝟏. Erfüllt für kleine Streuwinkel (𝜃𝜃 → 0), große Wellenlängen (𝜆𝜆 ≫ 𝑅𝑅𝐺𝐺 ), kleine Teilchen (𝑅𝑅𝐺𝐺 → 0). Ist 𝑷𝑷(𝜽𝜽) ≪ 𝟏𝟏, ermöglicht die Winkel-Abhängigkeit der Streustrahlung die Bestimmung des Gyrationsradius. 𝐾𝐾𝐾𝐾 = 𝑅𝑅𝜃𝜃 1 1 1 16𝜋𝜋 2 ∙ 𝑅𝑅𝐺𝐺2 𝜃𝜃 ∙ � + 2𝐵𝐵𝐵𝐵� = + ∙ sin2 � ∙ � + 2𝐵𝐵𝐵𝐵� �1 2 2 2 𝑀𝑀𝑟𝑟 3𝜆𝜆 2 16𝜋𝜋 ∙ 𝑅𝑅𝐺𝐺 𝜃𝜃 𝑀𝑀𝑟𝑟 ∙ sin2 1− 2 2 3𝜆𝜆 Im Gegensatz zur Lichtstreuung an einer realen Lösung kleiner Teilchen zeigt eine reale makromolekulare Lösung eine Abhängigkeit der Streuintensität von 𝒄𝒄 und dem Streuwinkel. In einem Streuungs-Experiment muss daher die Streuintensität 𝒊𝒊𝒔𝒔 und damit das Rayleigh-Verhältnis 𝑹𝑹𝜽𝜽 für verschiedene Streuwinkel und Konzentrationen bestimmt werden. Daraus können Molekülmasse, Gyrationsradius und Virialkoeffizient der streuenden Moleküle erhalten werden. Die Molekülmasse wird über Extrapolation von 𝐾𝐾𝐾𝐾 𝑅𝑅𝜃𝜃 für 𝑐𝑐 → 0 und 𝜃𝜃 → 0 erhalten. 1 𝐾𝐾𝐾𝐾 = c→0 𝑅𝑅𝜃𝜃 𝑀𝑀𝑟𝑟 lim 𝜃𝜃→0 Für diese Extropolation eignet sich die Auftragung in einem Zimm-Diagramm. Hier ist 𝜃𝜃 𝐾𝐾𝐾𝐾 𝑅𝑅𝜃𝜃 gegen sin2 2 + 𝑚𝑚𝑚𝑚 aufgetragen, wobei 𝑚𝑚 eine beliebige Konstante ist, die einen vernünftigen Maßstab auf der Abszisse liefert. Jede Messung von 𝑅𝑅𝜃𝜃 bei einem bestimmten Streuwinkel und einer bestimmten Konzentration ergibt einen Messpunkt im Zimm-Digramm. • • Ist die Konzentration konstant, so liegen die Messpunkte für verschiedene Streuwinkel auf der Kurve A. Der untere Endpunkt der Kurve für 𝜃𝜃 = 0° hat den x-Wert 𝑚𝑚𝑚𝑚. Für unterschiedliche Konzentrationen bei konstantem Winkel ergeben sich (fast) senkrecht zu A verlaufende Kurven B. Die Endpunkte aller Kurven (𝜃𝜃 = 0°) bilden eine Gerade mit der Geradengleichung: 1 𝐾𝐾𝐾𝐾 |𝜃𝜃 =0° = + 2𝐵𝐵𝐵𝐵 𝑀𝑀𝑟𝑟 𝑅𝑅𝜃𝜃 Der y-Achsen-Schnittpunkt dieser Geraden (𝑐𝑐 = 0, 𝜃𝜃 = 0°) liefert die Molekülmasse, ihre Steigung den zweiten Virialkoeffizienten. 𝜃𝜃 Der linke Endpunkt der Kurven B entspricht sin2 2 . Die Endpunkte aller Kurven liegen wieder auf einer Gerade mit der Geradengleichung 𝐾𝐾𝐾𝐾 16𝜋𝜋 2 ∙ 𝑅𝑅𝐺𝐺2 1 𝜃𝜃 |𝑐𝑐=0 = ∙ sin2 � �1 + 2 𝑅𝑅𝜃𝜃 3𝜆𝜆 𝑀𝑀𝑟𝑟 2 Der y-Achsen-Schnittpunkt liefert ebenfalls die Molekülmasse (gemeinsamer Schnittpunkt!), die Steigung liefert den Gyrationsradius. Zur Ableitung der Teilchendimensionen aus dem Gyrationsradius muss die Form (Kugel, Stab…) der Moleküle bekannt sein. Messtechnik Als Lichtquelle dient meist ein Laser, dessen monochromatische Strahlung über ein optisches System auf die Streuzelle fokussiert wird. Die emittierte Streustrahlung wird mit einem Photomultiplier registriert. Dieser ist auf einem drehbaren Arm montiert, sodass Messungen bei unterschiedlichen Streuwinkeln möglich sind. Die Streuung des Lösungmsittels muss getrennt gemessen und von der Streuung der Lösung abgezogen werden. Quasi-elastische Streuung Elastische Streuung liefert Intensität, Konzentrations- und Winkelabhängigkeit der Streuung. Quasielastische Streuung ermöglicht die Analyse der Frequenz der Streustrahlung als weitere Informationsquelle. Die spektrale Verteilung des Streulichts hat eine wesentlich höhere Halbwertsbreite (~10kHz) als die des Primärlichts. Die Ursache der Verbreiterung ist die thermische molekulare Bewegung der streuenden Partikel. Die Frequenz der emittierten Streustrahlung wird geringfügig von der Frequenz des eingestrahlten Lichts abweichen; Grund ist der Dopplereffekt aufgrund der thermischen Bewegung (Translation und Rotation). Rein elastische Streuung tritt also so gut wie gar nicht auf! Der Dopplereffekt beschreibt die Änderung der emittierten Wellenlänge aufgrund der Bewegung von Teilchen. In Bewegungsrichtung wird sie kleiner, entgegengesetzt der Bewegungsrichtung wird sie größer. Da sich Teilchen zufällig in alle Richtungen bewegen, resultiert eine Linienverbreiterung. Ein Molekül benötigt die Zeit t, um die Strecke x zurückzulegen. Es gilt 𝑡𝑡~𝑥𝑥 2 /𝐷𝐷 (𝐷𝐷=Diffusionskoeffizient). Die spektrale Verteilung des Streulichts hat die Form einer Lorentz-Kurve: q = Streuvektor Halbwertsbreite der Lorentzkruve: Für kugelförmige Teilchen ist D über Stokes-Einstein-Relation gegeben: |𝑞𝑞| = Δ𝑣𝑣 = 4𝜋𝜋 𝜆𝜆 𝐷𝐷𝑞𝑞 2 2𝜋𝜋 𝑘𝑘𝑘𝑘 𝜃𝜃 sin 2 𝐷𝐷 = 6𝜋𝜋𝜋𝜋𝜋𝜋 𝐼𝐼(𝑣𝑣) = 𝐷𝐷𝑞𝑞 2 2𝜋𝜋 ∙ 1 2 𝐷𝐷 𝑞𝑞 2 (𝑣𝑣−𝑣𝑣0 )2 +� � 2𝜋𝜋 Aus der HWB lässt sich direkt der Diffusionskoeffizient ermitteln. Bei bekannter Viskosität der Lösung kann der hydrodynamische Radius der Teilchen bestimmt werden. Anwendungsbeispiele Amphipatische Moleküle wie Seifen neigen in Lösung zur Aggregat-Bildung. Die Micellen-Bildung erfolgt bei Überschreiten eines kritischen Wertes der Teilchen-Konzentration (cmc). Die sprunghafte Zunahme der Streuintensität bei der Ausbildung von Micellen (Streuung der monomeren Einheiten sehr gering) ermöglicht die Bestimmung der kritischen Micellen-Bildungskonzzentration mit der Methode der elastischen Lichtstreuung. Gleichzeitig lässt sich die Masse der Micellen bestimmen. Raman-Spektroskopie Die Raman-Spektroskopie ist eine Streumethode (nichtresonante Wechselwirkung zwischen Licht und Materie), die auf der inelastischen Streuung basiert. Die Streustrahlung enthält damit, zusätzlich zu dem einfallenden Licht, Frequenz-verschobene Banden (Raman-Spektrum). Die Frequenz-Verschiebung liegt im Energiebereich der Vibrations- und Rotationsübergänge. Die eingestrahlten Photonen können dabei die entsprechende Energie dem Molekül entziehen (Herabsetzung des Energieniveaus) oder sie dem Molekül zuführen (Anregung in höheres Energieniveau). Aus der Frequenz-Verschiebung der Raman-Linien in Bezug zur Frequenz des eingestrahlten Lichts resultieren direkt die Frequenzen der Molekülschwingungen. Die RamanSpektroskopie deckt wie die IR-Spektroskopie den Bereich zwischen 150 und 4000 𝑐𝑐𝑚𝑚−1 ab und liefert vergleichbare Information. Physikalische Grundlagen Der Raman-Effekt lässt sich anhand der Polarisierbarkeit 𝛼𝛼 eines Moleküls beschreiben. In einem statischen E-Feld wirkt auf die positiven Kerne und die negativen Elektronen eine Kraft. Diese versucht die Ladungszentren zu trennen, wodurch ein induziertes elektrisches Dipolmoment resultiert und das Molekül polarisiert wird. Die Größe des induzierten Dipols 𝝁𝝁 = 𝜶𝜶𝜶𝜶 ist von der Feldstärke E abhängig. Da das elektrische Feld der EM-Strahlung mit der Frequenz 𝑣𝑣0 und der Maximalamplitude 𝐸𝐸0 zeitabhängig am Ort des Moleküls oszilliert, wird auch das induzierte Dipolmoment zeitabhängig: 𝐸𝐸 = 𝐸𝐸0 cos 2𝜋𝜋𝑣𝑣𝑜𝑜 𝑡𝑡 → 𝜇𝜇(𝑡𝑡) = 𝛼𝛼𝐸𝐸0 cos 2𝜋𝜋𝑣𝑣𝑜𝑜 𝑡𝑡 Aufgrund der Molekülschwingungen kommt es zur Zeitabhängigkeit der Polarisierbarkeit α. Ändern die Kerne ihre Lage, so folgen die Elektronen dieser Bewegung. Die Fähigkeit Elektronen durch ein äußeres Feld zu verschieben (= Polarisierbarkeit), ist demnach vom Kern-Kern-Abstand abhängig. Damit wird die Polarisierbarkeit durch die Frequenz der Molekülschwingung 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 moduliert: 𝛼𝛼(𝑡𝑡) = 𝛼𝛼0 + 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 cos 2𝜋𝜋𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 𝑡𝑡 𝛼𝛼0 ist Polarisierbarkeit des Moleküls in Gleichgewichtslage der Kerne und 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 die Änderung der Polarisierbarkeit mit der Kernbewegung. Polarisierbarkeit zeitlich konstant Polarisierbarkeit moduliert mit der Zeit => Schwebung (Molekülschwingung langsamer als Oszillation des E-Feldes => Molekülschwingung ist überlagert) Das Resultat ist eine Schwebung (Überlagerung einer Grundfrequenz mit einer dazu verschobenen Frequenz => Schwebungsfrequenz ist die Differenz der beiden Schwingungsfrequenzen). Damit sollte das gestreute Licht gegenüber dem Anregungslicht eine verschobene Frequenzkomponente enthalten. Neben der Frequenz der elastischen Streuung (Rayleigh-Bande) müssen demnach zu niedrigeren oder höheren Frequenzen verschobene Raman-Banden auftreten. Die Zahl der Banden ist von der Zahl der Molekülschwingungen abhängig. • • Die zu niedrigeren Frequenzen verschobenen Banden heißen Stokes-Banden (Energie wurde von Photonen abgegeben, „Absorptionsbanden“). Die zu höheren Frequenzen verschobenen heißen Anti-Stokes (Energie wurde von Photonen aufgenommen, „Emissionsbanden“). Mathematisch lassen sich die Gleichungen für 𝝁𝝁(𝒕𝒕) und 𝜶𝜶(𝒕𝒕) kombinieren und über die 1 2 geometrische Identität cos 𝑎𝑎 ∙ cos 𝑏𝑏 = (cos(𝑎𝑎 + 𝑏𝑏) + cos(𝑎𝑎 − 𝑏𝑏)) umformen. Die resultierende Gleichung für 𝜇𝜇(𝑡𝑡) zeigt, dass der oszillierende Dipol drei Frequenzkomponenten aufweist: die des eingestrahlten Lichts 𝒗𝒗𝟎𝟎 sowie Komponenten bei 𝒗𝒗𝟎𝟎 ± 𝒗𝒗𝒗𝒗𝒗𝒗𝒗𝒗 . Das Streulicht enthält die Frequenzen der Molekülschwingungen. 1 1 𝜇𝜇(𝑡𝑡) = 𝛼𝛼0 𝐸𝐸0 ∙ cos[2𝜋𝜋𝑣𝑣𝑜𝑜 𝑡𝑡] + 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 𝐸𝐸0 ∙ cos[2𝜋𝜋(𝑣𝑣0 + 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 )𝑡𝑡] + 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 𝐸𝐸0 ∙ cos[2𝜋𝜋(𝑣𝑣0 − 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 )𝑡𝑡] 2 2 Schwingungen sind nur dann Raman-aktiv, wenn sich die Polarisierbarkeit während der Schwingung ändert, also 𝜶𝜶𝒗𝒗𝒗𝒗𝒗𝒗 ≠ 𝟎𝟎 ist. Ansonsten würde nur die eingestrahlte Frequenz sichtbar sein. Raman-Effekt als 2-Photonen Prozess Ein Modell zur Vorstellung des Raman-Effektes ist die Annahme eines 2-Photonen-Prozesses. Dabei kann das Molekül Photonen-Energie vom Schwingungsgrundzustand sowie vom angeregten Schwingungszustand aufnehmen (Absorption) und nach Emission wieder in einer der beiden Zustände landen. Dabei liegt das Molekül in einem höheren, aber virtuellen Anregungszustand vor, der nicht unbedingt einem elektronischen Übergang entsprechen muss. Nach ~10−11 𝑠𝑠 wird dieser Zwischenzustand wieder verlassen. • • Absorption vom angeregten Niveau, Emission in den Grundzustand => Antistokes (Energiegewinn des Photons, Blauverschiebung). Absorption vom Grundzustand, Emission in das angeregte Niveau => Stokes (Energieverlust des Photons, Rotverschiebung). Da das Anregungsniveau für die Stokes-Bande energetisch niedriger liegt (höhere Besetzung) sind Stokes-Übergänge wahrscheinlicher und im Raman-Spektrum intensiver. Resonanz-Raman-Spektroskopie Wenn die Frequenz des eingestrahlten Lichts im Bereich einer Absorptionsbande liegt, treten im Streulicht ebenfalls Raman-Banden auf. Die Raman-Streuung nach Anregung im Bereich der Absorptionsbande eines Chromophors ist eine direkte Emission im Bereich von 𝟏𝟏𝟏𝟏−𝟏𝟏𝟏𝟏 𝒔𝒔 (nicht zu verwechseln mit Fluoreszenz: 𝟏𝟏𝟏𝟏−𝟖𝟖 𝒔𝒔 existiert hier der angeregte Zustand). Auftretende Fluoreszenz erschwert die Aufnahme eines Raman-Spektrums erheblich. Eine Unterscheidung zwischen Raman- und Fluoreszenz-Banden kann aufgrund des Zeitunterschieds oder der Frequenzabhängigkeit erfolgen: Fluoreszenz tritt unabhängig von der Anregungswellenlänge immer an derselben Stelle im Spektrum auf. Raman-Banden haben einen definierten Frequenzunterschied zur Rayleigh-Bande und verschieben sich daher im Frequenzspektrum mit der Anregungsfrequenz. Auswahlregeln Es ist von der Art der Schwingung abhängig, ob diese nur IR-aktiv, nur Raman-aktiv oder beides ist. • • IR: Änderung des Dipolmomentes während der Schwingung. Raman: Änderung der Polarisierbarkeit während der Schwingung (Deformierbarkeit der Elektronenwolke muss sich ändern). Die Änderung von α und 𝝁𝝁 kann entlang der Normalkoordinate Q (Abweichung vom Gleichgewichtsabstand) betrachtet werden. Negative Werte für Q repräsentieren eine Stauchung, positive Werte eine Streckung des Kern-Kern-Abstandes im Vergleich zum Gleichgewichtsabstand. Die Entscheidung über Raman- und IR-Aktivität erfolgt über die erste Ableitung von α und 𝝁𝝁 nach Q an der Gleichgewichtsposition 𝑸𝑸 = 𝟎𝟎 (dieser Wert entspricht der zuvor verwendeten Größe 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 ). U • • Haben 𝛼𝛼(𝑄𝑄) bzw. 𝜇𝜇(𝑄𝑄) bei 𝑄𝑄 = 0 eine Steigung, ist die Schwingung Raman- bzw. IR-aktiv. Resultiert eine Horizontale Tangente, dann sind die Schwingungen inaktiv. Die symmetrische Streckschwingung eines linearen Moleküls A-B-A ist Raman-aktiv. Die Deformierbarkeit der Elektronenwolke ist in der gestauchten Form verschieden von der der gestreckten Form. Das Dipolmoment ändert sich jedoch nicht bei dieser Schwingung, sodass sie IR-inaktiv ist. Bei der asymmetrischen Streckschwingung eines linearen Moleküls A-B-A ist die Situation gerade umgekehrt. Die Polarisierbarkeit ist in gestauchter und gestreckter Form gleich und durchläuft in der Gleichgewichtslage ein Minimum, weshalb die Schwingung Raman-inaktiv ist. Die Dipolmomentänderung ist jedoch gegeben, weshalb die Schwingung IR-aktiv ist. Eine symmetrische Streckschwingung eines nicht-linearen Moleküls A-B-A ist Raman- und IR-aktiv. Bei der Betrachtung der Änderung des Dipolmoments auf Ladungsschwerpunkt achten. Bei der Betrachtung der Änderung der Polarisierbarkeit auf Länge/Winkel der Bindungen achten. Die Änderung der Polarisierbarkeit und des Dipolmoments ist nicht auf eine Ebene beschränkt, sondern kann in drei Raumrichtungen verschieden sein. Die Polarisierbarkeit muss daher korrekt durch einen Tensor mit neun Elementen wiedergegeben werden. Eine Schwingung ist dann Ramanaktiv, wenn die Ableitung mindestens einer Komponente des Tensors nach Q an der GG-Position ungleich null ist. Dies bedeutet, dass die Raman-Spektroskopie auch Aussagen über Molekül-Symmetrie, -Orientierung und –Struktur liefert. Nichtaktive Schwingungen können durch Kopplung mit anderen Schwingungen aktiv werden, wenn dadurch höhere als die erste Ableitung ungleich null werden. Messtechnik Als Lichtquelle dienen Edelgas gefüllte Laser-Röhren (Argon-Ionen-Laser, Helium-Neon-Laser) oder Stickstoff-Laser. Sie emittieren definierte Linien im UV/VIS-Bereich des Lichts. Hohe Frequenzen (kleine Wellenlängen => UV) werden bevorzugt, da die Intensität des Streulichts mit 𝒗𝒗𝟒𝟒 steigt (also lieber 488 nm Linie des Argon-Lasers als die 632,8nm Linie des He-Ne-Lasers; Intensitätsfaktor: 2,8). Für ResonanzRaman-Untersuchungen wird ein durchstimmbarer, also in der Lichtfrequenz variabler FarbstoffLaser verwendet. Das Laser-Licht durchstrahlt die Probe, wonach das Streulicht in einem Winkel von 90° zur Einstrahlrichtung „aufgefangen“ und auf das Gitter eines Monochromators umgelenkt wird. Hier erfolgt die spektrale Zerlegung der Streustrahlung. Der Monochromator muss die RayleighStreuung, die um einen Faktor 𝟏𝟏𝟏𝟏𝟓𝟓 größer ist, von den Raman-Banden trennen und ist maßgeblich für die Auflösung des Spektrums verantwortlich. Daher werden Doppel- oder Dreifachmonochromatoren verwendet. Ein Doppelmonochromator schafft im Abstand von 50𝑐𝑐𝑚𝑚−1 vom Maximum der Rayleigh-Bande eine Intensitäts-Minderung der Rayleigh-Bande um einen Faktor 1010 . Dreifachmonochromatoren ermöglichen Aufnahmen von Raman-Banden bis zu einem Abstand von 10𝑐𝑐𝑚𝑚−1 von der Rayleigh-Bande. Dies ist allerdings nur dann interessant, wenn Rotationsniveaus betrachtet werden sollen, da Vibrationsniveaus ohnehin einen größeren Abstand zur Rayleigh-Bande aufweisen. Die Weglängen zwischen Spiegel und Gitter liegen im Bereich von 1m und bestimmen die Dimension des Spektrometers. Das Spektrum wird mithilfe eines Photomultipliers über die „Photon counting“-Technik berechnet. Dabei löst jedes auf den Detektor fallende Photon einen Impuls aus, der als Signal in einem Vielkanalanalysator gespeichert wird. Aus dem Inhalt der Kanäle ergibt sich das Raman-Spektrum. Die aufsummierte und gemittelte Streuintensität wird als Funktion der Wellenzahl, also dem Abstand vom Maximum der Rayleigh-Bande in 𝒄𝒄𝒎𝒎−𝟏𝟏 aufgezeichnet. Das RamanSpektrum sieht dann genauso aus wie das IR-Spektrum, mit Ausnahme der Signalintensitäten. Diese hängen im IR und Raman-Spektrum von dem Ausmaß der Änderung des Dipolmoments bzw. der Polarisierbarkeit mit der Zeit ab. Anwendungsbeispiele Aus der Intensität und Breite der Raman-Banden können inter- und intramolekulare Wechselwirkungen abgeleitet werden – genau wie bei der IR-Spektroskopie. Spezifische Frequenzverschiebungen erlauben Aussagen über Konformationsänderungen oder z.B. die Ausbildung von H-Brücken. Raman-Spektren von Proteinen Schwingungen des Peptid-Gerüsts und der Seitengruppen der AS können empirisch durch Vergleich zugeordnet werden. Im gezeigten Spektrum sieht man einen Teil der Rayleigh-Bande ganz rechts bei niedrigen Frequenzen. Neben den Amid-Banden können insbesondere die Aromaten-Schwingungen gut aufgelöst werden. Über die Verschiebung der Amid-I-Bande von 1650𝑐𝑐𝑚𝑚−1 (α-Helix) zu 1665𝑐𝑐𝑚𝑚−1 (β-Faltblatt) lassen sich wie bei der IR-Spektroskopie Konformationsänderungen beobachten. Phasenumwandlungen in Lipiden Das Spektrum der Lipid-Membranen ist hauptsächlich durch die Schwingungen des CH-Bereichs gekennzeichnet. Man unterscheidet die Bereiche „akustische Schwingungen“, „optische Schwingungen“ und den Bereich der CH-Schwingungen. „akustische Schwingungen“ (LAM, longitudinal acoustic modes) sind die Zieharmonika-ähnlichen longitudinalen Schwingungen der gesamten CH2-Kette. Der Bereich dieser Schwingungen liegt sehr eng an der Rayleigh-Bande (100-300𝒄𝒄𝒎𝒎−𝟏𝟏 ). Die Frequenz der Schwingung nimmt mit steigender Kettenlänge ab, sodass aus der Frequenz eine Aussage über die Länge eines schwingenden Kettenbereichs und damit über Wechselwirkungen z.B. mit Proteinen gemacht werden kann. „optische Schwingungen“ (SOM, sceletal optical modes) liegen im Bereich um 1100 𝒄𝒄𝒎𝒎−𝟏𝟏 . Deutlich sichtbar sind drei Banden, die typisch für C-C-Streckschwingungen in trans-Konformation sind. Die mittlere überdeckt eine Raman-Bande, die charakteristisch für C-CSchwingungen in gauche-Konformationen ist. Beim Durchlaufen der Phasenumwandlung von kristallin zu flüssigkristallin nimmt die gauche-Konformation stark zu, weshalb das Verhältnis der Banden ebenfalls zunehmen muss. CH-Streckschwingungen liegen zwischen 2800 und 3000 𝒄𝒄𝒎𝒎−𝟏𝟏 und liefern Informationen über die Kettenpackungsdichte. Sie können auch zur Charkaterisierung von Lipid-Phasen herangezogen werden. Die geringe Streuintensität des Wassers erlaubt eine im Vergleich zur IR-Absorption problemlose Messung von Raman-Spektren. Resonanz-Raman-Spektroskopie Raman-Streuung im Bereich einer Absorptionslinie zeigt eine um einige Größenordnungen verstärkte Streuintensität. Nichtresonante Streubanden erscheinen wegen der fehlenden Verstärkung durch die Absorption nur im Untergrund des resonanten Spektrums. So können in ganzen biologischen Materialen (z.B. Karotte) definierte Bereiche um einen Chromophor (hier: β-Carotin) untersucht werden. Untersuchungen an z.B. Häm-Proteinen erlauben Aussagen über die Schwingungsstruktur des Prophyrin-Ringes und damit über konformative Änderungen z.B. bei der Oxygenierung oder bei der Anlagerung anderer Liganden. Es kann spezifisch die Konformation und die Wechselwirkung vieler Metallproteine oder anderer Chromophore untersucht werden. Röntgen- und Neutronen-Beugung Strahlung wird beim Auftreffen auf Moleküle teilweise oder vollständig elastisch gestreut. Bei der Streuung an einem Kristall resultiert nur in Richtung der einfallenden Strahlung eine beobachtbare Streulicht-Intensität, da für alle anderen Winkel destruktive Interferenz resultiert. Ist dagegen die Wellenlänge der einfallenden Strahlung von gleicher Größenordnung wie die Gitterkonstante des Kristalls, beobachtet man ein oder mehrere gebeugte Strahlenbündel, deren Richtung von der Einfallsrichtung abweicht. Dies trifft für den Bereich der Röntgenstrahlung, aber auch für Elektronen und thermische Neutronen zu. Diese Sonden unterscheiden sich in ihrer Wechselwirkung mit Materie: Röntgenstrahlen werden an Elektronen gestreut, Neutronen an den Atomkernen und Elektronen am elektrostatischen Potential der Elektronen. Kristallographische Grundbegriffe Bravis-Gitter Der Begriff Kristallstruktur bezeichnet die periodische Anordnung der Atome oder Moleküle in Festkörpern. Das Bravis-Gitter ist ein Konzept, das die relevante Periode des Kristalls durch eine periodische Anordnung von Punkten beschreibt. Es existieren zwei äquivalente Definitionen für das Bravis-Gitter: • • Ein Bravis-Gitter ist eine unendliche Anordnung von Punkten und alle diese Punkte sind äquivalent in dem Sinne, dass von jedem Punkt ausgesehen diese Anordnung vollkommen identisch aussieht. Ein dreidimensionales Bravis-Gitter besteht aus allen Punkten, deren Ortsvektoren R in der Form 𝑅𝑅�⃗ = 𝑛𝑛1 𝑎𝑎⃗1 + 𝑛𝑛2 𝑎𝑎⃗2 + 𝑛𝑛3 𝑎𝑎⃗3 geschrieben werden können. Die Vektoren 𝑎𝑎⃗𝑖𝑖 heißen primitive Vektoren. Sie können in drei Dimensionen nicht alle gleichzeitig in einer Ebene liegen. Die Koeffizienten 𝑛𝑛𝑖𝑖 sind ganze Zahlen. Die Abbildung zeigt ein zweidimensionales BravisGitter. Es wurden Ursprung 0 und die zwei Punkte A und B definiert, die über eine Linearkombination der primitiven Vektoren ausgedrückt werden können: 𝑅𝑅�⃗𝐴𝐴 = 3𝑎𝑎⃗1 + 𝑎𝑎⃗2 𝑅𝑅�⃗𝐵𝐵 = 𝑎𝑎⃗1 − 𝑎𝑎⃗2 Wichtige dreidimensionale Gittertypen sind z.B. das einfache kubische Gitter (sc, Würfel mit acht Atomen an den Ecken), das kubisch raumzentrierte Gitter (bcc, einfaches kubisches Gitter mit einem Atom in der Mitte) und das kubisch flächenzentrierte Gitter (fcc, einfaches kubisches Gitter mit einem Atom in der Mitte einer jeden Würfelfläche). Das einfache kubische Gitter kann mit den drei primitiven Vektoren 𝑎𝑎⃗1 = (𝑎𝑎, 0,0), 𝑎𝑎⃗2 = (0, 𝑎𝑎, 0), 𝑎𝑎⃗3 = (0,0, 𝑎𝑎) dargestellt werden. Die Abbildung zeigt das kubisch raumzentrierte Gitter. Mit den Vektoren für das einfache kubische Gitter können die Atome in der Mitte nicht erreicht werden, weshalb hier als primitive Vektoren folgende verwendet werden: 𝑎𝑎⃗1 = 𝑎𝑎 (−1,1,1), 2 𝑎𝑎⃗2 = 𝑎𝑎 (1, −1,1), 2 𝑎𝑎⃗3 = 𝑎𝑎 (1,1, −1) 2 In einem Bravis-Gitter hat jeder Punkt bzw. jedes Atom die gleiche Anzahl direkter Nachbarn. Sie ist definiert durch die Koordinationszahl. Für die drei angesprochenen Gittertypen ist die Koordinationszahl 6 (sc), 8 (bcc) bzw. 12 (fcc). Insgesamt gibt es im dreidimensionalen Raum 14 verschiedene Bravis-Gitter inklusive den sich daraus ergebenenden Einheitszellen. Sie lassen sich in sieben Kristallsysteme klassifizieren (kubisch, hexagonal, trigonal, tetragonal, orthorhombisch, monoklin, triklin). Die Einheitszelle Jedem Bravis-Gitter ist eine Einheitszelle zuzuordnen, wobei man vier Arten von Einheitszellen unterscheidet. Es handelt sich um das kleinste Volumen im Raum, das durch Translation durch den Vektor 𝑅𝑅�⃗ den ganzen Raum ausfüllt. Die Einheitszelle definiert damit den Kristall. Warum benutzen wir dann Bravis-Gitter? Der Vorteil der Bravaisgitter ist, dass sie die jeweils größtmögliche Symmetrie unmittelbar erkennen lassen. Einheitszellen sind Parallelepipede, welche jeweils einen Gitterpunkt pro Ecke aufweisen. Sie werden von zwei bzw. drei Gittervektoren (2D bzw. 3D) aufgespannt. Zu ihrer Beschreibung gibt man die Längen der Kantenvektoren und die Winkel zwischen ihnen an. Zwecks Eindeutigkeit werden an die EZ drei Bedingungen gestellt: möglichst kleines Volumen, möglichst kurze Kanten (Gittervektoren) und Winkel nahe 90°. Kristall = Gitter + Basis Betrachtet man in einer Kristallstruktur nur die translatorisch äquivalenten Punkte (Atome), bilden diese das zu der Struktur gehörende Raumgitter (Translationsgitter). Es wird durch drei Gitterverktoren charakterisiert, die im Sinne der analytischen Geometrie eine Basis darstellen. Die Kristallstruktur wird durch das Bravis-Gitter und der Basis definiert. Unter der Basis versteht man eine Anordnung von Atomen bzw. Punkten, die durch die zulässigen Translationen des Bravis-Gitters die Kristallstruktur wiedergeben. Die Basis ist die Struktureinheit des Kristalls. Das Bravis-Gitter definiert die Vorschrift für die Aneinanderreihung der Basis-Vektoren, was zum Raumgitter führt. Im Bravis-Gitter sind 𝑎𝑎⃗𝑖𝑖 die Basis-Vektoren. Gitterebenen / Netzebenen Unter der Gitterebene versteht man eine Ebene, die mindestens drei nicht kolineare (= nicht auf einer Linie liegende) Gitterpunkte beinhaltet. Durch eine Parallelverschiebung einer solchen Ebene in einem bestimmten Abstand d baut sich das Kristallgitter auf. Unter einer Familie von Gitterebenen versteht man eine Menge solcher paralleler Gitterebenen, die alle den gleichen Abstand voneinander haben und zusammen sämtliche Gitterpunkte des Bravis-Gitters enthalten. Reziprokes Gitter Das Bravis-Gitter ist die Menge aller Gitterpunkte, deren Ortsvektoren in der Form 𝑅𝑅�⃗ = 𝑛𝑛1 𝑎𝑎⃗1 + 𝑛𝑛2 𝑎𝑎⃗2 + 𝑛𝑛3 𝑎𝑎⃗3 (Gittervektor) dargestellt werden können. Diese Ortsvektoren liegen im Ortsraum (auch direkter Raum genannt). Sie definieren das Raumgitter (auch direkte Gitter oder Kristallgitter genannt). Gitterpunkte im reziproken Gitter erfüllen die Gleichung 𝐺𝐺⃗ = ℎ𝑏𝑏�⃗1 + 𝑘𝑘𝑏𝑏�⃗2 + 𝑙𝑙𝑏𝑏�⃗3 (reziproker Gittervektor). Sie liegen im Phasenraum (auch k-Raum genannt). Ortsraum und Phasenraum stehen über die Gleichung 𝑒𝑒 𝑖𝑖𝑖𝑖𝑖𝑖 = 1 in Verbindung. Daraus ergibt sich direkt die Bedingung 𝐺𝐺𝐺𝐺 = 2𝜋𝜋𝜋𝜋 mit 𝑁𝑁 ∈ ℤ. Die primitiven Vektoren des reziproken Gitters berechnen sich über eine einfache Transformationsvorschrift aus den primitiven Vektoren des Bravis-Gitters. Im Nenner steht jeweils das Volumen, das die Basis-Vektoren aufspannen: 𝑉𝑉 = 𝑎𝑎⃗1 (𝑎𝑎⃗2 × 𝑎𝑎⃗3 ). 𝑏𝑏�⃗1 = 2𝜋𝜋 ∙ 𝑎𝑎⃗2 × 𝑎𝑎⃗3 , 𝑉𝑉 𝑏𝑏�⃗2 = 2𝜋𝜋 ∙ 𝑎𝑎⃗3 × 𝑎𝑎⃗1 , 𝑉𝑉 𝑏𝑏�⃗3 = 2𝜋𝜋 ∙ 𝑎𝑎⃗1 × 𝑎𝑎⃗2 𝑉𝑉 Es ergibt sich für die Gittervektoren ein einfacher Zusammenhang: Es gilt 𝑏𝑏𝑖𝑖 𝑎𝑎𝑗𝑗 = 2𝜋𝜋𝛿𝛿𝑖𝑖𝑖𝑖 = � 2𝜋𝜋 0 𝑖𝑖 = 𝑗𝑗 𝑖𝑖 ≠ 𝑗𝑗 Neben den Basisvektoren des Ortsraums und des Phasenraums (𝑎𝑎⃗𝑖𝑖 bzw. 𝑏𝑏�⃗𝑖𝑖 ) sind auch die Indizes (𝑛𝑛𝑖𝑖 bzw. 𝑘𝑘𝑖𝑖 ) miteinander verknüpft. Die Indizes des reziproken Gitters 𝑘𝑘𝑖𝑖 = ℎ, 𝑘𝑘, 𝑙𝑙 (Millersche Indizes) ergeben sich aus den Koeffizienten 𝑛𝑛𝑖𝑖 des Ortsraums dadurch, dass man die 𝑛𝑛𝑖𝑖 invertiert und die sich ergebenden Brüche so multipliziert, dass sie teilerfremde, ganze Zahlen ergeben. Eigenschaften des reziproken Gitters bzw. reziproken Raums: • • • • Das reziproke Gitter erfüllt alle Kriterien eines Bravis-Gitters und ist damit selbst wieder ein Bravis-Gitter. Das reziproke Gitter des reziproken Gitters ist wieder das ursprüngliche Bravis-Gitter. Das reziproke Gitter existiert im Phasenraum (auch reziproker Raum oder k-Raum). Die Vektoren des reziproken Gitters haben die Einheit einer inversen Länge. Zwischen reziprokem Raum und Ortsraum kann über Fourier-Transformation gewechselt werden. Miller Indizes Die Miller-Indizes bieten eine einfache Möglichkeit alle Ebenen einer Familie zu beschreiben. Die Miller-Indizes einer Gitterebene im Ortsraum sind die Koordinaten des reziproken Gittervektors im Phasenraum. Der reziproke Gittervektor steht senkrecht auf der Gitterebene (hkl). Da die Gittervektoren des reziproken Raumes auch senkrecht auf den Netzebenen des direkten Raumes stehen, lassen sich die Millerschen Indizes dazu nutzen, den Abstand zweier Netzebenen zu ermitteln. Es gilt: 𝑑𝑑 = 2𝜋𝜋/�𝐺𝐺⃗ � . Anders formuliert: Für eine Familie von Ebenen, die alle den Abstand d voneinander haben, existiert eine Untermenge der reziproken Gittervektoren 𝐺𝐺⃗ , die senkrecht zu der Familie der Ebenen sind und der kürzeste Vektor hat die Länge �𝐺𝐺⃗ � = 2𝜋𝜋/𝑑𝑑. Insgesamt gibt es zahlreiche Kristallnetzebenen, die mit den Millerschen Indizes (hkl) angegeben werden. Die Indizes erhält man aus den Schnittpunkten der betrachteten Netzebene mit den Kristallachsen, indem man das kleinste, ganzzahlige Verhältnis der reziproken Achsenabschnitte bildet. Schneidet die Netzebene die Achsen bei a/h, b/k und c/l, wird die Netzebenenschar durch (hkl) gekennzeichnet. Zu jeder Netzebenenschar des Kristalls gehört bei gegebener Wellenlänge ein Winkel 𝜽𝜽𝒉𝒉,𝒌𝒌,𝒍𝒍 , unter dem Reflexion zu beobachten ist. Die Reflexe im Beugungsbild des Kristalls lassen sich damit den zugehörigen Netzebenen zuordnen. Aus Zahl, Lage und Symmetrie der Reflexe im Beugungsbild lässt sich die Kristallstruktur bestimmen. reziprokes Gitter, Laue Gleichungen und Ewald Konstruktion Der Nutzen des reziproken Gitters erschließt sich, wenn man Streuung betrachtet. Das Maximum der gestreuten Strahlung tritt dort auf, wo der Gangunterschied zwischen den Strahlen ein ganzzahliges Vielfaches der Wellenlänge beträgt. Betrachtet man zwei Gitterpunkte in einem dreidimensionalen Gitter, welche durch die primitive Translation 𝑎𝑎⃗𝑛𝑛 beschrieben werden, so wird ein einfallender Strahl dann maximal gestreut, wenn gilt: 𝑎𝑎⃗𝑛𝑛 (𝑠𝑠⃗ − 𝑠𝑠⃗0 ) = ℎ𝜆𝜆 . Diese Gleichung wird Laue-Gleichung genannt. 𝑠𝑠⃗ und 𝑠𝑠⃗0 stehen hier für die Richtungsvektoren des einfallenden und des gebeugten Strahls (siehe Abbildung), h ist eine beliebige ganze Zahl. Die Laue-Gleichung lässt sich mithilfe der Bedingung für den reziproken Raum leicht umformulieren (𝐺𝐺⃗ 𝑅𝑅�⃗ = 2𝜋𝜋ℎ mit 𝑅𝑅�⃗ = 𝑎𝑎⃗𝑛𝑛 ersetzt ℎ in obiger Gleichung => (𝑠𝑠⃗ − 𝑠𝑠⃗0 ) = 𝜆𝜆𝐺𝐺⃗ /2𝜋𝜋; dann nur noch �𝑘𝑘�⃗ � = 2𝜋𝜋/𝜆𝜆 einsetzen => �𝑘𝑘�⃗ �(𝑠𝑠⃗ − 𝑠𝑠⃗0 ) = 𝐺𝐺⃗ => 𝑘𝑘�⃗ − 𝑘𝑘�⃗0 = 𝐺𝐺⃗ ). Als Bedingung für die maximale �⃗ = 𝐺𝐺⃗ . Das heißt die Differenz der Wellenvektoren Streuamplitude resultiert letztlich 𝑘𝑘�⃗ − 𝑘𝑘�⃗0 = 𝐾𝐾 aus einfallender und gestreuter Welle muss gleich dem reziproken Gittervektor sein. Der Satz G der reziproken Gittervektoren, der durch die einzelnen hkl-Ebenen definiert ist, bestimmt damit die möglichen Beugungsreflexe. Hier wurden nur zwei Gitterpunkte betrachtet. Da aber das Gitter eine Widerholung der betrachteten primitiven Translation darstellt, lässt sich das Prinzip auf beliebig viele Gitterpunkte erweitern. Ist diese Bedingung nicht erfüllt, findet keine konstruktive Interferenz statt. Die Beträge der Einzelwellen löschen sich aus. Der Zusammenhang zwischen G und K sowie die Laue-Bedingung lassen sich geometrisch über die Ewald-Konstruktion verdeutlichen. Die Abbildung zeigt die Ewald-Kugel im zweidimensionalen reziproken Gitter. Die Kugel wird wiefolgt konstruiert: (1) Man zeichnet die Punkte des reziproken Gitters des Kristalls auf. (2) In dieses Netz wird der Wellenzahlvektor 𝑘𝑘�⃗ der einfallenden Welle so eingezeichnet, dass er am Gitterpunkt (00) endet. Der Anfangspunkt des Vektors sei A, der idR nicht mit einem Gitterpunkt zusammenfällt. (3) Um den Punkt A wird nun eine Kugel (2D: Kreis) mit dem Radius �𝑘𝑘�⃗0 � gezeichnet. (4) Da für elastische Streuung �𝑘𝑘�⃗ � = �𝑘𝑘�⃗0 � (nur Richtung des einfallenden Strahls, nicht der Betrag ändert sich durch Streuung) gilt, liegt auch das Ende von �𝑘𝑘�⃗ �, ausgehend vom Punkt A auf der Oberfläche der Kugel. �⃗ = 𝐺𝐺⃗ für das Auftreten eines Beugungsmaximums gilt, ist (5) Da nun die Laue-Bedingung ∆𝑘𝑘�⃗ = 𝐾𝐾 dies genau für die gebeugten Wellenvektoren �𝑘𝑘�⃗ � der Fall, die von A ausgehend auf Punkte des reziproken Gitters zeigen (also die Gitterpunkte, die auf der Oberfläche der Ewald-Kugel liegen). In der Abbildung ist dies für einen Wellenvektor und dem dazugehörigen reziproken Gittervektor illustriert. An dieser Konstruktion wird anschaulich klar, warum bei großen Wellenlängen (kleine Wellenzahl k) keine Beugung am Kristall stattfinden kann: Es gibt keine Wellenvektoren 𝑘𝑘�⃗ mehr, welche die Laue- Bedingung erfüllen können, da die Ewald-Kugel zu klein wird. Über den Zweck des reziproken Gitters Der Phasenraum und das reziproke Gitter sind letztlich eine mathematische Konstruktion, sodass die Laue-Bedingung formuliert werden kann. Die Gitterpunkte werden im Phasenraum durch diejenigen Wellenvektoren dargestellt, welche die Periodizität des Gitters aufweisen. Die einzelnen Gitterpunkte stehen dann nicht mehr für eine Einheitszelle, sondern stellen eine ganze Gitterebene bezüglich des jeweiligen K-Vektors dar. �⃗ Eine ebene Welle der Form 𝒆𝒆𝒊𝒊𝒌𝒌�⃗𝒓𝒓 wird in der Regel nicht die Periodizität des zugrunde liegenden Bravis-Gitters aufweisen. Dies ist nur für bestimmte Wellenvektoren 𝑘𝑘�⃗ der Fall. Die Menge aller �⃗ = �𝒌𝒌⃗ − �𝒌𝒌⃗𝟎𝟎 , die zu ebenen Wellen führen, welche die Periodizität des BravisWellenvektoren �𝑲𝑲 Gitters aufweisen, nennt man das reziproke Gitter. Erzeugung von Röntgenstrahlung Allgemein betrachtet wird Röntgenstrahlung in einer evakuierten Röhre dadurch erzeugt, dass Elektronen, welche an einer Glühkathode austreten, durch ein elektrisches Feld beschleunigt und auf ein Anodenmaterial geschossen werden. Die angelegte Beschleunigungsspannung zwischen Kathode und Anode ist typischerweise 20-50 kV. Die dadurch entstehende Strahlung besitzt ein gewisses Spektrum, welches sich aus einem kontinuierlichen und einem diskreten Teil zusammensetzt und charakteristisch für das verwendete Anodenmaterial ist. Weiße Röntgenstrahlung Die weiße Röntgenstrahlung entspricht dem kontinuierlichen Teil des Spektrums. Es beginnt bei einer minimalen Wellenlänge und steigert seine Intensität bis zu einem Maximum, wonach die Intensität für größere Wellenlängen wieder absinkt. Die minimale Wellenlänge hängt direkt von der Beschleunigugnsspannung ab: 𝜆𝜆min = hcU/e . Der kontinuierliche Teil des Spektrums entsteht durch Abbremsung der Elektronen bei Auftreffen auf die Anode; man spricht daher auch von Bremsstrahlung. Dabei verlieren die Elektronen kinetische Energie, was in einem Schritt (minimale Wellenlänge) oder in mehreren Schritten (größere Wellenlängen) erfolgen kann. Bei einer erhöhten Beschleunigungsspannung steigt auch die kinetische Energie der Elektronen, was zu kleineren minimalen Wellenlängen führt. Die Röntgenstrahlung entspricht 1% der eingestrahlten Energie, 99% wird in Form von Wärme abgegeben. Charakteristische Röntgenstrahlung Die charakteristische Röntgenstrahlung entspricht einem diskrteten Spektrum und besteht idR aus zwei Spektrallinien. Wenn die kinetische Energie der Elektronen einen gewissen Wert überschreitet sind diese in der Lage Elektronen aus der Hülle eines Aoms zu schlagen. Die so entstehende Lücke wird von einem Elektron aus einer höheren Schale besetzt, wobei die überschüssige Energie (Energiedifferenz der elektronischen Niveaus) in Form eines Photons abgestrahlt wird. Teilchenbeschleuniger Eine weitere Möglichkeit Röntgenstrahlung zu erzeugen sind Teilchenbeschleuniger, insbesondere bei Beschleunigung von Elektronen. Hier entsteht, wenn der Teilchenstrahl in einem starken Magnetfeld abgelenkt und dadurch quer zu seiner Ausbreitungsrichtung beschleunigt wird, Synchrotonstrahlung, eine Art der Bremsstrahlung. Synchrotronstrahlung entsteht aufgrund der Maxwellschen Gesetze, wenn eine Ladung mit relativistischen Geschwindigkeiten einer Kreisbahn folgt. Bis zu einer Maximalenergie enthält die Synchrotonstrahlung das gesamte elektromagnetische Spektrum, darunter für passene Magnetfeldstärken und Teilchenenergie auch Röntgenstrahlung. Die Intensität ist um einige Größenordnungen höher als von Röntgenstrahlung aus konventionellen Röntgenröhren. Röntgen-Beugung Die geometrischen Bedingungen für konstruktive Interferenz lassen sich mithilfe der Braggschen Reflexionsbedingung oder mit den drei Laue-Gleichungen beschreiben Braggsche Bedingung Einfallende Strahlung wird an den parallel zueinander angeordneten Netzebenen (Abstand 𝒅𝒅) des Kristalls mit dem Winkel 𝜽𝜽 reflektiert. Für das Auftreten konstruktiver Interferenz der reflektierten Strahlung (Entstehung eines gestreuten Strahlenbündels) gilt die Braggsche Reflexionsbedingung. Braggsche Reflexionsbedingung: 𝟐𝟐𝟐𝟐 ∙ 𝐬𝐬𝐬𝐬𝐬𝐬 𝜽𝜽 = 𝒏𝒏𝒏𝒏 , 𝑛𝑛 = 0,1,2 … Der Gangunterschied zweier, an aufeinanderfolgenden Netzebenen reflektierter Strahlen ist 2𝑑𝑑 ∙ sin 𝜃𝜃. Für konstruktive Interferenz muss dieser Gangunterschied einem ganzzahligen Vielfachen der Wellenlänge, also 𝑛𝑛𝑛𝑛 entsprechen. Die Braggsche Reflexionsbedingung zeigt umgekehrte Proportionalität zwischen Streuwinkel 𝜽𝜽 und Abstand 𝒅𝒅 der zugehörigen Netzebene des Kristalls. • • Die Röntgen-Kleinwinkel-Streuung liefert daher Informationen über periodische Anordnungen mit großem Abstand. Die Röntgen-Weitwinkel-Streuung liefert Informationen über die Feinstruktur des Untersuchungsobjekts. Jedoch birgt die Herleitung der Bragg-Bedingung eine kleine Schwäche in sich. Man geht bei der Herleitung nämlich von willkürlich gewählten Gitterebenen aus. Es ist daher wünschenswert eine alternative Bedingung ableiten zu können, welche allgemein gefasst ist und ohne Wahl von Gitterebenen auskommt. Bragg Laue Laue Gleichungen Der Kristall wird bei diesem Modell als ein aus drei Scharen eindimensionaler äquidistanter Punktreihen aufgebautes Gitter betrachtet (Gitterebenen hkl im Ortsraum = Gitterpunkte im Phasenraum; Bragg Laue). Jedes der identischen Objekte kann zur Streuung des Lichts führen. Die Darstellung der Röntgenbeugung geht von der Streuung der Röntgenstrahlung an den Elektronen der Atomhüllen eines Kristalls aus. Treffen parallele Röntgenstrahlen auf eine Punktreihe, so kann Verstärkung der gebeugten Strahlen nur dann auftreten, wenn der Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge ist. Für alle anderen Gangunterschiede (also andere Streurichtungen) wird bei genügend großer Anzahl an Streuzentren die Streustrahlung vollständig ausgelöscht. Die einfallende Strahlung trifft unter dem Winkel α0 auf eine Reihe von Streuzentren mit dem Abstand a. Als Bedingung für konstruktive Interferenz, der unter dem Winkel α gestreuten Strahlung gilt: 𝐡𝐡𝐡𝐡 = 𝐚𝐚(𝐜𝐜𝐜𝐜𝐜𝐜 𝛂𝛂 − 𝐜𝐜𝐜𝐜𝐜𝐜 𝛂𝛂𝟎𝟎 ) , h = 0,1,2 … Für einen dreidimensionalen Kristall mit den Abständen a, b und c der Streuzentren in den jeweiligen Raumrichtungen kommen zwei weitere Bedingungen hinzu. 𝛼𝛼, 𝛽𝛽, 𝛾𝛾 sowie 𝛼𝛼0 , 𝛽𝛽0 , 𝛾𝛾0 geben die Winkel der einfallenden bzw. gestreuten Röntgen-Strahlung in Bezug auf die jeweilig betrachtete Raumrichtung an. Die drei Bedingungen entsprechen den Laue-Gleichungen. ℎ𝜆𝜆 = 𝑎𝑎(cos 𝛼𝛼 − cos 𝛼𝛼0 ) 𝑘𝑘𝑘𝑘 = 𝑏𝑏(cos 𝛽𝛽 − cos 𝛽𝛽0 ) 𝑙𝑙𝑙𝑙 = 𝑐𝑐(cos 𝛾𝛾 − cos 𝛾𝛾0 ) Jede der Laue-Gleichungen modelliert eine Kegelschar. Die Richtung der Streustrahlung wird durch die Kegelmäntel dargestellt, deren Achse eine eindimensionale Reihe der Streuzentren ist. Der geometrische Ort für die Richtungen, in denen Beugungsmaxima entstehen, ist eine koaxiale Kegelschar, d.h. zu jedem ganzzahligen h gehört ein Kegel mit unterschiedlichem Öffnungshalbwinkel. Jeder auf einem Kegelmantel liegender Vektor 𝒔𝒔 = 𝒉𝒉𝒉𝒉 ist eine Lösung der obigen Gleichung. 1D (koaxiale Kegelschar) 1D Beziehungen zwischen Bragg und Laue Befindet sich der Kristall unter dem Winkel 2𝜃𝜃 bezüglich der Einfallsrichtung der Röntgenstrahlung, resultiert der Streuwinkel 𝜃𝜃 (siehe Abbildung). Zu jeder Netzebenenschar (hkl) gibt es im Spektrum eine Wellenlänge, für die die Bragg-Bedingung erfüllt ist und konstruktive Interferenz resultiert. Aus den Reflexpositionen erhält man mithilfe der Braggschen Gleichung direkt die Netzebenenabsstände (d-Werte). Diese sind eine Funktion der Gitterparameter der Einheitszellen (a, b, c, α, β, γ) und der Millerschen Indizes (hkl). Die Zusammenhänge variieren daher für verschiedene Kristallsysteme. Unter Berücksichtigung der Winkelbeziehungen (Richtungskosinus) zwischen 𝜃𝜃 und 𝛼𝛼, 𝛽𝛽, 𝛾𝛾 sowie 𝛼𝛼0 , 𝛽𝛽0 , 𝛾𝛾0 erhält man als Verallgemeinerung der Braggschen Reflexionsbedingung für einen orthorhombischen Kristall (rechtwinkliges Kristallsystem mit drei 90°-Winkeln, ohne gleichlange Achsen): 1/2 ℎ2 𝑘𝑘 2 𝑙𝑙 2 𝜆𝜆 � 2 + 2 + 2 � 𝑎𝑎 𝑏𝑏 𝑐𝑐 = 2 sin 𝜃𝜃 Die Werte für ℎ, 𝑘𝑘, 𝑙𝑙 charakterisieren eine NetzebenenSchar, die für die beobachteten Streulichtreflexe unter dem zugehörigen Streuwinkel 𝜃𝜃ℎ,𝑘𝑘,𝑙𝑙 verantwortlich ist. Aufnahme von Beugungsbildern (Messmethoden) Laue Verfahren 3D Im Laue-Verfahren wird ein Einkristall polychromatischer Röntgenstrahlung ausgesetzt. Die BraggGleichung wird hier durch Variation der Wellenlängen erfüllt, sodass mehrere Gitterebenen gleichzeitig die Beugungsbedingung erfüllen. Damit ist das Laue-Verfahren sehr viel schneller als die in anderern Verfahren verwendete Beugung mit monochromatischer Röntgenstrahlung (Linienspektrum). Aufgrund der geringeren Zeit für die Aufnahme mit dem Laue-Verfahren, können dynamische Prozesse an Kristallen verfolgt werden. Besonders bei Proteinkristallen lassen sich Änderungen der Proteinstruktur im Kristall beobachten. Nachteil ist die Unkenntniss darüber welcher Reflex von welcher Wellenlänge stammt (Indizierungsproblem). Während das Laue-Verfahren sehr schnell ist, ist die späte Datenverarbeitung sehr zeitaufwendig. Auf dem fotographischen Film sind punktförmige Reflexe zu erkennen. Bild in der Ewald-Kugel: Es werden verschieden große Ewald-Kugeln gezeichnet, deren Mittelpunkte auf der Geraden des eingestrahlten Wellenvektors mit der kleinsten Wellenlänge (größtes k) liegen (dieser gehört zur Ewald-Kugel mit dem größten Radius). Der Endpunkt ist immer derselbe Gitterpunkt (00). Dadurch liegen mehrere Gittervektoren auf den verschiedenen Kreisen und die Laue-Bedingung wird für verschiedene EwaldKugeln erfüllt. Drehkristallmethode Für eine gegebene Netzebenenschar (hkl) bei fester Wellenlänge ist nur bei Einstrahlung unter einem Winkel 𝜃𝜃ℎ,𝑘𝑘,𝑙𝑙 die Reflexionsbedingung erfüllt. Zur Untersuchung von Einkristallen wird der Kristall um eine Achse senkrecht zur Einfallsrichtung der Strahlung gedreht, um damit für verschiedene Netzebenen die Laue-Bedingungen zu erfüllen. Die Lage der einzelnen Reflexe im Beugungsbild ermöglicht die Bestimmung der Dimensionen der Elementarzelle des Kristalls. Für diese Methode ist die Ewald-Kugel von besonderem Interesse: Ein Reflex entsteht, falls ein Gitterpunkt mit der Kugeloberfläche zusammenfällt. Im Allgemeinen gibt es keinen Reflex. Durch Drehen des Kristalls kann aber die Bedingung erfüllt werden. Bild in der Ewald-Kugel: Die Ewald-Kugel ist ortsfest, während sich das reziproke Gitter unter der Ewald-Kugel durchdreht. Dadurch landen verschiedene Gitterpunkte im Verlaufe der Drehung auf dem Kreis der Ewald-Kugel, wodurch verschiedene Reflexe während der Kristall-Drehung resultieren. Debye-Scherrer-Verfahren (Pulvermethode) Als Probe dient ein Pulver aus kleinen, statistisch orientierten Kristallen. Daher liegt bereits für jede Netzebene die geeignete Orientierung zur Erfüllung der Laue-Gleichungen vor (keine Drehung erforderlich). Das Beugungsbild besteht nicht mehr aus einzelnen Reflexen. Die Reflexe jeder Netzebene bilden einen Kreis um das Zentrum des Beugungsbildes. Je nach Symmetrie des Kristalls (Ausrichtung, periodische Strukturen) resultiert ein Beugungsmuster aus Ringen, Bögen oder Punkten. Rückschlüsse auf Strukturen der Elementarzelle sind möglich. Bild in der Ewald-Kugel: Der reziproke Raum besteht nicht mehr aus Punkten wie bei einem Einkristall, sondern aus Kugeln mit Radien der möglichen, reziproken Gittervektoren. Diese Kugeln schneiden sich mit der fixen Ewaldkugel in Breitenkreisen. Die Primärstrahlrichtung und damit auch die Ewald-Kugel sind ortsfest. Da es sich um ein polykristallines Gefüge handelt, können die Vektoren des reziproken Gitters G jede beliebige Richtung einnehmen. Die Gitterpunkte müssen auf den so gennanten Bragg-Kugelschalen liegen, damit Reflexion beobachtet wird. Gegenüberstellung Probe Strahlung Laue Einkristall Polychromatische Bremsstrahlung Prinzip Zu jeder Netzebenenschar (hkl) gibt es im Spektrum eine Wellenlänge für die die BragBedingung erfüllt ist. Beugungsbild Punktmuster, Symmetrie Drehkristallmethode Einkristall, epitaktische Schicht monochromatisch Debye-Scherrer Polykristallines Kristallpulver monochromatisch Vergrößerung des Winkels θ bei Mitführung des Detektors um 2θ bis Bragg-Bedingung erfüllt ist. Röntgenstrahlen, die an Netzproblemen mit gleichen Indizes reflektiert werden, liegen auf Kegelmantel um einfallenden Strahl (2θ) Winkelabhängige Intensitätsmaxima verschiedener Beugungsordnungen (punktförmig) Konzentrische Bogenstücke um den Strahlaustritt Anwendung Vororientierung der Kristalle Bestimmung der Gitterkonstanten, Halbwertsbreiten Gitterkonstante, Phasenanalyse, Gitterstörungen Bestimmung von Elektronendichten Das Beugungsmuster liefert Informationen zur Geometrie der Elementarzelle, während die Intensität der Reflexe Informationen zur Elektronendichteverteilung der Strukturen enthalten. Es sei ein periodisches 2D-Gitter aus parallel angeordneten zweiatomigen Molekülen (Atom A und B) innerhalb der xy-Ebene betrachtet. Bestimmte Ebenen durch die A Atome erfüllen die Laue-Bedingung (Die Teilwellen, ausgehend von allen Gitterpunkten (A-Atome) sind in Phase = Phasenunterschied beträgt ein Vielfaches der Wellenlänge). Dies gilt wegen der parallelen Anordnung auch für B. Zwischen der gestreuten Strahlung von A und B besteht jedoch eine Phasendifferenz. ℎ𝑥𝑥 𝑎𝑎 + 𝑘𝑘𝑘𝑘 � 𝑏𝑏 ℎ𝑥𝑥 𝑎𝑎 + 𝑘𝑘𝑘𝑘 𝑏𝑏 Abstände zwischen den Molekülen AB: in x-Richtung: a | in y-Richtung: b Abstände zwischen den Atomen A und B: in x-Richtung: x | in y-Richtung: y ΔΦ = 2𝜋𝜋 � Dreidimensional gilt: ΔΦ = 2𝜋𝜋 � Die Intensität der am Molekül AB gestreuten Wellen mit den Phasen ΦA = 0 und Φ𝐵𝐵 = ΔΦ Für N Atome im Molekül gilt (𝐴𝐴𝑗𝑗 sind Streufaktoren der Atome): Für n Moleküle pro Elementarzelle, ist die resultierende Intensität je Zelle auch proportional zu n. 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 ist der Strukturfaktor. Die Beträge der Strukturfaktoren sind proportional zur Wurzel aus den ReflexIntensitäten. Aus den Intensitäten lassen sich somit die Beträge der Strukturfaktoren, aber nicht 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 = |𝐹𝐹ℎ𝑘𝑘𝑘𝑘 | ∙ 𝑒𝑒 𝑖𝑖𝛼𝛼 ℎ 𝑘𝑘𝑘𝑘 und somit auch nicht die Phase 𝛼𝛼ℎ𝑘𝑘𝑘𝑘 bestimmen (siehe Phasenproblem). 𝑙𝑙𝑙𝑙 𝑐𝑐 + � = Φ𝐵𝐵 2 𝐼𝐼ℎ𝑘𝑘𝑘𝑘 ~�𝐴𝐴0 𝑒𝑒 𝑖𝑖Φ 𝐴𝐴 + 𝐵𝐵0 𝑒𝑒 𝑖𝑖Φ 𝐵𝐵 � 2 𝑖𝑖Φ 𝑗𝑗 𝐼𝐼ℎ𝑘𝑘𝑘𝑘 ~�∑𝑁𝑁 � = 𝑗𝑗 =1 𝐴𝐴𝑗𝑗 𝑒𝑒 �∑𝑗𝑗𝑁𝑁=1 𝐴𝐴𝑗𝑗 𝑒𝑒 2𝜋𝜋𝜋𝜋 ∙�ℎ𝑥𝑥 𝑗𝑗 +𝑘𝑘𝑦𝑦 𝑗𝑗 +𝑙𝑙𝑧𝑧𝑗𝑗 � � 2 2 2𝜋𝜋𝜋𝜋 ∙�ℎ𝑥𝑥 𝑗𝑗 +𝑘𝑘𝑦𝑦 𝑗𝑗 +𝑙𝑙𝑧𝑧 𝑗𝑗 � 𝐼𝐼ℎ𝑘𝑘𝑘𝑘 ~ �𝑛𝑛 ∙ ∑𝑁𝑁 � = |𝐹𝐹ℎ𝑘𝑘𝑘𝑘 |2 𝑗𝑗 =1 𝐴𝐴𝑗𝑗 𝑒𝑒 Vergleich zwischen berechneten Reflex-Intensitäten für verschiedene Positionen der Atome und den beobachteten Intensitäten ermöglicht Rückschlüsse auf Molekülanordnung im Kristall. Anstelle der Streufaktoren kann die Elektronendichte 𝝔𝝔(𝒙𝒙, 𝒚𝒚, 𝒛𝒛) verwendet werden. 𝑉𝑉𝐸𝐸𝐸𝐸 ist das Volumen der Elementarzelle. Das Integral hat die Form eines Fourierintegrals: 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 ist die Fouriertransformierte der Elektronendichteverteilung 𝜚𝜚(𝑥𝑥, 𝑦𝑦, 𝑧𝑧). Umgekehrt ergibt sich die Elektronendichte als Fouriertransformierte des Strukturfaktors. 2𝜋𝜋𝜋𝜋 ∙�ℎ𝑥𝑥 𝑗𝑗 +𝑘𝑘𝑦𝑦 𝑗𝑗 +𝑙𝑙𝑧𝑧 𝑗𝑗 � 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 = ∑𝑛𝑛𝑛𝑛 = 𝑗𝑗 =1 𝐴𝐴𝑗𝑗 𝑒𝑒 ∫𝑉𝑉 𝐸𝐸𝐸𝐸 𝜚𝜚(𝑥𝑥, 𝑦𝑦, 𝑧𝑧) ∙ 𝑒𝑒 𝜚𝜚(𝑥𝑥, 𝑦𝑦, 𝑧𝑧) = ∫𝑉𝑉 𝐸𝐸𝐸𝐸 2𝜋𝜋𝜋𝜋 ∙� ℎ 𝑥𝑥 𝑘𝑘𝑘𝑘 𝑙𝑙𝑙𝑙 + + 𝑎𝑎 𝑏𝑏 𝑐𝑐 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 ∙ 𝑒𝑒 � −2𝜋𝜋𝜋𝜋 ∙� 𝑑𝑑𝑑𝑑 ℎ 𝑥𝑥 𝑘𝑘𝑘𝑘 𝑙𝑙𝑙𝑙 + + � 𝑎𝑎 𝑏𝑏 𝑐𝑐 𝑑𝑑𝑑𝑑 Im Experiment wird das Beugungsmuster aus der Struktur erzeugt: Wir wollen aber aus dem Beugungsmuster die Struktur ermitteln: Ist 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 für eine bestimmte Netzebene (hkl) bekannt, so lässt sich die Elektronendichte-Verteilung 𝝔𝝔(𝒙𝒙, 𝒚𝒚, 𝒛𝒛) bestimmen und man erhält ein Abbild der Elementarzelle des Kristalls. Die Elektronendichte ist eine dreidimensionale Funktion mit der Einheit 𝑒𝑒/Å3 , welche beschreibt wo sich in der Einheitszelle des Kristalls die Elektronen (also auch die Atome) befinden. Sie enthält also das Bild der Struktur, das wir bestimmen wollen. Wichtig: Jeder Reflex (hkl) des Beugungsmusters trägt zur Elektronendichte in jeder einzelnen Position (xyz) der Einheitszelle des Kristalls bei. Durch Auftragung der Elektronendichte-Verteilung in Form von Linien gleicher Elektronendichte, erhält man Elektronenkarten. Phasenproblem und Lösungen Was ist das Phasenproblem? Die Elektronendichte-Verteilung lässt sich jedoch aus den gemessenen Reflexintensitäten nur bei Kenntnis der jeweils zugehörigen Phase bestimmen (Phasenproblem), über die keine Informationen aus dem Beugungsbild gewonnen werden können (zeigt nur konstruktive Interferenz, also In-PhaseAnteile; aber keine weiteren Phasenbeziehungen). Im Beugungsexperiment werden Intensitäten von Wellen gemessen, die von Ebenen (hkl) im Kristall gestreut werden. Die Amplitude der Welle |𝐹𝐹ℎ𝑘𝑘𝑘𝑘 | ist proportional zur Wurzel der gemessenen Intensitäten am Detektor. Um die Elektronendichte in der Position (xyz) der Einheitszelle eines Kristalls zu berechnen wird die Summation über alle hkl-Ebenen benötigt. Sprich: Elektronendichte bei (xyz) = Summe aus allen Wellen-Beiträgen im Punkt (xyz), die in der Ebene (hkl) gestreut wurden; Deren Amplituden sind abhängig von der Anzahl der Elektronen in der Ebene und der korrekten relativen Phasenbeziehung. Mathematisch formuliert: 𝑖𝑖𝛼𝛼 ℎ 𝑘𝑘𝑘𝑘 |𝐹𝐹ℎ𝑘𝑘𝑘𝑘 | ∙ 𝑒𝑒� 𝜚𝜚(𝑥𝑥, 𝑦𝑦, 𝑧𝑧) = 1/𝑉𝑉 � �� ���� �� ∙ 𝑒𝑒 −2𝜋𝜋𝜋𝜋 ∙(ℎ𝑥𝑥+𝑘𝑘𝑘𝑘 +𝑙𝑙𝑙𝑙) 𝐹𝐹ℎ 𝑘𝑘𝑘𝑘 Hier ist V das Volumen der Einheitszelle und 𝛼𝛼ℎ𝑘𝑘𝑘𝑘 die Phase, welche mit der Struktur-Faktor Amplitude |𝐹𝐹ℎ𝑘𝑘𝑘𝑘 | assoziiert ist. Wir können die Amplitude messen, aber die Phase geht im Experiment verloren. Dies ist das Phasenproblem. Übersicht über Methoden zur Lösung des Phasenproblems Es gibt keine Beziehung zwischen Amplituden und Phasen, außer über die Molekulare Struktur bzw. die Elektronendichte. Wenn wir also etwas über die Elektronendichte oder Struktur wissen, kann dies zu Werten für die Phasen führen. Dies ist die Basis für alle Methoden zur Lösung des Phasenproblems. Man unterscheidet verschiedene Ansätze zur Lösung des Phasenproblems: (1) (2) (3) (4) (5) (6) (7) (8) Direkte Methode Multiple isomorphous replacement (MIR) Single isomorphous replacement (SIR) Molecular Replacement (MR) + Patterson-Methode Multiwavelength anomalous diffraction (MAD) Single wavelength anomalous dispersion (SAD) Anomalous Scattering (AS) MIRAS und SIRAS (MIR+AS bzw. SIR+AS) Direkte Methoden Diese Methoden sind nur für kleine Moleküle mit subatomarer Auflösung (Sub-Angstrom-Bereich) anwendbar. Für einfache Moleküle nimmt man eine realistisch erscheinende Struktur an und berechnet daraus die Strukturfaktoren und die Phase. Das berechnete Beugungsbild wird mit den gemessenen Reflexintensitäten verglichen. So kann die angenommene Struktur verfeinert werden. Im Grunde werden einfach einzelne Werte für Phasen durchprobiert werden, bis eine sphärische Struktur in der resultierenden Elektronendichte-Karte beobachtet werden kann. Bei der direkten Methode werden statistische Beziehungen ausgenutzt, die zwischen Sätzen von Strukturfaktoren bestehen, um mögliche Werte für die jeweilige Phase abzuleiten. Ausgehend von einigen wenigen Reflexen, deren Phasen bekannt sind (Startreflexe), können die unbekannten Phasen der anderen Reflexe abgeschätzt werden. Die Wahrscheinlichkeit dafür, dass die so abgeschätzte Struktur die richtige ist, wächste mit der Anzahl der für die Lösung zur Verfügung stehenden Reflexe. Mit dem mathematisch sehr aufwendigen Verfahren lässt sich die Struktur der Basis entschlüsseln, wenn sie bis zu 100 Atomen enthält. Direkte Methoden basieren auf der Ladung und Atomzahl einer Elektronendichte, die zu Phasenbeziehungen zwischen den normalisierten Strukturfaktoren führen. So konnten bisher Protein-Strukturen mit bis zu 1000 Atomen bestimmt werden. Die direkte Methode wird auch für die Bestimmung von Substrukturen in hohen Auflösungen verwendet (Physik-Nobelpreis 1985). Molecular Replacement (MR) und Patterson-Methode Wenn ein Homologie-Modell zur Verfügung steht, kann die MR-Methode angewendet werden. In der MR-Methode wird das Phasenproblem gelöst, indem ein ähnliches Molekül in der korrekten Orientierung und Position in der asymmetrischen Einheit der kristallisierten unbekannten Struktur positioniert wird. Das bekannte Molekül muss eine ähnliche Struktur zur kristallisierten haben (Daumenregel: Rückgrat-Atome müssen weniger als 1,5Å rms aufweisen; dies wird erreicht bei einer Sequenzidentität von ca. 30%). Heutzutage werden 2/3 aller Strukturen mit dieser Methode gelöst. Über die Patterson-Methode wird die erste Orientierung der Modell-Struktur in der neuen Einheitszelle bestimmt und anschließend die Translation des korrekt orientierten Modells relativ zum Ursprung der Einheitszelle erreicht. Die Patterson-Funktion kann aus dem experimentellen Beugungsbild ohne Phasen sowie ausgehend von einer bereits bekannten Struktur berechnet werden. Das verwendete Struktur-Modell ist natürlich nicht identisch mit der Zielstruktur, sodass die entsprechenden Patterson-Funktionen nicht identisch sind. P(u,v,w) der Modell-Struktur enhtält nur intramuolekulare Vektoren, während P(u,v,w) aus den Beugungsdaten intra- und intermolekulare Vektoren enthält. Die Patterson-Methode kann direkt die Positionen von schweren Atomen bestimmen. Sie kann nur verwendet werden, wenn schwere Atome im Kristall vorkommen oder wenn ein bedeutender Anteil der Struktur bereits bekannt ist. Die Gefahr bei solchen Methoden ist eine falsche Struktur: So führt die Berechnung einer Elektronendichte-Karte aus den Amplituden eines Beugungsbildes einer Ente und den Phasen der Beugung an einer Katze zu der Katzen-Struktur. Phasen enthalten damit mehr Informationen als Amplituden! Single / Multiple Isomorphous Replacement (SIR/MIR) Der Austausch von schweren Atomen wurde zunächst für kleine Moleküle zur Lösung des Phasenproblems verwendet. Die veränderten Intensitäten ermöglichen Rückschlüsse auf die Positionierung einzelner Atome im Kristall. Protein-Kristalle können in Schwermetalllösungen inkubiert werden, um isomorphe Schwermetall-Atom Derivate (gleiche Einheitszelle, gleiche Orientierung des Proteins in der Zelle) zu erhalten. Aus den resultierenden Intensitäts-Änderungen können die Positionen der Schweratome abgeleitet werden. Zur Ableitung der Phase sind drei Schritte notwendig: (1) Normierung der Strukturfaktoren |𝐹𝐹𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘)| und |𝐹𝐹𝑃𝑃𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘)| auf dieselbe Skala: 𝑅𝑅 = 100 ∙ ∑ℎ𝑘𝑘𝑘𝑘 �|𝐹𝐹𝑃𝑃𝑃𝑃 | − |𝐹𝐹𝑃𝑃 |� / ∑ℎ𝑘𝑘𝑘𝑘 |𝐹𝐹𝑃𝑃 |. (2) Bestimmung der Positionen der schweren Atome (𝐹𝐹𝐻𝐻 ) über die Differenzen |𝐹𝐹𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘)| − |𝐹𝐹𝑃𝑃𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘)|. (3) Berechnung von 𝛼𝛼𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘) aus 𝐹𝐹𝐻𝐻 , |𝐹𝐹𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘)| und |𝐹𝐹𝑃𝑃𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘)|. Die Intensitätsänderungen durch isomorphen Ersatz wirken sich auf alle Beugungspunkte aus. Der Grund: Jedes Atom einer Einheitszelle ist an jeder einzelnen Reflektion im Beugungsmuster beteiligt – an einigen mehr, an anderen weniger. Es wird ein Atom mit dem Streufaktor A1 durch ein schweres Atom mit dem Streufaktor A2 ausgetauscht. Die Intensitätsunterschiede in den Beugungsbildern entsprechen einer Streuung an einem hypothetischen Kristall mit dem Streufaktor A2-A1. Die Struktur des hypothetischen Kristalls lässt sich einfach bestimmen, da nur ein Atom vorliegt (Beugungsbild des Schwereatoms allein in der Zelle des Proteins). So lässt sich das austauschbare Atom lokalisieren. Anschließend kann der Beitrag des Atoms zu jedem Strukturfaktor des Kristalls berechnet werden. In der Harker-Konstruktion (siehe Abbildung) resultieren für den Fall eines SIR-Experiments (single isomorphous replacement) zwei mögliche Werte für 𝛼𝛼𝑃𝑃 (ℎ𝑘𝑘𝑘𝑘). Dieses Problem kann über verschiedene Wege behoben werden: • • • • Dichte-Modifikation Ein zweites Schweratom-Derivat (MIR) Einführen von anomaler Streuung (SIRAS) Beides: MIRAS. Über MIR gibt es in der Harker-Konstruktion nur eine mögliche Lösung: Die Derivatisierung selbst kann über verschiedene Wege erfolgen. Beispiele sind Cokristallisation, quick-soaking und kovalente Modifikation des Proteins (z.B. Se-Met statt Met) oder der DNA (z.B. BrU statt T). Die Verbesserung der Phase Es ist eher selten, dass die experimentell bestimmten Phasen genau genug sind, um eine interpretierbare Elektronendichte-Karte zu erzeugen. Experimentelle Phasen sind oft der StartPunkt für Phasen-Verbesserungen über eine Vielzahl von Methoden der Dichte-Modifikation, die ebenso auf bekannte Struktur-Eigenschaften basieren. Eine wichtige Methode dieser DichteModifikation ist z.B. das Entfernen negativer Elektronendichte im Bereich des Lösungsmittels (solvent flattening), sodass die Elektronendichte des Proteins kontrastreicher vom Hintergrund hervorsticht. Es handelt sich um einen zyklischen Prozess: In vielen Fällen wird ein erster Satz von Phasen bestimmt und die Elektronendichte-Karte für das Beugungsmuster berechnet. Diese Elektronendichte-Karte wird dann verwendet, um Teile der Struktur zu bestimmen. Die Struktur dient zur Modellierung einer modifizierten Elektronendichte, die dann rücktransformiert wird, um eine modifizierte Phase zu erhalten. Dieser neue Satz an Phasen wird als Verfeinerung (Refinement) bezeichnet. Die Phasen werden nun auf die original Amplituden (Beugungsmuster) angewendet und eine verbesserte Elektronendichte-Karte abgeleitet, aus der die Struktur korrigiert werden kann. Dies wird fortgesetzt, bis der Zyklus konvergiert bzw. bis ein Fehler-Term (Rfree) einen zufriedenstellenden Wert erreicht hat. Anomalous Scattering (AS) Der atomare Streufaktor hat drei Komponenten: ein normaler Streu-Term, der vom Bragg-Winkel abhängig ist und zwei Terme, die nicht vom Streuwinkel abhängig sind, aber von der Wellenlänge. Die letzten beiden Terme repräsentieren anormale Streuung (anomalous scattering), die auftritt, wenn die Röntgenstrahlung absorbiert wird und ein Elektron aus der inneren Schale des Atoms herauslöst. Dies führt zur Phasenverschiebung, die dazu genutzt werden kann anomale Streuer zu lokalisieren. Die anormale Differenz kann auf dieselbe Weise wie die isomorphe Differenz in der Patterson- oder Direkten Methode dazu genutzt werden die anormalen Streuuer zu lokalisieren. Phasen für die nativen Struktur-Faktoren können dann ähnlich wie bei SIR oder MIR abgeleitet werden. Eine Kombination der Methoden führt zu SIRAS und MIRAS (single bzw. multple isomorphous replacement with anomalous scattering). Multiwavelength / Singlewavelength anomalous diffraction (MAD/SAD) SIR/MIR hat verschiedene Probleme, darunter der Nicht-Isomorphismus zwischen den Kristallen (Änderungen der Einheitszelle, Reorientierung des Proteins, Konformationsänderungen, Änderungen in Salz- und Lösungsmittel-Ionen). Diese Probleme werden von MAD bewältigt. Dabei werden typischerweise drei Wellenlängen verwendet, die im Bereich der Absorption liegen, um die Absorptionseffekte zu maximieren. In der MAD-Methode absorbieren innere Elektronen der Atome Röntgenstrahlung verschiedener Wellenlängen. Nach einer gewissen Zeitverzögerung wird die Röntgenstrahlung emittiert, wobei aufgrund der Zeitverzögerung eine Phasenverschiebung resultiert. Diese wird als anomalous dispersion effect beschrieben. Die Analyse der Phasenverschiebung ergibt eine Lösung für die Phasen. Für diese Methode ist Synchroton-Strahlung erforderlich. Neutronen/Elektronen-Beugung Neutronen-Beugung Nach de Broglie hat jedes Teilchen die Wellenlänge 𝝀𝝀 = 𝒉𝒉/𝒑𝒑 . Mit der mittleren Energie der 1 3 Neutronen 𝐸𝐸 = 2 𝑚𝑚𝑣𝑣 2 = 2 𝑘𝑘𝑘𝑘 ergibt sich damit 𝝀𝝀 = 𝒉𝒉/√𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐 . Bei 𝑻𝑻 = 𝟔𝟔𝟔𝟔𝟔𝟔𝟔𝟔 beträgt die Wellenlänge von Neutronen etwa 0,1nm und liegt damit in der Größenordnung der Kristallgitterkonstanten. Für Beugungsexperimente werden daher thermische Neutronen verwendet (Neutronen aus Kernspaltungen, die durch Kollision mit schwerem Wasser auf die entsprechenden Energien abgebremst werden). Mithilfe von Neutronenbeugung lassen sich Strukturen mit Wasserstoff-Atomen untersuchen. Die Röntgen-Beugung, die durch Wechselwirkung mit der Elektronenhülle der Atome erfolgt und daher mit der Zahl der Elektronen im streuenden Atom zunimmt, ist dafür nicht geeignet (H-Streuung wird durch Streuung großer Atome überdeckt). Die Streuung von Neutronen erfolgt dagegen aufgrund von Kernkräften und Wechselwirkungen zwischen magnetischen Momenten von Neutron und Atomkern. Als Maß für die Streukraft der Teilchen wird die Streulänge angeführt. Die Neutronen-Streulänge von H und D ist innerhalb eines Faktors 2-3 betragsmäßig vergleichbar mit den Streulängen von schweren Atomen. Leichte Atome liefern also ebenso einen wesentlichen Beitrag zur Streuintensität. Bei der Röntgenstrahlung nimmt die Streulänge mit steigender Molekülmasse zu. Die Streulängen bei Neutronenbeugung von H und D tragen unterschiedliches Vorzeichen. Negatives Vorzeichen bedeutet, dass die gestreute Strahlung um 180° gegenüber der Streustrahlung an anderen Atomen mit positiver Streulänge phasenverschoben sind. Diese Phasenverschiebung beeinflusst die Interferenzterme zwischen H und anderen Termen. Eine wichtige Anwendung findet diese Eigenschaft bei der Einstellung des Lösungsmittelkontrastes. Durch Variation des Lösungsmittelverhältnisses H2O/D2O lässt sich der Kontrast zwischen Lömi und gelöster Substanz verändern. Das Lömi bestimmt wesentlich das beobachtete Beugungsbild der Neutronenstrahlen. Mithilfe der Kontrastanpassung können verschiedene Bestandteile eines Objekts selektiv hervorgehoben werden. Neutronenbeugung Thermische Neutronen Schwache Streuung im wesentlichen an Kernen Probleme: Intensität, Monochromasie Vorteile: hohe Nachweisempfindlichkeit (Isotopen, leichte und schwere), Bestimmung der magnetischen Struktur und von Phononenspektren. Elektronenbeugung Wesentlich stärkere Wechselwirkung (größere Streuintensität geringere mengen). Oberflächen-nahe Bereiche und dünne Schichten. Vorteile: geringerere Linienverbreiterung, kürzere Belichtungszeiten, leichte Atome gut lokalisierbar. Teil 2: Elektrochemie und Membranbiophysik Kapitel 4/5: Basics zum Chemischen Potential und zur Gibbs-Energie Chemisches Potential Das chemische Potential ist eine partielle molare Größe. Im Falle einer reinen Substanz ist 𝜇𝜇 einfach die auf 1 mol bezogene Freie Enthalpie: 𝝁𝝁 = 𝑮𝑮/𝒏𝒏 (n ist die Stoffmenge, G die freie Enthalpie). Das chemische Potential gibt an, wie viel Arbeit aufzubringen ist, um in einem System bei konstantem Druck p, konstanter Temperatur T und konstanten Stoffmengen n anderer Systemkomponenten, die Menge der Substanz i von 𝑛𝑛𝑎𝑎 auf 𝑛𝑛𝑒𝑒 zu erhöhen. Das chemische Potential ist ein Maß für die Fähigkeit der Substanz i chemische Reaktionen einzugehen oder elektrische, mechanische und osmotische Arbeit zu leisten. Unter den genannten Bedingungen ist die aufzubringende Arbeit gleich der Änderung der Gibbs-Energie des Systems. 𝜕𝜕𝜕𝜕 𝜇𝜇𝑖𝑖 = � � → 𝑑𝑑𝑑𝑑 = � 𝜇𝜇𝑖𝑖 𝑑𝑑𝑛𝑛𝑖𝑖 𝜕𝜕𝑛𝑛𝑖𝑖 𝑃𝑃,𝑇𝑇,𝑛𝑛 𝑖𝑖 𝑗𝑗 Bei einer Mischung ist das chemische Potential der Komponente i also die partielle Ableitung von G nach der Stoffmenge 𝑛𝑛𝑖𝑖 unter Konstanhaltung von T,p,n. Wegen des extensiven Charakters von G gilt: 𝐺𝐺 = ∑𝑖𝑖 𝜇𝜇𝑖𝑖 𝑛𝑛𝑖𝑖 . Die Gibbs-Duhem-Gleichung ist das vollständige Differential des chemischen Potentials. Bei konstentem T und p (isotherme, isobare Prozessführung) gilt ∑𝑖𝑖 𝑛𝑛𝑖𝑖 𝑑𝑑𝑑𝑑𝑖𝑖 = 0. Gibbs-Duhem: ∑𝑖𝑖 𝑑𝑑𝑑𝑑𝑖𝑖 𝑛𝑛𝑖𝑖 = −𝑆𝑆𝑆𝑆𝑆𝑆 + 𝑉𝑉𝑉𝑉𝑉𝑉 Wie bei jeder thermodynamischen Energiegröße ist das chemische Potential einer gegebenen Substanz nur bis auf eine willkürliche additive Konstante bestimmt. Da bei allen Anwendungen nur Differenzen chemischer Potentiale vorkommen, ist diese Konstante belanglos. Chemisches Potential für ideale Gase Aus 𝑑𝑑𝑑𝑑 = 𝑉𝑉𝑉𝑉𝑉𝑉 − 𝑆𝑆𝑆𝑆𝑆𝑆 folgt bei konstanter Temperatur 𝑑𝑑𝑑𝑑 = 𝑉𝑉𝑉𝑉𝑉𝑉. Mit der Definitionsgleichung des chemischen Potentials folgt weiter 𝑑𝑑𝑑𝑑 = 𝑑𝑑𝑑𝑑/𝑛𝑛 = (𝑉𝑉/𝑛𝑛)𝑑𝑑𝑑𝑑. Mit der idealen Gasgleichung 𝑝𝑝𝑝𝑝 = 𝑛𝑛𝑛𝑛𝑛𝑛 → 𝑉𝑉/𝑛𝑛 = 𝑅𝑅𝑅𝑅/𝑝𝑝 folgt: 𝑑𝑑𝑑𝑑 = 𝑉𝑉 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 = 𝑑𝑑𝑃𝑃, 𝑛𝑛 𝑝𝑝 𝜇𝜇 𝑝𝑝 1 𝑑𝑑𝑑𝑑 𝑝𝑝 0 𝑝𝑝 � 𝑑𝑑𝑑𝑑 = 𝑅𝑅𝑅𝑅 � 𝜇𝜇 0∗ 𝝁𝝁 = 𝝁𝝁∗𝟎𝟎 + 𝑹𝑹𝑹𝑹 𝐥𝐥𝐥𝐥 𝑷𝑷 𝑷𝑷𝟎𝟎 → 𝜇𝜇 − 𝜇𝜇0∗ = 𝑅𝑅𝑅𝑅(ln 𝑃𝑃 − ln 𝑃𝑃0 ) Meist wird 𝑝𝑝0 = 1𝑏𝑏𝑏𝑏𝑏𝑏 gesetzt. In 𝜇𝜇 = 𝜇𝜇0∗ + 𝑅𝑅𝑅𝑅 ln 𝑝𝑝 ist dann p eine reine Zahl (Maßzahl des in bar angegebenen Drucks). 𝛍𝛍 ist nur bis auf die Konstante 𝛍𝛍∗𝟎𝟎 festgelegt, die vom Referenzdruck p0 , von der Temperatur und von der chemischen Natur des Gases abhängig ist. Das chemische Potential eines Gases nimmt mit steigendem Druck p zu. Ein hochkomprimiertes Gas, das zu großer Arbeitsleistung befähigt ist, besitzt ein hohes chemisches Potential. Chemisches Potential für ideale und reale Lösungen Das chemische Potential einer ideal verdünnten Lösung (keine WW zwischen den Molekülen, erfüllt für hinreichend kleine c) kann direkt aus dem des idealen Gases erhalten werden: 𝑉𝑉 = 𝑛𝑛𝑛𝑛𝑛𝑛 → 𝑝𝑝 = (𝑛𝑛/𝑉𝑉)𝑅𝑅𝑅𝑅 = 𝑐𝑐𝑐𝑐𝑐𝑐 𝜇𝜇 = 𝜇𝜇0∗ + 𝑅𝑅𝑅𝑅 ln 𝑝𝑝 → 𝜇𝜇 = 𝜇𝜇0∗ + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐𝑐𝑐𝑐𝑐 = 𝜇𝜇0∗ + 𝑅𝑅𝑅𝑅 ln 𝑅𝑅𝑅𝑅 + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐 = 𝜇𝜇0 + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐 𝝁𝝁 = 𝝁𝝁𝟎𝟎 + 𝑹𝑹𝑹𝑹 𝐥𝐥𝐥𝐥 𝒄𝒄 Bei konzentrierten Lösungen muss man die WW zwischen den gelösten Molekülen berücksichtigen. Statt der Konzentration wird die Aktivitätt 𝒂𝒂 verwendet, die eine Funktion der Konzentration darstellt: 𝒂𝒂 = 𝒇𝒇(𝒄𝒄) ∙ 𝒄𝒄 . Hier ist 𝒇𝒇(𝒄𝒄) der Aktivitätskoeffizient. Für 𝑐𝑐 → 0 folgt 𝑓𝑓 → 1, sodass für verdünnte Lösungen die Aktivität gleich der Konzentration ist. Bei Lösungen ungeladener Substanzen ist 𝑓𝑓 für kleine Konzentrationen konstant. Bei höheren Konzentrationen resultiert eine Zunahme von 𝒇𝒇, also eine Erhöhung der effektiven Konzentration im Vergleich zur tatsächlichen Konzentration. Die Zunahme von 𝑓𝑓 resultiert aus der WW der gelösten Moleküle mit den Lömi-Molekülen. Im Falle geladener Teilchen: elektrostatische WW mit den H2ODipolen, wodurch es zur Bildung der Hydrathülle kommt (Erniedrigung des Wasser-Anteils = Erhöhung der effektiven Konzentration). Debye-Hückel-Theorie Die Debye-Hückel-Theorie ist ein theoretischer Ansatz zur Beschreibung der Ionenwechselwirkungen in Lösungen. Sie liefert eine Interpretation für die elektrische Leitfähigkeit starker Elektrolyte sowie einen Ansatz zur Abschätzung von Aktivitätskoeffizienten für Elektrolyte. Die Grundlage dieser Theorie ist die Annahme, dass sich solvatisierte Ionen so verteilen, dass ihre Positionen durch anziehende und abstoßende elektrostatische Kräfte sowie die thermische Bewegung kT bestimmt werden. Aufgrund der Coulomb-Kraft ergibt sich um ein beliebiges Zentralatom eine kugelförmige Schale aus Gegenionen. Dies steht im Gegensatz zur statistischen Verteilung der Teilchen wie in einem Gas. Jedes geladene Teilchen ist Zentralion seiner eigenen Ionenwolke und gleichzeitig Bestandteil der Ionenwolken entgegengesetzt geladener Ionen. Über die Zeit gemittelt befinden sich neben jedem beliebigen Ion die passenden Gegen-Ionen (Ionenhülle). Debye-Hückel macht folgende Annahmen: • • • • • Der Elektrolyt ist vollständig dissoziiert, bei allen Konzentrationen. Ionen sind kugelförmige, nicht polarisierbare Ladungen (kugelförmiges E-Feld). Ionenradien sind klein gegenüber dem Abstand der Ionen. Das Lösungsmittel beeinflusst die Coulomb-WW der Ionen durch Bildung einer Solvathülle der Dielektrizitätskonstanten ε. Die Coulomb-WW der Ionen ist klein gegenüber kT nur für verdünnte Lösungen < 0,01 M. Ionenwolken Ionenwolken mit Hydrathüllen Der Radius β der Ionenwolke (auch Debye’scher Radius genannt) ergibt sich für T=25°C in wässrigen Lösungen zu: 𝜀𝜀𝜀𝜀0 𝑘𝑘𝐵𝐵 𝑇𝑇 0,304 ∙ 10−9 𝑚𝑚𝑚𝑚𝑚𝑚 � 𝛽𝛽 = � = , 2𝑁𝑁𝐴𝐴 𝑒𝑒 2 𝐼𝐼 𝑙𝑙 √𝐼𝐼 [𝛽𝛽] = 𝑚𝑚, [𝐼𝐼] = 𝑚𝑚𝑚𝑚𝑚𝑚 𝑙𝑙 Mit steigender Ionenkonzentration nimmt die Durchdringung der Ionenwolken zu, sodass die Coulomb-WW stärker wird. Um Reaktionen einzugehen, muss das Ion zusätzliche Arbeit aufwenden, um die Ionenhülle abzustreifen. Ein Ion in realer Lösung ist damit weniger reaktiv als ein isoliertes Ion in idealer verdünnter Lösung. Der Reaktionsverlust steigt mit der Dichte der Elektronenwolke und damit mit der Ionenstärke der Lösung. Um die tatsächlich wirksame Konzentration gelöster Ionen beschreiben zu können, verwendet man die Aktivität. Die Aktivitätskoeffizienten aller geladenen Teilchen fallen mit zunehmender Konzentration zunächst ab. Ursache ist nach Debye-Hückel wie beschrieben die elektrostatische WW zwischen den Ionen bzw. mit der Ionenhülle, die zu einer Verringerung des chemischen Potentials führt. Nach Durchlaufen eines Minimums überwiegt auch bei hochkonzentrierten Lösungenen geladener Teilchen der Anstieg der effektiven Konzentration aufgrund der WW mit den Lösungsmittelmolekülen. Für sehr niedrige Konzentrationen ist der Aktivitätskoeffizient nach Debye-Hückel gegeben durch log 𝑓𝑓 = −𝐴𝐴|𝑧𝑧+ 𝑧𝑧− | ∙ √𝐼𝐼 (Debye-Hückelsches Grenzgesetz), wobei 𝐴𝐴 eine Temperatur- und Lösungsmittel-abhängige Konstante und 𝐼𝐼 die Ionenstärke darstellt. Eine Verfeinerung des Modells von Debye-Hückel ist das Modell nach Debye-Hückel-Onsager, wo zusätzlich die Hydrodynamik mitberücksichtigt wird. Dies geschieht auf ähnliche Weise wie im Kapitel Elektrophorese beschrieben (Hydrodynamische Bremsung durch in entgegengesetzter Richtung wandernde Ionenwolke). Verteilungsgleichgewicht Bringt man eine Substanz A in ein Zweiphasen-System, die sich in beiden Phasen löst, resultiert nach einiger Zeit ein Verteilungsgleichgewicht. In Phase I herrscht dann die Konzentration c‘, in Phase II die Konzentration c‘‘. Werden 𝑑𝑑𝑑𝑑 Mole der Substanz A von der Phase I in die Phase II überführt, so ist die gesamte Änderung 𝑑𝑑𝑑𝑑 der Freien Enthalpie die Summe der Änderungen in beiden Phasen. Bei konstantem Druck und konstanter Temperatur gilt 𝑑𝑑𝑑𝑑 = 𝜇𝜇𝜇𝜇𝜇𝜇. Weiter gilt beim Übertritt der 𝑑𝑑𝑑𝑑 Mole A von I nach II die Beziehung: 𝑑𝑑𝑑𝑑′′ = −𝑑𝑑𝑑𝑑′ = 𝑑𝑑𝑑𝑑. • • 𝑑𝑑𝑑𝑑 = 𝑑𝑑𝐺𝐺 ′ + 𝑑𝑑𝐺𝐺 ′′ = 𝜇𝜇′ 𝑑𝑑𝑛𝑛′ + 𝜇𝜇′′ 𝑑𝑑𝑛𝑛′′ = (𝜇𝜇′′ − 𝜇𝜇′ )𝑑𝑑𝑑𝑑 Ein spontaner Übertritt von A aus Phase I in Phase II erfolgt dann, wenn 𝜇𝜇′ > 𝜇𝜇′′ (Übergang von hohem zu niedrigem chemischen Potential), weil 𝑑𝑑𝑑𝑑 < 0 für spontane Prozesse. Das Verteilungsgleichgewicht ist dann erreicht, wenn 𝜇𝜇′ = 𝜇𝜇′′ , weil 𝑑𝑑𝑑𝑑 = 0 für Prozesse im Gleichgewicht. Die Gleichgewichtsbedingung ermöglicht die Berechnung der Konzentrationen beider Phasen im Gleichgewicht. Dazu einfach die chemischen Potentiale in beiden Phasen gleich setzen und nach dem Konzentrationsverhältnis auflösen. Die Standardwerte des chemischen Potentials 𝜇𝜇0′ und 𝜇𝜇0′′ sind verschieden, da sich die Moleküle der Substanz A in beiden Phasen in einer unterschiedlichen Umgebung befinden. Die Differenz 𝜇𝜇0′ − 𝜇𝜇0′′ wird als −∆𝐺𝐺0 zusammengefasst. GG-Bedingung: 𝜇𝜇′ = 𝜇𝜇0′ + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐 ′ = 𝜇𝜇0′′ + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐 ′′ = 𝜇𝜇′′ (𝜇𝜇0′ − 𝜇𝜇0′′ ) 𝑐𝑐 ′′ = ln 𝑐𝑐 ′′ − ln 𝑐𝑐 ′ = ln ′ 𝑅𝑅𝑅𝑅 𝑐𝑐 ′ ′′ �𝝁𝝁𝟎𝟎 −𝝁𝝁𝟎𝟎 � −∆𝑮𝑮𝟎𝟎 𝒄𝒄′′ 𝑹𝑹𝑹𝑹 𝑹𝑹𝑹𝑹 = 𝜸𝜸 = 𝒆𝒆 = 𝒆𝒆 𝒄𝒄′ Der Verteilungskoeffizient 𝜸𝜸 ist nur noch von der Temperatur abhängig. Das Konzentrationsverhältnis ist demnach eine temperaturabhängige Konstante. Die Änderung der freien Enthalpie durch Transfer von 1 mol von Phase I nach II kann durch Integration aus 𝑑𝑑𝑑𝑑 = (𝜇𝜇′′ − 𝜇𝜇′ )𝑑𝑑𝑑𝑑 bestimmt werden. Unter der Annahme, dass sich die Konzentrationen c‘ und c‘‘ unwesentlich ändern (n‘ und n‘‘ sind hinreichend groß), bleiben die chemischen Potentiale µ‘ und µ‘‘ praktisch konstant. Es gilt: ∆𝐺𝐺 = 𝜇𝜇′′ − 𝜇𝜇′ = (𝜇𝜇0′′ − 𝜇𝜇0′ ) + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐 ′′ = ∆𝐺𝐺0 𝑐𝑐 ′ ∆𝐺𝐺0 ist damit die Änderung der Freien Enthalpie von 1 mol Substanz (∆𝐺𝐺), unter der Bedingung 𝑐𝑐′ = 𝑐𝑐′′, wodurch der lnTerm wegfällt. Bei positivem ∆𝐺𝐺0 (𝜇𝜇0′′ > 𝜇𝜇0′ ) ist der Verteilungskoeffizient 𝛾𝛾 < 0 (A reichert sich in Phase I an). Massenwirkungsgesetz und Energetik chemischer Reaktionen Bei einer Reaktion 𝑣𝑣𝐴𝐴 𝐴𝐴 + 𝑣𝑣𝐵𝐵 𝐵𝐵 → 𝑣𝑣𝑃𝑃 𝑃𝑃 + 𝑣𝑣𝑄𝑄 𝑄𝑄 gilt für die Änderung der Freien Enthalpie 𝑑𝑑𝑑𝑑: 𝑑𝑑𝑑𝑑 = 𝜇𝜇𝐴𝐴 𝑑𝑑𝑛𝑛𝐴𝐴 + 𝜇𝜇𝐵𝐵 𝑑𝑑𝑛𝑛𝐵𝐵 + 𝜇𝜇𝑃𝑃 𝑑𝑑𝑛𝑛𝑃𝑃 + 𝜇𝜇𝑄𝑄 𝑑𝑑𝑛𝑛𝑄𝑄 Annahme: Die Konzentrationen aller Reaktanden sind konstant (erfüllt bei großem Volumen des Reaktionsgefäßes bzw. hohen Konzentrationen der Reaktanden endlicher Stoffumsatz ohne Einfluss auf Konzentrationsverhältnisse). Somit können auch die chemischen Potentiale der Reaktanden als konstant betrachtet werden. Die einzelnen Stoffmengenänderungen 𝑑𝑑𝑛𝑛𝑖𝑖 sind über die stöchiometrischen Koeffizienten miteinander verknüpft. Außerdem müssen bei den Edukten ein negatives Vorzeichen ergänzt werden. Es folgt für die Änderung der freien Enthalpie pro Formelumsatz ∆𝑮𝑮: ∆𝐺𝐺 = �𝜇𝜇𝑃𝑃 𝑣𝑣𝑃𝑃 + 𝜇𝜇𝑄𝑄 𝑣𝑣𝑄𝑄 � − (𝜇𝜇𝐴𝐴 𝑣𝑣𝐴𝐴 + 𝜇𝜇𝐵𝐵 𝑣𝑣𝐵𝐵 ) Für ideal verdünnte Lösungen folgt weiter mit 𝜇𝜇𝑖𝑖 = 𝜇𝜇𝑖𝑖0 + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐𝑖𝑖 : ∆𝐺𝐺 = �𝜇𝜇𝑃𝑃0 𝑣𝑣𝑃𝑃 + 𝜇𝜇𝑄𝑄0 𝑣𝑣𝑄𝑄 � − �𝜇𝜇𝐴𝐴0 𝑣𝑣𝐴𝐴 + 𝜇𝜇𝐵𝐵0 𝑣𝑣𝐵𝐵 � + 𝑅𝑅𝑅𝑅�𝑣𝑣𝑃𝑃 ln 𝑐𝑐𝑃𝑃 + 𝑣𝑣𝑄𝑄 ln 𝑐𝑐𝑄𝑄 � − 𝑅𝑅𝑅𝑅(𝑣𝑣𝐴𝐴 ln 𝑐𝑐𝐴𝐴 + 𝑣𝑣𝐵𝐵 ln 𝑐𝑐𝐵𝐵 ) ∆𝐺𝐺 = ∆𝐺𝐺 0 + 𝑅𝑅𝑅𝑅 ln 𝑣𝑣 𝑣𝑣 𝑐𝑐𝑃𝑃𝑃𝑃 ∙ 𝑐𝑐𝑄𝑄𝑄𝑄 𝑣𝑣 𝑣𝑣 𝑐𝑐𝐴𝐴 𝐴𝐴 ∙ 𝑐𝑐𝐵𝐵𝐵𝐵 Für die Konzentrationen sind die entsprechenden Konzentrationen vor Einstellung des Gleichgewichts einzusetzen! Sind alle Konzentrationen gleich eins, so folgt ∆𝐺𝐺 = ∆𝐺𝐺 0 (Änderung der freien Enthalpie unter Standardbedingungen). Die Reaktion verläuft dann spontan von links nach rechts, wenn 𝜇𝜇𝐴𝐴 𝑣𝑣𝐴𝐴 + 𝜇𝜇𝐵𝐵 𝑣𝑣𝐵𝐵 > 𝜇𝜇𝑃𝑃 𝑣𝑣𝑃𝑃 + 𝜇𝜇𝑄𝑄 𝑣𝑣𝑄𝑄 , da für spontane Prozesse ∆𝐺𝐺 < 0 gilt. Selbst wenn ∆𝐺𝐺 0 positiv ist, kann die Reaktion spontan ablaufen, wenn die Konzentration der Endprodukte klein gehalten wird (z.B. bei Folgereaktion). Im Gleichgewicht gilt ∆𝑮𝑮 = 𝟎𝟎. Es folgt damit: 0 −∆𝐺𝐺 = 𝑅𝑅𝑅𝑅 ln 𝑣𝑣 𝑣𝑣 𝑐𝑐𝑃𝑃𝑃𝑃 ∙ 𝑐𝑐𝑄𝑄𝑄𝑄 𝑣𝑣 𝑐𝑐𝐴𝐴 𝐴𝐴 ∙ 𝑣𝑣 𝑐𝑐𝐵𝐵𝐵𝐵 ∆𝐺𝐺 0 = 𝑅𝑅𝑅𝑅 ln 𝐾𝐾 → 𝐾𝐾 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 Für die Konzentrationen der Reaktanden sind die Konzentrationen im Gleichgewicht einzusetzen! Da ∆𝐺𝐺 0 Konzentrations-unabhängig ist, muss das Argument im 𝑙𝑙𝑙𝑙 eine Konstante sein, die als 𝐾𝐾 bezeichnet wird. 𝑲𝑲 ist die Gleichgewichtskonstante der Reaktion und definiert das Massenwirkungsgesetz. Sie ist abhängig von der chemischen Natur der Reaktanden, von der Temperatur und vom Druck. Die Einheit der Gleichgewichtskonstanten ist abhängig von der Anzahl an Edukten und Produkten. Im Fall, dass es sich nicht um ideal verdünnte Lösungen handelt, sind die Konzentrationen durch Aktivitäten zu ersetzen. Hinreaktion und Rückreaktion laufen auch im Gleichgewicht ständig ab. Die Standardänderung der Freien Enthalpie ∆𝑮𝑮𝟎𝟎 Der Standardzustand ist durch die Konzentration 1 M definiert. Je stärker ∆𝐺𝐺 0 negativ ist, desto größer ist K (GG umso mehr auf der Seite der Produkte). Reaktionen mit hohen Gleichgewichtskonstanten werden als irreversibel bezeichnet. Sind Wasserstoffionen an der Reaktion beteiligt, so wird als Standardzustand eine Wasserstoffionen-Konzentration von 10−7 𝑀𝑀 (pH=7) ′ gewählt. Die Standardenthalpie wird mit ∆𝐺𝐺 0 bezeichnet. Für komplizierte Reaktionen kann ∆𝐺𝐺 0 aus den ∆𝐺𝐺 0 -Werten einfacher Reaktionen zusammengesetzt werden, die tabelliert sind. Die Reaktion muss dazu in Teilreaktionen zerlegt werden und die einzelnen ∆𝐺𝐺 0 -Werte der Teilreaktionen aufaddiert werden. Gekoppelte Reaktionen: exergone und endergone Reaktionen ′ Die Raktion Glucose + 𝑃𝑃𝑖𝑖 Glucose-6-Phosphat + H2O läuft nicht spontan ab, da ∆𝐺𝐺 0 1 = ′ 13,8𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚. Durch Kopplung an die Reaktion ATP+H2O ADP + 𝑃𝑃𝑖𝑖 + H+ mit ∆𝐺𝐺 0 2 = −30,5𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚 ′ ′ kann die Gesamtreaktion spontan ablaufen (∆𝐺𝐺 0 1 + ∆𝐺𝐺 0 2 = −16,7𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚). Die Kopplung erfolgt über das Enzym Hexokinase, die das Phosphat von ATP direkt auf Glucose überträgt. • • ∆𝐺𝐺 < 0: exergone Reaktion, läuft spontan ab. ∆𝐺𝐺 > 0: endergone Reaktion, läuft nicht spontan ab. Enthalpie und Entropie bei chemischen Reaktionen Gibbs-Helmholtz-Gleichung: ∆𝐺𝐺 = ∆𝐻𝐻 − 𝑇𝑇∆𝑆𝑆 Endotherme Reaktion: ∆𝐻𝐻 > 0, Wärme wird aus der Umgebung aufgenommen Exotherme Reaktion: ∆𝐻𝐻 < 0, Wärme wird an die Umgebung abgegeben Standardbedingungen (T=298,15K): ∆𝐺𝐺 0 = ∆𝐻𝐻 0 − 𝑇𝑇∆𝑆𝑆 0 ∆𝐻𝐻 0 ∆𝑆𝑆 0 𝑅𝑅 Gleichgewichtskonstante: 𝐾𝐾 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 ∙ 𝑒𝑒 − Läuger, Kapitel 6: Elektrochemie Elektrolytische Leitung Das Gesetz von Faraday Elektrolyte sind Stoffe, die in Wasser in frei bewegliche Ionen dissoziieren und daher elektrische Leiter darstellen. Durch Eintauchen von Elektroden aus einem inerten Metall (z.B. Platin) kann der Leitungsvorgang in Lösung beobachtet werden. Bei Anlegen einer Spannung 𝑉𝑉 fließt ein Strom 𝐼𝐼 durch die Lösung. Der Ladungstransport entspricht einer Wanderung von positiven Kationen zur Kathode und negativen Anionen zur Anode innerhalb der wässrigen Lösung. Im Inneren der Metallelektroden besteht der Ladungstransport in einer Wanderung von Elektronen. An der Grenzfläche Elektrode/Lösung findet also ein Übergang von einem elektronischen zu einem ionischen Leitungsmechanismus statt. Dies hat zur Folge, dass an den Elektroden chemische Reaktionen ablaufen (Elektrolyse). Bei einer HCl-Lösung reagieren zwei Protonen mit zwei Elektronen der Kathode zu H2-Gas, während zwei Chlorid-Ionen zwei Elektronen an die Anode abgeben und als Cl2-Gas der Lösung entweichen. Die Kathode ist damit Elektronendonor, während die Anode Elektronenakzeptor ist. Fließt während der Zeit 𝑡𝑡 ein konstanter Strom 𝐼𝐼, so wird insgesamt die Ladung 𝑸𝑸 = 𝑰𝑰𝑰𝑰 [𝑪𝑪 = 𝑨𝑨𝑨𝑨] transportiert. Die an den Elektroden umgesetzten Stoffmengen sind der transportierten Ladung proportional. Für die Abscheidung von 1 mol einer einwertigen Ionensorte benötigt man 𝑁𝑁𝐴𝐴 𝑒𝑒 = 𝐹𝐹 = 96485𝐶𝐶/𝑚𝑚𝑚𝑚𝑚𝑚 (Faraday-Konstante). Die allgemeine Form dieser Beziehung: 𝑸𝑸 = 𝒏𝒏𝒏𝒏𝒏𝒏 ist das Gesetz von Faraday (n = Anzahl der Mole, z = Ladung). Ionenwanderung im elektrischen Feld, Ionenbeweglichkeit und Leitfähigkeit Die Konzentrations-Abhängigkeit der Leitfähigkeit einer Elektrolytlösung kann über eine zylindrische Leitfähigkeitszelle vom Querschnitt 𝐴𝐴 und der Länge 𝑙𝑙 gemessen werden, die eine verdünnte Lösung eines völlig dissoziierten Elektrolyten 𝐴𝐴𝐴𝐴 ⇌ 𝐴𝐴+ + 𝐵𝐵− enthält. Die von außen angelegten elektrischen Potentiale der Elektroden 1 und 2 erzeugen eine Potentialdifferenz/Spannung von 𝑉𝑉 = 𝜑𝜑1 − 𝜑𝜑2 , die mit einem elektrischen Feld in x-Richtung verbunden ist. Dabei wird von einer linearen Abhängigkeit des elektrischen Potentials von der Ortskoordinate x ausgegangen. 𝐸𝐸𝑥𝑥 = − 𝑑𝑑𝑑𝑑 𝜑𝜑1 − 𝜑𝜑2 𝑉𝑉 = = 𝑙𝑙 𝑑𝑑𝑑𝑑 𝑙𝑙 ��⃗+ = 𝒆𝒆𝑬𝑬 �⃗ ; auf das Im elektrischen Feld wirkt auf das einwertige Kation der Ladung 𝒆𝒆 die Kraft 𝑲𝑲 ��⃗− = −𝒆𝒆𝑬𝑬 �⃗ . Schaltet man das E-Feld ein, so nehmen die Ionen Anion der Ladung – 𝑒𝑒 wirkt die Kraft 𝑲𝑲 �⃗+ = 𝒖𝒖+ �𝑬𝑬⃗ und 𝒗𝒗 �⃗− = −𝒖𝒖− �𝑬𝑬⃗ an, bei der die innerhalb kurzer Zeit konstante Geschwindigkeiten 𝒗𝒗 Reibungskraft mit der elektrischen Kraft im GG ist. 𝑢𝑢+ und 𝑢𝑢− sind die Ionenbeweglichkeiten (Einheit: 𝑐𝑐𝑚𝑚2 𝑉𝑉 −1 𝑠𝑠 −1 , Geschwindigkeit des Ions unter Wirkung der Feldstärke 1𝑉𝑉𝑉𝑉𝑚𝑚−1 , qualitativer Zusammenhang zum Diffusionskoeffizienten). Die Beweglichkeit kleiner Ionen in Wasser bei RT ist im Bereich 10−3 𝑐𝑐𝑚𝑚2 𝑉𝑉 −1 𝑠𝑠 −1 und daher sehr langsam (0,01mm pro Sekunde bei einer Feldstärke von 1𝑉𝑉𝑉𝑉𝑚𝑚−1 ). Die Elektrolytlösung enthält pro Volumenelement 𝑁𝑁+ Kationen und 𝑁𝑁− Anionen. Der durch die Bewegung der Ionen erzeugte elektrische Strom 𝑰𝑰 entspricht der Ladung 𝑸𝑸 pro Zeitintervall ∆𝒕𝒕, die durch eine senkrecht zur Bewegungsrichtung anzunehmende Querschnittsfläche 𝑨𝑨 hindurchtritt. In der Zeit ∆𝑡𝑡 legt das Ion die Strecke 𝒔𝒔 = 𝒗𝒗∆𝒕𝒕 zurück. Durch die Querschnittsfäche A treten in ∆𝑡𝑡 also alle Ionen durch, die sich in einem Zylinder des Volumens 𝑨𝑨𝑨𝑨∆𝒕𝒕 befinden, insgesamt also: ∆𝑵𝑵 = 𝑵𝑵𝑵𝑵𝑵𝑵∆𝒕𝒕 Ionen. Es resultiert ein Strombeitrag von 𝑰𝑰 = ∆𝑸𝑸/∆𝒕𝒕 = 𝒆𝒆∆𝑵𝑵/∆𝒕𝒕. Angewandt auf Kationen und Anionen ergibt sich (Die entgegengesetzten Bewegungsrichtungen der Kationen und Anionen können nicht registriert werden, da beide parallel zum E-Feld laufen. Es resultieren in beiden Fällen positive Strombeträge; für die Geschwidnigkeiten werden Beträge verwendet!): 𝐼𝐼+ = 𝑒𝑒𝑁𝑁+ 𝐴𝐴𝑣𝑣+ , 𝐼𝐼− = 𝑒𝑒𝑁𝑁− 𝐴𝐴𝑣𝑣− , → 𝐼𝐼 = 𝑒𝑒𝑒𝑒(𝑁𝑁+ 𝑣𝑣+ + 𝑁𝑁− 𝑣𝑣−) Mit 𝑁𝑁 = 𝑐𝑐𝑁𝑁𝐴𝐴 = 𝑐𝑐𝑐𝑐/𝑒𝑒 (𝑭𝑭 = 𝑵𝑵𝑨𝑨 𝒆𝒆 ) sowie 𝑣𝑣 = 𝑢𝑢𝑢𝑢 = 𝑢𝑢𝑢𝑢/𝑙𝑙 folgt weiter: U 𝑰𝑰 = 𝒄𝒄𝒄𝒄𝒄𝒄(𝒖𝒖+ + 𝒖𝒖− ) 𝑽𝑽 𝒍𝒍 Damit ist der elektrische Strom proportional zur angelegten Spannung, die als Triebkraft für die Ionenbewegung wirkt. Das Verhältnis von |𝑰𝑰/𝑽𝑽| (Strom:Spannung) ist der elektrische Leitwert (Einheit: 𝑆𝑆 = 1𝐴𝐴/𝑉𝑉). Er ist damit von den Dimensionen der Leitfähigkeitszelle (𝑨𝑨 und 𝒍𝒍) sowie von den Eigenschaften der Elektrolytlösung (𝒄𝒄 und 𝒖𝒖) abhängig. Werden ausschließlich die Eigenschaften der Elektrolytlösung berücksichtigt, definiert sich die elektrische Leitfähigkeit 𝝀𝝀 als der auf die Flächeneinheit und die Längeneinheit bezogene Leitwert (Leitwert der Einheitszelle: A=1cm², l=1cm). |𝐼𝐼/𝑉𝑉| ∙ 𝑙𝑙 = 𝝀𝝀 = 𝒄𝒄𝒄𝒄(𝒖𝒖+ + 𝒖𝒖− ) , 𝐴𝐴 [𝐴𝐴𝑉𝑉 −1 𝑐𝑐𝑚𝑚−1 = 𝑆𝑆𝑆𝑆𝑚𝑚−1 ] Die entsprechend reziproken Größen sind elektrischer Widerstand (Einheit: Ω = 𝑉𝑉/𝐴𝐴 = 1/𝑆𝑆) und spezifischer elektrischer Widerstand (Einheit: 𝑉𝑉𝐴𝐴−1 𝑐𝑐𝑐𝑐). Um eine von der Konzentration unabhängige Vergleichsgröße zu erhalten wird die molare elektrische Leitfähigkeit definiert: 𝚲𝚲 = 𝝀𝝀/𝒄𝒄 . Die Leitfähigkeit von Elektrolytlösungen (Ionenleitung) ist viel geringer als die von Metallen (Elektronenleitung): Für 1M KCl bei 25°C gilt 𝜆𝜆 = 0,11𝑆𝑆𝑆𝑆𝑚𝑚−1 (realer Messwert, berechneter Wert liegt bei 0,15𝑆𝑆𝑆𝑆𝑚𝑚−1 , da diese Gleichungen keine interionische WW berücksichtigen -> bewirkt Reduktion der Leitfähigkeit), während für gut leitende Metalle 𝜆𝜆 = 106 𝑆𝑆𝑆𝑆𝑚𝑚−1 gilt. 𝑧𝑧 𝑧𝑧 Berücksichtigung der Ladungszahl z und Dissoziationszahl n der Ionen 𝐾𝐾𝑛𝑛 ++ 𝐴𝐴𝑛𝑛−− : Interionische Wechselwirkung 𝝀𝝀 = 𝒄𝒄𝒄𝒄(𝒏𝒏+𝒛𝒛+𝒖𝒖+ + 𝒏𝒏−𝒛𝒛−𝒖𝒖−) Es wurde bisher vorausgesetzt, dass die Ionen unabhängig voneinander wandern (keine interionische WW), was nur bei hochverdünnten Lösungen zutrifft. Zwei Ladungen q im Abstand r ziehen sich mit �⃗𝑪𝑪 an. Dabei tritt die Coulomb-Energie 𝑾𝑾𝑪𝑪 auf. 𝑟𝑟⃗0 ist der Einheitsvektor in der Coulomb-Kraft �𝑲𝑲 Verbindungsrichtung der beiden Ladungen. �𝑲𝑲 �⃗𝑪𝑪 = 𝒒𝒒+𝒒𝒒− �⃗ , 𝒓𝒓 𝟒𝟒𝟒𝟒𝟒𝟒𝜺𝜺𝟎𝟎 𝒓𝒓𝟐𝟐 𝟎𝟎 𝑾𝑾𝑪𝑪 = − 𝒒𝒒+𝒒𝒒− 𝟒𝟒𝟒𝟒𝟒𝟒𝜺𝜺𝟎𝟎 𝒓𝒓 Würde nur die Coulomb-Kraft wirken, würden die Ionen in Wasser nicht dissoziieren. Ursache der Dissoziation ist die thermische Molekularbewegung aufgrund der thermischen Energie 𝑾𝑾𝒕𝒕𝒕𝒕 = 𝒌𝒌𝑩𝑩 𝑻𝑻 = 𝟒𝟒, 𝟏𝟏 ∙ 𝟏𝟏𝟏𝟏−𝟐𝟐𝟐𝟐 𝑱𝑱 . Ist die Coulomb-Energie kleiner als die thermische, so erfolgt die Dissoziation. Für einen Abstand 𝑟𝑟 = 0,5𝑛𝑛𝑛𝑛 (5-facher Ionenradius von Na+) würde in Wasser (𝜀𝜀 = 80) die Coulomb-Energie zweier einwertiger Ionen (𝑞𝑞+ 𝑞𝑞− = −𝑒𝑒 2 ) 𝑊𝑊𝐶𝐶 = 5,8 ∙ 10−21 𝐽𝐽 betragen. Dies entspricht 2,9 ∙ 10−21 𝐽𝐽 < 𝑊𝑊𝑡𝑡ℎ pro Ion. Die thermische Energie ist damit ausreichend für die Dissoziation, jedoch nicht groß genug, um eine völlige unabhängige Bewegung von Kationen und Anionen in Lösung zu ermöglichen. Damit ist die Aufenthaltswahrscheinlichkeit eines Kations in der Nähe eines Anions größer, als man es für eine unabhängige Bewegung erwarten würde. Kationen und Anionen stören sich bei der Bewegung im E-Feld, was zur Konzentrations-Abhängigkeit der molaren Leitfähigkeit führt. Für verdünnte Lösungen gilt: 𝚲𝚲(𝐜𝐜) = 𝚲𝚲𝟎𝟎 − 𝒂𝒂√𝒄𝒄 Hier ist Λ 0 der Grenzwert von Λ für 𝑐𝑐 → 0 und 𝑎𝑎 eine positive Konstante. Bei 1mM KCl beträgt der Korrekturfaktor 2%, bei größeren Konzentrationen kann er erheblich ansteigen. Die Reduktion der molaren Leitfähigkeit entspricht phänomenologisch einer Reduktion der effektiven IonenKonzentration. Dies wurde bereits anhand der Aktivität 𝑎𝑎 = 𝑓𝑓(𝑐𝑐)𝑐𝑐 festgestellt, wobei der Aktivitätskoeffizient 𝑓𝑓(𝑐𝑐) Konzentrationsabhängig ist (für Ionen: Reduktion der effektiven Konzentration bei geringen Konzentrationen aufgrund interionischer WW). Beziehungen zwischen Ionenbeweglichkeit und Ionenradius Da bei konstanter Geschwindigkeit im E-Feld ein GG zwischen Reibungskraft und elektrischer Kraft �⃗𝑟𝑟 = −𝐾𝐾 �⃗+ bzw. 𝐾𝐾 �⃗𝑟𝑟 = −𝐾𝐾 �⃗−. Für kugelförmige makroskopische Teilchen und herrscht gilt: 𝐾𝐾 �⃗𝑟𝑟 = −6𝜋𝜋𝜋𝜋𝜋𝜋𝑣𝑣⃗ = −6𝜋𝜋𝜋𝜋𝜋𝜋𝑢𝑢𝐸𝐸�⃗ . Es näherungsweise auch für mikroskopische gilt das Stokesche Gesetz 𝐾𝐾 folgt (da u positiv sein muss und z negativ für Anionen, muss ein negatives Vorzeichen ergänzt werden): −6𝜋𝜋𝜋𝜋𝜋𝜋𝜋𝜋𝐸𝐸�⃗ = 𝑧𝑧𝑧𝑧𝐸𝐸�⃗ , → 𝒖𝒖+/− = ± 𝒛𝒛+/− ∙ 𝒆𝒆 𝟔𝟔𝟔𝟔𝟔𝟔 ∙ 𝒓𝒓+/− Ionenbeweglichkeit ist demnach umgekehrt proportional zum Ionenradius, wobei der Radius des hydratisierten Ions zu betrachten ist. Die Verhältnisse hier (Li+aq > Na+aq > K+aq) sind umgekehrt als bei den Ionenradien ohne Hydrathülle (Li+ < Na+ < K+). Eine Sonderrolle nimmt das Proton ein, das eine besonders hohe Beweglichkeit besitzt. Dies liegt an dem Ordnungsgrad des Wassers, dass Protonentransport längs H-Brückenbindungen erlaubt (Grothhuß-Mechanismus). Überführungszahlen Da Kation und Anion unterschiedliche Beweglichkeiten besitzen, sind die Beiträge zum Gesamtstrom 𝑰𝑰 = 𝑰𝑰+ + 𝑰𝑰− unterschiedlich groß. Es werden Überführungszahl des Kations 𝑡𝑡+ = 𝐼𝐼+ /𝐼𝐼 = 𝑢𝑢+/(𝑢𝑢+ + 𝑢𝑢−) und des Anions 𝑡𝑡− (äquivalent) definiert, wobei 𝑡𝑡+ + 𝑡𝑡− = 1. Für HCl gilt z.B. 𝑡𝑡+ = 0,82, d.h. der Strom wird zu 82% durch Protonen getragen, aufgrund der hohen Beweglichkeit der Protonen. Ionengleichgewichte an Membranen: Das elektrochemische Potential Ionenselektive Membranen Es werden zwei Phasen zu unterschiedlichen NaCl-Konzentrationen betrachtet, die über eine Membran getrennt sind, die nur für eine Ionensorte permeabel sei (Ionenselektivität). Ionenselektive Membranen sind z.B. Ionenaustauscher-Membranen, die aus einem hochpolymeren porösen Netzwerk mit hoher Konzentration fixierter elektrischer Ladungen trägt. Kationenselektivität wird z.B. durch fixierte COO -Gruppen bewerkstelligt. Die porösen Zwischenräume enthalten dann neben Wasser Kationen, welche die fixierten negativen Ladungen neutralisieren. Die Anionen-Konzentration ist sehr gering. Aufgrund des Konzentrationsgradienten hat Na+ die Tendenz von der Seite höherer Konzentration (c‘‘) zur Seite niedrigerer Konzentration (c‘) zu wandern. Es kommt nicht zum Konzentrationsausgleich, da sich eine Potentialdifferenz 𝜑𝜑 ′ − 𝜑𝜑′′ = 𝑉𝑉𝑚𝑚 über der Membran aufbaut (Membranpotential). (1) Zunächst wird dabei 𝜑𝜑′ > 𝜑𝜑′′ , da die linke Seite der Membran (Plattenkondensator) durch die positiven Na+-Ionen positiv aufgeladen wird. (2) Dies führt zu einem elektrischen Feld im Inneren der Membran, dessen Vektor von links nach rechts orientiert ist. (3) Das elektrische Feld induziert eine Kraft in Gegenrichtung der wandernden, positiv geladenen Teilchen, die den Transport zum Erliegen bringt. Der Gleichgewichtszustand entspricht keinem Konzentrationsausgleich, sondern einem hinreichend großen Membranpotential. Elektrochemisches Potential, Membranpotential unter Gleichgewichtsbedingungen Obwohl sich ein Gleichgewichtszustand einstellt, ist die für ungeladene Teilchen gültige ′ Gleichgewichtsbedingung 𝜇𝜇′ = 𝜇𝜇′′ für das permeable Kation nicht mehr gültig, da 𝑐𝑐 ′ ≠ 𝑐𝑐 ′′ → 𝜇𝜇𝑁𝑁𝑎𝑎 + ≠ ′′ 𝜇𝜇𝑁𝑁𝑎𝑎 + . Es muss der Beitrag der elektrischen Potentialdifferenz berücksichtigt werden. Das elektrochemische Potential ist die Summe aus elektrischem und chemischem Potential: 𝜇𝜇�𝑖𝑖 = 𝜇𝜇𝑖𝑖 + 𝑧𝑧𝑖𝑖 𝐹𝐹𝐹𝐹 = 𝜇𝜇𝑖𝑖0 + 𝑅𝑅𝑅𝑅 ln 𝑎𝑎𝑖𝑖 + 𝑧𝑧𝑖𝑖 𝐹𝐹𝐹𝐹 𝒛𝒛𝒊𝒊 𝑭𝑭𝑭𝑭 ist die elektrostatische Energie, die aufgewendet werden muss, um 1 mol Ionen der Gesamtladung 𝒛𝒛𝒊𝒊 𝑭𝑭 vom Unendlichen (Potential Null) an einen Ort des Potentials 𝝋𝝋 zu transferieren. Für das permeable Ion gilt demnach die Gleichgewichtsbeziehung 𝜇𝜇� ′ = 𝜇𝜇�′′ . Für das permeable Kation gilt damit: ′ ′′ 𝜇𝜇+ + 𝑧𝑧+ 𝐹𝐹𝜑𝜑′ = 𝜇𝜇+ + 𝑧𝑧+ 𝐹𝐹𝜑𝜑′′ 0 0 𝜇𝜇+ + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐+′ + 𝑧𝑧+ 𝐹𝐹𝜑𝜑′ = 𝜇𝜇+ + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐+′′ + 𝑧𝑧+ 𝐹𝐹𝜑𝜑′′ 𝑧𝑧+ 𝐹𝐹𝜑𝜑′ − 𝑧𝑧+ 𝐹𝐹𝜑𝜑′′ = 𝑅𝑅𝑅𝑅 ln 𝑉𝑉𝑚𝑚 = 𝜑𝜑′ − 𝜑𝜑′′ = 𝑐𝑐+′′ 𝑐𝑐+′ 𝑅𝑅𝑅𝑅 𝑐𝑐 ′′ ln 𝑧𝑧𝑧𝑧 𝑐𝑐 ′ Für z.B. Na+ gilt mit 𝑧𝑧+ = 1 für 𝑇𝑇 = 298𝐾𝐾 folgende Gleichung. Für einwertig negative geladene Ionen wie Cl- würde derselbe Betrag mit anderem Vorzeichen (𝑧𝑧− = −1) resultieren. 𝑉𝑉𝑚𝑚 = 59𝑚𝑚𝑚𝑚 ∙ log10 𝑐𝑐 ′′ 𝑐𝑐 ′ Unter Berücksichtigung der spezifischen Membrankapazität C, errechnet sich eine akkumulierte Ladung von 𝑄𝑄 = 𝐶𝐶𝐶𝐶 = 5,8 ∙ 10−8 𝐶𝐶 = 3,6 ∙ 1011 𝑒𝑒 pro cm² Membranfläche. Gleichungen für Membranpotentiale im Gleichgewichtszustand werden als Nernst-Gleichungen bezeichnet. Bei diesen Berechnungen wird immer die Elektroneutralitätsbedingung berücksichtigt. Diese besagt, dass auf jeder Seite der Membran gleich viele Kationen wie Anionen vorliegen müssen (jedes intrazelluläre Kompartiment ist für sich elektroneutral). Die Diffusion von Kationen über die Membran bewirkt demnach, dass Anionen nachdiffundieren – Sie kommen allerdings nicht über die Membran. Die Potentialdifferenz kommt ausschließlich dadurch zustande, dass die Membran auf ihren beiden Seiten Ionen verschiedenen Vorzeichens aufnehmen kann – Sie wird nur durch die Ladungen bestimmt, die dicht an der Membran anliegen. Die durch die Membran transportierten Kationen akkumulieren also an der Membran auf der gegenüberliegenden Seite, die Anionen auf der entgegengesetzten Membranseite (Aufladung des Membrankondensators). Donnan-Gleichgewicht Das Donnan-Gleichgewicht beschreibt das Membranpotential, wenn eine für kleine Kationen und Anionen permeable Membran mit der Lösung eines impermeablen Polyelektrolyten (hochmolekulare, ioinisierte Verbindung, z.B. Protein) in Kontakt steht. In Lösung werden die auf dem Polyelektrolytmolekül fixierten Ladungen durch gelöste kleine Gegenionen kompensiert. Im Durchschnitt trägt ein Proteinat etwa 10 Ladungen. Es wird eine für Na+ und Cl- permeable Membran betrachtet. Im Gleichgewichtszustand gilt 𝑐𝑐+′ = 𝑐𝑐+′′ sowie 𝑐𝑐−′ = 𝑐𝑐−′′ , wenn lediglich der niedermolekulare Elektrolyt NaCl vorhanden ist. Das Membranpotential ist null. Die Zugabe eines Proteins zur Phase II bewirkt über die überschüssig fixierten Ladungen 𝒛𝒛𝑷𝑷 die Aufnahme von Ionen aus der Lösung. Dadurch stellt sich ein neues Gleichgewicht ein, bei dem 𝑐𝑐+′ = 𝑐𝑐+′′ sowie 𝑐𝑐−′ = 𝑐𝑐−′′ nicht mehr gelten. Zudem ist das Membranpotential nicht mehr null. • ′ ′′ Ausgangspunkt der Betrachtung sind wieder die Gleichgewichtsbedingungen 𝜇𝜇�+ = 𝜇𝜇�+ und + ′ ′′ 𝜇𝜇�− = 𝜇𝜇�− für Na bzw. Cl . Einsetzen der elektrochemischen Potentiale für verdünnte Lösungen und Addition der beiden Gleichungen ergibt die Donnan-Gleichung 𝒄𝒄′+ 𝒄𝒄′− = 𝒄𝒄′′+ 𝒄𝒄′′− . In beiden Lösungen muss damit das Produkt der Konzentrationen von permeablen Kationen und Anionen gleich groß sein. • • In der Protein-freien Phase I gilt die Elektroneutralitätsbedingung 𝒄𝒄′+ = 𝒄𝒄′− = 𝒄𝒄′ , sodass die Donnan-Gleichung zur quadratischen Gleichung (𝒄𝒄′ )𝟐𝟐 = 𝒄𝒄′′+ 𝒄𝒄′′− wird. Enthält die Phase II ein positiv geladenes Protein, so ist 𝒄𝒄′′− > 𝒄𝒄′′+ , da die Ladung des Proteins durch einen Cl--Überschuss kompensiert werden muss (Konzentration der Gegen-Ionen in der Proteinlösung erhöht, der Co-Ionen erniedrigt im Vergleich zur Protein-freien Lösung). Es gilt hier als Elektroneutralitätsbedingung 𝒄𝒄′′− = 𝒛𝒛𝑷𝑷 𝒄𝒄𝑷𝑷 + 𝒄𝒄′′+ . Durch Einsetzen der Gleichung für 𝑐𝑐−′′ und 𝑐𝑐+′′ in die quadratische Donnan-Gleichung und Auflösung über die pq-Formel (NullstellenBestimmung) ergeben sich folgende Beziehugen: (𝑐𝑐 ′ )2 = 𝑐𝑐+′′ (𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 + 𝑐𝑐+′′ ) bzw. (𝑐𝑐 ′ )2 = 𝑐𝑐−′′ (𝑐𝑐−′′ − 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 ) 0 = (𝑐𝑐+′′ )2 + 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 𝑐𝑐+′′ − (𝑐𝑐 ′ )2 bzw. 0 = (𝑐𝑐−′′ )2 − 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 𝑐𝑐−′′ − (𝑐𝑐 ′ )2 𝑐𝑐+′′ = − 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 2 + �(𝑐𝑐 ′ )2 + � � , 2 2 𝑐𝑐−′′ = 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 2 + �(𝑐𝑐 ′ )2 + � � 2 2 (nach der pq-Formel sollte vor der Wurzel ± stehen; für das minus-Zeichen würde aber eine negative Konzentration resultieren, was physikalisch keinen Sinn macht) Grenzfälle: • • • Befindet sich kein Protein in Lösung (𝑐𝑐𝑃𝑃 = 0) oder befindet es sich am isoelektrischen Punkt (𝑧𝑧𝑃𝑃 = 0), resultiert 𝑐𝑐+′′ = 𝑐𝑐−′′ = 𝑐𝑐′′. Hohe Salzkonzentration: Vernachlässigung des zweiten Terms unter der Wurzel, da 𝑧𝑧 𝑐𝑐 ′′ = 𝑐𝑐 ′ ∓ 𝑃𝑃 𝑃𝑃 𝑐𝑐 ′ ≫ |𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 | → 𝑐𝑐+/− 2 Niedrige Salzkonzentration: 𝑐𝑐 ′ ≪ |𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 | → 𝑐𝑐−′′ = 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 , 𝑐𝑐+′′ = 2 �𝑐𝑐 ′ � 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 ≪ 𝑐𝑐 ′ . Hier ist die Proteinlösung praktisch frei von Natrium-Ionen, obwohl sie durch die Membran diffundieren können. Das bei Donnan-Gleichgewicht vorliegende Membranpotential (Donnan-Potential) berechnet sich über die normale Nernst-Gleichung 𝑉𝑉𝑚𝑚 = (𝑐𝑐 ′ )2 = 𝑐𝑐+′′ 𝑐𝑐−′′ zu: 𝑅𝑅𝑅𝑅 𝑐𝑐 ′′ ln 𝑐𝑐 ′ 𝐹𝐹 𝑉𝑉𝑚𝑚 = 𝜑𝜑′ − 𝜑𝜑′′ = unter Berücksichtigung der Donnan-Gleichung 𝑅𝑅𝑅𝑅 𝑐𝑐+′′ 𝑅𝑅𝑅𝑅 𝑐𝑐−′′ ln ′ = ln ′ 𝑐𝑐 𝑐𝑐 𝐹𝐹 𝐹𝐹 Für ein positiv geladenes Protein nimmt die Protein-freie Lösung I ein positives Potential an (vergleiche Formel für 𝑐𝑐−′′ : für 𝑧𝑧𝑃𝑃 > 0 folgt hier 𝑐𝑐−′′ > 𝑐𝑐 ′ ). Erklärung: Für ein positiv geladenes Protein gilt nach der Gleichung 𝑐𝑐−′′ = 𝑧𝑧𝑃𝑃 𝑐𝑐𝑃𝑃 + 𝑐𝑐+′′ die Beziehung 𝑐𝑐−′′ > 𝑐𝑐+′′ . Der Überschuss an permeablen Anionen würde einen Nettotransport in die Protein-freie Lösung bewirken. Dieser wird durch das Membranpotential verhindert. Kolloidosmotischer Druck ignoriert S.207 Redoxprozesse und elektrochemische Zellen Ionen können teilweise in verschiedenen Oxidationsstufen vorkommen, die durch Aufnahme oder Abgabe eines Elektrons ineinander übergehen. Im Reaktionsablauf treten freie Elektronen jedoch nie in Erscheinung. Solche Reaktionen treten daher entweder gekoppelt auf (Elektronendonor = Reduktionsmittel und Elektronenakzeptor = Oxidationsmittel) oder finden unter Beteiligung von Metallelektroden statt. Eine allgemeine Redoxreaktion läuft nach dem Schema: (𝑂𝑂𝑂𝑂)1 + (𝑅𝑅𝑅𝑅𝑅𝑅)2 ⇌ (𝑅𝑅𝑅𝑅𝑅𝑅)1 + (𝑂𝑂𝑂𝑂)2 Analog zu einem konjugierten Säure-Base-Paar HA/A- treten Reduktionsmittel und Oxidationsmittel als konjugierte Redox-Paare auf. 𝐻𝐻𝐻𝐻 ⇌ 𝐴𝐴− + 𝐻𝐻 + entspricht damit 𝑅𝑅𝑅𝑅𝑅𝑅 ⇌ 𝑂𝑂𝑂𝑂 + 𝑒𝑒 −. Vorgänge an Elektrodenoberflächen, Elektronenmotorische Kraft E Eine spezielle Art eines Redox-Paares ist ein Metall in Kontakt mit einer Lösung seiner Ionen, wie ein Ag-Stab in einer Lösung von Ag+-Ionen. An der Grenzfläche Metall/Lösung findet je nach Ag+Konzentration in der Lösung einer der beiden Prozesse ab: (1) Anlagerung von Ag+ an die Metalloberfläche unter positiver Aufladung des Metalls. (2) Auflösung von metallischem Ag zu Ag+, das in die Lösung übergeht, unter negativer Aufladung des Metalls. Es baut sich also zwischen Metall und Lösung eine elektrische Potentialdifferenz ∆𝝋𝝋 = 𝝋𝝋𝑴𝑴 − 𝝋𝝋𝑳𝑳 auf, die schließlich eine weitere Aufladung des Metalls verhindert. Zur Ermittlung der Potentialdifferenz ∆𝜑𝜑 ist eine elektrische Verbindung zwischen Metall/Lösung und einem Voltmeter erforderlich, was nur über eine zweite Metallelektrode möglich ist. Auch diese zweite Elektrode hat jedoch eine Potentialdifferenz gegenüber der Lösung (Voltmeter zeigt Differenz zweier Potentialdifferenzen). Diese Anordnung heißt elektrochemische Zelle. Die beiden Elektroden tauchen entweder in dieselbe oder in verschiedene Lösungen, die über eine Salzbrücke (häufig konz. KCl, da hier die störenden Diffusionspotentiale an der Grenzfläche Salzbrücke/Lösung gering sind) verbunden sind, um einen elektrischen Kontakt zwischen Ihnen zu gewährleisten. Die Slazbrücke ermöglicht Potentialdifferenzen verschiedener Lösungen zu vergleichen (z.B. Zn-Elektrode in Zn+-Lösung vs. Cu-Elektrode in Cu+-Lösung). Die beiden Elektroden sind mit einem hochohmigen Voltmeter verbunden, der die Differenz 𝑬𝑬 = 𝝋𝝋𝒓𝒓𝑴𝑴 − 𝝋𝝋𝒍𝒍𝑴𝑴 der elektrischen Potentiale zwischen rechter (r) und linker (l) Elektrode misst. Vernachlässigt man Störpotentiale, sind die elektrischen Potentiale der Lösungen identisch, da sie über Salzbrücke verbunden sind: 𝝋𝝋𝑳𝑳 = 𝝋𝝋𝒓𝒓𝑳𝑳 = 𝝋𝝋𝒍𝒍𝑳𝑳 . Daher gilt: 𝑟𝑟 𝑙𝑙 𝑟𝑟 𝑙𝑙 𝑟𝑟 𝑙𝑙 𝐸𝐸 = 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝑀𝑀 = 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 + 𝜑𝜑𝐿𝐿 = (𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 ) − �𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 � → 𝐸𝐸 = ∆𝜑𝜑𝑟𝑟 − ∆𝜑𝜑𝑙𝑙 Bei unendlich hohem Innenwiderstand des Voltmeters würde die Spannungsmessung stromlos erfolgen. Damit befände sich die Messzelle im thermodynamischen GG. Die hier beobachtete Spannung E heißt Elektromotorische Kraft (EMK) der elektrochemischen Zelle. Sie entspricht der Quellenspannung einer elektrischen Spannungsquelle (kein Verlust durch Widerstände). Ersetzt man das Voltmeter durch einen Widerstand R, so fließt ein Strom durch Zelle und äußeren Stromkreis. Bei der Stromrichtung von rechts nach links (Bewegung positiver Ladungen, technische Stromrichtung) findet die Erzeugung der Elektronen an der linken Elektrode statt, indem das Elektrodenmaterial sich zu positiv geladenen Ionen auflöst. Die Elektronen wandern zur rechten Elektrode, wo sie mit den positiv geladenen Ionen in der Lösung unter Abscheidung von neutralem Metall reagieren. Bei diesen Vorgängen gibt die elektrochemische Zelle elektrische Energie ab (in Form des durch den Widerstand fließenden Stroms). Die Energie wird durch die an den Elektroden ablaufenden chemischen Reaktionen geliefert (Umwandlung von chemischer in elektrischer Energie). Zusammenhang zwischen EMK und Konzentration c Für die allgemeine Redox-Reaktion 𝐴𝐴+𝑧𝑧 + 𝑧𝑧𝑒𝑒 − ⇌ 𝐴𝐴 gilt für die Konzentrationsabhängigkeit der Potentialdifferenz im Gleichgewichtszustand ausgehend von ∆𝐺𝐺 = 𝜇𝜇�𝐴𝐴 − (𝜇𝜇�𝐴𝐴+𝑧𝑧 + 𝑧𝑧𝜇𝜇�𝑒𝑒 − ) = 0: 𝑅𝑅𝑅𝑅 ln 𝑎𝑎𝐴𝐴+𝑧𝑧 , ∆𝜑𝜑 = 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 = 𝜑𝜑0 + 𝑧𝑧𝑧𝑧 𝜇𝜇𝐴𝐴0 +𝑧𝑧 + 𝑧𝑧𝜇𝜇𝑒𝑒0− − 𝜇𝜇𝐴𝐴 𝜑𝜑0 = 𝑧𝑧𝑧𝑧 Falls 𝑎𝑎𝐴𝐴+𝑧𝑧 = 1, folgt somit ∆𝜑𝜑 = 𝜑𝜑0 . Ansonsten steigt ∆𝜑𝜑 mit dem Logarithmus der Ionenaktivität in Wasser an. Eine Erhöhung der Ionenaktivität entzieht dem Metall damit mehr Elektronen, wodurch ein positiveres elektrisches Potential im Metall resultiert. Bei Betrachtung der elektrochemischen Zelle unter Konstanthaltung der Ionenkonzentrationen der linken Seite (Referenzelektrode), ergibt sich für die Spannung E mit der Konzentrationsabhängigkeit der Potentialdifferenz die Beziehung: 𝐸𝐸 = ∆𝜑𝜑𝑟𝑟 − ∆𝜑𝜑𝑙𝑙 = 𝜑𝜑𝑟𝑟0 + 𝐸𝐸 = 𝐸𝐸0 + 𝑅𝑅𝑅𝑅 +𝑧𝑧 ln 𝑎𝑎𝑟𝑟𝐴𝐴 , 𝑧𝑧𝑧𝑧 𝑅𝑅𝑅𝑅 +𝑧𝑧 ln 𝑎𝑎𝑟𝑟𝐴𝐴 − ∆𝜑𝜑𝑙𝑙 𝑧𝑧𝑧𝑧 𝐸𝐸0 = 𝜑𝜑𝑟𝑟0 − ∆𝜑𝜑𝑙𝑙 Falls 𝑎𝑎𝐴𝐴+𝑧𝑧 = 1, folgt somit 𝐸𝐸 = 𝐸𝐸0 . Wählt man als Referenzelektrode die NormalWasserstoffelektrode, nennt man 𝑬𝑬𝟎𝟎 das Standard-Elektrodenpotential des Systems 𝐴𝐴/𝐴𝐴+𝑧𝑧 (für 𝐴𝐴𝐴𝐴/𝐴𝐴𝑔𝑔+ ist 𝐸𝐸𝐻𝐻0 = 0,8𝑉𝑉). Die hergeleitete Beziehung kann zur potentiometrischen Konzentrationsbestimmung über die Messung der Spannung verwendet werden. Berechnung der EMK elektrochemischer Zellen Über tabellierte Standardpotentiale ist die Berechnung von Zellspannungen E unterschiedlicher Metalle in Lösungen ihrer jeweiligen Ionen möglich. Für die Spannung schreibt man unter Berücksichtigung des elektrischen Potentials der Normal-Wasserstoffelektrode 𝝋𝝋𝑯𝑯 (wurde einmal subtrahiert und einmal addiert, die Klammerausdrücke entsprechen dann den EMKs der rechten und linken Elektrode, jeweils gegen die Normal-Wasserstoffelektrode): 𝑙𝑙 𝑟𝑟 𝐸𝐸 = (𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐻𝐻 ) − �𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐻𝐻 � = �(𝐸𝐸𝐻𝐻0 )𝑟𝑟 + 𝑅𝑅𝑅𝑅 𝑅𝑅𝑅𝑅 +𝑧𝑧 +𝑧𝑧 ln 𝑎𝑎𝑟𝑟𝐴𝐴 � − �(𝐸𝐸𝐻𝐻0 )𝑙𝑙 + ln 𝑎𝑎𝑙𝑙𝐴𝐴 � 𝑧𝑧𝑟𝑟 𝐹𝐹 𝑧𝑧𝑙𝑙 𝐹𝐹 Die Standardpotentiale sind Tabellen zu entnehmen, die Logarithmen werden zusammengefasst. 𝐸𝐸 = (𝐸𝐸𝐻𝐻0 )𝑟𝑟 − (𝐸𝐸𝐻𝐻0 )𝑙𝑙 +𝑧𝑧 𝑅𝑅𝑅𝑅 𝑎𝑎𝑟𝑟𝐴𝐴 + ln 𝑧𝑧𝑧𝑧 𝑎𝑎𝑙𝑙𝐴𝐴 +𝑧𝑧 Für die Daniell-Zelle (rechts: Cu, links: Zn) gilt z.B. 𝐸𝐸 = 1,1𝑉𝑉 + 𝑎𝑎 2+ 𝑅𝑅𝑅𝑅 ln 𝑎𝑎 𝐶𝐶𝑢𝑢 𝑧𝑧𝑧𝑧 𝑍𝑍𝑛𝑛 2+ Wird in beiden Halbzellen dasselbe Elektrodenmaterial und dieselben Lösungen in unterschiedlichen Konzentrationen verwendet, spricht man von Konzentrationsketten. Es gilt (𝐸𝐸𝐻𝐻0 )𝑟𝑟 = (𝐸𝐸𝐻𝐻0 )𝑙𝑙 , sodass kein Standardpotential zur Berechnung notwendig ist. IUPAC: • • Potentialdifferenz ist immer: rechte Elektrode minus linke Elektrode Formelumsätze immer als Reduktionen formulieren Redoxreaktionen an Edelmetallelektroden Edelmetalle lösen sich nicht in Wasser, weshalb die bisher besprochenen Reaktionen nicht möglich sind. Dennoch können Edelmetalle Elektronen aufnehmen und Abgeben, wobei das Elektronengas des Metalls als Reservoir für Redoxreaktionen fungiert. Steht z.B. eine Platinelektrode mit einer wässrigen Fe2+/Fe3+-Lösung in Kontakt, überwiegt je nach Konzentrationsverhältniss der zwei Ionensorten eher die Elektronenaufnahme oder –Abgabe, wodurch sich die Platinelektrode entweder positiv oder negativ gegenüber der Lösung auflädt. Platinelektroden werden in Normal-Wasserstoffelektroden als Referenzelektroden verwendet. Eine elektrochemische Zelle kann rechts (Messzelle) eine Lösung des zu untersuchenden Redox-Systems, wo eine Platinelektrode Übergänge zwischen Red und Ox in beiden Richtungen ermöglicht, und links (Referenzzelle) eine Platinelektrode als Normal-Wasserstoffelektrode in einer 1M Wasserstoffionen-Lösung unter 𝑝𝑝 = 1𝑏𝑏𝑏𝑏𝑏𝑏 enthalten. Beide Halbzellen sind verbunden über eine Salzbrücke. Je stärker oxidierend das in der rechten Halbzelle vorhandene Redoxpaar (schwaches Redmittel, starkes Oxmittel) ist, desto positiver ist das Potential der Messelektrode gegenüber der Referenzelektrode. Es resultiert ein Stromfluss, der durch folgende Reaktionen definiert wird: • • • Messelektrode: 𝑂𝑂𝑂𝑂 + 𝑒𝑒 − → 𝑅𝑅𝑅𝑅𝑅𝑅. Referenzelektrode: 1/2𝐻𝐻2 → 𝐻𝐻 + + 𝑒𝑒 −. Elektronen fließen im äußeren Kreis von der Referenzelektrode zur Messelektrode. Ist das Redoxpaar stark reduzierend (schwaches Oxmittel, starkes Redmittel), laufen die inversen Prozesse ab: • • • Messelektrode: 𝑅𝑅𝑅𝑅𝑅𝑅 → 𝑂𝑂𝑂𝑂 + 𝑒𝑒 −. Referenzelektrode: 𝐻𝐻 + + 𝑒𝑒 − → 1/2𝐻𝐻2 . Elektronen fließen von der Messelektrode zur Referenzelektrode. Bei hinreichend großen Widerständen (sehr kleine Ströme), bleibt das System (𝐻𝐻 + + 𝑅𝑅𝑅𝑅𝑅𝑅 → 1/2𝐻𝐻2 + 𝑂𝑂𝑂𝑂 bzw. 1/2𝐻𝐻2 + 𝑂𝑂𝑂𝑂 → 𝐻𝐻 + + 𝑅𝑅𝑅𝑅𝑅𝑅) sehr nahe am Gleichgewicht. Dies entspricht einer quasi-reversiblen Führung der chemischen Reaktion. Bei der Reaktion wird Energie frei. Redoxpotential, Nernst-Gleichung 𝐸𝐸 = 𝜑𝜑𝑀𝑀𝑒𝑒 − 𝜑𝜑𝑅𝑅𝑅𝑅 wird in diesen Zusammenhängen als Redoxpotential bezeichnet, wobei die Vorzeichenkonvention vorgibt: Messelektrode (Me) minus Referenzelektrode (Re). • • Ein stark oxidierendes Redox-Paar (Tendenz der Messelektrode Elektronen zu entziehen) ergibt einen stark positiven Wert von E. Ein stark reduzierendes Redox-Paar (Tendenz Elektronen an die Messelektrode abzugeben) ergibt einen stark negativen Wert von E. Unter Berücksichtigung, dass n mol Elektronen beim Umsatz von 1mol Ox in 1 mol Red ausgetauscht werden (𝑂𝑂𝑂𝑂 + 𝑛𝑛𝑒𝑒 − ⇄ 𝑅𝑅𝑅𝑅𝑅𝑅) ergibt sich für den Formelumsatz der Reaktion im Gleichgewicht: ∆𝐺𝐺𝑀𝑀 = 𝜇𝜇�𝑟𝑟𝑟𝑟𝑟𝑟 − (𝜇𝜇�𝑜𝑜𝑜𝑜 + 𝑛𝑛𝜇𝜇�𝑒𝑒 − ) = 0. Nach Einsetzen der elektrochemischen Potentiale ergibt sich analog zu oben: ∆𝜑𝜑𝑀𝑀𝑀𝑀 = 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 = 𝜑𝜑0 + 𝑅𝑅𝑅𝑅 𝑎𝑎𝑜𝑜𝑜𝑜 ln , 𝑛𝑛𝑛𝑛 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 𝐸𝐸 = ∆𝜑𝜑𝑀𝑀𝑀𝑀 − ∆𝜑𝜑𝑅𝑅𝑅𝑅 = 𝜑𝜑0 + 𝐸𝐸 = 𝐸𝐸0 + 𝑅𝑅𝑅𝑅 𝑎𝑎𝑜𝑜𝑜𝑜 ln , 𝑛𝑛𝑛𝑛 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 𝜑𝜑0 = 0 0 𝜇𝜇𝑜𝑜𝑜𝑜 + 𝑛𝑛𝜇𝜇𝑒𝑒0− − 𝜇𝜇𝑟𝑟𝑟𝑟𝑟𝑟 𝑛𝑛𝑛𝑛 𝑅𝑅𝑅𝑅 𝑎𝑎𝑜𝑜𝑜𝑜 ln − ∆𝜑𝜑𝑅𝑅𝑅𝑅 𝑛𝑛𝑛𝑛 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 𝐸𝐸0 = 𝜑𝜑0 − ∆𝜑𝜑𝑅𝑅𝑅𝑅 Die Gleichungen charakterisieren einen Gleichgewichtszustand. Die letzte Formulierung wird als Nernst-Gleichung für das Redoxpotential E bezeichnet. Sie beschreibt die Abhängigkeit des Redoxpotentials von den Konzentrationen der oxidierten und reduzierten Form des Redoxpaares. E ist umso stärker positiv, je größer die Aktivität des Oxidationsmittels und je kleiner die Aktivität des konjugierten Reduktionsmittels. E wird negativ, wenn die Aktivität des Reduktionsmittels größer ist als die Aktivität des Oxidationsmittels (𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 > 𝑎𝑎𝑜𝑜𝑜𝑜 → ln 𝑎𝑎𝑜𝑜𝑜𝑜 / 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 wird negativ). Übergang auf Zehnerlogarithmus (ln 𝑥𝑥 = 2,3 log10 𝑥𝑥) unter Berücksichtigung, dass 𝑅𝑅𝑅𝑅/𝐹𝐹 = 0,0257𝑉𝑉 für 𝑇𝑇 = 298𝐾𝐾: 𝐸𝐸 = 𝐸𝐸0 + 0,0592𝑉𝑉 𝑎𝑎𝑜𝑜𝑜𝑜 log10 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 𝑛𝑛 Eine Vergrößerung von 𝒂𝒂𝒐𝒐𝒐𝒐 /𝒂𝒂𝒓𝒓𝒓𝒓𝒓𝒓 um das Zehnfache führt für n=1 zu einer Erhöhung von E um 59,2 mV. Die Konzentrationsabhängigkeit des Redoxpotentials ist in der Abbildung gezeigt. Das StandardRedoxpotential 𝑬𝑬𝑯𝑯 𝟎𝟎 ergibt sich, wenn die Aktivitäten der oxidierten und reduzierten Form gleich groß sind und die Messung mit der Normal-Wasserstoffelektrode als Referenzelektrode durchgeführt wird. Je stärker positiv 𝐸𝐸0 desto stärker oxidierend ist das betreffende Redoxsystem. • • Red1/Ox1: Fe2+/Fe3+: 𝐸𝐸0𝐻𝐻 = 0,771𝑉𝑉 Red2/Ox2: Ce3+/Ce4+: 𝐸𝐸0𝐻𝐻 = 1,61𝑉𝑉 Redoxpotential und freie Enthalpie Bei einer äquimolaren Mischung der beiden Lösungen (Fe und Ce; ablaufende Reaktion: 𝑂𝑂𝑥𝑥1 + 𝑅𝑅𝑅𝑅𝑑𝑑2 ⇌ 𝑅𝑅𝑅𝑅𝑑𝑑1 + 𝑂𝑂𝑥𝑥2 ), würde Fe2+ zu Fe3+ oxidiert und Ce4+ zu Ce3+ reduziert werden. Diese Reaktion wäre irrversibel! Eine reversible Reaktion wäre über eine Verbindung beider Lösungen in einer elektrochemischen Zelle mit Platinelektroden möglich. Durch Wahl geeigneter Ausgangskonzentrationen der Redoxpaare kann so die Reaktion gesteuert werden. Bei Wahl eines Messgeräts mit hohem Innenwiderstand läuft die Reaktion sehr langsam ab. Für 𝐼𝐼 → 0 wird die EMK gemessen, die den Gleichgewichtszustand charakterisiert (𝑅𝑅𝑖𝑖 → ∞ = Ablauf der Reaktion gehemmt). Dieses Gleichgewicht unterscheidet sich jedoch vom chemischen GG, das bei Vermischung der Reaktanden beobachtet wird. 𝐻𝐻 Für den Grenzfall 𝑰𝑰 → 𝟎𝟎 gilt für die EMK (hier wurden wieder ∆𝜑𝜑𝑅𝑅𝑅𝑅 addiert und subtrahiert): 𝐻𝐻 ) 𝐻𝐻 ) 𝐸𝐸 = ∆𝜑𝜑2 − ∆𝜑𝜑1 = (∆𝜑𝜑2 − ∆𝜑𝜑𝑅𝑅𝑅𝑅 − (∆𝜑𝜑1 − ∆𝜑𝜑𝑅𝑅𝑅𝑅 Die Redoxpotentiale der beiden Redox-Paare ∆𝜑𝜑2 = 𝐸𝐸2 und ∆𝜑𝜑1 = 𝐸𝐸1 sind dabei über das entsprechende 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 der beiden Halbzellen definiert. Einsetzen der Nernst-Gleichung für das Redox-Potential und auflösen: 𝐻𝐻 ) 𝐻𝐻 ) 𝐸𝐸 = (∆𝜑𝜑2 − ∆𝜑𝜑𝑅𝑅𝑅𝑅 − (∆𝜑𝜑1 − ∆𝜑𝜑𝑅𝑅𝑅𝑅 = �(𝐸𝐸0𝐻𝐻 )2 + 𝐸𝐸 = 𝐸𝐸0 + 𝑅𝑅𝑅𝑅 𝑎𝑎𝑜𝑜𝑜𝑜 2 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 1 ln , 𝑛𝑛𝑛𝑛 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 2 𝑎𝑎𝑜𝑜𝑜𝑜 1 𝑅𝑅𝑅𝑅 𝑎𝑎𝑜𝑜𝑜𝑜 2 𝑅𝑅𝑅𝑅 𝑎𝑎𝑜𝑜𝑜𝑜 1 ln � − �(𝐸𝐸0𝐻𝐻 )1 + ln � 𝑛𝑛𝑛𝑛 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 2 𝑛𝑛𝑛𝑛 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 1 𝐸𝐸0 = (𝐸𝐸0𝐻𝐻 )2 − (𝐸𝐸0𝐻𝐻 )1 Im Chemischen Gleichgewicht: Durch Erniedrigung des Innenwiderstands fließt ein endlicher Strom, der die Reaktion in das chemische GG überführt. Im GG herrscht dann I=0, jetzt aber bei beliebigem endlichen Widerstand. Da I=0 gilt auch 𝐸𝐸 = 𝑅𝑅𝑖𝑖 𝐼𝐼 = 0 (vorher galt dies nicht, da 𝑅𝑅𝑖𝑖 𝐼𝐼 = ∞ ∙ 0 nicht definiert ist). Mit E=0 folgt aus der obigen Gleichung weiter: 𝐸𝐸0 = − 𝑅𝑅𝑅𝑅 𝑎𝑎�𝑜𝑜𝑜𝑜 2 𝑎𝑎�𝑟𝑟𝑟𝑟𝑟𝑟 1 𝑅𝑅𝑅𝑅 ln =− ln 𝐾𝐾 𝑛𝑛𝑛𝑛 𝑎𝑎�𝑟𝑟𝑟𝑟𝑟𝑟 2 𝑎𝑎�𝑜𝑜𝑜𝑜 1 𝑛𝑛𝑛𝑛 Hier sind für die Aktivitäten die Werte im Gleichgewichtszustand einzusetzen! Der Gleichgewichtszustand wird dann durch die Gleichgewichtskonstante K definiert. Umgeformt ergibt sich: ln 𝐾𝐾 = − 𝑛𝑛𝑛𝑛((𝐸𝐸0𝐻𝐻 )2 − (𝐸𝐸0𝐻𝐻 )1 ) 𝑛𝑛((𝐸𝐸0𝐻𝐻 )2 − (𝐸𝐸0𝐻𝐻 )1 ) =− 𝑅𝑅𝑅𝑅 0,0257𝑉𝑉 Da 𝐾𝐾 = 𝑒𝑒 −∆𝐺𝐺0 /𝑅𝑅𝑅𝑅 → ln 𝐾𝐾 = −∆𝐺𝐺0 /𝑅𝑅𝑅𝑅 folgt weiter: ∆𝐺𝐺0 = 𝑛𝑛𝑛𝑛((𝐸𝐸0𝐻𝐻 )2 − (𝐸𝐸0𝐻𝐻 )1 ) Damit kann die freie Standardenthalpie von Redoxreaktionen durch Messung von Redoxpotentialen bestimmt werden. Ist das Redox-Paar 1 stärker oxidierend als das Redox-Paar 2, folgt (𝐸𝐸0𝐻𝐻 )1 > (𝐸𝐸0𝐻𝐻 )2 und weiter ∆𝐺𝐺0 < 0; Die Reaktion läuft demnach spontan ab (von links nach rechts unter Standardbedingungen). Der Rest des Kapitels 6 ignoriert Läuger, Kapitel 7: Grenzflächenphänomene Kapitel 7.1 ignoriert Adsorption an Grenzflächen Im Allgemeinen sind die Mischungskomponenten in den einander berührenden Phasen nicht gleichförmig verteilt. Die Grenzfläche kann im Vergleich zur angrenzenden Volumenphase an bestimmten Mischungskomponenten angereichert oder verarmt sein, wodurch es zur Änderung der Grenzflächenspannung kommt. Wenn sich eine gelöste Substanz (grenzflächenaktive Verbindung = Tensid) an der Grenzfläche anreichert (Adsorption an die Grenzfläche), wird die Grenzflächenspannung gegenüber der des Lömis erniedrigt. Die Filmwaage Eine Flüssigkeit ist bestrebt eine minimale Oberfläche einzunehmen. Die Triebkraft für diesen Prozess ist die Oberflächenspannung 𝜸𝜸. Die Oberflächenspannung einer reinen Flüssigkeit 𝜸𝜸𝟎𝟎 kann durch Zumischung einer weiteren Komponente erniedrigt werden, sodass 𝜸𝜸 ≪ 𝜸𝜸𝟎𝟎 . Wasser hat eine hohe Oberflächenspannung (𝛾𝛾0 = 72,8𝑚𝑚𝑚𝑚 𝑚𝑚−1 = 72,8𝑚𝑚𝑚𝑚 𝑚𝑚−2 ) gegenüber seinem Dampf bzw. Luft. Für Wasser oberflächenaktive Verbindungen sind amphiphil (z.B. Hexanol). Hexanol akkumuliert aus energetischen Gründen an der Oberfläche (OH-Gruppe in Wasser). Dies ist gleichbedeutend mit einer Erniedrigung der Oberflächenspannung: Die energetisch ungünstige Anordnung der Wassermoleküle, wird durch die energetisch günstige Anordnung der HexanolMoleküle ersetzt (0,03M Hexanol reduziert 𝛾𝛾 auf 38,5𝑚𝑚𝑚𝑚/𝑚𝑚). Die Veränderung der Oberflächenspannung kann über eine Filmwaage (auch Langmuir-Waage) gemessen werden. Sie besteht aus einem flachen Gefäß mit einer auf der Oberfläche schwimmenden Barriere und einer daran befestigten Membran. Diese trennt die Lösung von einer zu untersuchenden Substanz. Die unterschiedlichen Oberflächenspannungen 𝜸𝜸 und 𝜸𝜸𝟎𝟎 auf beiden Seiten der Barriere sorgen für eine Nettokraft auf die bewegliche Barriere, die durch eine Gegenkraft K über eine Waage kompensiert werden muss. Beide Oberflächen besitzen eine mehr oder weniger große Tendenz sich zu verkleinern (Richtung der Kräfte beachten!). Befindet sich die oberflächenaktive Substanz links und das Lömi rechts von einer Barriere der Länge 𝑙𝑙: Dann wirkt die Kraft 𝒍𝒍𝜸𝜸𝟎𝟎 von links nach rechts und die Kraft 𝒍𝒍𝒍𝒍 von rechts nach links. Die zu kompensierende Nettokraft 𝑲𝑲 = 𝒍𝒍(𝜸𝜸𝟎𝟎 − 𝜸𝜸) wirkt von links nach rechts, da 𝜸𝜸𝟎𝟎 > 𝛾𝛾. Die Differenz 𝝅𝝅 = 𝜸𝜸𝟎𝟎 − 𝜸𝜸 ist der Spreitungsdruck (Kraft pro Länge oder Energie pro Fläche). Über die Filmwaage lässt sich direkt die Konzentrationsabhängigkeit der Oberflächenspannung 𝜸𝜸(𝒄𝒄) = 𝜸𝜸𝟎𝟎 − 𝝅𝝅(𝒄𝒄) bestimmen. Es gibt auch Oberflächenaktive Substanzen, welche die Oberfläche meiden und daher die Oberflächenspannung gegenüber dem reinen Lömi erhöhen (z.B. wässrige Lösung von Salzen: 0-5M NaCl zeigt lineare Erhöhung der Oberflächenspannung von 72,8 auf 81 mN/m). Im Allgemeinen bleibt 𝛾𝛾 für Lösungen oberflächenaktiver Substanzen groß genug, um die Ausbildung einer minimalen Oberfläche aufrechtzuerhalten. Für 𝝅𝝅 ≈ 𝜸𝜸𝟎𝟎 → 𝜸𝜸 ≈ 𝟎𝟎 würde eine kleinste Störung des Systems zu Ausstülpungen (Vergrößerung der Oberfläche) führen, die kein/kaum Energieaufwand benötigen würde. Dies gilt auch für Grenzflächen wie Membran/Wasser in biologischen Zellen (hier ist die Ausbildung der Membran energetisch günstig aufgrund der Oberflächenaktivität von Lipiden). Tenside Tenside erniedrigen die Oberflächenspannung des Wassers häufig auf Werte von ca. 25 mJ/m² oder auf viel kleinere Werte. Kleine 𝛾𝛾-Werte bei Tensidlösungen führen zur Schaumbildung durch mechanisches Rühren, da die Oberflächenvergrößerung nur geringe Energiezufuhr benötigt. Neben dem GG zwischen gelöstem und oberflächengebundenem Tensid tritt Micellenbildung (Assoziate aus 50-200 Molekülen) auf, wenn die Lösungsoberfläche bereits vollständig mit Tensidmolekülen besetzt ist. Dazu muss die kritische Mizellkonzentration (CMC) erreicht sein. Nach Erreichen der CMC resultiert keine weitere Erniedrigung der Oberflächenspannung mit zunehmenden TensidKonzentrationen mehr. Dafür resultieren eine Abnahme der molaren Leitfähigkeit und eine Zunahme der Lichtstreuung. CMC und mittlere Tensidmolekül-Anzahl pro Mizelle sind stark von der Konzentration der Gegenionen abhängig, da die negativen Ladungen der Tensidkopfgruppen ohne Stabilisierung über anorganische Kationen zur Abstoßung und Destabilisierung der Mizellen führen. Tenside erleichtern die Bildung von Emulsionen (z.B. Wasser-Tropfen in Öl oder Lipid-Tropfen in Wasser) nach Schütteln, indem sie die Grenzfläche zwischen den zwei Phasen stabilisieren (hydrophiler Teil in Wasser, hydrophober Teil in Öl). Tenside als Detergentien (z.B. langkettige Fettsäure) lösen Verschmutzungen, indem sie ihre Suspendierung erleichtern (Emulsion-Bildung), wobei auf der gereinigten Faser eine Tensidmonoschicht zurückbleibt, die mit den hydrophoben Teilen der Faser interagiert. Dies führt zu einer hohen Benetzbarkeit der Faser durch wässrige Lösungen. Die Löslichkeit kleiner hydrophober Moleküle kann durch Einbau in Mizellen erhöht werden (Solubilisierung). So kann die CMC über eine Zunahme der Fluoreszenz von hydrophoben Farbstoffen bestimmt werden. Membranproteine können über geeignete Detergentien solubilisiert werden. Dabei werden die Membranlipide in Tensid-haltige Mizellen-artige Strukturen überführt, wobei auch die Membranproteine mit den hydrophoben Teilen der Detergentien interagieren. Zur Vermeidung der Denaturierung werden die schonenderen zwitterionischen und nichtionischen Tenside eingesetzt. Nichtionische Tenside werden auch zur schonenden Permeabilisierung der Plasmamembran verwendet, um Zugang zum Zytoplasma zu erhalten. Die Plasmamembran wird nicht solubilisiert, sondern in ihren Barriereeigenschaften erheblich beeinträchtigt. SDS ist ebenso zur Solubilisierung fähig, bewirkt aber die Denaturierung der Proteine. Es wird für die SDS-PAGE verwendet. Dabei bindet ca. 1,4mg SDS an 1mg Protein, wodurch das Protein aufgrund der vollständig dissoziierten Sulfonatgruppen in SDS eine erhebliche negative Nettoladung erhält (Eigenladung vernachlässigbar). Da die Wanderungsgeschwindigkeit im E-Feld proportional zur Ladung proportional zur Oberfläche proportional zur Masse ist, kann die Molmasse über die Wanderungsstrecke bestimmt werden. Die Gibb‘sche Adsorptionsisotherme Die Oberflächenphase der Fläche 𝐴𝐴𝑠𝑠 einer Mischung aus zwei Komponenten 1 und 2 (z.B. Wasser und Hexanol) hat spezifische Oberflächenkonzentrationen Γ1 = 𝑛𝑛𝑠𝑠1 /𝐴𝐴𝑠𝑠 und Γ2 = 𝑛𝑛𝑠𝑠2 /𝐴𝐴𝑠𝑠 . Diese sind über die Stoffmengen pro Fläche definiert. Die Oberflächenphase hat eine endliche Dicke d, in der alle Oberflächen-spezifischen Phänomene auftreten können. Diese wird für die Überlegungen nicht benötigt, da sich die Oberflächenkonzentration auf die Fläche, nicht auf das Volumen der Oberflächenphase bezieht. Ohne Oberflächen-spezifische Phänomene wäre das Verhältnis der Oberflächenkonzentration gleich dem Verhältnis der Volumenkonzentration (Γ2 /Γ1 = 𝑐𝑐2 /𝑐𝑐1 ), während für eine Verarmung oder Anreicherung der Komponente 2 das Verhältnis ungleich wird. Es wird nach der Konzentrationsabhängigkeit der Oberflächenkonzentrationen 𝚪𝚪𝟐𝟐 (𝒄𝒄𝟐𝟐 ) und 𝚪𝚪𝟏𝟏 (𝒄𝒄𝟐𝟐 ) sowie der Oberflächenspannung 𝜸𝜸(𝒄𝒄𝟐𝟐 ) gefragt. Die Konzentration 𝑐𝑐2 ist niedrig, sodass für das chemische Potential 𝜇𝜇2 die Beziehung für eine ideal verdünnte Lösung gilt: 𝜇𝜇2 = 𝜇𝜇2,0 + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐2 Annahme: es herrscht thermodynamisches GG, d.h. alle intensiven Zustandsvariablen im Grenzflächensystem (s) und im Volumensystem sind gleich (z.B. 𝑇𝑇𝑠𝑠 = 𝑇𝑇, 𝑝𝑝𝑠𝑠 = 𝑝𝑝), so auch 𝜇𝜇𝑠𝑠1 = 𝜇𝜇1 und 𝜇𝜇𝑠𝑠2 = 𝜇𝜇2 . Für Volumenphase und Grenzflächenphase können separat entsprechende Gibbs-DuhemGleichungen aufgestellt werden: • • Gibbs-Duhem Gleichung für Volumenphase: 𝑛𝑛1 𝑑𝑑𝜇𝜇1 = −𝑛𝑛2 𝑑𝑑𝜇𝜇2 o Division durch das Volumen: 𝑐𝑐1 𝑑𝑑𝜇𝜇1 = −𝑐𝑐2 𝑑𝑑𝜇𝜇2 → 𝑑𝑑𝜇𝜇1 = −𝑐𝑐2 /𝑐𝑐1 ∙ 𝑑𝑑𝜇𝜇2 Gibbs-Duhem Gleichung für Oberflächenphase: 𝐴𝐴𝑠𝑠 𝑑𝑑𝑑𝑑 = −𝑛𝑛𝑠𝑠1 𝑑𝑑𝜇𝜇1 − 𝑛𝑛𝑠𝑠2 𝑑𝑑𝜇𝜇2 o Division durch die Oberfläche: 𝑑𝑑𝑑𝑑 = −Γ1 𝑑𝑑𝜇𝜇1 − Γ2 𝑑𝑑𝜇𝜇2 o Gibbsche Adsorptionsgleichung für n Komponenten in der Mischung: 𝑑𝑑𝑑𝑑 = − ∑𝑛𝑛𝑖𝑖 Γi 𝑑𝑑𝜇𝜇𝑖𝑖 Es ergibt sich durch Einsetzen von 𝑑𝑑𝜇𝜇1 und 𝑑𝑑𝜇𝜇2 = 𝑑𝑑�𝜇𝜇2,0 + 𝑅𝑅𝑅𝑅 ln 𝑐𝑐2 � = 𝑅𝑅𝑅𝑅 ∙ 𝑑𝑑𝑐𝑐2 /𝑐𝑐2 in die Gibbsche Adsorptionsgleichung: 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑐𝑐2 =− �Γ2 − Γ1 � 𝑑𝑑𝑐𝑐2 𝑐𝑐1 𝑐𝑐2 Der Klammerausdruck heißt Oberflächenüberschuss. • • • Wären die Konzentrationsverhältnisse in Oberflächenphase und Volumenphase identisch (Γ2 = 𝑐𝑐2 , Γ1 = 𝑐𝑐1 ), würde sich der Klammerausdruck zu null auflösen und damit 𝒅𝒅𝒅𝒅/𝒅𝒅𝒄𝒄𝟐𝟐 = 𝟎𝟎 resultieren (keine Änderung der Oberflächenspannung bei Änderung der Konzentration des gelösten Stoffes). Ist die Substanz 2 oberflächenaktiv, resultiert eine Anreicherung von 2 an der Grenzfläche. Der Oberflächenüberschuss ist positiv, es folgt: 𝒅𝒅𝒅𝒅/𝒅𝒅𝒄𝒄𝟐𝟐 < 0 (Abnahme der Oberflächenspannung mit zunehmender Konzentration). Bei wässrigen Lösungen von Salzen resultiert eine Verarmung von 2 an der Grenzfläche. Der Oberflächenüberschuss ist negativ, es folgt: 𝒅𝒅𝒅𝒅/𝒅𝒅𝒄𝒄𝟐𝟐 > 0. Mithilfe der Filmwaage kann direkt 𝒅𝒅𝒅𝒅/𝒅𝒅𝒄𝒄𝟐𝟐 gemessen werden (Einzelexperimente bei unterschiedlichen Konzentrationen Steigung des Graphen). Damit kann der Oberflächenüberschuss für eine bestimmte Konzentration 𝑐𝑐2 berechnet werden. Die Größen 𝚪𝚪𝟐𝟐 und 𝚪𝚪𝟏𝟏 sind jedoch nicht einzeln bestimmbar, weshalb der Oberflächenüberschuss als Γ(c2 ) zusammengefasst wird. Liegen zusätzliche molekulare Kenntnisse über das Grenzflächensystem vor, kann Γ2 getrennt ermittelt werden. Bei langkettigen Alkoholen liegt eine Monoschicht mit Ausrichtung der Moleküllängsachsen senkrecht zur Lösungsoberfläche vor. Der Oberflächenüberschuss entspricht also der Oberflächenkonzentration des Tensids in der Monoschicht. Bei einem Vergleich molekularer Strukturen von Grenzflächen resultiert, dass Γ2 ≫ 𝑐𝑐2 /𝑐𝑐1 ∙ Γ1 , sodass Γ(c) = Γ2 − c2 /c1 Γ1 ≈ Γ2 (Oberflächenüberschuss gleich Oberflächenkonzentration des Tensids). Für die Anwendung dieser Näherung muss die zuvor undefinierte Dicke 𝑑𝑑 der Grenzfläche auf 1-2 Moleküllängen festgelegt werden, da über diesen Abstand die für die strukturellen Eigenschaften der Grenzfläche verantwortlichen intermolekularen Wechselwirkungen stattfinden. Die abgeleiteten Gleichungen gelten für alle Grenzflächen: flüssig/gasförmig, flüssig/flüssig, flüssig/fest, wobei die adsorbierende Substanz nicht in der zweiten Volumenphase auftreten darf. Die Langmuir-Isotherme Bei einer Lösung einer oberflächenaktiven Substanz liegt oft eine Konzentrations-Abhängigkeit des Spreitungsdruckes 𝝅𝝅 vor, die empririsch ermittelt wurde: 𝜋𝜋 = 𝛾𝛾0 − 𝛾𝛾 = 𝑅𝑅𝑅𝑅 Γ∞ ln(1 + Kc) Γ∞ und K sind Konzentrations-unabhängige, Temperatur-abhängige, empirische Konstanten. Einsetzen der empirische Gleichung für 𝛾𝛾 in die Gibbsche Adsorptionsgleichung und Differentiation: 𝑑𝑑𝛾𝛾 𝑅𝑅𝑅𝑅 Γ Kc =− Γ(c) → Γ(c) = Γ∞ ⟺ Kc = 𝑑𝑑𝑐𝑐2 𝑐𝑐2 Γ∞ − Γ 1 + Kc Diese Langmuir’sche Adsorptionsisotherme gilt für die Adsorption eines Liganden an eine Grenzfläche unter isothermen Bedingungen (K=Konstant). Das theoretische Modell setzt voraus, dass an der Grenzfläche maximal 𝐍𝐍∞ Bindungsplätze (für je ein oberflächenaktives Molekül) vorhanden sind. Es resultiert ein dynamisches GG zwischen Adsorption und Desorption an diesen Bindungsplätzen. Wenn 𝑁𝑁 Moleküle gebunden sind, ist die Geschwindigkeit der Adsorption 𝑣𝑣𝑎𝑎 proportional zur Anzahl der freien Bindungsstellen 𝑁𝑁∞ − 𝑁𝑁 und proportional zur Konzentration freier Liganden 𝑐𝑐. Die Proportionalitätskonstante ist die Geschwindigkeitskonstante der Adsorption 𝑘𝑘𝑎𝑎 . Die Geschwindigkeit der Desorption 𝑣𝑣𝑑𝑑 ist proportional zur Anzahl 𝑁𝑁 der gebundenen Moleküle, wobei 𝑘𝑘𝑑𝑑 die Geschwindigkeitskonstante der Desorption ist. 𝑣𝑣𝑎𝑎 = 𝑘𝑘𝑎𝑎 (𝑁𝑁∞ − 𝑁𝑁)𝑐𝑐, 𝑣𝑣𝑑𝑑 = 𝑘𝑘𝑑𝑑 𝑁𝑁 Im Gleichgewicht müssen beide Geschwindigkeiten gleich sein. K ist die Gleichgewichtskonstante der Bindung. 𝒗𝒗𝒂𝒂 = 𝒗𝒗𝒅𝒅 → 𝑲𝑲𝑲𝑲 = 𝑵𝑵 , 𝑵𝑵∞ − 𝑵𝑵 𝑲𝑲 = 𝒌𝒌𝒂𝒂 𝒌𝒌𝒅𝒅 Setzt man anstelle der Bindungsstellen-Anzahl molare Oberflächenkonzentrationen (Γ = 𝑁𝑁/𝑁𝑁𝐴𝐴 𝐴𝐴𝑠𝑠 , Γ∞ = 𝑁𝑁∞ /𝑁𝑁𝐴𝐴 𝐴𝐴𝑠𝑠 ) ein, ergibt sich die Langmuirsche Adsorptionsisotherme. • • 𝚪𝚪∞ ist damit die Gesamtkonzentration an Bindungsplätzen an der Oberfläche. 𝐊𝐊 ist die Gleichgewichtskonstante für die Bindung an diese Plätze. Die Oberflächenkonzentration 𝚪𝚪 zeigt nach diesem Modell ein Sättigungsverhalten: Mit steigender Konzentration c nähert sich diese asymptotisch dem 𝚪𝚪∞ -Wert an. Der Spreitungsdruck 𝜋𝜋, der experimentell über die Filmwaage gemessen werden kann, zeigt kein Sättigungsverhalten. Kann experimentell nachgewiesen werden, dass der Spreitungsdruck 𝜋𝜋 die Konzentrations-Abhängigkeit der obigen Gleichung (𝜋𝜋 = 𝑅𝑅𝑅𝑅 Γ∞ ln(1 + Kc)) zeigt, kann sofort auf die Sättigungskonstante Γ∞ und die Bindungskonstante K geschlossen werden. Die Langmuirsche Adsorptionsisotherme ist formal und inhaltlich analog zur Michaelis-MentenKinetik der Enzyme sowie zur Liganden-Bindung an Proteine. Sie wird z.B. angewandt bei der Bindung von Hormonen an Rezeptoren der Plasmamembran (nur ohne Kooperativität!). Das zweidimensionale ideale Oberflächengas In vielen Fällen ist die Oberflächenkonzentration Γ direkt gegeben, aber die Konzentration c in der Volumenphase unmessbar klein (z.B. bei Lipidmonoschichten). Hier kann die Oberflächenspannung γ als Funktion der Oberflächenkonzentration dargestellt werden. Durch einsetzen von 𝐾𝐾𝐾𝐾 = Γ Γ ∞ −Γ in die empirische Formel für 𝜋𝜋 und Anwendung der Näherung Γ ≪ Γ∞ (kleine Oberflächenkonzentrationen) ergibt sich die Beziehung 𝜋𝜋 = 𝑅𝑅𝑅𝑅 Γ. Wegen Γ = ns /As folgt ein zweidimensionales Analogon zur idealen Gasgleichung: 𝝅𝝅𝑨𝑨𝒔𝒔 = 𝒏𝒏𝒔𝒔 𝑹𝑹𝑹𝑹 . Dies setzt voraus, dass keine Wechselwirkung zwischen den Molekülen existiert. Dies ist gegeben, da geringe Oberflächenkonzentrationen vorausgesetzt wurden. D.h. die adsorbierten Moleküle bewegen sich infolge der Wärmebewegung auf der zweidimensionalen Oberfläche genauso wie ein ideales Gas im Raum). Die entsprechende Beziehung gilt jedoch auch im asymptotischen Grenzfall, also auch für höhere Oberflächenkonzentrationen 𝚪𝚪 ≈ 𝚪𝚪∞ (siehe Diagramm für niedrige Spreitungsdrücke unten). 𝜋𝜋 = 𝑅𝑅𝑅𝑅 Γ∞ ln �1 + Γ Γ ∞ −Γ � = 𝑅𝑅𝑅𝑅 Γ∞ ln � Γ∞ Γ ∞ −Γ � = −𝑅𝑅𝑅𝑅 Γ∞ ln � Γ ∞ −Γ Γ∞ � = −𝑅𝑅𝑅𝑅 Γ∞ ln �1 − Γ Γ∞ � ≈ −𝑅𝑅𝑅𝑅 Γ∞ ∙ �− Γ Γ∞ � = RT Γ Hier wurde zuletzt ln(1 − 𝑥𝑥) ≈ −𝑥𝑥 für |𝑥𝑥| ≪ 1 verwendet, sodass dieses Ergebnis formal nur für Γ ≪ Γ∞ gilt, also nicht im asymptotischen Grenzfall. Unter Berücksichtigung der pro Molekül zur Verfügung stehenden molekularen Oberfläche („Größe der Bindungsstelle“) 𝑎𝑎𝑠𝑠 = 𝐴𝐴𝑠𝑠 /𝑁𝑁𝐴𝐴 𝑛𝑛𝑠𝑠 , ergibt sich aus der idealen Zustandsgleichung 𝜋𝜋 = 𝑘𝑘𝐵𝐵 𝑇𝑇/𝑎𝑎𝑠𝑠 . Monomolekulare und bimolekulare Lipidschichten Die Grundbausteine biologischer Membranen sind stark oberflächenaktiv, was eine Ausbildung von Aus- und Einstülpungen der Membranen erleichtert. Lipidmonoschichten Alkalisalze langkettiger Fettsäuren können in nennenswerten Konzentrationen gelöst werden (CMC im Bereich 10−3 − 10−2 𝑀𝑀). Die undissoziierten Formen (z.B. bei pH=2) oder die stark hydrophoben Phospholipide sind praktisch unlöslich. Sie bilden eine Monoschicht auf der Wasseroberfläche, ohne in die Volumenschicht einzudringen. Geringe Konzentrationen der zu untersuchenden Substanz werden in einem flüchtigen Lömi gelöst auf die wässrige Phase aufgetragen. Nach Verdampfen des Lömis und Ausbreitung des Tensids auf der Oberfläche kann die Studie über eine Filmwaage beginnen. Die Untersuchung von Myristinsäure (C14-FS) bei pH=2 und T=14°C ergibt charakteristische Zustandskurven bei sehr kleinen und hohen Spreitungsdrücken 𝜋𝜋. Die Variation des Spreitungsdruckes im Experiment erfolgt durch Verkleinerung der Monoschicht, d.h. durch Reduzierung der zur Verfügung stehenden Oberfläche (bewegliche Barriere). Die Langmuir-Isotherme sollte nur für sehr kleine Oberflächenkonzentrationen (niedrige Spreitungsdrücke, große Oberfläche pro Molekül) gelten (siehe Herleitung). Die linke Abbildung zeigt, dass die Abweichung zwischen Messkurve und Langmuir-Isotherme wie erwartet mit der Fläche pro Molekül 𝑎𝑎𝑠𝑠 abnimmt. Das Verhalten ähnelt dem eines zweidimensionalen idealen Gases. Bei kleineren Werten für 𝒂𝒂𝒔𝒔 treten Abweichungen vom idealen Verhalten auf, die auch bei realen Gasen beobachtet werden. • • Bei 𝜋𝜋 = 0,2𝑚𝑚𝑚𝑚 𝑚𝑚−1 und > 𝑎𝑎𝑠𝑠 = 8,5𝑛𝑛𝑚𝑚2 : „Kondensation des zweidimensionalen Gases“ 𝑎𝑎𝑠𝑠 < 0,5𝑛𝑛𝑚𝑚2 : zweidimensionale Flüssigkeit (flüssig-expandierte Monoschicht) Das Verhalten kann näherungsweise durch eine der Van-der-Waals-Gleichung für reale Gase äquivalente Gleichung beschrieben werden. 𝛼𝛼 und 𝛽𝛽 sind hier die zweidimensionalen Van-der-Waals Konstanten. �𝜋𝜋 + 𝛼𝛼 � (𝑎𝑎𝑠𝑠 − 𝛽𝛽) = 𝑘𝑘𝐵𝐵 𝑇𝑇 𝑎𝑎𝑠𝑠2 Niedrige Spreitungsdrücke (hohe Oberfläche pro Molekül), gestrichelte Linie = Langmuir-Isotherme für sehr kleine Oberflächenkonzentrationen Hohe Spreitungsdrücke (niedrige Oberfläche pro Molekül) Zusätzlich ist für Myristinsäure der Übergang zwischen flüssig-expandierter und kondensierter Phase zu beobachten (rechte Abbildung). Dieser Erstarrungsvorgang bei 𝜋𝜋 = 8𝑚𝑚𝑚𝑚 𝑚𝑚−1 führt von einer Oberfläche pro Molekül von etwa 0.35nm² auf eine von 0,22-0,25nm². Letztere kommt einer kristallinen Packung von Paraffinketten sehr nahe. Oberhalb von 𝜋𝜋 ≈ 15𝑚𝑚𝑚𝑚 𝑚𝑚−1 liegen dann alle CH-Ketten der Myristinsäure gestreckt in dichtester Packung und senkrecht zur Wasseroberfläche vor. Die Druck-Flächen-Diagramme zeigen, dass die Myristinsäure- genauso wie die DPPC-Isotherme analog zur Isotherme bei der Gaskompression beschreibbar sind. • • • • • „Kein Druck“: gasphase-ähnlich Niedriger Druck: flüssig-expandiert (FS-Ketten in gauche-trans-gauche). Kompression hoher Druck: flüssig-kondensiert (FS-Ketten in all-trans Konformation). Noch höherer Druck: flüssig-kristallin (dichteste Packung) Noch höherer Druck: Kollaps! Monoschicht wird zur Bimolekularen Lipidschicht Phosphatidylcholine bilden ebenso Monoschichten auf der Oberfläche der wässrigen Volumenphase. Der Spreitungsdruck ist abhängig von der Länge der CH-Ketten. Die Messungen fanden bei T=22°C an DPPC statt. • • • Kürzere Ketten zeigen einen flachen Kurvenverlauf im Druck-Flächen-Digramm (bei allen Spreitungsdrücken liegen die Lipide im flüssig-expandierten Zustand vor), Längere Ketten zeigen einen steilen Kurvenverlauf (bei allen Spreitungsdrücken liegen die Lipide im kondensierten Zustand vor). Für C16 ist ein Übergang zwischen zwei verschiedenen Steilheitsbereichen zu beobachten (Übergang von flüssig-expandiert zu kondensiert bei hohen Spreitungsdrücken). Der Phasenübergang erfolgt bei etwa 𝜋𝜋 = 8𝑚𝑚𝑚𝑚 𝑚𝑚−1 . Er beginnt bei 𝑎𝑎𝑠𝑠 ≈ 0,75𝑛𝑛𝑚𝑚2 und endet bei 𝑎𝑎𝑠𝑠 = 0,48𝑛𝑛𝑚𝑚2 bei hohen Spreitungsdrücken. In allen Zuständen ist die molekulare Oberfläche von PC damit doppelt so groß wie für FS (Grund: 2 CH-Ketten), weshalb man auch hier von einer dichtesten Packung sprechen kann. Abhängigkeit von PC-Kettenlänge Vereinfachte Übersichtsdarstellung für Monoschichten. Lipid-Doppelschicht-Systeme Phospholipide bilden in Wasser bimolekulare Schichten, die höhere lamellare Strukturen ausbilden können. Voraussetzung zur Ausbildung dieser Strukturen ist ein Überschuss an Wasser. Man unterscheidet verschiedene Modellmembran-Systeme, die zur Untersuchung von Membrangebundenen Prozessen wie Transportmechanismen dienen. (1) Vesikel / Liposomen (2) Schwarze Membranen (BLM) = planare Lipidmembranen (3) Festkörpergestützte Membranen (SSM) Der Anspruch an die Modellmembran ist eine Übereinstimmung zwischen Zellmembran und Modellsystem (freie Einstellung der physikalisch chemischen Eigenschaften wie laterale Beweglichkeit der Lipide und chemische Zusammensetzung der Lipidmembran; hohe Langzeitstabilität, Reproduzierbarkeit) Vesikel bilden in wässrigen Lösungen abgeschlossene Kompartimente, die eine wässrige-Innenphase von der wässrigen Außenphase trennen. Liposomen werden nach steigendem Durchmesser in SUV’s (small unilamellar vesicles; Ø = 20-100 nm), LUV’s (large unilamellar vesicles; Ø = 100-500 nm) und MLV’s (multilamellar vesicles; Ø > 100 nm) eingeteilt. Die Herstellung von unilamellaren Vesikeln erfolgt über die Extrusionsmethode nach Hope. Dabei wird eine Suspension multimlamellarer Vesikel oberhalb der Phasenumwandlungstemperatur des jeweiligen Lipids oder der Lipidmischung mehrmals durch eine Polycarbonatmembran definierter Porengröße gedrückt. Die entstehenden Vesikel sind unilamellar; die Größenverteilung ist von der Porengröße des Filter abhängig (100𝑛𝑛𝑛𝑛 80 ± 25𝑛𝑛𝑛𝑛). Vesikel eigenen sich als Modellsystem zur Untersuchung aktiver Membranproteine. Nachteil: nach der Präparation besteht kein Zugang zum Inneren des Vesikels. Anwendungen von Vesikel als Modellmembranen finden sich bei kalorimetrischen und optischen Untersuchungen. Planare Lipidmembranen können mithilfe verschiedener Techniken über ein kreisförmiges Loch (Durchmesser ca. 𝟎𝟎, 𝟑𝟑 − 𝟑𝟑𝒎𝒎𝒎𝒎) gespannt werden. Zur Herstellung der BLM wird ein geeignetes Lipid oder Lipidgemisch in organischem Lösungsmittel gelöst und die Lösung anschließend über das Loch in einer Teflonplatte gestreift. Durch Verdampfen des Lösungsmittels und self-assembly der Lipidmoleküle entsteht spontan eine Lipiddoppelschicht. Das Loch befindet sich in einer dünnen Festkörperschicht (elektrisch isoliertes Material, Teil einer Küvette), die zwei wässrige Phasen voneinander trennt. Der Stofftransport zwischen den Lösungen funktioniert nur über die planare Lipidmembran. Mit zwei Elektroden, einer Spannungsquelle und einem Voltmeter kann über Strommessung der Ionentransport über die Membran detektiert werden. So können elektrische Eigenschaften von Membranen und Membranproteinen gemessen werden. Vorteile von BLM liegen in der Zugänglichkeit beider Kompartimente, den guten elektrischen Eigenschaften und der Möglichkeit zur Einzelkanaluntersuchung. Ein Nachteil sind die verwendeten organischen Lömis, da nicht ausgeschlossen werden kann, dass noch Lömi-Reste innerhalb der Membran vorliegen und die Messungen beeinflussen. Außerdem liegt eine geringe Langzeitstabilität der BLM im Bereich einiger Stunden vor. Der relativ große Durchmesser der kreisförmigen Membran erlaubt auch optische Untersuchungen: Durch Messung der Intensität des reflektierenden Lichts kann die Membrandicke gemessen werden. Planare Lipidmembranen erscheinen im reflektierten Licht fast schwarz, da sich die an der Vorderund Rückseite der Membran reflektierten Lichtanteile durch Interferenz beinahe auslöschen. Sie werden daher auch als schwarze Lipidmembranen (BLM) bezeichnet. Planare Lipidmembranen können verwendet werden, um die Oberflächenspannung von Lipiddoppelschichten zu messen. Hierzu wird die Membran auf einer Seite zur Halbkugel ausgebeult (z.B. durch Erhöhung des Wasserspiegels auf einer Seite) und die dazu nötige Druckdifferenz gemessen. Es resultiert ein sehr kleiner Wert von 𝛾𝛾 = 0,9𝑚𝑚𝑚𝑚𝑚𝑚−2 . Amphiphile Verbindungen ermöglichen damit über die Ausbildung von Lipiddoppelschichten eine Reduktion der Oberflächenspannung um 2 Größenordnungen (für n-Heptan läge die Grenzflächenspannung bei 𝛾𝛾 = 100𝑚𝑚𝑚𝑚𝑚𝑚−2 ). Festkörpergestützte Membranen wurden aufgrund der Nachteile der BLM entwickelt. Sie zeigen eine sehr hohe Stabilität und erlauben die Anwendung verschiedener oberflächensensitiver Methoden (Anwendungen: MS, Ellipsometrie, ATR-IR, Rasterkraftmikroskopie, Impedanzspektroskopie). Die Präparation festkörpergestützter Membranen kann über Vesikelfusion oder Langmuir-BlodgettÜbertrag (LB-Übertrag) erfolgen. • • Bei der Vesikelfusion wird das Substrat für einige Zeit in einer Vesikelsuspension von unilamellaren Vesikeln definierter Größe inkubiert. Das Spreiten der an der Oberfläche adherierten Vesikel führt zu einer festkörpergestützten Membran. Die WW zwischen Vesikel und FK-Oberfläche kann elektrostatisch oder entropisch sein (Funktionalisierung der FK-Oberfläche mit geladenen bzw. amphipatischen Molekülen). Die Lipide können auch über funktionelle Gruppen an der Kopfgruppe eine quasikovalente Bindung mit dem Substrat eingehen (über Thiolgruppe, die an Goldoberfläche chemisorbiert). Beim LB-Übertrag wird ein hydrophiles Substrat (z.B. Glas, Silizium, Gold) in die Subphase des wassergefüllten Teflontrogs der Filmwaage gehängt, das Lipid an der Wasser-LuftGrenzfläche gespreitet und das Substrat unter kontantem Druck der Lipide langsam aus dem Wasser gezogen. Die Lipide bilden auf der Oberfläche des Substrats eine Monoschicht. In einem weiteren Übertrag kann durch Eintauchen (horizontal oder vertikal) des Substrats in die wässrige Phase eine zweite Monoschicht präpariert werden. Nachteile: Die ersten SSMs zeigten eine geringe Lebensdauer, da die Membranen hier lediglich auf dem Substrat physisorbiert (Van-der-Waals-Bindung) waren. Aufgrund der Wechselwirkung der unteren Monoschicht mit der Substratoberfläche, war der Einbau integraler Proteine durch den FK sterisch behindert. Ein weiteres Problem ist die Einschränkung der lateralen Diffusion in der unteren Lipidschicht aufgrund der Bindung der Lipide an das Susbtrat. Alle diese Probleme werden durch festkörpergestützte Membranen mit Abstandhalter (tBLM = tethered bilayer membrane) gelöst. Durch eine dünne Polyelektrolytschicht zwischen Substrat und Lipidschicht (packing- und Anchor-Moleküle) wird mehr Platz für Proteine und laterale Diffusion geschaffen. Der Abstand zwischen Lipidschicht und Substrat kann auch über Spacerlipide vergrößert werden, die z.B. über ein Thiol an das Goldsubstrat anbinden; die hier vorhandene Chemisorption (chemische, meist kovalente Bindung) ist wesentlich stabiler als die Physisorption und sorgt für wesentlich längere Lebensdauern. Bei der tBLM sind Membran und Substrat entkoppelt, weshalb die Oberfläche keinen Einfluss mehr auf die Membraneigenschaften hat. Phaseneigenschaften von Lipiddoppelschichten Bei lamellaren Phospholipid-Wasser-Systemen kann man Phasenübergänge beobachten, die den Monoschicht-Umwandlungen „flüssig-expandiert“ ⇌ „kondensiert“ ähneln. Die lamellaren Systeme eignen sich besser zur Untersuchung der Phaseneigenschaften über kalorimetrische oder spektroskopische Methoden, bei denen relativ scharfe Änderungen der Messgrößen (wie Wärmekapazität) in Abhängigkeit von der Temperatur beobachtet werden. Die spezifische Wärmekapazität von DPPC zeigt bei 𝑇𝑇𝑐𝑐 = 41°𝐶𝐶 ein charakteristisches Maximum. Die � (𝑇𝑇) = 𝐻𝐻(𝑇𝑇0 ) + 𝑐𝑐𝑝𝑝 (𝑇𝑇)𝑑𝑑𝑑𝑑 spezifische Enthalpie 𝐻𝐻 zeigt eine drastische Zunahme mit der Temperatur. Der Übergang ähnelt einem Phasenübergang erster Ordnung (scharfe Schmelzumwandlung). Da die Zustandsänderung nicht sehr scharf ist, sind die Verhältnisse bei der Umwandlung von LipidDoppelschichten jedoch komplizierter (mesomorphe Umwandlung). Die molekulare Anordnung der CH-Ketten unterhalb der Umwandlungstemperatur 𝑇𝑇𝑐𝑐 entspricht einer quasikristallinen Packung der gestreckten Ketten. Oberhalb der Umwandlungstemperatur nehmen die Ketten durch Rotation um C-C-Bindnungen verschiedene Konformationen ein, was zu einer Abnahme der Ordnung und zu einer Zunahme der Fluidität führt (fluid-kristalliner Zustand). Es handelt sich um keinen Schmelzvorgang! Die mesomorphe Umwandlung ist ein Übergang von einem erstarrten quasikristallinen Zustand (Gel-Phase) in eine flüssig-kristalline Phase unter Erhaltung der Doppelschicht-Struktur. • • Die Umwandlungstemperatur steigt mit der Kettenlänge (für Diacyl-Phosphatidylcholine gilt: C14: 24°C, C16: 41°C, C18: 55°C). Doppelbindungen erniedrigen den Grad der Ordnung in der quasikristallinen Packung, was zu einer Reduktion der Umwandlungstemperatur führt (C18 mit einer Doppelbindung: -22°C; Reduktion um 77°C!). Lipidmischungen in Lipiddoppelschichten Phasenübergänge von Mono- und Doppelschichtsystemen aus reinen Phospholipiden zeigen damit ein Phasenverhalten, das einem Schmelzgleichgewicht eines Einkomponentensystems sehr ähnlich ist. Das Phasenverhalten von Lipidmischungen kann ebenso näherungsweise analog zu den Phasengleichgewichten von Mehrkomponentensystemen beschrieben werden. Die Abbildung zeigt Phasendiagramme (x-Achse: Anteil an C18-PC, y-Achse: Temperatur) von lamellaren Mischsystemen aus Diacyl-PC verschiedener Kettenlängen in wässriger Suspension. Oben ist ein binäres System aus zwei PCs gezeigt, die sich in ihrer Länge um zwei CH2-Gruppen unterscheiden. Das Phasendiagramm entspricht einem Schmelzdiagramm eines (dreidimensionalen) binären Systems mit vollständiger Mischbarkeit der beiden Komponenten in beiden Phasen (flüssig und fest). Dadurch konnte auf die vollständige (zweidimensionale) Mischbarkeit der beiden Komponenten in beiden Phasen (flüssig-kristallin und quasikristallin) geschlossen werden. Es ist außerdem zu erkennen, dass bei konstanter Temperatur, durch Anreicherung bzw. Verarmung einer PC-Art, fluid-kristalline und quasikristalline Phase nebeneinander existieren können (Zweiphasengebiet, F+S). Die Phasen sind streifenförmig oder Inselförmig voneinander abgetrennt. Bei niedrigeren oder höheren Temperaturen resultieren Einphasengebiete, sodass die gesamte Membran ausschließlich in quasikristallinen (S) bzw. fluid-kristallinen (F) Zustand vorliegt. Der Übergang vom Zweiphasengebiet in das Einphasengebiet (durch Temperatur- oder MolenbruchÄnderung) wird als laterale Phasentrennung bezeichnet. Unten ist ein binäres System aus zwei PCs gezeigt, die sich in ihrer Länge um vier CH2-Gruppen unterscheiden. Das Phasendiagramm zeigt hier, dass die zwei Komponenten im kristallinen Einphasengebiet nur beschränkt mischbar sind. Es handelt sich um ein monotektisches Phasendiagramm, da es einer Hälfte des eutektischen Phasendiagramms entspricht. Im eutektischen Phasendiagramm (völlige Mischbarkeit in der einen und völlige Entmischbarkeit in der anderen Phase) gibt es einen eutektischen Punkt, in dem drei Phasen des Systems im Gleichgewicht sind (Solidus- und Liquidus-Linie berühren sich, siehe rechte Abbildung). Dies ist hier nicht der Fall. Das Phasendiagramm zeigt, dass die kristalline Phase (S) aus reinem DSL besteht oder zumindest eine DSL-reiche Phase darstellt (feste Phase bei hohen Temperaturen nur bei hohem DSL-Anteil möglich). Unterhalb der Temperatur TDML (reines monotektisches Verhalten) existiert ein erstarrter Bereich mit DML und DSL nebeneinander. In Plasmamembranen kommt Cholesterin in relativ hoher Konzentration vor (𝑥𝑥𝐶𝐶ℎ𝑜𝑜𝑜𝑜 = 0,3). Dies ist die Ursache für Phasenverhalten mit ausgedehnten Zweiphasengebieten. Das Phasenverhalten natürlicher Membranen ist aufgrund der Vielzahl an Komponenten (mehr thermodynamische Freiheitsgrade als ein binäres System) wesentlich komplexer. Dennoch sind Bereiche im Phasendiagramm zu erwarten, in denen Phasen im Gleichgewicht stehen. Wichtige Regulationsvorgänge an Membranen beruhen auf zweidimensionalen Phasentrennungen, die durch Änderung der Konzentration stark oberflächenaktiver Membranbestandteile induziert werden. Dadurch könnten verschiedene Membran-gebundene Enzym- oder Transportfunktionen an- oder abgeschaltet werden, wenn der zugehörige Membranbereich erstarrt oder fluidisiert wird oder, wenn seine Zusammensetzung in Bezug auf funktionswichtige Membranbestandteile verschoben wird. Lipid Rafts sind angereichert an Sphingolipiden und Cholesterin und scheinen zur Verankerung und Aggregation spezieller Membranproteine zu dienen. Sie sind in ihrer Struktur Festkörper-ähnlich und schwimmen auf dem fluid-kristallinen See der Membran. Sie entstehen durch laterale Phasentrennung. Läuger, Kapitel 8 Transporterscheinungen in kontinuierlichen Systemen sind irreversibel und umfassen Diffusion, Sedimentation und Elektrophorese. Viskosität Definition Die Viskosität 𝜼𝜼 ist über die Kraft K definiert, die notwendig ist, um eine obere Platte (Position d, Fläche A) mit konstanter Geschwindigkeit gegen eine untere Platte (Position 0, Fläche A) zu verschieben. Zwischen den Platten befinden sich einzelne Flüssigkeitsschichten, deren Geschwindigkeiten von 𝑣𝑣 = 0 (Position 𝑧𝑧 = 0) bis zur Geschwindigkeit 𝑣𝑣0 (Geschwindigkeit der oberen Platte, Position 𝑧𝑧 = 𝑑𝑑) linear mit dem Abstand 𝑧𝑧 zunimmt. Diese Linearität gilt nur für laminare (wirbelfreie) Strömungen (Flüssigkeitsbewegung ist ausschließlich durch innere Reibung bestimmt, Voraussetzung: kleine Geschwindigkeiten). Im turbulenten Fall wäre die Viskosität keine Materialkonstante mehr, sondern von 𝑣𝑣0 abhängig. Die Viskosität sinkt mit der Temperatur. Fluidität ist der Kehrwert der Viskosität. 𝐾𝐾 = 𝜂𝜂𝜂𝜂 ∙ 𝑣𝑣0 𝐾𝐾𝐾𝐾 𝑑𝑑𝑑𝑑 = 𝜂𝜂𝜂𝜂 ∙ → 𝜂𝜂 = , 𝑑𝑑 𝐴𝐴𝑣𝑣0 𝑑𝑑𝑑𝑑 Viskoses Fließen in einer Kapillare � 𝑁𝑁𝑁𝑁 𝑁𝑁𝑁𝑁 𝑘𝑘𝑘𝑘 = 2= � ∙ 𝑚𝑚/𝑠𝑠 𝑚𝑚 𝑚𝑚𝑚𝑚 𝑚𝑚2 Fließt eine Flüssigkeit der Dichte 𝜌𝜌 von einem höheren Reservoir in ein tieferes, ist die treibende Kraft der Druckunterschied ∆𝑃𝑃 = 𝜌𝜌𝜌𝜌ℎ, wobei ℎ die Höhe der Flüssigkeitssäule ist. An der Kapillarwand (Rauigkeit) hat die Flüssigkeitsschicht 𝑣𝑣 = 0, im Zentrum ist 𝑣𝑣 = 𝑣𝑣𝑚𝑚𝑚𝑚𝑚𝑚 . Bei konstanter Strömung resultiert ein parabolisches Geschwindigkeitsprofil in der Kapillare. In einer bestimmten Zeit ∆𝑡𝑡 fließt das Volumen ∆𝑉𝑉 durch die Kapillare. Die entsprechende Beziehung heißt Hagen-Poiseuillesche Gleichung. 𝑅𝑅 ist Kapillarradius, 𝐿𝐿 die Kapillarlänge. Beachte die Proportionalität zu 𝑅𝑅 4 (Verdopplung des Radius => 16faches transportiertes Volumen pro Zeit). ∆𝑉𝑉 = 𝜋𝜋 𝜌𝜌𝜌𝜌ℎ𝑅𝑅 4 ∙ ∙ ∆𝑡𝑡 𝜂𝜂𝜂𝜂 8 Viskositätsmessung geht über ein Kapillarviskosimeter nach Ostwald (ignoriert). Sie geben Informationen über Eigenschaften von Makromolekülen. Viskosität makromolekularer Lösungen Viskosität gibt Aufschluss über Größe und Form von Makromolekülen. Die Viskosität steigt mit der Konzentration 𝑐𝑐 [𝑔𝑔/𝑐𝑐𝑚𝑚3 ] des Makromoleküls an (Potenzreihenentwicklung der Konzentrationsabhängigkeit). Die Viskosität des reinen Lösungsmittels ist 𝜂𝜂0 (y-Achsen-Schnittpunkt). Für kleine Konzentrationen resultiert linearer Anstieg nach der Geradengleichung 𝜂𝜂(𝑐𝑐) = 𝜂𝜂0 (1 + [𝜂𝜂]𝑐𝑐) mit der Steigung 𝜂𝜂0 [𝜂𝜂]. [𝜂𝜂] (erster Koeffizient der Potenzreihe) ist die Intrinsic-Viskosität und beschreibt die Veränderung der Viskosität durch die gelöste makromolekulare Komponente. Dadurch ermöglicht [𝜼𝜼] Aussagen über die Form des Makromoleküls. • • Für kugelförmige Teilchen der Dichte 𝜌𝜌 ist [𝜂𝜂]𝜌𝜌 = 2,5. Anhand von [𝜂𝜂]𝜌𝜌 kann das Halbachsenverhältnis für ellipsoide Moleküle bestimmt werden, wenn bekannt ist, ob es sich um ein Stäbchen oder ein Scheibchen handelt: Stäbchenförmige Teilchen erhöhen mit zunehmendem Halbachsenverhältnis a/b die Viskosität wesentlich stärker als Scheibchenförmige Teilchen (Stäbchen bewirken eine stärkere Störung der Lömi-Strömung). Lineare Moleküle können in flexible Fadenmoleküle und langgestreckte starre Stäbchen unterteilt werden. Eine Unterscheidung ist über eine Molmassenabhängigkeit von [𝜂𝜂] möglich. Reibungskoeffizient Teilchen erfahren in Flüssigkeiten der Viskosität 𝜂𝜂 einen Reibungswiderstand, der durch den Reibungskoeffizienten charakterisiert ist. Die Reibungskraft ist proportional zur �⃗) �⃗ = 𝒒𝒒𝑬𝑬 Teilchengeschwindigkeit und wirkt der auslösenden Kraft (z.B. Coulomb-Anziehung �𝑲𝑲 �⃗ . entgegen: ��⃗ 𝑹𝑹 = −𝒇𝒇𝒗𝒗 Der Reibungskoeffizient 𝒇𝒇 [𝑁𝑁𝑁𝑁/𝑚𝑚 = 𝑘𝑘𝑘𝑘/𝑠𝑠] lässt sich für makroskopische Teilchen definierter Geometrie berechnen. Für eine Kugel gilt das Gesetz von Stokes: 𝒇𝒇 = 𝟔𝟔𝟔𝟔𝟔𝟔𝟔𝟔 (kann auch für mikroskopische Teilchen verwendet werden). Die Bewegungsgleichung eines Teilchens in viskoser Lösung, auf das eine konstante Kraft K wirkt lautet 𝑚𝑚𝑣𝑣⃗̇ = 𝐾𝐾 − 𝑓𝑓𝑣𝑣⃗ . Die Lösung dieser Differentialgleichung ergibt die Geschwindigkeit: 𝑣𝑣(𝑡𝑡) = 𝑓𝑓 𝐾𝐾 �1 − 𝑒𝑒 −𝑚𝑚 𝑡𝑡 � 𝑓𝑓 Die Geschwindigkeit des Teilchens nimmt damit hyperbolisch bis zur Endgeschwindigkeit ��⃗ = −𝑹𝑹 ��⃗ und damit die Beschleunigung gleich null wird. 𝒗𝒗𝒎𝒎𝒎𝒎𝒎𝒎 = 𝑲𝑲/𝒇𝒇 zu, da hier 𝑲𝑲 Die Beschleunigung kann durch die Relaxationszeit 𝝉𝝉 = 𝒎𝒎/𝒇𝒇 beschrieben werden, nach der das Teilchen bis auf 1/e seine Endgeschwindigkeit erreicht hat (63,2% von 𝑣𝑣𝑚𝑚𝑚𝑚𝑚𝑚 ). In Wasser (𝜂𝜂 = 0,001𝑔𝑔𝑔𝑔𝑚𝑚−1 𝑠𝑠 −1 ) resultieren damit für Proteine Werte im Bereich von 𝜏𝜏 = 10−11 𝑠𝑠, für Zellen im Bereich von 𝜏𝜏 = 10−5 𝑠𝑠. Es wird demnach sehr schnell die Maximalgeschwindigkeit erreicht. Brownsche Molekularbewegung und Reibungskoeffizient Die Ursache der Brownschen Molekularbewegungen sind thermisch bedingte Zusammenstöße mit Molekülen der umgebenden Flüssigkeit. Aufgrund der ungeordneten Wärmebewegung der Moleküle, kommt es zu Zufallsbewegungen. Die mittlere Verschiebung ���� 𝚫𝚫𝒙𝒙 für n Einzelverschiebungen ist null, da positive Richtung und negative �����𝟐𝟐 (Ausmaß der Richtung gleich wahrscheinlich sind. Das mittlere Verschiebungsquadrat 𝜟𝜟𝒙𝒙 Zitterbewegung) steigt mit zunehmender thermischer Energie 𝑘𝑘𝐵𝐵 𝑇𝑇 (𝑘𝑘𝐵𝐵 = 𝑅𝑅/𝑁𝑁𝐴𝐴 = 1,38 ∙ 1023 𝐽𝐽/𝐾𝐾 ist die Boltzmannkonstante) und abnehmendem Reibungskoeffizient 𝑓𝑓 (und logischerweise mit der Beobachtungszeit 𝛥𝛥𝛥𝛥): �����2 = 2𝑘𝑘𝐵𝐵 𝑇𝑇 𝛥𝛥𝛥𝛥 𝛥𝛥𝑥𝑥 𝑓𝑓 �����2 lässt sich damit 𝑓𝑓 eines Teilchens bestimmen. Für die Projektion der Durch Messung von 𝛥𝛥𝑥𝑥 Bewegung auf die y- und z-Achse gelten identische Beziehungen. Im dreidimensionalen gilt dann: �����2 = ����� �����2 + 𝛥𝛥𝑧𝑧 �����2 = 6𝑘𝑘𝐵𝐵 𝑇𝑇 𝛥𝛥𝛥𝛥 𝛥𝛥𝑠𝑠 𝛥𝛥𝑥𝑥 2 + 𝛥𝛥𝑦𝑦 𝑓𝑓 Diffusion Diffusion ist Materietransport aufgrund von Konzentrationsunterschieden. Die Diffusion ist mechanistisch an die Brownsche Molekularbewegung gekoppelt. Diffusion und Brownsche Molekularbewegung Bei Überschichtung eines gelösten Farbstoffs der Konzentration 𝑐𝑐0 mit reinem Lösungsmittel erfolgt mit der Zeit t ein Konzentrationsausgleich. Zur quantitativen Beschreibung des Diffusionsvorgangs wird der Diffusionsfluss 𝑱𝑱𝒙𝒙 [𝑚𝑚𝑚𝑚𝑚𝑚 ∙ 𝑠𝑠 −1 ] definiert: Es ist die Stoffmenge pro Zeiteinheit ∆𝒏𝒏/∆𝒕𝒕 , die netto und in positiver x-Richtung durch einen senkrecht zur x-Richtung angeordneten, ebenen Querschnitt der Fläche A hindurchtritt (Vergleiche: Definition des Stromflusses bei Elektrolyse). U Bezieht sich der Diffusionsfluss auf einen Querschnitt der Einheitsfläche, spricht man von der Diffusionsflussdichte oder dem spezifischen Diffusionsfluss 𝚽𝚽𝒙𝒙 = 𝑱𝑱𝒙𝒙 /𝑨𝑨 [𝑚𝑚𝑚𝑚𝑚𝑚 ∙ 𝑐𝑐𝑚𝑚−2 ∙ 𝑠𝑠 −1 ] . Der Diffusionsfluss und die Diffusionsflussdichte sind Vektorgrößen! Hier wird lediglich immer eine Komponente (in x-Richtung) betrachtet. Das 1. Ficksche Gesetz beschreibt die Proportionalität zwischen dem Fluss 𝑱𝑱𝒙𝒙 und der betrachteten Querschnittsfläche 𝑨𝑨 sowie dem Konzentrationsgefälle −(𝒅𝒅𝒅𝒅/𝒅𝒅𝒅𝒅)𝒕𝒕 in x-Richtung. Die Proportionalitätskonstante ist der Diffusionskoeffizient 𝑫𝑫. Der Diffusionskoeffizient beschreibt die Geschwindigkeit der Diffusion und ist mit der inneren Reibung verknüpft, die das Teilchen während seiner Bewegung vom umgebenden Medium erfährt. D ist daher von der Viskosität des Mediums abhängig. Das Minus-Zeichen wird verwendet, um 𝐽𝐽 und 𝐷𝐷 positiv zu definieren, wenn 𝑑𝑑𝑐𝑐/𝑑𝑑𝑑𝑑 negatives Vorzeichen hat (positiver Fluss in x-Richtung, wenn Abnahme der Konzentration in x-Richtung). 𝒅𝒅𝒅𝒅 𝑱𝑱𝒙𝒙 = −𝑫𝑫𝑫𝑫 � � 𝒅𝒅𝒅𝒅 𝒕𝒕 Die Konzentration 𝑐𝑐(𝑥𝑥, 𝑡𝑡) ist aufgrund der Diffusion sowohl ortsabhängig als auch zeitabhängig. Daher enthält das 1. Ficksche Gesetz die partielle Ableitung der Konzentration c nach der Ortskoordinate x. Diese Gleichung gilt damit unabhängig von der Zeit. Die Zeit- und Orts-Abhängigkeit der Konzentration ist Gegenstand des 2. Fickschen Gesetzes. Dieses wird später 𝑑𝑑𝑑𝑑 betrachtet: � � = 𝐷𝐷 � 𝑑𝑑𝑑𝑑 𝑥𝑥 𝑑𝑑 2 𝑐𝑐 � 𝑑𝑑𝑥𝑥 2 𝑡𝑡 Die Fickschen Gesetze beschreiben einen gerichteten Materie- oder Teilchenstrom, beruhen aber allein auf der ungerichteten Brownschen Molekularbewegung der einzelnen diffundierenden Teilchen. Aus dem mittleren Verschiebungsquadrat der Brownschen Molekularbewegung, lässt sich das Ficksche Gesetz direkt herleiten (S296, ignoriert). Sie führt also bei Konzentrationsunterschieden zu einer gerichteten Bewegung. Darüber hinaus wird eine Definitionsgleichung für den Diffusionskoeffizienten erhalten, die so genannte Einstein-Gleichung. Aus der Gleichung ist zu erkennen, dass die Wärme als Triebkraft für die Diffusionsbewegung fungiert (𝑘𝑘𝐵𝐵 𝑇𝑇 im Zähler), während die Viskosität als bremsende Kraft wirkt (6𝜋𝜋𝜋𝜋𝜋𝜋 im Nenner). 𝐷𝐷 = �����2 𝑘𝑘𝐵𝐵 𝑇𝑇 𝛥𝛥𝑥𝑥 𝑘𝑘𝐵𝐵 𝑇𝑇 = = ⏟ 2∆𝑡𝑡 𝑓𝑓 𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾 6𝜋𝜋𝜋𝜋𝜋𝜋 Die Kenntnis des Diffusionskoeffizienten ermöglicht die Berechnung der maximal möglichen Verschiebung ������ 𝜟𝜟𝒙𝒙𝟐𝟐 innerhalb eines Zeitintervalls ∆𝑡𝑡 sowie über die zweite Beziehung die Berechnung des Reibungskoeffizienten 𝒇𝒇 bei gegebener Temperatur. Diese Gleichungen ermöglichen z.B. für einen Substrattransport die Berechnung der notwendigen Diffusionszeit ∆𝒕𝒕 für eine gegebene Wegstrecke ������ 𝜟𝜟𝒙𝒙𝟐𝟐 , wenn 𝑫𝑫 oder 𝒇𝒇 bekannt sind. Als abgewandelte Formulierung des 1. Fickschen Gesetzes wird die Diffusionsflussdichte verwendet. 𝑑𝑑𝑑𝑑 𝐽𝐽𝑥𝑥 = Φ𝑥𝑥 = −𝐷𝐷 𝐴𝐴 𝑑𝑑𝑑𝑑 In vielen Fällen ist eine 1D-Betrachtung der Diffusion nicht ausreichend, da die Konzentrationsverteilung nicht unbedingt linear, sondern auch Kugel- oder Zylinder-symmetrisch (z.B. in einer Zelle) sein kann. Für die drei Raumrichtungen 𝑥𝑥, 𝑦𝑦, 𝑧𝑧 gelten entsprechend identische Formulierungen. Für eine kugelsymmetrische Zelle ist die Konzentration nur vom Abstand r zum Zellmittelpunkt abhängig, sodass auch hier einfach Φ𝑟𝑟 verwendet werden kann, wenn der Koordinaten-Ursprung im Zellmittelpunkt gewählt wird. Stationäre Diffusion durch eine Trennwand Nun soll eine stationäre Diffusion des Stoffes S zwischen zwei Lösungsräumen, getrennt durch eine feinporige Wand, eindimensional (x-Richtung) betrachtet werden. Werden beide Lösungsräume kontinuierlich durchmischt (Magnetrührer), ist die Konzentration der Lösungsräume ortsunabhängig. Das Konzentrationsgefälle beschränkt sich auf die Lösungsmittelgefüllten Poren der Trennwand. Das Konzentrationsgefälle ist für lange Diffusionszeiten und große Lösungsräume (beides = Konzentrationsdifferenz in Lösungsräumen konstant) linear. Damit fällt die Konzentration von S in den Poren linear von 𝒄𝒄𝑰𝑰𝑰𝑰 auf 𝒄𝒄𝑰𝑰 ab. Durch Einsetzen von 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑐𝑐(𝑥𝑥) = 𝑐𝑐 𝐼𝐼𝐼𝐼 − =− �𝑐𝑐 𝐼𝐼𝐼𝐼 −𝑐𝑐 𝐼𝐼 � 𝑑𝑑 (𝑐𝑐 𝐼𝐼𝐼𝐼 − 𝑐𝑐 𝐼𝐼 ) 𝑑𝑑𝑑𝑑 𝑥𝑥 = 𝑐𝑐 𝐼𝐼𝐼𝐼 − 𝑥𝑥, 𝑑𝑑 𝑑𝑑𝑑𝑑 0 ≤ 𝑥𝑥 ≤ 𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑡𝑡 in das 1. Fickschen Gesetz 𝐽𝐽𝑥𝑥 = −𝐷𝐷𝐷𝐷 � � ergibt sich: 𝐽𝐽𝑥𝑥 = 𝐷𝐷𝐷𝐷 (𝑐𝑐 𝐼𝐼𝐼𝐼 − 𝑐𝑐 𝐼𝐼 ) 𝑑𝑑 Als Folge der Diffusion nimmt die Konzentratiosdifferenz 𝑐𝑐 𝐼𝐼𝐼𝐼 − 𝑐𝑐 𝐼𝐼 mit der Zeit ab, sodass 𝐽𝐽𝑥𝑥 mit der Zeit ebenso kleiner wird. Sind die Lösungsräume sehr groß, ändert sich die Konzentrationsdifferenz nur unwesentlich und der Fluss ist stationär (zeitlich konstant). Über diese Anordnung kann der Diffusionskoeffizient gemessen werden. Der Fluss 𝐽𝐽𝑥𝑥 = Δn/Δ𝑡𝑡 wird erhalten, indem im Zeitintervall Δ𝑡𝑡 die durch die Trennwand diffundierte Stoffmenge Δ𝑛𝑛 gemessen wird. 𝐴𝐴 ist der effektive Querschnitt (Summe der Querschnittsflächen aller Poren), 𝑑𝑑 die effektive Dicke der Trennwand (𝑑𝑑/𝐴𝐴 wird über Eichung mit einer Substanz mit bekanntem Diffusionskoeffizienten über dieselbe Gleichung bestimmt). 𝐷𝐷 = Δn 𝑑𝑑 1 ∙ ∙ 𝐼𝐼𝐼𝐼 Δ𝑡𝑡 𝐴𝐴 (𝑐𝑐 − 𝑐𝑐 𝐼𝐼 ) Zeitabhängigkeit der Diffusion durch eine Trennwand (einfacher Fall) Die zeitabhängige Konzentrationsdifferenz zwischen den Lösungsräumen sei ∆𝑐𝑐 = 𝑐𝑐 𝐼𝐼𝐼𝐼 − 𝑐𝑐 𝐼𝐼 (Fluss von II nach I). Die zeitliche Änderungen der Stoffmengen 𝑛𝑛𝐼𝐼 und 𝑛𝑛𝐼𝐼𝐼𝐼 in den beiden Lösungsräumen entsprechen direkt den Flüssen und können daher über das 1. Ficksche Gesetz geschrieben werden. Die unterschiedlichen Vorzeichen beschreiben, dass die Zunahme der Konzentration im Lösungsraum I von der Abnahme in Lösungsraum II unterschieden werden muss. 𝑑𝑑𝑛𝑛𝐼𝐼𝐼𝐼 𝑉𝑉 𝐼𝐼𝐼𝐼 𝑑𝑑𝑐𝑐 𝐼𝐼𝐼𝐼 = = −𝐽𝐽𝑥𝑥 , 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 → 𝑑𝑑𝑐𝑐 𝐼𝐼𝐼𝐼 1 = − 𝐼𝐼𝐼𝐼 ∙ 𝐽𝐽𝑥𝑥 𝑑𝑑𝑑𝑑 𝑉𝑉 𝑑𝑑𝑛𝑛𝐼𝐼 𝑉𝑉 𝐼𝐼 𝑑𝑑𝑐𝑐 𝐼𝐼 = = 𝐽𝐽𝑥𝑥 , 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 → 𝑑𝑑𝑐𝑐 𝐼𝐼 1 = 𝐼𝐼 ∙ 𝐽𝐽𝑥𝑥 𝑑𝑑𝑑𝑑 𝑉𝑉 Die zeitliche Änderung der Konzentrationsdifferenz ergibt sich aus der Subtraktion der rechten Gleichungen (links minus recht): ⟺ 𝑑𝑑𝑐𝑐 𝐼𝐼𝐼𝐼 𝑑𝑑𝑐𝑐 𝐼𝐼 1 1 − = − 𝐼𝐼𝐼𝐼 ∙ 𝐽𝐽𝑥𝑥 − 𝐼𝐼 ∙ 𝐽𝐽𝑥𝑥 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑉𝑉 𝑉𝑉 ∆𝑐𝑐 1 1 𝒅𝒅∆𝒄𝒄 = −𝐷𝐷𝐷𝐷 � 𝐼𝐼𝐼𝐼 + 𝐼𝐼 � = −𝜷𝜷𝜷𝜷∆𝒄𝒄 , 𝑑𝑑 𝑉𝑉 𝑉𝑉 𝒅𝒅𝒅𝒅 𝛽𝛽 = 𝐴𝐴 1 1 � 𝐼𝐼𝐼𝐼 + 𝐼𝐼 � 𝑑𝑑 𝑉𝑉 𝑉𝑉 𝛽𝛽 ist die „Apparate Konstante“ der Anordnung. Die Lösung der Differentialgleichung (rot markiert) unter Berücksichtigung der Konzentrationsdifferenz ∆𝑐𝑐0 im Anfangszustand ermöglicht die Bestimmung des Diffusionskoeffizienten, wenn Konzentrationsdifferenz ∆𝑐𝑐 zur Zeit t bekannt ist. ∆𝑐𝑐 = ∆𝑐𝑐0 𝑒𝑒 −𝛽𝛽𝛽𝛽𝛽𝛽 ↔ 𝐷𝐷 = ln(∆𝑐𝑐0 /∆𝑐𝑐) 𝛽𝛽𝛽𝛽 Der wesentliche Schritt für die zeitabhängige Betrachtung ist die Berücksichtigung der Stoffmengenbilanzen der zwei Lösungsräume. Das 2. Ficksche Gesetz ermöglicht eine allgemeine Formulierung der Stoffmengenbilanzen bei Diffusionsvorgängen. Die lila markierten Bestimmungsgleichungen, einmal für den stationären und einmal für den zeitabhängigen Fall, können beide zur Berechnung von D herangezogen werden. Bisher unberücksichtigt: Der Diffusionskoeffizient nimmt mit zunehmender Konzentration ab. Faustregel: In einer 1%igen Lösung (Massenprozent) ist D um 1-2% gegenüber dem Wert bei einer unendlich verdünnten Lösung erniedrigt. 2. Ficksches Gesetz und Diffusion in freier Lösung Für Diffusionsprozesse in freier Lösung (keine poröse Wand) ist das 1. Ficksche Gesetz unzureichend. Es wird das 2. Ficksche Gesetz angewendet. Wir betrachten die Konzentrationsbilanz in einer dünnen Scheibe der Dicke 𝒅𝒅𝒅𝒅 und der Querschnittsfläche 𝑨𝑨. Die erste Oberfläche befindet sich an Position 𝑥𝑥 (hier ist der Zufluss von Teilchen möglich), die andere an Position 𝑥𝑥 + 𝑑𝑑𝑑𝑑 (Abfluss von Teilchen). Die Änderung 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 der Stoffmenge 𝑛𝑛 = 𝑉𝑉𝑉𝑉 = 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 der diffundierenden Teilchen in der flachen Scheibe beruht auf der Differenz von Zufluss und Abfluss: 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝐴𝐴𝐴𝐴𝐴𝐴 � � = 𝐽𝐽(𝑥𝑥) − 𝐽𝐽(𝑥𝑥 + 𝑑𝑑𝑑𝑑) 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑥𝑥 Umformen zum Differentialquotienten („Division“ durch dx): 𝑑𝑑𝑑𝑑 𝐽𝐽(𝑥𝑥) − 𝐽𝐽(𝑥𝑥 + 𝑑𝑑𝑑𝑑) 𝐽𝐽(𝑥𝑥 + 𝑑𝑑𝑑𝑑) − 𝐽𝐽(𝑥𝑥) 𝑑𝑑𝑑𝑑 𝐴𝐴 � � = =− � �=− � � 𝑑𝑑𝑑𝑑 𝑥𝑥 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 Für J das 1. Ficksche Gesetz einsetzen: 𝐽𝐽𝑥𝑥 = −𝐷𝐷𝐷𝐷 � � 𝑑𝑑𝑑𝑑 𝑡𝑡 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑 �𝐷𝐷𝐷𝐷 � � � 𝑑𝑑 �� � � 𝑑𝑑𝑑𝑑 𝑑𝑑2 𝑐𝑐 𝑑𝑑𝑑𝑑 𝑡𝑡 𝑑𝑑𝑑𝑑 𝑡𝑡 𝐴𝐴 � � = � � = 𝐷𝐷𝐷𝐷 � � = 𝐷𝐷𝐷𝐷 � 2 � 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑥𝑥 𝑡𝑡 𝑑𝑑𝑑𝑑 𝑥𝑥 𝒅𝒅𝒅𝒅 𝒅𝒅𝟐𝟐 𝒄𝒄 → � � = 𝑫𝑫 � 𝟐𝟐 � 𝒅𝒅𝒅𝒅 𝒙𝒙 𝒅𝒅𝒙𝒙 𝒕𝒕 Diese Gleichung beschreibt Orts- und Zeitabhängigkeit der Konzentration, wobei D auch hier als Konzentrationsunabhängig vorausgesetzt wird. Für 3D ist 𝑑𝑑 2 𝑐𝑐/𝑑𝑑𝑥𝑥 2 zu ersetzen durch ∑ 𝑖𝑖 = 𝑥𝑥, 𝑦𝑦, 𝑧𝑧. 𝑑𝑑 2 𝑐𝑐 𝑑𝑑𝑖𝑖 2 mit Da das 2. Ficksche Gesetz für alle existierenden Diffusionsprobleme gilt, muss die allgemeine Lösung der Differentialgleichung vieldeutig sein. Erst durch Beachtung von spezifischen Anfangsbedingungen und Randbedingungen des Problems resultiert eine eindeutige Lösung. Daher muss für das zweite Ficksche Gesetz die Lösung immer anhand des vorliegenden Problems neu hergeleitet werden. Betrachtung einer eindimensionalen Diffusion einer Phase mit gelöster Substanz S gegen eine reine Lösungsmittelphase ohne Trennwand; die Phasengrenze liegt bei x=0. • • Anfangsbedingungen gelten zum Zeitpunkt 𝑡𝑡 = 0. o 𝑐𝑐 = 𝑐𝑐0 für 𝑥𝑥 < 0. o 𝑐𝑐 = 0 für 𝑥𝑥 > 0. Randbedingungen gelten an geometrischen Grenzen des Diffusionsproblems im Verlaufe des Diffusionsprozesses, also für 𝑡𝑡 ≥ 0. Wir gehen davon aus, dass die Konzentrationen an den Enden der Diffusionsküvette konstant bleiben (es wird von einer unendlich großen Diffusionsküvette ausgegangen, jedoch gilt diese Bedingung auch für Küvetten mit Längen im 𝑐𝑐𝑐𝑐-Bereich bei Beschränkung der Diffusionszeit auf mehrere Tage) o o 𝑐𝑐 = 𝑐𝑐0 für 𝑥𝑥 = −∞ 𝑐𝑐 = 0 für 𝑥𝑥 = ∞. Unter diesen Bedingungen lautet die Lösung des 2. Fickschen Gesetzes 𝑐𝑐(𝑥𝑥, 𝑡𝑡) mit der Fehlerfunktion 𝝋𝝋(𝒖𝒖): 𝑐𝑐0 𝑐𝑐(𝑥𝑥, 𝑡𝑡) = [1 − 𝜑𝜑(𝑢𝑢)] , 2 𝜑𝜑(𝑢𝑢) = 2 √𝜋𝜋 𝑢𝑢 2 � 𝑒𝑒 −𝑦𝑦 𝑑𝑑𝑑𝑑 , 0 𝑢𝑢 = 𝑥𝑥 2√𝐷𝐷𝐷𝐷 Das Integral lässt sich nur numerisch lösen: 𝜑𝜑(𝑢𝑢) = 0 für 𝑢𝑢 = 0 und geht für große 𝑢𝑢-Werte schnell → 1. Die Fehlerfunktion ist außerdem symmetrisch 𝜑𝜑(−𝑢𝑢) = −𝜑𝜑(𝑢𝑢). Durch differenzieren der Fehlerfunktion nach der oberen Grenze erhält man: 𝑥𝑥 2 𝑐𝑐0 𝑑𝑑𝑑𝑑 − 4𝐷𝐷𝐷𝐷 =− 𝑒𝑒 𝑑𝑑𝑑𝑑 √4𝜋𝜋𝜋𝜋𝜋𝜋 Konzentrationsgradient −𝑑𝑑(𝑐𝑐/𝑐𝑐0 )/𝑑𝑑𝑑𝑑 vs. Diffusionsstrecke x Konzentrationsververhältnis 𝑐𝑐/𝑐𝑐0 vs. Diffusionsstrecke x 𝐷𝐷 = 3 ∙ 10−6 𝑐𝑐𝑚𝑚2 𝑠𝑠 −1 , z.B. ATP (4𝐷𝐷 = 1𝑐𝑐𝑚𝑚2 𝑑𝑑−1 macht Rechnung einfacher, wenn für t=d eingesetzt wird). Die Abbildung zeigt, dass die Diffusion für makroskopische Entfernungen (𝑐𝑐𝑐𝑐-Bereich) sehr langsam ist. 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 zeigt jedoch sehr große Änderungen bei kleinen x-Werten. Es findet eine gerichtete Bewegung der Teilchen von der Phase I (negative x-Werte) in die Lösungsmittel-Phase II (positve x-Werte) statt: • • Untere Abbildung: Zeigt die Konzentrationsverhältnisse 𝑐𝑐/𝑐𝑐0 in Abhängigkeit von dem Abstand zur Phasengrenze. Bei t=0 ist hier eine Treppenfunktion zu erkennen, wobei an der Phasengrenze x=0 die Konzentration abrupt von 𝑐𝑐 = 𝑐𝑐0 bzw. 𝑐𝑐/𝑐𝑐0 = 1 für negative x-Werte auf null für positive x-Werte abfällt. Zu späteren Zeiten nähern sich beide Phasen der Konzentration 𝑐𝑐 = 0,5𝑐𝑐0 bzw. 𝑐𝑐/𝑐𝑐0 = 0,5 an. Die Kurven zeigen einen sigmoidalen Verlauf. Obere Abbildung: Zeigt die Steigung des Graphen der unteren Abbildung (Achtung: y-Achse zeigt den negativen Gradienten!), also die Änderung des Konzentrationsverhältnisses mit der Position x. Für x-Werte nahe null (Nahe der Phasengrenze) sind die Konzentrationsänderungen am größten. Für negative und positive x-Werte nimmt das Ausmaß der Änderung ab, bis es bei großen Entfernungen zur ursprünglichen Phasengrenze null wird. Die Kurve nähert sich für lange Zeiten einer horizontalen Geraden an. Für den typischen Durchmesser einer Zelle von 80 µm benötigt ein Teilchen über Diffusion lediglich 1,6 s (für 8 cm sind es 18,7 Tage). Die Diffusionsprozesse limitieren damit auch die Kompartimentierung biologischer Systeme. Ähnliche Werte gelten für Proteine und Lipide in der Lipidmembran (1-2 µm pro Sekunde). Die experimentelle Bestimmung von 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 mithilfe der schlierenoptischen Methode ermöglicht die Berechnung des Diffusionskoeffizienten. Dabei wird der Gradient des Brechnungsindex 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 gemessen, wobei 𝑛𝑛 = 𝜅𝜅𝜅𝜅 (Formeln ignoriert, S305). Sedimentation-Kapitel ignoriert Diffusion von Ionen Eine Kapillare verbindet zwei Lösungsräume mit unterschiedlich konzentrierten, vollständig dissoziierten Elektrolyten 𝑀𝑀+ 𝑋𝑋 −. • • Am Ende der Kapillare sei die Konzentration konstant und so groß wie im entsprechenden Lösungsraum (stetige Durchmischung, große Räume): 𝑐𝑐(𝑥𝑥 = 0) = 𝑐𝑐′ und 𝑐𝑐(𝑥𝑥 = 𝑙𝑙) = 𝑐𝑐 ′′ . Kapillare ist in einem quasi-stationären (annähernd zeitunabhängigen) Zustand: 𝑑𝑑𝑑𝑑(𝑥𝑥)/𝑑𝑑𝑑𝑑 = 0. Die Flüsse der einzelnen Ionen 𝑴𝑴+ und 𝑿𝑿− sind trotz unabhängiger Bewegung (in verdünnten Lösungen) und unterschiedlichen Diffusionskoeffizienten identisch. Für 𝑫𝑫+ > 𝑫𝑫− hat das Kation die Tendenz dem Anion bei der Diffusion vorauszueilen. So wandern zunächst geringfügig mehr Kationen als Anionen aus der konzentrierten in die verdünnte Lösung. Dadurch kommt es zu einem positiven elektrischen Potential in der verdünnten Lösung gegenüber der konzentrierten. Das in der Kapillare entstehende elektrische Feld vermindert den Fluss von Kationen und erhöht den Fluss von Anionen, sodass die Flüsse beider Ionensorten gleich groß werden. Die Wanderung von Ionen unter gleichzeitiger Wirkung eines Konzentrationsgradienten und eines elektrischen Potentialgradienten heißt Elektrodiffusion. Die sich entlang der Diffusionsstrecke aufbauende Spannung 𝑽𝑽𝑫𝑫 = 𝝋𝝋′ − 𝝋𝝋′′ heißt Diffusionspotential. Nernst-Planck-Gleichung Die Flussdichte muss damit als Summe eines Diffusionsanteils und eines durch das elektrische Feld zustande kommenden Anteils geschrieben werden, wobei 𝑖𝑖 für eine Ionensorte steht: Φ𝑖𝑖 = (Φ𝑖𝑖 )𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 + (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 = −𝐷𝐷𝑖𝑖 𝑑𝑑𝑐𝑐𝑖𝑖 + (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 𝑑𝑑𝑑𝑑 Nun soll (𝚽𝚽𝐢𝐢 )𝐞𝐞𝐞𝐞 berechnet werden Auf jedes Ion wirkt eine Kraft aufgrund des elektrischen Feldes. Für die x-Komponente dieser Kraft gilt: 𝑒𝑒𝑒𝑒 = 𝑞𝑞𝑖𝑖 𝐸𝐸𝑥𝑥 = −𝑞𝑞𝑖𝑖 𝐾𝐾𝑥𝑥,𝑖𝑖 𝑑𝑑𝑑𝑑 , 𝑑𝑑𝑑𝑑 𝑞𝑞𝑖𝑖 = 𝑧𝑧𝑖𝑖 𝑒𝑒 𝜑𝜑(𝑥𝑥) ist das elektrische Potential in der Kapillare. Die elektrische Kraft stellt nach einer kurzen Zeit (Gleichgewichtsbedingung: 𝐾𝐾 = −𝑅𝑅) eine konstante Geschwindigkeit ein, entsprechend dem Reibungskoeffizienten 𝑓𝑓 des Ions. 𝑣𝑣𝑥𝑥,𝑖𝑖 = 𝑞𝑞𝑖𝑖 𝑞𝑞𝑖𝑖 𝑑𝑑𝑑𝑑 𝐸𝐸𝑥𝑥 = − ∙ 𝑓𝑓𝑖𝑖 𝑓𝑓𝑖𝑖 𝑑𝑑𝑑𝑑 Mit der Einsteinschen Beziehung (𝐷𝐷𝑖𝑖 = 𝑘𝑘𝐵𝐵 𝑇𝑇/𝑓𝑓𝑖𝑖 ) lässt sich der Reibungskoeffizient ersetzen: 𝑣𝑣𝑥𝑥,𝑖𝑖 = −𝐷𝐷𝑖𝑖 ∙ 𝑞𝑞𝑖𝑖 𝑑𝑑𝑑𝑑 ∙ 𝑘𝑘𝐵𝐵 𝑇𝑇 𝑑𝑑𝑑𝑑 Nun ein paar Naturkonstanten austauschen (𝑒𝑒 = 𝐹𝐹/𝑁𝑁𝐴𝐴 , 𝑘𝑘𝐵𝐵 = 𝑅𝑅/𝑁𝑁𝐴𝐴 ): 𝑣𝑣𝑥𝑥,𝑖𝑖 = −𝐷𝐷𝑖𝑖 ∙ 𝑧𝑧𝑖𝑖 𝐹𝐹 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 ∙ = −𝑢𝑢𝑖𝑖 ∙ 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 𝒖𝒖𝒊𝒊 ist die Beweglichkeit und steht hier für die gerichtete Bewegung der Ionen im elektrischen Feld. Sie lässt sich durch den Diffusionskoeffizienten ausdrücken, der wiederum aus der ungerichteten Brownschen Molekularbewegung herleitbar ist. Auch hier basiert also die gerichtete Bewegung auf einer ungerichteten! Die elektrische Flussdichte (𝚽𝚽𝒊𝒊 )𝒆𝒆𝒆𝒆 ist das Produkt aus Konzentration und Geschwindigkeit. Damit gilt: (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 = 𝑐𝑐𝑖𝑖 𝑣𝑣𝑥𝑥,𝑖𝑖 = −𝑐𝑐𝑖𝑖 𝐷𝐷𝑖𝑖 ∙ 𝑧𝑧𝑖𝑖 𝐹𝐹 𝑑𝑑𝑑𝑑 ∙ 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 Damit ergibt sich die Nernst-Planck-Gleichung, die grundlegende Gleichung für Elektrodiffusion: 𝑑𝑑𝑐𝑐𝑖𝑖 𝐹𝐹 𝑑𝑑𝑑𝑑 + 𝑧𝑧𝑖𝑖 𝑐𝑐𝑖𝑖 ∙ ∙ � Φ𝑖𝑖 = (Φ𝑖𝑖 )𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 + (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 = −𝐷𝐷𝑖𝑖 � 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 Sie gilt unabhängig davon, ob die elektrische Feldstärke 𝑬𝑬𝒙𝒙 = − 𝒅𝒅𝒅𝒅 𝒅𝒅𝒅𝒅 durch Ionendiffusion (Diffusionspotential) erzeugt wird oder durch eine von außen angelegte Spannung entsteht. Nernst-Planck: Diffusionspotential eines 1:1-wertigen Elektrolyten Versuchsanordnung/Bedingungen wie in Abbildung zu Beginn des Kapitels. Weitere Voraussetzungen: • • In der Kapillare fließt kein Strom, d.h. es wandern gleich viele Kationen wie Anionen von links nach rechts: Φ+ = Φ− → Φ+ − Φ− = 0 Jedes Volumenelement der Kapillare enthält gleich viele Kationen wie Anionen (Elektroneutralitätsbedingung): 𝑐𝑐+ (𝑥𝑥) = 𝑐𝑐− (𝑥𝑥) = 𝑐𝑐(𝑥𝑥) Nernst-Planck-Gleichung mit 𝑧𝑧+ = 1 bzw. 𝑧𝑧− = −1 einsetzen: 𝑑𝑑𝑐𝑐+ 𝐹𝐹 𝑑𝑑𝑑𝑑 𝑑𝑑𝑐𝑐− 𝐹𝐹 𝑑𝑑𝑑𝑑 + 𝑐𝑐+ ∙ ∙ � + 𝐷𝐷− � − 𝑐𝑐− ∙ ∙ � Φ+ − Φ− = 0 = −𝐷𝐷+ � 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 Die Gleichung auflösen nach 𝐷𝐷+ − 𝐷𝐷− 𝑅𝑅𝑅𝑅 1 𝑑𝑑𝑑𝑑 𝛼𝛼 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 =− ∙ ∙ ∙ =− ∙ 𝐷𝐷+ + 𝐷𝐷− 𝐹𝐹 𝑐𝑐 𝑑𝑑𝑑𝑑 𝑐𝑐 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 Integration der Differentialgleichung zwischen 𝑥𝑥 = 0 und 𝑥𝑥 = 𝑙𝑙 (Länge der Kapillare). Achtung: Das ist etwas merkwürdig: die Gleichung wird mit dx erweitert, um nach dx integrieren zu können; letztlich wird dadurch aber dx gekürzt, sodass die rechte Seite nach dc und die linke nach 𝑑𝑑𝑑𝑑 integriert werden kann, wobei die Grenzen eben für x gesetzt bleiben (Formalismus, muss man nich verstehen xD). 𝑙𝑙 � 0 𝑙𝑙 𝑑𝑑𝑑𝑑 1 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = −𝛼𝛼 � ∙ 𝑑𝑑𝑥𝑥 𝑑𝑑𝑑𝑑 0 𝑐𝑐 𝑑𝑑𝑑𝑑 𝑙𝑙 𝑙𝑙 → � 𝑑𝑑𝑑𝑑 = −𝛼𝛼 � 0 0 1 ∙ 𝑑𝑑𝑑𝑑 𝑐𝑐 → 𝜑𝜑(𝑙𝑙) − 𝜑𝜑(0) = −𝛼𝛼 ln 𝑐𝑐(𝑙𝑙) 𝑐𝑐(0) Da die Werte von 𝜑𝜑 und c an den Enden der Kapillare genauso groß sind wie in den Lösungsräumen (𝜑𝜑(𝑙𝑙) = 𝜑𝜑′′, 𝜑𝜑(0) = 𝜑𝜑′, 𝑐𝑐(𝑙𝑙) = 𝑐𝑐′′, 𝑐𝑐(0) = 𝑐𝑐′), folgt für das Diffusionspotential 𝑽𝑽𝑫𝑫 (𝛼𝛼 wurde wieder eingesetzt): 𝜑𝜑′′ − 𝜑𝜑′ = − Grenzbetrachtungen: • • • 𝐷𝐷+ − 𝐷𝐷− 𝑅𝑅𝑅𝑅 𝑐𝑐 ′′ ∙ ∙ ln ′ 𝐷𝐷+ + 𝐷𝐷− 𝐹𝐹 𝑐𝑐 𝑉𝑉𝐷𝐷 = 𝜑𝜑′ − 𝜑𝜑′′ = | ∗ (−1) 𝐷𝐷+ − 𝐷𝐷− 𝑅𝑅𝑅𝑅 𝑐𝑐′′ ∙ ∙ ln ′ 𝐷𝐷+ + 𝐷𝐷− 𝐹𝐹 𝑐𝑐 Für 𝐷𝐷+ = 𝐷𝐷− (Anionen und Kationen haben denselben Diffusionskoeffizient) wird 𝑉𝑉𝐷𝐷 = 0 Für 𝐷𝐷+ > 𝐷𝐷− ist 𝑉𝑉𝐷𝐷 = 𝜑𝜑′ − 𝜑𝜑′′ > 0 für 𝑐𝑐 ′′ > 𝑐𝑐′. Die verdünnte Lösung 𝐼𝐼 hat damit gegenüber der konzentrierten 𝐼𝐼𝐼𝐼 ein positives Potential. Für 𝐷𝐷+ ≫ 𝐷𝐷− bzw. Für 𝐷𝐷+ ≪ 𝐷𝐷− geht das Diffusionspotential in das Nernst-Potential für das Kation bzw. das Anion über: 𝑉𝑉𝐷𝐷 Messung des Membranpotentials ≈ 𝐷𝐷+ ≫𝐷𝐷− 𝐷𝐷+ ≪𝐷𝐷− 𝑐𝑐′′ + 𝑅𝑅𝑅𝑅 ∙ ln ′ − 𝐹𝐹 𝑐𝑐 Diffusionspotentiale sind bei elektrochemischen Messungen oft störend. Bei der Messung des Membranpotentials führt man in die Zelle eine Glaskapillare mit KCl-Lösung ein, die über einen chlorierten Silberdraht an den äußeren Messkreis angeschlossen ist. Die zweite Elektrode befindet sich in der umgebenden Lösung der Zelle. Das Voltmeter zeigt die Potentialdifferenz zwischen Elektrolytfüllungen der beiden Elektroden an: 𝑉𝑉 = 𝜑𝜑𝐸𝐸1 − 𝜑𝜑𝐸𝐸2 . Die gemessene Potentialdifferenz ist von verschiedenen Potentialdifferenzen abhängig: (𝜑𝜑𝐸𝐸1 𝑉𝑉 = �� − �� 𝜑𝜑𝑖𝑖 ) + (𝜑𝜑 ����� ������� ��� �� 𝑖𝑖 − 𝜑𝜑 𝑎𝑎 ) + (𝜑𝜑 𝑎𝑎 − 𝜑𝜑𝐸𝐸2 ) 𝑉𝑉𝐷𝐷 1 𝑉𝑉𝑀𝑀 −𝑉𝑉𝐷𝐷 2 𝑉𝑉𝐷𝐷1 und 𝑉𝑉𝐷𝐷2 sind die entsprechenden Diffusionspotentiale an den Spitzen der Elektroden 1 (Differenz Elektrodenlösung minus Zellinneres) und 2 (Differenz Zelläußeres minus Elektrodenlösung). Ursache dieser Potentialdifferenzen sind die Ionen-Konzentrationsgradienten in der Übergangszone zwischen Elektrodenlösung und Außenmedium. Sie verfälschen das eigentlich zu messende Membranpotential 𝑉𝑉𝑀𝑀 . Um 𝑉𝑉𝐷𝐷1 und 𝑉𝑉𝐷𝐷2 klein zu halten, müssen zwei Bedingungen erfüllt sein: • Elektrodenfüllung muss ein Salz sein, für das 𝑫𝑫+ = 𝑫𝑫− gilt, damit 𝑉𝑉𝐷𝐷1 und 𝑉𝑉𝐷𝐷2 ungefähr gleich groß werden und sich wegen des unterschiedlichen Vorzeichens aufheben (KCl). • Hohe Konzentrationen sind notwendig, damit in der Übergangszone das Diffusionspotential ausschließlich von KCl bestimmt wird und nicht von anderen Ionen in der Zelle/Lösung. Elektrisch geladene Grenzflächen Geladene Oberflächen (Zellen, Proteine) tragen meist negative und positive Ladungen, in ungleicher Zahl, wodurch eine Nettoladung resultiert. Sie sind gleichzusetzen mit einer elektrisch geladenen, ebenen Wand. Elektrisches Potential in der Nähe einer geladenen Wand Eine ebene Wand mit fixierten positiven Ladungen 𝑊𝑊 + sei in Kontakt mit einem vollständig dissoziierten Elektrolyten 𝑀𝑀+ 𝑋𝑋 −. Da das Gesamtsystem (Wand + Lösung) elektrisch neutral sein muss, werden 𝑊𝑊 +durch 𝑋𝑋 − neutralisiert. Dies geschieht durch einen Überschuss von 𝑋𝑋 − (Gegen-Ion, entgegengesetzte Ladung im Vergleich zu 𝑊𝑊 +) und ein Defizit von 𝑀𝑀+ (Co-Ion, gleiche Ladung wie 𝑊𝑊 +) in der Nähe der Wand. Die Schicht aus fixierten 𝑾𝑾+-Ladungen und diffusen 𝑿𝑿−-Ladungen bilden die elektrische Doppelschicht. Die Bildung der elektrischen Doppelschicht geht einher mit der Bildung eines elektrischen Potentials (ganz allgemein: Galvani-Potential) zwischen Wand und Lösung. Der Verlauf der Konzentrationen 𝑐𝑐+ (𝑥𝑥) und 𝑐𝑐− (𝑥𝑥) in der Nähe der Wand wird durch den Verlauf des elektrischen Potentials 𝜑𝜑(𝑥𝑥) bestimmt. 𝑊𝑊 + erzeugt unmittelbar an der Wand (𝑥𝑥 = 0) ein positives elektrisches Potential 𝜑𝜑0 (Grenzflächenpotential), das in der Grenze 𝑥𝑥 → ∞ null wird (Referenz). Der Verlauf 𝜑𝜑(𝑥𝑥) wird durch verschiedene Theorien beschrieben. Das Helmholtz-Schicht-Modell beschreibt die starre Bindung der hydratisierten Ionen an die Elektroden-Grenzfläche, wobei die Hydratationssphären den Abstand zwischen Ionen und Grenzfläche limitieren und das Ladungsverhältnis zwischen fixierten (Elektrode) und frei beweglichen (Ionen) Ladungen genau 1:1 ist. Es entsteht eine planare Ionen-Schicht, die äußere Helmholtz-Schicht (OHP) im Abstand von einem Ionenradius r zur Elektroden-Grenzfläche. Zwischen den beiden Ladungsschichten ist ein ladungsfreier Raum (Ladungsdichte 𝜌𝜌 = 0). Ohne Quellen oder Senken des elektrischen Potentials, ändert sich dieses nur linear mit dem Ort. Aus der Poissoin-Gleichung folgt durch zweimalige Integration: 𝜌𝜌 𝑑𝑑2 𝜑𝜑 =− , 𝜌𝜌 = 0 → 𝜑𝜑(𝑥𝑥) = 𝐶𝐶1 𝑥𝑥 + 𝐶𝐶2 2 𝜀𝜀𝑟𝑟 𝜀𝜀0 𝑑𝑑𝑥𝑥 Eine Verfeinerung des Modells beschreibt, dass Ionen ihre Hydrathülle abwerfen und direkt über chemische Bindung an die Elektroden-Oberflächen binden können. Dabei bildet sich eine innere Helmholtz-Schicht (IHP). Das Helmholtz-Schicht-Modell vernachlässigt jedoch die thermische Energie und die damit verbundene diffuse Bewegung der Ionen, welche die rigiden Hemlholtz- Schichten zerstört. Das Helmholtz-Schicht-Modell kann jedoch mehr oder weniger gut für sehr hochkonzentrierte Elektrolyt-Lösungen angewendet werden. Das Gouy-Chapman-Modell berücksichtigt eine diffuse elektrische Doppelschicht, ähnlich wie auch die Debye-Hückel-Theorie die diffuse Hydrathülle eines Ions beschreibt. Es wird lediglich das einzelne Zentral-Ion durch eine unendliche, planare Elektrode ersetzt. Im Gouy-Chapman Modell befinden sich mehr Gegen-Ionen in der Nähe der Elektroden-Oberfläche als Co-Ionen. • • Debye-Hückel: Gegenseitige Wechselwirkung der Ionen einer Elektrolytlösung. Radialsymmetrische Geometrie Ionenwolke. Gouy-Chapman: Wechselwirkung zwischen fixierten Ionen einer Wand und Ionen einer angrenzenden Lösung. Ebene Geometrie Raumladungszone. Unter Voraussetzung kleiner Werte für 𝜑𝜑0 , resultiert aus der Gouy-Chapman-Theorie: |𝜑𝜑0 | ≪ 𝑅𝑅𝑅𝑅 ≈ 25𝑚𝑚𝑚𝑚 𝐹𝐹 → 𝜑𝜑(𝑥𝑥) = 𝜑𝜑0 ∙ 𝑒𝑒 𝑥𝑥 − 𝑙𝑙 𝐷𝐷 𝒍𝒍𝑫𝑫 ist der Abstand, in dem 𝝋𝝋 auf 1/e von 𝝋𝝋𝟎𝟎 abgefallen ist (Debye-Länge). Die Debye-Länge ist abhängig von der Konzentration des Elektrolyten und der Dielektrizitätskonstanten: 𝑙𝑙𝐷𝐷 = 1 𝜀𝜀𝜀𝜀0 𝑅𝑅𝑅𝑅 ∙� 𝐹𝐹 2𝑐𝑐 Für wässrige Lösungen (𝜀𝜀 = 80) bei RT: • • • • 𝑐𝑐 𝑐𝑐 𝑐𝑐 𝑐𝑐 = 0,001𝑀𝑀 → 𝑙𝑙𝐷𝐷 = 9,6𝑛𝑛𝑛𝑛 = 0,01𝑀𝑀 → 𝑙𝑙𝐷𝐷 = 3𝑛𝑛𝑛𝑛 = 0,1𝑀𝑀 → 𝑙𝑙𝐷𝐷 = 0,96𝑛𝑛𝑛𝑛 = 1𝑀𝑀 → 𝑙𝑙𝐷𝐷 = 0,3𝑛𝑛𝑛𝑛 Mit zunehmender Elektrolytkonzentration nimmt die Debye-Länge ab, sodass der beschriebene Abfall des elektrischen Potentials in kleineren Wandabständen vollzogen ist. Unter physiologischen Bedingungen (𝒄𝒄 ≈ 𝟎𝟎, 𝟏𝟏𝟏𝟏) resultiert 𝒍𝒍𝑫𝑫 ≈ 𝟏𝟏𝟏𝟏𝟏𝟏 (etwa 4-5 Schichten Wassermoleküle). Potentialverlauf für verschiedene Elektrolytkonzentrationen Es resultiert eine Überschussladung im Bereich der Grenzfläche! Probleme bei der Gouy-Chapman-Theorie: (1) Versagen bei hohen Elektrolytkonzentrationen. (2) Viel zu hohe Kapazitätswerte. (3) Anderer Kapazitätsverlauf bei größeren Potentialdifferenzen. Weder das Helmholtz- noch das Gouy-ChapmanModell ermöglichen eine gute Beschreibung der Struktur der elektrischen Doppelschicht. Während ersteres die Rigidität der lokalen Lösung zu sehr betont, vernachlässigt letzteres die rigide Struktur zu sehr. Beide Modelle werden daher im Stern-Modell kombiniert. Hier werden die Ionen, die der Elektrode am nächsten sind, in eine Helmholtz-Schicht gezwungen (lineare Abnahme des Potentials), während Ionen außerhalb dieser Schicht sich wie im Gouy-Chapman Modell verhalten (exponentielle Abnahme des Potentials). Somit resultiert für die Kapazität eine Reihenschaltung zweier Kapazitäten: 1 1 1 1 1 = 𝐻𝐻𝐻𝐻𝐻𝐻𝐻𝐻 + 𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺 = + 𝐴𝐴 𝐴𝐴 𝐶𝐶𝑑𝑑 𝐶𝐶𝑑𝑑 𝐶𝐶𝑑𝑑 𝜀𝜀0 𝜀𝜀𝐻𝐻𝐻𝐻𝐻𝐻𝐻𝐻 ∙ 𝜀𝜀0 𝜀𝜀𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺 ∙ 𝑑𝑑 𝑑𝑑 Eine weitere Verfeinerung stellt das Stern-Grahame-Modell dar, das die innere Helmholtz-Schicht mit berücksichtigt (über van-der-Waals Kräfte spezifisch adsorbierte Ionen und Wassermoleküle mit orientiertem Dipol). Die OHP enthält dann Ladungen mit demselben Vorzeichen wie die Elektrode bzw. mit entgegengesetztem Vorzeichen zur IHP. Dieses Modell ermöglicht die Beschreibung mittels drei verschiedener Werte für die Permitivität. In dielektrisch gesättigten, wässrigen Lösungen ist für die innere Schicht 𝜀𝜀 ≈ 6. In der äußeren Schicht ist das Feld wesentlich geringer (𝜀𝜀 ≈ 30). In der diffusen Gouy-Schicht wird eine Permittivität von 𝜀𝜀 ≈ 78, also die von reinem Wasser angenommen. Die Kapazität ergibt sich demnach aus der Reihenschaltung dreier Kapazitäten. Ionenstärke Wenn in der Lösung n verschiedene Ionensorten mit unterschiedlichen Wertigkeiten 𝑧𝑧𝑖𝑖 und zu unterschiedlichen Konzentrationen 𝑐𝑐𝑖𝑖 vorliegen, so muss in die Gouy-Chapman-Gleichung statt die Konzentration die Ionenstärke 𝑱𝑱 eingesetzt werden. 𝐽𝐽 ist eine mittlere Konzentration, bei der die Ionensorten entsprechend dem Quadrat ihrer Wertigkeit gewichtet werden. 𝒏𝒏 𝟏𝟏 𝑱𝑱 = � 𝒛𝒛𝟐𝟐𝒊𝒊 𝒄𝒄𝒊𝒊 𝟐𝟐 𝒊𝒊=𝟏𝟏 Grundgleichungen der Elektrostatik (gelten für Punktladungen) 𝟏𝟏 𝒒𝒒𝟏𝟏 𝒒𝒒𝟐𝟐 �⃗ 𝒓𝒓 �⃗| 𝟒𝟒𝟒𝟒𝜺𝜺𝟎𝟎 𝒓𝒓𝟐𝟐 |𝒓𝒓 𝟏𝟏 𝒒𝒒𝟏𝟏 𝒒𝒒𝟐𝟐 𝟒𝟒𝟒𝟒𝜺𝜺𝟎𝟎 𝒓𝒓 �𝑭𝑭⃗𝑪𝑪 (𝒓𝒓 �⃗) = −𝒈𝒈𝒈𝒈𝒈𝒈𝒈𝒈�𝑼𝑼(𝒓𝒓 �⃗)� = �𝑬𝑬⃗(𝒓𝒓 �⃗)𝒒𝒒𝟐𝟐 = �⃗) = 𝑼𝑼(𝒓𝒓 �⃗ 𝒓𝒓 �⃗′ )𝒅𝒅𝒓𝒓 �⃗′ − ∫𝒓𝒓�⃗ �𝑭𝑭⃗(𝒓𝒓 𝟎𝟎 ��⃗(𝒓𝒓 �⃗)𝒒𝒒𝟐𝟐 = = 𝝋𝝋 �𝑭𝑭⃗ 𝒒𝒒𝟏𝟏 �⃗ 𝒓𝒓 𝟐𝟐 �⃗| 𝟎𝟎 𝒓𝒓 |𝒓𝒓 𝟏𝟏 𝒒𝒒𝟏𝟏 𝟒𝟒𝟒𝟒𝜺𝜺𝟎𝟎 𝒓𝒓 𝟏𝟏 �⃗(𝒓𝒓 �⃗) = −𝒈𝒈𝒈𝒈𝒈𝒈𝒈𝒈�𝝋𝝋 ��⃗(𝒓𝒓 �⃗)� = 𝑪𝑪 = 𝑬𝑬 𝒒𝒒 𝟒𝟒𝟒𝟒𝜺𝜺 ��⃗(𝒓𝒓 �⃗) = 𝝋𝝋 �⃗ 𝒓𝒓 �⃗′ )𝒅𝒅𝒓𝒓 �⃗′ − ∫𝒓𝒓�⃗ �𝑬𝑬⃗(𝒓𝒓 𝟎𝟎 = 𝟐𝟐 �⃗) 𝑼𝑼(𝒓𝒓 𝒒𝒒𝟐𝟐 = Ionenkonzentration in der Nähe einer geladenen Wand Die in der Nähe der Wand befindlichen Ionen besitzen je nach Vorzeichen ihrer Ladung eine erhöhte oder erniedrigte potentielle Energie: 𝑈𝑈(𝑥𝑥) = 𝑞𝑞 ∙ 𝜑𝜑(𝑥𝑥), 𝑞𝑞 = 𝑧𝑧𝑧𝑧 Nach der Boltzmann-Verteilung gilt für das Verhältnis zwischen Konzentrationen derselben Ionensorte mit einer spezifischen Energiedifferenz: 𝑈𝑈 −𝑈𝑈 𝑐𝑐2 − 2 1 = 𝑒𝑒 𝑘𝑘 𝐵𝐵 𝑇𝑇 𝑐𝑐1 Die eine Ionen-Population befindet sich hinreichend weit von der Membran entfernt, sodass 𝜑𝜑(𝑥𝑥) bereits auf null gesunken ist, wodurch auch 𝑈𝑈(𝑥𝑥) = 𝑈𝑈1 = 0 (aufgrund der kleinen Debye-Länge kann so ein Abstand leicht in der Zelle erreicht werden; der Grenzwert 𝑥𝑥 → ∞ muss nicht vorliegen). Die Konzentration dieser Ionen-Population sei 𝑐𝑐1 = 𝑐𝑐. Sowohl Anionen als auch Kationen liegen in gleicher Konzentration vor (Ionen-Population ist hinreichend weit von der Membran entfernt). Für die zweite Ionen-Population wird 𝑼𝑼𝟐𝟐 = 𝑼𝑼(𝒙𝒙) gesetzt. Hier müssen die Konzentrationen von Anionen und Kationen getrennt betrachtet werden. Für einwertige Anionen bzw. Kationen gilt dann 𝑈𝑈(𝑥𝑥) = −𝑒𝑒𝑒𝑒(𝑥𝑥) bzw. 𝑈𝑈(𝑥𝑥) = +𝑒𝑒𝑒𝑒(𝑥𝑥). Mithilfe der Boltzmann-Verteilung können für Anionen und Kationen getrennt die Konzentrationsverhältnisse zwischen den Energieniveaus 𝑈𝑈1 = 0 und 𝑈𝑈2 = ±𝑒𝑒𝑒𝑒(𝑥𝑥) berechnet werden. 𝑒𝑒𝑒𝑒 (𝑥𝑥) 𝑐𝑐+ (𝑥𝑥) − = 𝑒𝑒 𝑘𝑘 𝐵𝐵 𝑇𝑇 𝑐𝑐 𝑒𝑒𝑒𝑒 (𝑥𝑥) 𝑐𝑐− (𝑥𝑥) = 𝑒𝑒 𝑘𝑘 𝐵𝐵 𝑇𝑇 𝑐𝑐 𝑭𝑭𝑭𝑭(𝒙𝒙) 𝑹𝑹𝑹𝑹 𝒄𝒄+ (𝒙𝒙) = 𝒄𝒄𝒆𝒆− 𝒄𝒄− (𝒙𝒙) = 𝒄𝒄𝒆𝒆 𝑭𝑭𝑭𝑭(𝒙𝒙) 𝑹𝑹𝑹𝑹 Bei einer positiv geladenen Wand (also: 𝜑𝜑(𝑥𝑥) > 0 für alle Abstände x, außer im Unendlichen) ist die Kationenkonzentration in Wandnähe erniedrigt (𝑐𝑐+(𝑥𝑥) < 𝑐𝑐, da e-Funktion < 1). Die negative Überschussladung kompensiert die fixierten positiven Ladungen der Wand. Eine Folgerung ist, dass an einer elektrisch geladenen Grenzfläche der pH-Wert verschieden ist vom pH-Wert der Lösung. Scheinbares Paradoxon: Innerhalb einer elektrisch leitenden Phase (Wand-nahe Elektrolytlösung) ist ein elektrisches Feld vorhanden (𝑈𝑈𝑥𝑥 = −𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑), ohne dass gleichzeitig ein Strom fließt (kein NettoLadungsfluss). Erklärung: Der Feld-induzierte Ladungstransport (Gegen-Ionen in Richtung der Elektrode, Co-Ionen in entgegengesetzter Richtung) wird durch Diffusion der Kationen und Anionen entlang ihres Konzentrationsgradienten 𝒅𝒅𝒄𝒄+ /𝒅𝒅𝒅𝒅 und 𝒅𝒅𝒄𝒄− /𝒅𝒅𝒅𝒅 kompensiert. Es stellt sich somit ein Gleichgewicht ein, das durch die entsprechenden Ionen-Konzentrationen in jedem beliebigen Abstand zur Elektrode definiert ist. Potential- und Konzentrationsgradient sind an jeder Stelle sowohl für Kation als auch für Anion betragsmäßig gleich groß (unterschiedliches Vorzeichen), sodass die Nernst-Planck-Gleichung gleich 0 ist 𝑑𝑑𝑐𝑐𝑖𝑖 𝐹𝐹 𝑑𝑑𝑑𝑑 Φ𝑖𝑖 = −𝐷𝐷𝑖𝑖 � + 𝑧𝑧𝑖𝑖 𝑐𝑐𝑖𝑖 ∙ ∙ � = 0, 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑: 𝑑𝑑𝑐𝑐𝑖𝑖 𝐹𝐹 𝑑𝑑𝑑𝑑 = −𝑧𝑧𝑖𝑖 𝑐𝑐𝑖𝑖 ∙ ∙ 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 In den Gleichungen für c(x) geht daher das Verhältnis der Energie des E-Feldes (Ladung mal elektrisches Potential durch Elektrode) und der thermischen Energie kBT (Ursache der Brownschen Molekularbewegung und damit der Diffusion) ein. Zusammenhang zwischen Flächenladungsdichte und Grenzflächenpotential Die Anzahl der auf der Wand fixierten elektrischen Ladungen (Flächenladungsdichte 𝝈𝝈 [𝐶𝐶𝑚𝑚−2 ]) bestimmt das Grenzflächenpotential 𝝋𝝋𝟎𝟎 . Die Ladungsdichte ist durch die Struktur der Grenzfläche und den pH-Wert der Lösung vorgegeben und ist konstant bei Variation der Ionenstärken. Eine elektrische Doppelschicht kann durch einen Plattenkondensator dargestellt werden. Die elektrischen Feldlinien entspringen aus positiven Ladungen und enden auf gleich vielen negativen Ladungen. Die Dichte der Feldlinien ist damit bei den Gegen-Ionen in Lösung und dem Plattenkondensator für dieselbe Flächenladungsdichte identisch, sofern ein unmittelbar an die Wand angrenzendes Gebiet der Lösung betrachtet wird (d.h. für 𝐸𝐸𝑥𝑥 = −𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 Feldstärke bei x=0 einsetzen). Die Flächenladungsdichte ist allgemein über definiert. 𝜎𝜎 = 𝑄𝑄 𝐴𝐴 • Für eine Membran (Plattenkondensator) folgt dann mit der E-Feldstärke 𝐸𝐸 = (Q ist der Betrag der Ladung auf einer Platte) für die Flächenladungsdichte 𝑑𝑑𝑑𝑑 𝜎𝜎 = 𝜀𝜀𝜀𝜀0 𝐸𝐸𝑥𝑥 = 𝜀𝜀𝜀𝜀0 � 𝑑𝑑𝑑𝑑 � 𝑥𝑥=0 𝑈𝑈 𝑑𝑑 = 𝑄𝑄 𝜀𝜀𝜀𝜀 0 𝐴𝐴 . • Für eine Flächenladung (gleichmäßig geladene, ausgedehnte dünne Platte) würde mit der • E-Feldstärke 𝐸𝐸 = 𝑄𝑄 2𝜀𝜀𝜀𝜀 0 𝐴𝐴 für die Flächenladungsdichte folgen: 𝜎𝜎 = 2𝜀𝜀𝜀𝜀0 𝐸𝐸𝑥𝑥 . Für einen Kugelkondensator (z.B. Vesikel) würde gelten: 𝐸𝐸 = Herleitung der Beziehung zwischen Grenzflächenpotential und Ladungsdichte: (1) (2) (3) (4) (5) − 𝑄𝑄 4𝜋𝜋𝑟𝑟 2 𝜀𝜀𝜀𝜀 0 => 𝜎𝜎 = 4𝜋𝜋𝜋𝜋𝜀𝜀0 𝐸𝐸𝑥𝑥 . x Für φ(x) die Gouy-Chapman-Gleichung (φ(x) = φ0 ∙ e l D ) einsetzen, Nach x differenzieren, 𝑥𝑥 = 0 setzen, sodass die e-Funktion 1 wird, nach 𝜑𝜑0 auflösen; rechts wurde Debye-Länge eingesetzt und die Konstanten zusammengefasst: 𝜑𝜑0 = 𝜎𝜎𝑙𝑙𝐷𝐷 𝜎𝜎 𝑅𝑅𝑅𝑅 𝜎𝜎 = ∙� = 𝐾𝐾 ∙ 𝜀𝜀𝜀𝜀0 𝐹𝐹 2𝜀𝜀𝜀𝜀0 𝐽𝐽 �𝐽𝐽 Bei gegebener Ladungsdichte nimmt das Grenzflächenpotential mit zunehmender Ionenstärke ab. Ähnlich verkleinert sich auch mit zunehmender Ionenstärke der Bereich des Abfalls von 𝜑𝜑(𝑥𝑥) (mehr Ionen in Lösung, weniger Einfluss einer geladenen Membran in einer bestimmten Entfernung). Der Abfall des Potentials wird durch die Debye-Länge bestimmt. Das Grenzflächenpotential ist unabhängig von der Debye-Länge (Permitivität steht im Nenner!). Verlauf der elektrischen Feldstärke Die Bewegung wird quantitativ durch die elektrische Kraft 𝐾𝐾𝑥𝑥,𝑖𝑖 = 𝑧𝑧𝑖𝑖 𝑒𝑒𝐸𝐸𝑥𝑥 = −𝑧𝑧𝑖𝑖 𝑒𝑒 ein Teilchen der Ladung 𝑧𝑧𝑖𝑖 𝑒𝑒 wirkt und von der geladenen Membran herrührt. • • 𝐸𝐸𝑥𝑥 = − 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 bestimmt, die auf 𝑥𝑥 𝑥𝑥 𝑑𝑑𝑑𝑑 1 𝜎𝜎 − − = −𝜑𝜑0 ∙ 𝑒𝑒 𝑙𝑙 𝐷𝐷 ∙ �− � = ∙ 𝑒𝑒 𝑙𝑙 𝐷𝐷 𝑑𝑑𝑑𝑑 𝑙𝑙𝐷𝐷 𝜀𝜀𝜀𝜀0 Damit ist die elektrische Feldstärke 𝑬𝑬𝒙𝒙 (𝒙𝒙 = 𝟎𝟎) = 𝝈𝝈 𝜺𝜺𝜺𝜺𝟎𝟎 an der Membran unabhängig von der Ionenstärke, im Gegensatz zum elektrischen Potential an der Membran (Grenzflächenpotential). Für 𝒙𝒙 > 0 nimmt die elektrische Feldstärke jedoch mit zunehmender Ionenstärke ab, wobei die Abnahme durch die Debye-Länge bestimmt wird (wie beim Potentialverlauf). Der elektrische Potentialverlauf durch eine BLM Eine BLM ist für kleine anorganische Ionen nahezu impermeabel, da aufgrund des hydrophoben Membraninneren (𝜀𝜀 = 2) ein relativ großer Potentialberg überwunden werden muss. Der Verlauf des Potentials ist maßgeblich vom Grenzflächenpotential nach dem Gouy-Chapman-Modell (beeinflusst duch hydrophile Kopfgruppen) und der Born-Energie (Potentialberg im Zentrum der Membran) abhängig. Zudem spielt u.a. der Bildpunktladungseffekt eine Rolle (negative Punktladung erzeugt durch Dipol-Dipol-WW eine positive Bildladung an der Membran, was zu einer attraktiven WW führt). Die Abbildung zeigt die Summe aller Beiträge. Die Lage der Minima sind abhängig von Größe, Ladung und chemischer Struktur des Ions. Der Potentialberg wird maßgeblich durch die BornEnergie beschrieben: 𝑊𝑊𝐵𝐵 (𝑟𝑟) = Anwendungsbeispiele • 𝑧𝑧 2 𝑒𝑒 2 1 1 ∙� − � 8𝜋𝜋𝜀𝜀0 𝑟𝑟 𝜀𝜀𝑀𝑀 𝜀𝜀𝐻𝐻2 𝑂𝑂 Cyctochrom c ist (wie die meisten peripheren Membranproteine) über elektrostatische Wechselwirkung an die negativ geladene innere mitochondriale Membran gebunden. Durch Waschen mit konzentrierten Salzen wie NaCl (Ionenstärke wird erhöht) kann das Protein von der Membran gelöst werden. Man spricht von milden Bedingungen. Im Gegensatz dazu müssen integrale Proteine durch Zerstörung der Membranstruktur über Behandlung mit Detergentien gelöst werden (harte Bedingungen). • Zwei Proteine mit gleicher Oberflächen-Nettoladung stoßen sich in Lösung ab, wenn sich die Raumladungszonen an Gegen-Ionen durchdringen. Die Dicke der Ionenwolke ist etwa gleich der Debye-Länge und nimmt daher mit zunehmender Ionenstärke ab. Bei hohen Elektrolytkonzentrationen können die Anziehungskräfte überwiegen (geringe Ionenwolke) und Protein-Aggregation erfolgen. Elektrophorese Elektrophorese ist die Wanderung großer geladener Teilchen (Proteine, Zellen) unter dem Einfluss eines elektrischen Feldes. Die Wanderungsgeschwindigkeit ist von der Teilchenladung abhängig (Prinzip der Trennmethode). Das elektrische Feld wirkt nicht nur auf die geladenen Teilchen selbst, sondern auch auf die Raumladungswolke an Gegenionen. Ohne Berücksichtigung der Gegenionen würde die Wanderungsgeschwindigkeit nach Einschalten des Feldes schnell eine konstante Geschwindigkeit 𝑣𝑣𝑚𝑚𝑚𝑚𝑚𝑚 erreichen (siehe Viskosität, 𝑢𝑢 = 𝑞𝑞/𝑓𝑓 ist die Beweglichkeit, 𝐾𝐾 = 𝑞𝑞𝑞𝑞 die Kraft auf das Teilchen durch das elektrische Feld 𝐸𝐸, 𝑞𝑞 = 𝑧𝑧𝑧𝑧 die Ladung des Teilchens, 𝑓𝑓 der Reibungskoeffizient): 𝑣𝑣⃗ (𝑡𝑡) = �⃗ �⃗ 𝑞𝑞𝐸𝐸�⃗ 𝑓𝑓𝑓𝑓 𝐾𝐾 𝐾𝐾 �1 − 𝑒𝑒 − 𝑚𝑚 � → 𝑣𝑣⃗𝑚𝑚𝑚𝑚𝑚𝑚 = = = 𝑢𝑢𝐸𝐸�⃗ 𝑓𝑓 𝑓𝑓 𝑓𝑓 Diese Geschwindigkeit ist bei Annahme eines kugelförmigen Körpers (Stokes-Gesetz: 𝑓𝑓 = 6𝜋𝜋𝜋𝜋𝜋𝜋) nur von der Ladung der Teilchen 𝑞𝑞, ihrem Radius 𝑟𝑟 und der Viskosität 𝜂𝜂 des Mediums abhängig (abgesehen von der elektrischen Feldstärke, der Ursache der Bewegung xD). Berücksichtigung der Gegenionen: Das Teilchen und die entgegengesetzt geladene Ionenwolke (diffuse Gouy-Chapman Schicht) wandern im elektrischen Feld in eine entgegengesetzte Richtung. Die Ionenwolke wird dabei an der Vorderseite des Teilchens stetig neu gebildet. Dadurch kommt es zu einer hydrodynamischen Bremsung des Teilchens durch die Ionenwolke. Die Wanderungsgeschwindigkeit ist von der Form des Teilchens abhängig, was die Bestimmung der elektrophoretischen Wanderungsgeschwindigkeit ebenso erschwert. Das Ergebnis wird unter der folgenden Prämisse einfach: Der kleinste Krümmungsradius des Teilchens (im Bereich der stärksten Krümmung der Teilchenform zu suchen) muss größer als die Debye-Länge (Dicke der Doppelschicht) sein. Diese Bedingung ist nur für große Teilchen wie Zellen [µm] erfüllt, nicht aber für Proteine [nm]. Die Geschwindigkeit steigt dann linear mit der Debye-Länge, da bei kleiner Debye-Länge die Ionenwolke enger an dem Teilchen anliegt, wodurch eine stärkere hydrodynamische Bremsung resultiert. • • 𝑣𝑣⃗ = 𝜎𝜎𝐸𝐸 𝑙𝑙𝐷𝐷 𝐸𝐸�⃗ 𝜂𝜂 �⃗/𝜼𝜼 ist hier ebenso gegeben, wie in der Gleichung ohne �⃗~𝑬𝑬 Die Proportionalität 𝒗𝒗 Berücksichtigung der Ionenwolke. Die Abhängigkeit vom Radius 𝑟𝑟 des Teilchens fehlt völlig. Statt der Ladung 𝑞𝑞, taucht hier die elektrophoretisch wirksame Ladungsdichte 𝝈𝝈𝑬𝑬 auf. Sie unterscheidet sich von der eigentlichen Ladungsdichte 𝜎𝜎, weil Oberflächenrauigkeiten einen Teil der Gegenionen bei der Wanderung des Teilchens mitschleppen (entspricht HelmholtzSchicht) – Der Absolutbetrag von 𝝈𝝈 sinkt. In Analogie zur Beziehung zwischen Ladungsdichte 𝜎𝜎 und Grenzflächenpotential 𝜑𝜑0 führt man das Zeta-Potential 𝝃𝝃 ein, das 𝜎𝜎𝐸𝐸 statt 𝜎𝜎 enthält. Der Unterschied zwischen dem Zeta-Potential und dem Grenzflächenpotential entspricht dem Beitrag der mitgeführten Flüssigkeitsschicht (HelmholtzSchicht). Mit dem Zeta-Potential lässt sich die Geschwindigkeits-Gleichung umformulieren: 𝜑𝜑0 = 𝝃𝝃 = → 𝑣𝑣⃗ = 𝜎𝜎𝑙𝑙𝐷𝐷 𝜀𝜀𝜀𝜀0 𝝈𝝈𝑬𝑬 𝒍𝒍𝑫𝑫 𝜺𝜺𝜺𝜺𝟎𝟎 𝜀𝜀𝜀𝜀0 𝜉𝜉 𝐸𝐸�⃗ 𝜂𝜂 Die neue Gleichung für die Geschwindigkeit kann zur Bestimmung des Zeta-Potentials herangezogen werden. Dadurch ist die effektive Ladungsdichte bestimmbar. Die reale Ladungsdichte ist experimentell nicht zugänglich! Das Zeta-Potential charakterisiert die Abstoßungsenergie zwischen den Teilchen. Eine Erhöhung des Zeta-Potentials steigert die Intermolekularen Abstoßungskräfte, wodurch die Aggregationsfähigkeit vermindert ist. Summary: Die bei Bewegung der Partikel in der Flüssigkeit auftretenden Scherkräfte beeinflussen die fest an die Oberfläche gebundene Helmholtz-Schicht nicht! Die Helmholtz-Schicht definiert die Scherebene. Diese definiert damit die elektrophoretisch wirksame Ladungsdichte 𝝈𝝈𝑬𝑬 und das Zeta- Potential. Die hydrodynamische Bremsung kommt lediglich durch die Neubildung der diffusen Gouy-Chapman-Schicht zustande, wodurch die veränderte Geschwindigkeitsbeziehung resultiert. Gelelektrophorese ignoriert. S.340 Kapitel 9: Biologische Membranen Membranen bilden eine passive Barriere für viele Substanzen, steuern selektiv den Durchtritt einzelner Verbindungen und ermöglicht die asymmetrische Orientierung von Proteinen und Lipiden, die wesentlich zur Funktion beitragen. Fettsäuren mit einem hydrophoben Schwanz bilden Micellen, Lipide mit zwei hydrophoben Schwänzen bilden Doppelschichten. Hydrophobe Wechselwirkung Der Hydrophobe Effekt (=Hydrophobe Wechselwirkung) führt zur Selbstaggregation von hydrophoben Molekülen in wässriger Lösung aufgrund der starken Wechselwirkung zwischen Wassermolekülen. Das Verteilungsgleichgewicht von n-Alkanen zwischen Wasser und einem apolaren Lösungsmittel wird über den Verteilungskoeffizienten γ angegeben, wobei 𝑐𝑐𝑤𝑤 die Alkan-Konzentration in Wasser und 𝑐𝑐𝑎𝑎 die Alkan-Konzentration im apolaren Lömi ist. 𝛾𝛾 = Δ𝐺𝐺 0 𝑐𝑐𝑎𝑎 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 𝑐𝑐𝑤𝑤 𝚫𝚫𝑮𝑮𝟎𝟎 ist die Änderung der freien Enthalpie bei der Überführung von 1 mol n-Alkan aus Wasser in das apolare Lömi unter Standardbedingungen. 𝚫𝚫𝑮𝑮𝟎𝟎 hängt linear von der Zahl 𝒗𝒗 der C-Atome im Alkan ab: Δ𝐺𝐺 0 = ΔH0 − 𝑇𝑇ΔS0 = −𝐴𝐴 − 𝐵𝐵𝐵𝐵, (𝐴𝐴, 𝐵𝐵 = 𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘. > 0, 𝑣𝑣 ≥ 4) 𝚫𝚫𝑮𝑮𝟎𝟎 ist negativ und wird mit jeder CH2-Gruppe des Alkans um etwa 4kJ/mol negativer, sodass der Übergang in die apolare Phase begünstigt ist. Der Verteilungskoeffizient 𝑐𝑐𝑎𝑎 /𝑐𝑐𝑤𝑤 wird damit für jede CH2-Gruppe um einen konstanten Faktor größer. Die Bestimmung von ΔH 0 aus der Temperaturabhängigkeit von 𝛾𝛾 ergibt für kleine Kettenlängen sogar positive Werte (Butan: 3,4 kJ/mol), sodass der Prozess nicht enthalpisch getrieben sein kann. In der Umgebung einer CH-Kette haben die Wassermoleküle eine erhöhte Ordnung. Entzieht sich die CH-Kette dem Kontakt mit Wasser, bricht dieser Ordnungszustand zusammen und die Entropie nimmt zu (treibende Kraft für Membran-Bildung und Proteinfaltung). H-Brücken im Wasser werden von der Größe der hydrophoben Moleküle beeinflusst: • • Kleine unpolare Moleküle bewirken kaum ein Aufbrechen der H-Brücken zwischen Wassermolekülen. Es resultiert lediglich Umorientierung der Wassermoleküle. Bei großen unpolaren Molekülen ist das Aufrechterhalten des Wassernetzwerkes nicht mehr möglich. Die Anzahl der H-Brücken wird reduziert. Die Entropie ist Es wird angenommen, dass Wasser um hydrophobe Moleküle in einem höher geordneten Zustand vorliegen. Man spricht von Clathrat-Hydraten (Käfigartige Struktur aus Wassermolekülen um ein „Gastmolekül“). Für große hydrophobe Moleküle resultiert eine dünne wasserfreie „VakuumSchicht“ an der Oberfläche („trockene Schicht“). Kleine Moleküle sind „nass“ (Dichte von Wasser an deren Oberfläche erhöht). Van-der-Waals-Kräfte bewirken die Verminderung des Trocknungseffekts und damit eine Destabilisierung der Clathrat-Hydrate. Der HE wird dominiert durch Entropie bei RT und Enthalpie bei höherer Temperatur! • • Enthalpie: bei steigender Temperatur werden die H-Brücken schwächer. Entropie: durch höhere Temperatur erfolgt Ausdehnung des Wassernetzwerkes, was zur Zunahme des freien Volumens für hydrophobe Moleküle führt. Der Graph zeigt Δ𝐺𝐺/4𝜋𝜋𝑅𝑅 2 gegen den Molekülradius. Für kleine Moleküle ist der hydrophobe Effekt damit stärker als für große. • • Für kleine Moleküle steigt Δ𝐺𝐺 linear mit dem Volumen des Teilchens an (Δ𝐺𝐺~𝑅𝑅 3 ; im Graph lineare Steigung für kleine R). Für große Moleküle steigt Δ𝐺𝐺 linear mit der Oberfläche des Teilchens an (Δ𝐺𝐺~4𝜋𝜋𝑅𝑅 2 𝛾𝛾 mit der Oberflächenspannung 𝛾𝛾). Enthalpie und Entropie haben für kleine und große Teilchen unterschiedlichen Einfluss: • • Kleine Teilchen: Entropie dominiert Große Cluster: Enthalpie dominiert. Ab kritischer Größe sind Cluster energetisch günstiger als einzelne Teilchen. Δ𝐺𝐺 steigt mit Temperatur hydrophober Effekt nimmt zu. • • Bei Kälte bildet Wasser mehr H-Brücken, sodass die Entropie per se schon gering ist (durch Hydrophoben Stoff werden H-Brücken nicht erhöht). Der Entropiegewinn bei einer Verkleinerung hydrophober Oberflächen ist damit minimal (Kältedenaturierung). Bei warmen Wasser sind weniger H-Brücken vorhanden, da ungeordnetere Zustände. Die Entropie wird damit durch hydrophobe Stoffe (Ausbildung von H-Brücken zwischen Wasser und hydrophobem Stoff) verringert. Durch Aggregation der hydrophoben Stoffe wird die Entropie wieder stark erhöht, was die Ausbildung von Membranen und Proteinfaltung bei RT begünstigt. Die Verteilungsfunktion (pcf) beschreibt die Abhängigkeit der freien Energie von dem Abstand der hydrophoben Moleküle (genauso auch für interagierende Ionen) unter Berücksichtigung der Größe der Hydrathülle (𝑤𝑤(𝑟𝑟)~Δ𝐺𝐺 0 ). Eigenschaften der Plasmamembran Geometrische Dimensionen Der Abstand der polaren Gruppen von C16 und C18 Fettsäureketten beträgt ca. 4 nm. Die voll gestreckte Länge zweier C18 Ketten beträgt jedoch 2*18*0,125 = 4,5 nm. Die Differenz kommt daher, dass die Ketten bei physiologischen Temperaturen nicht völlig gestreckt und parallel vorliegen. Die Gesamtdicke der Plasmamembran ist durch an- und eingelagerte Proteine auf 6-10 nm erhöht. Je nach Dicke des hydrophoben Protein-Bereichs eines Membranproteins kann die Dicke der Membran über die Lipid-Zusammensetzung angepasst werden. Phosphatidylcholin ist für gerade Membranflächen – Phosphoatidylethanolamin für stark gekrümmte Membranflächen geeignet. Membranfluidität Bei physiologischen Temperaturen liegt die Membran in einem flüssig-kristallinen Zustand vor. Dies ermöglicht schnelle Diffusion: Die laterale Platzwechselzeit liegt bei 𝟏𝟏𝟏𝟏−𝟕𝟕 𝒔𝒔 (Zeit, die zwei Lipide im Mittel benötigen, aufgrund der thermischen Bewegung ihre Plätze zu tauschen). Dies entspricht einem Diffusionskoeffizienten der Lipidmoleküle in der Membranebene von 𝑫𝑫 = 𝟏𝟏𝟏𝟏−𝟖𝟖 − 𝟏𝟏𝟏𝟏−𝟕𝟕 𝒄𝒄𝒎𝒎𝟐𝟐 𝒔𝒔−𝟏𝟏 . Die transversale Austauschzeit zwischen den Monoschichten der Doppelschicht besitzt Größenordnungen von mindestens Stunden oder Tagen. Die Diffusion von Membranproteinen kann über Markierung von Membranarealen mit fluoreszierenden Antikörpern und anschließender zeitabhängiger Messung der Ausdehnung des fluoreszierenden Membranflecks bestimmt werden. Der Fleck hat sich nach einer Zeit 𝝉𝝉 auf den Durchmesser 𝟐𝟐𝟐𝟐 vergrößert. Der Diffusionskoeffizient kann dann ermittelt werden über 𝑫𝑫 = 𝒂𝒂𝟐𝟐 /𝟐𝟐𝟐𝟐 , woraus Werte im Bereich 𝑫𝑫 ≈ 𝟏𝟏𝟏𝟏−𝟗𝟗 𝒄𝒄𝒎𝒎𝟐𝟐 𝒔𝒔−𝟏𝟏 resultieren. In Wasser würde für ein Protein ähnlicher Größe ein 100-1000fach größerer Diffusionskoeffizient resultieren. Einige Proteine sind jedoch mit dem Zytoskelett verbunden und nicht frei diffusibel. Elektrische Eigenschaften: Ersatzschaltbild Das Innere einer Lipid-Doppelschicht (CH-Ketten) entspricht einem Medium mit hohem elektrischen Widerstand R, das zwei Elektrolytlösungen mit niedrigem Widerstand voneinander trennt. Membran und Elektrolytlösungen sind ein Plattenkondensator der Kapazität C: Die elektrisch leitenden Lösungen entsprechen den Metallplatten, die durch das Membraninnere als Dielektrikum niedriger Leitfähigkeit voneinander getrennt sind. Der tatsächliche Widerstand der Membran wird durch Ionenkanäle bestimmt. Elektrischer Widerstand Der elektrische Widerstand 𝑹𝑹 = 𝑼𝑼 𝑰𝑰 einer Membran ist umgekehrt proportional zur Membranfläche A (Widerstand sinkt für größere Membran). Der spezifische Membranwiderstand 𝑹𝑹𝒎𝒎 = 𝑹𝑹 ∙ 𝑨𝑨 [Ω𝑐𝑐𝑚𝑚2 ] ist auf die Membranfläche normiert. Membranleitfähigkeit 𝒈𝒈 = 𝟏𝟏/𝑹𝑹 und spezifische Membranleitfähigkeit 𝒈𝒈𝒎𝒎 = 𝟏𝟏/𝑹𝑹𝒎𝒎 sind die entsprechenden reziproken Werte. Im Vergleich zu 𝑔𝑔𝑚𝑚 [𝑆𝑆𝑆𝑆𝑚𝑚−2 ] bezieht sich die elektrische Leitfähigkeit homogener Lösungen 𝜆𝜆 auf die Einheitszelle (Einheit: 𝑆𝑆𝑆𝑆𝑚𝑚−1 ). Bei genügend großen Zellen kann 𝑅𝑅 durch Einführen einer Mikroelektrode direkt ermittelt werden: gemessen wird die aus einer Spannungsänderung Δ𝑈𝑈 resultierende Stromänderung Δ𝐼𝐼. Alternative ist die patch-clamp Technik. Die 𝑹𝑹𝒎𝒎 -Werte verschiedener Zellmembranen liegen bei 𝟏𝟏 − 𝟏𝟏𝟏𝟏𝟓𝟓 𝛀𝛀𝒄𝒄𝒎𝒎𝟐𝟐 . Bei künstlichen, Proteinfreien Lipiddoppelschichten ist 𝑹𝑹𝒎𝒎 ≈ 𝟏𝟏𝟏𝟏𝟖𝟖 𝛀𝛀𝒄𝒄𝒎𝒎𝟐𝟐 (in 0,1M NaCl). Die Lipide tragen damit maßgeblich zum Widerstand bei, während die Proteine die Leitfähigkeit erhöhen. In Anbetracht der geringen Membrandicken handelt es sich in allen Fällen um extrem hohe Widerstände. So hat eine 0,1 M NaCl Lösung der Dicke einer Membran einen Widerstand von 𝑹𝑹𝒎𝒎 ≈ 𝟏𝟏𝟏𝟏−𝟒𝟒 𝛀𝛀𝒄𝒄𝒎𝒎𝟐𝟐 . Im Vergleich zu einer gleich dicken wässrigen Lösung ist der Widerstand der Membran um den Faktor 104 − 109 höher. Die Eigenschaft eines Widerstandes wird über lineare IV-Kennlinien dargestellt. Elektrische Kapazität elektrische Kapazität C spezifische Membrankapazität 𝐶𝐶 = 𝜀𝜀𝜀𝜀0 𝐴𝐴 [µ𝐹𝐹] 𝑑𝑑 𝜀𝜀𝜀𝜀0 ≈ 0,44µ𝐹𝐹𝐹𝐹𝑚𝑚−2 𝑑𝑑 [µ𝐹𝐹𝐹𝐹𝑚𝑚−2 = 10−6 𝐶𝐶𝑉𝑉 −1 𝑐𝑐𝑚𝑚−2 ] 𝐶𝐶𝑚𝑚 = 𝜀𝜀0 = 8,85 ∙ 10−12 𝐶𝐶𝑉𝑉 −1 𝑚𝑚−1 𝜀𝜀 = 2 für CH-Kette 𝐴𝐴 = Membranfläche 𝑑𝑑 = Membrandicke (4nm) Achtung! Theoretischer Wert weicht vom gemessenen (1µ𝐹𝐹𝐹𝐹𝑚𝑚−2 ) ab! Die Membrankapazität kann bestimmt werden, indem zum Zeitpunkt t=0 ein konstanter Strom zwischen den beiden Stromelektroden eingeschaltet wird und die zeitliche Veränderung der Potentialdifferenz U(t) zwischen den beiden Spannungselektroden mithilfe eines Oszillographen verfolgt wird. Die Membran hat gleichzeitig einen Widerstand und eine Kapazität, sodass diese im Ersatzschaltbild parallel geschaltet sind. Wird zur Zeit 𝑡𝑡 = 0 der Strom 𝐼𝐼 eingeschaltet, so steigt die Spannung von 𝑈𝑈 = 0 allmählich auf den Endwert 𝑉𝑉∞ = 𝐼𝐼𝐼𝐼 an. Der verzögerte Anstieg der Spannung resultiert aus der Aufladung der Membrankapazität 𝐶𝐶 mit der Ladung 𝑄𝑄 = 𝐶𝐶𝑉𝑉∞ . 𝑈𝑈(𝑡𝑡) = 𝐼𝐼𝐼𝐼 �1 − 𝑒𝑒 𝑡𝑡 − 𝜏𝜏 𝑚𝑚 �, 𝑅𝑅𝑚𝑚 𝜏𝜏𝑚𝑚 = 𝑅𝑅𝑅𝑅 = � ∙ 𝐶𝐶𝑚𝑚 𝐴𝐴� = 𝑅𝑅𝑚𝑚 𝐶𝐶𝑚𝑚 𝐴𝐴 𝜏𝜏𝑚𝑚 ist die Zeit, nach der der Endwert 𝑉𝑉∞ = 𝐼𝐼𝐼𝐼 bis auf 1/e erreicht ist. Sie wird auch RC-Zeit genannt (Vergleiche RC-Zeit bei BLM) • • • Der Widerstand kann aus der Messung von 𝑉𝑉∞ und dem eingestellten Strom 𝐼𝐼 aus 𝑉𝑉∞ = 𝐼𝐼𝐼𝐼 berechnet werden. Die Kapazität kann aus der gemessenen Zeitkonstanten und dem berechneten Widerstand über 𝜏𝜏𝑚𝑚 = 𝑅𝑅𝑅𝑅 berechnet werden. Die spezifische Membrankapazität lässt sich nur bei bekannter Membranfläche ermitteln. Die spezifische Membrankapazität bei verschiedenen Zelltypen liegt immer im Bereich von etwa 𝑪𝑪𝒎𝒎 = 𝟏𝟏µ𝑭𝑭𝑭𝑭𝒎𝒎−𝟐𝟐, Im Gegensatz zu dem bei verschiedenen Zelltypen in weiten Grenzen variierenden spezifischen Widerstand 𝑅𝑅𝑚𝑚 . Der Unterschied zur berechneten spezifischen Membrankapazität von 𝑪𝑪𝒎𝒎 = 𝟎𝟎, 𝟒𝟒𝟒𝟒µ𝑭𝑭𝑭𝑭𝒎𝒎−𝟐𝟐 kommt daher, dass die Dielektrizitätskonstante der Membran durch Einbau von Proteinen größer ist als der angenommene Wert von 𝜀𝜀 = 2. Über Messung der Kapazität lässt sich auch die Ladungsverschiebung über die Membran bestimmen. Beispiel: 𝑄𝑄 = 𝐶𝐶𝐶𝐶 = 30𝑝𝑝𝑝𝑝 ∙ 90𝑚𝑚𝑚𝑚 = 2,7 ∙ 10−12 𝐶𝐶 = 3 ∙ 1017 𝑚𝑚𝑚𝑚𝑚𝑚. Die letzte Umrechnung erfolgt über Division durch die Elementarladung 𝑒𝑒. Der dazu notwendige Verschiebungsstrom 𝑰𝑰 = 𝑪𝑪𝑪𝑪𝑪𝑪/𝒅𝒅𝒅𝒅 ist ebenso zeitabhängig. Die Spannung der Membran reagiert auf das Ein- und Ausschalten eines Stroms mit einem exponentiellen Zeitverlauf der Spannung, der sich asymptotisch der Maximalspannung annähert. Die Membran verzerrt also den Zeitverlauf eines angelegten Stimulationssignals. Kanäle und Pumpen im Ersatzschaltbild Kanäle verhalten sich wie eine Batterie (Spannungsquelle) mit Widerstand. Die Polung der Spannungsquelle und die Spannung [V] selbst orientieren sich an der Richtung und dem Betrag des elektrochemischen Gradienten. Der Widerstand (repräsentiert eine Leitfähigkeit) beschreibt die endliche Wahrscheinlichkeit, dass ein Ion entgegen des elektrochemischen Gradienten wandern kann. Spannung und Polung können mit der Zeit variieren: je mehr transportiert wird, desto geringer wird der Gradient und desto geringer die Wahrscheinlichkeit für den nächsten, gerichteten Transport. Die Spannungsquellen (Batterien) des Modells ersetzen die über der Membran vorhandenen Aktivitätsunterschiede der verschiedenen Ionensorten, d.h. sie stehen für das Nernst´sche Gleichgewichtspotential des jeweiligen Ions. Die zu den Batterien seriell geschalteten Widerstände stellen die selektiven Ionenpermeabilitäten der Zellmembran, also die Leitfähigkeiten der einzelnen Ionensorten, dar. Die Spannung über den gesamten Schaltkreis stellt das Membranpotential dar und kann an einem Spannungsmeßgerät abgelesen werden. Pumpen hingegen verhalten sich wie ein Gleichstrom-Generator, da immer dieselbe TransportEinheit mit demselben Energie-Aufwand in dieselbe Richtung mit konstanter Geschwindigkeit übertragen wird. Im Gegensatz zum Kanal ist keine „Umkehr“ des Transports möglich – es existiert also keine Wahrscheinlichkeit für einen Rückwärts-Transport (kein Widerstand seriell geschaltet). Pumpen ermöglichen damit einen eindeutig definierten gerichteten Stromfluss (GleichstromGenerator), während bei Kanälen ein negatives Ion auch vom (+)-Pol zum (–)-Pol (entgegen des elektrischen Gradienten) „springen“ kann. Letzteres ist nur unter Berücksichtigung einer (gepolten) Spannungsquelle möglich. Sind mehrere Kanäle oder Pumpen in die Membran eingelagert, so werden die einzelnen Kanäle/Pumpen im Ersatzschaltbild parallel gezeichnet. Unter Berücksichtigung der BLM müssten die einzelnen Kanäle/Pumpen parallel zum Widerstand und dem Kondensator der Membran eingezeichnet werden. Transport durch Membranen: Grundlagen und passiver Transport Permeabilitätskoeffizient Eine elektrisch neutrale Substanz S liegt auf zwei Seiten der Membran mit unterschiedlichen Konzentrationen vor. Die Membran ist nur für S, nicht für das Lösungsmittel permeabel. Der Diffusionsfluss 𝚽𝚽 von S über die Membran ist dann proportional zur Konzentrationsdifferenz Δ𝑐𝑐 (Das Vorzeichen von Φ ist so definiert, dass 𝚽𝚽 > 0 bei Transport von Lösung I mit 𝒄𝒄′ nach Lösung II mit 𝒄𝒄′′ , unabhängig von der Größe der Konzentrationen). Die Proportionalitätskonstante ist der Permeabilitätskoeffizient 𝑷𝑷𝒅𝒅 [𝑐𝑐𝑐𝑐 ∙ 𝑠𝑠 −1 ] der Membran für S. 𝑃𝑃𝑑𝑑 ist unabhängig von der Konzentrationsdifferenz, kann aber eine Funktion der mittleren Konzentration 𝑐𝑐 = (𝑐𝑐 ′ + 𝑐𝑐 ′′ )/2 sein. U Φ = 𝑃𝑃𝑑𝑑 (𝑐𝑐 ′ − 𝑐𝑐 ′′ ) = 𝑃𝑃𝑑𝑑 Δ𝑐𝑐, [𝑚𝑚𝑚𝑚𝑚𝑚 ∙ 𝑐𝑐𝑚𝑚−2 ∙ 𝑠𝑠 −1 ] Experimentelle Bestimmung des Permeabilitätskoeffizienten Zur Zeit 𝑡𝑡 = 0 wird S der Konzentration 𝑐𝑐𝑎𝑎 in das Außenmedium zu einer Zellsuspension gegeben. In bestimmten Zeitabständen werden Zellen vom Medium abgetrennt und die in die Zellen aufgenommene Menge S bestimmt. Für Bestimmung von Membranpermeabilitäten werden meist radioaktiv markierte Substanzen S verwendet. Bedingungen an das System: • • • • Außenvolumen ist sehr viel größer als Zellvolumen (𝒄𝒄𝒂𝒂 über die Zeit konstant). Diffusion von S im Zytoplasma ist schnell (Aufnahme in die Zelle wird nur durch Permeation bestimmt). Rein passive Aufnahme von S (nur durch Konzentrationsgradient getrieben). S ist eine nicht-metabolisierbare Substanz (wird in der Zelle nicht verändert, Innenkonzentration muss charakteristisch mit der Zeit ansteigen). Für die Aufnahme gilt dann folgendes Zeitgesetz, wie für alle Prozesse mit Sättigungsverhalten: 𝑐𝑐𝑖𝑖 = 𝑐𝑐𝑎𝑎 �1 − 𝑒𝑒 −𝑡𝑡/𝜏𝜏 �, 𝜏𝜏 = 𝑉𝑉 𝐴𝐴𝑃𝑃𝑑𝑑 Die Innenkonzentration 𝑐𝑐𝑖𝑖 steigt demnach über eine Sättigungskurve von 𝑐𝑐𝑖𝑖 = 0 auf den Endwert 𝑐𝑐𝑖𝑖 (∞) = 𝑐𝑐𝑎𝑎 an, wobei die Zeitkonstante 𝝉𝝉 vom Permeabilitätskoeffizient, der mittleren Zelloberfläche und dem mittleren Zellvolumen abhängig ist. Zur Bestimmung von 𝑷𝑷𝒅𝒅 müssen daher die Zellmaße bekannt sein. Transport Lipid-löslicher Substanzen Der Transport lipidlöslicher Substanzen kann in erster Näherung über einen einfachen Diffusionsmechanismus beschrieben werden. Sie besitzen einen großen Verteilungskoeffizienten zwischen Membranphase m und Wasser w: 𝛾𝛾 = 𝑐𝑐𝑚𝑚 /𝑐𝑐𝑤𝑤 . • • • • + + - Ionen wie Na , K und Cl sind extrem lipidunlöslich, da die elektrostatische Energie für die Überführung einer Ladung aus einem Medium mit hohem 𝜀𝜀 (Wasser) in ein Medium mit kleinem 𝜀𝜀 (Membran) sehr hoch ist. Für Verbindungen, die viele H-Brücken zu Wasser ausbilden (z.B. Zucker) ist 𝛾𝛾 ebenso klein. Wasser nimmt eine mittlere Stellung zwischen lipidlöslichen und lipidunlöslichen Verbindungen ein. Einige Verbindungen kommen in einer lipidlöslichen Form und einer weniger lipidlöslichen, ionisierten Form vor + (NH3/NH4 , COOH/COO ). Es sind einige, vereinfachende Annahmen erforderlich: (1) Membran = homogener Flüssigkeitsfilm => ortsunabhängiger Verteilungskoeffizient und ortsunabhängiger Diffusionskoeffizient von S in der Membran. (2) Schneller Austausch von S zwischen Membran und Wasser => An der Grenzfläche Wasser/Membran ist direkt das Verteilungsgleichgewicht eingestellt. Wegen Annahme 1 stellt sich innerhalb der Membran ein linearer Konzentrationsverlauf 𝒄𝒄(𝒙𝒙) ein. Die Flussdichte Φ im Membraninneren ist durch das 1. Ficksche Gesetz ′ ′′ = 𝑐𝑐𝑚𝑚 (0) und 𝑐𝑐𝑚𝑚 = 𝑐𝑐𝑚𝑚 (𝑑𝑑) sind die gegeben. 𝑐𝑐𝑚𝑚 Konzentrationen von S innerhalb der Membran an den beiden Grenzflächen. Φ = −𝐷𝐷 ′′ ′ 𝑑𝑑𝑐𝑐𝑚𝑚 𝑐𝑐𝑚𝑚 − 𝑐𝑐𝑚𝑚 = −𝐷𝐷 𝑑𝑑𝑑𝑑 𝑑𝑑 Wegen Annahme 2 sind die Konzentrationen an den Grenzflächen innerhalb und außerhalb der Membran über den Verteilungskoeffizienten verknüpft. 𝛾𝛾 = ′ ′′ 𝑐𝑐𝑚𝑚 𝑐𝑐𝑚𝑚 = , 𝑐𝑐𝑤𝑤′ 𝑐𝑐𝑤𝑤′′ → Φ = −γD ∙ 𝑐𝑐𝑤𝑤′′ − 𝑐𝑐𝑤𝑤′ 𝑐𝑐𝑤𝑤′ − 𝑐𝑐𝑤𝑤′′ = γD ∙ 𝑑𝑑 𝑑𝑑 Mit der Definition Φ = 𝑃𝑃𝑑𝑑 (𝑐𝑐 ′ − 𝑐𝑐 ′′ ) = 𝑃𝑃𝑑𝑑 Δ𝑐𝑐 folgt dann 𝑷𝑷𝒅𝒅 = 𝛄𝛄𝛄𝛄/𝐝𝐝 . Bei lipidlöslichen Substanzen kann der Permeabilitätskoeffizient aus dem Verteilungskoeffizienten und dem Diffusionskoeffizienten ermittelt werden. 𝐷𝐷 ist wenig, 𝛾𝛾 stark von der chemischen Struktur der Substanz abhängig. Damit liegt 𝐷𝐷 für viele Moleküle im selben Bereich, während 𝛾𝛾 stark variieren kann. 𝑃𝑃𝑑𝑑 variiert demnach stark mit dem Verteilungskoeffizienten: Je größer γ, desto steiler ist bei gegebener äußerer Konzentrations-differenz 𝒄𝒄′𝒘𝒘 − 𝒄𝒄′′𝒘𝒘 der Konzentrationsgradient innerhalb der Membran (𝒄𝒄′𝒎𝒎 − 𝒄𝒄′′𝒎𝒎 )/𝒅𝒅. Diese Proportionalität zwischen 𝑃𝑃𝑑𝑑 und 𝛾𝛾 gilt für zahlreiche Nichtelektrolyte und wurde bereits von Ernest Overton gefunden (Overton-Regel). Für kleine hydrophile Moleküle wie Wasser oder Harnstoff findet man Abweichungen von der Overton-Regel. Diese Abweichungen sind bei einer Auftragung von log 𝑃𝑃𝑑𝑑 vs. log 𝛾𝛾 sichtbar (Collander-Plot), da die Datenpunkte für Harnstoff und Wasser nicht auf der Geraden liegt, deren Steigung durch das Verhältnis 𝐷𝐷/𝑑𝑑 definiert wird. Die Permeabilitätskoeffizienten für biologische Membranen umspannen zehn Größenordnungen (𝑷𝑷𝑴𝑴 = 𝟏𝟏𝟏𝟏−𝟏𝟏𝟏𝟏 − 𝟏𝟏𝟏𝟏−𝟐𝟐 𝒄𝒄𝒄𝒄 𝒔𝒔−𝟏𝟏 ). Collander-Plot für verschiedene Substanzen. Substanzen 5 (Wasser), 9 (Harnstoff) und 10 (Glycerin) zeigen hohe Abweichungen von der Geraden. Experimentell wird der Verteilungskoeffizient über eine Kohlenwasserstoff-Phase statt einer Membran bestimmt. Die Permeabilität von Protonen liegt mit 𝑷𝑷𝑴𝑴 = 𝟏𝟏𝟏𝟏−𝟒𝟒 𝒄𝒄𝒄𝒄 𝒔𝒔−𝟏𝟏 sehr hoch, sodass große Abweichungen von der Gerade im Collander-Plot vorliegen. Erklärungen für diese hohe Permeabilität liefert z.B. das Grothus-Modell: Aufgrund thermischer Dichtefluktuationen entstehen transiente Verbindungen aus Wassermolekülen durch die Membran. Währenddessen kann das Proton über eine Serie von H-Brücken von Wassermolekül zu Wassermolekül springen. Unidirektionale Flüsse, Flussmessungen mit Isotopen Bei jedem beobachteten Fluss, setzt sich die Nettoflussdichte 𝚽𝚽 aus zwei unidirektionalen Flussdichten zusammen, von denen eine von I (z.B. Außenmilieu einer Zelle) nach II (z.B. Zytoplasma) und eine von II nach I gerichtet ist (genauso gilt es auch für die Diffusion: Teilchen können sich nach links und nach rechts bewegen; Nettoergebnis ist dann die beobachtete Diffusion). Für 𝑐𝑐 ′′ < 𝑐𝑐 ′ entspräche Φ𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁𝑁 = Φ′ − Φ′′ dann Nettoeinstrom = Einstrom – Ausstrom. Wenn die Nettoflussdichte null ist, weil die Konzentrationen auf beiden Seiten der Membran gleich sind, sind dennoch unidirektionale Flussdichten vorhanden. Solche Flüsse lassen sich über Isotopenmarkierung beobachten, wobei die Substanz in I als rad markiert und die Substanz in II als stab markiert wird. • • ′ Srad-Fluss von I nach II: Φ′ = Φ𝑟𝑟𝑟𝑟𝑟𝑟 ′′ Sstab-Fluss von II nach I: Φ′′ = Φ𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 • Annahme: Srad und Sstab sind für die Membran ununterscheidbar Meist wird auf der Seite I der Membran nur ein Teil der Substanz radioaktiv markiert, während der Rest der Substanz einem stabilen Isotop entspricht, wie es auch auf der anderen Seite der Membran vorliegt. • • • • ′ ′ Für die Konzentration von S auf Seite I gilt: 𝑐𝑐 ′ = 𝑐𝑐𝑟𝑟𝑟𝑟𝑟𝑟 + 𝑐𝑐𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 ′ ′ Gesamte unidirektionale Flussdichte von I nach II: Φ′ = Φ𝑟𝑟𝑟𝑟𝑟𝑟 + Φ𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 ′ Verhältnis Konzentration des radioaktiven Isotops : Gesamtkonzentration S: 𝛼𝛼 ′ = 𝑐𝑐𝑟𝑟𝑟𝑟𝑟𝑟 /𝑐𝑐 ′ ′′ ′′ Konzentrationen von S auf Seite II: 𝑐𝑐 ′′ = 𝑐𝑐𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 , 𝑐𝑐𝑟𝑟𝑟𝑟𝑟𝑟 (𝑡𝑡 = 0) = 0 Durch Messung der Radioaktivität auf Seite II nach einer bestimmten Zeit, lässt sich der unidirektionale Fluss des radioaktiv markierten Isotops bestimmen (Φ = ∆n/∆t). Über die Beziehung zwischen Flussdichte-Verhältnis und Konzentrationsverhältnis ist die gesamte unidirektionale Flussdichte aus der Flussdichte des radioaktiven Isotops berechenbar: ′ Φ′ 𝑐𝑐 ′ 1 Φ𝑟𝑟𝑟𝑟𝑟𝑟 ′ = = → Φ = ′ ′ Φ𝑟𝑟𝑟𝑟𝑟𝑟 𝑐𝑐𝑟𝑟𝑟𝑟𝑟𝑟 𝛼𝛼 ′ 𝛼𝛼′ ′′ Ebenso kann der Permeabilitätskoeffizient ermittelt werden. Da Φ𝑟𝑟𝑟𝑟𝑟𝑟 = 0 liegen radioaktive=gemessene Flüsse nur von I nach II vor. Vorteil: Bei dieser Versuchsanordnung wird 𝑷𝑷𝒅𝒅 in einem stationären Zustand bestimmt, da Die Gesamtkonzentrationen in I und II zeitunabhängig sind Flusskopplung Φrad = ′ Φrad = ′ 𝑃𝑃𝑑𝑑 𝑐𝑐𝑟𝑟𝑟𝑟𝑟𝑟 ′ Φrad → 𝑃𝑃𝑑𝑑 = ′ crad Gemachte Annahmen: • • Differenzen Δ𝑐𝑐𝐴𝐴 und Δ𝑐𝑐𝐵𝐵 sind hinreichend klein. Es gelten die Gesetze für verdünnte Lösungen (alle Aktivitätskoeffizienten sind 1). Treten gleichzeitig mehrere Teilchensorten durch die Membran, können sich die einzelnen Flüsse beeinflussen. Die bekannten Gleichungen der einzelnen Flussdichten der Substanzen A und B müssen dann mithilfe der Thermodynamik irreversibler Prozesse erweitert werden: Φ𝐴𝐴 = 𝑃𝑃𝐴𝐴 Δ𝑐𝑐𝐴𝐴 + 𝑃𝑃𝐴𝐴𝐴𝐴 Δ𝑐𝑐𝐵𝐵 , Φ𝐵𝐵 = 𝑃𝑃𝐵𝐵 Δ𝑐𝑐𝐵𝐵 + 𝑃𝑃𝐵𝐵𝐵𝐵 Δ𝑐𝑐𝐴𝐴 Der Fluss von A ist also auch von Δ𝑐𝑐𝐵𝐵 abhängig und umgekehrt. 𝑷𝑷𝑨𝑨𝑨𝑨 bzw. 𝑷𝑷𝑩𝑩𝑩𝑩 sind Kreuzkoeffizienten. Diese sind direkt durch die Onsager-Relation 𝑷𝑷𝑨𝑨𝑨𝑨 𝒄𝒄𝑩𝑩 = 𝑷𝑷𝑩𝑩𝑩𝑩 𝒄𝒄𝑨𝑨 verknüpft. Die unabhängige Wanderung von A und B ist ein Spezialfall, sodass 𝑃𝑃𝐴𝐴𝐴𝐴 = 𝑃𝑃𝐵𝐵𝐵𝐵 = 0 gilt und die gewöhnlichen Gleichungen ohne Erweiterung durch die Thermodynamik irreversibler Prozesse verwendet werden kann. Aus den Gleichungen für Φ𝐴𝐴 und Φ𝐵𝐵 lässt sich durch Kombination Φ𝐴𝐴 (Φ𝐵𝐵 ) oder Φ𝐵𝐵 (Φ𝐴𝐴 ) darstellen, sodass die Flusskopplung beschrieben wird (die Φ𝐵𝐵 -Gleichung nach Δ𝑐𝑐𝐵𝐵 auflösen und dann in die andere einsetzen ergibt Φ𝐴𝐴 (Φ𝐵𝐵 )). Φ𝐴𝐴 = �𝑃𝑃𝐴𝐴 − 𝑃𝑃𝐴𝐴𝐴𝐴 𝑃𝑃𝐵𝐵𝐵𝐵 𝑃𝑃𝐴𝐴𝐴𝐴 � Δ𝑐𝑐𝐴𝐴 + Φ 𝑃𝑃𝐵𝐵 𝑃𝑃𝐵𝐵 𝐵𝐵 Die Gleichung zeigt auch, dass selbst für 𝚫𝚫𝒄𝒄𝑨𝑨 = 𝟎𝟎 noch ein Fluss der Substanz A beobachtbar ist, wenn Δ𝑐𝑐𝐵𝐵 ≠ 0 und eine Kopplung zwischen A und B (𝑃𝑃𝐴𝐴𝐴𝐴 ≠ 0) existiert. So kann bei einem Konzentrationsgradienten der Substanz B die Substanz A gegen ihren Konzentrationsgradienten mit transportiert werden. • • Transport durch Kanäle: Positive Flusskopplung (Symport) Carrier-Transport: Positive und Negative Flusskopplung (Symport und Antiport); bei Antiport ist dann 𝑃𝑃𝐴𝐴𝐴𝐴 < 0. Osmose an nicht-semipermeablen Membranen, Staverman-Gleichungen S.371-375 ignoriert Grundlage: Osmose (Kapitel 4) Carriertransport (erleichterte Diffusion) Hydrophile oder geladane Substanzen S haben eine verschwindende Permeabilität (geringe Diffusion), die selektiv durch einen Carrier C erhöht werden kann (erleichterte Diffusion). Der Carrier befindet sich innerhalb der Membran und kann mit der Substanz S einen Komplex CS eingehen. Die Aufnahme und Abgabe von S erfolgt immer an den Grenzflächen Membran/Lösung. Dabei gibt es zwei Mechanismen: • • Translatorische Carrier diffundieren innerhalb der Membran zwischen den beiden Grenzflächen. Valinomycin transportiert Kalium und andere Alkaliionen passiv durch die Membran, indem es innerhalb der Membran frei diffundieren kann. Sechs von 12 CarbonylSauerstoffatome bilden einen Käfig, in dem ein K+ Ion eingeschlossen werden kann. Die Außenseite des Komplexes ist stark hydrophob. Valinomycin ist hochspezifisch für K+ (Na+Transport ist 1000fach ineffizienter). Bei hoher K+-Konzentration transportiert ein Valinomycin-Molekül etwa 𝟏𝟏𝟏𝟏𝟒𝟒 K+-Ionen pro Sekunde durch die Membran. Carrier, die über Konformationsänderungen die Bindetasche abwechselnd zu der einen Grenzfläche und der anderen Grenzfläche exponieren. Permeasen sind passive Transportsysteme, welche die formalen Kriterien des Carriermodels erfüllen. Die Aufklärung des genauen Transportmechanismus erweist sich bei diesen jedoch als schwierig. Die Laktose-Permease (LacY) erreicht eine Wechselzahl von 1000/min. Der Transport ist rein passiv, erfolgt also entlang des elektrochemischen Gradienten von S. Im Gleichgewichtszustand (verschwindender Nettotransport) sind die Konzentrationen CS, C und S durch das Massenwirkungsgesetz verknüpft (m=Membran, w=Wasser). K ist die Gleichgewichtskonstante der Komplexbildung. 1/K ist die Konzentration von S, bei der die Hälfte der Carriermoleküle als Komplex CS vorliegen. 𝐾𝐾 = [𝐶𝐶𝐶𝐶]𝑚𝑚 [𝐶𝐶]𝑚𝑚 [𝑆𝑆]𝑤𝑤 Sättigungskinetik des Carriertransports Es wird der Import von extrazellulärem S in die Zelle beobachtet. Bei 𝒕𝒕 = 𝟎𝟎 sei 𝒄𝒄𝒔𝒔,𝒊𝒊 = 𝟎𝟎. Mit zunehmender Außenkonzentration 𝒄𝒄𝒔𝒔,𝒂𝒂 steigt der einwärtsgerichtete Fluss zunächst linear und dann asymptotisch gegen den Maximalwert 𝑱𝑱𝒎𝒎𝒎𝒎𝒎𝒎 an. Die Sättigung des Flusses entspricht der Tatsache, dass bei hohen Konzentrationen alle Carrier an der Außenseite der Membran als CSKomplexe vorliegen – eine weitere Steigerung des Flusses ist nicht möglich. Die Wechselzahl 𝒘𝒘 = 𝑱𝑱𝒎𝒎𝒎𝒎𝒎𝒎 /𝑵𝑵 des Carriers lässt sich aus der Zahl der Carriermoleküle N und dem maximalen Fluss bei Sättigung bestimmen. Sie entspricht der Anzahl an Teilchen, die ein CarrierMolekül pro Sekunde transportieren kann. Typische Werte liegen bei 𝟏𝟏𝟏𝟏𝟏𝟏𝒔𝒔−𝟏𝟏 . Negative Flusskopplung (Gegentransport) Negative Flusskopplung tritt auf, wenn zwei Verbindungen R und S um dieselbe Bindungsstelle eines Carriers konkurieren. Auf beiden Seiten einer Membran liegt S in gleichen Konzentrationen vor. Die Konzentration von S ist so hoch, dass sich C in Sättigung befindet. Durch Zugabe von R mit der gleichen Konzentration wie S auf Seite II der Membran, herrscht eine Konkurrenz zwischen R und S um die Bindung von C an der Grenzfläche Membran / Seite II. Ein Teil des Carriers geht dann an dieser Grenzfläche in die Form CR über, wodurch in der Membran ein Konzentrationsgradient für CS entsteht, obwohl die Konzentrationen für S in den Außenphasen gleich groß sind. Dies führt zu einem Fluss von S von Seite I nach Seite II, während R in entgegengesetzte Richtung transportiert wird. Dieser Transportmechanismus funktioniert auch dann noch, wenn die Außenkonzentration größer ist als die Innenkonzentration, sodass der Transport gegen den Konzentrationsgradienten erfolgt. Beispiel: Alanin wird von Streptokokken in hoher Konzentration synthetisiert, während Serin durch Kopplung an den Alanin-Fluss entgegen des Konzentrationsgradienten aus dem Medium aufgenommen wird. Austauschtransport Ist die Beweglichkeit des unkomplexierten Carriers in der Membran gering, wird der Rücktransport des unkomplexierten Carriers behindert (z.B. wenn Carrier elektrisch geladen ist: 𝐶𝐶 2− + 𝑆𝑆 2+ ⇄ 𝐶𝐶𝑆𝑆). Dies kann verhindert werden, indem auf der anderen Seite der Membran eine Verbindung zurück transportiert wird. Beispiele für Austauschtransportsysteme sind das Bicarbonat/Chlorid-Austauschsystem in der Erythrozytenmembran und das ATP/ADP-Austauschsystem in der inneren Mitochondrienmembran. NhaA (Na+H+-Austauscher von E.coli) erreicht eine Wechselzahl von 90k/min. Positive Flusskopplung (Cotransport) Bei positiver Flusskopplung hat der Carrier zwei verschiedene Bindestellen für R und S, wobei nur der Komplex CSR über die Membran diffundieren kann. Beispiel hierfür ist der Na+-gekoppelte Glucosetransport in Epithelzellen des Dünndarms. Transport durch Kanäle Ein Carrier hat Bindestellen, die abwechselnd von der einen und von der anderen Seite der Membran zugänglich sind, aber nicht gleichzeitig! Ein Kanal ist gleichzeitig von beiden Seiten zugänglich. Die Wechselzahl eines translatorischen Carriers ist durch die Viskosität beschränkt. In Membrandurchspannenden Kanälen können dagegen viel höhere Transportraten auftreten (Na+-Kanal in Neuronen und Ach-aktivierter Ionen-Kanal in subsynaptischer Membran der Muskelendplatte: 𝟏𝟏𝟏𝟏𝟕𝟕 Ionen pro Sekunde). Das 15 AS lange Peptid Gramicidin bildet Kanäle aus zwei Kopf-an-Kopf verknüpften helikalen Molekülen, die für monovalente Kationen spezifisch sind. Die hydrophoben Reste zeigen nach außen, das Ion wird durch die helikale Struktur transportiert. Bei 1M NaCl Lösung und einer Membranspannung von 100 mV ist die Wechselzahl ebenso bei 107 Ionen pro Sekunde. Die Zahl der transportierten Ionen pro Zeiteinheit (selbe Aussage wie Wechselzahl! Aber keine Sättigungskinetik, daher andere Methode zur Bestimmung notwendig) kann durch Einzelkanalexperimente bestimmt werden. Der Einbau einzelner Ionenkanäle führt zu einer signifikanten Zunahme der Leitfähigkeit einer Lipidmembran. Ionenkanäle sind dynamische Strukturen, die zwischen verschiedenen Leitfähigkeitszuständen fluktuieren, z.B. zwischen einem offenen und einem geschlossenen Zustand: 𝐺𝐺 ⇄ 𝑂𝑂. Dementsprechend zeigt der elektrische Strom bei konstanter Membranspannung stufenförmige Fluktuationen. Aus deren Amplitudenstrom 𝑖𝑖 (Strom ist Ladung pro Zeit) kann die Anzahl 𝑛𝑛 an Ionen der Ladung 𝑞𝑞 = 𝑧𝑧𝑧𝑧 pro Zeiteinheit 𝑡𝑡 ermittelt werden. makroskopisch: 𝑸𝑸 = 𝒛𝒛𝒛𝒛𝒛𝒛 = 𝑰𝑰𝑰𝑰 → mikroskopisch: 𝒛𝒛𝒛𝒛𝒛𝒛 = 𝒊𝒊𝒊𝒊 → 𝒊𝒊 = 𝒏𝒏𝒏𝒏𝒏𝒏 𝒕𝒕 In der Versuchsanordnung überspannt die bimolekulare Lipidmembran die kreisrunde Öffnung (1mm² Fläche) in einer dünnen Trennwand aus Teflon. Auf beiden Seiten der Membran befinden sich wässrige Salzlösungen, die durch Elektroden kontaktiert werden. Diese sind mit einer Spannungsquelle und einem Strommessgerät verbunden. Diese Experimente waren der wesentliche Schritt zu Einzelkanalexperimenten im Rahmen der PatchClamp Technik. Das Auftreten solcher Stromfluktuationen wird als experimenteller Beweis für das Vorliegen eines Kanalmechanismus angesehen. Bei Vorliegen eines Carriermechanismus ist der Strombeitrag einzelner Carriermoleküle um mehrere Größenordnungen geringer (siehe typische Wechselzahlen), weshalb er in Einzelkanalexperimenten nicht aufgelöst werden könnte. Kanäle ermöglichen wie Carrier positive Flusskopplung: In engen Kanälen passen nie zwei Moleküle nebeneinander durch den Kanal. Hintereinander angeordnete Moleküle können ihre Plätze also nicht tauschen, weshalb die Flüsse verschiedener Teilchensorten gekoppelt sein müssen. Dies wurde für den K+-Kanal der Nervenmembran bewiesen: Durch Anlegen von Spannung wird der KaliumTransport induziert und Wassermoleküle mitgeführt. Transport durch Membranen: aktiver Transport Aktiver Transport liegt vor, wenn eine Substanz entgegen ihres elektrochemischen Gradienten (Konzentrationsgradient + elektrischer Gradient) transportiert wird. Aktiver Transport kann nur über Kopplung an einen energieliefernden Prozess stattfinden, sodass die Gesamtbilanz der Freien Enthalpie negativ ist. Achtung: Die bisher besprochene Flusskopplung, die zu einem gerichteten Antiport oder Cotransport führen kann, kann sowohl aktiv als auch passiv sein. Beispiele: Colibakterien können gewisse Zucker aus dem Medium bis zu einem Konzentrationsverhältnis 𝑐𝑐 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 𝑐𝑐𝑎𝑎𝑎𝑎 ß𝑒𝑒𝑒𝑒 = 103 anreichern. Das Epithel der Magenschleimhaut sezerniert Protonen aus dem Zellinneren (pH=7) in den Magensaft (pH=1). Das Konzentrationsverhältnis ist 106 . Sind 𝑎𝑎′ und 𝑎𝑎′′ die Aktivitäten der zu transportierenden Substanz in Lösung I und Lösung II, 𝜑𝜑′ und 𝜑𝜑′′ � ′ und 𝝁𝝁 � ′′ : die elektrischen Potentiale, so sind die elektrochemischen Potentiale 𝝁𝝁 𝜇𝜇�′ = 𝜇𝜇0 + 𝑅𝑅𝑅𝑅 ln 𝑎𝑎′ + 𝑧𝑧𝑧𝑧𝜑𝜑 ′ , 𝜇𝜇�′′ = 𝜇𝜇0 + 𝑅𝑅𝑅𝑅 ln 𝑎𝑎′′ + 𝑧𝑧𝑧𝑧𝜑𝜑 ′′ � = 𝝁𝝁 � ′ − 𝝁𝝁 � ′′ = ∆𝑮𝑮𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻 , also der elektrochemische Entscheidend ist die Größe der Differenz ∆𝝁𝝁 Gradient. Er entspricht der freien Enthalpie, die beim Transport von 1 mol der Substanz von Lösung II nach Lösung I verbraucht wird. ∆𝑮𝑮𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝒓𝒓𝒓𝒓 = 𝑹𝑹𝑹𝑹 𝐥𝐥𝐥𝐥 𝒂𝒂′ + 𝒛𝒛𝒛𝒛(𝝋𝝋′ − 𝝋𝝋′′ ) 𝒂𝒂′′ Aufgrund der Definition von 𝚽𝚽 (positiv, wenn Fluss von Lösung I � = 𝝁𝝁 � ′ − 𝝁𝝁 � ′′ gilt: nach Lösung II) und der Vorgabe ∆𝝁𝝁 • • �<0 für den aktiven Transport: 𝚽𝚽 ∙ ∆𝝁𝝁 �>0 für den passiven Transport: 𝚽𝚽 ∙ ∆𝝁𝝁 � entspricht der Änderung der freien Enthalpie, die mit dem betrachteten Das Produkt 𝚽𝚽 ∙ ∆𝝁𝝁 Transportvorgang pro Flächen- und Zeiteinheit verknüpft ist. Für den Transport eines Nichtelektrolyten ist 𝑧𝑧 = 0, sodass gilt: ∆𝜇𝜇� = 𝑅𝑅𝑅𝑅 ln 𝑎𝑎′ 𝑎𝑎′′ Bei verdünnten Lösungen kann in den Gleichungen die Aktivität 𝑎𝑎 durch die Konzentration 𝑐𝑐 ersetzt werden. Arten des aktiven Transports • • • • Primär aktiver Transport wird durch eine primäre Energiequelle wie ATP-Hydrolyse (Natrium-Kalium-Pumpe), Licht (Bakteriorhodopsin) oder Redoxenergie (Cytochrom-Oxidase) getrieben. Sekundär aktiver Transport wird durch Kopplung des Transports an den Transport einer anderen Substanz, die entlang ihres Gradienten transportiert wird, erreicht (z.B. Na+-Glucose Cotransport zwecks Glucose-Anreicherung in den Dünndarmzellen). Der Konzentrationsgradient wird durch einen primär aktiven Transport (hier: Natrium-KaliumPumpe) aufrecht erhalten. Tertiär aktiver Transport nutzt den Konzentrationsgradient, den ein sekundär aktiver Transport auf der Basis eines primär aktiven Transports aufgebaut hat (im Dünndarm werden Di- und Tripeptide über diesen Mechanismus aufgenommen). Gruppentranslokation: Hier werden z.B. Monosaccharide durch die Membran transportiert und dabei direkt chemische verändert (z.B. phosphoryliert), wodurch kein Konzentrationsgradient abgebaut wird (z.B. Phosphotransferase-System zum Glucose-Import in E.coli; Energie stammt aus dem Phosphat von PEP). Energiebilanz des primär aktiven Transports Annahme: Pro mol hydrolysiertes ATP werden 𝒗𝒗 mol der Substanz S von Phase I nach Phase II transportiert. Für den Transport ist also ein Betrag der freien Enthalpie der Größe 𝑣𝑣 ∙ ∆𝐺𝐺𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 erforderlich. Die Hydrolyse von ATP (∆𝐺𝐺 = −30𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚) liefert freie Enthalpie der Größe −∆𝐺𝐺 = 30𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚 (∆𝐺𝐺 ist negativ; da man Energie „rausbekommt“ muss negatives Vorzeichen ergänzt werden). Soll der Gesamtvorgang spontan ablaufen, muss gelten: 𝑣𝑣 ∙ ∆𝐺𝐺𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 < −∆𝐺𝐺 𝑣𝑣 �𝑅𝑅𝑅𝑅 ln 𝑎𝑎′′ + 𝑧𝑧𝑧𝑧(𝜑𝜑′′ − 𝜑𝜑′ )� < −∆𝐺𝐺 𝑎𝑎′ Die Gleichung legt fest, bis zu welchem Aktivitätsverhältnis 𝒂𝒂′′ /𝒂𝒂′ eine Substanz bei gegebenem Membranpotential 𝝋𝝋′′ − 𝝋𝝋′ akkumuliert werden kann. Ist S elektrisch neutral (z=0) und der Transport gehorcht einer 1:1 Stöchiometrie (v=1) sowie findet in einer verdünnten Lösung statt (ac), folgt aus der Gleichung: ∆𝐺𝐺 𝑐𝑐 ′′ − 𝑅𝑅𝑅𝑅 < 𝑒𝑒 𝑐𝑐 ′ ′ Die ATP-Hydrolyse unter Standardbedingungen liefert −∆𝐺𝐺 = −∆𝐺𝐺 0 = 𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑/𝒎𝒎𝒎𝒎𝒎𝒎 Energie. Die ATP-Hydrolyse unter physiologischen Bedingungen liefert bis zu −∆𝐺𝐺 = −∆𝐺𝐺𝑐𝑐ℎ𝑒𝑒𝑒𝑒 = 𝟔𝟔𝟔𝟔𝟔𝟔𝟔𝟔/𝒎𝒎𝒎𝒎𝒎𝒎 Energie. Dies liegt an den sehr unterschiedlichen verwendeten Konzentrationen (1M unter Standardbedingungen, 0,01M unter physiologischen Bedingungen). Außerdem ist der Wert wegen der höheren Temperatur (37°C statt 25°C) um wenige kJ/mol erhöht. Zusätzlich ist der Wert pHabhängig. ∆𝐺𝐺𝑐𝑐ℎ𝑒𝑒𝑒𝑒 = 𝑅𝑅𝑅𝑅 ln 𝐾𝐾 = 𝑅𝑅𝑅𝑅 ln [𝑃𝑃𝑖𝑖 ][𝐴𝐴𝐴𝐴𝐴𝐴] 1,5𝑚𝑚𝑚𝑚 ∗ 0,05𝑚𝑚𝑚𝑚 = 𝑅𝑅𝑅𝑅 ln [𝐴𝐴𝐴𝐴𝐴𝐴] 8𝑚𝑚𝑚𝑚 Mit 𝑅𝑅𝑅𝑅 = 2,5𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚 folgt für Standardbedingungen 𝑐𝑐 ′′ /𝑐𝑐 ′ < 𝑒𝑒 12 = 2 ∙ 105 und für physiologische Bedingungen 𝑐𝑐 ′′ /𝑐𝑐 ′ < 𝑒𝑒 24 = 2 ∙ 1010 . Die tatsächlich erzielte Anreicherung ist jedoch nierdiger. Gründe hierfür sind: • • Unvollständige Kopplung. Passiver Rücktransport von S. Beispiel für primär aktiven Transport: Die Natrium-Kalium-Ionen-Pumpe Damit aufgrund des Na+-Glucose-Symports oder anderer Transport-Mechanismen, die den NatriumGradienten ausnutzen, nicht allmählich Δ𝜇𝜇𝑁𝑁𝑁𝑁 → 0 und damit der Symport zum Erliegen kommt, müssen die Natrium-Ionen aktiv aus der Zelle exportiert werden. Die meisten tierischen Zellen besitzen im Zytoplasma eine hohe Kalium-Konzentration (136mM) und eine niedrige Natrium-Konzentration (19mM), während im extrazellulären Medium das Konzentrationsverhältnis umgekehrt ist (5 mM bzw. 120 mM, die Angaben beziehen sich auf Erythrozyten). Die zytoplasmatischen Konzentrationen von Kalium und Natrium sind wichtig für die Konstanthaltung des Zellvolumens, für die Erregbarkeit von Nervenzellen und die Akkumulierung von Zuckern und Aminosäuren durch Cotransportsysteme. Die Zellmembran besitzt eine signifikante passive Permeabilität für Na+ und K+. Damit müssen die Konzentrationsgradienten ständig aktiv aufrecht erhalten werden. Die Na+-K+-Ionen-Pumpe bewerkstelligt dies, indem sie unter ATP-Hydrolyse Na+ exportiert und K+ importiert. In homogener Lösung können enzymatische Eigenschaften studiert werden, wobei der vektorielle Charakter der Reaktion nicht mehr vorhanden ist. Untersuchungen des Proteins nach Einbau in die Erythrozytenmembran ermöglichten die Aufklärung des Mechanismus: (1) (2) (3) (4) ATP wirkt in Form von MgATP nur auf der cytosolischen Seite. + In Gegenwart von intrazellulärem Na wird das Enzym durch ATP an einem Aspartylrest phosphoryliert. + Das phosphorylierte Protein wird in Gegenwart von extrazellulärem K dephosphoryliert. + + Für jedes hydrolysierte ATP werden 2 K -Ionen nach innen und 3 Na -Ionen nach außen transportiert. Die entsprechenden Konzentrationsgradienten im Gleichgewichtszustand (Na/K Transport-Gleichgewicht: + + + Na -K -Pumpen-Aktivität, passive Permeabilität, Na -Glucose-Symport sind im Gleichgewicht => stationärer Zustand => Konzentrationen über die Zeit konstant) können nur aufrecht erhalten werden, wenn die Pumpe orientiert in die Membran eingebaut wurde. Wären die natürlichen Gradienten für Na+ und K+ umgekehrt, so würde die Na+-K+-Pumpe „rückwärts“ laufen und gleichzeitig ATP-Synthese betreiben. Da ungleich viele Ladungen importiert und exportiert werden, handelt es sich um einen elektrogenen Transport. Die Na+-K+-Pumpe ist damit Stromquelle. Die Aktivität der Na+-K+-Pumpe kann damit auch durch die elektrische Spannung über der Membran gesteuert werden. Der Reaktionsmechanismus beinhaltet einen Übergang von einer Konformation E1 mit einwärts gerichteten zu einer Konformation E2 mit auswärts gerichteten Ionenbindestellen. Im Zustand E1 kann das Enzym 3 Na+-Ionen mit hoher Affinität binden, wonach die Phosphorylierung einen Übergang zur Konformation E2 induziert. In diesem Zustand sind die Bindestellen nach außen orientiert, während die Affinität zu Na+ niedrig ist. Dies bewirkt die Dissoziation von Na+ und die Aufnahme von 2 K+ Ionen, wodurch eine Dephosphorylierung den Übergang in die Konformation E1 induziert. Die E1-E2-Übergänge verlaufen über Zwischenzustände, in denen die gebundenen Ionen im Protein eingeschlossen sind. Im Vergleich zu einem Ionenkanal ist die Transportrate mit 100 Zyklen pro Sekunde bei 37°C sehr klein. Erythrozyten besitzen etwa 50 Kopien der Na+-K+-Pumpe je Zelle; Zellen der Nierentubuli besitzen bis zu 4 ∙ 106 Kopien. Energetik der Na+-K+-Pumpe 𝑎𝑎 Für den Transport von 3 mol Na+ nach außen (𝑎𝑎, 𝑐𝑐𝑁𝑁𝑁𝑁 = 140𝑚𝑚𝑚𝑚, 𝑐𝑐𝐾𝐾𝑎𝑎 = 5𝑚𝑚𝑚𝑚) und 2 mol K+ nach 𝑖𝑖 innen (𝑖𝑖, 𝑐𝑐𝑁𝑁𝑁𝑁 = 10𝑚𝑚𝑚𝑚, 𝑐𝑐𝐾𝐾𝑖𝑖 = 150𝑚𝑚𝑚𝑚) wird bei einem Membranpotential von ∆𝜑𝜑 = 𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 = −60𝑚𝑚𝑚𝑚 benötigt: 𝑎𝑎 𝑖𝑖 −∆𝐺𝐺𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 = 3�𝜇𝜇𝑁𝑁𝑁𝑁 − 𝜇𝜇𝑁𝑁𝑁𝑁 � + 2�𝜇𝜇𝐾𝐾𝑖𝑖 − 𝜇𝜇𝐾𝐾𝑎𝑎 � = −42,2kJ/mol Der Anteil von Natrium: a 𝑘𝑘𝑘𝑘 cNa 𝜑𝜑𝑖𝑖 ) = (19,6 + 17,4) = 𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑/𝒎𝒎𝒎𝒎𝒎𝒎 = 3RT ln i + 3F (𝜑𝜑 ����� 𝑎𝑎 − �� 𝑚𝑚𝑚𝑚𝑚𝑚 cNa ��� +60mV Der Anteil von Kalium: ~ln 10 cKi 𝑘𝑘𝑘𝑘 = 2RT ln a + 2F (𝜑𝜑 = 𝟓𝟓, 𝟐𝟐𝟐𝟐𝟐𝟐/𝒎𝒎𝒎𝒎𝒎𝒎 ����� �� 𝑖𝑖 − 𝜑𝜑 𝑎𝑎 ) = (16,8 − 11,6) cK 𝑚𝑚𝑚𝑚𝑚𝑚 � ~ln 10 −60mV Bedingung für einen spontanen Prozess: −∆𝐺𝐺𝑐𝑐ℎ𝑒𝑒𝑒𝑒 = 60𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚 > 42,2𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚 = ∆𝐺𝐺𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 . Insgesamt wird dabei also die Energie 𝟔𝟔𝟔𝟔𝟔𝟔𝟔𝟔/𝒎𝒎𝒎𝒎𝒎𝒎 − 𝟒𝟒𝟒𝟒, 𝟐𝟐𝟐𝟐𝟐𝟐/𝐦𝐦𝐦𝐦𝐦𝐦 = 𝟏𝟏𝟏𝟏, 𝟖𝟖𝟖𝟖𝟖𝟖/𝐦𝐦𝐦𝐦𝐦𝐦 > 0 nicht verwendet. Dies bedeutet, dass die Na+-K+-Pumpe fern des elektrochemischen Gleichgewichts arbeitet. Bedeutung der Natrium-Kalium-Pumpe Die Bedeutung der Natrium-Kalium-Pumpe ist sehr weitreichend für alle Organismen: • Wiederherstellung des korrekten Konzentrationsverhältnisses nach einem Aktionspotential. • • • Natrium-Export ist die Triebkraft für zahlreiche sekundär aktiven Transporter, die Glucose, Aminosäuren und andere Nährstoffe über den Natriumgradienten importieren. Aufrechterhaltung des Zellvolumens: Da die Zellmembran eine wesentlich geringere Permeabilität für Natrium, als für Kalium aufweist, haben die Natrium-Ionen eine Tendenz draußen zu bleiben. Es resultiert ein Nettoverlust an Ladung innerhalb der Zelle, was den Wassereinstrom (Osmose Lyse der Zelle) verhindert. Signaltransduktion: Die Natrium-Kalium-Pumpe bindet Src-Kinase und inhibiert sie. Infolge der Ligand-Bindung wird sie freigesetzt und kann MAPK und PLC-Wege induzieren. Energiebilanz des sekundär aktiven Transports S wird durch Kopplung an den Bergabtransport von R bergauf transportiert. Für den Transport von S entgegen des elektrochemischen Gradienten ist – Φ𝑆𝑆 Δ𝜇𝜇𝑆𝑆 > 0 aufzuwenden. Damit der Gesamtprozess spontan abläuft, muss gelten: Φ𝑅𝑅 Δ𝜇𝜇𝑅𝑅 >– Φ𝑆𝑆 Δ𝜇𝜇𝑆𝑆 Beispiel für sekundär aktiven Transport: Cotransport von Na+ und organischen Substraten Die Epithelzellen des Dünndarms akkumulieren Glucose aus dem Darmlumen entgegen eines Konzentrationsgradienten durch Kopplung an den Natrium-Import entlang des elektrochemischen Gradienten. Der Gesamtvorgang läuft spontan ab, wenn: Φ𝐺𝐺𝐺𝐺 Δ𝜇𝜇𝐺𝐺𝐺𝐺 + ΦNa Δ𝜇𝜇𝑁𝑁𝑁𝑁 > 0 Annahme: die Kopplung ist vollständig und pro Glucose-Molekül wird ein Natrium-Ion transportiert. Φ𝐺𝐺𝐺𝐺 = ΦNa > 0, → Δ𝜇𝜇𝐺𝐺𝐺𝐺 + Δ𝜇𝜇𝑁𝑁𝑁𝑁 > 0 , 𝑎𝑎 𝑖𝑖 𝑎𝑎 𝑖𝑖 → �𝜇𝜇𝐺𝐺𝐺𝐺 − 𝜇𝜇𝐺𝐺𝐺𝐺 − 𝜇𝜇𝑁𝑁𝑁𝑁 � + �𝜇𝜇𝑁𝑁𝑁𝑁 �>0 Wobei a für Außenmedium und i für Innenmedium steht. Nun nimmt man eine verdünnte Lösung an (Konzentrationen statt Aktivitäten) und berücksichtigt, dass Glucose keine Ladung trägt: 𝑅𝑅𝑅𝑅 ln [G]a [𝑁𝑁𝑎𝑎+ ]𝑎𝑎 > −𝑅𝑅𝑅𝑅 ln − 𝐹𝐹(𝜑𝜑𝑎𝑎 − 𝜑𝜑𝑖𝑖 ) [𝐺𝐺]𝑖𝑖 [𝑁𝑁𝑎𝑎+ ]𝑖𝑖 [𝐆𝐆]𝐢𝐢 [𝑵𝑵𝒂𝒂+ ]𝒂𝒂 −𝑭𝑭(𝝋𝝋𝒂𝒂−𝝋𝝋𝒊𝒊 ) 𝑹𝑹𝑹𝑹 > 𝒆𝒆 [𝑮𝑮]𝒂𝒂 [𝑵𝑵𝒂𝒂+ ]𝒊𝒊 Diese Gleichung gibt das maximale Anreicherungsverhältnis von Glucose an. Es ist von dem NatriumKonzentrationsverhältnis sowie von dem Membranpotential abhängig. Für [𝑵𝑵𝒂𝒂+ ]𝒂𝒂 /[𝑵𝑵𝒂𝒂+]𝒊𝒊 = 𝟏𝟏𝟏𝟏 und 𝝋𝝋𝒂𝒂 − 𝝋𝝋𝒊𝒊 = −𝟔𝟔𝟔𝟔𝟔𝟔𝟔𝟔 folgt [𝐆𝐆]𝐢𝐢 /[𝐆𝐆]𝐚𝐚 = 𝟏𝟏𝟏𝟏𝟏𝟏. Bei nicht vollständiger Kopplung wird dieser Wert unterschritten. Möglicher Transportmechanismus: Carrier hat zwei Bindestellen, eine für Natrium und eine für Glucose, und kann nur durch die Membran diffundieren, wenn beide Substanzen gebunden haben. Chemiosmotische Theorie Die oxidative Phosphorylierung in Mitochondrien und die Photophosphorylierung in Chloroplasten � 𝑯𝑯 Gradienten zur Synthese von ATP. nutzt den ∆𝝁𝝁 Mitchell postulierte 1961, dass die Redoxenergie für die Reaktion 𝐴𝐴𝐴𝐴𝐴𝐴 + 𝑃𝑃𝑖𝑖 → 𝐴𝐴𝐴𝐴𝐴𝐴 intermediär in der Differenz des elektrochemischen Potentials von H+ über der inneren Mitochondrienmembran gespeichert wird. Grund: Es wurde kein energiereiches Zwischenprodukt nachgewiesen, dass die Energie für die Reaktion liefern könnte. In der Elektronentransportkette der Mitochondrien wird zu Beginn ein Wasserstoff-reiches Substrat 𝑅𝑅𝐻𝐻2 oxidiert. Die entzogenen Elektronen werden am Ende der Kette auf 𝑂𝑂2 übertragen. Zu einem gerichteten Transmembrantransport kommt es, wenn die integralen Redoxproteine der Elektronentransportkette in der Membran orientiert vorliegen: • • • 𝑅𝑅𝐻𝐻2 → 2𝑒𝑒 − + 2𝐻𝐻 + + 𝑅𝑅 (Protonen werden nach außen abgegeben). 1 𝑂𝑂 2 2 + 2𝑒𝑒 − + 2𝐻𝐻 + → 𝐻𝐻2 𝑂𝑂 (Protonen werden von innen aufgenommen). Zusätzlich wird oft direkt ein Elektronentransfer mit einem Protonenexport gekoppelt (Redox-getriebene Protonenpumpen). Dabei sind Elektronen-Aufnahme und –Abgabe gekoppelt an Übergängen zwischen Konformationen mit einwärts und auswärts orientierten Protonenbindestellen (ähnlich Mechanismus der NaK-Pumpe). Durch den gerichteten Protonen-Transport baut sich eine pH-Differenz und eine elektrische Potentialdifferenz auf, wobei der mitochondriale Innenraum ein negatives Potential annimmt (𝝋𝝋𝒊𝒊 − 𝝋𝝋𝒂𝒂 < 0) und einen geringeren pH-Wert aufweist (𝒑𝒑𝑯𝑯𝒊𝒊 − 𝒑𝒑𝑯𝑯𝒂𝒂 = ∆𝒑𝒑𝒑𝒑 < 𝟎𝟎): ∆𝜇𝜇�𝐻𝐻 = 𝑅𝑅𝑅𝑅 ln 𝑖𝑖 𝑎𝑎𝐻𝐻 𝑎𝑎 + 𝐹𝐹(𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 ) = −2,3𝑅𝑅𝑅𝑅∆𝑝𝑝𝑝𝑝 + 𝐹𝐹∆𝜑𝜑, 𝑎𝑎𝐻𝐻 ln 𝑎𝑎 = 2,3 log 𝑎𝑎 , 𝑝𝑝𝑝𝑝 = − log 𝑎𝑎 Die protonenmotorische Kraft (PMF) oder das Protonenpotential ist als elektrische Spannung definiert. Die PMF ist die gesamte effektive Potentialdifferenz, die auf das Proton wirkt. Die pHDifferenz wird durch den Faktor 2,3𝑅𝑅𝑅𝑅/𝐹𝐹 = 59𝑚𝑚𝑚𝑚 bei 𝑇𝑇 = 298𝐾𝐾 in eine elektrische Potentialdifferenz umgerechnet. ∆𝑝𝑝 = ∆𝜇𝜇�𝐻𝐻 𝑅𝑅𝑅𝑅 = −2,3 ∆𝑝𝑝𝑝𝑝 + ∆𝜑𝜑 = −59𝑚𝑚𝑚𝑚∆𝑝𝑝𝑝𝑝 + ∆𝜑𝜑 𝐹𝐹 𝐹𝐹 Welchen Einfluss ∆𝒑𝒑𝒑𝒑 und ∆𝝋𝝋 auf die PMF haben, ist von den physiologischen Bedingungen abhängig. • • Ausgehend vom Gleichgewichtszustand (∆𝑝𝑝𝑝𝑝 = 0, ∆𝜑𝜑 = 0), baut sich schnell unter Aufladung der Membrankapazität eine Potentialdifferenz auf, während der pH-Unterschied wegen der Pufferkapazität der wässrigen Medien beiderseits der Membran klein bleibt. Ist die Membran für andere Ionen permeabel, induziert ∆𝜑𝜑 einen passiven Ladungstransport, der die Tendenz hat |∆𝜑𝜑| zu verkleinern. Zum Ausgleich für diesen Ladungstransport dauert der Redox-getriebene Protonen-Transport weiter an, sodass |∆𝑝𝑝𝑝𝑝| ansteigt. Im stationären Zustand wird die Größe von ∆𝑝𝑝𝑝𝑝 und ∆𝜑𝜑 beeinflusst von der passiven Permeabilität für Protonen und andere Ionen, von der ATP-Synthese-Rate sowie anderer energetischer Kopplungen. ATP-Synthese ′ Unter Standardbedingungen wird für die ATP-Synthese ∆𝐺𝐺 0 = 30𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚 benötigt, die nach der chemiosmotischen Theorie durch Protonen-Transport entlang des elektrochemischen Gradienten aufgebracht werden. Mit der Stöchiometrie 3 Protonen für 1 ATP muss gelten: ′ ′ ∆𝜇𝜇�𝐻𝐻 ∆𝐺𝐺 0 ∆𝐺𝐺 0 |3∆𝜇𝜇�𝐻𝐻 | > �∆𝐺𝐺 � → |∆𝜇𝜇�𝐻𝐻 | > � � → |∆𝒑𝒑| = � � ≈ 𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏 � > � 3 𝐹𝐹 3𝐹𝐹 0′ Bei den Konzentration von ATP, ADP und 𝑷𝑷𝒊𝒊 ist die vorliegende PMF (|∆𝒑𝒑| = |−𝟓𝟓𝟓𝟓𝟓𝟓𝟓𝟓∆𝒑𝒑𝒑𝒑 + ∆𝝋𝝋|) größer als die erforderlichen 100 mV, nämlich im Bereich von 200 mV. Die Photophosphorylierung der Chloroplasten verläuft auf ähnliche Weise, wobei hier während dem lichtgetriebenen Elektronentransport Protonen ins Innere der Thylakoide gepumpt werden. Energetische Kopplung des Protonen-Flusses bei E.coli (1) Anreicherung von Lactose und Prolin im Zytoplasma durch positive Flusskopplung. (2) Export von Na+ und Ca2+ durch negative Flusskopplung. (3) Beim Import frei werdende Energie wird für den Antrieb der Flagellenrotation verwendet. Transport durch Membranen: Membranpotential im GG und Nicht-GG Die Differenz der elektrischen Potentiale zwischen Zellinnerem und Außenmedium 𝑉𝑉𝑚𝑚 = 𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 wird als Membranspannung oder Membranpotential bezeichnet. Berechnung des Membranpotentials im Gleichgewicht Die Membran sei nur für Kalium permeabel, dann resultiert ein Kaliumausstrom, da die Innenkonzentration größer ist als die Außenkonzentration. Dieser Ausstrom kommt im Gleichgewicht zum Erliegen, da der Konzentrationsgradient durch den sich aufbauenden, entgegen gerichteten elektrischen Gradienten kompensiert wird. Für das Membranpotential in diesem Gleichgewichtszustand gilt die Nernst-Gleichung. 𝐸𝐸𝐾𝐾 ist das Kaliumgleichgewichtspotential bei 𝑇𝑇 = 298𝐾𝐾. 𝑅𝑅𝑅𝑅 𝑐𝑐𝐾𝐾𝑎𝑎 𝑐𝑐𝐾𝐾𝑎𝑎 ln 𝑖𝑖 = 59,2𝑚𝑚𝑚𝑚 log 𝑖𝑖 = 𝐸𝐸𝐾𝐾 𝑉𝑉𝑚𝑚 = 𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 = 𝐹𝐹 𝑐𝑐𝐾𝐾 𝑐𝑐𝐾𝐾 Tatsächlich ist die Zellmembran für mehrere Ionensorten permeabel (meist für K+, Na+ und Cl-), wobei jede Ionensorte ein anderes Konzentrationsverhältnis 𝑐𝑐 𝑎𝑎 /𝑐𝑐 𝑖𝑖 besitzt. Daher ist ein Gleichgewichtszustand über die Membran nicht möglich: Wäre eine Ionensorte im Gleichgewicht, so wäre es eine andere aufgrund des unterschiedlichen Konzentrationsverhältnisses eben nicht. Das Membranpotential stellt sich daher auf einen Mittelwert der einzelnen Gleichgewichtspotentiale ein. Das Membranpotential ist nicht mehr thermodynamisch definiert – es sind Modelle erforderlich! Berechnung des Membranpotentials im Nichtgleichgewicht Die Membran sei nur für K+, Na+ und Cl- permeabel. Es gelten folgende Annahmen: (1) Membran ist im stationären Zustand (konstante Ionenkonzentrationen innen und außen). (2) Membran ist homogene Phase (ortsunabhängiges D und γ, unabhängige Wanderung der Ionen in der Membran). (3) An der Grenzfläche Membran/Wasser herrscht für alle Ionen Verteilungsgleichgewicht (Diffusion im Membraninneren bestimmt Geschwindigkeit des Ionentransports). (4) E-Feld in der Membran ist konstant (𝜑𝜑 ist linear von x abhängig = Membran ist ideales Dielektrikum = Ionenkonzentration in Membran ist null bzw. in erster Näherung klein). Für die 𝑑𝑑 = 10 𝑛𝑛𝑛𝑛 dicke Membran gilt das Prinzip der makroskopischen Elektroneutralität nicht, da 𝑑𝑑 < 𝑙𝑙𝑑𝑑 (Debye-Länge ist größer als die Membrandicke; Elektroneutralität gilt nur in Abständen größer als 𝑙𝑙𝑑𝑑 ). Die Flussdichte der Ionensorte 𝑣𝑣 in der Membran im stationären Zustand ist durch die Nernst-PlanckGleichung gegeben: 𝑑𝑑𝑐𝑐𝑣𝑣 𝐹𝐹 𝑑𝑑𝑑𝑑 + 𝑧𝑧𝑣𝑣 𝑐𝑐𝑣𝑣 � Φ𝑣𝑣 = −𝐷𝐷𝑣𝑣 � 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 Mit Annahme 4 ergibt sich das reduzierte Membranpotential 𝒖𝒖: 𝑑𝑑𝑑𝑑 𝜑𝜑𝑎𝑎 − 𝜑𝜑𝑖𝑖 𝑉𝑉𝑚𝑚 𝑅𝑅𝑅𝑅 𝑢𝑢 = =− =− ∙ , 𝑑𝑑𝑑𝑑 𝑑𝑑 𝑑𝑑 𝐹𝐹 𝑑𝑑 Die Nernst-Planck-Gleichung vereinfacht sich zu: Φ𝑣𝑣 = −𝐷𝐷𝑣𝑣 � 𝑢𝑢 = 𝐹𝐹𝑉𝑉𝑚𝑚 1 = ∙ 𝑉𝑉 𝑅𝑅𝑅𝑅 25𝑚𝑚𝑚𝑚 𝑚𝑚 𝑑𝑑𝑐𝑐𝑣𝑣 𝑢𝑢 − 𝑧𝑧𝑣𝑣 𝑐𝑐𝑣𝑣 � 𝑑𝑑𝑑𝑑 𝑑𝑑 Diese Differentialgleichung für die unbekannte Funktion 𝑐𝑐𝑣𝑣 (𝑥𝑥) muss gelöst werden. Aus Annahme 3 resultieren die Randbedingungen: An den Grenzflächen Membran/Lösung soll das Verhältnis der Konzentrationen innerhalb und außerhalb der Membran gleich dem Verteilungskoeffizienten sein. 𝑐𝑐𝑣𝑣 (0) 𝑐𝑐𝑣𝑣𝑖𝑖 = 𝑐𝑐𝑣𝑣 (𝑑𝑑) = 𝛾𝛾𝑣𝑣 𝑐𝑐𝑣𝑣𝑎𝑎 Die Differentialgleichung lässt sich damit lösen. Das Ergebnis zeigt, dass 𝑐𝑐𝑣𝑣 (𝑥𝑥) eine nicht-lineare Funktion von x ist (𝜑𝜑 dagegen ist linear von x abhängig), sondern exponentiell von x abhängig ist (ne Menge Gleichungen und Herleitung ignoriert S.400). Letztlich ergibt sich für die Ionenflussdichte Φ𝑣𝑣 in Abhängigkeit von den Ionenkonzentrationen außen und innen und vom Membranpotential u folgende Beziehung. Über diese Gleichung kann der Permeabilitätskoeffizient unter beliebigen Bedingungen (𝑉𝑉𝑚𝑚 ≠ 0) mit Hilfe von Isotopenflussmessungen bestimmt werden. 𝚽𝚽𝒗𝒗 = 𝑷𝑷𝒗𝒗 𝒛𝒛𝒗𝒗 𝒖𝒖 ∙ 𝒄𝒄𝒊𝒊𝒗𝒗 𝒆𝒆𝒛𝒛𝒗𝒗𝒖𝒖 − 𝒄𝒄𝒂𝒂𝒗𝒗 𝒆𝒆𝒛𝒛𝒗𝒗𝒖𝒖 − 𝟏𝟏 Aus den Flussdichten 𝚽𝚽𝒗𝒗 aller permeablen Ionensorten erhält man die Stromdichte 𝒋𝒋 über die Membranfläche 𝑨𝑨𝒎𝒎 . Flüsse von Kationen und Anionen in gleicher Richtung entsprechen nach der Gleichung einer elektrischen Stromdichte entgegengesetzten Vorzeichens. 𝑗𝑗 = 𝐼𝐼 = 𝐹𝐹 � 𝑧𝑧𝑣𝑣 Φ𝑣𝑣 , 𝐴𝐴𝑚𝑚 𝑣𝑣 [𝑄𝑄/𝐴𝐴 ∙ 𝑡𝑡] Im stationären Zustand des Systems ist das Membranpotential zeitlich konstant (man spricht von einem Fließgleichgewicht, aber: stationärer Zustand ≠ thermodynamischer Gleichgewichtszustand). Damit ist der elektrische Strom über die Membran gleich null (𝒋𝒋 = 𝟎𝟎). Damit gilt für eine Membran, die nur für Na+, K+ und Cl- permeabel ist: Φ𝑁𝑁𝑁𝑁 + Φ𝐾𝐾 − Φ𝐶𝐶𝐶𝐶 = 0 Mit der Gleichung für Φ𝑣𝑣 und der Resubstitution von u folgt die Goldmann-Gleichung als verallgemeinerte Nernst-Gleichung. Die Beiträge der einzelnen Ionensorten sind hier über die Permeabilitätskoeffizienten gewichtet. 𝑉𝑉𝑚𝑚 = 𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 = 𝑖𝑖 𝑎𝑎 𝑅𝑅𝑅𝑅 𝑃𝑃𝐾𝐾 𝑐𝑐𝐾𝐾𝑎𝑎 + 𝑃𝑃𝑁𝑁𝑁𝑁 𝑐𝑐𝑁𝑁𝑁𝑁 + 𝑃𝑃𝐶𝐶𝐶𝐶 𝑐𝑐𝐶𝐶𝐶𝐶 ln 𝑎𝑎 𝑖𝑖 𝐹𝐹 𝑃𝑃𝐾𝐾 𝑐𝑐𝐾𝐾𝑖𝑖 + 𝑃𝑃𝑁𝑁𝑁𝑁 𝑐𝑐𝑁𝑁𝑁𝑁 + 𝑃𝑃𝐶𝐶𝐶𝐶 𝑐𝑐𝐶𝐶𝐶𝐶 Im Grenzfall, wo die Membran überwiegend für K+ permeabel ist (𝑷𝑷𝑲𝑲 ≫ 𝑷𝑷𝑪𝑪𝑪𝑪 , 𝑷𝑷𝑲𝑲 ≫ 𝑷𝑷𝑵𝑵𝑵𝑵 ), geht die Goldmann-Gleichung in die Nernst-Gleichung für Kalium über: 𝑉𝑉𝑚𝑚 = 𝑅𝑅𝑅𝑅 𝑐𝑐𝐾𝐾𝑎𝑎 ln 𝐹𝐹 𝑐𝑐𝐾𝐾𝑖𝑖 Liegt für ein Ion 𝑣𝑣 an der Membran ein Gleichgewicht vor (𝑐𝑐𝑣𝑣𝑎𝑎 /𝑐𝑐𝑣𝑣𝑖𝑖 ist durch Nernst-Gleichung gegeben), so verschwindet der Fluss dieser Ionensorte, weshalb der Beitrag nicht in der GoldmannGleichung berücksichtigt werden muss. Die allgemeine Form der Goldmann-Gleichung lautet (A=Anionen, K=Kationen): 𝑽𝑽𝒎𝒎 = 𝑹𝑹𝑹𝑹 ∑ 𝑷𝑷𝑲𝑲 𝒄𝒄𝒂𝒂𝑲𝑲 + ∑ 𝑷𝑷𝑨𝑨 𝒄𝒄𝒊𝒊𝑨𝑨 𝐥𝐥𝐥𝐥 𝑭𝑭 ∑ 𝑷𝑷𝑲𝑲 𝒄𝒄𝒊𝒊𝑲𝑲 + ∑ 𝑷𝑷𝑨𝑨 𝒄𝒄𝒂𝒂𝑨𝑨 Die Goldmann-Gleichung wurde unter Berücksichtigung der passiven Ionenströme abgeleitet. Dabei wurde der Strombeitrag von Ionenpumpen vernachlässigt! Die Gültigkeit der GoldmannGleichung kann überprüft werden, indem die Permeabilitätskoeffizienten der einzelnen Ionen in unabhängigen Experimenten bestimmt werden. Elektrisch erregbare Membranen Der Erregungsvorgang findet im Wesentlichen an der Nervenmembran statt, während das AxonInnere (Axoplasma) hauptsächlich als passiver elektrischer Leiter und Ionenreservoir fungiert. Die ersten elektrophysiologischen Untersuchungen wurden am Riesenaxon von Tintenfischen durchgeführt, dessen Na+/K+/Cl- Konzentrationen innen und außen denen der meisten tierischen Zellen entsprechen (Innen wenig Na+, viel K+, wenig Cl-; außen umgekehrt). Die Gradienten werden durch ATPgetriebene Ionenpumpen aufrecht erhalten. Die Abbildung zeigt zur Orientierung physiologische und nichtphysiologische Strombereiche im Vergleich. Das Ruhepotential der Axonmembran Der unerregte Zustand des Tintenfischaxons ist durch 𝑉𝑉𝑚𝑚 = 𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 = −60𝑚𝑚𝑚𝑚 charakterisiert (Bei Säugern findet man typischerweise 𝑉𝑉𝑚𝑚 = −70𝑚𝑚𝑚𝑚 in Nervenzellen). Das Ruhepotential wird hauptsächlich durch K+, weniger durch Na+ bestimmt. Dies ist auf die Aktivität der Na+-K+-Pumpe zurückzuführen (Spannungsabhängige Na+- und K+-Kanäle sind geschlossen), wobei die Membran für Natrium weitgehend impermeabel, aber für Kalium aufgrund anderer geöffneter Kalium-Kanäle permeabel ist (solche K+-Kanäle haben keinen S4 Sensor und können nicht auf verschiedene Spannungen reagieren). Damit werden Natrium-Ionen über die Na+K+-Pumpe nach außen transportiert und bleiben dort. Kalium-Ionen wandern über die Pumpe nach Innen und gelangen über den sich aufbauenden Gradienten über Kanäle wieder nach außen (hohe Permeabilität). Daher bestimmt der Kalium-Diffusionsgradient das Ruhepotential, bei dem sich ein Fließgleichgewicht zwischen Kalium-Diffusion nach Außen über Kanäle und Kalium-Transport nach Innen über die Pumpe eingestellt hat. Die Goldmann-Gleichung lautet für das Ruhepotential: 𝑎𝑎 𝑅𝑅𝑅𝑅 𝑃𝑃𝐾𝐾 𝑐𝑐𝐾𝐾𝑎𝑎 + 𝑃𝑃𝑁𝑁𝑁𝑁 𝑐𝑐𝑁𝑁𝑁𝑁 𝑉𝑉𝑚𝑚 = ln 𝑖𝑖 𝐹𝐹 𝑃𝑃𝐾𝐾 𝑐𝑐𝐾𝐾𝑖𝑖 + 𝑃𝑃𝑁𝑁𝑁𝑁 𝑐𝑐𝑁𝑁𝑁𝑁 Daraus ergibt sich mit 𝑽𝑽𝒎𝒎 = −𝟔𝟔𝟔𝟔𝟔𝟔𝟔𝟔 ein Permeabilitätsverhältnis für den Ruhezustand einer Nervenfaser von 𝑷𝑷𝑲𝑲 /𝑷𝑷𝑵𝑵𝑵𝑵 = 𝟏𝟏𝟏𝟏. Dies zeigt ebenso, dass das Ruhepotential hauptsächlich durch die Permeabilität von Kalium zustande kommt. Mittels Nernst-Gleichung lässt sich das Membran-Potential berechnen, das entsteht, wenn die Membran ausschließlich für Kalium-Ionen permeabel ist. Der Unterschied zwischen gemessenem und berechnetem Wert kommt durch eine (geringe) Permeabilität für Natrium- und Chlorid-Ionen zustande. EK = [K + ] RT ⋅ ln o+ = −91mV zF [Ki ] Das Ersatzschaltbild einer Nervenmembran Das Ruhemembranpotential lässt sich auch durch das Ersatzschaltbild einer Nervenmembran (Kanäle = parallel geschaltete Batterien mit Widerstand) unter Verwendeung der Knotenregel (In einem Knotenpunkt eines elektrischen Netzwerkes ist die Summe der zu- und abfließenden Ströme identisch) berechnen, wenn Gleichgewichtspotentiale und Leitfähigkeiten der einzelnen Kanäle bekannt sind. Die Ionenleitfähigkeit lässt sich über verschiedene Techniken getrennt bestimmen (Membranleitfähigkeit mittels voltage-clamp messen und dann selektiv nur eine Ionensorte ins Außenmedium geben oder selektiv Ionenkanäle blockieren) Aus Knotenregel folgt: −𝐼𝐼𝑁𝑁𝑁𝑁 = 𝐼𝐼𝐾𝐾 → 𝐼𝐼𝑁𝑁𝑁𝑁 + 𝐼𝐼𝐾𝐾 = 0 Für i=K,Na ergeben sich die jeweilige Beiträge zum anliegenden Membranpotential aus der Summe aus dem Ionen-Gleichgewichtspotential und der Spannung U=IR=I/g. 𝑉𝑉𝑚𝑚 = 𝐸𝐸𝑖𝑖 + 𝐼𝐼𝑖𝑖 → 𝐼𝐼𝑖𝑖 = 𝑔𝑔𝑖𝑖 ∙ (𝑉𝑉𝑚𝑚 − 𝐸𝐸𝑖𝑖 ) 𝑔𝑔𝑖𝑖 Einsetzen in 𝐼𝐼𝑁𝑁𝑁𝑁 + 𝐼𝐼𝐾𝐾 = 0 ergibt die folgende Beziehung (rechts allgemein formuliert). Aktionspotentiale 𝑉𝑉𝑚𝑚 = (𝐸𝐸𝑁𝑁𝑁𝑁 ∙ 𝑔𝑔𝑁𝑁𝑁𝑁 ) + (𝐸𝐸𝐾𝐾 ∙ 𝑔𝑔𝐾𝐾 ) ∑𝑖𝑖 𝐸𝐸𝑖𝑖 ∙ 𝑔𝑔𝑖𝑖 → 𝑉𝑉𝑚𝑚 = ∑𝑖𝑖 𝑔𝑔𝑖𝑖 𝑔𝑔𝑁𝑁𝑁𝑁 + 𝑔𝑔𝐾𝐾 Die Messung von Aktionspotentialen erfolgt durch Reizung des Nervenendes über einen Strompuls. Die Richtung des Strompulses muss die Ladung der Membrankapazität an der Reizstelle betragsmäßig vermindern (z.B. von -60mV auf -30mV). Mit zwei Mikroelektroden in einem Abstand 𝒂𝒂 kann eine zeitlich um ∆𝒕𝒕 verzögerte, vorübergehende Änderung der Membranspannung von negativen auf positive Werte beobachtet werden. Aus 𝑣𝑣 = 𝑎𝑎/∆𝑡𝑡 kann die Fortleitungsgeschwindigkeit des Nervenimpulses bestimmt werden. Sie steigt mit dem Durchmesser der Nervenfaser. Bei einer Riesenfaser mit 0,5mm Durchmesser sind Werte von 𝒗𝒗 = 𝟓𝟓𝟓𝟓𝟓𝟓/𝒔𝒔 möglich. Kabeleigenschaften des Axons Ein Axon besitzt einen elektrisch gut leitenden Kern (Axoplasma) und eine schlecht leitende Hülle (Membran), weshalb es einem Kabel gleicht. Kabel leiten elektrische Signale passiv weiter (elektrotonische Weiterleitung), während Nervenaxone zusätzlich aktive Weiterleitung ermöglichen (hier vernachlässigt). Am Ende des Kabels liegt die Spannung 𝑽𝑽𝟎𝟎 zwischen Axoplasma und Außenphase an. Da über die Membran ein elektrischer Strom vom Axoplasma in die Außenphase fließen kann und der spezifische Widerstand an jedem Punkt des Axons gleichgroß ist (𝑅𝑅 = 𝑈𝑈/𝐼𝐼 = 𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾; wenn I kleiner wird, muss auch U kleiner werden), nimmt die am Ende des Kabels angelegte Spannung längs des Kabels ab. Die abnehmende Spannung ist damit eine Folge der Spannungsteilung zwischen Axoplasma und Membran. Im elektrischen Ersatzschaltbild wird ein Axonabschnitt näherungsweise als Tiefpass gezeichnet: Im Zytoplasma herrscht in jedem Axonabschnitt ein Innenwiderstand. Das Zytoplasma ist über eine Membran (Kondensator) mit der extrazellulären Lösung verbunden. Der Widerstand der Membran ist hier vernachlässigt. Nach Ausschalten der Eingansfunktion resultiert exp. Abfall! Die elektrotonische Weiterleitung führt damit zu einer exponentiellen Abschwächung des elektrischen Signals V mit dem Abstand x zur Spannungsquelle des Axons. Die Längskonstante 𝝀𝝀 ist der Abstand, in dem das Signal auf 1/e seines Anfangswertes abgefallen ist. Sie ist abhängig vom Radius 𝑟𝑟 des Axoplasmas, dem spezifischen Widerstand 𝑅𝑅𝑖𝑖 des Axoplasmas sowie dem spezifischen Flächenwiderstand 𝑅𝑅𝑚𝑚 der Membran. 𝑉𝑉 = 𝑉𝑉0 𝑒𝑒 −𝑥𝑥/𝜆𝜆 , 𝑟𝑟𝑅𝑅𝑚𝑚 𝜆𝜆 = � 2𝑅𝑅𝑖𝑖 Ein hochwertiges Kabel besitzt eine große Längskonstante. In der Biologie führt die Erhöhung von Membran-Widerstand über Myelierung (gute Isolierung, siehe Nervenzellen von Vertebraten) oder des Querschnitts der Zelle (Leitungsdurchmesser erhöht, siehe Riesenaxon von Tintenfischen) zu einer Vergrößerung der Längskonstante, während der Widerstand des Axoplasmas kaum beeinflussbar ist. • • Transatlantik-Kabel: 𝜆𝜆 = 100 − 1000𝑘𝑘𝑘𝑘 Riesenaxon: 𝜆𝜆 = 5𝑚𝑚𝑚𝑚 (𝑟𝑟 = 0,25𝑚𝑚𝑚𝑚, 𝑅𝑅𝑀𝑀 = 700Ω𝑐𝑐𝑚𝑚2 , 𝑅𝑅𝑖𝑖 = 30Ω𝑐𝑐𝑐𝑐) Da das Signal in einem Riesenaxon längs des gesamten Axons nahezu dieselbe Amplitude hat, ist dies nicht durch elektrotonische Weiterleitung zu erklären. Damit die Impulsamplitude konstant bleibt, muss eine Energiequelle her: es handelt sich um einen aktiven Mechanismus. Für die Weiterleitung ist nur die Axonmembran erforderlich: Nach Entfernung des Axoplasmas und Durchströmung mit geeigneter Elektrolytlösung (Perfusion) ist immer noch eine Weiterleitung zu messen. Während Axons einen aktiven Nervenfortsatz darstellen (Leitfähigkeiten sind vom momentanen Membranpotential und von der Zeit 𝑡𝑡 abhängig), also nicht alleine durch die Kabeleigenschaften definiert sind, stellen Dendriten einen passiven Nervenfortsatz (Leitfähigkeiten sind Konstanten), weshalb die Ausbreitung des elektrischen Signals hier vollständig durch die Kabelgleichung beschrieben ist. Schwellenwertverhalten des Aktionspotentials Zur Messung des Aktionspotentials an einem Riesnaxon muss die Außenelektrode die Form eines koaxialen Zylinders aufweisen. Durch kurze Stromimpulse kann das im Ruheszustand auf der Innenseite negative Membranpotential in Richtung positiver Werte (Depolarisation) oder in Richtung negativer Werte (Hyperpolarisation) verschoben werden. Bei Hyperpolarisation und schwacher Depolarisation resultiert ein rein passives Verhalten der Axonmembran (Verhalten wie Parallelschaltung von Widerstand und Kapazität). Bei stärkerer Depolarisation über einen bestimmten Schwellenwert resultiert ein Aktionspotential, das den schnellen Anstieg des Membranpotentials auf positive Werte und die sofortige Rückkehr zum Ruhepotential induziert (Kurve 4). Die Form des Aktionspotentials ist von der Stärke des Reizes fast unabhängig. Aktionspotentiale können über verschiedene Mechanismen ausgelöst werden: • • Mechanischer oder chemischer Reiz bewirkt Änderung in Ionenpermeabilitäten, was entsprechend der GoldmanGleichung eine Depolarisation der Axonmembran zur Folge hat. An Synapsen wird die Ionenpermeabilität der Axonmembran über die Ausschüttung einer Transmittersubstanz beeinflusst. Neben den Ohm’schen Kanälen gibt es Kanäle, die keine lineare Abhängigkeit zwischen Strom und Membranpotential haben. Ursache ist eine Abhängigkeit der Leitfähigkeit vom Membranpotential. Aus den Strom-Spannungskennlinien lässt such aus der Steigung direkt die Leitfähigkeit ablesen. Ist diese kontant (Geradengleichung), so handelt es sich um ein Ohmsches Verhalten. Strom-Spannungskennlinie eines Ohmschen Kanals Strom-Spannungskennlinie eines Nicht-Ohmschen Kanals Strom-Spannungskennlinie einer Nervenmembran Ionenströme bei der Nervenerregung Während des Aktionspotentials zeigen Membranpotential und Strom durch die Membran kompliziertes Zeitverhalten. Mithilfe der Spannungsklemme (voltage clamp) kann dieses Verhalten vereinfacht werden, indem die Spannung über die Membran konstant gehalten wird. Dabei werden in das Axon eine stromzuführende Elektrode und eine Spannungsmesselektrode eingeführt, die über eine Regelschaltung verbunden sind; Der durch die Membran fließende Strom 𝐼𝐼 wird durch die stromzuführende Elektrode so reguliert, dass das Membranpotential 𝑉𝑉𝑚𝑚 den einstellbaren, zeitlich konstanten Wert 𝑉𝑉𝑒𝑒 beibehält. Der Anstieg vom Ruhepotential auf 𝑉𝑉𝑚𝑚 = 𝑉𝑉𝑒𝑒 ist dabei sprunghaft (< 0,1𝑚𝑚𝑚𝑚). Für Voltage-Clamp gilt als Vorzeichenkonvention für den Membranstrom 𝐼𝐼: 𝑰𝑰 > 0, wenn positive Ladungen von innen nach außen fließen. Beim Ruhepotential ist der Membranstrom definitionsgemäß null. Bei schneller Änderung von 𝑽𝑽𝒎𝒎 resultiert aufgrund der Entladung der sehr hohen Membrankapazität eine kapazitive Stromspitze 𝑰𝑰𝒌𝒌𝒌𝒌𝒌𝒌 . Es folgt ein nach innen gerichteter Strom, der nach etwa 1 ms in einen nach außen gerichteten Strom übergeht. Der Gesamtstrom 𝐼𝐼𝐺𝐺𝐺𝐺𝐺𝐺 = 𝐼𝐼𝑁𝑁𝑁𝑁 + 𝐼𝐼𝐾𝐾 + 𝐼𝐼𝐿𝐿 setzt sich additiv aus einem durch Na+ und einem durch K+ getragenen Strom zusammen. Es kommt ein Leckstrom 𝑰𝑰𝑳𝑳 hinzu, der hauptsächlich durch Cl--Transport verursacht wird. Die relativen Anteile von 𝑰𝑰𝑵𝑵𝑵𝑵 und 𝑰𝑰𝑲𝑲 am Gesamtstrom verändern sich über die Zeit des Aktionspotentials erheblich: Gezeigt werden konnte dies durch selektive Blockade einzelner Ionenströme über: Austausch von Ionen im Außenmedium; Veränderung der Ionen im Zellinneren bei perfundierten Axonen; Inhibition der Ströme durch Gifte. + + • Na gegen Cholin im Außenmedium austauschen oder Blockade des Natriumstroms durch Terodotoxin (TTX, wirkt an der Außenseite des Axons) Nur Ausstromsignal bleibt übrig. Der frühe Einwärtsstrom besteht damit fast ausschließlich aus einem passiven Natriumstrom. • Tetraethylamonium (TEA wirkt an der axoplasmatischen Seite des Axons) blockiert den Kaliumstrom Nur Einstromsignal bleibt übrig. Der späte Auswärtsstrom kommt durch einen passiven Kaliumstrom zustande. • Die Ströme sind rein passiver Natur. Bestätigt wird dies dadurch, dass perfundierte Axonen über längere Zeit Erregbarkeit zeigen, obwohl keine metabolischen Energiequellen vorhanden sind. Voraussetzung ist nur die Aufrechterhaltung der physiologischen Na+/K+ Konzentrationen. Umkehrpotential Wenn nur Natrium-Ionen über die Membran fließen können (z.B. durch Einwirkung von TEA), sollte beim NatriumGleichgewichtspotential kein Nettofluss vorliegen (kein Strom messbar). Das Natriumgleichgewichtspotential ist durch die Nernst-Gleichung gegeben: 𝐸𝐸𝑁𝑁𝑁𝑁 = 𝑎𝑎 𝑅𝑅𝑅𝑅 𝑐𝑐𝑁𝑁𝑁𝑁 𝑅𝑅𝑅𝑅 460𝑚𝑚𝑚𝑚 ln 𝑖𝑖 = ln = +55𝑚𝑚𝑚𝑚 𝐹𝐹 𝑐𝑐𝑁𝑁𝑁𝑁 𝐹𝐹 50𝑚𝑚𝑚𝑚 Wird also 𝑉𝑉𝑚𝑚 = 𝑉𝑉𝑒𝑒 = 𝑬𝑬𝑵𝑵𝑵𝑵 = +𝟓𝟓𝟓𝟓𝟓𝟓𝟓𝟓 eingestellt, so findet kein Nettofluss von Natrium-Ionen statt, da der Konzentrationsgradient von außen nach innen durch das innen gegen außen positive elektrische Potential von +55 𝑚𝑚𝑚𝑚 kompensiert wird. Für 𝑉𝑉𝑚𝑚 > 55𝑚𝑚𝑚𝑚 resultiert Auswärtsstrom, für 𝑉𝑉𝑚𝑚 < 55𝑚𝑚𝑚𝑚 Einwärtsstrom. Das Membranpotential, bei dem der Strom seine Richtung umkehrt heißt Umkehrpotential. Quantitative Betrachtung des Natriumeinstroms Die Anzahl notwendiger Na+-Ionen Δ𝑛𝑛 = Δ𝑄𝑄/𝑧𝑧𝑧𝑧 (𝑧𝑧 = 1), um die Membrankapazität vom Ruhepotential (-60mV) auf den Maximalwert des Aktionspotentials (+40mV) umzuladen, ist direkt aus der notwendigen Ladung Δ𝑄𝑄 zugänglich. Bei Betrachtung der Einheitsfläche der Membran (Kapazität 𝐶𝐶𝑚𝑚 ), benötigt man für eine Spannungsänderung Δ𝑉𝑉𝑚𝑚 demnach: 𝛥𝛥𝛥𝛥 = 𝛥𝛥𝛥𝛥 𝐶𝐶𝑚𝑚 𝛥𝛥𝑉𝑉𝑚𝑚 1µ𝐹𝐹𝐹𝐹𝐹𝐹−2 ∙ 100𝑚𝑚𝑚𝑚 = = = 10−12 𝑚𝑚𝑚𝑚𝑚𝑚 𝑐𝑐𝑚𝑚−2 𝐹𝐹 𝐹𝐹 105 𝐶𝐶𝐶𝐶𝐶𝐶𝑙𝑙 −1 Die Anzahl an Ionen pro Aktionspotential können auch über Messung mit radioaktiven Isotopen (24Na+, 42K+) erhalten werden. Der experimentelle Wert liegt etwa bei ∆𝒏𝒏 = 𝟑𝟑 ∙ 𝟏𝟏𝟏𝟏−𝟏𝟏𝟏𝟏 𝒎𝒎𝒎𝒎𝒎𝒎 𝒄𝒄𝒎𝒎−𝟐𝟐 Na+-Ionen, die bei einem Aktionspotential in das Axon importiert werden; dabei werden etwa gleich viele K+-Ionen exportiert. Dies sind damit nur geringfügig mehr, als für die Umladung der Membrankapazität notwendig ist. Der Faktor 3 erklärt sich dadurch, dass sich Natrium-Einstrom und Kalium-Ausstrom zeitlich teilweise überlagern und daher mehr Natrium-Ionen notwendig sind, um die gegebene Peak-Spitze zu erreichen. Die durch das Aktionspotential im Axoplasma eingetretenen Konzentrationsänderungen werden durch die ATP-getriebene Na,K-Pumpe langsam wieder rückgängig gemacht. Mechanismus des Aktionspotentials Die Natrium- und Kalium-Kanäle werden durch das elektrische Feld gesteuert: Sie sind beide im Ruhezustand der Membran geschlossen. Der Na-Kanal öffnet sich nach der Depolarisation für kurze Zeit, wonach er schnell wieder inaktiviert wird – Inaktivierung und Aktivierung verlaufen nach unterschiedlichen Mechanismen (offener, geschlossener, inaktiver Zustand). Der K-Kanal öffnet sich nach der Depolarisation zeitlich verzögert und bleibt geöffnet, solange die Depolarisation aufrechterhalten wird (offener, geschlossener Zustand). Im Ruhezustand ist das Aktivierungstor des Na-Kanals geschlossen, das Inaktivierungstor geöffnet. Beim maximalen Na-Einstrom sind beide Tore geöffnet, während das Tor des K-Kanals noch geschlossen ist. Beim maximalen K-Ausstrom ist das Inaktivierungstor des Na-Kanals geschlossen und das Aktivierungstor des K-Kanals geöffnet. • • • • • • Depolarisation von -60mV auf -40mV (Schwellenwert) öffnet einige Na+-Kanäle. Der Na+-Einstrom bewirkt die Öffnung weiterer Na+-Kanäle, wodurch sich das Depolarisationssignal verstärkt. Maximal könnte das Mambranpotential bis zum Na+-Gleichgewichtspotential von +55mV ansteigen, wobei es tatsächlich einen Wert von +40mV erreicht. Durch den Inaktivierungsmechanismus des Na+-Kanals wird dieser nach 2 ms geschlossen. Gleichzeitig wird der K+-Kanal geöffnet, wodurch das Membranpotential wieder auf negative Werte absinkt. Die K+-Kanäle schließen sich allmählich, wenn das Membranpotential negativ geworden ist. Zudem kehren die Na+-Kanäle in den Ausgangszustand zurück (Inaktivierung aufgehoben, Kanal aber geschlossen). Die Zelle ist in ihr Ruhepotential zurückgekehrt (elektrisch wieder gleich, die Konzentrationen von Natrium- und Kalium-Ionen innen und außen sind aber vertauscht). Die Na+K+-ATPase pumpt die Natrium und Kalium Ionen, die während des Aktionspotentials die Seiten getauscht haben, wieder zurück. Einige ms nach dem Aktionspotential ist das Axon aufgrund der „falschen“ Konzentrationsverhältnisse von Natrium und Kalium unerregbar (Refraktärperiode). Hauptgrund ist jedoch die Inaktivierung der Na+-Kanäle, die keine weitere Reizung zulässt. Nach einem Aktionspotential bringen die geöffneten K+-Kanäle das Membranpotential in die Nähe des K+-Gleichgewichtspotentials. Diese Tatsache erklärt das negative Nachpotential am Ende des Aktionspotentials: Das K+-Gleichgewichtspotential liegt niedriger als das GG der Na,K-Pumpe, sodass sich das Ruhepotential erst langsam wieder einstellt (Pumpen arbeiten langsamer als Kanäle). Dynamik der Kalium- und Natrium-Leitfähigkeit Abhängigkeit vom Membranpotential Abhängigkeit von der Dauer des Reizes Vergleich der Einzelkanal-Leitfähigkeiten mit dem Aktionspotential Der Auslöser der Aktionspotentiale ist meist ein Transmitter aus einer Nachbarzelle, der die Öffnung chemisch gesteuerter Ionenkanäle induziert. Wird der Schwellenwert überschritten öffnen sich die Spannungs-gesteuerten Ionenkanäle, wodurch es zum Aktionspotential kommt. Die lokal erzeugte Depolarisation wird über die Kabeleigenschaften des Axons passiv auf benachbarte Teile des Axons übertragen, wodurch auch hier die Schwelle zum Aktionspotential erreicht wird (Aktionspotential wandert entlang des Axons). In myelierten Fasern spielt sich der Erregungsvorgang an den Schnürringen ab, welche die Myelinscheiden in regelmäßigen Abständen unterbrechen. Nur an den Schnürringen steht die Axonmembran in Kontakt mit extrazellulärem Medium. Das Aktionspotential zwischen den Schnürringen breitet sich passiv anhand der Kabeleigenschaften aus. Die Längskonstante des myelierten Axons ist aufgrund der guten Isolation sehr hoch, sodass am nächsten Schnürring das neue Aktionspotential erreicht wird (saltatorische Erregungsleitung). Wegen der niedrigen elektrischen Kapazität der Myelinscheiden werden an myelinierten Fasern ähnlich hohe Leitungsgeschwindigkeiten erreicht wie an Riesenaxonen. Die Ausbreitungs-Geschwindigkeit ist an den Schnürringen (Auslösung des Aktionspotentials) wesentlich niedriger, als in myelierten Bereichen (passive Weiterleitung). Die Geschwindigkeit ist antiproportional zum Membranwiderstand und zum Axondurchmesser. Spannungsabhängige Steuerung von Ionenkanälen, Torströme Der Steuerungsmechanismus beruht auf einer Konformationsänderung, induziert durch das elektrische Feld. Bei einer 5 nm dicken Membran und einer transmembranären Spannung von 100 mV resultiert eine Feldstärke von 10−4 𝑘𝑘𝑘𝑘/5 ∙ 10−6 𝑚𝑚𝑚𝑚 = 𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐/𝒎𝒎𝒎𝒎 , die der Durchbruchsfeldstärke vieler Materialien nahe kommt (z.B. Luft ~2kV/mm, Glas 10kV/mm, PCV 30kV/mm). Elektrische Felder greifen an Ladungen an, sodass die Konformationsänderung durch eine Verschiebung geladener Gruppen oder eine Rotation elektrischer Dipole (z.B. Carbonylgruppen) eingeleitet wird. Dabei wandert eine positive Ladung des Kanals immer zur Membranseite mit negativem Potential, wobei an die Ladung eine mechanische Barriere gekoppelt ist, welche den Kanal öffnet oder schließt. Die hierfür verantwortliche Kanal-Region heißt Spannungs-Sensor. Übergänge zwischen geschlossener und offener Konformation gleichen einer monomolekularen Reaktion. 𝑁𝑁 ist die Zahl der geschlossenen bzw. offenen Kanäle und 𝐾𝐾 die Gleichgewichtskonstante der Reaktion: ∆𝐺𝐺 0 𝑁𝑁𝑜𝑜 = 𝐾𝐾 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 𝑁𝑁𝑔𝑔 ∆𝐺𝐺 0 ist die Änderung der freien Enthalpie beim Übergang von 1 mol Kanalprotein vom geschlossenen in den offenen Zustand. Da Ladungen durch das E-Feld verschoben werden, beinhaltet ∆𝐺𝐺 0 einen elektrostatischen Anteil ∆𝐺𝐺𝑒𝑒𝑒𝑒0 = −𝑧𝑧𝑧𝑧𝑁𝑁𝐴𝐴 ∙ 𝑉𝑉𝑚𝑚 = −𝑧𝑧𝑧𝑧 ∙ 𝑉𝑉𝑚𝑚 (elektrische Energie = Ladung mal Spannung), wobei z Elementarladungen pro Kanalprotein über die Membran verschoben werden. Das Minuszeichen kommt wegen der Definition des Membranpotentials: negatives 𝑉𝑉𝑚𝑚 = 𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 erhöht die Zahl geschlossener Kanäle und 0 korreliert sein. ∆𝐺𝐺�0 muss daher mit einem positiven ∆𝐺𝐺𝑒𝑒𝑒𝑒 ist die Änderung der freien Enthalpie ∆𝐺𝐺 0 bei 𝑉𝑉𝑚𝑚 = � ist die Gleichgewichtskonstante 𝐾𝐾 bei 𝑉𝑉𝑚𝑚 = 0. 0. 𝐾𝐾 ∆𝐺𝐺 0 = ∆𝐺𝐺�0 + ∆𝐺𝐺𝑒𝑒𝑒𝑒0 = ∆𝐺𝐺�0 − 𝑧𝑧𝑧𝑧 ∙ 𝑉𝑉𝑚𝑚 𝑧𝑧𝑧𝑧∙𝑉𝑉𝑚𝑚 𝑧𝑧𝑧𝑧∙𝑉𝑉𝑚𝑚 ∆𝐺𝐺 0 ∆𝐺𝐺� 0 𝑁𝑁𝑜𝑜 − − � ∙ 𝑒𝑒 𝑅𝑅𝑅𝑅 𝑅𝑅𝑅𝑅 = 𝐾𝐾 = 𝑒𝑒 = 𝑒𝑒 𝑅𝑅𝑅𝑅 ∙ 𝑒𝑒 𝑅𝑅𝑅𝑅 = 𝐾𝐾 𝑁𝑁𝑔𝑔 Da der Natrium-Strom 𝑰𝑰𝑵𝑵𝑵𝑵 proportional zur Zahl 𝑵𝑵𝒐𝒐 offener Natriumkanäle ist, kann man aus der Spannungsabhängigkeit von 𝑰𝑰𝑵𝑵𝑵𝑵 die Zahl der verschobenen Ladungen pro Kanal bestimmen. Für den Na+-Kanal wurde z=6, für den K+-Kanal z=4,5 gezeigt. Diese Werte bedeuten, dass sich entweder z=6 bzw. z=4,5 Ladungen über die gesamte Membran oder entsprechend größere Ladungen über eine geringere Distanz bewegen. Die Ladungsverschiebung entspricht einem kurzzeitigen elektrischen Strom. Dieser Torstrom (gating current) kann experimentell nachgewiesen werden. Schwierigkeiten sind die Überdeckung durch den viel größeren Ionenstrom durch den Kanal und durch den kapazitiven Aufladestrom, der im selben Zeitbereich wie der Torstrom liegt. Der Torstrom 𝑰𝑰𝑻𝑻 ergibt sich als Differenz der transienten Membranströme nach einem depolarisierenden (−𝟕𝟕𝟕𝟕𝟕𝟕𝟕𝟕 → 𝟎𝟎𝟎𝟎𝟎𝟎) und einem hyperpolarisierenden (−𝟕𝟕𝟕𝟕𝟕𝟕𝟕𝟕 → −𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏) Spannungssprung, wodurch der kapazitive Strom herausgemittelt wurde. Übertragung des Nervenimpulses über Synapsen Neuronen sind über Synapsen indirekt miteinander verknüpft. Der synaptische Spalt zwischen den miteinander verbundenen Zellen misst 20 bis 50nm. Die präsynaptische Zelle (sensorische Zelle oder Neuron) überträgt den Impuls über die Synapse zur postsynaptischen Zelle (Neuron, Drüßenzelle oder Muskelzelle). Verbindungen zwischen Neuron und Muskelzelle werden „neuromuscular junctions“ genannt. Hier ist ein Motoraxon mit den Muskelfibrillen des Skelettmuskels verbunden. In den synaptischen Endknöpfchen befinden sich viele Vesikel, in denen Neurotransmitter (z.B.: Acetylcholin, Norepinephrin) gespeichert werden, welche mit der postsynaptischen Zelle interagieren, indem sie die Impulse zum Skelettmuskel oder Herzmuskel übertragen. Wenn ein Impuls das synaptische Endknöpfchen erreicht, induziert die Depolarisation das Öffnen von voltage-gated Calcium-Kanälen an der präsynaptischen Membran. Dadurch strömen Calcium Ionen in die Zelle und erhöhen die Ca2+-Konzentration um das tausendfache um die Kanäle herum. Calcium initiiert die Fusion eines oder weniger Vesikel mit der präsynaptischen Membran, wodurch die Neurotransmitter in den synaptischen Spalt entlassen werden. Sie diffundieren in Richtung postsynaptischer Membran und binden spezifisch an Membran-assoziierte Rezeptoren. • • Der gebundene Neurotransmitter aktiviert das Öffnen von Kation-selektiven Kanälen (Influx von Natrium-Ionen Depolarisation weniger negatives Membran-Potential). Dies kann zu einem Aktionspotential führen. Der gebundene Neurotransmitter aktiviert das Öffnen von Anion-selektiven Kanälen (Influx von Chlorid-Ionen Hyperpolarisation negativeres Membran-Potential). Dies inhibiert Aktionspotentiale. Die meisten Nervenzellen im Gehirn empfangen exzitatorische und inhibitorische Signale von verschiedenen präsynaptischen Neuronen. Die Summe der Impulse entscheidet, ob ein Aktionspotential ausgelöst wird oder nicht. Ob ein Neurotransmitter eine aktivierende oder inhibierende Wirkung hat, hängt von den Rezeptoren ab (ACh inhibiert Kontraktion des Herzens und aktiviert Kontraktion des Skelettmuskels). Innerhalb des Gehirns wirkt Glutamat als primärer exzitatorische Neurotransmitter, während γ-Aminobuttersäure (GABA) als primärer inhibitorischer Neurotransmitter fungiert. Wirkung von Drogen auf die Nervenreizweiterleitung Die im synaptischen Spalt befindlichen Neurotransmitter müssen nach einer kurzen Zeit eliminiert werden, um eine Dauerreizung der postsynaptischen Zelle zu verhindern. Dies geschieht über zwei Wege, welche die Dauer eines Impulses auf nur wenige ms reduzieren. • • Enzyme zerstören die Neurotransmitter im synaptischen Spalt. Proteine transportieren die Neurotransmitter zurück zum synaptischen Endknöpfchen. Wenn die Acetylcholin-Esterase durch das Nervengas DFP (Diisopropylfluorophosphat) inhibiert wird, kontrahieren alle Muskeln unkontrolliert (ACh ist ständig im synaptischen Spalt präsent). Kokain verhindert die Wiederaufnahme des Neurotransmitters Dopamin, das vom limbischen System (Belohnungszentrum) freigesetzt wird, wodurch ein Gefühl der Euphorie und das Bedürfnis die Aktivität ständig zu wiederholen, entsteht. Amphetamine agieren ebenso mit Dopamin sezernierenden Neuronen: sie beschleunigen die Abgabe von Dopamin und verlangsamen die Wiederaufnahme. Gentechnisch veränderte Mäuse, welche keinen Dopamin-Transporter (DAT) zur Wiederaufnahme aufweisen zeigen dieselben Symptome wie normale Mäuse, die Kokain oder Amphetamine nehmen. Δ9-Tetrahydrocannabinol (Wirkstoff von Marihuana) bindet an Cannabinoid-Rezeptoren (CB1) bestimmter Neuronen und reduziert damit die Wahrscheinlichkeit, dass diese Neuronen Neurotransmitter freisetzen (Schutz vor Reizüberflutung). CB1 interagiert normalerweise mit Endocannabinoiden, welche von der postsynaptischen Membran nach ihrer Depolarisation synthetisiert werden. Diese Substanzen diffundieren rückwärts durch die präsynaptische Membran, wo sie an CB1 binden und die synaptische Aktivität herabsetzen. CB1 ist hauptsächlich am Hippocampus und Cerebellum des Gehirns lokalisiert (deshalb geringere Erinnerungs- und motorische Koordinations-Funktionen). Synaptische Plastizität Synapsen zeigen erstaunliche dynamische Fähigkeiten (synaptische Plastizität), welche bei der Entwicklung des neuronalen Kreislaufs besonders in der Kindheit wichtig sind. Der Hippocampus ist wichtig für Lernvorgänge und das Kurzzeit-Gedächtnis und es ist einer der Hauptbereiche, die durch Alzheimer zerstört werden. Wenn Neuronen im Hippocampus wiederholend kurzzeitig stimuliert werden, so werden die Synapsen, welche diese Neuronen verbinden durch long-term-potentiation (LTP) verstärkt. Diese Verstärkung kann Tage, Wochen oder länger anhalten. Der NMDA-Rezeptor ist einer der verschiedenen Rezeptor-Typen, welcher Glutamat bindet. Wenn Glutamat an diesen postsynaptischen Rezeptor bindet, öffnet sich ein interner Kationen-Kanal, der den Einstrom von Calcium-Ionen in die postsynaptische Zelle induziert. Calcium ist für eine SignalKaskade verantwortlich, welche zum LTP führt. Nach einer LTP können die Neuronen auf geringere Signale reagieren und können eine intensivere Antwort bei postsynaptischen Zellen hervorrufen. LTP spielt eine entscheidende Rolle für Lernprozesse (wird LTP inhibiert, wird auch die Fähigkeit neue Information aufzunehmen erheblich reduziert). Hodgin-Huxley-Gleichungen Die Hodgin-Huxley-Gleichungen: Mathematische Beschreibung des Aktionspotentials (S419-422 ignoriert). Die Hodkin-Huxley-Gleichungen sind Differentialgleichungen, welche den Zeitverlauf sowie die Ortsabhängigkeit (Ausbreitung wie eine Welle entlang des Axons) des Aktionspotentials beschreiben. Messung von Einzelkanal-Strömen mit der Saugpipetten-Technik Einzelkanalexperimente am Na+-Kanal der Nervenmembran Einzelkanalfluktuationen werden bei konstanter Membranspannung detektiert. Dies ist beim Spannungs-abhängigen Na+-Kanal der Nervenmembran wegen seines Inaktivierungsverhaltens nicht möglich. Erklärung: Der Na+-Kanal öffnet sich nur einmal, wonach er lange Zeit nicht mehr geöffnet werden kann. Es ist also kein statistisches Öffnen/Schließen beobachtbar, wie bei anderen Kanälen. Die Inaktivierung wird erst wieder im Ruhepotential rückgängig gemacht, wonach der Kanal wieder Spannungsabhängig geöffnet werden kann. Die Inaktivierung erfordert demnach eine Messung über Spannungssprünge! Daher werden während der Saugpipetten-Anordnung unter dem Membranfleck (enthält ein bis mehrere Na+-Kanäle) depolarisierende Spannungssprünge durchgeführt, um den Kanal zu öffnen. Nach dem Spannungssprung wird der Pipettenstrom 𝑰𝑰 etwa 20 ms detektiert, wonach die Spannung wieder auf den Ruhewert zurückgestellt wird (1s Erholzeit) und der nächste Spannungssprung folgen kann. Die Stromspuren der einzelnen Spannungssprünge zeigen Kanalöffnungsereignisse. Dabei sind Latenzzeit zwischen Spannungssprung und Kanalöffnung sowie Lebensdauer des offenen Zustandes statistisch verteilt. Außerdem besteht eine Wahrscheinlichkeit, dass nach dem Spannungssprung keine Kanalöffnung beobachtet wird. Über Summation einzelner Stromspuren, ergibt sich der mittlere Strom, der in seinem Zeitverhalten mit dem makroskopischen Na+-Einwärtsstrom übereinstimmt. Damit liefert die Einzelkanalmessung wesentlich detailliertere Ergebnisse als die Vielkanalmessung. Für den Na+-Kanal kann damit folgendes kinetisches Schema abgeleitet werden: (1) Nach dem depolarisierenden Spannungssprung geht der geschlossene Zustand G nach einer statistisch verteilten Latenzzeit in den offenen Zustand O über. (2) Nach einer wiederum statistisch verteilten Wartezeit geht O in den inaktivierten Zustand I über. (3) Gelegentlich kann der Kanal von O in G zurückspringen und dann wieder in O übergehen (mehrfache Öffnungsereignisse). (4) Aus dem Auftreten von Stromspuren ohne Öffnungsereignisse folgt, dass auch direkte Übergänge von G nach I möglich sind. Bei der im Experiment gewählten Spannung sind GI und OI irreversibel (keine Kanalöffnungsereignisse bei langen Zeiten). Struktur von Kanälen Beispiele für Kanäle • • • • Aquaporine Porine der äußeren Membran gramnegativer Bakterien transportieren viele niedermolekulare Substanzen wie Zucker Kanäle können auch entfaltete Proteine transportieren. Kanalartige Strukturen dienen auch als hydrophile Zugangskanäle zu Bindestellen aktiver Transporter (Pumpen) innerhalb der Membran oder stellen den Ausgang in die gegenüberliegende wässrige Phase dar. Dies gilt für Na,K-Pumpe sowie Bakteriorhodopsin. Grundsätzliches Bauprinzip: hydrophobes Äußeres, Hydrophiler Kanalinnenraum (z.B. Gramicidin A). Die Außenmembranproteine gramnegativer Bakterien sind aus β-Faltblattstrukturen aufgebaut, während die Ionenkanäle erregbarer Membranen aus α-helikalen Elementen bestehen. TolC besteht aus einem Porin-artigen Kanal aus einem β-Fass in der äußeren Membran von gramnegativen Bakterien. An diesen Kanal schließt sich ein α-helikaler Tunnel an, der den periplasmatischen Raum zwischen äußerer Membran und zytoplasmatischer Membran der Bakterien überbrückt. Hier sind demnach beide Grundstrukturen vorhanden. TolC entspricht einem Zylinder mit 3,5 nm Durchmeser, durch den verschiedene Moleküle, auch Proteine transportiert werden können. Die Ionenkanäle der Plasmamembran tierischer Zellen weisen einen erheblich geringeren Durchmesser (Zehntel nm) auf, wodurch zwischen Ionen verschiedener Durchmesser oder Ladungen unterschieden werden kann (Ionenselektivität). Der Selektivitätsfilter kann mehr oder weniger ausgeprägt sein. Na+-Kanäle haben für Na+ eine 1000mal höhere Leitfähigkeit als für K+. Spannungsabhängige Ionenkanäle bestehen aus vier Untereinheiten, die identisch (K+-Kanal) oder verschieden (Na+-Kanal) sein können. Jede Untereinheit besteht aus sechs transmembranen α-Helices (S1-S6). Die Helix S4 trägt eine Reihe positiver Ladungen und ist für die Spannungsabhängige Steuerung der Kanäle verantwortlich. Zwischen S5 und S6 befindet sich eine ausgeprägte Schleife, die den Kanaleingang (von der Außenseite her gesehen) bildet. Durch Zusammenlagerung der vier Untereinheiten entsteht ein Kanal, der durch S5 und S6 gebildet wird, mit der Eingangsstelle im Bereich der vier Schleifen, welche für die Ionenselektivität verantwortlich sind. An eine zytosolische Domäne (T1) jeder Untereinheit ist über eine flexible Kette eine kugelförmige Struktur geknüpft. Diese dringt in den Kanal ein und blockiert/inaktiviert ihn auf diese Weise. Teil 3: Membranbiophysik am MPI (BPC2-Praktikum) Bakteriorhodopsin (BR) Struktur und Funktion Bei BR handelt es sich um ein integrales Membranprotein, das 75 Massenprozent der Purpurmembran (bis zu 5 µm große Membran-Bereiche) des halophilen Bakteriums Halobacterium salinarium ausmacht. BR-Moleküle sind in Trimeren organisiert und in der Purpurmembran in einem kristallinen hexagonalen Gitter angeordnet. BR stellt daher ein sehr gutes Modellprotein dar, weil es aufgrund seiner Häufigkeit sehr leicht zu isolieren und außerdem sehr resistent gegen Umwelteinflüsse (hohe Stabilität und Langlebigkeit) ist. BR fungiert als zellauswärtsgerichtete lichtgetriebene Protonenpumpe, die in vivo die Erzeugung eines elektrochemischen Gradienten bewirkt, aus dem direkt ATP gewonnen werden kann (außerdem dient der Gradient zur Phototaxis sowie zur + + + Aufrechterhaltung eines niedrigen intrazellulären Na -Pools über den Na /H -Antiporter). Halobacterium salinarium zeigt damit eine sehr spezielle Form der Photosynthese, die in Sauerstoff-armen Milieus die ATPProduktion über die Atmungskette unterstützen und ersetzen kann. Das Protein besteht aus 248 Aminosäuren (26 kDa), die in 7 nahezu parallelen α-Helices angeordnet sind und eine Pore innerhalb der Membran bilden. Die Pore beinhaltet ein zentrales, über eine Schiffsche Base an die ε-NH2-Gruppe von Lys216 kovalent gebundenes Retinalmolekül. Retinal ist für die Purpur-Farbe des Bakteriums verantwortlich und ein Derivat des Vitamin A. Es kann unter physiologischen Bedingungen sowohl in all-trans, als auch in 13-cis Konfiguration vorliegen. Der Übergang von all-trans zu 13-cis erfolgt unter Lichteinwirkung, während die Reisomerisierung ein Prozess der thermischen Relaxation darstellt. Der Photozyklus von BR (1) 𝑩𝑩𝑩𝑩 → 𝑩𝑩𝑹𝑹∗: Durch Absorption eines Photons der Wellenlänge 568 nm erfolgt ein Übergang vom BR Grundzustand zum photokativierten angeregten Zustand BR* innerhalb von 200 fs. BR* fällt nur über thermische Relaxation in den elektronischen Grundzustand zurück, entweder direkt oder unter Durchlaufen des Photozyklus (Dauer: ~10 ms bei 22°C). (2) 𝑩𝑩𝑹𝑹∗ → 𝑱𝑱: Der Photozyklus beginnt mit der Isomerisierung am C13-Atom des Retinals: Der protonierte all-trans Zustand des Retinals geht innerhalb von 500 fs in den protonierten 13-cis Zustand über. (3) 𝑱𝑱 → 𝑲𝑲 → 𝑳𝑳 → 𝑴𝑴: Es folgen drei weitere schnelle Übergänge, bis der M Zustand gebildet ist. Während des Übergangs von L nach M innerhalb von 50 µs wird das Proton der Schiff-Base an den primären Protonenakzeptor Asp85 weiter gegeben. Von dort wird das Proton über weitere Bindestellen im Protein an die extrazelluläre Seite der Membran weiter gereicht. (4) 𝑴𝑴 → 𝑵𝑵: Retinal ist im M-Zustand also deprotoniert, jedoch immernoch in 13-cisKonfiguration. Der Zerfall des M-Komplexes in den Zustand N, welcher mit der Aufnahme eines Protons vom primären Protonendonor Asp96 und somit mit der Reprotonierung der Schiff-Base verbunden ist, dauert mit 3 ms relativ lange. Der Protonendonor erhält sein Proton über mehrere Proton-Bindestellen im Protein letztlich aus der intrazellulären Seite der Membran. (5) 𝑵𝑵 → 𝑶𝑶 → 𝑩𝑩𝑩𝑩: Über die Reisomerisierung des Retinals von 13-cis zu all-trans während des N-Zerfalls innerhalb einer ms, erfolgt nach weiteren 5 ms über den Zustand O die Wiederherstellung des BR Grundzustandes. BR-Zustand L-Zerfall: Asp85Protonierung M-Zerfall: Asp96Deprotonierung + Asp85-Deprotonierung N-Zustand: Asp96Reprotonierung Je Zyklus wird ein Proton von der intrazellulären Seite der Membran auf die extrazelluläre Seite transportiert, wobei das in Zyklus 1 zur Reprotonierung der Schiff Base verwendete Proton erst in Zyklus 2 die extrazelluläre Seite erreicht. Der Protonendonor Asp96 ist näher an der intrazellulären Seite gelegen, während sich der Protonenakzeptor Asp85 an der extrazellulären Seite befindet. Die verschiedenen Affinitäten der Protonen-Donoren und –Akzeptoren werden über zeitlich veränderte pK-Werte der Schiffschen Basen und Carboxylgruppen aufgrund von Konformationsveränderungen moduliert. Da die verschiedenen Zustände im Photozyklus unterschiedliche Konformationen aufweisen, resultieren auch unterschiedliche Absorptionsmaxima. Durch Absorption von Licht dieser speziellen Wellenlängen, relaxiert das System sofort in den photoaktivierten Grundzustand zurück, wodurch das Proton zu einer gewissen Wahrscheinlichkeit nicht seinen Bestimmungsort erreicht (je nachdem welcher Zustand im Zyklus angeregt wird). BR-Mutante D96N Es existiert eine BR-Mutante, bei der der primäre Protonendonor Asp96 durch ein Asparagin ersetzt ist. Diese Mutante zeigt eine erheblich reduzierte Protonentransportaktivität. Da das Protein im Grundzustand protoniert im all-trans Zustand vorliegt und ebenso wie der Wildtyp photoaktivierbar ist, gelangt die BR-Mutante in den L-Zustand und von dort durch schnelle Deprotonierung in den M-Zustand. Der M-Zerfall, welcher mit einer Reprotonierung der Schiff-Base verbunden ist, ist jedoch erheblich erschwert, da der Protonendonor Asp96 nicht vorhanden ist. Daher zeigt der M-Zustand der Mutante eine wesentlich höhere Lebensdauer als im Wildtyp Protein. BLM Experimentelles Setup Die BLM (black lipid membrane) ist eine Methode Membranproteine elektrophysiologisch zu charakterisieren. Dazu wird eine spezielle Küvette aus Teflon, die zwei Kammern, verbunden über eine bimolekulare Membran innerhalb eines Septums enthält, mit einem Elektrolyt-Puffer gefüllt. Die zwei Kammern sind wiederum über Salzbrücken aus Agar mit den Elektroden verbunden. Wird über die Öffnung in der Trennwand (Septum) der Teflon-Kammer eine Lösung von Lipid, das in einer organischen Substanz gelöst ist, gestrichen, so bildet sich zunächst eine dicke Flüssigkeitslamelle. Nach einigen Minuten fließt überflüssiges Lösungsmittel und Lipid zum Rand des Septums ab. Durch Selbstorganisation bildet sich dabei eine Lipid-Doppelschicht aus. Das Septum, welche die beiden Kammern verbindet wird zunächst mit dem Lipid DiphytanoylPhosphatidylcholin (PC; 0,5% w/v in Hexan) imprägniert, anschließend wird die Elektrolytlösung in die Kammern gegeben (100 mM NaCl, 20 mM HEPES, pH=7,3), ein Rührfisch in die Kammern eingesetzt und das Septum mit PC (1,5% w/v in Decan) und zusätzlich Octadecylamin (PC/Octa 60/1 w/w) versetzt, wodurch die zwei Kammern nun über eine bimolekulare Lipidmembran getrennt sind. Während das aufgegebene Lipid-Lösungsmittelgemisch bei Beleuchtung mit weißem Licht anfangs durch Reflexion und Interferenzeffekte an der Lösungsmittel-Lipidmultischicht in allen Spektralfarben schillert, so erscheint die anschließend entstehende Lipiddoppelschicht schwarz, da aufgrund ihrer Dicke von nur 4 – 6 nm eine destruktive Interferenz auftritt. Zur Überprüfung der Membran-Güte werden Leitfähigkeit und Kapazität der Membran gemessen. Eine hohe Leitfähigkeit deutet darauf hin, dass die Membran durchlässig für Ionen ist. Dies sollte bei der Messung der Aktivität einer Protonenpumpe verhindert werden. Die Zugabe von BR erfolgt über das lichtabgewandte Kompartiment. BR wird in Form von Membranfragmenten der Purpurmembran in die Lösung gegeben, die sich an die BLM anlagern. Damit stehen zwei Lipiddoppelschichten in Kontakt (selbstgezogene BLM und Protein-haltiges Membranfragment), die über eine dünne Lösungsmittelschicht getrennt sind. Nach 30 Minuten rühren sollten sich die Membranen am Septum zusammengelagert haben. Der Versuchsaufbau ist damit vollständig. Die Anlagerung von BR an die BLM findet so statt, dass die Protonen von der Küvettenkammer in das Lumen zwischen den beiden bimolekularen Lipiddoppelschichten transportiert werden. Indem BR nun über Licht der Wellenlänge 568 nm angeregt wird, erfolgt die Induktion des Photozyklus und der Transport von Protonen, wodurch sich das elektrische Potential über die Membran verändert, was über die Elektroden detektiert wird. Berechnung der spezifischen Kapazität, Leitfähigkeit und Dicke der planaren Lipidmembran Nachdem die bimolekulare Lipidmembran auf das Septum der BLM-Küvette aufgezogen wurde, erfolgt die Messung der Kapazität und Leitfähigkeit. Die Kapazität (gespeicherte Ladung Q pro angelegte Spannung U) kann durch Anlegen einer Dreiecksspannung (𝑈𝑈 = 20 𝑚𝑚𝑚𝑚, ∆𝑡𝑡 = 1𝑠𝑠) ermittelt werden. Dabei resultierte eine Stromdifferenz von ∆𝐼𝐼 = 25𝑝𝑝𝑝𝑝 zwischen Maximum und Minimum im Intervall von einer Sekunde. Über folgende Gleichung wurde die Kapazität berechnet. 𝐶𝐶 = 𝑄𝑄 ∆𝐼𝐼 ∙ ∆𝑡𝑡 25 ∙ 10−12 𝐴𝐴 ∙ 1𝑠𝑠 = = = 1,25𝑛𝑛𝑛𝑛 𝑈𝑈 𝑈𝑈 20 ∙ 10−3 𝑉𝑉 Zur Messung der Leitfähigkeit wurde eine konstante Spannung von 𝑈𝑈 = 30𝑚𝑚𝑚𝑚 angelegt. Dabei resultierte ein Peakstrom von 𝐼𝐼 = 1,7𝑝𝑝𝑝𝑝. Die Leitfähigkeit ist definiert als der Kehrwert des Widerstandes R: Es ergibt sich demnach 𝐺𝐺 = 𝑈𝑈 [𝑉𝑉] Angelegte Spannung 𝐼𝐼 1,7 ∙ 10−12 𝐴𝐴 = = 56𝑝𝑝𝑝𝑝 𝑈𝑈 30 ∙ 10−3 𝑉𝑉 𝑈𝑈 [𝑉𝑉] Angelegte Spannung ∆𝑡𝑡 = 1𝑠𝑠 30 mV Rechteckspannung 20 mV Dreieckspannung 𝑡𝑡 [𝑠𝑠] 𝑄𝑄 [𝑉𝑉] Ladung am Kondensator 𝑡𝑡 [𝑠𝑠] Ableitung Stromantwort 𝑡𝑡 [𝑠𝑠] -10 mV 𝑄𝑄 [𝑉𝑉] Ladung am Kondensator 𝐼𝐼 [𝐴𝐴] = 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 +10 mV 𝐼𝐼 = 1,7𝑝𝑝𝑝𝑝 𝑡𝑡 [𝑠𝑠] 𝐼𝐼 [𝐴𝐴] = 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 Stromantwort 𝐼𝐼 = 25𝑝𝑝𝑝𝑝 𝑡𝑡 [𝑠𝑠] Messung der Leitfähigkeit Messung der Kapazität Die spezifische Leitfähigkeit und Kapazität kann unter Berücksichtigung der Membranfläche erhalten werden. Die Membranfläche entspricht der Fläche der Küvettenpore von 1𝑚𝑚𝑚𝑚2 𝐺𝐺𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = 𝐶𝐶𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = 𝐺𝐺 56 ∙ 10−12 𝑆𝑆 𝑆𝑆 = = 5,6 ∙ 10−9 2 𝐴𝐴 0,01𝑐𝑐𝑐𝑐 𝑐𝑐𝑐𝑐2 𝐶𝐶 1,25 ∙ 10−9 𝐹𝐹 𝐹𝐹 = = 1,25 ∙ 10−7 2 𝐴𝐴 0,01𝑐𝑐𝑐𝑐 𝑐𝑐𝑐𝑐2 Die Membrandicke 𝒅𝒅 lässt sich mithilfe der Annahme, dass es sich bei der Membran um einen Kondensator handelt, berechnen. Dann entspricht die Membrandicke dem Abstand zwischen den Kondensatorplatten 𝑑𝑑. Die Berechnung erfolgt über die Kapazitätsformel, wobei die Dielektrizitätskonstante im hydrophoben Innenbereich der Membran 𝜀𝜀 = 2 beträgt und die Fläche 𝐴𝐴 wieder der Fläche der Küvettenpore von 1𝑚𝑚𝑚𝑚2 entspricht. 𝐶𝐶 = 𝜀𝜀𝜀𝜀0 10−6 𝑚𝑚2 𝐴𝐴 𝐴𝐴 𝐴𝐴𝐴𝐴 ⟺ 𝑑𝑑 = 𝜀𝜀𝜀𝜀0 = 2 ∙ 8,8542 ∙ 10−12 ∙ = 1,417 ∙ 10−8 𝑚𝑚 = 14𝑛𝑛𝑛𝑛 𝑑𝑑 𝐶𝐶 𝑉𝑉𝑉𝑉 1,25 ∙ 10−9 𝐹𝐹 Erklärung des zeitlichen Verlaufs des transienten Stroms und des Ersatzschaltbildes Die bimolekulare Membran am Septum der BLM-Küvette trennt zwei Puffer-Lösungen, die über eine Salzbrücke aus Agar mit den Elektroden verbunden sind. Die Membran hat eine für sich charakteristische Leitfähigkeit und Kapazität, die im Ersatzschaltbild als RC-Parallelschaltung eingezeichnet ist. Der durch die Anordnung fließende Strom 𝑰𝑰 ist demnach die Summe der Ströme durch den Widerstand 𝑰𝑰𝑹𝑹 und den Kondensator 𝑰𝑰𝑪𝑪 . Dabei ist der ohmsche Strom der momentanen Spannung an der Membran proportional, während der kapazititve Strom dem zeitlichen Spannungsgradienten folgt. 𝐼𝐼 = 𝐼𝐼𝑅𝑅 + 𝐼𝐼𝐶𝐶 = 𝑈𝑈 𝑑𝑑𝑑𝑑 + 𝐶𝐶 𝑅𝑅 𝑑𝑑𝑑𝑑 Berücksichtigt man die Anlagerung der BR-haltigen Purpurmembran, liegt eine Reihenschaltung zweier RC-Parallelschaltungen vor. Zusätzlich muss im zweiten RC-Glied noch BR als Stromgenerator berücksichtigt werden, sodass für den Gesamststrom gilt: 𝐼𝐼 = 𝐼𝐼𝑅𝑅 + 𝐼𝐼𝐶𝐶 + 𝐼𝐼𝑃𝑃 . Der entsprechende Schaltkreis ist dann identisch zu dem einer SSM. Oben: Ersatzschaltbild BLM ohne Purpurmembran (Spannungsquelle zur Messung von C und G der BLM) Links: Ersatzschaltbild BLM mit Purpurmembran (keine Spannungsquelle, da Stromfluss durch BR über Licht angeregt wird) Da BR eine Protonen-Pumpe darstellt ist hier die Stromquelle 𝐼𝐼𝑃𝑃 parallel zum RC-Glied der Purpurmembran zu zeichnen. Der BR-induzierte Strom (Protonen-Fluss) beeinflusst die Leitfähigkeit der Membran. Die Stromquelle (BR) und die damit verbundene Leitfähigkeitsänderung der Membran ist Licht-abhängig (Photoinduzierbarkeit von BR). Die Begrenzung der Zeitauflösung erfolgt über die Anstiegszeit des Stromverstärkers (im µs-Bereich) und dem Zugriffswiderstand über Elektrolyt und Elektroden (letztere wurden hier vernachlässigt). Messprinzip: Kapazitive Kopplung Erklärung des Prinzips anhand der BLM bzw. SSM: (1) Zum Zeitpunkt 𝒕𝒕 = 𝟎𝟎 ist das Membranpotential bei einem relativ niedrigen Wert (kein elektrischer Gradient über die Membran) im Gleichgewicht (stationärer Strom). (2) Durch Belichtung bei 𝒕𝒕 = 𝟏𝟏 werden Protonen in den Raum zwischen Purpurmembran und BLM (Abbildung: in das Proteoliposom) gepumpt. Die positive Ladung des Lumens führt durch kapazitive Kopplung zu einem Fluss negativer Ladung durch den äußeren Stromkreis inklusive Strommessgerät und Elektrode in Richtung der BLM innerhalb der anderen Elektrolytkammer (Abbildung: in Richtung Goldschicht). (3) Bei 𝒕𝒕 = 𝟐𝟐 diffundieren Protonen aufgrund des elektrochemischen Potentials durch die Membran zurück in die Elektrolytlösung, wodurch der Nettotransport gleich null wird und das Membranpotential sein Maximum erreicht hat. Damit wird auch der messbare Stromfluss gleich null (Ladungsausgleich ist beendet). (4) Bei 𝒕𝒕 = 𝟑𝟑 wird das Licht ausgeschaltet, wodurch kein Protonenimport mehr stattfindet. Das Membranpotential nimmt durch Diffusion der Protonen aus dem Lumen bzw. Liposom ab. Die negativen Ladungen auf der anderen Seite der BLM bzw. in der Goldschicht wandern zurück; die Stromrichtung kehrt sich um. Kapazitive Kopplung bedeutet, dass die Aufladung des einen Membrankondensators (Purpurmembran) mit der Aufladung des anderen Membrankondensators (BLM) gekoppelt ist und erst diese Kopplung zu dem gemessenen Stromfluss über den äußeren Stromkreis führt. Der durch konstante Belichtung für 2 Sekunden induzierte, gemessene Strom ist damit transient (Ursache ist die kapazitive Kopplung); stationäre, also konstante Ströme (entspricht Vergrößerung der Leak-Ströme) können über die Inkorporation von Ionophoren in die BLM und die Purpurmembran erhalten werden (Zugabe in beide Elektrolytkammern). Dabei müssen die Ionophore permeabel für die Ionen sein, die durch die Proteine im BLM-adhärierten Membranfragment transportiert werden (in diesem Fall: H+-Ionophore). Es wird somit ein kontinuierlicher Fluss von Ladung ermöglicht (BLM ist keine Barriere mehr für Ionenfluss). Zeitlicher Verlauf des Stromsignals Die gemessenen transienten Ströme sind kapazitive Ströme, die allein durch die kapazitive Kopplung zwischen Purpurmembran und BLM möglich sind. Das Stromsignal nach Einschaltung des Lichts besteht aus zwei exponentiellen Kurven, die durch zwei Zeitkonstanten beschrieben werden. Die sehr schnelle Zeitkonstante 𝝉𝝉𝟏𝟏 beschreibt den Anstieg bis zum Erreichen des Peakstroms. Ursache ist die sich anfangs beschleunigende ProtonenTransportgeschwindigkeit, die mit einem hohen Elektronenfluss durch das Strommessgerät aufgrund der kapazitiven Kopplung verbunden ist. Die Größe des Peakstroms ist abhängig von der PumpLeistung von BR und von den Leakströmen. Die erheblich langsamere Zeitkonstanten 𝝉𝝉𝟐𝟐 (Abklingkonstante) beschreibt den Abfall des Signals bis zum Erreichen des konstanten Membranpotentials. Ursache ist der langsamer werdende Anstieg der Protonenkonzentration (Abbremsung der Protonen-Transportgeschwindigkeit) im Lumen zwischen BLM und Purpurmembran (aufgrund niedrigerer Pump-Leistung sowie die Diffusion der Protonen zurück in die Elektrolytlösung) und der damit verbundene geringere kapazitive Stromfluss. Im GG sollte dann der kapazitive Stromfluss gleich null sein, da die Ionenkonzentrationen an der BLM und im Lumen zwischen Purpurmembran und BLM konstant sind. Tatsächlich stellt sich aber ein stationärer Stromfluss ein: Es handelt sich um einen Leakstrom aufgrund von Löcher innerhalb der BLM und der Purpurmembran, wodurch der Stromkreis „geschlossen“ ist und ein kontinuierlicher Stromfluss ermöglicht wird. Diese Zeitkonstante wird auch RC-Zeit genannt, da sie direkt und ausschließlich von den Membran-Eigenschaften (Widerstand, Kapazität) abhängig ist. Die Abklingkonstante ist gegeben durch (𝑈𝑈 ist eine Konstante mit der Einheit einer Spannung): 𝜏𝜏2 = 𝑅𝑅𝐺𝐺𝐺𝐺𝐺𝐺 ∙ 𝐶𝐶𝐺𝐺𝐺𝐺𝐺𝐺 = 𝐶𝐶𝑚𝑚 + 𝐶𝐶𝑝𝑝 𝐶𝐶𝐺𝐺𝐺𝐺𝐺𝐺 = 𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺 𝐺𝐺𝑚𝑚 + 𝐺𝐺𝑝𝑝 + 𝐼𝐼𝑝𝑝 ⁄𝑈𝑈 Leakstrom exponentieller Signalanstieg mit Belichtung Start exponentieller Signalabfall mit Baseline Peakstrom Belichtung Ende BR kann maximal einen Protonengradienten von vier pH-Einheiten erzeugen, wonach sich ein Gleichgewicht zwischen Protonenfluss nach außen durch Löcher innerhalb der Membran (Leakströme) und Protonenfluss nach Innen durch die Aktivität von BR, eingestellt hat. Besitzt die Membran (idealerweise) eine Leitfähigkeit von null (keine Leakströme), so nähert sich das abklingende Signal der Baseline an. Liegt eine relevante Leitfähigkeit vor, so liegt die Asymptote des abklingenden Signals tiefer als die Baseline, da der Leakstrom (unter Annahme der Langzeitstabilität der BLM) konstant ist, und daher im Gleichgewicht auch eine konstante Menge Protonen pro Zeit durch BR ins Lumen gepumpt wird. Die Messungen werden verfälscht, wenn die Membran instabil ist, da dies einer Erhöhung des Leakstroms mit der Zeit entspricht (Daten nicht mehr vergleichbar). Die Richtung des Peakstroms (positiv oder negativ) ist von der Polung der Spannungsquelle abhängig. Elektronen fließen immer von der Kammer mit Protein-haltigem Membranfragment zur Kammer mit der BLM. „Springen“ sie dabei über die Spannungsquelle von + nach – resultiert ein negativer Peak-Strom. „Springen“ sie von – nach +, was der natürlichen Richtung der negativ geladenen Elektronen entspricht, resultiert ein positiver Peakstrom (evtl. umgekehrt, da technische Stromrichtung der Wanderung positiver Ladung entspricht). Flash Photolyse Die Flash-Photolyse (Laserblitzlichtphotolyse = LFP) beruht auf der Messung der optischen Dichte (OD, Absorption) in Abhängigkeit von der Zeit und ist eine Methode um die Kinetik reaktiver Zwischenprodukte, die durch einen Laserpuls erzeugt werden, zu untersuchen (Laser hier: 580 nm, zur Anregung des BR-Grundzustandes und Induktion des Photozyklus). Bei der Messung der OD liegen einige Messpunkte zeitlich vor dem Auftreffen des Laserstrahls auf die Probe, wonach die Photolyseprodukte erzeugt werden. Nach dem Laserpuls ändert sich die OD sofort, da in der Analysezelle eine veränderte Produktzusammensetzung vorliegt. Reaktive Zwischenprodukte setzen sich in Abhängigkeit von ihrer Lebensdauer 𝛕𝛕 unterschiedlich schnell in weitere Produkte um. Diese Prozesse lassen sich in der zeitlichen Veränderung der 𝐎𝐎𝐎𝐎 beobachten. Im Experiment wird eine Kurve erhalten, welche die Zeit 𝑡𝑡 gegen die 𝑂𝑂𝑂𝑂(𝜆𝜆, 𝑡𝑡) bei einer bestimmten Wellenlänge darstellt (diese Auftragung wird als Transientenspur bezeichnet). Außerdem können Transientenspektren erhalten werden, wenn dieselbe Messung bei verschiedenen Wellenlängen durchgeführt wurde und die Differenz der OD bei konstanten Zeitpunkten gegen die einzelnen Wellenlängen aufgetragen werden. Über die Transientenspur kann die Lebensdauer des entsprechenden Intermediats bestimmt werden, indem die erhaltene Kurve über eine Kinetik erster Ordnung, d.h. über [𝑨𝑨]𝟎𝟎 = [𝑨𝑨]𝒕𝒕 𝒆𝒆−𝒌𝒌𝒌𝒌 durch ein Computerprogramm gefittet wird. Die Lebensdauer 𝜏𝜏 des Intermediats ist dann genau die Zeitspanne, in der seine Konzentration auf 1/𝑒𝑒 seiner Ursprungskonzentration abgefallen ist. Aus den vom Computerprogramm erhaltenen Parametern lässt sich damit die Lebensdauer berechnen. Apparativer Aufbau Beim LFP-Experiment strahlt der Laser orthogonal zur optischen Bank ein, sodass so wenig wie möglich Laserstrahlen den Detektor erreichen. Der Brennpunkt des Lasers liegt vor der Probe, sodass die Probe gleichmäßig angeregt werden kann. Der Strahlengang des Lasers kann durch einen Shutter unterbrochen werden. Als Analyselicht wird eine Xenonlampe verwendet, deren Brennpunkt innerhalb der Probe liegt. Durch spezifische Filter können die benötigten Wellenlängen selektiv eingestrahlt werden, um bestimmte Intermediate innerhalb der Probe zu detektieren. Das Analyselicht einer bestimmten Wellenlänge wird abhängig von der Zusammensetzung der Probe unterschiedlich stark absorbiert und gelangt dann direkt zur Detektionseinheit. Diese besteht aus einem Monochromator, welcher nur die gewünschte zu detektierende Wellenlänge durchlässt, einer Photodiode, welche die Photonen detektiert, und einem Photomultiplier, welcher das Signal verstärkt. Letzterer ist an einem Oszilloskop angeschlossen, welches das Messsignal visualisiert. Da der Zerfall kurzlebiger Intermediate sehr schnell stattfinden kann, bedarf es einer zeitlich hohen Auflösung des Detektors im µs-Bereich und relativ kurzen Pulsdauern im ns-Bereich. Bei der Flash-Photolyse wurde die BR-Probe auf eine OD von 0,5 verdünnt. Die Verdünnung der zu vermessenden Probe ist kritisch, da die OD hoch genug sein muss, um einen Effekt zu sehen, aber nicht zu hoch, da ansonsten das Analyselicht nicht durchstrahlt. Das Messlicht wird einmal auf 421 nm eingestellt, um den M-Zustand zu detektieren und ein weiteres mal auf 562 nm, um den Grundzustand zu detektieren. Es ist darauf zu achten, dass das Messlicht bei der Detektion des Grundzustandes nicht der Wellenlänge des Lasers (580 nm zur Anregung des BR-Grundzustandes) entspricht, da ansonsten auch das an der Probe gestreute Laserlicht detektiert werden kann, was zu Messfehlern führen würde. Patch Clamp an Channelrhodopsin Channelrhodopsine Channelrhodopsine (ChR) sind eine Protein-Subfamilie der Opsin-Proteine und fungieren als Lichtgesteuerte Ionenkanäle. Sie dienen als sensorische Photorezeptoren in einzelligen Grünalgen und kontrollieren dort die Phototaxis. In anderen Organismen ermöglichen sie u.a. die Regulation der intrazellulären Azidität, des Calcium-Einstroms oder des Membranpotentials durch Licht. Es sind derzeit drei ChR-Proteine bekannt, von denen alle Kationen-Kanäle sind, die Protonen, Natrium, Kalium und Calcium Ionen transportieren. • • • ChR1 wurde als selektiver Licht-aktivierter Protonen-Kanal in der Grünalge Chlamydomonas reinhardtii im Jahr 2002 entdeckt. ChR2, aus demselben Organismus isoliert, hat im Vergleich zu ChR1 eine zweimal höhere Lebensdauer des leitenden Zustands, was in höheren stationären Strömen, aber langsamerer Kinetik resultiert. Es handelt sich bei ChR2 im Gegensatz zum ChR1 um einen unspezifischen Kationen-Kanal. Das dritte Channelrhodopsin VChR1 wurde in der multizellulären Alge Volvox entdeckt. Strukturell sind alle Proteine der Rhodopsin-Familie Retinal-haltige 7-Transmembran Proteine. Das Chromophor ist im inaktiven Zustand in Form von all-trans-Retinal über eine Schiff-Base an ein Lysin des Apoproteins verknüpft. Das C-terminale Ende von ChR2 ist in den intrazellulären Raum extendiert und kann an fluoreszierende Proteine fusioniert werden, ohne die Proteinfunktion zu stören, wodurch die Morphologie ChR2-exprimierender Zellen visualisiert werden kann. In diesem Experiment wird ebenso ein Fusionsprodukt exprimiert, um erfolgreiche Transfektionen nachzuweisen und nur solche Transfektanden mit ausreichend hoher Fluoreszenzintensität mittels Patch-Clamp zu analysieren. ChR2 absorbiert blaues Licht am Absorptionsmaximum bei 𝜆𝜆 = 480𝑛𝑛𝑛𝑛, wodurch all-trans-Retinal zum 13-cis-Retinal umgewandelt wird. Diese Konformationsänderung induziert eine weitere Konformationsänderung im Protein, wodurch sich die Pore um bis zu 𝟔𝟔Å öffnet. Innerhalb von millisekunden relaxiert das Retinal zurück in den all-trans-Zustand, wodurch die Pore wieder geschlossen und der Ionenfluss beendet wird. Patch Clamp Die Patch-Clamp Technik ermöglicht kinetische Messungen an Einzelkanälen oder mehreren Ionenkanälen innerhalb einer Zelle. Zentrales Element dieser Methode ist eine hitzepolierte Glas-Mikropipette mit einem inneren Spitzen-Durchmesser von ca. 𝟏𝟏 − 𝟐𝟐 𝝁𝝁𝝁𝝁. Die Pipette ist mit einer wässrigen Elektrolytlösung gefüllt, die mit einer Ag/AgCl-Elektrode in Kontakt steht und so an eine Spannungsquelle und einen Stromverstärker angeschlossen ist. So kann das Öffnen/Schließen einzelner Ionenkanäle im Membranfleck nachgewiesen werden. Da der außerhalb der Pipette befindliche Teil der Zellmembran aufgrund seiner viel größeren Fläche einen elektrischen Kurzschluss darstellt, bleibt die Spannung über den Membranfleck zeitlich konstant, unabhängig vom Öffnen/Schließen von Kanälen. Daher die Bezeichnung patchclamp (am Membranfleck erscheint die Spannung geklemmt). Ein elektrischer Kurzschluss ist eine nahezu widerstandslose Verbindung zweier Schaltungspunkte mit normalerweise verschiedenem Potential, wodurch die Spannung zwischen diesen Punkten auf null abfällt; Das Resultat: extremer Stromfluss zwischen diesen Punkten. Die Pipettenlösung kann in ihrer Zusammensetzung beliebig verändert werden, sodass die Ionenkanäle unter verschiedenen Bedingungen untersucht werden können. Die Patch-Pipette wird mittels Mikromanipulator und inversem Mikroskop direkt über eine Zelle justiert, sodass sich darunter ein Stück Membran – der Patch oder Membranfleck – befindet. Anschließend wird ein leichter Unterdruck angelegt, sodass dieser Patch angesaugt wird. Dabei entsteht ein enger Kontakt zwischen Membrangrenzfläche und Glaswand, der zu einem extrem hohen elektrischen Abdichtwiderstand 𝑅𝑅𝑎𝑎 ≈ 1010 − 1012 Ω zwischen Pipettenlösung und Badlösung führt. Dieser Widerstand wird als „gigaohm seal“ oder einfach „gigaseal“ bezeichnet. „Seal“ bezeichnet dabei die Versiegelung zwischen Membran und Glaspipette. Damit ist die cell-attached Konfiguration der Patch-Clamp Technik erreicht. Aufgrund des geringen Durchmessers der Glaselektrode kann davon ausgegangen werden, dass sich lediglich ein einzelner Ionenkanal innerhalb des Patches befindet. Somit können Einzelkanalmessungen durchgeführt werden. Der elektrische Strom durch einen einzelnen Ionenkanal kann durch eine Treppenfunktion dargestellt werden, die zwischen zwei Zuständen fluktuiert. Aus dem Stromsignal lässt sich die Größe des Einzelkanalstroms 𝒊𝒊 (Höhe der Treppenstufe) und hieraus die Einzelkanalleitfähigkeit 𝚲𝚲 = 𝒊𝒊/𝑽𝑽 (V ist angelegte Spannung) ermitteln. Außerdem kann die mittlere Lebensdauer 𝝉𝝉 des offenen Kanalzustands bestimmt werden (Mittelwert der Breite über alle Treppenstufen). Da EinzelkanalLeitfähigkeiten zwischen 𝟓𝟓𝟓𝟓𝟓𝟓 𝒇𝒇𝒇𝒇 und 𝟏𝟏𝟏𝟏𝟏𝟏 𝒑𝒑𝒑𝒑 liegen, haben sie bei 𝑽𝑽𝒎𝒎 = 𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏 in der Regel Amplituden von wenigen 𝒑𝒑𝒑𝒑. Eine Stromamplitude von 1pA entspricht einem Durchtritt von 𝒊𝒊/𝒛𝒛𝒛𝒛 = 𝟓𝟓 ∙ 𝟏𝟏𝟏𝟏𝟔𝟔 einwertigen Ionen pro Sekunde. Es können kurzzeitige Kanalöffnungsereignisse von Dauern herab bis zu 0,1 ms beobachtet werden, was einem Durchtritt von ca. 500 Ionen entspricht. Damit solche geringen Ströme messbar sind, muss der Abdichtwiderstand sehr hoch sein, weshalb der Gigaseal essentiell ist. Darüber hinaus sind wegen der geringen Ströme eine gute Abschirmung der gesamten Messapparatur über einen Faraday-Käfig, sowie einem Schwingungsgedämpften Messtisch notwendig. Sollten mehrere Kanäle im Patch vorliegen, ist dies direkt an den Signalamplituden erkennbar (Abbildung oben: 1 Kanal; unten: 5 Kanäle). In der Summe ergibt sich der makroskopische Stromverlauf aus einer exponentiell steigenden und einer exponentiell fallenden Kurve (siehe z.B. auch Aktionspotential). Die Saugpipetten-Technik liefert neben den Amplituden der Einzelkanalströme Informationen über das statistische Öffnungs-/Schließungsverhalten von Ionenkanälen. Aus statistischen Parametern wie die mittlere Offenzeit des Kanals können kinetische Modelle für den Kanal abgeleitet werden. Oft ist die Annahme von zwei Zuständen (offen und geschlossen) ausreichend. In anderen Fällen müssen mehrere geschlossene Zustände angenommen werden: 𝐺𝐺1 ⇌ 𝐺𝐺2 ⇌ ⋯ 𝐺𝐺𝑛𝑛 ⇌ 𝑂𝑂 Bei vielen Kanälen ist die Übergangswahrscheinlichkeit zwischen den einzelnen Zuständen von der Membranspannung abhängig. In anderen Fällen kann sich der Kanal erst infolge einer AktivatorBindung öffnen (z.B. Ca2+, Ach, GABA). Befinden sich 𝑁𝑁 Kanäle mit der Übergangswahrscheinlichkeit 𝑝𝑝 für den Übergang in den offenen Zustand innerhalb der Membran, gilt für den mittleren elektrischen Strom 𝐼𝐼 durch diese Kanäle: 𝐼𝐼 = 𝑁𝑁𝑁𝑁𝑁𝑁 (𝑖𝑖 ist der elektrische Strom durch den offenen Kanal). Der Einzelkanalstrom 𝒊𝒊 zeigt meist ein Ohmsches Verhalten. Der makroskopische Strom 𝑰𝑰 kann eine nicht-lineare Funktion der Membranspannung sein, wenn die Wahrscheinlichkeit des offenen Zustandes Spannungs-abhängig ist. Interpretation: Dies ist der Grund, weshalb Membranen als nicht-Ohmscher Widerstand zu betrachten sind. Es handelt sich bei der in den 1970er Jahren entwickelten Patch Clamp Technik um eine Verfeinerung der „traditionellen“ Voltage-Clamp Technik, die in den 1940er Jahren entwickelt wurde. Bei letzterer werden zwei Elektroden in die Zelle gestochen (jeweils eine Referenzelektrode in der Badlösung), wobei eine dazu dient eine Haltespannung vorzugeben, während die zweite Elektrode die auftretenden Ströme über die Membran aufzeichnet. Über traditionelles Voltage-Clamp kann nur die Summe aller Einzelströme durch die Zellmembran gemessen, aber niemals einzelne Anteile aufgelöst werden. Im Gegensatz hierzu nutzt die Patch-Clamp Technik nur eine Elektrode zur Messung des Membranpotentials, sowie eine Referenzelektrode in der Badlösung zur Messung der Sollspannung, mit der das Membranpotential abgeglichen wird. Sollten Membranpotential und Sollspannung voneinander abweichen, wird ein Kompensationsstrom durch die Pipettenelektrode in die Zelle injiziert, sodass die Spannungen wieder gleich sind. Dieser Kompensationsstrom wird letztlich gemessen und ermöglicht Rückschlüsse über Leitfähigkeiten in der Membran, deren Ursache die Ionenkanäle darstellen. Patch-Clamp Verstärker sind meist differentielle Verstärker, welche die Referenz-Elektrode in der Badlösung nutzen, um den Nullwert des Stroms zu setzen. Dadurch kann die Spannung konstant gehalten und die Änderungen im Strom durch die Pipettenelektrode gemessen werden (VoltageClamp). Umgekehrt kann auch der Strom konstant gehalten werden und Änderungen in der Spannung detektiert werden (Current-Clamp). Die kapazitiven Eigenschaften der Membran müssen bei voltage oder current clamp (gilt auch für TEVC) nicht berücksichtigt werden, da die Umladungsprozesse mit einer Dauer von ca. 1 ms deutlich vor den ausgewerteten Stromwerten (300ms-3s nach Beginn einer Spannungsänderung) abgeschlossen sind. Anordnungen in der Patch-Clamp Technik Neben der „Cell-Attached“ Konfiguration können (ausgehend von dieser) weitere Anordnungen erreicht werden, welche Aufschlüsse über unterschiedliche Charakteristika der untersuchten Zelle bzw. der exprimierten Ionenkanäle geben. Bei der „cell-attached“ Konfiguration sind die Zellmembran, sowie das Innere der Zelle intakt. Durch einen erhöhten Unterdruck oder durch kurze Pulse elektrischer Spannung an der Pipetten-Elektrode kann der Patch geöffnet werden und die Pipettenlösung steht in direktem Kontakt mit dem Cytoplasma. So kann das Gesamtverhalten aller Ionenkanäle der betreffenden Zelle untersucht werden. Der Gigaseal bleibt intakt, da Pipette und Cytoplasma über die Zellmembran und die Glaselektrode von der Badlösung isoliert sind. Diese Konfiguration wird als „whole-cell“ bezeichnet. Da in dieser Konfiguration die Pipettenlösung das Innere der Zelle füllt, sollte sie der Zusammensetzung des Cytosols relativ ähnlich sein (Die Zusammensetzung der Pipettenlösung bleibt dabei nahezu unverändert, da ihr Volumen im Vergleich zum Zellvolumen wesentlich größer ist. Dadurch läßt sich während der Messungen das intrazelluläre Milieu kontrollieren). Im Praktikum wird diese Anordnung für alle Versuchsteile verwendet. Wenn nach Erreichen der „cell-attached“ Konfiguration die Pipette von der Zelle abgezogen wird, löst sich der Patch von der Zellmembran und bleibt wegen des Unterdrucks an der Pipette hängen. Dadurch ist die cytoplasmatische Seite der Membran nun der Badlösung zugewandt, während sich die extrazelluläre Membranseite innerhalb der Pipette befindet. Es handelt sich dabei um die „inside-out“ Konfiguration. Sie ermöglicht wie die „cell-attached“ Konfiguration die Messung einzelner Ionenkanäle, wobei zusätzlich das Milieu der cytoplasmatischen Seite der Membran über die Zusammensetzung der Badlösung manipuliert werden kann. Simuliert die Pipettenlösung das Extrazelluläre Medium kann die Ionenkanal-Aktivität in Abhängigkeit von der Badlösung (Simulation des Cytosols) untersucht werden. Ausgehend von der „whole-cell“ Konfiguration kann ebenso die Pipette von der Zelle abgezogen werden, wodurch sich ein Teil der Membran von der Zelle löst, sich nach Innen umstülpt und durch Assemblierung der Lipide einen neuen Patch an der Pipettenspitze bildet. Dadurch befinden sich die cytoplasmatische Seite der Membran zur Pipettenlösung und die extrazelluläre Seite hin zur Badlösung gerichtet. Es handelt sich um die „outside-out“ Konfiguration, in der das Milieu des extrazellulären Raums über die Badlösung moduliert werden kann, während das cytosolische Milieu über die Pipettenlösung erhalten bleibt. Inside-out und outside-out Konfigurationen werden auch als Excised Patch bezeichnet, da der Membranfleck mitsamt Pipette durch Abziehen von der Zelle entfernt wird. Der Patch-Clamp Verstärker Zum Einstellen des Membranpotentials auf einen beliebigen, konstanten Wert wird ein Rückkopplungsmechanismus ausgenutzt, bei dem das membranpotential gemessen und mit dem gewünschten Wert (Kommandospannung, Sollspannung) verglichen wird. Unterscheiden sich Sollspannung und Membranpotential, so fließt ein Strom über die Zellmembran. Dadurch wird ein Regler aktiviert, der einen entgegengesetzten Strom in die Zelle injiziert. Diesen Kompensationsstrom kann man messen und dadurch die Leitfähigkeit der Zellmembran berechnen. Wichtige Komponenten des Schaltbildes sind der sogenannte Operationsverstärker (OPA, ope- ration amplifier) und ein Rückkopplungswiderstand R (f = feedback). Der OPA besitzt zwei Eingänge: Am Minus-Eingang (Punkt1 in f Abbildung 8) liegt die Spannung der Pipette (U ) an. Am anderen Eingang wird über ein Kabel die Sollspannung U soll pip von der Steuereinheit des Verstärkers eingespeist. Weichen Pipettenpotential und Kontrollspannung voneinander ab, so liefert der OPA am Ausgang eine Spannung, die proportional zur Differenz der beiden Eingangsspannungen, aber verstärkt ist. Daher herrscht zu diesem Zeitpunkt eine unterschiedliche Spannung zwischen Punkt 1 und Punkt 2, so daß ein Strom durch den Rückkopplungswiderstand fließt. An R entsteht f dadurch eine Spannung, die proportional zum Strom ist. Dies ergibt sich aus dem Ohm´schen Gesetz (𝑈𝑈𝑓𝑓 = 𝑅𝑅𝑓𝑓 × 𝐼𝐼). Der Operationsverstärker besitzt einen sehr hohen Eingangswiderstand (ca. 10^12 Ω), so daß der Strom nicht in den OPA fließen kann, sondern ausschließlich in die Pipette fließt. Der Strom ändert das Potential an Punkt 1, also U , und fließt so lange bis kein Unterschied zwischen den beiden Eingängen besteht, d.h. bis sich das pip Pipettenpotential dem Kommandopo- tential angeglichen hat. Somit gleicht die Schaltung Differenzen zwischen Pipettenpotential und Sollspannung aus, wobei an R eine Spannung erzeugt wird, die dem in die Zelle applizierten f Strom proportional ist. Bei dem Schaltkreis handelt es sich daher um einen Strom-Spannungs- Wandler. Der Ausgleich zwischen Pipetten- und Kommandopotential erfolgt so schnell, daß beide Werte zu jedem Zeitpunkt identisch sind. Die Ausgangsspannung wird zur Steuereinheit fortgeleitet und kann von dort ausgelesen und in den Strom (abhängig von R ) umgerechnet werden. Eigentlich addiert sich zur Ausgangsspannung auch noch die f Sollspannung, doch diese wird durch einen Differenzverstärker wieder abgezogen. Die bisherige Darstellung des Rückkopllungswiderstands R stellt allerdings eine Idealisierung dar. 𝑅𝑅𝑓𝑓 ist kein reiner f Ohm´scher Widerstand, sondern besitzt auch kapazitive Eigenschaften. Bei jedem Spannungssprung fließen zunächst Ladungen auf die Oberfläche des Widerstandes, um ihn umzuladen. Diese Eigenschaft ist bedeutsam für die Messung, weil bei jeder Änderung der Spannung Zeit für das Umladen des Kondensators verloren geht, so daß schnell veränder- liche Signale, z.B. senkrecht ansteigende Signale von Einzelkanalströmen, verzögert werden. Der Verstärker enthält Korrekturschaltkreise, die ein dem Kondensator umgekehrtes Fre- quenzverhalten aufweisen, wodurch die Verluste ausgelöscht und die Antwortzeit auf wenige Mikrosekunden herabgesetzt wird. Messung der spezifischen Membrankapazitäten Zunächst müssen die spezifischen Kapazitäten der Patch-Pipette gemessen werden (patchen eines Öl-Tropfens). Zwecks Vergleich wird auch die spezifische Kapazität der verwendeten Zellen ohne Chr2-Expression bestimmt, um den Einfluss von Chr2 auf die Kapazität zu bestimmen. Außerdem werden die Kapazitäten zwecks Vergleichs auf die Zellgröße geeicht. Dazu wurden die Ladungen 𝑄𝑄 = ∆𝐼𝐼 ∙ ∆𝑡𝑡 gemessen, die bei bestimmten Haltepotentialen über die Membran übertragen wurden. Die Messung erfolgt bei unterschiedlichen Haltepotentialen zwischen -140 mV und +40 mV, welche über die Badelektrode in 20 mV-Schritten hochreguliert wurden. Anschließend wird die Kapazität 𝐶𝐶 = 𝑄𝑄/𝑈𝑈 für die einzelnen Haltespannungen U berechnet. Die nicht Chr2-exprimierenden Zellen zeigen sehr konstante Membrankapazitäten für alle Haltespannungen. Im Mittelwert war die Membrankapazität der Chr2-exprimierenden Zellen größer. Durch Einbau zusätzlicher Proteine in die Membran wird eine Erhöhung der Dielektrizitätskonstanten von 𝜀𝜀 = 2 (reine Lipidmembran) erwartet, weshalb die Kapazität 𝐶𝐶 = 𝜀𝜀0 𝜀𝜀 ∙ 𝐴𝐴/𝑑𝑑 gestiegen ist. Verlauf des Stromsignals (1) Der vor der ChR2-Aktivierung gemessene Strom ist der Leckstrom. Er entsteht durch den Ladungsfluss über die Membran durch andere Kanäle, Transporter oder Lecks innerhalb der Membran. (2) Direkt nach der Aktivierung des Kanals werden alle Kanäle gleichzeitig aus dem inaktiven Zustand in den aktiven Zustand überführt, wodurch der maximale Ladungstransport und somit der Peakstrom erreicht wird. (3) Da sich die Kanäle automatisch nach wenigen ms wieder inaktivieren, nimmt das Potential zunächst schneller ab, wobei sich langsam ein stationärer Strom einstellt. Ursache des stationären Stroms ist ein Verlust der Kohärenz von gleichzeitigem Öffnen und Schließen aller Kanäle. So stellt sich ein Gleichgewichts-Ladungstransport über die Membran ein, der durch alle aktiven ChR2 Moleküle zustande kommt, wobei sich aktive und nicht-aktive ChR2 Moleküle im Gleichgewicht befinden. (4) Sobald die kontinuierliche Lichteinstrahlung unterbrochen wird, fällt der stationäre Strom wieder zurück auf Leckstrom-Niveau, da sich die Kanäle wieder schließen und nicht erneut die Öffnung angeregt wird. 𝑰𝑰 [𝒑𝒑𝒑𝒑] 𝟎𝟎 Leckstrom Baseline ChR2-Schließung mit Zeitkonstante 𝝉𝝉𝟑𝟑 Stationärer Strom ChR2-Öffnung mit Zeitkonstante 𝝉𝝉𝟏𝟏 Peakstrom ChR2-Relaxation mit Zeitkonstante 𝝉𝝉𝟐𝟐 Belichtung Start Belichtung Ende Zwei-Elektroden Voltage-Clamp an Oozyten 𝒕𝒕 [𝒔𝒔] Purino-Rezeptoren Der P2X2-Rezeptor gehört zu den P2-Rezeptoren, einer Gruppe Liganden-aktivierter Ionenkanäle. Allen gemein ist die Aktivierung durch ATP, weshalb sie auch als Purino- oder Nukleotid-Rezeptoren (ATP ist ein Purin-Nukleotid) bezeichnet werden. Es existieren viele Purin- und Pyrimidin-Rezeptoren in fast allen Zellarten. Sie sind an zahlreichen physiologischen, aber auch pathologischen Prozessen beteiligt. Extrazelluläre Purine und Pyrimidine beeinflussen z.B. die Kontraktilität der glatten Muskeln, die exogene und endogene Sekretion, die Immunantwort sowie die ThrombozytenAggregation. Klassifizierung, Struktur und Funktion der P2-Rezeptoren Fast jede Säugerzelle weist P2-Rezeptoren an ihrer Oberfläche auf. Diese können in zwei große Rezeptor-Familien kategorisiert werden: die P1-Purinorezeptoren (P1R) und die P2Purinorezeptoren (P2R). • • P1R zeigen Affinitäten für Adenosin und sind alle an G-Proteine gekoppelt. Man unterscheidet weiter insgesamt vier Subtypen, auf die nicht näher eingegangen werden soll. Bei den P2R lassen sich zwei Subtypen voneinander unterscheiden. Die P2X-Rezeptoren (P2XR) sind Liganden-aktivierte Kationenkanäle, während die P2Y-Rezeptoren (P2YR) G-Protein-gekoppelte Rezeptoren darstellen. o P2Y ist ein G-Protein-gekoppelter Rezeptor mit 7-Transmembranhelices, drei extrazellulären und drei intrazellulären Schleifen, wobei vier extrazellulär lokalisierte Cystein-Reste über zwei Disulfidbrücken miteinander verbunden sind. Der NTerminus ist extrazellulär lokalisiert, während sich der C-Terminus im Zytosol befindet. o P2X hat lediglich zwei Transmembrandomänen, die über eine große extrazelluläre Schleife verbunden sind. Diese beinhaltet eine ATP-Bindestelle, Regulator-Domänen, sowie Glykosylierungsstellen. N-, sowie C-Terminus sind intrazellulär lokalisiert, wobei der C-Terminus in seiner Länge zwischen den P2X Subtypen stark variiert. Die P2Y-Rezeptorfamilie Die evolutionär sehr früh entstandene P2Y-Rezeptorfamilie gehört zur Rhodopsinfamilie G-Proteingekoppelter Rezeptoren (Klasse 1 GPCR), die alle eine 7 Transmembran-Topologie aufweisen. Es wurden bisher 8 verschiedene Typen kloniert. Aufgrund von Homologiemerkmalen lassen sich zwei Gruppen unterscheiden. Die Proteine der ersten Gruppe (P2Y1, P2Y2, P2Y4, P2Y6, P2Y11) sind Gq-Protein gekoppelt und führen zur Aktivierung der Phospholipase C (PLC). Die PLC hydrolysiert Phosphatidylinositol-4,5-phosphat (PIP2) zu Diacylglycerol (DAG) und Inositol-1,4,5-trisphosphat (IP3). IP3 setzt Calcium aus intrazellulären Speichern, wie dem ER frei. Zusammen mit Ca2+ kann DAG unter anderem die Aktivierung der Proteinkinase C (PKC) bewirken. Es folgt eine Signalkaskade, welche in glatten Muskelzellen eine Kontraktion, in Adipozyten und Hepatozyten die Gluconeogenese und den Glykogenabbau, in Thrombozyten die Aggregation sowie in sezernierenden Zellen die Sekretion von Botenstoffen induziert. Die Proteine der zweiten Gruppe (P2Y12, P2Y13, P2Y14) haben verschiedene Funktionen und unterscheiden sich von den GPCR der ersten Gruppe aufgrund ihrer unterschiedlichen AS-Sequenz. Der Rezeptor P2Y12 ist in die Thrombozyten-Aggregation involviert. Der P2Y13 Rezeptor wird durch ADP aktiviert, wobei die Funktion in der Literatur noch nicht beschrieben ist. Bei P2Y14 handelt es sich um einen Rezeptor für UDP-Zucker, die an GProteine gekoppelt sind. Es wird für diesen Rezeptor eine Rolle im Immunsystem angenommen. Die P2X-Rezeptorfamilie Hierbei handelt es sich um nichtselektive Liganden-gesteuerte Kationenkanäle, die für monovalente und bivalente Kationen (wie Na+, K+ und Ca2+) permeabel (manche Rezeptoren sind auch für größere Moleküle durchlässig) sind und über mikromolare Konzentrationen von extrazellulärem ATP aktiviert werden. Sie spielen eine wichtige Rolle bei der schnellen Erregungsübertragung zwischen Neuronen im zentralen und peripheren Nervensystem, kommen aber auch u.a. in Epithel- und Endothelzellen und im Skelettmuskel vor. Insgesamt sind bisher auch hier 8 Subtypen in Säugerzellen beschrieben. Alle Subtypen zeigen eine 30-50% identische AS-Sequenz und weisen demnach auch eine ähnliche Hauptstruktur auf. N- und C-Termini sind intrazellulär lokalisiert und dienen als Ziele für PKvermittelte Phosphorylierung. Während der N-Terminus bei allen Subtypen näherungsweise gleich groß ist, schwankt die Länge des C-Terminus erheblich (zwischen 30 AS bei P2X6 und 240 AS für P2X7). Die zwei Transmembran-Regionen sind am Aufbau der Ionenpore beteiligt. Die extrazelluläre Schleife besitzt 10 Cysteinreste, die paarweise Disulfidbrücken bilden und somit die Tertiärstruktur der Schleife prägen. Die extrazelluläre H5 Region am Porenvorhof ist für die Regulation des Rezeptors durch verschieden Kationen (u.a. Zink und Protonen) verantwortlich. Außerdem existieren mehrere Glykosilierungsstellen. Die ATP-Bindestellen der extrazellulären Schleife befinden sich in der Nähe der Transmembran-Regionen. Für die Quartiärstruktur wurde ein gestreckter Trimer postuliert, wobei sowohl Homomere, als auch Heteromere P2X-Rezeptoren existieren können, die sich in ihren pharmakologischen Eigenschaften unterscheiden. Universeller Agonist für die P2X-Rezeptoren ist ATP, jedoch zeigen auch ATPverwandte Verbindungen wie ADP, UTP, CTP und ATP-Derivate unterschiedliche Affinitäten für die Rezeptoren. Im Praktikumsversuch wird der Rezeptor-Subtyp P2X2 verwendet. Er ist für die synaptische Übertragung zwischen Neuronen, sowie zwischen Neuronen und glatten Muskelzellen verwantwortlich. Es sind insgesamt sechs Transkriptionsvarianten des P2X2-Gens bekannt, die für sechs verschiedene Isoformen codieren. Elektrophysiologie der P2X-Subtypen Die einzelnen P2X-Rezeptortypen zeigen stark unterschiedliche elektrophysiologische Eigenschaften, wobei vor allem die Desensibilisierung der einzelnen Ionenkanäle stark variiert. Unter Desensibilisierung versteht man die Kinetik der Kanal-Inaktivierung einer gesamten Population von Ionenkanälen nach Aktivierung des Transports (hier: durch ATP-Zugabe), sowie die notwendige Erholungszeit, die bis zur Rückkehr der ursprünglichen Agonisten-Empfindlichkeit benötigt wird. Die Schließung der Kanäle kann in elektrophysiologischen Messungen als exponentiell abfallender Strom detektiert werden. Die Kanalöffnung entspricht der meist wesentlich schneller ansteigenden exponentiellen Funktion, die im Peakstrom endet. Die Ursache der Desensibilisierung ist weitestgehend unbekannt. Die Desensibilisierung (Inaktivierungszeit, sowie Erholungszeit) ist abhängig von der AgonistenKonzentration, sowie der Affinität für den entsprechenden Agonisten. Je höher die Affinität und je größer die Konzentration, desto schneller und ausgeprägter ist die Desensibilisierung. Inaktivierungszeit und Erholungszeit variieren zwischen den P2X Rezeptoren erheblich und sind Konzentrations-abhängig. Die Konzentrationsabhängigkeit der Inaktivierungszeit ist in der Abbildung dargestellt: Je höher die ATP-Konzentration, desto schneller wird der Strom wieder null (Inaktivierung der Kanäle). Bei P2X1 und P2X3 entwickelt sich eine vollständige Desensibilisierung innerhalb einiger Millisekunden und setzt direkt nach Aktivierung des Kanals ein. Bei P2X2 sowie P2X4 erfolgt die Desensibilisierung innerhalb von Zehntel-Sekunden, wobei die Aktivität des Kanals über mehrere Sekunden konstant ist. Die Abbildung zeigt Desensibilisierungskurven von sechs homomeren P2XRezeptoren. Es sind die zeitlichen Verläufe der Nettoströme nach Druckapplikation von 30 µM ATP auf P2X-exprimierende HEK293 Zellen gezeigt. Diese wurden 48 Stunden vor dem Experiment mit 1 µg/ml P2X-Rezeptor-cDNA transfiziert. Oben: Die ATP-Applikation erfolgte für 2s, hier ist kaum ein Unterschied zwischen P2X2, P2X4 und P2X7 zu erkennen. P2X1 desensibilisiert wesentlich schneller als P2X3. Unten: Die ATP-Applikation erfolgte für 60s, es ist zu erkennen, dass P2X4 und P2X2 wesentlich schneller Desensibilisieren, als P2X7, dessen Population nach 60s immer noch vollständig geöffnet ist. Die Erholungszeit ist im Vergleich zur Inaktivierungszeit wesentlich länger. Die Desensibilisieurng des P2X1 Rezeptors ist mit 30 Minuten langanhaltend. Nach einer halben Stunde in ATP-freier Lösung kann erst wieder eine maximale Stromantwort erzielt werden. Nach fünf Minuten in ATP-freier Lösung resultiert ein Strom, der etwa 25% der Primärantwort nach erster ATP-Gabe entspricht: Die Abbildung zeigt die Erholungszeit von P2X1. Nach jeder Messung wurde die Zelle 5 Minuten in ATPfreier Lösung inkubiert. Xenopus Oozyten Die P2X2 Rezeptoren werden 1-3 Tage vor Experiment-Beginn in Form von in vitro-synthetisierter mRNA in die Oozyten von Xenopus laevis (glatter Krallenfrosch) injiziert. Xenopus Oozyten eignen sich hervorragend zur heterologen Genexpression, sowie für Knockdown-Studien. Sie sind mit ungefähr 1 mm Durchmesser sehr groß, wodurch die Injektion fremder RNA und die anschließende Analyse über elektrophysiologische oder molekularbiologische Techniken wesentlich erleichtert ist. Außerdem stehen die Oozyten in großem Umfang zur Verfügung. Ein Weibchen produziert 10.000 bis 15.000 pro Jahr, die während einer Operation aus dem großen Ovargewebe isoliert werden können und nach enzymatischer Trennung der adhärierten Follikelzellen mittels Kollagenase direkt für die Experimente zur Verfügung stehen (sollten die Follikelzellen nicht vollständig abgetrennt worden sein, resultiert eine verzögerte Stromantwort im TEVC Experiment, da die ATP-Bindestellen der P2-Rezeptoren durch die Zellen verdeckt werden und nicht direkt erreichbar sind). Nach wenigen Monaten hat das Weibchen neue Eizellen produziert. Die Oozyten sind ungefähr zwei Wochen nach Isolierung in ORI (Oozyten Ringer Lösung, eine spezielle NaClLösung) haltbar. Bei den Xenopus laevis Weibchen ist die Oogenese ein kontinuierlicher, asynchroner Prozess, sodass das Ovar Eizellen jeden Entwicklungsstadiums enthält. Die Oozyten durchlaufen insgesamt sechs Stadien der Oogenese und wachsen dabei von einer Größe von 50 µm auf eine Größe von 1,3 mm an. Oozyten später Stadien besitzen eine dunkel pigmentierte Hälfte, die animale Hemisphäre und eine nur schwach pigmentierte Hälfte, die vegetale Hemisphäre (siehe Abbildung). Im Stadium VI sind diese Hälften durch den nicht-pigmentierten äquatorialen Ring voneinander getrennt. Der Zellkern, welcher das 100fache Volumen eines typischen somatischen Zellkerns hat und daher als Keimbläschen bezeichnet wird, befindet sich in den unteren Entwicklungsstadium im Zentrum der Zelle und wandert ab Stadium IV in die sich ausbildende animale Hemisphäre. Im Zentrum der Oozyte entsteht die mitochondriale Wolke, die u.a. Mitochondrien und Ribosomen enthält. Für den Praktikumsversuch eignen sich die Oozyten besonders, da sie wenige Kanäle und demnach kaum endogene Leitfähigkeiten aufweisen. Darüber hinaus existieren keine endogenen ATPaktivierten Kanäle, welche die Messergebnisse am P2X2 Kanal verfälschen könnten. Zur heterologen Genexpression eignen sich die Xenopus Oozyten aus zwei Gründen besonders gut. (1) Sie besitzen alle notwendigen Strukturen und Proteine für posttranslationale Modifikationen. (2) Es findet eine selektive Amplifikation ribosomaler RNA schon im Stadium I der Oogenese zur Produktion eines umfangreichen maternalen Vorrats von Ribosomen statt. Am vegetalen Pol der Oozyte wird in den frühen Entwicklungsstadien eine besondere Gruppe maternaler mRNA-Moleküle angereichert, die für bestimmte Transkriptionsfaktoren und Signalmoleküle codieren. Ab Stadium III wird an diesem Pol das Speicherprotein Vitellogenin eingelagert, das mit seinen Spaltprodukten über die Hälfte der gesamten Proteinmenge ausmacht. Die Synthese des Proteins erfolgt durch die Leber von Xenopus laevis und die Aufnahme durch Mikropinozytose. Innerhalb der Oozyten erfolgen die Spaltung von Vitellogenin und die Einlagerung der Spaltprodukte in Dotterschollen. Der Abbau dieser Proteine liefert die Energie für die Embryonalentwicklung bis zum Kaulquappenstadium. Eines der Spaltprodukte von Vitellogenin (Lipovitellin) ist mit Lipiden assoziiert, weshalb die zwei Elektroden im TEVC Experiment immer von der animalen, dunklen Seite in die Zelle injiziert werden sollten, um eine repräsentative Stromantwort zu erhalten. Außerdem bleibt nach Isolation der Oozyten eine Vitellogenin-Hülle um die Zelle herum erhalten, die ebenso vor dem TEVC-Experiment entfernt werden muss. Zweielektroden Spannungsklemme Die TEVC-Methode (Two-Electrode Voltage-Clamp) wurde schon in den 1940er Jahren entwickelt und seither immer weiter verbessert. Im Vergleich zum Patch-Clamp werden hier die Elektroden direkt in die Zelle eingestochen. Darüber hinaus werden im TEVC zwei Elektrodenpaare (hier: Glasmikroelektroden), im Patch-Clamp nur ein Elektrodenpaar verwendet. In den frühen Phasen der TEVC Methode wurden die Ursachen für das Auftreten von Aktionspotentialen in Riesen-Axonen von Tintenfischen aufgeklärt. Für diese Arbeiten gab es 1963 den Medizin Nobelpreis. Heute ist es möglich auch wesentlich kleinere Zellen mit dieser Methode zu untersuchen, da Mikroelektroden mit ca. einem µm Durchmesser verwendet werden. Darüber hinaus lässt sich Voltage-Clamp auch mit einer einzelnen Elektrode durchführen (Single-Electrode Voltage-Clamp, SEVC). Für große Zellen mit niedrigem Eingangswiderstand ist SEVC jedoch nicht anwendbar. Zur Messung des Membranpotentials zu Beginn des Expriments wird nur ein Elektrodenpaar benötigt: Die Potentialelektrode innerhalb der Zelle und die Badelektrode außerhalb der Zelle. Die intrazelluläre Elektrode misst mit hohem Eingangswiderstand des Verstärkers (kein Stromfluss) die an der Zellmembran anliegende elektrische Spannung. Anhand der Spannungsmessung können erste Vermutungen über vorhandene Leitfähigkeiten angestellt werden (hohes Membranpotential ist Indiz für geringe Leitfähigkeit). Eindeutige Charakterisierung benötigt jedoch das TEVC-Experiment. Im TEVC Experiment induziert die intrazelluläre Stromelektrode eine Spannung innerhalb der Zelle („Injektion von Ladung“), während die intrazelluläre Potentialelektrode die „Stromantwort“ misst. Zur Messung durch die Potentialelektrode wird eine Referenz benötigt, welche die Badelektrode liefert (Messung der Potentialdifferenz). Die Stromelektrode benötigt eine geerdete (warum geerdet?), zweite Badelektrode, um das Membranpotential aktiv durch Anlegen einer Spannung zu verändern und über die gesamte Messung konstant zu halten (daher: Spannungsklemme). Die angelegten Spannungen variieren typischerweie zwischen -150 mV und +100 mV. Durch Auftragung des gemessen Stroms gegen die angelegten Spannungen werden IV-Kennlinien erhalten, so wie auch beim Patch-Clamp. Charakteristische Parameter der IV-Kennlinien sind Steigung, Form und Umkehrpotential. Statt der Spannungsklemme, lässt sich auch eine Stromklemme durchführen, wobei hier der Strom konstant ist und das Membranpotential gemessen wird. Current Clamp und Voltage Clamp basieren prinzipiell auf dem Ohm’schen Gesetz U=RI, wobei die Widerstände meist spannungsabhängig sind, was zu nicht-linearen Kennlinien führt. Grund: • Spannungs-abhängige Kanäle basieren auf dem Ohmschen Gesetz und zeigen lineare IVKennlinien; Aufgrund Inaktivierungs-Mechanismen und unterschiedlichen Schwellenwerten gehorchen auch eine Kombination verschiedener Spannungs-abhängiger Kanäle als Gesamtheit nicht mehr dem Ohmschen Gesetz. • Spannungs-unabhängige Kanäle, nämlich solche die Ligand-gesteuert sind wie die P2XRezeptoren, zeigen nicht-lineare IV-Kennlinien. Das folgende Ersatzschaltbild zeigt die Voltage-Clamp Schaltung mit einer Stromelektrode (CE) und einer Potentialelektrode (PE). Um eine Zellmembran auf ein bestimmtes Membranpotential VM, nämlich das Kommandopotential VC, zu klemmen, muss ein Potential VCl vorgegeben werden, dass groß genug ist, um den Spannungsabfall an dem Elektrodenwiderstand RCE zu kompensieren. Es lässt sich quantitativ darstellen über 𝑉𝑉𝐶𝐶𝐶𝐶 = 𝑉𝑉𝑚𝑚 (𝑅𝑅𝑀𝑀 + 𝑅𝑅𝐶𝐶𝐶𝐶 )/𝑅𝑅𝑀𝑀 . Da sich der Membranwiderstand RM und gelegentlich auch der Elektrodenwiderstand RCE während eines Experiments ändert, ist es notwendig das Membranpotential VM stetig mithilfe der Potentialelektrode PE mit dem Kommandopotential VC zu vergleichen und das Klemmpotential VCl entsprechend nachzuregeln. Um diesen regulatorischen Prozess zu automatisieren, werden Operationsverstärker (op-amp) eingesetzt. Die Glasmikroelektoden werden aus Glaskapillaren hergestellt, die mit einem Mikroelektrodenpuller fein ausgezogen werden. Nach Füllung mit 3 M KCl wird der der elektrische Kontakt zur Elektronik über einen chlorierten Silberdraht (AgCl-Elektrode), der in die Elektrodenfülllösung eintaucht hergestellt. Vor Beginn der Messungen muss der Eigenwiderstand der Mikroglaselektroden bestimmt werden. Dazu werden diese in die Lösung eingetaucht. Er sollte < 2𝑀𝑀Ω sein. Anschließend wird die gemessene Potentialdifferenz zwischen Messelektrode und Badelektrode zu null abgeglichen (Eichung der Messapparatur). Für alle elektrophysiologischen Messungen wurden zwei P2X2 exprimierende Oozyten, sowie drei nicht-transfizierte Kontrollzellen verwendet, die mit dem animalen Pol nach oben in die Flüssigkeits-gefüllte Messkammer pipettiert wurden (siehe Abbildung). Anschließend werden die zwei Glasmikroelektroden langsam an die Oozyte herangefahren, bis sie die Zellmembran leicht eindrücken und anschließend eingestochen. Durch den Einstich fällt das Membranpotential plötzlich ab, wodurch der Membrandurchstoß erkannt werden kann. Zum Wechsel des Außenmediums wird der Medienwechsler über der Oozyte positioniert und die entsprechende Lösung, sowie die Absaugvorrichtung aktiviert. Damit steht die Oozyte in einem kontinuierlichen Fluss von Außenmedium, das computergesteuert in seiner Zusammensetzung schnell verändert werden kann. Messungen des Ruhepotentials Zur Messung des Ruhepotentials wird nur eine Glasmikroelektrode, die Spannungselektrode, in die Oozyte eingestochen. Die Messung soll die Abhängigkeit des Ruhepotentials vom Außenmedium zeigen. Es werden die drei Medien ORI, ORI-90K, sowie ORI-ATP verwendet. • • • ORI ist eine 90 mM konzentrierte NaCl Lösung mit 1 mM KCl, 2 mM MgCl2 und 5 mM HEPES bei pH=7,4. Bei ORI-90K ist die Konzentration von KCl 90 mM und die von NaCl 1mM. Bei der Lösung ORI-ATP sind in der ORI Lösung zusätzlich 100 µM ATP enthalten. In ORI- und ORI-90K Lösung zeigen Kontrollzellen und P2X2-exprimierende Zellen vergleichbare Ruhepotentiale, da die inaktiven P2X2-Rezeptoren keinen Einfluss auf das Ruhepotential haben. Für die ORI-Lösung ist das Membranpotential negativer als für die ORI-90K Lösung, da im Außenmedium angereicherte Kalium-Ionen über Kalium-Kanäle entlang ihres elektrochemischen Gradienten in die Zelle diffundieren und somit eine Verringerung des Membranpotentials bewirken (Natrium-Ionen können nicht hinein diffundieren). Wenn größtenteils Natrium-Ionen im Außenmedium vorliegen, so ist keine Diffusion über die Membran möglich und der hohe elektrochemische Gradient bleibt erhalten und wirkt sich auf das Membranpotential aus. Die ORI-ATP Lösung bewirkt bei den Kontrollzellen keine nennenswerte Verschiebung des Ruhepotentials im Vergleich zur ORI-Lösung (eine geringe Verschiebung in Richtung positiven Werten ist aufgrund der zusätzlichen negativen Ladungen in ATP außerhalb der Zelle zu beobachten). Da keine durch ATP aktivierbaren Ionen-Kanäle innerhalb der Membran vorliegen, wird das Potential nicht beeinflusst. In P2X2-exprimierenden Zellen hingegen erfolgt eine durch ATP-vermittelte Aktivierung der Kationen-Diffusion über P2X2, wodurch alle Kationen entlang ihres elektrochemischen Gradienten über die Membran diffundieren können und das Membranpotential somit hin zu positiven Werten verändern. Messungen der Membrankapazität und Leitfähigkeit Nun wird auch die Stromelektrode in die Zelle eingestochen und diese auf ein Haltepotential von 60 mV geklemmt. Es ist darauf zu achten, dass der Haltestrom bei -60 mV nicht -100 nA übersteigt, da ansonsten die Oozyten elektrisch undicht sind. Um die Kapazität zu erhalten, wird eine Sägezahnspannung angelegt. Es ist von Bedeutung, dass für diese Messung kein ATP in der ORI Lösung vorhanden ist, da ATP die Öffnung von P2X2 Kanälen bewirkt und damit zusätzliche Ionen in die Zelle einströmen. Dieser zusätzliche Einstrom von Ionen überlagert den kapazitiven Strom. Ohne die Kapazitiven Eigenschaften der Plasmamembran würde die Stromantwort einen identischen Verlauf zeigen, wie die Spannungsvorgabe. Die kapazitiven Ströme sind durch einen sprunghaften Anstieg infolge eines Vorzeichenwechsels der Steigung 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 charakterisiert. Der sprunghafte Anstieg liegt daran, dass die Umladung des Kondensators mit einer sehr schnellen Zeitkonstante geschieht. 𝑼𝑼 −𝟔𝟔𝟔𝟔 𝒎𝒎𝒎𝒎 𝒅𝒅𝒅𝒅 𝒎𝒎𝒎𝒎 = 𝟏𝟏 𝒅𝒅𝒅𝒅 𝒎𝒎𝒎𝒎 −𝟏𝟏𝟏𝟏𝟏𝟏 𝒎𝒎𝒎𝒎 𝟒𝟒𝟒𝟒 𝒎𝒎𝒎𝒎 𝟖𝟖𝟖𝟖 𝒎𝒎𝒎𝒎 −𝟐𝟐𝟐𝟐 𝒎𝒎𝒎𝒎 𝑰𝑰 −𝟔𝟔𝟔𝟔 𝒎𝒎𝒎𝒎 𝑰𝑰𝟏𝟏 = 𝑰𝑰𝑪𝑪 𝑰𝑰𝟐𝟐 = 𝟐𝟐𝑰𝑰𝟏𝟏 𝟒𝟒𝟒𝟒 𝒎𝒎𝒎𝒎 𝒕𝒕 𝟒𝟒𝟒𝟒 𝒎𝒎𝒎𝒎 Spannungsprotokoll zur Messung der Membrankapazität, sowie Leitfähigkeit. 𝚫𝚫𝑰𝑰 𝚫𝚫𝒕𝒕 𝟖𝟖𝟖𝟖 𝒎𝒎𝒎𝒎 𝑰𝑰𝟑𝟑 = 𝑰𝑰𝟐𝟐 𝑰𝑰𝟒𝟒 = 𝑰𝑰𝟏𝟏 𝟒𝟒𝟒𝟒 𝒎𝒎𝒎𝒎 𝒕𝒕 Stromantwort auf das Spannungsprotokoll. Der mit Ic markierte Abschnitt dient zum Ablesen des kapazitiven Stroms. Der Kapazitive Strom und die Kapazität stehen über folgende Gleichung in direktem Zusammenhang. 𝐶𝐶 = 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 Da die Steigung der Geraden genau 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝐼𝐼𝐼𝐼𝐼𝐼 =1 𝑚𝑚𝑚𝑚 𝑚𝑚𝑚𝑚 ⟹ 𝐼𝐼𝐶𝐶 = 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝑑𝑑𝑑𝑑 𝐶𝐶𝐶𝐶𝐶𝐶 entspricht, vereinfacht sich die Gleichung zu 𝐼𝐼𝐶𝐶 = 𝐶𝐶 ∙ 1𝑚𝑚𝑚𝑚/𝑚𝑚𝑠𝑠 ⟺ 𝐶𝐶 = 𝐼𝐼𝐶𝐶 ∙ 1𝑚𝑚𝑠𝑠/𝑚𝑚𝑚𝑚, weshalb die Kapazität direkt im Graphen in Form des kapazitiven Stroms abgelesen werden konnte. Nach obiger Gleichung sollten alle vier durch das Spannungsprotokoll im I-t Diagramm sichtbaren kapazitiven Ströme identisch sein, da 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 im gesamten Spannungsprotokoll mit 1 mV/ms eine feste Größe darstellt. Wegen des Vorzeichenwechsels sind die Ströme I2 und I3 jedoch um einen Faktor 2 zu groß. Zur Berechnung der Leitfähigkeit 𝐺𝐺 = 1/𝑅𝑅 muss beachtet werden, dass es sich um eine Spannungsabhängige Leitfähigkeit handelt. Damit ist das Ohmsche Gesetz 𝑅𝑅 = ∆𝑈𝑈/∆𝐼𝐼 zur Berechnung des Widerstandes nicht anwendbar (R ist spannungsabhängig: Voltage Dependent Resistence, VDR). Der Widerstand eines VDR-Elementes in der Elektrotechnik verringert sich exponentiell mit wachsender Spannung, wodurch der Zusammenhang zwischen R und U nicht mehr linear ist, wie im Ohmschen Gesetz verankert. P2X2 hat unterschiedliche Leitfähigkeiten für die einzelnen Haltepotentiale (2 Ursachen: Anzahl der offenen Kanäle variiert mit der Spannung; Konzentrationsgradienten) und entspricht demnach einem VDR-Element. Ausgangspunkt für die Berechnung der Leitfähigkeit ist die im betrachteten Intervall (Spannungsanstieg von −20 𝑚𝑚𝑚𝑚 auf −100 𝑚𝑚𝑚𝑚; 𝑑𝑑𝑑𝑑 = −80𝑚𝑚𝑚𝑚) resultierende Stromdifferenz 𝑑𝑑𝑑𝑑 der Stromantwort. Es wird dann das Ohmsche Gesetz angewendet. Der Kehrwert von 𝑅𝑅 = 𝑈𝑈/𝐼𝐼 ist dann direkt die Leitfähigkeit 𝐺𝐺 = 𝐼𝐼/𝑈𝑈. Wäre 𝐺𝐺 = 0, so wäre auch die Steigung 𝑑𝑑𝑑𝑑/𝑑𝑑𝑑𝑑 = 0. Je größer diese Steigung, desto mehr Ionen pro Zeit passieren die Membran, desto größer ist die Leitfähigkeit. Damit kann die Leitfähigkeit auch grob im I-t Diagramm abgeschätzt werden. Wenn man eine spezifische Membrankapazität von 1 µ𝐹𝐹/𝑐𝑐𝑐𝑐2 annimmt, lässt sich die Zelloberfläche der Zellen bestimmen. Für die Zelloberfläche gilt dann 𝐴𝐴 = 𝐶𝐶𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 𝐶𝐶𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 𝐶𝐶𝑚𝑚𝑚𝑚𝑚𝑚𝑚𝑚 = 3 = 2 𝐶𝐶𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 10 𝑛𝑛𝑛𝑛/𝑐𝑐𝑚𝑚 10 𝑛𝑛𝑛𝑛/𝑚𝑚𝑚𝑚2 Bei Betrachtung der Kapazitäten sind Unterschiede zwischen P2X2 exprimierenden Zellen und Kontrollzellen festzustellen. Diese Unterschiede sind theoretisch möglich, da die Kapazität von der Membran-Fläche, sowie der Anzahl an eingebauten Proteinen (Veränderung des Dielektrikums) abhängig ist. Da keine statistisch aussagekräftige Menge Oozyten gemessen wurden, kann die Größe und somit Membran-Fläche stark variieren und daher diese Unterschiede erzeugen. Theoretisch ist eine Erhöhung der relativen Permittivität und somit der Kapazität zu erwarten, da die MembranDomänen der Proteine leicht hydrophiler sind als die Lipide der Membran. Bei den Leitfähigkeiten, sollten keine oder nur geringe Abweichungen zwischen Kontrollzellen und P2X2 exprimierenden Zellen resultieren, da der Einbau von Ionen-Kanälen keinen Einfluss auf die Leitfähigkeit hat, solange sie inaktiv sind. Messungen der P2X2 Rezeptorströme Strom-Spannungs-Kennlinien (IV-Kurven) der Oozyten werden in ORI sowie in ORI-ATP (30 µM) gemessen. Dazu wird das Membranpotential auf -60 mV geklemmt, worauf Spannungssprünge für jeweils 500 ms auf -120 mV bis +60 mV in Zehnerschritten folgen. Zwischen den Spannungssprüngen wird das Membranpotential zurück auf -60 mV gesetzt, damit die Kanäle nach jedem Spannungssprung wieder zurück in den Ursprungszustand relaxieren können. Die maximalen Stromantworten werden gegen die Spannungen der einzelnen Spannungssprünge aufgetragen und ergeben so die IV-Kurven. Die Stromantworten der Kontrollzellen sind mit und ohne ATP alle identisch, sodass die Stromantworten unabhängig von der ATP-Konzentration sein müssen. Die Kontrollzellen zeigen desweiteren, so wie auch die P2X2-exprimierenden Zellen ohne ATP im Außenmedium, einen über die Zeit konstanten Strom für jede angelegte Spannung. Für die P2X2-exprimierenden Oozyten in ATP-haltigem Außenmedium ist die maximale Stromantwort erst nach einer längeren Zeit erreicht. Während dieser Zeit erfolgt die Adaption der Kanäle innerhalb des makroskopischen System an das neue Haltepotential (es öffnen sich mehr Kanäle, je größer das Haltepotential) und es resultiert ein stark hyperbolischer Kurvenverlauf. Der konstante Bereich der Stromantwort wird zur Messung der maximalen Stromantwort verwendet. 𝑼𝑼 Spannungsprotokoll +𝟔𝟔𝟔𝟔 𝒎𝒎𝒎𝒎 𝟎𝟎 𝒎𝒎𝒎𝒎 −𝟔𝟔𝟔𝟔 𝒎𝒎𝒎𝒎 −𝟏𝟏𝟏𝟏𝟏𝟏 𝒎𝒎𝒎𝒎 𝟏𝟏 𝒔𝒔 …. 𝒕𝒕 Stromantwort für P2X2 exprimierende Zellen mit ATP im Außenmedium Stromantwort für P2X2 exprimierende Zellen ohne ATP im Außenmedium Die Stromantworten der Kontrollzelle zeigen für die ORI und die ORI-ATP Lösung einen nahezu identischen linearen Verlauf zeigen. Die Differenz der Stromantworten (Differenzkennlinie) ergibt eine Null-Linie. Dies zeigt, dass ATP keinen Einfluss auf die Stromantwort der Kontrollzellen hat. Bei der P2X2 exprimierenden Oozyte ergibt die ORI-Lösung ohne ATP eine lineare IV-Kennlinie, die keinen nennenswerten Unterschied zur IV-Kennlinie der Kontrollzellen zeigt. Damit hat der Einbau des P2X2 Rezeptors keinen Einfluss auf die Stromantwort, solange er inaktiv ist. Die Differenzkennlinie entspricht nahezu der stark hyperbolischen Kurve für die ORI-ATP Lösung, da die resultierenden Ströme mit ATP-Zusatz wesentlich größer sind, als in reiner ORI Lösung. Dies ist Beweis für eine ATP-abhängige Ionen-Translokation aufgrund der P2X2 Kanäle. Die Umkehrpotential der IV-Kurven sind die Spannungen, bei denen kein Strom über die Zellmembran fließt. Bei diesen Haltespannungen sind keine Nettoströme über die Membran detektierbar, da das Ruhepotential der Zelle exakt der angelegten Haltespannung entspricht. Für die Kontroll-Oozyten liegt das Umkehrpotential bei ca. -22 mV. Für die P2X2-exprimierenden Oozyten in ORI-Lösung ergibt sich das gleiche Umkehrpotential wie auch für die Kontroll-Oozyten. Für die ATPhaltige Lösung ist das Umkehrpotential stark nach rechts verschoben und liegt bei -2 mV. Um lediglich den Einfluss der P2X2 Kanäle auf die Stromantwort zu betrachten, muss das Umkehrpotential der Differenzkennlinie verwendet werden, da hier der lineare Anstieg der Stromantwort mit dem Haltepotential heraus gerechnet ist. Das Umkehrpotential liegt hier bei ca. +8 mV. Die Differenzkennlinie, welche das direkte IV-Verhalten des P2X2 Rezeptors wiedergibt, ist stark hyperbolisch und erreicht bei positiven Haltepotentialen ihre Sättigung, wobei die maximale Stromantwort ungefähr +70 nA beträgt. Ursache für diese Sättigung ist die Tatsache, dass P2X2 lediglich Kationen in die Zelle transportieren kann, aber nicht hinaus (einwärts gleichrichtender Kanal). Bei positiven Haltepotentialen ist der elektrische Gradient nach außen gerichtet, weshalb kein einwärts-Transport möglich ist (konstante Stromantwort für stark positive Haltepotentiale). Für negative Haltepotentiale steigt der Betrag der Stromantwort jedoch immer weiter und stärker an, da der elektrische Gradient nach innen gerichtet ist und P2X2 dein einwärts-Transport ermöglicht. ATP-Dosiswirkungskurven Um ATP-Dosiswirkungskurven zu erhalten, wird das System auf eine Spannung von -60 mV geklemmt und ein ATP-Konzentrationsprotokoll gefahren. Es ist darauf zu achten, dass nach jedem Konzentrationssprung, zunächst erneut die 30 µM konzentrierte ATP-Lösung gemessen, und anschließend mit ORI Lösung für eine längere Zeit gespült wird. So wird jeder gemessene Strom bei einer bestimmten ATP Konzentration auf die darauffolgende Messung der 30 µM konzentrierten ATP-Lösung normiert. So kann der Einfluss von Veränderungen innerhalb der P2X2 Aktivität (z.B. durch leichte Desensibilisierung oder eventueller Veränderung der Anzahl aktiver/erreichbarer/vorhandener Kanäle in der Membran) auf die Dosis-Wirkungskurve minimiert werden. Für ideale Messbedingungen würden konstante Stromlinien für die 0 µM und die 30 µM ATP-Applikation sprechen. Für höhere ATP-Konzentrationen resultiert eine vermehrte Aktivierung der P2X2 Population innerhalb der Membran, womit eine Verstärkung der Stromantwort verbunden ist. Die Stromantworten für 0 µM ATP und 30 µM ATP sind für alle Zeiten konstant, was darauf hinweist, dass keine Desensibilisierung vorliegt. [𝑨𝑨𝑨𝑨𝑨𝑨] 𝟏𝟏𝟏𝟏𝟏𝟏 µ𝑴𝑴 𝟑𝟑𝟑𝟑𝟑𝟑 µ𝑴𝑴 𝟏𝟏 𝒎𝒎𝒎𝒎 𝟑𝟑 µ𝑴𝑴 𝟏𝟏𝟏𝟏 µ𝑴𝑴 𝟑𝟑𝟑𝟑 µ𝑴𝑴 𝟎𝟎 µ𝑴𝑴 Ruhepotential 𝟑𝟑𝟑𝟑 µ𝑴𝑴 𝒕𝒕 ATP-Konzentrationsprotokoll Stromantwort für 𝑈𝑈 = −60𝑚𝑚𝑚𝑚 Es werden aus diesem Graphen jeweils die maximalen Stromantworten abgelesen, auf die jeweils folgende Stromantwort von 30 µM ATP normiert und in einem c-I Diagramm aufgetragen, das der Dosis-Wirkungskurve entspricht. Diese kann mit der Hill-Gleichung gefittet werden, aus der letztlich der EC50 Wert und der Hill-Koeffizient n der Bindung bestimmt werden können. Der EC50 Wert entspricht der ATP-Konzentration, für die eine Halbmaximale Transport-Aktivität resultiert. Bei dieser ATP-Konzentration sind somit die Hälfte der Kanäle geöffnet. 𝐼𝐼 = 𝐼𝐼𝑚𝑚𝑚𝑚𝑚𝑚 𝐸𝐸𝐸𝐸 𝑛𝑛 1 + � 50 � [𝐴𝐴𝐴𝐴𝐴𝐴] In der Literatur ist das Ergebnis aus Einzelkanalexperimenten beschrieben. Die Grafiken A und B zeigen die Öffungswahrscheinlichkeiten der Kanäle in Abhängigkeit von der ATP-Konzentration. Die Öffnungswahrscheinlichkeit P gegen die ATP-Konzentration geplottet ergibt eine sigmpoidale Kurve (Grafik C). Der sigmoidale Verlauf ist aufgrund der lag-Phase zwischen 0 und 10 µM kaum zu sehen; der Sättigungsverlauf der Kurve ab 100 µM ATP ist stark dominant. Qualitiativ dieselbe Kurve wird erhalten, wenn die maximalen Stromantworten gegen die einzelnen ATP-Konzentrationen geplottet werden (Beobachtung aller Kanäle der gesamten Zelloberfläche). Ein Fit über die Hill-Gleichung ergibt 𝑛𝑛 = 2,3 und 𝐸𝐸𝐶𝐶50 = 11,2µ𝑀𝑀 bei einer maximalen Öffnungswahrscheinlichkeit von 𝑃𝑃 = 0,61. Aus n=2,3 resultiert, dass mindestens 3 ATP-Bindestellen für einen funktionalen Kanal existieren müssen. Da es sich bei P2X2 um einen Homomer handelt, muss der funktionale Kanal aus drei Untereinheiten bestehen. Stopped-Flow mit Na-K-ATPase Spannungssensitive Fluoreszenzfarbstoffe Fluoreszenzfarbstoffe, deren Fluoreszenz abhängig ist von der Spannung, werden häufig zur Messung des Membranpotentials eingesetzt. In diesem Experiment werden die anionischen, spannungssensitiven Chromophore Oxonol V und VI, sowie der Farbstoff RH421 verwendet. Durch Innen positive Potentiale wird die Bindung des Farbstoffs an Lipidvesikel gefördert, was zu einer Rotverschiebung des Absorptions- und Emissionsspektrums führt. Nach Kalibrierung des Fluoreszenzsignals bei bekannten Membranpotentialen lässt sich die Fluoreszenz eines Farbstodds zur Messung unbekannter Potentiale verwenden. Zur Potentialeichung verwendet man KaliumDiffusionspotentiale in gegenwart des Ionophors Valinomycin. Hierbei handelt es sich um SteadyState-Messungen. Bei niedrigen Farbstoff/Lipid-Verhältnissen tritt eine Fluoreszenzerhöhung auf, da die Bewegung des Farbstoffs eingeschränkt ist und der Farbstoff in der Lipidphase vor Quenchenden Agenzien geschützt ist. Bei hohen Farbstoffkonzentrationen wird wieder ein quenching beobachtet, das vermutlich auf Farbstoffaggregation zurückzuführen ist. Im Experiment soll auch die Kinetik der Wechselwirkung von Oxonol V mit Liposomen untersucht werden, wobei keine Steady-State-Messungen, sondern zeitaufgelöste Messungen der Änderung des Membranpotentials (z.B. hervorgerufen durch die Aktivität eines elektrogenen Transportproteins) erforderlich sind. Dieser Wechselwirkung liegen zwei Prozesse mit unterschiedlichen Geschwindigkeitskonstanten zugrunde. Zunächst erfolgt die schnelle Bindung des Farbstoffs an die Vesikelmembran, wonach die langsamere Diffusion innerhalb der Membran bis zu einer Gleichverteilung erfolgt. Beide Zeitkonstanten werden durch einen biexponentiellen Fit erhalten. Den Farbstoff RH421 zeichnet eine sehr schnelle Reaktion auf die Änderung des lokalen elektrischen Feldes aus, sodass auch schnelle Änderungen des elektrischen Feldes durch Konformationsänderungen oder schnelle Transportprozesse aufgelöst werden können. Er kommt in diesem Experiment bei der Analyse von Konformationsübergängen der Na+-K+-ATPase zum Einsatz. Die Veränderung des Spektrums der Fluoreszenzfarbstoffe wird durch eine Störung des elektronischen Systems des Farbstoffs aufgrund der Membranpotential-Änderung hervorgerufen. Diese Störung kann mehrere Auswirkungen haben: (1) (2) (3) (4) Potential-abhängiger Verteilungskoeffizient zwischen wässriger und lipidischer Phase Wechsel der Farbstoff-Orientierung in der Lipidmembran Veränderung des Aggregationsgrades des Farbstoffs in wässriger bzw. lipidischer Phase Direkter elektrochromer Effekt des Potentials auf die Elektronenkonfiguration des Farbstoffs Zudem beeinflussen die experimentellen Bedinungen die Fluoreszenz (Wasser/Lipid-Verhältnis, pH, Ionenstärke, Temperatur). Stopped-Flow Es handelt sich um eine Strömungsmethode zur Messung kinetischer Parameter. Dazu werden zwei Lösungen, die jeweils einen Reaktionspartner enthalten in zwei getrennte Spritzen gefüllt, die gleichzeitig, pneumatisch in dieselbe Mischkammer entleert werden. Bis die Lösungen gemeinsam von der Mischkammer aus die Beobachtungskammer erreichen, sind bereits je nach Fließgeschwindigkeit und Wegstrecke 1-3 ms vergangen. In der Beobachtungskammer findet dann die Zeitabhängige Analyse der Vorgänge innerhalb der Mischung statt. Daher können nur Prozesse beobachtet werden, die wesentlich länger als 3 ms andauern. Ist die Beobachtungskammer gefüllt, so löst die Stoppspritze dahinter einen Kontakt aus, welcher die Detektionseinheit aktiviert. Die ablaufenden Prozesse können über die Absorption, Zirkulardichroismus oder Lichtstreuung verfolgt werden, wobei in unserem Experiment die Fluoreszenz zeitlich verfolgt wird. Dynamische Lichtstreuung Es handelt sich um eine Methode, bei der die Größe von Partikeln innerhalb einer Lösung oder Suspension bestimmt werden kann. Dabei wird die Probe mit einem Laser, dessen Fokus in einem sehr kleinen Bereich der Probenkammer liegt, bestrahlt. Daher kann angenommen werden, dass sich pro Zeitintervall lediglich ein einziges Partikel im Fokus des Lasers befindet, weshalb die Konzentration der Probe nicht bekannt sein muss. Dieses Partikel bewegt sich mit einer bestimmten Geschwindigkeit aufgrund der Brownschen Molekularbewegung. Dies bewirkt eine Veränderung der Streuung des kohärenten Laserstrahls über die Zeit. Durch Detektion der Laserstreuung im 90° Winkel zur Einstrahlachse (kilocounts per second [kcps]) lassen Rückschlüsse auf die Geschwindigkeit der Partikelbewegung zu, mit Hilfe derer die Diffusionskoeffizienten berechnet werden können. Aus diesen wiederum lässt sich die Größe der Partikel ableiten. Neben der Streuintensität wird bei der Messung die Temperatur detektiert, welche als zweite Variable zur Berechnung der Partikelgröße essentiell ist. Experimentelle Ergebnisse Anregungs- und Emissionsspektren von Oxonol VI Bei der Aufnahme von Anregungsspektren wird die Probe im Wellenlängenbereich von 400 bis 700 nm bestrahlt und die Fluoreszenzintensität bei 660 nm als Funktion der Einstrahlwellenlänge detektiert. Es wird hier analysiert bei welcher Einstrahlwellenlänge das System Strahlung absorbiert, um dann letztlich bei 660 nm Fluoreszenzstrahlung zu emittieren. Hier ist der Peak bei 660 nm auf die Streuung derselben Anregungswellenlänge zurückzuführen. Für die Aufnahme von Emissionsspektren wird die Wellenlänge der Anregungsstrahlung bei 580 nm über einen Monochromator konstant gehalten und die Intensitätsverteilung der Emission zwischen 450 und 700 nm detektiert. Im Emissionsspektrum entspricht der Peak bei 580 nm dem gestreuten Anregungslicht. Es werden jeweils 0,13 µM Oxonol VI in 1 ml (A) wässrigen Puffer, (B) Ethanol und (C) wässrigen Puffer, der 50 µg Liposomen enthält, gegeben und am Fluorometer die genannten Spektren aufgenommen. In dem auf das lokale Maximum normierte Spektrum ist eine Rotverschiebung der Fluoreszenz, sowohl im Emissionsspektrum, als auch im Anregungsspektrum gut zu erkennen. Die Wellenlänge und Intensität von Fluoreszenzspektren ist abhängig von der Temperatur, Bindung, Viskosität und Polarität des Lösungsmittels. Wellenlängenverschiebungen treten immer dann auf, wenn die Energien der Grund- und angeregten Zustände durch äußere Faktoren (wie zum Beispiel der Wechselwirkung mit der Lösungsmittelumgebung) verändert wird. Polare Lösungsmittel wechselwirken über Dipole sowohl mit Grund- als auch angeregtem Zustand polarer Fluoreszenzfarbstoffe, wodurch eine Absenkung des angeregten Zustandes und eine längerwellige Fluoreszenz resultiert (Stokes-Shift). Da die meisten Farbstoffe einen polaren Anteil aufweisen resultiert typischerweise mit zunehmender Apolarität der Lösungsmittelumgebung eine Blauverschiebung des Absorptionsmaximums. Dies wird als Bathochromer Effekt beschrieben. In Ausnahmefällen, bei vorwiegend apolaren Farbstoffen, wie bei Oxonol VI, resultiert jedoch auch eine Verschiebung hin zu kleineren Wellenlängen (Rotverschiebung, Hypsochromer Effekt). Neben der Wellenlängenverschiebung ist tendenziell eine Zunahme der Fluoreszenzintensität mit der Apolarität des Lösungsmittels zu beobachten. Ursache hierfür ist eine Abnahme der QuenchingEffekte, die von polaren Lösungsmitteln vermittelt werden. Einfluss von Valinomycin auf die Anregungs- und Emissionsspektren von Oxonol VI Valinomycin ist ein Makrolidantibiotikum aus 12 zyklisch verbundenen Aminosäuren, das als Ionophor fungiert, indem es einen Kanal in der Membran bildet und über die hydrophilen Carboxylgruppen selektiv Kalium-Ionen komplexiert kann, die so durch die Membran gelangen. Dadurch wird das Membranpotential abgebaut, wodurch die Zelle stirbt. Im Experiment wird durch die Veränderung des Membranpotentials durch Valinomycin eine Veränderung der Oxonol-VIFluoreszenz induziert. Der Puffer, in dem die Liposomen generiert wurden enthält 2 mM Kalium-Ionen (1mM 𝐾𝐾2 𝑆𝑆𝑂𝑂4 ), weshalb zu Beginn des Experiments, sowohl außerhalb der Liposomen, als auch im Liposomen-Lumen 2 mM 𝐾𝐾 + vorliegen. Die Kalium-Konzentration des Puffers soll nun über die sequentielle Zugabe von 𝐾𝐾2 𝑆𝑆𝑂𝑂4 auf 5 mM, 10 mM und letztlich auf 20 mM erhöht werden, wonach jeweils ein Emissionsspektrum aufgenommen wird. Durch die Zugabe von 𝐾𝐾2 𝑆𝑆𝑂𝑂4 wird sich die KaliumKonzentration innerhalb der Liposomen kaum verändern. Es wird also angenommen, dass für alle Messungen gilt: 𝑐𝑐𝑖𝑖𝑖𝑖 ≈ 2𝑚𝑚𝑚𝑚. Das aus der Zugabe von Kaliumsulfat resultierende Membranpotential korreliert mit dem Konzentrationsunterschied außerhalb und innerhalb der Liposomen und kann durch die Nernstgleichung berechnet werden: ∆𝝓𝝓 = 𝑹𝑹𝑹𝑹 𝒄𝒄𝒐𝒐𝒐𝒐𝒐𝒐 𝒄𝒄𝒐𝒐𝒐𝒐𝒐𝒐 ∙ 𝒍𝒍𝒍𝒍 = 𝟐𝟐𝟐𝟐, 𝟐𝟐𝟐𝟐𝟐𝟐𝟐𝟐 ∙ 𝒍𝒍𝒍𝒍 𝒁𝒁𝒁𝒁 𝒄𝒄𝒊𝒊𝒊𝒊 𝒄𝒄𝒊𝒊𝒊𝒊 Damit ergeben sich für die einzelnen Konzentrationen die in der folgenden Tabelle 1 aufgelisteten Membranpotentiale, die den entsprechenden gemessenen Fluoreszenzintensitäten 𝐹𝐹 bei 642 nm entsprechen. Die Wellenlänge 642 nm wurde aufgrund des erwarteten Verhältnisses zwischen den Fluoreszenzintensitäten unterschiedlicher Kalium-Konzentrationen ausgewählt. 𝒄𝒄𝒐𝒐𝒐𝒐𝒐𝒐 2 mM 5 mM 10 mM 20 mM ∆𝝓𝝓 0 mV 23,13 mV 40,64 mV 58,13 mV 𝑭𝑭 𝐹𝐹0 = 77,85 𝐹𝐹1 = 81,2 𝐹𝐹2 = 84,03 𝐹𝐹3 = 86,43 ∆𝑭𝑭 = 𝑭𝑭 − 𝑭𝑭𝟎𝟎 0 3,35 6,18 8,58 ∆𝑭𝑭/𝑭𝑭𝟎𝟎 0 43,03 ∙ 10−3 79,38 ∙ 10−3 110,21 ∙ 10−3 Die folgende Abbildung 3 zeigt den Verlauf der Fluoreszenzintensität in Abhängigkeit von der KaliumKonzentration. Wie zu erwarten, ist ein mit steigender Kalium-Konzentration bzw. höherem Membranpotential steigendes Fluoreszenzsignal, zumindest ab einer Wellenlänge von ca. 628 nm zu beobachten. Vor dieser Wellenlänge verhalten sich die Fluoreszenzsignale genau umgekehrt. Abbildung 3: Emissionsspektrum von Oxonol VI in Abhängigkeit von verschiedenen KaliumKonzentrationen, sowie unter Einfluss von Valinomycin. Das rechte Spektrum zeigt eine Vergrößerung der gewählten Wellenlänge für den Vergleich der Fluoreszenzintensitäten. Es ist mit zunehmendem Membranpotential eine geringe Rotverschiebung der Amplitude zu beobachten. Ursächlich hierfür ist eine durch das Membranpotential geförderte Bindung von Oxonol VI an die Membran und die damit verbundene Rotverschiebung des Fluoreszenzspektrums (Kontakt mit polarem Teil der Membran bewirkt hypsochromen Effekt). Zur Darstellung der Fluoreszenzänderung wird eine Wellenlänge gewählt, für die sich die Fluoreszenzintensitäten zwischen den einzelnen membranpotentialen am stärksten unterscheiden. Dazu wurden die Datenpunkte bei 642 nm ausgewählt. Als Referenz-Fluoreszenzintensität fungiert 𝐹𝐹0 , die für ∆ϕ = 0mV gemessen wurde. In Folgender Abbildung wurde die Fluoreszenz über 𝐹𝐹𝑛𝑛𝑛𝑛𝑛𝑛𝑛𝑛 = ∆𝐹𝐹 𝐹𝐹0 = 𝐹𝐹−𝐹𝐹0 𝐹𝐹0 normiert. Es ergibt sich ein linearer Zusammengang zwischen normierter Fluoreszenz und dem Membranpotential. Abbildung 4: Gegenüberstellung des Membranpotentials zur Änderung der Fluoreszenzintensität. Visualisierung der in Tabelle 1 gezeigten Daten. Die Datenpunkte wurden linear mittels Origin 7.5 gefittet. Stopped Flow Messung der Wechsewlrikung von Oxonol V mit Liposomen In diesem Teilexperiment wurde eine Oxonol V haltige Puffer-Lösung schnell mit einer Liposomenhaltigen Puffer-Lösung gemischt und das resultierende biphasische Fluoreszenzsignal aufgezeichnet. Die Signalzunahme ist sehr schnell und entspricht der Anlagerung von Oxonol V an die LiposomenMembran, die von der Diffusionskonstanten beeinflusst wird. Die langsame Signalabnahme ist einer Umlagerungsreaktion von Oxonol V in die innere Lipidmembran zuzuordnen. Die Einstellung des Verteilungsgleichgewichts ist wesentlich langsamer als die Diffusion an die Membran. In der folgenden Abbildung ist die Signalabnahme gezeigt, aus deren Fitting über zwei exponentielle Funktionen 𝑦𝑦 = −𝐴𝐴1 ∙ exp(−𝑅𝑅1 𝑥𝑥) − 𝐴𝐴2 ∙ exp(−𝑅𝑅2 𝑥𝑥) + 𝐶𝐶 die kinetische Ratenkonstante für den Prozess der Umlagerung bestimmt wurde. Abbildung 5: Biphasisches Fluoreszenzsignal der Oxonol V Wechselwirkung mit Liposomen. Der schnelle Prozess entspricht der Anlagerung von Oxonol V an die Membran, der langsamere Prozess der Umlagerung in die innere Lipidmembran. Die folgende Tabelle zeigt die Fitting-Parameter, wobei die A-Werte Amplituden entsprechen und die R-Werte den Ratenkonstanten zuzuordnen sind. Die Ratenkonstante R entspricht der Geschwindigkeitskonstanten 𝑘𝑘 und ist angegeben in 𝑠𝑠 −1 , weshalb der größere Wert dem schnellen Prozess, also der Diffusion entspricht. Tabelle 2: Übersicht über die Fitting-Parameter für den Fit des Fluoreszenzsignals in Abbildung 5 Fitting Parameter 𝐴𝐴1 𝑅𝑅1 𝐴𝐴2 𝑅𝑅2 Wert 5003 32,981 𝑠𝑠 −1 648,18 4,847 𝑠𝑠 −1 Fehler ±74 ±0,77 ±59 ±0,95 Nun soll die Geschwindigkeitskonstante 𝑘𝑘1 für die Oxonol V Bindung an die Membran bestimmt werden (Maßgeblich hierfür ist 𝑅𝑅2 ). Der Bindungsprozess kann über folgende reversible Reaktion beschrieben werden, wobei sich die Geschwindigkeitskonstante des Gesamtprozesses, die letztlich durch das Fitting ermittelt wurde, ergibt zu 𝒌𝒌𝟏𝟏 𝑶𝑶 + 𝑽𝑽 ⇌ 𝑶𝑶𝑶𝑶 𝒌𝒌−𝟏𝟏 ⟹ 𝒌𝒌 = 𝒌𝒌𝟏𝟏 ∙ 𝒄𝒄𝑽𝑽 − 𝒌𝒌−𝟏𝟏 Die Annahme, dass Oxonol V, in der Gleichung angegeben mit O, einmal an das Vesikel (in der Gleichung mit V bezeichnet) gebunden, nicht mehr abdiffundieren kann, also, dass 𝑘𝑘−1 = 0 ist, vereinfacht die Betrachtung erheblich, da so eine Reaktion zweiter Ordnung anstelle einer reversiblen Reaktion vorliegt. Bevor jedoch 𝑘𝑘1 = 𝑘𝑘/𝑐𝑐𝑉𝑉 berechnet werden kann, muss die Vesikelkonzentration 𝑐𝑐𝑉𝑉 ermittelt werden. Dazu wird lediglich die Anzahl an Lipidmolekülen pro Vesikel n und die Konzentration der Lipide 𝑐𝑐𝐿𝐿 in der Lösung benötigt. Zunächst erfolgt die Berechnung der Lipidmoleküle pro Vesikel. Hierfür wird der durch dynamische Lichtstreuung ermittelte effektive Außenradius der Liposomen benötigt. Zunächst muss nach folgender Gleichung das Molekulargewicht der Liposomen berechnet werden. In dieser Gleichung ist 𝑁𝑁𝐴𝐴 die Avogadro Konstante und 𝑉𝑉 ≈ 0,985𝑐𝑐𝑐𝑐3 /𝑔𝑔 das spezifische Volumen der Lipide innerhalb der Vesikelmembran. 𝑟𝑟𝑎𝑎 ist der gemessene Außenradius des Vesikels und 𝑟𝑟𝑖𝑖 = 𝑟𝑟𝑎𝑎 − 4𝑛𝑛𝑛𝑛 der Innenradius, wobei die Membrandicke 4 nm ist. 𝑵𝑵𝑨𝑨 𝟒𝟒 6,022 ∙ 1023 𝑚𝑚𝑚𝑚𝑚𝑚 −1 4 𝟑𝟑 𝟑𝟑 𝑴𝑴𝑽𝑽 = ∙ 𝝅𝝅�𝒓𝒓𝒂𝒂 − 𝒓𝒓𝒊𝒊 � = ∙ 𝜋𝜋([122,5𝑛𝑛𝑛𝑛]3 − [118,5𝑛𝑛𝑛𝑛]3 ) 𝑽𝑽 𝟑𝟑 0,985 ∙ 107 𝑛𝑛𝑛𝑛3 𝑔𝑔−1 3 = 2,561 ∙ 1017 𝑔𝑔 𝑛𝑛𝑛𝑛3 𝑚𝑚𝑚𝑚𝑚𝑚 ∙ 174259𝑛𝑛𝑛𝑛3 = 4,463 ∙ 1022 𝑔𝑔/𝑚𝑚𝑚𝑚𝑚𝑚 Die Anzahl an Lipidmoleküle pro Vesikel entspricht nun dem Verhältnis der Molekulargewichte von Vesikel und Lipid. Als Lipid wurde DOPC eingesetzt, dessen Molekulargewicht 786,14𝑔𝑔/𝑚𝑚𝑚𝑚𝑚𝑚 beträgt. 𝒏𝒏 = 𝑴𝑴𝑽𝑽 4,463 ∙ 1022 𝑔𝑔/𝑚𝑚𝑚𝑚𝑚𝑚 = = 5,677 ∙ 1019 𝑴𝑴𝑳𝑳 786,14𝑔𝑔/𝑚𝑚𝑚𝑚𝑚𝑚 Nun kann die Vesikelkonzentration berechnet werden: Da die Oxonol V haltige Lösung keine Lipide enthält und die Liposomen Lösung 40 µg/ml konzentriert ist, ist 𝑐𝑐𝐿𝐿 = 20µ𝑔𝑔/𝑚𝑚𝑚𝑚. 20 ∙ 109 𝑔𝑔/𝑙𝑙 𝒄𝒄𝑳𝑳 𝑚𝑚𝑚𝑚𝑚𝑚 786,14𝑔𝑔/𝑚𝑚𝑚𝑚𝑚𝑚 2,54 ∙ 107 𝑚𝑚𝑚𝑚𝑚𝑚/𝑙𝑙 = = = 4,4742 ∙ 10−13 = 44,7𝑝𝑝𝑝𝑝 𝒄𝒄𝑽𝑽 = 19 19 𝒏𝒏 5,677 ∙ 10 5,677 ∙ 10 𝑙𝑙 Damit ergibt sich letztlich 𝒌𝒌 4,847𝑠𝑠 −1 = = 1,0833 ∙ 1013 𝑠𝑠 −1 𝑀𝑀−1 𝒌𝒌𝟏𝟏 = 4,4742 ∙ 10−13 𝑀𝑀 𝒄𝒄𝑽𝑽 Typische Diffusionskontrollierte Reaktionen in Lösung weisen Geschwindigkeitskonstanten in der Größenordnung von 1010 𝑠𝑠 −1 𝑀𝑀−1 auf, da 𝑘𝑘𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 ≈ 1010 𝑠𝑠 −1 𝑀𝑀−1 . Das Ergebnis ist daher durchaus plausibel. Zur Betrachtung des Fehlers von 𝑘𝑘1 wird die Gleichung für die Fehlerfortpflanzung angwendet. Die zugrundeliegenden Fehler sind der Fehler bei der Bestimmung der Ratenkonstante durch den FittingVorgang und der Fehler bei der Berechnung des effektiven Vesikeldurchmessers durch dynamische Lichtstreuung. Der Fehler der Vesikelkonzentration ist bekannt und ergibt sich zu ε(cV ) = 0,1 ∙ cV . 1 2 𝜕𝜕𝑘𝑘1 2 2 𝜕𝜕𝑘𝑘1 2 2 𝑘𝑘 2 � 𝜀𝜀 (𝑘𝑘) + � � 𝜀𝜀 (𝑐𝑐𝑉𝑉 ) = �� � 𝜀𝜀 2 (𝑘𝑘) + �− 2 � 𝜀𝜀 2 (𝑐𝑐𝑉𝑉 ) 𝜀𝜀(𝑘𝑘1 ) = �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝑐𝑐𝑉𝑉 𝑐𝑐𝑉𝑉 𝑐𝑐𝑉𝑉 = �� 2 2 1 4,847 𝑠𝑠 −1 −1 )2 + �− (0,95 � 𝑠𝑠 � (0,1 ∙ 4,4742 ∙ 10−13 𝑀𝑀)2 (4,4742 ∙ 10−13 𝑀𝑀)2 4,4742 ∙ 10−13 𝑀𝑀 = �4,50834 ∙ 1024 𝑠𝑠 −2 𝑠𝑠 −2 + 1,17358 ∙ 1024 2 = 2,384 ∙ 1012 𝑠𝑠 −1 𝑀𝑀−1 2 𝑀𝑀 𝑀𝑀 ⟹ 𝒌𝒌𝟏𝟏 = �𝟏𝟏, 𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎 ∙ 𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏 ± 𝟐𝟐, 𝟑𝟑𝟑𝟑𝟑𝟑 ∙ 𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏 �𝒔𝒔−𝟏𝟏 𝑴𝑴−𝟏𝟏 In der Literatur ist die Geschwindigkeitskonstante mit (1,18 ± 0,05) ∙ 1011 𝑠𝑠 −1 𝑀𝑀−1 angegeben (Clarke et al.). Der Prozess der Anlagerung von Oxonol V an die Liposomen hat also um einen Faktor 100 schneller stattgefunden, als bei den Versuchsbedingungen von Clarke et al der Fall gewesen ist. Konformationsänderungskinetik der Na+K+ ATPase an der Stopped Flow Apparatur Mithilfe des Fluoreszenzfarbstoffs RH421, der sehr schnell auf Änderungen des lokalen elektrischen Feldes reagiert, können Konformationsveränderungen der Na+K+ ATPase zeitlich aufgelöst werden. Lösung 1 enthält u.a. Natrium-Ionen und Na+K+ ATPase haltige Membranfragmente, sowie den Farbstoff RH421. Die Lösung 2 enthält ATP, was die Konformationsveränderung induziert. Die Messung findet in Abwesenheit der Kalium Ionen statt, sodass eine Rückreaktion aus dem E1P Zustand nicht erfolgt. Die ATPase liegt in Abwesenheit von ATP in der E1 Konformation vor. Nach der schnellen Mischung mit ATP in sättigender Konzentration erfolgt die schnelle Bindung von ATP und Phosphorylierung der ATPase (langsamer Prozess, niedrige Geschwindigkeitskonstante). Die durch Phosphorylierung induzierte Konformationsveränderung (E1P → E2P) und der dadurch vermittelte Transport der 3 Natrium-Ionen bewirkt eine Änderung des Membranpotentials (schneller Prozess, hohe Geschwindigkeitskonstante), worauf RH421 mit einer Fluoreszenzänderung reagiert, die detektiert wird. Das Fitting des Signals erfolgt erneut biexponentiell. Die Fitting-Parameter sind in folgender Tabelle gelistet. Abbildung 6: Biphasisches Fluoreszenzsignal von RH421 während der ATP-Hydrolyse (langsamer Prozess) und der Konformationsveränderung von E1P nach E2P (schneller Prozess) der Na+-K+-ATPase. Tabelle 3: Übersicht über die Fitting-Parameter für den Fit des Fluoreszenzsignals in Abbildung 6 Fitting Parameter 𝐴𝐴1 𝑅𝑅1 𝐴𝐴2 𝑅𝑅2 Wert 998 85,795 𝑠𝑠 −1 190,82 24,74 𝑠𝑠 −1 Fehler ±76 ±8,7 ±15 ±1 Für den schnellen Prozess wurde eine Ratenkonstante von 85,795 ± 8,7 𝑠𝑠 −1 und für den langsameren Prozess eine Ratenkonstante von24,74 ± 1 𝑠𝑠 −1 ermittelt. In der Literatur sind für die ATPase aus Hasennieren Werte für die Geschwindigkeitskonstanten von 164 ± 9 𝑠𝑠 −1 für den schnellen Prozess und 32 ± 6 𝑠𝑠 −1 für den langsameren Prozess zu findden (Clarke et al.). Unter den im Experiment gewählten versuchsbedingungen sind damit die Umlagerung von E1-P in E2-P um einen Faktor 2 und die Phosphorylierung um etwa 25% verlangsamt. Ursächlich für diese Abweichung können die unterschiedlichen Versuchsbedingungen (Temperatur, Puffer), aber auch die Verwendung einer anderen ATPase (hier: aus Zitteraal Electrophorus electricus) sein. Teil 4: Formeln Absorptionsspektroskopie 𝜆𝜆 ∙ 𝜈𝜈 = 𝑐𝑐 = 2,998 ∙ 108 𝑚𝑚/𝑠𝑠 Energie eines Lichtquants: 𝐸𝐸 = ℎ ∙ 𝜈𝜈 Induktionsflussdichte 𝐵𝐵 = 𝜇𝜇 ∙ 𝜇𝜇0 ∙ 𝐻𝐻 𝐸𝐸𝑥𝑥 = 𝐸𝐸𝑥𝑥0 ∙ cos 2𝜋𝜋𝜋𝜋𝜋𝜋 Feldstäkevektor (t) 𝐷𝐷01 = |𝜇𝜇01 |2 = 1,63 ∙ 10−38 ∙ 𝜀𝜀𝑚𝑚𝑚𝑚𝑚𝑚 ∙ Dipolstärke Multiplizität 𝑀𝑀 = 2𝑆𝑆 + 1 Quantifizierung der Absorption: 𝐼𝐼 = 𝐼𝐼0 ∙ 𝑒𝑒 −𝛼𝛼𝛼𝛼 , 𝛼𝛼 = 2,303 ∙ 𝜀𝜀 ∙ 𝑐𝑐 Lambert-Beer 𝐼𝐼 = 𝐼𝐼0 ∙ 10−𝜀𝜀𝜀𝜀𝑑𝑑 , lg Transmission 𝜀𝜀 −𝜀𝜀 ∥ Brechungsindex ⊥ 𝒏𝒏 = 𝒄𝒄𝟎𝟎 /𝒄𝒄 𝑑𝑑 𝜆𝜆 𝛼𝛼(𝜆𝜆) = 180° ∙ ∙ (𝑛𝑛𝐿𝐿 − 𝑛𝑛𝑅𝑅 ) Drehung lin. Pol. Lichts: (ORD) [𝛼𝛼]𝜆𝜆 = Spezifische Drehung: [𝑀𝑀]𝜆𝜆 = Molare Rotation: Elliptizität (CD): 𝛼𝛼(𝜆𝜆) 𝑐𝑐∙𝑑𝑑 𝛼𝛼(𝜆𝜆)∙𝑀𝑀 10∙𝑐𝑐∙𝑑𝑑 𝜃𝜃(𝜆𝜆) = ln 10 ∙ [𝜃𝜃]𝜆𝜆 = IR-Spektroskopie Hookesches Gesetz: = 𝜀𝜀𝜀𝜀𝑑𝑑 = 𝐴𝐴 = 𝐸𝐸 𝑑𝑑 = 𝜀𝜀 ∥ +𝜀𝜀 ⊥ Dichroitisches Verhältnis (LD): Harmonischer Oszillator: 𝐼𝐼0 𝐼𝐼 𝑇𝑇% = 𝐼𝐼/𝐼𝐼0 ∙ 100, 𝑂𝑂𝑂𝑂 = 1 → 𝑇𝑇% = 10 LD, CD ORD Wellenzahl: ∆𝜆𝜆 𝜆𝜆 𝑀𝑀∙𝜃𝜃(𝜆𝜆) 10∙𝑐𝑐∙𝑑𝑑 1 𝜆𝜆 180 2𝜋𝜋 = 3,3𝑀𝑀 ∙ ∆𝜀𝜀 𝑣𝑣� = → 𝐸𝐸 = ℎ𝑐𝑐𝑣𝑣� → 𝑣𝑣� = 𝐹𝐹 = −𝑘𝑘(𝑟𝑟 − 𝑟𝑟0 ) ∙ (𝜀𝜀𝐿𝐿′ − 𝜀𝜀𝑅𝑅′ ) ∙ 𝑐𝑐 ∙ 𝑑𝑑 ≈ 33 ∙ (𝜀𝜀𝐿𝐿′ − 𝜀𝜀𝑅𝑅′ ) ∙ 𝑐𝑐 ∙ 𝑑𝑑 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 𝑐𝑐 1 2 𝐸𝐸 = 𝑘𝑘 ∙ (𝑟𝑟 − 𝑟𝑟0 )2 Potentielle Energie: Vibrationsfrequenz: 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 = 1 2𝜋𝜋 ∙� 𝑚𝑚 1 𝑚𝑚 2 1 +𝑚𝑚 2 Reduzierte Masse: µ = 𝑚𝑚 Energieniveaus: 𝑘𝑘 µ 1 2 𝐸𝐸𝑣𝑣 = �𝑣𝑣 + � ℎ ∙ 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 1 2 Nullpunktenergie: 𝐸𝐸0 = ℎ𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 Resonanzbedingung: 𝐸𝐸𝑣𝑣 = 𝐸𝐸𝑣𝑣+1 − 𝐸𝐸𝑣𝑣 = ℎ𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 Fluoreszenz-Spektroskopie Quantenausbeute: kf 𝑘𝑘 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑄𝑄 Φ= 𝑁𝑁(𝑡𝑡) = 𝑁𝑁0 ∙ 𝑒𝑒 −𝑘𝑘 𝑓𝑓 ∙𝑡𝑡 , 𝝉𝝉𝑭𝑭 = 𝟏𝟏/𝒌𝒌𝒇𝒇 , 𝝉𝝉 = 𝝉𝝉𝑭𝑭 ∙ 𝚽𝚽 Fluoreszenzlebensdauer: Excimere Stern-Volmer Gleichung für Excimerenbildungsrate: 𝜙𝜙 𝐸𝐸 𝜙𝜙 𝑀𝑀 Bestimmung der Bildungsrate: Fluoreszenzlöschung Dynamisch: statisch: τ0 = 1 , 𝑘𝑘 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 Φ0 Φ =1+ Energieübertragungsrate bei FRET: 𝑘𝑘 𝑓𝑓𝑓𝑓 = 𝑘𝑘 𝑓𝑓𝑓𝑓 Φ0 Φ = 1 + 𝑘𝑘𝑄𝑄 τ0 , [𝑀𝑀𝑀𝑀]∗ , [𝑀𝑀 ∗ ] 𝐸𝐸𝑇𝑇 = 𝑘𝑘 Fluoreszenzpolarisation 𝑘𝑘 𝑇𝑇 𝑘𝑘 𝑇𝑇 +1/𝜏𝜏 𝐷𝐷 Polarisation und Anisotropie: Absorptionswahrscheinlichkeit 𝜃𝜃 = ∡(𝜇𝜇𝐴𝐴 , 𝐸𝐸)) = 𝑘𝑘 𝑇𝑇 𝐷𝐷 𝐷𝐷 𝐷𝐷 𝑇𝑇 +𝑘𝑘 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 𝐼𝐼 −𝐼𝐼 ⊥ 𝐼𝐼𝐸𝐸 𝐼𝐼𝑀𝑀 − 𝟏𝟏 = 𝒌𝒌𝒂𝒂 𝒄𝒄𝑸𝑸 Φ 𝐷𝐷 −𝐴𝐴 Φ 𝐷𝐷 , 𝟏𝟏 𝝉𝝉𝑫𝑫 −1= 1 𝑘𝑘 𝑎𝑎 ∙𝑐𝑐∙𝜏𝜏 0 = 𝑹𝑹 −𝟔𝟔 𝑹𝑹𝟎𝟎 𝑘𝑘 𝐷𝐷 𝑓𝑓 𝐷𝐷 𝐷𝐷 𝑘𝑘 𝑇𝑇 +𝑘𝑘 𝐷𝐷 𝑓𝑓 +𝑘𝑘 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 𝑘𝑘 𝐷𝐷 𝑓𝑓 𝐷𝐷 𝐷𝐷 𝑘𝑘 𝑓𝑓 +𝑘𝑘 𝐷𝐷 𝑖𝑖𝑖𝑖 +𝑘𝑘 𝑖𝑖𝑖𝑖𝑖𝑖 = 1 − 𝐸𝐸𝑇𝑇 ∙� � 𝐼𝐼 −𝐼𝐼 𝐴𝐴 = 𝐼𝐼 ∥+2𝐼𝐼⊥ = ∥ Φ Emax ΦE − 𝟏𝟏 = 𝑲𝑲𝒄𝒄𝑸𝑸 𝛕𝛕𝟎𝟎 (Stern-Volmer), 𝑰𝑰𝟎𝟎 𝑰𝑰 𝒌𝒌𝑻𝑻 = 𝑃𝑃 = 𝐼𝐼∥ +𝐼𝐼⊥ − 1 = 𝑘𝑘𝑎𝑎 ∙ 𝑐𝑐 ∙ 𝜏𝜏0 , 𝑰𝑰𝟎𝟎 𝑰𝑰 [𝑀𝑀𝑀𝑀] 𝑅𝑅06 𝑅𝑅 6 +𝑅𝑅06 ∥ ∙ 𝑘𝑘𝑎𝑎 𝑐𝑐 ∙ 𝜏𝜏𝐸𝐸 ~ 𝑘𝑘𝑎𝑎 = [𝑀𝑀][𝑄𝑄], Abstandsabhängigkeit der FRET-Effizienz: Abstandsbestimmung: 𝐸𝐸𝑇𝑇 = ΦM max ΦM ⊥ 𝐼𝐼∥ −𝐼𝐼⊥ 𝐼𝐼𝐺𝐺𝐺𝐺𝐺𝐺 𝑃𝑃(𝜃𝜃, 𝜑𝜑)~(𝜇𝜇𝐴𝐴 ∙ 𝐸𝐸)2 ~ cos2 𝜃𝜃 (Photoselektion -> kleine Winkel 3 5 1 5 Durch Photoselektion maximale Werte für Anisotropie: 𝐼𝐼∥ = , 𝐼𝐼⊥ = , 𝐴𝐴 = 0,4 (Grenzanisotropie) Berücksichtigung von 𝜸𝜸 = ∡(𝜇𝜇𝐴𝐴 , 𝜇𝜇𝐸𝐸 ) 𝑨𝑨 = Fundamentalanisotropie 𝟑𝟑 𝐜𝐜𝐜𝐜𝐜𝐜𝟐𝟐 𝜸𝜸−𝟏𝟏 (=1 für 𝛾𝛾 = 0 im Widerspruch zur Grenzanisotropie) 𝟐𝟐 𝑨𝑨 = 𝟎𝟎, 𝟒𝟒 ∗ 𝟑𝟑 𝐜𝐜𝐜𝐜𝐜𝐜𝟐𝟐 𝜸𝜸−𝟏𝟏 𝟐𝟐 (Limitierende Anisotropie −0,2 ≤ 𝐴𝐴0 ≤ 0,4) Berücksichtigung der Rotationsdiffusion im angeregten Zustand: Perrin-Gleichung (statisch) Perrin-Gleichung (dynamisch) FRAP 𝟏𝟏 𝑨𝑨 = 𝟏𝟏 �𝟏𝟏 𝑨𝑨𝟎𝟎 𝝉𝝉 + 𝝉𝝉𝑭𝑭 � , 𝜏𝜏𝑐𝑐 = 𝒄𝒄 𝑨𝑨(𝒕𝒕) = 𝑨𝑨𝟎𝟎 𝒆𝒆−𝒕𝒕/𝝉𝝉𝒄𝒄 1 , 6𝐷𝐷𝑟𝑟𝑟𝑟𝑟𝑟 𝐷𝐷𝑟𝑟𝑟𝑟𝑟𝑟 = 𝑘𝑘𝑘𝑘 𝑉𝑉 ℎ 𝜂𝜂 𝑎𝑎 2 𝐷𝐷 = 4𝜏𝜏 1/2 Ausdehnung des fluoreszierenden Flecks auf Durchmesser von 2a: ESR-Spektroskopie 𝑫𝑫 = 𝒂𝒂𝟐𝟐 /𝟐𝟐𝟐𝟐 Drehimpuls, magnetisches Moment Gesamtdrehimpulsquantenzahl Magnetische Momente: Magneton (Bohrsches Magneton) Landé-Faktor für ein Atom Freie Elektronen: Zeeman-Effekt Projektion von |S| auf B0: Spin Magnetische Quantenzahl von S: Einstellungsmöglichkeiten in B0: Projektion von 𝜇𝜇𝑆𝑆 auf B0 ±1,0012𝜇𝜇𝐵𝐵 ) 𝐽𝐽 = 𝐿𝐿 + 𝑆𝑆, |𝐽𝐽| = ℏ�𝐽𝐽(𝐽𝐽 + 1) = 𝑃𝑃𝐽𝐽 (Gesamtdrehimpuls) �𝜇𝜇𝐽𝐽 � = 𝛾𝛾 ∙ 𝑃𝑃𝐽𝐽 = 𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ 𝑃𝑃𝐽𝐽 𝜇𝜇 = 𝑞𝑞∙ℏ , 2𝑚𝑚 𝑔𝑔 = 1 + ( 𝜇𝜇𝐵𝐵 = 𝑒𝑒∙ℏ 2𝑚𝑚 𝑒𝑒 = 0,92 ∙ 10−23 𝐽𝐽/𝑇𝑇 ) 𝐽𝐽 (𝐽𝐽 +1)+𝑆𝑆(𝑆𝑆+1)−𝐿𝐿(𝐿𝐿+1) 2𝐽𝐽 (𝐽𝐽 +1) �𝜇𝜇𝐽𝐽 � = |𝜇𝜇𝑆𝑆 | = −𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ 𝑃𝑃𝑆𝑆 𝑷𝑷𝒛𝒛 = 𝒎𝒎𝒔𝒔 ℏ 𝑆𝑆 = ±1/2 𝑚𝑚𝑠𝑠 = 𝑆𝑆, 𝑆𝑆 − 1, 𝑆𝑆 − 2, … , −𝑆𝑆 𝟐𝟐𝟐𝟐 + 𝟏𝟏 𝝁𝝁𝒛𝒛 = 𝜸𝜸 ∙ 𝑷𝑷𝒛𝒛 = 𝜸𝜸 ∙ 𝒎𝒎𝒔𝒔 ℏ (für S=0,5 𝜇𝜇𝑧𝑧 = −𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ 𝑚𝑚𝑠𝑠 = Energieniveaus Energie eines magn. Dipols in B0: Für 𝑆𝑆 = 0,5 → 𝑚𝑚𝑠𝑠 = ±0,5 𝑬𝑬 = 𝝁𝝁𝒛𝒛 𝑩𝑩𝟎𝟎 = 𝜸𝜸𝒎𝒎𝒔𝒔 ℏ𝑩𝑩𝟎𝟎 1 2 1 2 𝐸𝐸+1/2 = + ℏ ∙ 𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ 𝐵𝐵0 und 𝐸𝐸−1/2 = − ℏ ∙ 𝑔𝑔 ∙ 𝜇𝜇𝐵𝐵 ∙ 𝐵𝐵0 Energiedifferenz: Resonanzbedingung: Boltzmann-Verteilung Larmor-Präzession Drehmoment Larmor-Frequenz: ∆𝑬𝑬 = 𝜸𝜸ℏ ∙ 𝑩𝑩𝟎𝟎 𝒉𝒉𝒉𝒉 = ∆𝑬𝑬 = 𝜸𝜸ℏ ∙ 𝑩𝑩𝟎𝟎 ∆𝑬𝑬 ∆𝐸𝐸 1 ~ 𝑘𝑘∙𝑇𝑇 200 𝒏𝒏+ = 𝒏𝒏− ∙ 𝒆𝒆−𝒌𝒌∙𝑻𝑻 , 𝚪𝚪 = 𝝁𝝁 × 𝑩𝑩𝟎𝟎 𝑣𝑣𝐿𝐿 = 𝛾𝛾∙𝐵𝐵0 ℏ ℎ = 𝛾𝛾∙𝐵𝐵0 2𝜋𝜋 𝑛𝑛 → 𝑛𝑛 − = 1,000007 + ↔ 𝝎𝝎𝟎𝟎 = 𝜸𝜸 ∙ 𝑩𝑩𝟎𝟎 Spin-Gitter-Relaxation T1 (Boltzmann-Verteilung) Spin-Spin-Relaxation T2 (Kohärenz; ausschlaggebend für ESR), ∆𝑬𝑬 ∙ 𝝉𝝉 = 𝒉𝒉 Spin-Bahn-Kopplung: Hyperfeinaufspaltung g=2,00232 (ohne), 1 < 𝑔𝑔 < 4 (Übergangsmetallionen) 𝑩𝑩𝒆𝒆𝒆𝒆𝒆𝒆 = 𝑩𝑩𝟎𝟎 + 𝑩𝑩𝒍𝒍𝒍𝒍𝒍𝒍 (WW mit magn. Moment des Atomkerns) Einstellungsmöglichkeiten des Kernspins in B0: Magnetische Quantenzahl von I: Resonanzen (Linien) bei: 2𝐼𝐼 + 1 (Aufspaltung der Linie) 𝑚𝑚𝐼𝐼 = 𝐼𝐼, 𝐼𝐼 − 1, 𝐼𝐼 − 2, … , −𝐼𝐼 0 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 = 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 − 𝑎𝑎𝑚𝑚𝐼𝐼 (Hyperfeinkopplungskonstante = 𝒂𝒂) ESR-Linien einer paramagnetischen Substanz: 𝟐𝟐𝟐𝟐(𝟐𝟐𝟐𝟐 + 𝟏𝟏) Anwendungen: Spektrale Anisotropie Molekulares System ist achsialsym. entlang z: 𝑔𝑔∥ = 𝑔𝑔𝑧𝑧𝑧𝑧 , 𝑎𝑎∥ = 𝑎𝑎𝑧𝑧𝑧𝑧 , 𝑔𝑔⊥ = 𝑔𝑔𝑥𝑥𝑥𝑥 = 𝑔𝑔𝑦𝑦𝑦𝑦 𝑎𝑎⊥ = 𝑎𝑎𝑥𝑥𝑥𝑥 = 𝑎𝑎𝑦𝑦𝑦𝑦 Orientierungen zwischen den Hauptachsen: 𝑔𝑔𝜃𝜃 = �𝑔𝑔∥2 cos 2 𝜃𝜃 + 𝑔𝑔⊥2 sin2 𝜃𝜃 𝑎𝑎𝜃𝜃 = �𝑎𝑎∥2 cos 2 𝜃𝜃 + 𝑎𝑎⊥2 sin2 𝜃𝜃 Isotropes Spektrum Es ergeben sich die isotropen Mittelwerte: 1 𝑎𝑎0 = (𝑎𝑎𝑧𝑧𝑧𝑧 + 𝑎𝑎𝑦𝑦𝑦𝑦 + 𝑎𝑎𝑥𝑥𝑥𝑥 ) 3 1 𝑔𝑔0 = (𝑔𝑔𝑧𝑧𝑧𝑧 + 𝑔𝑔𝑦𝑦𝑦𝑦 + 𝑔𝑔𝑥𝑥𝑥𝑥 ) 3 Für den Fall der Achsialsymmetrie gilt: 1 𝑎𝑎0 = (𝑎𝑎∥ + 2𝑎𝑎⊥ ) 3 1 𝑔𝑔0 = (𝑔𝑔∥ + 2𝑔𝑔⊥ ) 3 𝒂𝒂 −𝒂𝒂 𝒔𝒔 = 𝒂𝒂 ∥ −𝒂𝒂⊥ = Ordnungsgrad (beobachtete/maximale Hyperfeinaufsp.): 𝒛𝒛𝒛𝒛 Winkel zwischen Membran-Normale und Moleküllängsachse) Rotationskorrelationszeit für eine Kugel: Rotkor-Zeit für Segmentbewegung eines Proteins: 𝜏𝜏𝑅𝑅 = 𝒙𝒙𝒙𝒙 𝟑𝟑⟨𝐜𝐜𝐜𝐜𝐜𝐜𝟐𝟐 𝜽𝜽⟩−𝟏𝟏 (𝜃𝜃 ist der 𝟐𝟐 4𝜋𝜋𝜋𝜋 𝑎𝑎 3 3𝑘𝑘𝑘𝑘 ℎ 𝜏𝜏𝑅𝑅 = 6,5 ∙ 10−10 ∙ ∆𝐵𝐵0 ∙ �ℎ 0 − 1 −1 𝐷𝐷𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 = 6 ∙ 10−16 ∙ Diffusionskoeffizient (Austauschfrequenz, Sonden-Konzentration): Vernachlässigung einer Phasentrennung!) 𝑊𝑊𝑒𝑒𝑒𝑒 𝑐𝑐 (unter NMR-Spektroskopie Kernspin: Magnetisches Moment: FID 𝐹𝐹(𝑡𝑡) = Spektrum 𝑎𝑎 0 2 |𝐼𝐼| = ℏ�𝐼𝐼(𝐼𝐼 + 1) = 𝑃𝑃𝐼𝐼 𝜇𝜇𝐼𝐼 = 𝛾𝛾 ∙ 𝐼𝐼 = 𝑔𝑔𝑁𝑁 ∙ 𝜇𝜇𝑁𝑁 ∙ 𝐼𝐼 𝜇𝜇𝑁𝑁 = 𝑒𝑒∙ℏ 2𝑚𝑚 𝑝𝑝 = 5,05 ∙ 10−27 𝐽𝐽/𝑇𝑇 + 𝑎𝑎1 cos 𝑥𝑥 + 𝑎𝑎2 cos 2𝑥𝑥 + 𝑎𝑎3 cos 3𝑥𝑥 + ⋯ + 𝑏𝑏1 sin 𝑥𝑥 + 𝑏𝑏2 sin 2𝑥𝑥 + 𝑏𝑏3 sin 3𝑥𝑥 + ⋯ Chemische Verschiebung Induziertes B-Feld: Resonanzfrequenz: chem Versch. Spin-Spin-Kopplung: +∞ +∞ 𝐹𝐹(𝜔𝜔) = ∫−∞ 𝑓𝑓(𝑡𝑡)𝑒𝑒 𝑖𝑖𝑖𝑖𝑖𝑖 𝑑𝑑𝑑𝑑 = ∫−∞ 𝑓𝑓(𝑡𝑡) ∙ (cos 𝜔𝜔𝜔𝜔 + 𝑖𝑖 sin 𝜔𝜔𝜔𝜔)𝑑𝑑𝑑𝑑 𝑩𝑩𝒍𝒍𝒍𝒍𝒍𝒍 = 𝑩𝑩𝟎𝟎 − 𝑩𝑩𝒊𝒊𝒊𝒊𝒊𝒊, 𝐵𝐵𝑖𝑖𝑖𝑖𝑖𝑖 = 𝜎𝜎𝐵𝐵0 𝜔𝜔0 = 𝛾𝛾𝐵𝐵0 (1 − 𝜎𝜎) 𝛿𝛿 = 𝑣𝑣𝑅𝑅𝑅𝑅𝑅𝑅 −𝑣𝑣𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃𝑃 𝑣𝑣𝑅𝑅𝑅𝑅𝑅𝑅 ∙ 106 𝑝𝑝𝑝𝑝𝑝𝑝 0 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 = 𝐵𝐵𝑟𝑟𝑟𝑟𝑟𝑟 − 𝐽𝐽𝑚𝑚𝐼𝐼 Multiplizität bei n benachbarten Kernen mit Spin I: Gesamtmultiplizität des betrachteten Kerns: 𝒛𝒛 = ∏ 𝒛𝒛𝒊𝒊 𝒛𝒛 = 𝟐𝟐𝟐𝟐 ∙ 𝑰𝑰 + 𝟏𝟏 Relaxation: Spin-Gitter: Spin-Spin: Pulstechnik Abklingen des FIDs: 𝑴𝑴𝒛𝒛 = 𝑴𝑴𝟎𝟎 �𝟏𝟏 − 𝒆𝒆−𝒕𝒕/𝑻𝑻𝟏𝟏 � 𝑴𝑴𝒚𝒚 = 𝑴𝑴𝒚𝒚𝒚𝒚 �𝒆𝒆−𝒕𝒕/𝑻𝑻𝟐𝟐 � 𝜽𝜽 = 𝜸𝜸𝑩𝑩𝟏𝟏 𝒕𝒕𝒑𝒑 wobei 𝑡𝑡𝑝𝑝 ≪ 𝜏𝜏𝑟𝑟 und 1µ𝑠𝑠 < 𝑡𝑡𝑝𝑝 < 50µ𝑠𝑠 𝑑𝑑𝑀𝑀𝑦𝑦′ 𝑑𝑑𝑑𝑑 =− Inversion Recovery zur Messung von T1: Peak-Halbwertsbreite: ∆𝑣𝑣1/2 ≥ 𝑀𝑀𝑦𝑦′ 𝑇𝑇2 1 2𝜋𝜋∙𝑇𝑇2 𝐴𝐴 = 𝐴𝐴max �1 − 2e τ T1 − � , Nullstelle: τ = T1 ∙ ln 2 Licht-Streuung Elastische Streuung: 𝑥𝑥 𝑐𝑐 oszillierendes E-Feld des eingestrahlten Lichts: 𝐸𝐸 = 𝐸𝐸0 ∙ cos �2𝜋𝜋 ∙ 𝑣𝑣 �𝑡𝑡 − �� oszillierendes elektrisches Dipolmoment: E-Feld der Dipolstrahlung: Für polarisiertes Licht (𝐼𝐼~𝐸𝐸²): Für unpolarisiertes Licht: Streuung an verd. Gas (Clausius-Mosotti): 𝝁𝝁 = 𝜶𝜶𝜶𝜶 𝑰𝑰𝑺𝑺 𝑰𝑰𝟎𝟎 𝑰𝑰𝑺𝑺 𝑰𝑰𝟎𝟎 Für reale Lösungen…: …mit Rayleigh-Verhältnis Streuung an Makromolekülen: = 𝛼𝛼 2 ∙ 𝑟𝑟 2 ∙𝜆𝜆 4 ∙ sin2 Φ 16𝜋𝜋 4 = 1 4𝜋𝜋 2 = 𝑛𝑛 02 4𝜋𝜋 2 𝑑𝑑𝑑𝑑 2 𝑑𝑑𝑑𝑑 Linke Vertikale Linie im Zimm-Diagramm: Quasi-elastische Streuung: Streuvektor: Halbwertsbreite des Streulicht-Peaks Stokes-Einstein-Relation für Kugel: 16𝜋𝜋 4 𝑀𝑀 2 1 2 𝟏𝟏 𝒅𝒅𝒅𝒅 𝑴𝑴𝒓𝒓 ∙ ∙ 𝟐𝟐𝟐𝟐 𝒅𝒅𝒅𝒅 𝑵𝑵𝑨𝑨 ∙ � � ∙ 𝑁𝑁 𝑟𝑟2 ∙ 𝑟𝑟 2 ∙𝜆𝜆 4 ∙ (1 + cos2 θ) 𝐾𝐾∙𝑐𝑐 𝑅𝑅𝜃𝜃 𝐾𝐾𝐾𝐾 𝑅𝑅𝜃𝜃 = = 1 𝑀𝑀𝑟𝑟 1 𝑀𝑀𝑟𝑟 𝒊𝒊 𝑑𝑑𝑑𝑑 2 𝑑𝑑𝑑𝑑 ∙� � ∙ 𝐴𝐴 𝑀𝑀𝑟𝑟2 𝑁𝑁𝐴𝐴2 𝟎𝟎 1 𝑃𝑃(𝜃𝜃) ∙� 𝐾𝐾𝐾𝐾 𝜃𝜃→0 𝑅𝑅𝜃𝜃 = = lim c→0 𝐾𝐾𝐾𝐾 | 𝑅𝑅𝜃𝜃 𝜃𝜃=0° 𝐾𝐾𝐾𝐾 | 𝑅𝑅𝜃𝜃 𝑐𝑐=0 |𝑞𝑞| = Δ𝑣𝑣 = 𝐷𝐷 = = = 4𝜋𝜋 𝜆𝜆 16𝜋𝜋 4 𝑟𝑟 2 ∙𝜆𝜆 4 𝒓𝒓𝟐𝟐 𝑹𝑹𝜽𝜽 = 𝑰𝑰𝒔𝒔 ∙ 𝟏𝟏+𝐜𝐜𝐜𝐜𝐜𝐜𝟐𝟐 𝜽𝜽 𝐾𝐾𝐾𝐾 𝑅𝑅𝜃𝜃 ∙ + 2𝐵𝐵𝐵𝐵 + ⋯ 𝑃𝑃(𝜃𝜃) = 1 − Untere Horizontale Linie im Zimm-Diagramm: 1 2 = 𝛼𝛼 2 ∙ 𝑟𝑟 2 ∙𝜆𝜆 4 ∙ (1 + cos 2 θ) 𝒏𝒏 𝑛𝑛2 − 𝒏𝒏𝟐𝟐𝟎𝟎 = 4𝜋𝜋 ∙ 𝑁𝑁 ∙ 𝛼𝛼 → 𝜶𝜶 = 𝟐𝟐𝟐𝟐𝟎𝟎 ∙ 𝑰𝑰𝑺𝑺 𝑰𝑰𝟎𝟎 Für ideale Lösungen…: 16𝜋𝜋 4 𝑥𝑥 𝑐𝑐 ∙ cos �2𝜋𝜋 ∙ 𝑣𝑣 �𝑡𝑡 − �� 𝒏𝒏𝟐𝟐 − 𝟏𝟏 = 𝟒𝟒𝟒𝟒 ∙ 𝑵𝑵 ∙ 𝜶𝜶 → 𝜶𝜶 = 𝑰𝑰𝑺𝑺 𝑰𝑰𝟎𝟎 Streuung an gelösten Molekülen: 4𝜋𝜋 2 ∙sin Φ 𝑟𝑟 ∙𝜆𝜆 2 𝐸𝐸 = 𝛼𝛼 ∙ 𝐸𝐸0 ∙ 𝑘𝑘𝑘𝑘 6𝜋𝜋𝜋𝜋 𝑟𝑟 1 𝑀𝑀𝑟𝑟 1 𝑀𝑀𝑟𝑟 𝐾𝐾 = 𝜃𝜃 ∙ sin2 2 + 2𝐵𝐵𝐵𝐵 �1 + ∙ (1 + cos2 θ) und + 2𝐵𝐵𝐵𝐵� 16𝜋𝜋 2 ∙𝑅𝑅𝐺𝐺2 3𝜆𝜆 2 1 𝑀𝑀𝑟𝑟 sin 𝐷𝐷𝑞𝑞 2 2𝜋𝜋 1 𝑀𝑀𝑟𝑟 1 2 𝒅𝒅𝒅𝒅 𝑴𝑴𝒓𝒓 ∙ 𝒅𝒅𝒅𝒅 𝑵𝑵𝑨𝑨 16𝜋𝜋 2 ∙𝑅𝑅𝐺𝐺2 3𝜆𝜆 2 𝜃𝜃 2 (Diffusionskoeffizient) (Teilchenradius) 𝜃𝜃 ∙ sin2 2 � 2𝜋𝜋 2 ∙𝑛𝑛 02 𝑁𝑁𝐴𝐴 ∙𝜆𝜆 4 𝑑𝑑𝑑𝑑 2 𝑑𝑑𝑑𝑑 ∙� � Raman-Spektroskopie und inelastische Streuung Zeitabhängigkeit des osz. Dipolmom. 𝜇𝜇(𝑡𝑡) = 𝛼𝛼𝐸𝐸0 cos 2𝜋𝜋𝑣𝑣𝑜𝑜 𝑡𝑡 Zeitabhängigkeit der Polarisierbarkeit 𝛼𝛼(𝑡𝑡) = 𝛼𝛼0 + 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 cos 2𝜋𝜋𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 𝑡𝑡 3 Frequenz-Komponenten im Streulicht (Rayleigh, Anti-Stokes, Stokes): 1 2 1 2 𝜇𝜇(𝑡𝑡) = 𝛼𝛼0 𝐸𝐸0 ∙ cos[2𝜋𝜋𝑣𝑣𝑜𝑜 𝑡𝑡] + 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 𝐸𝐸0 ∙ cos[2𝜋𝜋(𝑣𝑣0 + 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 )𝑡𝑡] + 𝛼𝛼𝑣𝑣𝑣𝑣𝑣𝑣 𝐸𝐸0 ∙ cos[2𝜋𝜋(𝑣𝑣0 − 𝑣𝑣𝑣𝑣𝑣𝑣𝑣𝑣 )𝑡𝑡] Röntgen- und Neutronen-Beugung 𝑅𝑅�⃗ = 𝑛𝑛1 𝑎𝑎⃗1 + 𝑛𝑛2 𝑎𝑎⃗2 + 𝑛𝑛3 𝑎𝑎⃗3 Ortsvektoren des Bravis-Gitters (Gitterpunkte im Ortsraum): Ortsvektoren im reziproken Gitter (Gitterpunkte im Phasenraum): 𝐺𝐺⃗ = ℎ𝑏𝑏�⃗1 + 𝑘𝑘𝑏𝑏�⃗2 + 𝑙𝑙𝑏𝑏�⃗3 Zusammenhang Ortsraum <-> Phasenraum: 𝑒𝑒 𝑖𝑖𝑖𝑖𝑖𝑖 = 1 → 𝐺𝐺𝐺𝐺 = 2𝜋𝜋𝜋𝜋 , 𝑁𝑁 ∈ ℤ Zusammenhänge der Basisvektoren (primitive Gittervektoren des reziproken bzw. Bravis-Gitters): 𝑏𝑏�⃗1 = 2𝜋𝜋 ∙ Laue Gleichung: 𝑎𝑎⃗2 × 𝑎𝑎⃗3 , 𝑉𝑉 𝑏𝑏�⃗2 = 2𝜋𝜋 ∙ 𝑉𝑉 = 𝑎𝑎⃗1 (𝑎𝑎⃗2 × 𝑎𝑎⃗3 ), Wellenvektor: 𝑎𝑎⃗3 × 𝑎𝑎⃗1 , 𝑉𝑉 𝑏𝑏�⃗3 = 2𝜋𝜋 ∙ 2𝜋𝜋 𝑏𝑏𝑖𝑖 𝑎𝑎𝑗𝑗 = 2𝜋𝜋𝛿𝛿𝑖𝑖𝑖𝑖 = � 0 𝑎𝑎⃗1 × 𝑎𝑎⃗2 𝑉𝑉 𝑖𝑖 = 𝑗𝑗 𝑖𝑖 ≠ 𝑗𝑗 �⃗ = 𝐺𝐺⃗ 𝑎𝑎⃗𝑛𝑛 (𝑠𝑠⃗ − 𝑠𝑠⃗0 ) = ℎ𝜆𝜆 → 𝑘𝑘�⃗ − 𝑘𝑘�⃗0 = 𝐾𝐾 𝜆𝜆 = 2𝜋𝜋/𝑘𝑘�⃗ (Erklärung: Der Satz G reziproker Gittervektoren muss gleich der Differenz der einfallenden und reflektierten Wellenvektoren sein, damit konstruktive Interferenz resultiert) Braggsche Reflexionsbedinung: Streuung an Elektronenhüllen (1D): Laue Gleichungen (3D): 2𝑑𝑑 ∙ sin 𝜃𝜃 = 𝑛𝑛𝑛𝑛, 𝑛𝑛 = 1,2,3 … 𝒉𝒉𝒉𝒉 = 𝒂𝒂(𝐜𝐜𝐜𝐜𝐜𝐜 𝜶𝜶 − 𝐜𝐜𝐜𝐜𝐜𝐜 𝜶𝜶𝟎𝟎 ) , ℎ = 0,1,2 … ℎ𝜆𝜆 = 𝑎𝑎(cos 𝛼𝛼 − cos 𝛼𝛼0 ) 𝑘𝑘𝑘𝑘 = 𝑏𝑏(cos 𝛽𝛽 − cos 𝛽𝛽0 ) Laue + Bragg für kubisches Gitter: Strukturfaktor 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 , Streufaktoren 𝐴𝐴𝑗𝑗 Elektronendichteverteilung: Phasenproblem: 𝑙𝑙𝑙𝑙 = 𝑐𝑐(cos 𝛾𝛾 − cos 𝛾𝛾0 ) ℎ2 𝑎𝑎 2 𝜆𝜆 � + 𝑘𝑘 2 𝑏𝑏 2 + 1/2 𝑙𝑙 2 � 𝑐𝑐 2 = 2 sin 𝜃𝜃 2 2𝜋𝜋𝜋𝜋 ∙�ℎ𝑥𝑥 𝑗𝑗 +𝑘𝑘𝑦𝑦 𝑗𝑗 +𝑙𝑙𝑧𝑧 𝑗𝑗 � 𝐼𝐼ℎ𝑘𝑘𝑘𝑘 ~ �𝑛𝑛 ∙ ∑𝑁𝑁 � = |𝐹𝐹ℎ𝑘𝑘𝑘𝑘 |2 𝑗𝑗 =1 𝐴𝐴𝑗𝑗 𝑒𝑒 𝜚𝜚(𝑥𝑥, 𝑦𝑦, 𝑧𝑧) = ∫𝑉𝑉 𝐸𝐸𝐸𝐸 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 ∙ 𝑒𝑒 𝐹𝐹ℎ𝑘𝑘𝑘𝑘 = |𝐹𝐹ℎ𝑘𝑘𝑘𝑘 | ∙ 𝑒𝑒 𝑖𝑖𝛼𝛼 ℎ 𝑘𝑘𝑘𝑘 −2𝜋𝜋𝜋𝜋 ∙� ℎ 𝑥𝑥 𝑘𝑘𝑘𝑘 𝑙𝑙𝑙𝑙 + + � 𝑎𝑎 𝑏𝑏 𝑐𝑐 𝑑𝑑𝑑𝑑 1 2 3 2 𝝀𝝀 = 𝒉𝒉/𝒑𝒑 , 𝐸𝐸 = 𝑚𝑚𝑣𝑣 2 = 𝑘𝑘𝑘𝑘 → 𝜆𝜆 = ℎ/√2𝑚𝑚𝑚𝑚𝑚𝑚 De Broglie für thermische Neutronen: Chemisches Potential Reine Substanz: 𝝁𝝁 = 𝑮𝑮/𝒏𝒏 𝜕𝜕𝜕𝜕 � 𝜕𝜕𝑛𝑛 𝑖𝑖 𝑃𝑃,𝑇𝑇,𝑛𝑛 Mischung, Gibbs-Duhem Gelichung: 𝜇𝜇𝑖𝑖 = � Chemisches Potential, ideal verd. Lösung: 𝑗𝑗 → 𝑑𝑑𝑑𝑑 = ∑𝑖𝑖 𝜇𝜇𝑖𝑖 𝑑𝑑𝑛𝑛𝑖𝑖 𝝁𝝁 = 𝝁𝝁𝟎𝟎 + 𝑹𝑹𝑹𝑹 𝐥𝐥𝐥𝐥 𝒄𝒄 Aktivität: 𝒂𝒂 = 𝒇𝒇(𝒄𝒄) ∙ 𝒄𝒄 𝜀𝜀𝜀𝜀 0 𝑘𝑘 𝐵𝐵 𝑇𝑇 2𝑁𝑁𝐴𝐴 𝑒𝑒 2 𝐼𝐼 Ionenradius (Debye-Hückel): 𝛽𝛽 = � = 0,304∙10 −9 𝑚𝑚𝑚𝑚𝑚𝑚 � 𝑙𝑙 √𝐼𝐼 log 𝑓𝑓 = −𝐴𝐴|𝑧𝑧+ 𝑧𝑧− | ∙ √𝐼𝐼 Debye-Hückel-Grenzgesetz (niedrige c): 𝑑𝑑𝑑𝑑 = (𝜇𝜇′′ − 𝜇𝜇′ )𝑑𝑑𝑑𝑑 Verteilungsgleichgewicht (2 Phasen): Konzentrationsverhältnis im Gleichgewicht: Chemische Reaktion im Nicht-Gleichgewicht: 𝒄𝒄′′ 𝒄𝒄′ = 𝒆𝒆 �𝝁𝝁′𝟎𝟎 −𝝁𝝁′′ 𝟎𝟎 � 𝑹𝑹𝑹𝑹 0 −∆𝐺𝐺 = 𝑅𝑅𝑅𝑅 ln Enthalpie, Entropie: 𝑣𝑣 𝑣𝑣 = 𝜸𝜸 𝑣𝑣𝑄𝑄 𝑐𝑐𝑃𝑃 𝑃𝑃 ∙𝑐𝑐𝑄𝑄 𝑣𝑣 𝑣𝑣 𝑐𝑐𝐴𝐴 𝐴𝐴 ∙𝑐𝑐𝐵𝐵𝐵𝐵 𝑣𝑣𝑄𝑄 𝑐𝑐𝑃𝑃 𝑃𝑃 ∙𝑐𝑐𝑄𝑄 𝑣𝑣 𝑣𝑣 𝑐𝑐𝐴𝐴 𝐴𝐴 ∙𝑐𝑐𝐵𝐵𝐵𝐵 ∆𝐺𝐺 = ∆𝐻𝐻 − 𝑇𝑇∆𝑆𝑆, Elektrochemie −∆𝑮𝑮𝟎𝟎 𝑹𝑹𝑹𝑹 ∆𝐺𝐺 = ∆𝐺𝐺 + 𝑅𝑅𝑅𝑅 ln 0 Chem. Reaktion im Gleichgewicht: = 𝒆𝒆 ∆𝐺𝐺 0 = 𝑅𝑅𝑅𝑅 ln 𝐾𝐾 → 𝐾𝐾 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 𝐾𝐾 = 𝑒𝑒 ∆𝐻𝐻 0 𝑅𝑅𝑅𝑅 − ∙ 𝑒𝑒 ∆𝑆𝑆 0 𝑅𝑅 − Grundgleichungen der Elektrostatik (gelten für Punktladungen) �⃗ 𝒒𝒒𝟏𝟏 𝒒𝒒𝟐𝟐 𝒓𝒓 �⃗| 𝒓𝒓𝟐𝟐 |𝒓𝒓 𝟏𝟏 𝒒𝒒𝟏𝟏 𝒒𝒒𝟐𝟐 𝟒𝟒𝟒𝟒𝜺𝜺𝟎𝟎 𝒓𝒓 𝟏𝟏 �⃗𝑪𝑪 (𝒓𝒓 �⃗(𝒓𝒓 �⃗) = −𝒈𝒈𝒈𝒈𝒈𝒈𝒈𝒈�𝑼𝑼(𝒓𝒓 �⃗)� = 𝑬𝑬 �⃗)𝒒𝒒𝟐𝟐 = 𝑭𝑭 𝟒𝟒𝟒𝟒𝜺𝜺 �⃗ 𝒓𝒓 �⃗(𝒓𝒓 �⃗) = − ∫𝒓𝒓�⃗ 𝑭𝑭 �⃗′ )𝒅𝒅𝒓𝒓 �⃗′ = 𝝋𝝋 ��⃗(𝒓𝒓 �⃗)𝒒𝒒𝟐𝟐 = 𝑼𝑼(𝒓𝒓 𝟎𝟎 𝟎𝟎 �⃗ �⃗ 𝒓𝒓 �⃗(𝒓𝒓 ��⃗(𝒓𝒓 �⃗) = − ∫𝒓𝒓�⃗ 𝑬𝑬 �⃗′ )𝒅𝒅𝒓𝒓 �⃗′ = 𝝋𝝋 𝟎𝟎 𝟐𝟐 �⃗) 𝑼𝑼(𝒓𝒓 𝒒𝒒𝟐𝟐 Faraday-Gesetz (transportierte Ladung vs. an Elektroden umgesetzte Stoffmenge): 𝑸𝑸 = 𝑰𝑰𝑰𝑰 = 𝒏𝒏𝒏𝒏𝒏𝒏 Potentialdifferenz der Elektroden ist mit einem E-Feld in x-Richtung verbunden: Kraft auf Kation bzw. Anion: 𝐸𝐸𝑥𝑥 = − �⃗ 𝒒𝒒𝟏𝟏 𝒓𝒓 𝟐𝟐 |𝒓𝒓 �⃗| 𝒓𝒓 𝟎𝟎 𝟏𝟏 𝒒𝒒𝟏𝟏 𝟒𝟒𝟒𝟒𝜺𝜺𝟎𝟎 𝒓𝒓 𝑭𝑭 𝟏𝟏 �𝑬𝑬⃗(𝒓𝒓 �⃗) = −𝒈𝒈𝒈𝒈𝒈𝒈𝒈𝒈�𝝋𝝋 ��⃗(𝒓𝒓 �⃗)� = 𝑪𝑪 = 𝒒𝒒 𝟒𝟒𝟒𝟒𝜺𝜺 𝑑𝑑𝑑𝑑 𝜑𝜑1 − 𝜑𝜑2 𝑉𝑉 = = 𝑙𝑙 𝑑𝑑𝑑𝑑 𝑙𝑙 �𝑲𝑲 �⃗, �𝑲𝑲 �⃗ �⃗+ = 𝒆𝒆𝑬𝑬 �⃗− = −𝒆𝒆𝑬𝑬 = Konstante Geschwindigkeiten: �⃗, 𝒗𝒗 �⃗ �⃗+ = 𝒖𝒖+ 𝑬𝑬 �⃗− = −𝒖𝒖− 𝑬𝑬 𝒗𝒗 Zwischen den Elektroden fließender Strom Elektrischer Leitwert (reziprok: Widerstand): 𝐼𝐼 = 𝑐𝑐𝑐𝑐𝑐𝑐(𝑢𝑢+ + 𝑢𝑢− ) 𝑉𝑉 𝑙𝑙 𝐼𝐼/𝑉𝑉 = 𝑐𝑐𝑐𝑐𝑐𝑐(𝑢𝑢+ + 𝑢𝑢− )/𝑙𝑙 𝜆𝜆 = 𝐼𝐼𝐼𝐼/𝑉𝑉𝑉𝑉 = 𝑐𝑐𝑐𝑐(𝑢𝑢+ + 𝑢𝑢− ) Elektrische Leitfähigkeit (reziprok: spezifischer Widerstand): 𝜆𝜆 = 𝑐𝑐𝑐𝑐(𝑛𝑛+ 𝑧𝑧+𝑢𝑢+ + 𝑛𝑛− 𝑧𝑧−𝑢𝑢−) Dissoziationszahl und Ladungszahl berücksichtigt: Λ = 𝐹𝐹(𝑢𝑢+ + 𝑢𝑢− ) = 𝜆𝜆/𝑐𝑐 Molare elektrische Leitfähigkeit: Coulomb-Kraft und Energie: Thermische Energie induziert Dissoziation: �⃗𝐶𝐶 = 𝑞𝑞 + 𝑞𝑞 − 2 𝑟𝑟⃗0 , 𝑊𝑊𝐶𝐶 = − 𝑞𝑞 + 𝑞𝑞 − 𝐾𝐾 4𝜋𝜋𝜋𝜋 𝜀𝜀 𝑟𝑟 4𝜋𝜋𝜋𝜋 𝜀𝜀 𝑟𝑟 0 𝑾𝑾𝒕𝒕𝒕𝒕 = 𝒌𝒌𝑩𝑩 𝑻𝑻 = 𝟒𝟒, 𝟏𝟏 ∙ 𝟏𝟏𝟏𝟏−𝟐𝟐𝟐𝟐 𝑱𝑱 0 Konzentrationsabhängigkeit der Leitfähigkeit: Λ(c) = Λ 0 − 𝑎𝑎 √𝑐𝑐 Stokesches Gesetz Beweglichkeit vs. hydratisierter Ionenradius: �⃗𝑟𝑟 = −𝑓𝑓𝑣𝑣⃗ = −6𝜋𝜋𝜋𝜋𝜋𝜋𝑣𝑣⃗ 𝐾𝐾 𝑢𝑢 = 𝑞𝑞 𝑓𝑓 𝑧𝑧 = ± 6𝜋𝜋𝜋𝜋+/− ∙𝑟𝑟 ∙𝑒𝑒 +/− 𝑡𝑡+ = 𝐼𝐼+ /𝐼𝐼 = 𝑢𝑢+/(𝑢𝑢+ + 𝑢𝑢−) Anteil am Gesamststrom für Kation: Ionengleichgewichte an Membranen 𝜇𝜇�𝑖𝑖 = 𝜇𝜇𝑖𝑖 + 𝑧𝑧𝑖𝑖 𝐹𝐹𝐹𝐹 = 𝜇𝜇𝑖𝑖0 + 𝑅𝑅𝑅𝑅 ln 𝑎𝑎𝑖𝑖 + 𝑧𝑧𝑖𝑖 𝐹𝐹𝐹𝐹 Elektrochemisches Potential: Membranpotential im GG (Nernst-Gleichung): 𝜇𝜇�′ = 𝜇𝜇�′′ → 𝑉𝑉𝑚𝑚 = 𝜑𝜑′ − 𝜑𝜑′′ = Für Na+: 𝑉𝑉𝑚𝑚 = 59𝑚𝑚𝑚𝑚 ∙ log10 Donnan-Gleichung: Elektroneutralität bei Protein-freier Lösung: 𝒄𝒄′+ 𝒄𝒄′− = 𝒄𝒄′′+ 𝒄𝒄′′− 𝑐𝑐 ′′ 𝑐𝑐 ′ 𝒄𝒄′+ = 𝒄𝒄′− = 𝒄𝒄′ → (𝒄𝒄′ )𝟐𝟐 = 𝒄𝒄′′+ 𝒄𝒄′′− Elektroneutralität bei Protein-haltiger Lösung 𝒄𝒄′′− = 𝒛𝒛𝑷𝑷 𝒄𝒄𝑷𝑷 + 𝒄𝒄′′+ 𝑧𝑧𝑃𝑃 𝑐𝑐 𝑃𝑃 2 � 2 Einsetzen in Donnen-Gleichung: 𝑐𝑐+′′ = �(𝑐𝑐 ′ )2 + � Redoxprozesse, elektrochemische Zellen Potentialdifferenz einer elektrochem Zelle: − 𝑧𝑧𝑃𝑃 𝑐𝑐 𝑃𝑃 2 𝑧𝑧𝑃𝑃 𝑐𝑐 𝑃𝑃 2 � 2 , 𝑐𝑐−′′ = �(𝑐𝑐 ′ )2 + � 𝑟𝑟 𝑙𝑙 𝐸𝐸 = (𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 ) − �𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 � → 𝑅𝑅𝑅𝑅 ln 𝑎𝑎𝐴𝐴+𝑧𝑧 , 𝑧𝑧𝑧𝑧 𝜑𝜑0 = 𝜇𝜇 𝐴𝐴0 +𝑧𝑧 +𝑧𝑧𝜇𝜇 𝑒𝑒0− −𝜇𝜇 𝐴𝐴 𝑧𝑧𝑧𝑧 + 𝐸𝐸 = ∆𝜑𝜑𝑟𝑟 − ∆𝜑𝜑𝑙𝑙 Konzentrationsabhängigkeit der Potentialdifferenz an einer Elektrode im GG: ∆𝜑𝜑 = 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 = 𝜑𝜑0 + 𝑅𝑅𝑅𝑅 𝑐𝑐 ′′ ln ′ 𝑐𝑐 𝑧𝑧𝑧𝑧 𝑧𝑧𝑃𝑃 𝑐𝑐 𝑃𝑃 2 Für elektrochemische Zelle mit Referenzelektrode links unter Konstanthaltung der Konzentration gilt: 𝐸𝐸 = 𝐸𝐸0 + +𝑧𝑧 𝑅𝑅𝑅𝑅 ln 𝑎𝑎𝑟𝑟𝐴𝐴 𝑧𝑧𝑧𝑧 , 𝐸𝐸0 = 𝜑𝜑𝑟𝑟0 − ∆𝜑𝜑𝑙𝑙 EMK elektrochemischer Zelle ohne Referenzelektrode berechnet sich mithilfe des elektrischen Potentials der Normal-Wasserstoffelektrode (tabelliert): 𝐸𝐸 = (𝐸𝐸𝐻𝐻0 )𝑟𝑟 − (𝐸𝐸𝐻𝐻0 )𝑙𝑙 + +𝑧𝑧 𝑅𝑅𝑅𝑅 𝑎𝑎 𝐴𝐴 ln 𝑟𝑟𝐴𝐴 +𝑧𝑧 𝑧𝑧𝑧𝑧 𝑎𝑎 𝑙𝑙 Redoxpotential und Nernst-Gleichung (Re=Referenzelek, Me=Messelek, Konzentrationsverhältnis im GG!): ∆𝜑𝜑𝑀𝑀𝑀𝑀 = 𝜑𝜑𝑀𝑀 − 𝜑𝜑𝐿𝐿 = 𝜑𝜑0 + 𝐸𝐸 = 𝐸𝐸0 + 𝑅𝑅𝑅𝑅 𝑎𝑎 ln 𝑎𝑎 𝑜𝑜𝑜𝑜 𝑛𝑛𝑛𝑛 𝑟𝑟𝑟𝑟𝑟𝑟 𝐸𝐸 = 𝐸𝐸0 + 𝑅𝑅𝑇𝑇 𝑎𝑎 𝑎𝑎 ln 𝑎𝑎 𝑜𝑜𝑜𝑜 2 𝑎𝑎𝑟𝑟𝑟𝑟𝑟𝑟 1 𝑛𝑛𝑛𝑛 𝑟𝑟𝑟𝑟𝑟𝑟 2 𝑜𝑜𝑜𝑜 1 𝑅𝑅𝑅𝑅 𝑛𝑛𝑛𝑛 𝑎𝑎 ln 𝑎𝑎 𝑜𝑜𝑜𝑜 , 𝜑𝜑0 = 𝑟𝑟𝑟𝑟𝑟𝑟 , 𝐸𝐸0 = 𝜑𝜑0 − ∆𝜑𝜑𝑅𝑅𝑅𝑅 0 +𝑛𝑛𝜇𝜇 0− −𝜇𝜇 0 𝜇𝜇 𝑜𝑜𝑜𝑜 𝑒𝑒 𝑟𝑟𝑟𝑟𝑟𝑟 𝑛𝑛𝑛𝑛 Reversible Führung der Reaktion über Stromfluss gegen 0: , 𝐸𝐸0 = (𝐸𝐸0𝐻𝐻 )2 − (𝐸𝐸0𝐻𝐻 )1 Bei endlichem Strom resultiert chemisches Gleichgewicht: 𝐸𝐸 = 0, 𝐸𝐸0 = − ln 𝐾𝐾 = − ∆𝐺𝐺0 𝑅𝑅𝑅𝑅 𝑅𝑅𝑅𝑅 𝑛𝑛𝑛𝑛 𝑎𝑎� 𝑎𝑎� 𝑟𝑟𝑟𝑟𝑟𝑟 1 𝑎𝑎 𝑟𝑟𝑟𝑟𝑟𝑟 2 𝑎𝑎� 𝑜𝑜𝑜𝑜 1 ln �𝑜𝑜𝑜𝑜 2 =− 𝑅𝑅𝑅𝑅 𝑛𝑛𝑛𝑛 ln 𝐾𝐾 → ∆𝐺𝐺0 = 𝑛𝑛𝑛𝑛(𝐸𝐸0𝐻𝐻 )2 − (𝐸𝐸0𝐻𝐻 )1 Adsorption an Grenzflächen Filmwaage: 𝑲𝑲 = 𝒍𝒍(𝜸𝜸𝟎𝟎 − 𝜸𝜸) , 𝝅𝝅 = 𝜸𝜸𝟎𝟎 − 𝜸𝜸 , 𝜸𝜸(𝒄𝒄) = 𝜸𝜸𝟎𝟎 − 𝝅𝝅(𝒄𝒄) Gibbsche Adsorptionsisotherme Spezifische Oberflächenkonzentration der Komponente i: Gibbsche Adsorptionsgleichung: Oberflächenüberschuss: Langmuir-Isotherme 𝑑𝑑𝑑𝑑 = − ∑𝑛𝑛𝑖𝑖 Γi 𝑑𝑑𝜇𝜇𝑖𝑖 → 𝑐𝑐 Γ(c2 ) = �Γ2 − 𝑐𝑐2 Γ1 � Konzentrationsabhängigkeit des Speitungsdruckes: Langmuirsche Adsorptionsisotherme: Γ(c) = Γ∞ 2D ideales Oberflächengas: Kc 1+Kc 𝑑𝑑𝑑𝑑 𝑑𝑑𝑐𝑐2 =− Γ𝑖𝑖 = 𝑛𝑛𝑠𝑠,𝑖𝑖 /𝐴𝐴𝑠𝑠 𝑅𝑅𝑅𝑅 �Γ2 𝑐𝑐2 𝑐𝑐 − 𝑐𝑐2 Γ1 � 1 1 𝜋𝜋 = 𝛾𝛾0 − 𝛾𝛾 = 𝑅𝑅𝑅𝑅 Γ∞ ln(1 + Kc) ⟺ Kc = Γ Γ ∞ −Γ 𝝅𝝅𝑨𝑨𝒔𝒔 = 𝒏𝒏𝒔𝒔 𝑹𝑹𝑹𝑹 , 𝜋𝜋 = 𝑘𝑘𝐵𝐵 𝑇𝑇/𝑎𝑎𝑠𝑠 (𝑎𝑎𝑠𝑠 = Größe Bindestelle) Viskosität Definition über Kraft K, Platten der Fläche A im Abstand d gegeneinander zu verschieben: 𝐾𝐾 = 𝜂𝜂𝜂𝜂 ∙ 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝜂𝜂𝜂𝜂 ∙ 𝑣𝑣0 𝑑𝑑 → 𝜂𝜂 = 𝐾𝐾𝐾𝐾 𝐴𝐴𝑣𝑣0 𝜋𝜋 8 Hagen-Poiseuillesche Gleichung: transportiertes Volumen in Kapillare: ∆𝑉𝑉 = ∙ 𝑅𝑅�⃗ = −𝑓𝑓𝑣𝑣⃗ Reibungskraft eines Teilchens in viskoser Lösung: Reibungskoeffizient für Kugelförmige Teilchen, Gesetz von Stokes: Geschwindigkeitsprofil: 𝑓𝑓 𝐾𝐾 𝑓𝑓 𝐾𝐾 𝑓𝑓 Mittleres Verschiebungsquadrat der Brownschen MB (d = dimension: 1,2,3): Diffusion (eindimensionale Betrachtung) Erstes Ficksches Gesetz 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑡𝑡 𝐽𝐽𝑥𝑥 = −𝐷𝐷𝐷𝐷 � � , Diffusionskoeffizient (Einstein-Gleichung): 𝐷𝐷 = Erstes Ficksches Gesetz: 𝐽𝐽𝑥𝑥 = Zeitabhängigkeit: Änderung der Stoffmenge pro Zeit: 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 Δn Δ𝑡𝑡 = Φ𝑥𝑥 = −𝐷𝐷 ������ 𝛥𝛥𝑥𝑥 2 2∆𝑡𝑡 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝐷𝐷𝐷𝐷 𝑉𝑉𝑉𝑉𝑉𝑉 𝑑𝑑𝑑𝑑 → �����2 = 2𝑑𝑑𝑘𝑘 𝐵𝐵 𝑇𝑇 𝛥𝛥𝛥𝛥 𝛥𝛥𝑥𝑥 𝑓𝑓 𝚽𝚽𝒙𝒙 = 𝑱𝑱𝒙𝒙 /𝑨𝑨 𝑐𝑐(𝑥𝑥) = 𝑐𝑐 𝐼𝐼𝐼𝐼 − Lineares Konzentrationsgefälle: ∙ ∆𝑡𝑡 𝑓𝑓 = 6𝜋𝜋𝜋𝜋𝜋𝜋 𝑣𝑣(𝑡𝑡) = �1 − 𝑒𝑒 −𝑚𝑚 𝑡𝑡 � , 𝑣𝑣𝑚𝑚𝑚𝑚𝑚𝑚 = , 𝜏𝜏 = 𝑚𝑚/𝑓𝑓 Diffusionsflussdichte = spezifischer Diffusionsfluss: 𝜌𝜌𝜌𝜌 ℎ𝑅𝑅 4 𝜂𝜂𝜂𝜂 = 𝑘𝑘 𝐵𝐵 𝑇𝑇 𝑓𝑓 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = ⏟ 𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾𝐾 𝑥𝑥 = 𝑐𝑐 𝐼𝐼𝐼𝐼 − 𝑘𝑘 𝐵𝐵 𝑇𝑇 6𝜋𝜋𝜋𝜋𝜋𝜋 �𝑐𝑐 𝐼𝐼𝐼𝐼 −𝑐𝑐 𝐼𝐼 � 𝑑𝑑 ∆𝑐𝑐 𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 1 𝑉𝑉 𝑥𝑥 ∙ 𝐽𝐽𝑥𝑥 ∆𝑐𝑐 1 1 𝑑𝑑∆𝑐𝑐 = −𝐷𝐷𝐷𝐷 � 𝐼𝐼𝐼𝐼 + 𝐼𝐼 � = −𝛽𝛽𝛽𝛽∆𝑐𝑐 → ∆𝑐𝑐 = ∆𝑐𝑐0 𝑒𝑒 −𝛽𝛽𝛽𝛽𝛽𝛽 𝑑𝑑 𝑉𝑉 𝑉𝑉 𝑑𝑑𝑑𝑑 𝒅𝒅𝒅𝒅 𝒅𝒅𝒅𝒅 𝒙𝒙 Zweites Ficksches Gesetz: 𝒅𝒅𝟐𝟐 𝒄𝒄 � 𝒅𝒅𝒙𝒙𝟐𝟐 𝒕𝒕 � � = 𝑫𝑫 � Diffusion von Ionen Diffusionspotential, wegen Voraus-Diffusion des Ions mit dem größeren D oder wegen von außen angelegter Spannung: 𝑽𝑽𝑫𝑫 = 𝝋𝝋′ − 𝝋𝝋′′ Flussdichte der Ionensorte i: Φ𝑖𝑖 = (Φ𝑖𝑖 )𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 + (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 = −𝐷𝐷𝑖𝑖 Elektr. Kraft des E-Feldes auf ein Ion: 𝑑𝑑𝑐𝑐 𝑖𝑖 𝑑𝑑𝑑𝑑 𝑒𝑒𝑒𝑒 𝐾𝐾𝑥𝑥,𝑖𝑖 = 𝑞𝑞𝑖𝑖 𝐸𝐸𝑥𝑥 = −𝑞𝑞𝑖𝑖 + (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 , 𝑞𝑞𝑖𝑖 = 𝑧𝑧𝑖𝑖 𝑒𝑒 Beweglichkeit u und Geschwindigkeit v: 𝑣𝑣𝑥𝑥,𝑖𝑖 = −𝐷𝐷𝑖𝑖 ∙ 𝑧𝑧 𝑖𝑖 𝐹𝐹 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 ∙ (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 = 𝑐𝑐𝑖𝑖 𝑣𝑣𝑥𝑥,𝑖𝑖 = −𝑐𝑐𝑖𝑖 𝐷𝐷𝑖𝑖 ∙ Elektrischer Beitrag zur Flussdichte: = −𝑢𝑢𝑖𝑖 ∙ 𝑧𝑧 𝑖𝑖 𝐹𝐹 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 ∙ 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝑑𝑑𝑐𝑐 Nernst-Planck-Gleichung für Elektrodiffusion: Φ𝑖𝑖 = (Φ𝑖𝑖 )𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 + (Φ𝑖𝑖 )𝑒𝑒𝑒𝑒 = −𝐷𝐷𝑖𝑖 � 𝑑𝑑𝑑𝑑𝑖𝑖 + 𝑧𝑧𝑖𝑖 𝑐𝑐𝑖𝑖 ∙ Diffusionspotential für Elektrodiffusion durch Kapillare zwischen zwei Lösungsräumen: 𝐷𝐷 −𝐷𝐷 𝑅𝑅𝑅𝑅 𝐹𝐹 − 𝑉𝑉𝐷𝐷 = 𝜑𝜑′ − 𝜑𝜑′′ = 𝐷𝐷++𝐷𝐷− ∙ + 𝑐𝑐 ′′ ∙ ln 𝑐𝑐 ′ , (Nernst-Planck-Potential) 𝑉𝑉𝐷𝐷 ≈ ± 𝐷𝐷+ ≫𝐷𝐷− 𝐷𝐷+ ≪𝐷𝐷− 𝑅𝑅𝑅𝑅 𝐹𝐹 ∙ ln 𝐹𝐹 𝑅𝑅𝑅𝑅 ∙ 𝑑𝑑𝑑𝑑 � 𝑑𝑑𝑑𝑑 𝑐𝑐′′ (Nernst-Potential) 𝑐𝑐 ′ (𝜑𝜑𝐸𝐸1 (𝜑𝜑𝑎𝑎 − 𝜑𝜑𝐸𝐸2 ) 𝑉𝑉 = �� − �� 𝜑𝜑𝑖𝑖 ) + (𝜑𝜑 ����� ��� �� 𝑖𝑖 − 𝜑𝜑 𝑎𝑎 ) + ������� Messung des Membranpotentials: 𝑉𝑉𝐷𝐷 1 Elektrisch geladene Grenzflächen 𝑉𝑉𝑀𝑀 −𝑉𝑉𝐷𝐷 2 Helmholtz-Modell (Poisson-Gleichung ohne Ladungsdichte) 𝑑𝑑 2 𝜑𝜑 𝑑𝑑𝑥𝑥 2 =− 𝜌𝜌 , 𝜌𝜌 𝜀𝜀 𝑟𝑟 𝜀𝜀 0 = 0 → 𝜑𝜑(𝑥𝑥) = 𝐶𝐶1 𝑥𝑥 + 𝐶𝐶2 |𝜑𝜑0 | ≪ Gouy-Chapman (Potentialverlauf): Debye-Länge: 1 𝐹𝐹 𝑙𝑙𝐷𝐷 = ∙ � 1 𝐶𝐶𝑑𝑑 Stern-Modell: = 1 2 1 𝐶𝐶𝑑𝑑𝐻𝐻𝐻𝐻𝐻𝐻𝐻𝐻 𝜀𝜀𝜀𝜀 0 𝑅𝑅𝑅𝑅 2𝑐𝑐 + 𝑅𝑅𝑅𝑅 𝐹𝐹 ≈ 25𝑚𝑚𝑚𝑚 1 𝐽𝐽 = ∑𝑛𝑛𝑖𝑖=1 𝑧𝑧𝑖𝑖2 𝑐𝑐𝑖𝑖 Ionenstärke: 1 = 𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺 𝐶𝐶𝑑𝑑 𝐴𝐴 𝜀𝜀 0 𝜀𝜀 𝐻𝐻𝐻𝐻𝐻𝐻𝐻𝐻 ∙ 𝑑𝑑 → 𝜑𝜑(𝑥𝑥) = 𝜑𝜑0 ∙ 𝑒𝑒 + 1 𝜀𝜀 0 𝜀𝜀 𝐺𝐺𝐺𝐺𝐺𝐺𝐺𝐺 ∙ 𝑥𝑥 𝑙𝑙 𝐷𝐷 − 𝐴𝐴 𝑑𝑑 Ionenkonzentration in der Nähe der geladenen Wand (1=Anion, 2=Kation): 𝑐𝑐2 𝑐𝑐1 = 𝑒𝑒 𝐸𝐸 −𝐸𝐸 − 2 1 𝑘𝑘 𝐵𝐵 𝑇𝑇 , 𝐹𝐹𝐹𝐹 (𝑥𝑥) 𝑅𝑅𝑅𝑅 𝐸𝐸(𝑥𝑥) = 𝑞𝑞 ∙ 𝜑𝜑(𝑥𝑥) → 𝑐𝑐+ (𝑥𝑥) = 𝑐𝑐𝑒𝑒 − Flächenladungsdichte und Grenzflächenpotential: Flächenladungsdichte 𝜎𝜎 = 𝑄𝑄 𝐴𝐴 mit 𝐸𝐸 = 𝑄𝑄 𝜀𝜀𝜀𝜀 0 𝐴𝐴 𝜑𝜑0 = E-Feld: 𝐸𝐸𝑥𝑥 = − , 𝑐𝑐− (𝑥𝑥) = 𝑐𝑐𝑒𝑒 𝐹𝐹𝐹𝐹 (𝑥𝑥) 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 � 𝑑𝑑𝑑𝑑 𝑥𝑥=0 (Plattenkondensator): 𝜎𝜎 = 𝜀𝜀𝜀𝜀0 𝐸𝐸𝑥𝑥 = 𝜀𝜀𝜀𝜀0 � 𝜎𝜎𝑙𝑙𝐷𝐷 𝜎𝜎 𝑅𝑅𝑅𝑅 𝜎𝜎 = ∙� = 𝐾𝐾 ∙ 𝜀𝜀𝜀𝜀0 𝐹𝐹 2𝜀𝜀𝜀𝜀0 𝐽𝐽 �𝐽𝐽 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝜎𝜎 𝜀𝜀𝜀𝜀 0 ∙ 𝑒𝑒 𝑥𝑥 𝑙𝑙 𝐷𝐷 − Potentialberg innerhalb der Membran (Born-Energie): 𝑧𝑧 2 𝑒𝑒 2 0 𝑟𝑟 𝑊𝑊𝐵𝐵 (𝑟𝑟) = 8𝜋𝜋𝜀𝜀 ∙� 1 𝜀𝜀 𝑀𝑀 − 1 � 𝜀𝜀 𝐻𝐻 2 𝑂𝑂 Elektrophorese Geschwindigkeit ohne Gegenionen: �⃗ 𝐾𝐾 𝑓𝑓 𝑣𝑣⃗𝑚𝑚𝑚𝑚𝑚𝑚 = Geschwindigkeit mit Gegenionen: 𝑣𝑣⃗ = 𝜎𝜎𝐸𝐸 𝑙𝑙 𝐷𝐷 𝜂𝜂 Zeta-Potential (äquivalent zum Grenzflächenpotential): = 𝐸𝐸�⃗ 𝑞𝑞𝐸𝐸�⃗ 𝑓𝑓 = 𝑢𝑢𝐸𝐸�⃗ 𝜉𝜉 = Biologische Membranen, Kapitel 9 𝜎𝜎𝐸𝐸 𝑙𝑙 𝐷𝐷 𝜀𝜀𝜀𝜀 0 Kapazität: 𝐶𝐶 = 𝜀𝜀𝜀𝜀0 𝐴𝐴 𝑑𝑑 , 𝐶𝐶𝑚𝑚 = 𝜀𝜀𝜀𝜀 0 𝑑𝑑 𝑈𝑈 𝐼𝐼 𝑤𝑤 𝟏𝟏 𝑹𝑹 , 𝑅𝑅𝑚𝑚 = 𝑅𝑅 ∙ 𝐴𝐴 , 𝒈𝒈 = , 𝒈𝒈𝒎𝒎 = , , 𝑈𝑈(𝑡𝑡) = 𝐼𝐼𝐼𝐼 �1 − 𝑒𝑒 Ladungsverschiebung und Verschiebungsstrom: 𝑡𝑡 𝜏𝜏 𝑚𝑚 − 𝑰𝑰 = 𝑪𝑪𝑪𝑪𝑪𝑪/𝒅𝒅𝒅𝒅 Φ = 𝑃𝑃𝑑𝑑 (𝑐𝑐 ′ − 𝑐𝑐 ′′ ) = 𝑃𝑃𝑑𝑑 Δ𝑐𝑐 Flussdichte und Permeabilitätskoeffizient: Messung von Pd über Zeitkonstante des Transports: 𝟏𝟏 𝑹𝑹𝒎𝒎 � , 𝜏𝜏𝑚𝑚 = 𝑅𝑅𝑅𝑅 = 𝑅𝑅𝑚𝑚 𝐶𝐶𝑚𝑚 𝑄𝑄 = 𝐶𝐶𝐶𝐶 Transport über Membranen 𝐸𝐸�⃗ Δ 𝐺𝐺 0 𝑐𝑐 Δ𝐺𝐺 0 = ΔH0 − 𝑇𝑇ΔS0 = −𝐴𝐴 − 𝐵𝐵𝐵𝐵, (𝐴𝐴, 𝐵𝐵 = 𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘𝑘. > 0, 𝑣𝑣 ≥ 4) 𝑅𝑅 = 𝜀𝜀𝜀𝜀 0 𝜉𝜉 𝜂𝜂 𝛾𝛾 = 𝑐𝑐 𝑎𝑎 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 Verteilungskoeffizient (Konz in Lömi1 vs. Konz in Lömi2): Widerstand, Leitfähigkeit: → 𝑣𝑣⃗ = 𝑐𝑐𝑖𝑖 = 𝑐𝑐𝑎𝑎 �1 − 𝑒𝑒 −𝑡𝑡/𝜏𝜏 �, 𝜏𝜏 = Transport über Membran für lipidlösliche Substanzen (Overton-Regel): 𝑉𝑉 𝐴𝐴𝑃𝑃𝑑𝑑 𝑃𝑃𝑑𝑑 = γD/d Unidirektionaler Fluss durch teilweise Isotopenmarkierung im Außenmedium: 𝛼𝛼 ′ = Flusskopplung: ′ Φrad 𝑃𝑃𝑑𝑑 = ′ crad ′ 𝑐𝑐𝑟𝑟𝑟𝑟𝑟𝑟 𝑐𝑐 ′ , Φ′ = Φ ′𝑟𝑟𝑟𝑟𝑟𝑟 𝛼𝛼 ′ Φ𝐴𝐴 = 𝑃𝑃𝐴𝐴 Δ𝑐𝑐𝐴𝐴 + 𝑃𝑃𝐴𝐴𝐴𝐴 Δ𝑐𝑐𝐵𝐵 , Φ𝐵𝐵 = 𝑃𝑃𝐵𝐵 Δ𝑐𝑐𝐵𝐵 + 𝑃𝑃𝐵𝐵𝐵𝐵 Δ𝑐𝑐𝐴𝐴 Onsager-Relation zwischen den Kreuzkoeffizienten: Carriertransport: Φ𝐴𝐴 = �𝑃𝑃𝐴𝐴 − 𝑷𝑷𝑨𝑨𝑨𝑨 𝒄𝒄𝑩𝑩 = 𝑷𝑷𝑩𝑩𝑩𝑩 𝒄𝒄𝑨𝑨 𝑃𝑃𝐴𝐴𝐴𝐴 𝑃𝑃𝐵𝐵𝐵𝐵 𝑃𝑃𝐴𝐴𝐴𝐴 � Δ𝑐𝑐𝐴𝐴 + Φ 𝑃𝑃𝐵𝐵 𝑃𝑃𝐵𝐵 𝐵𝐵 [𝐶𝐶𝐶𝐶]𝑚𝑚 , 𝑚𝑚 [𝑆𝑆]𝑤𝑤 𝐾𝐾 = [𝐶𝐶] 𝒘𝒘 = 𝑱𝑱𝒎𝒎𝒎𝒎𝒎𝒎 /𝑵𝑵 (Wechselzahl bei Sättigung) Kanaltransport (Transport von n Ionen der Ladung q in der Zeit t; Strommessung): 𝐼𝐼 = Aktiver Transport: Elektrochemische Potentiale: 𝑞𝑞 𝑡𝑡 → 𝑛𝑛 𝑡𝑡 = 𝐼𝐼 𝑞𝑞 𝜇𝜇�′ = 𝜇𝜇0 + 𝑅𝑅𝑅𝑅 ln 𝑎𝑎′ + 𝑧𝑧𝑧𝑧𝜑𝜑 ′ , 𝜇𝜇�′′ = 𝜇𝜇0 + 𝑅𝑅𝑅𝑅 ln 𝑎𝑎′′ + 𝑧𝑧𝑧𝑧𝜑𝜑 ′′ 𝑎𝑎 ′ ∆𝜇𝜇� = 𝜇𝜇�′ − 𝜇𝜇�′′ = ∆𝑮𝑮𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻 = 𝑅𝑅𝑅𝑅 ln 𝑎𝑎 ′′ + 𝑧𝑧𝑧𝑧(𝜑𝜑 ′ − 𝜑𝜑′′ ) Elektrochemischer Gradient: Energiebilanz des primär aktiven Transports: 𝑣𝑣 ∙ ∆𝐺𝐺𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 < −∆𝐺𝐺 = 30𝑘𝑘𝑘𝑘/𝑚𝑚𝑚𝑚𝑚𝑚 𝑐𝑐 ′′ 𝑐𝑐 ′ Energiebilanz für elektrisch neutrales Teilchen: ∆𝐺𝐺 < 𝑒𝑒 −𝑅𝑅𝑅𝑅 Energiebilanz des sekundär aktiven Transports: Φ𝑅𝑅 Δ𝜇𝜇𝑅𝑅 >– Φ𝑆𝑆 Δ𝜇𝜇𝑆𝑆 Für Na/Glc-Symport 1:1: [G] [𝑁𝑁𝑎𝑎 + ] Φ𝐺𝐺𝐺𝐺 = ΦNa > 0, → Δ𝜇𝜇𝐺𝐺𝐺𝐺 + Δ𝜇𝜇𝑁𝑁𝑁𝑁 > 0 , [G]i [𝐺𝐺]𝑎𝑎 𝑅𝑅𝑅𝑅 ln [𝐺𝐺]a > −𝑅𝑅𝑅𝑅 ln [𝑁𝑁𝑎𝑎 +]𝑎𝑎 − 𝐹𝐹(𝜑𝜑𝑎𝑎 − 𝜑𝜑𝑖𝑖 ) 𝑖𝑖 𝑖𝑖 > [𝑁𝑁𝑎𝑎 + ]𝑎𝑎 [𝑁𝑁𝑎𝑎 + ]𝑖𝑖 𝐹𝐹�𝜑𝜑 𝑎𝑎 −𝜑𝜑 𝑖𝑖 � 𝑅𝑅𝑅𝑅 𝑒𝑒 − Für primär aktiven Transport über NaK Pumpe: 𝑎𝑎 𝑖𝑖 −∆𝐺𝐺𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 = 3�Δ𝜇𝜇𝑁𝑁𝑁𝑁 − Δ𝜇𝜇𝑁𝑁𝑁𝑁 � + 2�Δ𝜇𝜇𝐾𝐾𝑖𝑖 − Δ𝜇𝜇𝐾𝐾𝑎𝑎 � = −42,2kJ/mol Der Anteil von Natrium: = 3RT ln c aNa c iNa ci + 3F(𝜑𝜑𝑎𝑎 − 𝜑𝜑𝑖𝑖 ) = (19,6 + 17,4) = 2RT ln c Ka + 2F(𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 ) = (16,8 − 11,6) Der Anteil von Kalium: K 𝑘𝑘𝑘𝑘 𝑚𝑚𝑚𝑚𝑚𝑚 𝑘𝑘𝑘𝑘 𝑚𝑚𝑚𝑚𝑚𝑚 = 𝟑𝟑𝟑𝟑𝟑𝟑𝟑𝟑/𝒎𝒎𝒎𝒎𝒎𝒎 = 𝟓𝟓, 𝟐𝟐𝟐𝟐𝟐𝟐/𝒎𝒎𝒎𝒎𝒎𝒎 Chemiosmtische Hypothese: 𝑎𝑎 𝑖𝑖 ∆𝜇𝜇�𝐻𝐻 = 𝑅𝑅𝑅𝑅 ln 𝑎𝑎 𝐻𝐻𝑎𝑎 + 𝐹𝐹(𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 ) = −2,3𝑅𝑅𝑅𝑅∆𝑝𝑝𝑝𝑝 + 𝐹𝐹∆𝜑𝜑, ln 𝑎𝑎 = 2,3 log 𝑎𝑎 , 𝑝𝑝𝑝𝑝 = − log 𝑎𝑎 PMF: 𝐻𝐻 ∆𝑝𝑝 = � 𝐻𝐻 ∆𝜇𝜇 𝐹𝐹 = −2,3 ′ 𝑅𝑅𝑅𝑅 𝐹𝐹 ∆𝑝𝑝𝑝𝑝 + ∆𝜑𝜑 = −59𝑚𝑚𝑚𝑚∆𝑝𝑝𝑝𝑝 + ∆𝜑𝜑 Energiebilanz: |3∆𝜇𝜇�𝐻𝐻 | > �∆𝐺𝐺 0 � → |∆𝜇𝜇�𝐻𝐻 | > � ∆𝐺𝐺 0 3 ′ � → |∆𝒑𝒑| = � � 𝐻𝐻 ∆𝜇𝜇 � 𝐹𝐹 >� ∆𝐺𝐺 0 3𝐹𝐹 ′ � ≈ 𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏𝟏 Membranpotential Im GG: Nernst-Gleichung: 𝑉𝑉𝑚𝑚 = 𝜑𝜑𝑖𝑖 − 𝜑𝜑𝑎𝑎 = Im Nicht-GG: Nernst-Planck: 𝑑𝑑𝑐𝑐 Φ𝑣𝑣 = −𝐷𝐷𝑣𝑣 � 𝑑𝑑𝑑𝑑𝑣𝑣 + 𝑧𝑧𝑣𝑣 𝑐𝑐𝑣𝑣 Reduziertes Membranpotential u: 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝐹𝐹 𝑑𝑑𝑑𝑑 𝑅𝑅𝑅𝑅 𝑑𝑑𝑑𝑑 𝜑𝜑 𝑎𝑎 −𝜑𝜑 𝑖𝑖 𝑑𝑑 � =− 𝑅𝑅𝑅𝑅 𝑐𝑐 𝑎𝑎 ln 𝐾𝐾𝑖𝑖 𝐹𝐹 𝑐𝑐𝐾𝐾 𝑉𝑉𝑚𝑚 𝑑𝑑 =− = 59,2𝑚𝑚𝑚𝑚 log 𝑅𝑅𝑅𝑅 𝐹𝐹 𝑢𝑢 𝑑𝑑 ∙ , 𝑢𝑢 = 𝐹𝐹𝑉𝑉𝑚𝑚 𝑅𝑅𝑅𝑅 𝑐𝑐𝐾𝐾𝑎𝑎 𝑐𝑐𝐾𝐾𝑖𝑖 = 𝐸𝐸𝐾𝐾 = 1 25𝑚𝑚𝑚𝑚 ∙ 𝑉𝑉𝑚𝑚 Ionenflussdichte für Ion v: Φ𝑣𝑣 = 𝑃𝑃𝑣𝑣 𝑧𝑧𝑣𝑣 𝑢𝑢 ∙ 𝑐𝑐𝑣𝑣𝑖𝑖 𝑒𝑒 𝑧𝑧 𝑣𝑣 𝑢𝑢 −𝑐𝑐𝑣𝑣𝑎𝑎 𝑒𝑒 𝑧𝑧 𝑣𝑣 𝑢𝑢 −1 (vergleiche Flussdichte für ungeladene substanz: Φ𝑣𝑣 = 𝑃𝑃𝑣𝑣 ∆𝑐𝑐 – viel einfacher xD) Stromdichte: 𝑗𝑗 = 𝐼𝐼 𝐴𝐴𝑚𝑚 = 𝐹𝐹 ∑𝑣𝑣 𝑧𝑧𝑣𝑣 Φ𝑣𝑣 , im stationären Zustand ist j=0 Goldmanngleichung, wenn Membran für mehrere Ionen permeabel: Elektrisch erregbare Membranen 𝑽𝑽𝒎𝒎 = 𝑹𝑹𝑹𝑹 ∑ 𝑷𝑷𝑲𝑲 𝒄𝒄𝒂𝒂𝑲𝑲 + ∑ 𝑷𝑷𝑨𝑨 𝒄𝒄𝒊𝒊𝑨𝑨 𝐥𝐥𝐥𝐥 𝑭𝑭 ∑ 𝑷𝑷𝑲𝑲 𝒄𝒄𝒊𝒊𝑲𝑲 + ∑ 𝑷𝑷𝑨𝑨 𝒄𝒄𝒂𝒂𝑨𝑨 Ruhemembranpotential Goldmann: 𝑉𝑉𝑚𝑚 = 𝑅𝑅𝑅𝑅 𝑃𝑃 𝑐𝑐 𝑎𝑎 +𝑃𝑃 𝑐𝑐 𝑎𝑎 ln 𝐾𝐾 𝐾𝐾𝑖𝑖 𝑁𝑁𝑁𝑁 𝑁𝑁𝑁𝑁 𝑖𝑖 𝐹𝐹 𝑃𝑃𝐾𝐾 𝑐𝑐𝐾𝐾 +𝑃𝑃𝑁𝑁𝑁𝑁 𝑐𝑐𝑁𝑁𝑁𝑁 Aus dem Ersatzschaltbild (Knotenregel): 𝑉𝑉𝑚𝑚 = ∑𝑖𝑖 𝐸𝐸𝑖𝑖 ∙𝑔𝑔 𝑖𝑖 ∑𝑖𝑖 𝑔𝑔 𝑖𝑖 𝑟𝑟𝑅𝑅 𝑉𝑉 = 𝑉𝑉0 𝑒𝑒 −𝑥𝑥/𝜆𝜆 , 𝜆𝜆 = � 2𝑅𝑅𝑚𝑚 Kabelgleichung, Spannungsabfall längs des Kabels: Für Spannungsänderung benötigte Ionenanzahl: 𝛥𝛥𝛥𝛥 = Übergang zwischen offenen und geschlossenen Zustand: 𝛥𝛥𝛥𝛥 𝑧𝑧𝑧𝑧 = 𝐶𝐶𝑚𝑚 𝛥𝛥𝑉𝑉𝑚𝑚 𝑧𝑧𝑧𝑧 𝑖𝑖 = 10−12 𝑚𝑚𝑚𝑚𝑚𝑚 𝑐𝑐𝑚𝑚−2 𝑧𝑧𝑧𝑧∙𝑉𝑉𝑚𝑚 𝑧𝑧𝑧𝑧∙𝑉𝑉𝑚𝑚 ∆𝐺𝐺 0 ∆𝐺𝐺� 0 𝑁𝑁𝑜𝑜 � ∙ 𝑒𝑒 𝑅𝑅𝑅𝑅 = 𝐾𝐾 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 = 𝑒𝑒 − 𝑅𝑅𝑅𝑅 ∙ 𝑒𝑒 𝑅𝑅𝑅𝑅 = 𝐾𝐾 𝑁𝑁𝑔𝑔 MPI Paktikum ∆𝐺𝐺 0 = ∆𝐺𝐺�0 + ∆𝐺𝐺𝑒𝑒𝑒𝑒0 = ∆𝐺𝐺�0 − 𝑧𝑧𝑧𝑧 ∙ 𝑉𝑉𝑚𝑚 BLM Messung der Kapazität und Leitfähigkeit: Membrandicke: Strom durch eine BLM: Abklingkonstante des Stromsignals: Patch clamp: Einzelkanalleitfähigkeit 𝐶𝐶 = 𝑄𝑄 𝑈𝑈 = ∆𝐼𝐼∙∆𝑡𝑡 , 𝑈𝑈 𝐴𝐴 𝑑𝑑 𝐼𝐼 𝑈𝑈 𝐶𝐶 = 𝜀𝜀𝜀𝜀0 ⟺ 𝑑𝑑 = 𝜀𝜀𝜀𝜀0 𝐼𝐼 = 𝐼𝐼𝑅𝑅 + 𝐼𝐼𝐶𝐶 = 𝑈𝑈 𝑅𝑅 + 𝐶𝐶 𝜏𝜏2 = 𝑅𝑅𝐺𝐺𝐺𝐺𝐺𝐺 ∙ 𝐶𝐶𝐺𝐺𝐺𝐺𝐺𝐺 = 𝐺𝐺 𝚲𝚲 = 𝒊𝒊/𝑽𝑽 𝐶𝐶 𝐴𝐴 𝐺𝐺 = , 𝐶𝐶𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = , 𝐺𝐺𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = 𝐴𝐴 𝐶𝐶 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 𝐶𝐶𝑚𝑚 +𝐶𝐶𝑝𝑝 𝑚𝑚 +𝐺𝐺𝑝𝑝 +𝐼𝐼𝑝𝑝 ⁄𝑈𝑈 𝐺𝐺 𝐴𝐴



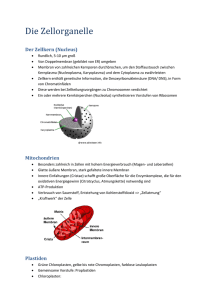

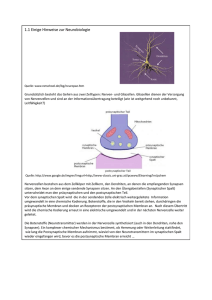



![Pressetext TROPF-BLUMAT 2 [download]](http://s1.studylibde.com/store/data/005763115_1-b3ad9922193c421f1daaa89af4d90417-300x300.png)

