Beispiele

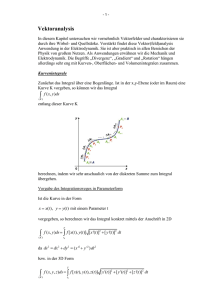
Vorlesungsfolien
Mathematik 3
WS 2010/11
Dr. Leonhard Wieser
UMIT
Einleitung
Begriff Vektoranalysis:
Kombination aus Linearer Algebra/Vektorrechnung
mit Differential- und Integralrechnung
Inhaltsangabe:
- Einführung (Wiederholung, Grundbegriffe)
- Differentialrechnung (Partielle Ableitung, Differentialoperatoren)
- Integralrechnung (Mehrdimensionale Integrale)
Raumkurven
Definition:
Beispiele: Bewegung eines Planeten im Schwerefeld
Beispiele: Gleichförmige Bewegung, Wurfparabel
Tangente, Tangentenvektor
Definition:
Beispiele:
- r(t) = (t², t³, 0)
- Wurfparabel
(s. Bild)
Bogenlänge von Kurven
Herleitung:
Summe über Längen der
Abschnitte, Grenzwertbildung
S=
Bogenlänge unabhängig von
Parametrisierung
Beispiele:
- Kreisbogen
- Spirale r(t) = (cos t, sin t, t)
Skalare Funktion, Vektorfelder
Skalare Funktion:
Beispiel (2D): f(x,y) = x e(-x²-y²)
0.5
0
-0.5
2
1
0
-1
-2
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Skalare Funktion, Vektorfelder
Vektorfeld:
Gravitationsfeld
Geschwindigkeitsfeld
rotierende Scheibe
Partielle Differentiale, Kettenregel
Partielle Ableitung:
Jacobi-Matrix: Darstellung aller partiellen Ableitungen als Matrix
Kettenregel:
Gradient
Definition:
Gegeben eine skalare Funktion f
Bemerkung: Der Gradient ist ein Vektorfeld.
Beispiele:
Gradienten bilden von:
1
-
0.8
0.6
0.4
-
f(x,y) = 1 –
x2
–
y4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
1
1
0
0.5
0
-0.5
-1
-1
Richtungsableitung
Idee:
Änderungsrate einer skalaren Funktion in einer
vorgegebenen Richtung
Definition:
Zusammenhang:
Beispiel:
Gradient von f(x,y) = 1 – x2 – y4 im Punkt (1, 0) mit
mit verschiedenen Richtungen
Gradient als Flächennormale
Fläche mit f als definierender Funktion Æ grad f steht normal auf Fläche
Beispiel:
- Sphäre: f(x,y,z) = x2 + y2 + z2 – R2
Potential
Definition:
Potential ist die skalare Funktion f zu einem Vektorfeld v
so, dass grad f = v ist.
Das Vektorfeld v heißt dann konservativ.
Beispiele:
- Konstantes Vektorfeld
- Coulombsches Kraftfeld
- Elektrisches Feld – Elektrisches Potential
- v(x,y,z) = (3x², 2yz, y²)
Beispiel Bildverarbeitung
Bild aus Magnetresonanztomographie als Grauwertbild (links)
und der Gradient davon ebenfalls als Grauwertbild (rechts)
Æ Kanten werden betont
Divergenz
Definition:
Gegeben ein Vektorfeld v
Beispiele:
- Divergenz von v(x,y,z) = (x-y, xy, z²)
- Divergenz des Elektrischen Feldes (Coulomb-Gesetz)
Kontinuitätsgleichung
Gegeben: Vektorfeld v (Geschwindigkeitsfeld), gewichtet mit Dichte u=ρv
Betrachte kleines Flächenstück
und betrachte Flüsse durch die
Kanten
Æ
=
Grenzübergang: Δt, Δx, Δy Æ 0
Divergenz, geometrische Deutung
Kontinuitätsgleichung:
Nettoflüsse durch infinitesimal kleine Flächenelemente (in 3D: Volumselemente)
y
Beispiele:
Gradientenfeld von f(x,y) = x e(-x²-y²) :
(1-2x2,
-2xy)
v = grad f = e(-x²-y²)
div v in den Punkten (1,0), (-1,0), (0,-1)?
Geschwindigkeitsfeld einer rotierenden Kreisscheibe:
v = ω (-y, x, 0)
div v = ?
x
Rotation
Definition:
Gegeben ein Vektorfeld v, die Rotation ist definiert
als das Vektorfeld
Definiert in 3D, in 2D entartet die Rotation zu einer skalaren Funktion.
Geometrische Deutung:
„Kleine Kreisscheiben“, die im
gegebenen Vektorfeld rotieren
Rotation
Beispiele: Rotation von
- v = ω (-y, x, 0)
Eigenschaften:
- div (rot v) = 0
- rot (grad f) = 0
Satz: Gegeben ein stetig partiell differenzierbares Vektorfeld v auf einem
einfach zusammenhängenden Gebiet.
Es gibt ein Potential f mit grad f = v genau dann, wenn rot v = 0.
Beispiele:
- v = (3x2, 2yz, y2)
- v = (yex, ex, 2z)
- Elektrisches Potential
Doppelintegral (Flächenintegral)
Integral einer Funktion
über eine Fläche --> Volumen
unter dem Funktionsgraphen
Unterteilung in Rechtecke
und Summation der Einzelvolumina
Æ Doppelintegral über
zwei Einzelintegrale
Doppelintegral ‐ Beispiele
Volumen unter einer Fläche:
R aufgespannt durch die Funktionen
y = x und y = x²
Funktion: f(x,y) = 1-xy
Schwerpunkt eines Halbkreises:
Volumsintegral
Integral einer Funktion f(x,y,z) über ein Gebiet im
Æ 3 aufeinanderfolgende Integrationen
Beispiel: Dichtefunktion f(x,y,z) = x²y²z²
z
Masse des Würfels 0 < x, y, z < 1 ?
x
y
Linienintegral
Motivation:
Verschiebungsarbeit an einem
Körper in einem Kraftfeld
Definition:
Beispiel:
- Wurfparabel im Schwerefeld
Linienintegral, konservative Vektorfelder
Gegeben:
Vektorfeld F und zugehöriges Potential f
Æ Linienintegral vom Weg unabhängig
Æ Linienintegral verschwindet über
geschlossene Kurven
Beispiel: f = x3+y2z, F = grad f = ?
C1: r(t) = (t, t2, 0)
C2: r(t) = (t, 0, 0)
C3: r(t) = (1, t, 0)
Integration von F über C1 und Integration über C2, C3
Parametrisierung Flächen
Parametrisierung der Oberfläche
Beschreibung der Tangentenebene
Beispiel: Sphäre mit Radius R
Oberflächenintegral, skalare Funktion
Betrachte kleines Flächenelement in der parametrisierten Fläche
Oberflächenintegral:
Beispiel: Oberfläche einer Sphäre mit Radius R
Oberflächenintegral, Vektorfelder
Fluss durch ein kleines Flächenelement
Flussintegral:
Orientierung von Flächen beachten
Möbius-Band: Beispiel für nicht orientierbare Fläche
Beispiele: Fluss durch die Sphäre mit Radius R
- F(x,y,z) = (x,y,z) = r
- F(x,y,z) =
= r/|r|³
Satz von Gauß
Anwendungsbeispiele
Elektrisches Feld (Coulomb-Gesetz)
-
Elektrischer Kraftfluss durch eine beliebige geschlossene Oberfläche hängt nur
von der Ladung im Inneren ab, nicht von der Beschaffenheit der Oberfläche
-
Anwendung des Satzes von Gauß liefert die Beziehung mit der Ladungsdichte ρ
(„Ladungen sind die Quellen des elektrischen Feldes“)
Wärmeleitungsgleichung
-
Gleichung zwischen Wärmefluss durch geschlossene Oberfläche und
Energieabnahme bzw. –zunahme im Inneren.
Anwendung des Satzes von Gauß liefert die Wärmeleitungsgleichung
T … Temperatur
Materialabhängige Größen: λ … Wärmeleitfähigkeit, κ … Spez. Wärmekapazität, ρ … Dichte