GeoGebra für Anfänger

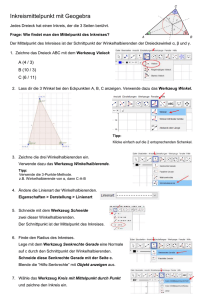
www.geogebra.at
Herzlich Willkommen
beim
Seminar
GeoGebra für Anfänger
Ihr Name
Viel Erfolg!
www.geogebra.at
Umkreis eines Dreiecks
Aufgabenstellung
Zeichnen Sie mit GeoGebra ein Dreieck mit den Eckpunkten
A (-5|-1), B (4|-2), C (2|3) und konstruieren Sie dessen Umkreis.
Konstruktionsanleitung
Mit der Werkzeugleiste
1
Konstruieren Sie mit dem Werkzeug Vieleck das Dreieck ABC.
2
Erzeugen Sie mit dem Werkzeug Streckensymmetrale die drei Seitensymmetralen
des Dreiecks. Benützen Sie die Gestaltungsleiste, um die Darstellung auf strichliert
zu ändern.
Hinweis: Blenden Sie die Gestaltungsleiste mit dem kleinen schwarzen Dreieck
rechts oben ein.
3
Beschriften Sie die Seitensymmetralen als sa, sb und sc.
Klicken Sie mit der rechten Maustaste auf das entsprechende
Objekt → Umbenennen.
Hinweis: Um etwas im Index zu schreiben, stellen Sie einen Unterstrich voran, etwa
s_a.
4
Erzeugen Sie mit dem Werkzeug Schneide zwei Objekte den Umkreismittelpunkt U
des Dreiecks.
5
Konstruieren Sie mit Hilfe des Werkzeugs Kreis mit Mittelpunkt durch Punkt den
Umkreis k des Dreiecks.
Mit der Eingabezeile
1
A = (-5, -1)
2
B = (4, -2)
3
C = (2, 3)
4
Vieleck[A, B, C]
5
s_a = Streckensymmetrale[a]
6
s_b = Streckensymmetrale[b]
7
U = Schneide[s_a, s_b]
8
k = Kreis[U, A]
Freitag, 1. Juni 2012
www.geogebra.at
Lineare Funktionen
Aufgabenstellung
Zeichnen Sie mit GeoGebra eine lineare Funktion y = k * x + d. k und d sollen dabei mittels
Schieberegler veränderbar sein.
Konstruktionsanleitung
1
Erzeugen Sie einen Schieberegler für k mit dem Werkzeug Schieberegler:
Minimum -5, Maximum 5, Schrittweite 0.5.
2
Fügen Sie einen Schieberegler für d hinzu: Minimum -5, Maximum 5, Schrittweite 0.5.
3
Zeichnen Sie g mittels der Eingabezeile: g: y = k * x + d.
4
Zeichnen Sie h mittels der Eingabezeile: h: y = k * x.
5
Konstruieren Sie die Strecke auf der y - Achse zwischen den beiden Geraden mit
dem Werkzeug Strecke zwischen zwei Punkten.
6
Fügen Sie mit dem Werkzeug Steigung das Steigungsdreieck von g hinzu.
7
Ergänzen Sie die Konstruktion mit dem Werkzeug Text mit Text.
Hinweis: Der Wert von Objekten, wie etwa einem Schieberegler, kann beim
Bearbeiten des Textes mit Objekte eingefügt werden.
8
Blenden Sie die Punkte A und B aus: Rechtsklick auf den Punkt → Objekt anzeigen
abwählen.
9
Formatieren Sie die Konstruktion, sowie die Achsen und das Koordinatengitter.
Hinweis: Einstellungen → Einstellungen → Graphik.
Freitag, 1. Juni 2012
www.geogebra.at
Satz von Thales
Aufgabenstellung
Visualisieren Sie mit Hilfe von GeoGebra die
Aussage des bekannten Satzes von Thales und
finden Sie einen graphischen Beweis.
Konstruktionsanleitung - Visualisierung
1
Konstruieren Sie die Strecke AB mit dem Werkzeug Strecke zwischen zwei
Punkten.
2
Fügen Sie den Halbkreis mit dem Werkzeug Halbkreis durch zwei Punkte hinzu.
3
Setzen Sie mit dem Werkzeug Neuer Punkt einen Punkt auf den Halbkreis.
4
Zeichnen Sie das Dreieck ABC mit dem Werkzeug Vieleck.
5
Zeichnen Sie die drei Winkel mit dem Werkzeug Winkel ein.
Hinweis: Um immer den Innenwinkel zu erhalten, markieren Sie die Punkte gegen
den Uhrzeigersinn.
6
Formatieren Sie die Konstruktion ansprechend.
Aufgabenstellung
Finden Sie mit Hilfe von GeoGebra einen
graphischen Beweis.
Konstruktionsanleitung – Beweis
1
Konstruieren Sie die Visualisierung wie oben beschrieben.
2
Finden Sie den Halbierungspunkt der Strecke AB mit dem Werkzeug Mittelpunkt.
3
Benennen Sie D in M um: Rechtsklick auf D → Umbenennen.
4
Verbinden Sie M nun mit dem Punkt C.
5
Löschen Sie den Winkel bei C mit dem Werkzeug Lösche Objekt.
6
Zeichnen Sie die Winkel ACM und MCB ein.
7
Formatieren Sie die Konstruktion und argumentieren Sie, warum damit der Satz
gelten muss!
Freitag, 1. Juni 2012
www.geogebra.at
Seiten - Seiten - Seiten - Satz
Aufgabenstellung
Konstruieren Sie ein Dreieck mit a = 2, b = 4 und c = 3.
Konstruktionsanleitung
1
Erzeugen Sie mit dem Werkzeug Neuer Punkt A (1|1).
2
Konstruieren Sie mit dem Werkzeug Kreis mit Mittelpunkt und Radius einen Kreis
mit dem Mittelpunkt A und Radius 3.
3
Erzeugen Sie mit dem Werkzeug Neuer Punkt den Punkt B auf dem eben
konstruierten Kreis.
4
Konstruieren Sie mit dem Werkzeug Kreis mit Mittelpunkt und Radius einen Kreis
mit dem Mittelpunkt A und dem Radius 4 und einen weiteren mit dem Mittelpunkt B
und dem Radius 2.
5
Schneiden Sie mit dem Werkzeug Schneide zwei Objekte die zuletzt erzeugten
Kreise.
Hinweis: Klicken Sie direkt auf den gewünschten Schnittpunkt, um nicht alle, sondern
nur diesen zu erhalten.
6
Konstruieren Sie mit dem Werkzeug Vieleck das Dreieck ABC.
7
Blenden Sie die Beschriftung der Seiten des Dreieckes ein und benennen Sie sie
gegebenenfalls um.
Hinweis: Rechtsklick auf die Strecke → Beschriftung anzeigen,
beziehungsweise Rechtsklick auf die Strecke → Umbenennen.
8
Blenden Sie mit dem Werkzeug Objekte anzeigen / ausblenden die Kreise aus.
Klicken Sie dazu nacheinander auf alle auszublendenden Objekte. Diese werden nun
dicker dargestellt. Wechseln Sie anschließend zu einem beliebigen anderen
Werkzeug.
Freitag, 1. Juni 2012
www.geogebra.at
Spiegeln
Aufgabenstellung
Spiegeln Sie mit GeoGebra ein Bild an einer Geraden.
Konstruktionsanleitung
1
Erzeugen Sie mit dem Werkzeug Neuer Punkt die Punkte A (2|1) und B (5|1).
2
Fügen Sie mit dem Werkzeug Bild einfügen das Bild ein.
3
Legen Sie die Postion des Bildes fest:
Rechtsklick auf das Bild → Eigenschaften → Postion,
bei Eckpunkt 1 A und bei Eckpunkt 2 B auswählen.
4
Erzeugen Sie mit dem Werkzeug Neuer Punkt die Punkte C (1|1) und D (2|4).
5
Konstruieren Sie mit dem Werkzeug Gerade durch zwei Punkte die Gerade durch
die Punkte C und D.
6
Spiegeln Sie mit dem Werkzeug Spiegle Objekt an Gerade das Bild an der
Geraden.
Freitag, 1. Juni 2012
www.geogebra.at
Größe eines Sees
Aufgabenstellung
Ermitteln Sie den Flächeninhalt eines Sees
anhand eines Bildes mit gegebenen Maßstab
näherungsweise.
Konstruktionsanleitung
1
Ändern Sie die Einstellungen des Zeichenblattes unter
Einstellungen → Einstellungen → Graphik:
Grundeinstellungen:
Minimum der x-Achse: -100 Maximum der x-Achse: 800
x-Achse : y-Achse = 1 : 1
x-Achse:
y-Achse:
Abstand: 100
y-Achse anzeigen abwählen
2
Erstellen Sie mit dem Werkzeug Neuer Punkt zwei Punkte A und B auf der x - Achse.
3
Fügen Sie das Bild des Sees mit dem Werkzeug Bild einfügen ein.
4
Legen Sie die Postion des Bildes fest:
Eigenschaften → Postion → Eckpunkt 1: A, Eckpunkt 2: B.
5
Verschieben Sie A und B mit dem Werkzeug Bewege so, dass der Maßstab des
Bildes mit der Skalierung der x - Achse übereinstimmt.
6
Setzen Sie die Deckkraft des Bildes etwas herab und bringen Sie es in den
Hintergrund:
Eigenschaften → Farbe → Deckkraft: etwas herabsetzen,
Eigenschaften → Grundeinstellungen → Hintergrundbild anwählen.
7
Bauen Sie mit dem Werkzeug Vieleck die Kontur des Sees nach.
8
Benützen Sie die Gestaltungsleiste, um den Wert (=Flächeninhalt) des Vieleckes
anzuzeigen.
Hinweis: Blenden Sie die Gestaltungsleiste mit dem kleinen schwarzen Dreieck
rechts oben ein. Wählen Sie bei angewähltem Vieleck als Art der Bezeichnung
„Wert“.
Freitag, 1. Juni 2012
www.geogebra.at
Statistik
Aufgabenstellung
Erstellen Sie einen Boxplot und versuchen Sie anschließend, folgende statistische Kennzahlen zu
interpretieren: Arithmetisches Mittel, Median, Quartile, Standardabweichung.
Konstruktionsanleitung
1
Wählen Sie die Perspektive Tabelle und Graphik.
Hinweis: Perspektiven → Tabelle und Graphik.
2
Geben Sie in die Zellen der Spalte A Werte ein, etwa 5, 7, 4, 1, 2, 4, 3, 5, 9, 10, 6, 8,
8, 5 in A1 bis A14.
3
Wählen Sie die Zellen mit den Daten aus und analysieren Sie sie mit dem Werkzeug
Analyse einer Variablen.
4
Wechseln Sie die Art des Diagramms von Histogramm auf Boxplot.
5
Betrachten Sie die statistischen Daten auf der linken Seite und finden Sie die
gesuchten Größen unter ihnen. Wie stehen sie im Zusammenhang mit dem Boxplot?
6
Kopieren Sie den Boxplot in die Zeichenfläche:
Rechtsklick → In die Zeichenfläche kopieren.
Freitag, 1. Juni 2012
www.geogebra.at
Tangenten einer Funktion
Aufgabenstellung
Zeichnen Sie mit GeoGebra die Funktion f(x) = sin(x). Legen Sie in den Punkten A (-π|0) und
B (π/2|1) jeweils eine Tangente an die Funktion f(x) und konstruiere den Schnittpunkt S.
Konstruktionsanleitung
1
Zeichnen Sie die Funktion f(x) = sin(x) mittels der Eingabezeile.
2
Ändern Sie die Einstellungen des Zeichenblattes unter
Einstellungen → Einstellungen → Graphik:
Minimum der x-Achse: -3 π Maximum der x-Achse: 3 π Abstand: π/2
Minimum der y-Achse: -1.2 Maximum der y-Achse: 1.2
Abstand: 0.1
Hinweis: Schreiben Sie π als „Pi“!
3
Fügen Sie mit dem Werkzeug Neuer Punkt zwei Punkte A und B auf f hinzu.
4
Bewegen Sie die Punkte A und B mit dem Werkzeug Bewege an die Stellen (-π|0),
beziehungsweise (π/2|1).
5
Legen Sie mit dem Werkzeug Tangenten in den Punkten A und B jeweils eine
Tangente an die Funktion f.
6
Schneiden Sie die beiden Tangenten mit dem Werkzeug Schneide zwei Objekte und
benennen Sie den Punkt in S um: Rechtsklick → Umbenennen.
7
Fügen Sie mit dem Werkzeug Text einfügen die Angabe der Koordinaten von S
hinzu.
Hinweis: Der Wert von Objekten, etwa eines Punktes, kann beim Bearbeiten des
Textes mit Objekte eingefügt werden.
Freitag, 1. Juni 2012
www.geogebra.at
Potenzfunktion
Aufgabenstellung
Zeichnen Sie mit GeoGebra die
Potenzfunktion n - ten Grades und
erstellen Sie eine Wertetabelle.
Konstruktionsanleitung
1
Wählen Sie die Perspektive Tabelle und Graphik.
Hinweis: Perspektiven → Tabelle und Graphik.
2
Blenden Sie die Eingabezeile mit Ansicht → Eingabezeile → Anzeigen ein.
3
Ändern Sie die Einstellungen des Zeichenblattes unter
Einstellungen → Einstellungen → Graphik:
Grundeinstellungen:
Minimum der x-Achse: -5.5 Maximum der x-Achse: 5.5
x-Achse : y-Achse = 1 : 1
4
Erzeugen Sie einen Schieberegler für n mit dem Werkzeug Schieberegler:
Minimum -5, Maximum 5, Schrittweite 1.
5
Zeichnen Sie die Potenzfunktion mittels der Eingabezeile: f(x) = x^n.
6
Fügen Sie mit dem Werkzeug Text einfügen die Funktionsgleichung von f hinzu.
Hinweis: Der Wert von Objekten, etwa eines Schiebereglers, kann beim Bearbeiten
des Textes mit Objekte eingefügt werden.
7
Geben Sie „-4“ in die Zelle A1 und „-3“ in die Zelle A2 ein, markieren Sie beide und
ziehen Sie sie bis A9 nach unten.
8
Geben Sie „f(A1)“ in die Zelle B1 ein und ziehen Sie sie bis B9.
9
Markieren Sie die Zellen A1 bis B9 und erstellen Sie mit dem Werkzeug
Tabelle erzeugen die Wertetabelle.
10
Formatieren Sie die Konstruktion ansprechend.
Freitag, 1. Juni 2012
www.geogebra.at
Zins- und Zinseszinsrechnung
Aufgabenstellung
Stellen Sie mit GeoGebra den Verlauf der Kapitalentwicklung bei einfacher Verzinsung und
jährlicher Mitverzinsung graphisch gegenüber.
Konstruktionsanleitung
1
Wählen Sie die Perspektive Tabelle und Graphik.
Hinweis: Perspektiven → Tabelle und Graphik.
2
Geben Sie „Kapital“ und „Zinssatz in %“ in die Zellen A1, beziehungsweise A2, ein.
3
Geben Sie das Anfangskapital und den Zinssatz (nach KeSt) in die Zellen B1 und B2
ein.
4
Geben Sie „Jahr“, „Einfache Verzinsung“ und „Zinseszinsrechnung“ in die Zellen A4
bis C4 ein.
5
Geben Sie „0“ in die Zelle A5 und „1“ in die Zelle A6 ein, markieren Sie beide und
ziehen Sie sie bis A14 nach unten.
6
Geben Sie „=$B$1 + A5 * $B$1 * $B$2 / 100“ in die Zelle B5 ein und ziehen Sie sie
bis B14.
7
Geben Sie „=B1“ in die Zelle C5 ein.
8
Geben Sie „=C5 * (1 + $B$2 / 100)“ in die Zelle C6 ein und ziehen Sie sie bis B15.
9
Markieren Sie A5 bis B14 und erstellen Sie mit dem Werkzeug Liste von Punkten
erzeugen eine Liste von Punkten.
10
Markieren Sie A5 bis A14 und C5 bis C14 und erstellen Sie mit dem Werkzeug Liste
von Punkten erzeugen eine Liste von Punkten.
Hinweis: Markieren Sie zuerst A5 bis A14 und dann bei gedrückter STRG – Taste
C5 bis C14.
11
Formatieren Sie die Tabelle und die Graphik ansprechend!
Freitag, 1. Juni 2012
www.geogebra.at
Ableitung einer Funktion
Aufgabenstellung
Zeichnen Sie mit GeoGebra die Funktion f(x) = ½ * x2, sowie die Tangente samt Steigungsdreieck
in einem Punkt A. Veranschaulichen Sie außerdem das Verhalten der Steigung von A in
Abhängigkeit von x.
Konstruktionsanleitung
1
Zeichnen Sie f(x) = 1/2 x^2 mittels der Eingabezeile.
2
Fügen Sie mit dem Werkzeug Neuer Punkt einen Punkt auf f hinzu.
3
Konstruieren Sie mit dem Werkzeug Tangenten die Tangente an f in A.
4
Zeichnen Sie mit dem Werkzeug Steigung das Steigungsdreieck der Tangente ein.
5
Konstruieren Sie nun den Punkt B mit Hilfe der Eingabezeile als B = (x(A), k).
Hinweis: x(A) gibt die x - Koordinate von A an.
6
Schalten Sie die Spur von B ein: Rechtsklick → Spur ein anwählen.
7
Formatieren Sie die Konstruktion ansprechend.
8
Ziehen Sie den Punkt A und interpretieren Sie die von B gezeichnete Spur!
Freitag, 1. Juni 2012
www.geogebra.at
Kurvendiskussion
Aufgabenstellung
Zeichnen Sie eine beliebige Polynomfunktion 3. Grades. Ermitteln Sie Nullstellen, Extrempunkte
und Wendepunkte der Funktion. Versuchen Sie die Vorgehensweise für die Berechnung von N, E
und W anschaulich darzustellen.
Konstruktionsanleitung
1
Geben Sie eine beliebige Polynomfunktion dritten Grades mit Hilfe der Eingabezeile
ein, etwa f(x) = 3 x^3 - 10 x^2 – x + 8.
2
Schneiden Sie mit dem Werkzeug Schneide zwei Objekte f mit der x - Achse,
um die Nullstellen von f zu erhalten.
3
Benennen Sie die Nullstellen, sofern vorhanden, als N1, N2 und N3.
Hinweis: Um etwas im Index zu schreiben, stellen Sie einen Unterstrich voran,
etwa N_1.
4
Leiten Sie f mit Hilfe der Eingabezeile ab: Ableitung[f].
5
Leiten Sie f' mit Hilfe der Eingabezeile ab: Ableitung[f'].
6
Konstruieren Sie nun die Nullstellen von f' wie oben.
7
Zeichnen Sie mit dem Werkzeug Senkrechte Gerade Normale auf die x - Achse
durch die Nullstellen von f' ein.
8
Schneiden Sie mit dem Werkzeug Schneide zwei Objekte die Normalen mit f.
9
Überlegen Sie, ob die Schnittpunkte Extremstellen sind, und benennen Sie sie
entsprechend.
10
Konstruieren Sie die Wendepunkte von f analog zu den Extremstellen über die
Nullstellen von f''.
11
Formatieren Sie die Konstruktion ansprechend!
Freitag, 1. Juni 2012