Integralrechnung I. Integrieren Händisches Integrieren ist für Potenz
Werbung
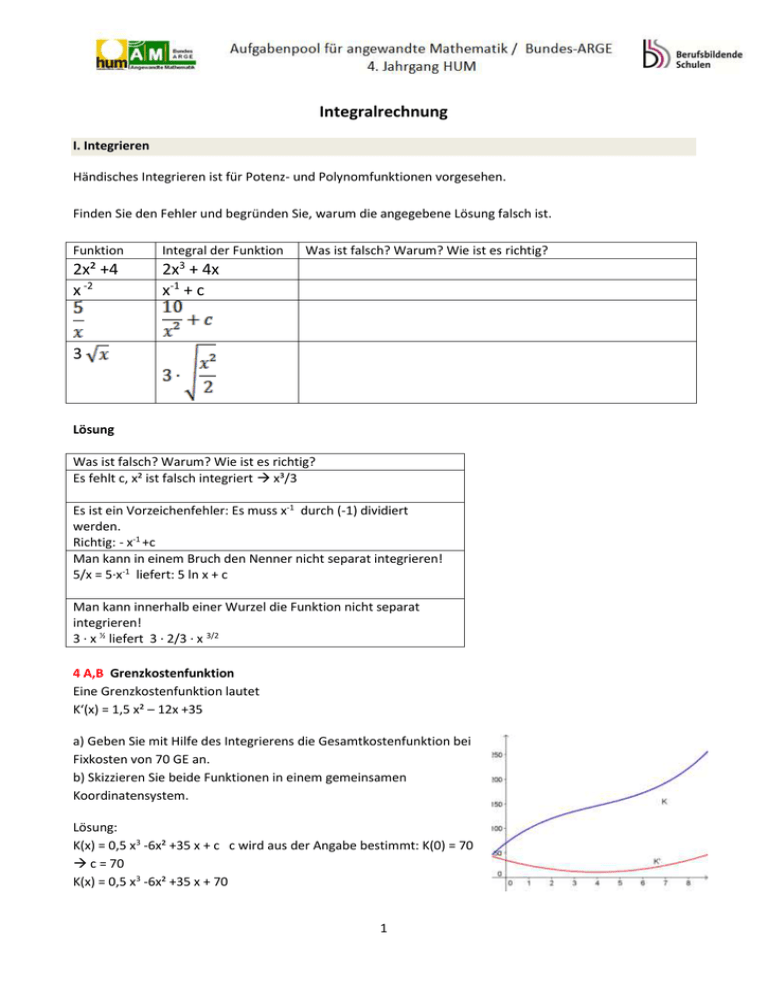
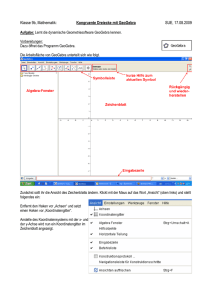
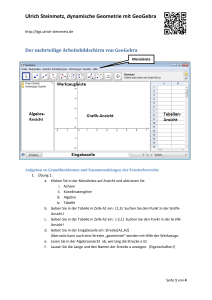
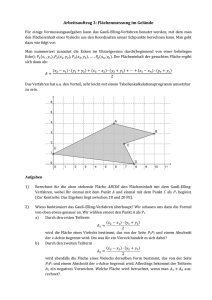
Integralrechnung I. Integrieren Händisches Integrieren ist für Potenz- und Polynomfunktionen vorgesehen. Finden Sie den Fehler und begründen Sie, warum die angegebene Lösung falsch ist. Funktion 2x² +4 x -2 Integral der Funktion Was ist falsch? Warum? Wie ist es richtig? 3 2x + 4x x-1 + c 3 Lösung Was ist falsch? Warum? Wie ist es richtig? Es fehlt c, x² ist falsch integriert x³/3 Es ist ein Vorzeichenfehler: Es muss x-1 durch (-1) dividiert werden. Richtig: - x-1 +c Man kann in einem Bruch den Nenner nicht separat integrieren! 5/x = 5∙x-1 liefert: 5 ln x + c Man kann innerhalb einer Wurzel die Funktion nicht separat integrieren! 3 ∙ x ½ liefert 3 ∙ 2/3 ∙ x 3/2 4 A,B Grenzkostenfunktion Eine Grenzkostenfunktion lautet K‘(x) = 1,5 x² – 12x +35 a) Geben Sie mit Hilfe des Integrierens die Gesamtkostenfunktion bei Fixkosten von 70 GE an. b) Skizzieren Sie beide Funktionen in einem gemeinsamen Koordinatensystem. Lösung: K(x) = 0,5 x3 -6x² +35 x + c c wird aus der Angabe bestimmt: K(0) = 70 c = 70 K(x) = 0,5 x3 -6x² +35 x + 70 1 II. Flächenberechnung und prismenartiges Volumen Die Abbildung zeigt eine Fläche, die von den Funktionsgraphen von f, g, h und der x-Achse begrenzt ist. Aus einem dünnen Brett 2 dm x 5 dm muss die abgebildete Form geschnitten werden. f(x) = 0,05(x - 5,6)² + 0,4 g(x) ist die Tangente an f(x) durch den Punkt bei x = 0 h: x = 5 Die Maße sind in dm angegeben a) Berechnen Sie die Gleichung der Tangente bei x = 0 an f(x). b) Erklären Sie, wie man die Fläche unterteilen kann, damit sie gut berechnet werden kann. Skizzieren Sie die Teilflächen und schreiben Sie die allgemeinen Berechnungsformeln an. (Es gibt mehrere Möglichkeiten – finden Sie zumindest zwei davon.) c) Berechnen Sie die Größe des Holzverschnitts (=Abfall) in Prozent. Lösung: a) Mit Technologie z.B. Geogebra Befehl: Tangente [ x-Wert, Funktion] g(x) = -0,56x + 1,97 b) A1 = A2 = A = A1 + A2 S ist die x-Koordinate des Schnittpunktes von g und x-Achse. A1 = A2 = (5 - S) T/2 T ist die y-Koordinate des Schnittpunktes von g mit h. A = A1 – A2 c) Die Fläche wird nach einer der Teilungen von Aufgabe b) gerechnet. Für den Verschnitt zieht man diese Fläche vom Rechteck ab. Geogebra Befehl: Integral [Funktion, Startw., Endw.] und IntegralZwischen[funktion1, funktion 2, Startw. Endw.] A1 = A2 = = 0,74 Verschnitt: 10 - 0,74 - 0,72 = 8,54 Das sind 85,4%. 2 4 A,B,D Becken Ein Becken hat den in der Abbildung dargestellten Grundriss und ist mit Wasser bis zum Rand gefüllt. Der Bereich zwischen den Funktionen f und g hat eine Tiefe von 1,20 m. Die Abteilung zwischen g und h ist 2,50 m tief. f(x)= - 0,04x² + 60 g(x) = 0,005x² + 30 h(x) = -20 x … wird in Metern (m) angegeben a) Stellen Sie eine allgemeine Formel auf, wie man die gesamte Wasseroberfläche berechnen kann. b) Berechnen Sie den Wasserbedarf in m³, der zur Füllung des Beckens notwendig ist. Erklären Sie Ihre Vorgangsweise. Lösung: a) A = b) Mit Technologieeinsatz gerechnet zB Geogebra: Zuerst werden die Schnittpunkte A und B berechnet. Befehl: Schneide [f,g] Das Becken hat 3 Teile: A1 … Fläche zwischen f und g mit der Tiefe 1,2 m A2 … Fläche zwischen g und der x-Achse mit der Tiefe 2,5 m A3 … Fläche zwischen x-Achse und h mit der Tiefe von 2,5 m Berechnung der Flächen, Befehl: Integral ( Funktion, Startw, Endwert) Volumen : 1032,8 ∙ 1,2 + (1606,58 + 1032,8) ∙2.5 = 7837,8 m³ 3 3,4 B,D Stahlträger Ein Stahlträger mit dem in der Grafik dargestelltem Profil hat eine Länge von L = 3 m und eine Dichte von ρ = 7,7 kg / dm³. Die Profilberandung wird mit den folgenden Funktionen für den 1. und 2. Quadranten des Koordinatensystems angeben. Die Profilfläche setzt sich im 3. und 4. Quadranten spiegelbildlich fort so dass ein x-förmiger Querschnitt des Trägers entsteht. Kurve oben: f(x) = 2,5 – 0,1x4 + x² Kurve seitlich: g(x) =(x²-1)0,5 x … Länge in dm a) Berechnen Sie mit TE die Schnittpunkte A und B der beiden Kurven auf 2 Nachkommastellen. b) Skizzieren Sie die Teilflächen, mit denen der Trägerquerschnitt berechnet wird. c) Geben Sie eine allgemeine Formel für die Berechnung der Teilflächen und der gesamten Querschnittsfläche an. d) Berechnen Sie das Volumen und die Masse des Trägers mit Technologieeinsatz. Es gilt: Masse = Volumen mal Dichte. Lösung: a) Schnittpunkte: TE –Eingabe z.B. mit Geogebra: Schneide [f(x),g(x),-4,4] A = (-3,09|2,92) B = (3,09|2,92) b) Skizze der Teilflächen A1 und A2: c) A1 = A2 = Die gesamte Fläche: A = 4 ∙ (A1-A2) d) L = 3 m = 30 dm, ρ =7,7 kg / dm³ mit TE V = 996,64 dm³, m = 7674,14 kg V = A ∙ L ∙ ρ = 4 . 30 ∙ 4 Hinweis zur vorherigen Aufgabe: Wenn man die Wurzelfunktion nicht mag, kann man ganz ähnlich mit der Funktion: g(x) = -0,39x² +3,11x -2,72 arbeiten. Kurze Berechnungen in Geogebra: 5