Ulrich Steinmetz, dynamische Geometrie mit GeoGebra

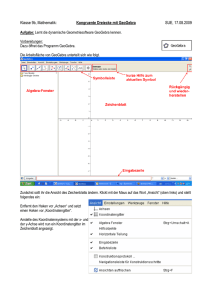
Ulrich Steinmetz, dynamische Geometrie mit GeoGebra
http://dgs.ulrich-steinmetz.de
Der mehrteilige Arbeitsbildschirm von GeoGebra
Menüleiste
Aufgaben zu Grundfunktionen und Zusammenhängen der Fensterbereiche
1. Übung 1:
a. Klicken Sie in der Menüleiste auf Ansicht und aktivieren Sie
i. Achsen
ii. Koordinatengitter
iii. Algebra
iv. Tabelle
b. Geben Sie in der Tabelle in Zelle A1 ein: (1,3) Suchen Sie den Punkt in der GrafikAnsicht!
c. Geben Sie in der Tabelle in Zelle A2 ein: (-2,1) Suchen Sie den Punkt in der GrafikAnsicht!
d. Geben Sie in der Eingabezeile ein: Strecke[A1,A2]
Alternativ kann auch eine Strecke „gezeichnet“ werden mit Hilfe der Werkzeuge.
e. Lesen Sie in der Algebraansicht ab, wie lang die Strecke a ist.
f. Lassen Sie die Länge und den Namen der Strecke a anzeigen. (Eigenschaften!)
Seite 1 von 4
Ulrich Steinmetz, dynamische Geometrie mit GeoGebra
http://dgs.ulrich-steinmetz.de
2. Übung 2:
a. Geben Sie in B1 eine 5 ein.
b. Geben Sie in der Eingabezeile ein: f(x)= B1 x -3 (Leerzeichen beachten!)
c. Ändern Sie in Zelle B1 die 5 zur 2! Beobachten Sie Veränderungen in der GrafikAnsicht.
3. Übung 3:
a. Geben Sie in der Eingabezeile ein: g(x)=B1 x^2 -3 (statt x^2 ginge auch x² oder x*x)
b. Ändern Sie den Wert in B1. (z.B. 0.5 mit Punkt eingeben!)
c. Geben Sie in der Eingabezeile ein: Ableitung[g(x)]
d. Fügen Sie einen neuen beweglichen Punkt der Parabel ein.
e. Lassen Sie eine Tangente durch den Punkt gehen.
f.
Zeigen Sie die Steigung der Tangente an.
4. Übung 4:
a. Öffnen Sie ein neues GeoGebra-Fenster
Strg+N oder Menübefehl Datei + Neues Fenster
b. Legen Sie zwei Schieberegler in die Grafik-Ansicht.
Sie sollen die Werte von – 10 bis +10 darstellen können und die Breite 200 (Pixel)
haben.
Schauen Sie nach, wie die Schieberegler-Variablen heißen.
(Eigenschaft, Algebraansicht)
c. Geben Sie dann eine Funktion 3.Grades + 2.Grades mit Verwendung der beiden
Schieberegler ein. (Beispiel f(x)= a x³ - b x² + 2)
Die Leerzeichen sind relevant, denn sonst denkt das Programm, es handle sich um
Variablen, die ax oder bx heißen!
d. Ändern Sie die Schieberegler und beobachten Sie.
Animieren Sie die Regler! (Eigenschaft Animation ein)
e. Ergänzen Sie die Nullstellen (Befehl Nullstelle[Funktionsname])
f. Ergänzen Sie die Scheitelpunkte (Befehl Extremum[Funktionsname])
g. Stellen Sie die 1. Ableitung der Funktion in roter Farbe dar. (Befehl Ableitung[f(x)])
(Es ginge auch die Eingabe f‘(x) für die erste Ableitung!)
h. Wenn Sie Spaß an Integralen haben: Eingabe Integral[f, -0.5, 2], wobei die beiden
Zahlen Anfangs- und Endwert sind. Sie sind beliebig eingebbar. „f“ ist der Name der
Funktion. Denkbar sind auch Schieberegler-Variablen für die Grenzen.
Seite 2 von 4
Ulrich Steinmetz, dynamische Geometrie mit GeoGebra
http://dgs.ulrich-steinmetz.de
5. Übung 5:
a. Denken Sie sich eine einfache Zuordnung aus, zu der Sie eine Wertetabelle erfassen
wollen. Proportional oder umgekehrt proportional.
b. Geben Sie innerhalb der Tabellenansicht die x-Werte in Spalte A und die y-Werte in
Spalte B ein. Keine Überschriften in die Spalten einfügen!
c. Versuchen Sie danach, die Punkte auch in der Grafikansicht erscheinen zu lassen.
Hierzu der Tipp:
Versuchen Sie in Spalte C die Daten in der Form (x,y) erscheinen zu lassen. Man kann
A1 und B1 weiterverwenden, =(A1,B1) wäre zulässig wie in Excel.
d. Stellen Sie in einer anderen Farbe als schwarz die zu den Daten in der
Zuordnungstabelle gehörige Funktion dar, indem Sie die Funktionsgleichung
eingeben.
6. Übung 6:
a. Stellen Sie ein allgemeines veränderbares Dreieck in blauer Farbe her. Die Höhe hc
soll in Rot erscheinen. Werkzeug Vieleck verwenden.
b. In einem Textfeld soll erscheinen:
„h = xx.xxx cm“
Hierzu müssen Sie ein Textfeld
anlegen. Texte in Anführungszeichen, Variablen mit „+“
anfügen.
c. Anspruchsvoller ist diese Aufgabe:
In einer weiteren Zeichnung soll ein veränderliches Dreieck mit einem dauerhaft
rechten Winkel bei C erstellt
werden. Sie brauchen
einen Thaleskreis dafür!
Versuchen Sie in Ihrer
Zeichnung den Höhensatz
anschaulich zu zeigen.
Stellen Sie z.B. h² als
Quadrat dar und p mal q als
Rechteck.
Optimal wäre auch die
Anzeige des rechten
Winkels bei C. (Werkzeug
Winkel)
Sie benötigen dazu folgende Werkzeuge:
i. Kreis mit Mittelpunkt und Radius, um p abzutragen (als Radius dann die
Variable eingeben!)
ii. Senkrechte und parallele Geraden
Seite 3 von 4
Ulrich Steinmetz, dynamische Geometrie mit GeoGebra
http://dgs.ulrich-steinmetz.de
iii. Schneide zwei Objekte, um Schnittpunkte zu bilden
iv. Textfelder für die Maßzahlen der Flächen, damit die Flächengleichheit klar
wird
7. Übung zur Weiterarbeit:
a. Konstruieren Sie ein Haus so wie im Beispiel:
http://ulrich-steinmetz.de/geogebra/Hausbau1.html
Tipp:
GeoGebra hat kein Tool, welches automatisch 3D zeichnen kann. Sie müssen mit
Geraden, Parallelen und Senkrechten vorgehen. Ebenso benötigen Sie Winkel mit
festen Gradzahlen (135°) und Zirkelfunktionen um z.B. halbe Längen abzutragen.
Zunächst soll es reichen, wenn das Haus fest ist und nicht mit Schiebereglern
gekoppelt ist. Das geht leichter. Sie dürfen es aber trotzdem versuchen, wenn Sie
mutig sind!
Seite 4 von 4