Ulrich Steinmetz, dynamische Geometrie mit GeoGebra
Werbung

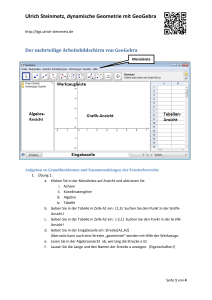
Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de Vorwort „des Schulministeriums“ Das NRW Schulministerium legt in dem Kernlehrplan Mathematik Hauptschule Folgendes fest: Prozessbezogene Kompetenz: Werkzeuge nutzen Zitat: Bereits ab Beginn der Jahrgangsstufe 5 nutzen die Schülerinnen und Schüler verschiedene (nicht-digitale) Werkzeuge für mathematisches Arbeiten. Beim Umgang mit den jeweils zur Verfügung stehenden fachlichen Gegenständen sollen sie die folgenden Werkzeuge nutzen können: Geodreieck Zirkel Regelheft (Merkheft) Im weiteren Verlauf bis zum Ende der Jahrgangsstufe 10 sollen die Schülerinnen und Schüler zusätzlich weitere (auch digitale) Werkzeuge nutzen können: Formelsammlung Taschenrechner Tabellenkalkulation Dabei sollen sie die Eigenschaften dieser Werkzeuge darstellen, die Werkzeuge der jeweiligen Situation angemessen auswählen und Vor- und Nachteile des Einsatzes der Werkzeuge sowie möglicher Alternativen beurteilen können. zusätzlich Mittlerer Schulabschluss: Die Schülerinnen und Schüler sollen Dynamische-Geometrie-Software zur Bearbeitung mathematischer Situationen nutzen können.1 … Eine abschlussbezogene Differenzierung mathematischer Kompetenz in der Doppeljahrgangsstufe 9/10 ergibt sich wiederum aus der entsprechenden Differenzierung in den inhaltsbezogenen Bereichen. Daher wird bei der Darstellung der prozessbezogenen Kompetenzen nicht nach Doppeljahrgangsstufen differenziert. Eine Differenzierung zwischen den beiden Abschlussniveaus ist nur im Bereich Werkzeuge nutzen ausgewiesen. Dies betrifft den Einsatz Dynamischer-GeometrieSoftware, der eng mit der inhaltsbezogenen Differenzierung im Gebiet Geometrie verbunden ist. … Zitat Ende 1 http://www.standardsicherung.schulministerium.nrw.de/lehrplaene/lehrplannavigator-si/hauptschule/mathematik/kernlehrplan/kompetenzen/ (Stand 3.10.2013) Seite 1 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de Das NRW Schulministerium legt in dem Kernlehrplan Mathematik Realschule Folgendes fest:2 Bereich Werkzeuge Kompetenzerwartungen am Ende der Jahrgangsstufe 8 Zitat Anfang Schülerinnen und Schüler Erkunden nutzen Tabellenkalkulation und Geometriesoftware zum Erkunden inner- und außermathematischer Zusammenhänge Berechnen nutzen den Taschenrechner Darstellen tragen Daten in elektronischer Form zusammen und stellen sie mit Hilfe einer Tabellenkalkulation dar Recherchieren nutzen Lexika, Schulbücher und Internet zur Informationsbeschaffung Kompetenzerwartungen am Ende der Jahrgangsstufe 10 Schülerinnen und Schüler Erkunden nutzen mathematische Werkzeuge (Tabellenkalkulation, Geometriesoftware, Funktionenplotter) zum Erkunden und Lösen mathematischer Probleme Berechnen wählen ein geeignetes Werkzeug ("Bleistift und Papier", Taschenrechner, Geometriesoftware, Tabellenkalkulation, Funktionenplotter) aus und nutzen es Darstellen wählen geeignete Medien für die Dokumentation und Präsentation aus Recherchieren nutzen selbstständig Print- und elektronische Medien zur Informationsbeschaffung Zitat Ende Tabellenkalkulation, Geometriesoftware, Funktionenplotter, das alles kann GeoGebra! 2 http://www.standardsicherung.schulministerium.nrw.de/lehrplaene/lehrplannavigator-si/realschule/mathematik/kernlehrplan/kompetenzen/kompetenzen.html (Stand 3.10.2013) Seite 2 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de Wo gibt es GeoGebra kostenlos? http://www.geogebra.org Der Arbeitsbildschirm von GeoGebra Menüleiste Aufgaben zu Grundfunktionen und Zusammenhängen der Fensterbereiche 1. Übung: a. Klicken Sie in der Menüleiste auf Ansicht und aktivieren Sie i. Algebra ii. Tabelle b. Klicken Sie mit rechter Maustaste in der Grafik Ansicht und aktivieren Sie i. Achsen ii. Koordinatengitter c. Geben Sie in der Tabelle in Zelle A1 ein: (1,3) Suchen Sie den Punkt in der GrafikAnsicht! d. Geben Sie in der Tabelle in Zelle A2 ein: (-2,1) Suchen Sie den Punkt in der GrafikAnsicht! e. Geben Sie in der Eingabezeile ein: Strecke[A1,A2] Alternativ kann auch eine Strecke „gezeichnet“ werden mit Hilfe der Werkzeuge. f. Lesen Sie in der Algebraansicht ab, wie lang die Strecke a ist. g. Lassen Sie die Länge und den Namen der Strecke a anzeigen. (Eigenschaften!) Seite 3 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de 2. Übung: a. Geben Sie in B1 eine 5 ein. b. Geben Sie in der Eingabezeile ein: f(x)= B1 x -3 (Leerzeichen beachten!) c. Ändern Sie in Zelle B1 die 5 zur 2! Beobachten Sie Veränderungen in der GrafikAnsicht. 3. Übung: a. b. c. d. Geben Sie in der Eingabezeile ein: g(x)=B1 x^2 -3 (statt x^2 ginge auch x² oder x*x) Ändern Sie den Wert in B1. (z.B. 0.5 mit Punkt eingeben!) Geben Sie in der Eingabezeile ein: Ableitung[g(x)] Fügen Sie einen neuen beweglichen Punkt der Parabel ein. e. Lassen Sie eine Tangente durch den Punkt gehen. f. Zeigen Sie die Steigung der Tangente an. 4. Übung: a. Bereiten Sie eine Zeichnung vor, welche ein einfaches Dreieck mit Innenwinkeln darstellt. Schüler sollen später damit die Winkelsumme herausfinden. Sie benötigen neue Werkzeuge. Ziel: b. Achten Sie auf die Farben und Nachkommastellen und Bezeichnungen. Kommt es auch mal zur Winkelsumme 181° oder 179° ? Wie gehen Sie damit um? Nachkommastellen berücksichtigen? 5. Schauen Sie sich auf YouTube dieses Video von Jörn Loviscach an: http://www.youtube.com/watch?v=OuImEm2Nwgo Er leitet die Winkelsumme im Dreieck auf eine andere Art her. Erstellen Sie dazu auch mal eine GeoGebra Konstruktion! Seite 4 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de 6. Übung: a. Öffnen Sie ein neues GeoGebra-Fenster Strg+N oder Menübefehl Datei + Neues Fenster b. Legen Sie zwei Schieberegler in die Grafik-Ansicht. Sie sollen die Werte von – 10 bis +10 darstellen können und die Breite 200 (Pixel) haben. Schauen Sie nach, wie die Schieberegler-Variablen heißen. (Eigenschaft, Algebraansicht) c. Geben Sie dann eine Funktion 3.Grades + 2.Grades mit Verwendung der beiden Schieberegler ein. (Beispiel f(x)= a x³ - b x² + 2) Die Leerzeichen sind relevant, denn sonst denkt das Programm, es handle sich um Variablen, die ax oder bx heißen! d. Ändern Sie die Schieberegler und beobachten Sie. Animieren Sie die Regler! (Eigenschaft Animation ein) e. Ergänzen Sie die Nullstellen (Befehl Nullstelle[Funktionsname]) f. Ergänzen Sie die Scheitelpunkte (Befehl Extremum[Funktionsname]) g. Stellen Sie die 1. Ableitung der Funktion in roter Farbe dar. (Befehl Ableitung[f(x)]) (Es ginge auch die Eingabe f‘(x) für die erste Ableitung!) h. Wenn Sie Spaß an Integralen haben: Eingabe Integral[f, -0.5, 2], wobei die beiden Zahlen Anfangs- und Endwert sind. Sie sind beliebig eingebbar. „f“ ist der Name der Funktion. Denkbar sind auch Schieberegler-Variablen für die Grenzen. 7. Schauen Sie sich weitere Übungen an, welche oft mit Schiebereglern ausgestattet sind: Sie finden eine Auswahl von meinen Aufgaben bei http://dgs.ulrich-steinmetz.de Die Links führen zu Aufgaben, die ich zuvor auf GeogebraTube hochgeladen habe. a. http://www.geogebratube.org/student/m80300 Hier werden Schieberegler für die Veränderung von Farben eingesetzt b. http://www.geogebratube.org/student/mxZrexqFB Hier ändern Schieberegler den Streckungsfaktor bei einer zentrischen Streckung c. http://www.geogebratube.org/student/moBFZ7gYg Schieberegler ändern eine Streckenlänge d. http://www.geogebratube.org/student/my6WMcNpH Ein Schieberegler ändert die Öffnung einer Parabel e. http://www.geogebratube.org/student/meevlRTld 2 Schieberegler ändern Dreiecksseiten Seite 5 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de 8. Die Links aus der vorhergehenden Aufgabe stellen nur eine kleine Auswahl der Anwendungsmöglichkeiten dar. Auf meiner für den Schulunterricht konzipierten Website (Adresse s.o.) befinden sich momentan diese Übungen. (Stand 13.10.2014) Klasse 5-8 Klasse 9/10+ alle Klassen/Diverses Erkenntnisse von Thales Pythagoras entdecken Der Nilforscher Steigung von Geraden Pythagoras mal anders Tangram Figuren Schnittpunkte im Pythagoras als Film Winkelgrößen Pythagoras Entscheidung der Bienen (I) Dreieck(Video)zeigen Winkel auf 90° stellen Der Perigal Pythagoras-Beweis Entscheidung der Bienen (II) und Raumdiagonale 6 Winkel einstellen Pythagoras Satz anschaulich Garfields Beweis des Spuren suchen im Dreieck Der "Stuhl der Braut" Beweis Hausbau in 3D (Perigal) Pythagoras Inkreis des Dreiecks Sechsecksfläche Zuordnung (proportional) Parabeln bei Brücken Das Volumen einer Zuordnung Parabeln bei Brücken Das Volumen einer Box optimieren (1) Spiegeln mit Eichhörnchen (A) Steinwurf Parabel bestimmen Wo liegt das neue (umgekehrt proportional) (inkl. Modellierung) Box optimieren (2) Kraftwerk? Spiegeln mit Eichhörnchen (P) Pi bestimmen im Viertelkreis Lösung mit Funktionsgraph Senkrechte oder Regentropfen im Vollkreis Der Fermat-Punkt in einem Schätze 2 Kreise und 2 Umfänge Satz von Viviani im Dreieck parallele suchen Strecke? Dreieck Schätze suchen (mit Hilfe) 2 Kreise und 2 Flächen Der RGB-Trainer Streckung an Quadraten Das Pyramidenvolumen Sternenkollision Beweis der Winkelsumme Pyramide und Quader im Die Herz-Ellipse bestimmen Quadranten lernen Die 1. binomische Formel Maria Agnesi: "Witch of Agnesi" Dreieck Vergleich Winkelbezeichnungen lernen Ein Rechteck im Kreis Das Goldene Dreieck (V1) Der Schmetterling (V1) Berechnungen an Quadraten Das Goldene Dreieck (V2) optimieren Der Schmetterling (V2) Der Höhensatz und die Die Dreiecksfläche Ortslinie Wurzeln des Die Parallelogramm-Fläche Ortslinie des InkreisHöhenschnittpunkts Winkelsummen Dreieck/Viereck Ortslinie des Schwerpunkts Mittelpunkts Zentrische Streckung und Einheitskreis und Sinus Vierecke Flächen ineinander parallel? Sinus und Cosinus verfolgen 11 Würfelnetze * Kugelstoßen auf 3 Planeten Koordinaten üben (1.Quadrant) Hypotenusen berechnen Koordinaten üben (alle Parabeln in Scheitelpunktform Koordinaten angeben Die Ziege frisst im Viertelkreis Quadranten) Winkel im Sehnenviereck Die frisst im Viertelkreis Teil Ziege 1 Zaunpfosten aufstellen Rechteck im Dreieck Teil 2 Haus des Nikolaus maximieren Mandala und Symmetrie Kreisflächen schätzen Polynome und Parabeln Aus 3 Punkten eine Der Ellipsenbaukasten Parabelgleichung Brennpunkt einer Parabel Brennpunkt einer Parabel LNB und Satellitenschüssel suchen Funktionen ausprobieren Seite 6 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de 9. Übung: a. Denken Sie sich eine einfache Zuordnung aus, zu der Sie eine Wertetabelle erfassen wollen. Proportional oder umgekehrt proportional. b. Geben Sie innerhalb der Tabellenansicht die x-Werte in Spalte A und die y-Werte in Spalte B ein. Keine Überschriften in die Spalten einfügen! c. Versuchen Sie danach, die Punkte auch in der Grafikansicht erscheinen zu lassen. Hierzu der Tipp: Versuchen Sie in Spalte C die Daten in der Form (x,y) erscheinen zu lassen. Man kann A1 und B1 weiterverwenden, =(A1,B1) wäre zulässig wie in Excel. d. Stellen Sie in einer anderen Farbe als schwarz die zu den Daten in der Zuordnungstabelle gehörige Funktion dar, indem Sie die Funktionsgleichung eingeben. 10. Übung: a. Stellen Sie ein allgemeines veränderbares Dreieck in blauer Farbe her. Die Höhe hc soll in Rot erscheinen. Werkzeug Vieleck verwenden. b. In einem Textfeld soll erscheinen: „h = xx.xxx cm“ Hierzu müssen Sie ein Textfeld anlegen. (Hinweis für ältere Geogebra Versionen: Texte in Anführungszeichen, Variablen mit „+“ anfügen.) c. Anspruchsvoller ist diese Aufgabe: In einer weiteren Zeichnung soll ein veränderliches Dreieck mit einem dauerhaft rechten Winkel bei C erstellt werden. Sie brauchen einen Thaleskreis dafür! Versuchen Sie in Ihrer Zeichnung den Höhensatz anschaulich zu zeigen. Stellen Sie z.B. h² als Quadrat dar und p mal q als Rechteck. Optimal wäre auch die Anzeige des rechten Winkels bei C. (Werkzeug Winkel) Sie benötigen dazu folgende Werkzeuge: i. Kreis mit Mittelpunkt und Radius, um p abzutragen (als Radius dann die Variable eingeben!) Seite 7 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de ii. Senkrechte und parallele Geraden iii. Schneide zwei Objekte, um Schnittpunkte zu bilden iv. Textfelder für die Maßzahlen der Flächen, damit die Flächengleichheit klar wird 11. Übung a. Schauen Sie sich den Beweis des Satzes des Pythagoras nach Henry Perigal an bei Wikipedia. b. Vergleichen Sie mit meiner ersten Version des GeoGebra Arbeitsblattes http://www.geogebratube.org/student/mP9f397F4 c. Vergleichen Sie mit meiner zweiten Version des GeoGebra Arbeitsblattes http://www.geogebratube.org/student/m88253 d. Versuchen Sie den Anfang dieser Konstruktion, indem Sie zunächst ein rechtwinkliges Dreieck und die Quadrate herstellen. Weitere Schritte erst nach Praxiserfahrung! 12. Übung: Der verletzte Forscher a. Zwei Forscher sind mit Ihren Landrovern in der Wüste westlich des Nils bei Ausgrabungen. Ein Forscher verletzt sich und benötigt dringend Hilfe und vor allem Wasser. Er ruft mit seinem GPS-Handy seinen Kollegen herbei, der nun auf dem kürzesten Weg Wasser holen muss und damit dann seinen Kollegen retten soll. Beschreiben Sie eine Strategie für sein Vorhaben! b. Lösen Sie die Aufgabe mit einer GeoGebra Konstruktion. Lassen Sie sich dabei Winkel anzeigen! c. Wie würde eine reine tafelorientierte Lösung aussehen? d. Stellen Sie das Ergebnis vor! (Teamarbeit) Seite 8 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de 13. Anzeigen von Meldungen unter Bedingungen In Aufgabenstellungen, bei denen Schülerinnen und Schüler etwas erkennen sollen oder etwas konstruieren sollen, ist es oft sinnvoll, dass eine Textmeldung auf dem Bildschirm erscheint, in der bestätigt wird, dass die Konstruktion richtig gemacht wurde. Objekte können unter selbst festgelegten Bedingungen erscheinen oder verborgen werden. a. Erstes Beispiel zum Einsatz: Zwei Geraden sollen so auf dem Bildschirm platziert werden, dass sie senkrecht zueinander sind. Die notwendige Bedingung ist also das „zueinander senkrecht sein“. (im folgenden Bild ist die Meldung noch nicht sinnvoll!) Anleitung: i. Neues Arbeitsblatt ohne Koordinatensystem mit Gitter ii. Zeichnen Sie 2 beliebige Geraden. iii. Legen Sie ein Textfeld mit dem entsprechenden Text an. Schwarzer Hintergrund, gelbe Textfarbe. Schön groß machen! iv. Nun beginnt die Eingabe einer Bedingung zur Anzeige des Textes, denn er darf nur dann erscheinen, wenn die Geraden senkrecht zueinander sind. v. Öffnen Sie die Eigenschaften des Textfeldes. Klicken Sie auf Erweitert. vi. Die Geraden heißen a und b. Geben Sie als Bedingung ein a ⊥ b Das Zeichen für senkrecht finden Sie, indem Sie auf das @ Zeichen in der Eingabezeile für die Bedingung klicken. Seite 9 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de b. Zweites Beispiel zum Einsatz: Ein beliebiges Dreieck soll so durch Ziehen an den Eckpunkten verändert werden, dass genau 2 Seiten gleich lang sind. Die Dreiecksseiten sind a, b, c. Wenn also a=b oder a=c oder b=c richtig ist, soll eine Meldung erscheinen, nicht aber wenn alle 3 Seiten gleich lang sind. Erste grundsätzliche Schwierigkeit ist hierbei, dass eine Längengleichheit von Strecken fast nie erreicht werden kann, weil sich Längen manchmal nur um 1/1000 cm unterscheiden. Man sollte also einen Schwellenwert bestimmen. Wenn 2 Seiten sich unterhalb dieses Schwellenwertes unterscheiden, ist die Aufgabe bereits gelöst. Vorschlag: wenn der Längenunterschied <=0.01 ist, soll es in Ordnung sein. Es ist hier sinnvoll eine Variable anzulegen: schwelle=0.01 in der Eingabezeile! i. Zum Zweiten muss man daran denken, dass Unterschiede als Absolutwert berechnet werden, damit keine negativen Differenzen auftauchen. Man kann abs(a-b) schreiben, die abs() Funktion entfernt das Vorzeichen. ii. Man benötigt bei der Eingabe das „oder“ Zeichen, es ist ein v und das „und“ Zeichen, es ist ein ^ (wie ein Dach). Beide Zeichen findet man wieder unter dem @ Zeichen bei der Eingabe. Sie können sich das nach einer ZP 10 Aufgabe entstandene Beispiel dazu ansehen: http://tube.geogebra.org/student/m180195 iii. Vorbereitung des Arbeitsblattes iv. Nun die Bedingungen als Eigenschaften des Textes schreiben! Der Anfang: abs(a - b) ≤ schwelle .... v. Es ist ratsam eine zusätzliche Bedingung zu definieren für den Fall, dass alle Seiten gleich lang sind. Ist diese Bedingung dann erfüllt, darf der Text nicht erscheinen. Gegebenenfalls erscheint dann ein anderer Text. Sie werden das Zeichen für nicht benötigen! So kann es aussehen: …∧ (¬allegleich) In der Klammer sehen Sie das „nicht“ Zeichen vor der Variablen allegleich, welches aus dem Bereich der Aussagenlogik bekannt ist. Seite 10 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de 14. Einsatz von Befehlsschaltflächen und Skripting-Befehlen a. Schaltflächen können Aufgaben übernehmen, die zuvor eingegeben wurden. Beispielsweise können ein paar Punkte im Koordinatensystem per Klick gesetzt werden, zu denen Schülerinnen und Schüler dann die Koordinaten ermitteln sollen. Sehen Sie sich dieses Beispiel an: http://www.geogebratube.org/student/m97708 Hier werden 8 Punkte mit Skripting Befehlen zufällig neu positioniert. b. Schaltflächen werden mit Skripting Befehlen programmiert. Die Skripting Befehle findet man alle auf der Website von GeoGebra. Es ist nicht sinnvoll, alle hier zu nennen, denn die Anzahl der möglichen Befehle wird regelmäßig größer. Auf http://www.geogebra.org/cms/de/ am besten auf Hilfe klicken, man kommt auf http://wiki.geogebra.org/de/Hauptseite und dort als Suchwort Skripting oder Befehle eingeben. Die Skripting Befehle sind die, die man oft gebrauchen kann, aber auch weitere Befehle sind nützlich. Screenshot 20.3.2014 c. Es gibt bei GeoGebra einige Tausend einsetzbare Befehle. Allein die Gruppierung stellt über 400 Seiten zu verschiedenen Themen dar. Auf jeder dieser Seiten findet man wieder themenorientierte Einzelbefehle. d. Beispielbefehle: Seite 11 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de e. Erstellen Sie ein neues GeoGebra Arbeitsblatt mit einem Koordinatensystem, welches ausschließlich den 1. Quadranten des Koordinatensystems zeigt. Einstellung über die Eigenschaften der Grafik-Ansicht. (Rechte Maustaste Klick) i. Erzeugen Sie auf „normale Art“ 4 Punkte. ii. Erzeugen Sie eine Schaltfläche „zufällige Punkte“ iii. Schreiben Sie Skripting Befehle zu der Schaltfläche, die bei Mausklick stattfinden sollen! SetzeKoordinaten(A,Zufallszahl[0,7],Zufallszahl[0,7]) Dieser Befehl setzt die Koordinaten des Punktes A auf neue Werte im Bereich 0 bis 7. Testen Sie Ihr neues Arbeitsblatt. Seite 12 von 13 Ulrich Steinmetz, dynamische Geometrie mit GeoGebra http://dgs.ulrich-steinmetz.de http://www.geogebratube.org/student/m88253 Abschluss: Ein Statement zur Einsetzbarkeit von GeoGebra. (Diskussion) Frei nach Hilbert Meyer, Professor für Schulpädagogik, Universität Oldenburg Alle sagten: "Das geht nicht." Dann kam einer, der wusste das nicht, und hat dynamische Geometrie mit seinen Schülern gemacht. Seite 13 von 13