Relativbewegungen, Kreisel und eulersche - Physik

Ergänzungen zu Physik I
Inhaltsverzeichnis
Ergänzungen zur Physik I
U. Straumann, 15. November 2016
Physik - Institut Universität Zürich
Inhaltsverzeichnis
1 Relativbewegungen
1.1 Relativitätsprinzip der Mechanik . . . . . . . . . . .
1.2 Die Kinematik in einem bewegten Bezugssystem . .
1.3 Die Dynamik in einem bewegten Bezugssystem . . .
1.4 Beispiele und Spezialfälle für bewegte Systeme . . .
1.4.1 Gleichförmig bewegtes System Sr . . . . . . .
1.4.2 Rein translatorisch beschleunigtes System Sr
1.4.3 Gleichförmig rotierendes System Sr . . . . . .
1.5 Trägheitseffekte auf der Erde . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Eigenschaften des Kreisels
2.1 Trägheitstensor und Eulersche Kreisel-Gleichungen . . . . . .
2.2 Der kräftefreie rotationssymmetrische Kreisel . . . . . . . . .
2.3 Stabilität der Drehachse für Körper ohne Rotationssymmetrie
2.4 Symmetrischer Kreisel im Schwerefeld (Präzession) . . . . . .
2.5 Rotationsenergie und Energiesatz für die allgemeine Drehung
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
2
3
4
5
5
5
6
7
.
.
.
.
.
9
9
13
15
16
18
1
Ergänzungen zu Physik I
1
Relativbewegungen
1 Relativbewegungen
Bei der Diskussion der Newtonschen Prinzipien wurde betont, dass diese nur in einem Inertialsystem gültig sind. Nach dem 1. Newtonschen Prinzip ist das ein solches Koordinatensystem,
in dem ein isolierter, also keinen Kräften unterworfener Massenpunkt sich mit konstanter Geschwindigkeit bewegt.1 Als Inertialsystem haben wir meist ein auf der Erdoberfläche verankertes Koordinatensystem benutzt2 . Die mit der Newtonschen Mechanik berechneten Bewegungen
stimmten ausgezeichnet mit den Messungen überein.
Es stellen sich dann die Fragen: Wie kann man verschiedene Inertialsysteme unterscheiden? Wie
lauten die Bewegungsgleichungen in Nicht-Inertialsystemen? Insbesondere die Beantwortung der
zweiten Frage ist von grosser praktischer Bedeutung, da wir sehen werden, dass Rechnungen oft
vereinfacht werden können, wenn man sie in einem beschleunigten Nicht-Inertialsystem ausführt.
1.1 Relativitätsprinzip der Mechanik
Ein Koordinatensystem können wir uns immer durch Vektoren in einem starren Körper realisiert
denken. In einem solchen Körper bleiben per definitionem die Abstände beliebiger Punktepaare
konstant. Wir betrachten zwei Systeme dieser Art, das S-System (z.B. Laborsystem) mit den
xyz-Achsen und das relative Sr -System mit den xr yr zr -Achsen (Abb. Seite 3). Der Ort eines
Massenpunktes m wird durch die Ortsvektoren ~r und ~rr festgelegt.
Dann gilt
~r = ~r◦ + ~rr .
(1)
Wir setzen voraus, dass in beiden Systemen die klassische, nicht-relativistische Mechanik gilt,
d.h. alle Geschwindigkeiten sind klein gegenüber der Lichtgeschwindigkeit (v c). Dann gelten
bis zu einer hohen Genauigkeit die klassischen Vorstellungen von Raum, Zeit und Masse:
a) In beiden Systemen werden die gleichen Massstäbe zur Längenmessung verwendet. Das
impliziert, dass die Standard-Massstäbe von S und Sr verglichen werden können.
b) Beide Systeme benutzen die gleiche Zeit. Wenn in S eine Zeit ∆t zwischen zwei Ereignissen
beobachtet wird, so wird in Sr das gleiche Intevall ∆tr = ∆t gemesen.
c) Der Massenpunkt hat in beiden Systemen die gleiche Masse.
In der Relativitätstheorie sind diese drei Annahmen nicht mehr haltbar, sobald die Geschwindigkeiten der Grösse nach mit c vergleichbar werden.
Wir wollen nun annehmen, durch Versuche habe sich erwiesen, dass S ein Inertialsystem sei.
Dann lässt sich sofort zeigen, dass auch Sr ein Inertialsystem ist, falls es sich gleichförmig geradlinig gegenüber S bewegt, d.h. wenn gilt
d~r◦
= ~v◦ = konst.
dt
1
2
(2)
Vgl. Halliday, Kap. 5-3.
und dabei die Rotation der Erde als kleinen Effekt vernachlässigt. Ein Labor auf der Erde ist bei genauer
Messung jedoch ein beschleunigtes Nicht-Inertialsystem mit den entsprechenden Schein- oder Trägheitskräften.
2
Ergänzungen zu Physik I
1
Relativbewegungen
Denn zweimalige Differenziation von Gl.(1) liefert
d~r
d~r◦ d~rr
= ~v =
+
= ~v◦ + ~vr
dt
dt
dt
und
d2~rr
d2~r
=
~
a
=
= ~ar .
dt2
dt2
Aus ~a = ~ar folgt aber, dass die Kräfte F~ = m~a und F~r = m~ar in beiden Systemen die gleichen
sind; demzufolge gilt auch in Sr die Newtonsche Mechanik, Sr ist auch ein Inertialsystem. Alle
Koordinatensysteme, die sich gleichförmig geradlinig gegenüber einem Inertialsystem bewegen,
sind also ebenfalls Inertialsysteme. Sie lassen sich nicht unterscheiden, und es ist daher unmöglich
festzustellen, ob eines dieser Systeme “absolut in Ruhe” ist. Dies ist das Relativitätsprinzip der
Mechanik.
Wenn Gl. (2) gilt, so lässt sich Gl. (1) auch in der Form der Galilei-Transformation
~r = ~rr + ~v◦ t
(3)
schreiben. Wenn diese Transformationsgleichung zwischen den Systemen S und Sr gültig ist, gilt
das Relativitätsprinzip der Mechanik, das man auch in folgenden Worten formulieren kann:
Es ist einem Beobachter unmöglich, mit Hilfe von mechanischen Experimenten
herauszufinden, ob sein Bezugssystem in Ruhe oder in gleichförmiger Bewegung ist.
Mittels anderer Wechselwirkungen wie z.B. elektrodynamischen oder optischen Versuchen ist
eine solche Unterscheidung ebensowenig möglich.
1.2 Die Kinematik in einem bewegten Bezugssystem
Wir behandeln jetzt eine beliebige Bewegung (auch Rotationen und damit beschleunigte Systeme) des Systems Sr gegenüber dem Inertialsystem S (im Folgenden Ruhe- oder Laborsystem
genannt. Ein ausgedehnter Körper mit einer allgemeinen Bewegung hat sechs Freiheitsgrade, 3
der Translation und 3 der Rotation. Es gelte wie oben die klassische Mechanik.
zr 6 ~
m ω
Das bewegte Bezugssystem sei ein starrer Raum Sr (xr , yr , zr ) (Fahr- z 6
u
Sr
zeug), der vom ruhenden System S(x, y, z) aus beschrieben wird mit
~r
1y
7 r
~r r
~r◦ , ~v◦ (Ortsvektor und Geschwindigkeit des Ursprungs von Sr ) und
ω
~ (Winkelgeschwindigkeit von Sr um eine Achse durch den Ursprung
xr
~r◦
von Sr ). Im relativen System Sr (xr , yr , zr ) wird eine Masse m mit ~rr ,
1
y
~vr und ~ar gekennzeichnet. Im ruhenden System beschreiben ~r, ~v und S ~a die Masse m.
x
Der Koordinatenursprung von Sr liegt auf der Drehachse. Die Winkelgeschwindigkeit ω ist (im
~ ◦ und dem Drehmoment M
~ ◦ ) unabhängig von der Wahl des BeGegensatz zum Drehimpuls L
zugspunktes.
3
Ergänzungen zu Physik I
1
Relativbewegungen
Für eine reine Translation von Sr wird durch ableiten von (1)
~v = ~vr + ~v◦
und
~a = ~ar + ~aT
(4)
~aT = d~v◦ /dt nennen wir die Führungsbeschleunigung für reine Translation. Sie tritt in einem
beschleunigten Fahrzeug auf.
Für eine reine Rotation von Sr mit konstanter Winkelgeschwnidigkeit ω
~ bekommt man für die
Beziehungen der Geschwindigkeiten anschaulich (für Herleitung siehe Demtroeder, Kapitel 3.3.2,
Formel 3.14)
~v = ~vr + ω
~ × ~rr
(5)
wobei der zweite Term die Rotationsgeschwindigkeit eines in Sr ruhenden Punktes angibt.
Die Beschleunigung wird daraus
~a =
d~v
d~vr
d~rr
=
+ω
~×
dt
dt
dt
(6)
In reiner Rotation ist ~rr = ~r und somit wird d~rr /dt = ~v . Die Ableitung von ~vr bekommt wieder
einen analogen Rotationsterm wie in (5):
d~vr
= ~ar + ω
~ × ~vr
dt
(7)
Zusammengefasst und nach Einsetzen von (5) ergibt sich:
~a = ~ar + 2 ω
~ × ~vr + ω
~ × (~
ω × ~rr )
(8)
~ar = ~a + 2 ~vr × ω
~ +ω
~ × (~rr × ω
~)
(9)
oder nach ~ar aufgelöst:
Wir nennen
~aZ
= ω
~ × (~rr × ω
~)
~aC
= 2 · ~vr × ω
~
Zentrifugal − Beschleunigung
Coriolisbeschleunigung
(10)
(11)
Diese Zentrifugal- und Coriolis-Beschleunigungen treten also in einem rotierenden System auf.
Falls ein Massenpunkt im rotierenden System in Ruhe ist, also ~vr = 0, dann tritt nur Zentrifugalbeschleunigung auf, bei im rotierenden System sich bewegenden Körpern ~vr 6= 0 auch noch
Coriolisbeschleunigung.
1.3 Die Dynamik in einem bewegten Bezugssystem
Das Aktionsprinzip der Bewegung eines Körpers mit Masse m im System S ist
m~a =
n
X
F~i = F~
i=1
4
Ergänzungen zu Physik I
1
Relativbewegungen
mit F~ gleich den resultierenden äusseren Kräften. Dann gilt auch (mit Gl. (1) und (9)):
m~a = m(~ar + ~aT − ~aZ − ~aC ) = F~ .
Ein in Sr mitbewegter Beobachter registriert nur die Relativbeschleunigung ~ar und findet deshalb
~ und m~aC = 2 · m(~vr × ω
~
für das Aktionsprinzip (mit −m~aT =: F~T , m~aZ =: Z
~ ) =: C)
~ +C
~
m~ar = F~ + F~T + Z
(Aktionsprinzip im bewegten System).
(12)
~ (die Zentrifugalkraft), C
~ (die Corioliskraft) und F~T (die translatorische Führungskraft) haZ
ben die Dimension einer Kraft; sie sind jedoch in S keine wahrhaft existierenden Kräfte, sondern
Schein- oder Trägheitskräfte, die ein bewegter Beobachter als Korrektur in die Newtonsche Bewegungsgleichung einführen muss, wenn er dort an Stelle der Beschleunigung ~a die Relativbeschleunigung ~ar einsetzt. Sie haben keine Reaktionskräfte. Obwohl sie nur Schein- oder Trägheitskräfte
sind, existieren sie als reale Kraft im bewegten System Sr . Ein beschleunigtes Bezugssystem ist
kein in sich abgeschlossenes Inertialsystem, es müssen von aussen Kräfte wirken, um das System
mit Massen zu beschleunigen.
1.4 Beispiele und Spezialfälle für bewegte Systeme
1.4.1 Gleichförmig bewegtes System Sr
Es ist ~vF = ~v◦ = konst, folglich ~aF = ~aC = 0 und somit ~ar = ~a. Dann ist auch Sr ein
Inertialsystem, wie wir schon in Abschnitt 1 diskutiert haben.
1.4.2 Rein translatorisch beschleunigtes System Sr
~ = 0 und damit m~ar =
In einem rein translatorisch beschleunigten Bezugssystem gilt ω
~ = 0, C
d~
v
F~ + F~T = F~ − m~aT . Mit ~vT = ~v◦ (t) folgt ~aT = dt◦ = ~a◦ . Damit spürt z.B. der Insasse eines
mit ~a◦ beschleunigten Fahrzeuges die Kraft m~ar = F~ − m~a◦ . Wenn die auf ihn wirkende Kraft
F~ = 0 ist, erfährt er die beschleunigende Trägheitskraft m~ar = −m~a◦ . S und Sr sind nicht mehr
äquivalent, in den beiden Systemen werden unterschiedliche Beschleunigungen gemessen.
Beispiel: Mathematisches Pendel auf einer vertikal beschleunigten Plattform
z
6
a◦
6
~ = −m~a◦ = −ma◦~k und damit die Bewegungsgleichung
Es ist Z
für die Tangentialkomponente
A
A
ϕA `
K
A
AA F ∗
Au
A
?
G
d2r ϕ
= −(mg + ma◦ ) sin ϕ.
dt2
Für kleine Ausschläge ist sin ϕ ' ϕ, also
d2r ϕ
g + a◦
+
ϕ = 0. Mit dem Ansatz
dt2
`
m`
Z
?
x-
5
Ergänzungen zu Physik I
1
r
ϕ(t) = ϕ◦ cos(Ωt − δ)
ist
Ω=
g + a◦
`
Relativbewegungen
die Kreisfrequenz des Pendels.
Fällt die Plattform frei, so ist g = −a◦ , also Ω = 0, d.h. die Schwingungsdauer T =
unendlich. Der freie Fall merkt keine Gravitationskraft.
2π
Ω
ist
1.4.3 Gleichförmig rotierendes System Sr
Die translatorische Bewegung verschwindet ~v◦ = 0. ω
~ ist konstant. Wir behandeln zwei Experimente auf dem Drehtisch.
a) Ein Massenpunkt m sei auf einer mit konstanter Winkelgeschwindigkeit ω
~ sich drehenden,
horizontalen Unterlage durch eine Feder mit der Drehachse verbunden. m sei relativ zur
Unterlage in Ruhe. Es herrscht scheinbares Gleichgewicht. Im ruhenden System beschreibt
m eine Kreisbahn. Die wahren Kräfte sind, wenn keine Reibungen vorhanden sind,
v2
= mrr ω 2 .
r
Ein mitbewegter Beobachter muss eine Scheinkraft einzuführen, um sich die relative Ruhe erklären zu können. Es
ist
~ =0
~vF = ω
~ × ~rr , ~vr = 0, also C
G=N
6
ω
~
~rr
~
-6
N
∼∼∼∼∼ u - Z
~
F~F ?
~
G
und
FF = m
ω
sowie ~v˙ ◦ = 0 und d~
= 0. Damit ergibt sich die
dt
Führungskraft aus Gl.(9) zu
~ = m~aZ = −m[~
Z
ω × (~
ω × ~rr )] , der Zentrifugalkraft3 . Ihr Betrag ist gerade Z = mrr ω 2
~ und F~F erfüllen also die Gleichgewichtsbedingung im beschleunigten
(da ω
~ ⊥ ~rr steht). Z
Relativsystem.
b) Vom Ursprung des ruhenden Systems S aus bewegt sich eine Masse m mit konstanter
Geschwindigkeit v◦ , es wirken keine äusseren Kräfte. Der Beobachter in Sr sieht eine
spiralförmig nach aussen bewegte Masse, für welche die Geschwindigkeit direkt angegeben werden kann; in Polarkoordinaten hat sie die Komponenten vrr = drdtrr = v◦ und
vrϕ = rr drdtϕr = −ωrr . Nach einer einfachen Integration erhält man hieraus auch die
Ortskoordinaten rr = v◦ t und ϕr = −ωt. Gemäss Gl.(12) gilt für den Beobachter das
Aktionsprinzip
~ +C
~ = m~aZ + m~aC = −m · ω
m~ar = Z
~ × (~
ω × ~rr ) − 2m · ω
~ × ~vr ,
d.h. er beobachtet eine Zentrifugalkraft und eine Corioliskraft. Letztere sucht die Richtung
der Geschwindigkeit dauernd zu ändern ohne den Betrag zu beeinflussen, wie dies auf der
Erde bei den Monsunen, Passatwinden und dem Golfstrom ebenfalls beobachtet wird.
Versucht der Beobachter in Sr die Masse festzuhalten, so muss er eine Reaktionskraft zu
~ +C
~ aufbringen.
Z
3
Zur Zentrifugalkraft: vgl. Formel (6-35) im Halliday, Kap.6-5.
6
Ergänzungen zu Physik I
1
Relativbewegungen
1.5 Trägheitseffekte auf der Erde
In den vorausgegangenen Beispielen spielte der Hörsaal und damit die Erde die Rolle des ruhenden Systems. Diese Wahl führte zu keinen Widersprüchen mit der Erfahrung, obwohl die
Erde ein bewegtes Bezugssystem ist. Der Grund liegt darin, dass auf der Erde Z und C viel
kleiner als mg sind. Es können aber terrestrische Versuche ausgeführt werden, die eindeutig die
Trägheitseffekte als Folge des Bewegungszustandes der Erde zeigen.
Ein Beispiel: Nachweis der Erdrotation mit dem Foucaultpendel
N
m
→
ω
→
ω
β
S
Ein schwingendes Pendel behält infolge der Trägheit seine
Schwingungsebene im Raum bei. Dieses eigentümliche Verhalten offenbart sich beim Foucault-Versuch4 (1850/51 in Paris).
Ein Ort auf der Erde mit der geographischen Breite β rotiert mit der Winkelgeschwindigkeit ω · sin β um eine zur Erdoberfläche senkrechte Achse; mit dieser Winkelgeschwindigkeit
dreht sich die Erde unter dem schwingenden Pendel hinweg. Die
effektive Umlaufszeit der Horizontalebene relativ zur Schwingungsebene des Pendels in der geographischen Breite β ist
T = 2π/ω sin β mit ω = 2π/24 Stunden. Zur Berechnung wurde hier ω
~ bei der geographischen Breite β in die Komponenten
senkrecht (ω⊥ ) und parallel (ωk ) zur Erdoberfläche zerlegt.5
Die Pendelebene bleibt bei der Drehung im Raum S erhalten, es gilt die Drehimpulserhaltung
~ = 2m(~vr × ω
und die Drehung ist direkt durch ω⊥ gegeben. Es gilt für die Corioliskraft C
~) =
2m(~vr × ω⊥ + ~vr × ωk ), wobei nur der erste Term zu einer Auslenkung führt. Für Zürich mit
β ≈ 47◦ ist T = 34h, am Pol erhalten wir T = 24h und am Äquator T = ∞.
Die Corioliskraft ist auch die Ursache dafür, dass Hochdruckgebiete auf der Nordhalbkugel im
Uhrzeigersinn rotieren, Tiefdruckgebiete in Gegenrichtung. Bei einem Tiefdruckgebiet strömt
die Luft aufgrund des Druckgefälles nach innen. Diese Strömung wird auf der Nordhalbkugel
durch die Corioliskraft nach rechts abgelenkt und es ergibt sich eine gegen den Uhrzeigersinn
gerichtete Rotation.
4
5
Für eine ausführlichere Darlegung siehe Halliday, Kap.16-10.
Dies ist nur deshalb möglich, weil es sich bei ω
~ um einen axialen Vektor handelt.
7
Ergänzungen zu Physik I
1
Relativbewegungen
Schematische Darstellung der athmosphr̈ischen Zirkulation. Temperaturunterschiede führen zu
Fall- und Steigströmungen (rechts dargestellt), die wiederum Hoch- und Tiefdruckgebiete erzeugen. Die Corioliskraft bewirkt, dass rotierende Wirbel entstehen. Tiefdruckwirbel können durch
bei der Kondensation der aufsteigenden Luftfeuchtigkeit freiwerdender Energie weiter angetrieben werden, sodass Wirbelstürme entstehen. Referenz:
http://www.techniklexikon.net/d/atmosphärische zirkulation/atmosphärische zirkulation.htm
8
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
2 Eigenschaften des Kreisels
2.1 Trägheitstensor und Eulersche Kreisel-Gleichungen
Auf Grund der formalen Ähnlichkeit von Impuls- und Drehimpulssatz, also von
~◦
d~
p
dL
= F~
und
= ~τ◦ ,
dt
dt
~
könnte man vermuten, dass der Beziehung p~ = m~v ein ähnlicher Zusammenhang zwischen L
und ω
~ bei der Rotation entspricht. Das ist aber im allgemeinen nicht der Fall. Die Beziehung
L◦z = I◦ ω gilt nur für ebene Bewegungen.6
Wird ein Punkt ◦ eines starren Körpers festgehalten, dann nennt man die Bewegung um ◦ eine
Kreiselung. Sie besitzt drei Rotationsfreiheitsgrade, die jedoch wesentlich komplizierter sind
als drei reine Translationsfreiheitsgrade. Die Schwierigkeiten mehrerer Rotationsfreiheitsgrade
haben folgende Gründe:
1. Es gibt keine Koordinaten, deren Ableitungen direkt Geschwindigkeiten darstellen, wie bei
den Translationen. Drehungen sind Pseudovektoren (axiale Vektoren), deren Reihenfolge
nicht wie bei polaren Vektoren vertauscht werden kann.
2. Die Trägheitsmomente hängen von der Achsenwahl ab. Ändert die Achse mit der Zeit die
Richtung, so wird I = I(t), während in Analogie für Translationen die Masse m konstant
ist.
~ 6= I~
~ im allgemeinen nicht die Richtung von ω
3. Für Drehungen gilt im allgemeinen L
ω , da L
~
hat. Das Trägheitsmoment muss daher durch einen Tensor7 I dargestellt werden, so dass
~ = I~
gilt L
ω.
Im Folgenden wird der Trägheitstensor rein buchhalterisch als Matrix eingeführt8 , wobei die
Rechenregeln in der Matrizendarstellung zwanglos einsichtig sind.
~ =
Ein Beispiel für die Aussage L
6 I~
ω ist die Hantel, deren Mitte mit einer vertikalen Achse
verbunden ist, die mit ω
~ rotiert, und die nicht einer Symmetrieachse entspricht.
→
dL o
m
→
→
Lo
dϕ
α
ω
→
→
→
→
r2
p2
m
.
→
p 1=p
→
r1=r
Die Hantel ist um den Winkel α gegen diese Drehachse geneigt.
~ ◦ der Hantel bezüglich ◦ ist L
~ ◦ = ~r1 × p~1 +
Der Drehimpuls L
~r2 × p~2 , was sich wegen −~r2 = ~r1 =: ~r und −~
p2 = p~1 =: p~ auch
~ ◦ = 2(~r × p~) = 2m(~r ×~v ) schreiben lässt. L
~ ◦ dreht sich mit
als L
der Winkelgeschwindigkeit ω
~ auf einem Kegelmantel um ω
~ mit
~
~
dL◦ /dt = L◦ sin α dϕ/dt = |~
ω × L◦ |; L◦ und ω
~ stehen also nicht
parallel zueinander. Diese Bewegung ist nur möglich mit einem
äusseren (z.B. durch Lagerkräfte aufgebrachten) Drehmoment
~◦
L
~ ◦ ; ohne Lagerkräfte dreht die Hantel, bis
~τ◦ := ddt
= ω
~ ×L
~◦ k ω
L
~ steht und ~τ◦ = 0 wird.
6
Der Kringel im Index steht jeweils um anzugeben, dass die entsprechenden Grössen bezüglich eines raumfesten
Bezugspunktes ◦ betrachtet werden.
7
Tensoren sind physikalische Objekte, die durch ihr Transfomationsverhalten definiert sind. Beispielsweise sind
Skalare Tensoren 0. Stufe; Vektoren sind Tensoren 1. Stufe. Tensoren 2. Stufe wie das Trägheitsmoment können
im einmal gewählten Koordinatensystem durch eine n × n Matrix dargestellt werden.
8
Eine eingehendere Einführung findet sich in den mathematischen Hilfsmitteln zur Physik I.
9
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
~ ◦ und ω
Wir wollen nun einen allgemeinen Zusammenhang zwischen L
~ finden und dann mit Hilfe
des Drehimpulssatzes Bewegungsgleichungen, die Eulerschen Kreiselgleichungen, aufstellen, die
für die Kreiselbewegung gelten, d.h. für Bewegungen eines starren Körpers, von dem ein Punkt
fest gehalten wird.
Wenn bei einer Kreiselung ein Punkt des Körpers im Raume fest bleibt, dann kann dieser Punkt
◦ als raum- (~ri ) und körperfester (~r´i ) Ursprung gewählt werden. Es ist dann ~ri = ~r´i und die
Zeitabhängigkeit steckt im raumfesten System in den Komponenten von ~ri und im körperfesten
System in den Basisvektoren ~´i,~´j,~k´ von ~r´i . Es gilt nach der Definition des Drehimpulses für einen
Massenpunkt ~l◦i = mi ~ri × (~
ω × ~ri ) und damit für n Massenpunkte
~◦ =
L
n
X
i=1
~l◦i =
n
X
mi ~ri × (~
ω × ~ri ) =
i=1
n
X
mi [ri2 ω
~ − (~ri · ω
~ ) ~ri ]
(13)
i=1
wobei im letzten Schritt wird die Vektoridentität
~a × (~b × ~c) = (~a · ~c) ~b − (~a · ~b) ~c
(14)
verwendet wurde.
Für einen ausgedehnten Körper ergibt sich
Z
Z
Z
Z
~ ◦ = ~r ×~v dm = ~r ×(~
L
ω ×~r) dm = [r2 ω
~ −(~r ·~
ω ) ~r ] dm = [r2 ω
~ −(xωx +yωy +zωz ) ~r ] dm.
(15)
Dabei hängt ω
~ in der Summe nicht von i und im Integral nicht von der Massenverteilung ab.
Es besteht jetzt das mathematische Problem, wie man ω
~ aus der Summe herausziehen resp. vor
~ ◦ = I◦ ω
das Integral stellen kann, um so die Beziehung L
~ aufstellen und den Trägheitstensor I◦
bestimmen zu können. Dazu berechnet man die drei Komponenten des Drehimpulses9
Z
Z
Z
2
2
L◦x = ωx (y + z ) dm −ωy yx dm −ωz zx dm
{z
}
| {z }
| {z }
|
Ixx
Cyx
Czx
Z
Z
Z
L◦y = ωy (x2 + z 2 ) dm −ωx xy dm −ωz yz dm
|
| {z }
| {z }
{z
}
Iyy
Cxy
Cyz
Z
Z
Z
L◦z = ωz (x2 + y 2 ) dm −ωx xz dm −ωy yz dm
|
{z
}
| {z }
| {z }
Izz
Cxz
Cyz
Die Trägheitsmomente I in den obigen Gleichungen sind in Analogie zum Trägheitsmoment der
ebenen Bewegung definiert. Die übrigen, nichtdiagonalen Terme C werden als Deviationsmomente
bezeichnet. Für alle drei Komponenten erhält man so in einer buchhalterischen
Anordnung10
:::::::::::::::::::::::::::
9
10
Natürlich erhält man das gleiche Ergebnis, wenn man in Gl.(15) direkt das dreifache Vektorprodukt ausrechnet.
Überprüfe mittels Matrix-Vektor-Multiplikation ( Multipliziere die einzelnen Zeilen-Terme der Matrix mit den
”
Spalten-Termen des Vektors“).
10
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels



L◦x =Ixx ωx −Cxy ωy −Cxz ωz
+Ixx −Cxy −Cxz
ωx
~ ◦ =: I ω
L◦y =Iyy ωy −Cyz ωz −Cyx ωx ⇒ L
~ =  −Cyx +Iyy −Cyz   ωy  ,
L◦z =Izz ωz −Czx ωx −Czy ωy
−Czx −Czy +Izz
ωz
(16)
d.h. man kann den Trägheitstensor I als (3 × 3)-Matrix auffassen. In ausgeschriebener Form
lautet er:
 R
I=
R
R

(y 2R+ z 2 ) dm R − xy dm
− R xz dm
− R yx dm
(x2R+ z 2 ) dm R − yz dm  .
− zx dm
− zy dm
(x2 + y 2 ) dm
(17)
Jede Komponente des Drehimpulses ist eine lineare Funktion von allen Komponenten der Winkelgeschwindigkeit ω
~ . Der Trägheitstensor I ist reell und symmetrisch (Cij = Cji ), und lässt sich
daher11 bezüglich eines geeigneten Koordinatensystems Ś in Diagonalform darstellen. Die Deviationsmomente Cij verschwinden somit allesamt, übrig bleiben nur noch die Trägheitsmomente
Iii der zum Hauptachsensystem Ś gehörigen Hauptachsen. Die Einheitsvektoren entlang dieser
Hauptachsen bezeichnen wir mit ~e1 , ~e2 , ~e3 . Wir haben also (mit den Abkürzungen: Ixx =: I1 ,
Iyy =: I2 , Izz =: I3 ) für ein Hauptachsensystem:


I1 0 0
~ ◦ = I1 ω1~e1 + I2 ω2~e2 + I3 ω3~e3 .
Í =  0 I2 0  und damit L
(18)
0 0 I3
Oft fallen die Hauptachsen mit den (Dreh-)Symmetrieachsen eines Körpers zusammen (Bsp.:
~ ◦ ist auch im Hauptachein Quader und die Achsen des Kartesischen Koordinatensystems). L
sensystem nicht parallel zu ω
~ , da (ausser für eine homogene Kugel) I1 6= I2 6= I3 ist.
Beispiel:
• •
•
Als einfaches Beispiel sei der Trägheitstensor eines zweiatomigen Moleküls (H2 , N2 , O2 ) im
körperfesten Hauptachsensystem berechnet:
r11 = −d,
r21 = +d,
6
2
r12 = 0,
r22 = 0,
r13 = 0,
r23 = 0,
2 + r2 + r2
ri2 = ri1
i2
i3

P
P
2
mP
mi ri1 ri2
−P mi ri1 ri3
i (ri − ri1 ri1 ) P−
2

mP
mi ri2 ri3
I =  − P mi ri2 ri1
i (ri − ri2 ri2 ) P
2
− mi ri3 ri1
− mi ri3 ri2
mi (ri − ri3 ri3 )


0 0 0

I = 2m 0 d2 0  und I1 = 0, I2 = 2md2 , I3 = 2md2 .
0 0 d2
 P
i=1
i=2
u
u
d
3
11
d
-
1
wie in der Linearen Algebra noch gezeigt werden wird
11
Ergänzungen zu Physik I
2
• •
Eigenschaften des Kreisels
•
Bildet man mit Gl.(16), die für ein raumfestes Koordinatensystem hergeleitet wurde, die Be~◦
L
wegungsgleichung (Drallsatz) ~τ◦ = ddt
, dann sind die Komponenten des Trägheitstensors
~ ◦ wird kompliziert – es treten jedoch im raumfesten
zeitabhängig I = I(t) und der Drehimpuls L
System keine Scheinkräfte auf. Im körperfesten und damit bewegten Hauptachsen-System ist der
Trägheitstensor diagonal und der Drehimpuls ist einfach entsprechend Gl.(18); dafür müssen im
rotierenden System Scheinkräfte eingeführt werden. (Das Hauptachsensystem dreht sich mit der
Winkelgeschwindigkeit ω
~ gegenüber dem raumfesten System.) Es war die Idee von Euler12 , die
Vorteile beider Systeme zu kombinieren und die Nachteile zu unterdrücken.
Wir befinden uns also im körperfesten, rotierenden System, und nehmen die Hauptachsen, in
dem der Trägheitstensor diagonal ist, als Bezugssytem. Das ist die entscheidende Annahme für
die Eulergleichungen. Damit müssen wir in diesem beschleunigten Bezugssystem Zentrifugalkräfte Z als Scheinkräfte einführen. Wir lassen im folgenden die Striche bei den Koordinaten
d
sind also im rotierenden System gemeint.
weg, r, v und L sowie die Ableitung dt
Mit der bei gemäss Gleichung (12) definierten Zentrifugalkraft wird
~ = −m(~
Z
ω × (~
ω × ~r))
(19)
Diese Scheinkraft erzeugt ein zusätzliches (scheinbares) Drehmoment τZ wofür wir nach einsetzen
von Z, unter Verwendung der Identität (14) erhalten:
~ = −~
~
τ~Z = ~r × Z
ω×L
(20)
wobei auch verwendet wurde, dass ~v und ~r senkrecht aufeinander stehen und ~v = ω
~ × ~r.
Im rotierenden System gilt also mit einem äusseren, “wirklichen” Drehmoment ~τ :
~τ + τ~Z =
~
dL
dt
(21)
oder umsortiert und eingesetzt:
~
dL
~
+ω
~ ×L
dt
das ist der Drallsatz im körperfest rotierenden System.
~τ =
(22)
Befinden wir uns ausserdem im Hauptachsensystem mit den orthonormierten Koordinaten i =
1, 2, 3 ist der Trägheitstensor diagonal und es gilt deshalb
Li = Ii ωi
12
(23)
Leonard Euler (1707-1783), in Basel geboren, der Vater war Pastor in Riehen, studierte in Basel Theologie
und dann Mathematik und Physik. Er war ein Anhänger der Wellentheorie des Lichtes, sein klassisches Werk
populärer Wissenschaft: “Lettres à une Princesse d’Allemagne”.
12
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
was wir koordinatenweise in den Drallsatz (22) einsetzen. Damit sind wir bei den gesuchten
Eulerschen Gleichungen angelangt:
τ1 = I1 dω1 − (I2 − I3 )ω2 ω3
dt
τ2 = I2 dω2 − (I3 − I1 )ω3 ω1
dt
die Eulerschen Gleichungen
im körperfesten
Hauptachsensystem [123]
(24)
τ3 = I3 dω3 − (I1 − I2 )ω1 ω2
dt
Mit diesem Rüstzeug kehren wir zum Kreisel zurück.
2.2 Der kräftefreie rotationssymmetrische Kreisel
Man betrachtet einen rotationssymetrischen starren Körper mit einem Fixpunkt. Rotationssymmetrie bedeutet in unserem Formalisums, dass zwei der drei Trägheitsmomente gleich sind, z.B.
I1 = I2 .
Auf einen kräftefreien Kreisel wirkt kein Drehmoment (~τ◦ = 0). Er kann im Schwerefeld realisiert werden, indem man ihn im Schwerpunkt aufhängt (der raumfeste Punkt ◦ ist dann gleich
dem Schwerpunkt S) oder eine kardanische Aufhängung wählt.13 Bei Rotationssymmetrie ist im
körpereigenen System I1 = I2 =: I und die 3-Achse ist die Figurenachse durch den Schwerpunkt.
3
S=o
2
1
Mit den Eulerschen Gleichungen und dLs = τs = τ◦ = 0
dt
ist
d
0 = I dω1 − (I − I3 )ω2 ω3
| I1 dt
···
dt
dω
0 = I 2 − (I3 − I)ω3 ω1
dt
0 = I3 dω3 − (I − I)ω1 ω2 = I3 dω3 ⇒ ω3 = konst.
dt
dt
3
S
Kombiniert man wie angedeutet die beiden ersten Gleichungen, so erhält man
0=
d2 ω1 I − I3 dω2
(I − I3 )(I3 − I)
ω3 = ω̈1 −
ω1 · ω32 =: ω̈1 + ω1 · ω◦2 .
−
dt2
I
dt
I ·I
(25)
Dies ist eine Schwingungsgleichung mit der konstanten Frequenz
ω◦ =
(I3 − I)
ω3
I
(26)
und den Lösungen
ω1 = c · sin(ω◦ t − δ)
13
(27)
~ am Schwerpunkt angreift.
Ein Diskus fliegt frei von Drehmomenten, da die Schwerkraft G
13
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
. Analog ergibt sich aus der umgekehrten Kombination der beiden Gleichungen ω2 = −c·cos(ω◦ t−
δ).
Beispiel Erde: Die Rotationsachse führt eine Nutationsbewegung aus mit einer Amplitude auf
der Oberfläche der Erde von etwa 6 m. Aus der bekannten Form und unter Annahme einer
konstanten Dichte erhält man eine Period von Tgerechnet = 304 Tage. Der gemessene Wert
beträgt Tgemessen = 433 Tage.
Der Unterschied kommt unter anderem dadurch zustande, dass die Erde kein starrer Körper ist,
sondern einen flüssigen Kern hat und natürlich keine homogene Dichteverteilung besitzt.
Zusätzlich zu dieser freien Nutation kommt noch eine erzwungene Schwingung dazu, die von
den jahreszeitlichen Massenverschiebungen auf der Erdoberfläche (Schnee etc.) und von unregelmässigen Ereignissen (z.B. Erdbeben) erzeugt werden. Die effektiv gemessene Nutationsamplitude schwant deshalb zwischen 2m und 8m.
Figurenachse
→
Gangpolkegel
3
ω
ω→3
ω→
→
ω2
→
ω1
2
1
c
"
korperfestes
System
2 =: c2 . ω und ω
Im körperfesten System ist ω12 + ω22 = ω⊥
1
2
sind die Komponenten eines Vektors ω
~ ⊥ , der in der senkrecht
zur 3-Achse stehenden Ebene mit der Winkelgeschwindigkeit
ω◦ rotiert. Da ω
~ =ω
~ ⊥ + ω3~e3 gilt, ist auch |~
ω | = konst. Somit muss sich ω
~ auf einem Kegel, dem Gangpolkegel, um
die Figurenachse14 drehen. Ist ω1 = ω2 = 0 und damit
ω
~ = ω
~ 3 = konst, dann bleibt der Kreisel in der Figurenachse stehen (ruhender Kreisel). Im raumfesten System ist
~ s = konst. Man wählt daher zweckmässig
der Drehimpuls L
~ s = I1 ω1~e1 + I2 ω2~e2 + I3 ω3~e3 (I hat
die z-Achse ↑↑ L
im körperfesten Hauptachsensystem nur Diagonalelemente). Die 3-Komponente des Drehimpulses ist Ls3 = I3 ω3 =
Ls cos ϑ = konst.
Man beobachtet folgende Bewegungen der einzelnen Axialvektoren:
z
Nutations- →
Ls
kegel
ϑ
3
Ls3
raumfestes System
CO
C
C
~s C
L
CO
C (I3 − I)ω3~e3 C I~
ω
C
14
ω
~ dreht auf dem Gangpolkegel um die Figurenachse 3 im körperfesten
Hauptachsensystem. Die Figurenachse 3 dreht unter dem konstanten
Winkel ϑ um die raumfeste z-Achse (Nutationskegel). Wie bewegt
sich ω
~ in Bezug auf die raumfeste z-Achse?
~ s = 1 ωz Lz =
Aus der Energiebetrachtung Krot = 21 ω
~ Is ω
~ = 12 ω
~ ·L
2
konst (siehe später, Gl.(32)) muss mit Lz = Ls = konst auch
ωz = konst gelten. Damit läuft ω
~ auf einem Kegel um die z-Achse
(Rastpolkegel).
~ s, ω
Wir überzeugen uns, dass dann alle drei Vektoren L
~ und ~e3 (=
ˆ
~
3-Achse) in jedem Moment in einer Ebene liegen. Es ist ja Ls =
I(ω1~e1 + ω2~e2 ) + I3 ω3~e3 = I~
ω⊥ + I3 ω3~e3 = I(~
ω − ω3~e3 ) + I3 ω3~e3 =
~ s liegt also in der durch die
I~
ω + (I3 − I)ω3~e3 . Der Summenvektor L
Komponentenvektoren ω
~ und ~e3 aufgespannten Ebene.
so die Bezeichnung für die Hauptachse mit dem grössten Trägheitsmoment
14
Ergänzungen zu Physik I
Nutationskegel
2
Eigenschaften des Kreisels
Da die relative Lage der drei Vektoren sich nicht ändert,
bleibt als einzig mögliche Bewegung die Drehung dieser Ebene um die raumfeste Ls -Richtung übrig. Da sich aber ω
~
~ sschon um die Figurenachse dreht und sich beide um die L
Achse drehen, haben wir folgendes Resultat für die
z
3
→
→
ω
Bewegung des symmetrischen Kreisels:15
Ls
Rastpolkegel
Gangpolkegel
prolater Kreisel I1 = I2 > I3
a) ω
~ dreht sich um Ls auf dem raumfesten Rastpolkegel.
b) ω
~ dreht sich um die Figurenachse 3 auf dem
körperfesten Gangpolkegel.
z
3
Nutationskegel
Rastpolkegel
~ s auf dem raumd) Die Figurenachse dreht sich um L
festen Nutationskegel.
ω→
Gangpolkegel
c) Beide Kegel rollen aufeinander ab, ω
~ bildet die gemeinsame Mantellinie.
Je nach Anfangsbedingungen ist natürlich auch der Spezialfall möglich, dass die ω
~ -Drehachse und die Figurenachse mit der Richtung des raumfesten Drehimpulses zusammenfallen.
→
Ls
oblater Kreisel I1 = I2 < I3
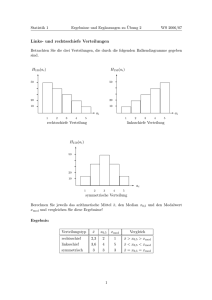
2.3 Stabilität der Drehachse für Körper ohne Rotationssymmetrie
Die Stabilität eines Systems z.B. im Schwerefeld kann untersucht werden, indem man kleine
Auslenkungen aus der Gleichgewichtslage untersucht und die resultierende Bewegungsgleichung
näherungsweise aufstellt.
Die Bewegungsgleichung ist dann vom Typ
stabil
indifferent
labil
ẍ + a2 x ≈ 0. Mit a2 > 0 erhält man eine Lösung
x(t) ≈ cos(at); x(t) bleibt endlich, ist also stabil.
Mit a2 < 0 ist x(t) ≈ eat und x(t) → ∞, die Lösung ist
labil.
Allgemein ist für eine kräftefreie Bewegung ~τ◦ = 0 und I1 =
6 I2 6= I3 im Hauptachsensystem.
Dreht sich der Körper bei Stabilität praktisch nur um eine Hauptachse, dann ist ω1 ≈ ω2 ≈ 0
15
Die Figuren beschreiben einen prolaten Kreisel (I1 = I2 > I3 ), bei dem der Rastpolkegel ausserhalb auf
dem Gangpolkegel läuft, und einen oblaten Kreisel (I1 = I2 < I3 ), bei dem der Rastpolkegel innerhalb des
Gangpolkegels läuft.
15
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
und ω3 6= 0 und die Eulerschen Gleichungen (Gl.(24)), wenn der quadratisch kleine Term ω1 ω2
vernachlässigt wird, sind
ω̇1 −
I2 − I3
ω2 ω3 = 0,
I1
ω̇2 −
I3 − I1
ω3 ω1 = 0,
I2
ω̇3 −
I1 − I2
ω1 ω2 = 0
I3 | {z }
≈0
⇒ ω3 = konst.
Durch Differenzieren der ersten beiden Gleichungen und Einsetzen erhält man für ω1 und ω2
(analog zu S.13) die Schwingungsgleichungen
ω̈1 −
|
I2 − I3 I3 − I1 2
ω3 ω1 = 0
I1
I
{z 2
}
2
a
und
ω̈2 −
|
I3 − I1 I2 − I3 2
ω3 ω2 = 0
I2
I
{z 1
}
2
a
3 I3 −I1
ã stabil für a2 > 0 ⇒ I2I−I
< 0, es muss dann I3 das grösste oder das kleinste
I2
1
Trägheitsmoment um die Hauptachse 3 sein.
ã instabil für a2 < 0 ⇒ I1 < I3 < I2 führt ω1 exponentiell von einer zunächst reinen
Rotation um die Hauptachse 3 weg ins Torkeln.
Die Hauptachsen mit dem grössten
Trägheitsmoment sind stabile Drehachsen.
und
dem
kleinsten
Anschauliche Betrachtung dieser Stabilitätsbedingungen: Bei gleicher kinetischer Rotationsenergie 21 Iω 2 entspricht die Rotation um die Hauptachse mit dem maximalen (minimalen)
Trägheitsmoment dem minimalen (maximalen) ω, d.h. ω kann bei erhaltener Energie der Rotation nicht mehr in beide Richtungen verändert werden.
Ein anderes Stabilitätsbeispiel ist das Problem des Lassowerfers: Das Lasso klappt beim Drehen
zu einem Stab zusammen, da das Trägheitsmoment für den Stab mit der Länge ` kleiner ist als
1
für einen Kreis mit dem Umfang 2` also IStab = 12
m`2 < IKreis = π12 m`2 . Man muss deshalb
beim Lassowerfen die Anfangsbedingungen besser wählen und das Lasso steifer machen.
2.4 Symmetrischer Kreisel im Schwerefeld (Präzession)
z 6
~◦
~rs k ω
~ kL
@
@ @
@
α ~rs
c
~
G
?
Wir kehren zum symmetrischen Kreisel zurück. Der Kreisel sei jetzt aber
nicht mehr im Schwerpunkt unterstützt, so dass das Gewicht ein Dreh~ ausübt und folglich L
~ ◦ nicht mehr konstant ist. Die
moment ~τ◦ = ~rs × G
daraus resultierende Bewegung der Drehimpulsachse nennt man Präzession.
Zur Vereinfachung nehmen wir an, die Figurenachse, Drehachse und Drehimpulsachse fallen zusammen und ~rs liege in der Figurenachse.
Es ist also
~◦ k ω
L
~ k ~rs .
16
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
Ferner sei ω3 sehr gross.16 Dann sind wir nicht mehr auf die Euler-Gleichungen angewiesen,
sondern können den
~
~ = dL◦
Drehimpulsatz ~τ◦ = ~rs × G
dt
bq
~◦
L
?
~◦
dL
?
~
τ◦
→
benützen.
~ ◦ , aber parallel zu dL
~ ◦ steht, muss dL
~ ◦ senkrecht auf
Da ~τ◦ senkrecht zu L
~
L◦ stehen. Dieser Sachverhalt gilt für jeden Augenblick, also muss sich die
~ ◦ -Vektors auf einem Kreis bewegen, L
~ ◦ selbst präzessiert auf
Spitze des L
~ ◦ ist also ein
einem Kegelmantel, dem Präzessionskegel, um die z-Achse. L
Vektor, der im Relativsystem (Hauptachse) konstant ist und im Absolutsystem nur seine Richtung, nicht aber seinen Betrag ändert. Die Ableitung
des Drehimpulses und somit das Drehmoment stehen deshalb senkrecht auf
L~◦ , man kann somit schreiben (siehe auch Ergänzungsblätter Relativbe”
wegungen“, Gl.(5), S.3.):
→
ωp
dL o
~τ◦ =
~◦
dL
~◦ .
=ω
~p × L
dt
→
Lo
α
ωp nennt man Präzessions-Kreisfrequenz. Der Drehimpulsvektor weicht
~ aus.
also der angreifenden Kraft G
dL
~
◦ ~ = rs G sin α = ω
~ ◦ = ωp L◦ sin α
Da |~τ◦ | = ~p × L
= ~rs × G
dt gilt, folgt
(28)
rs G
rs M g
ωp =
=
L◦
ω3 I3
die Präzessionsfrequenz
des rasch rotierenden
symmetrischen Kreisels
(unabhängig von α).
(29)
Infolge dieser Präzession hat der Kreisel einen kleinen Drehimpuls in der z-Richtung erhalten.
r Mg
Falls jedoch ωp ω3 ist, d.h. für ω32 sI , können wir diesen Drehimpuls vernachlässigen
3
~ ◦ rechnen.
und nur mit L
Eine genaue Rechnung mittels der Euler-Gleichungen zeigt, dass die Kreiselachse nicht eine einfache Präzession um die z-Achse ausführt, sondern dabei noch Schwankungen des Winkels α auftreten (Nutation). Immerhin gibt es immer einen bestimmten Winkel α, bei dem die Präzession
nutationsfrei ist. Insbesondere ist die senkrechte Lage α = 0 nutationsfrei, solange gilt
ω > ωkrit =
16
2p
M grs I1 .
I3
schlafender Kreisel
(30)
Der Grund für diese Annahme wird mit Gl.(29) klar.
17
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
Sieht man von der Nutation ab, so gelten für den Kreisel die folgenden Regeln:
→
Lo
→
1. Ein äusseres Drehmoment erzeugt bei einem frei beweglichen
~ ◦ , wobei die Änderung von L
~ ◦ die
Kreisel eine Präzession von L
Richtung von ~τ◦ besitzt.
ωp
2. Verhindert man eine Präzession durch Anbringen von
Führungen, so erzeugen die Führungen Kräfte, welche die Kreiselachse senken oder heben.
Wand
→
N
3. Will man eine Präzession der Drehachse erzwingen, so müssen
die Lager die entsprechenden Kräfte und Drehmomente aufbringen.
→
ω
Mg
Beispiel zu 2):
~
~τ = ~r × N
d
H
HH
j
~r Die Führungskraft N erzeugt ein Drehmoment
~
~τ = ~r × N
~ ◦ k ~τ . Die Kreiselachse senkt sich. Wirkt N
~ umund eine Änderung dL
gekehrt, d.h. versucht man die Präzession zu vergrössern, so steigt die
Kreiselachse.
0
→
→
Lo
→
→
F2
ω
F 1 Beispiel zu 3):
Wird die Kreiselachse in der Horizontalebene gedreht, 50
so müssen die Lager die Kräfte F~1 , F~2 ausüben, deren
→
~
Mo Drehmoment parallel zu dL◦ steht.
2.5 Rotationsenergie und Energiesatz für die allgemeine Drehung
Die kinetische Energie K eines Systems von Massenpunkten kann durch die Schwerpunktsgeschwindigkeit ~v und die die Relativgeschwindigkeit ~vsi der DrehungPum den Schwerpunkt
ausgedrückt werden, wobei das Schwerpunktssystem definiert ist durch ni=1 mi~vsi = 0:
1X
1
1X
1X
2
2
mi (~v + ~vsi )2 =
mi (~v 2 + 2~v~vsi + ~vsi
) = m~v 2 +
mi~vsi
.
K=
2
2
2
2
i
i
i
Für einen starren Körper gilt ~vsi = ω
~ × ~rsi mit ~rsi dem Ortsvektor im Schwerpunktssystem.
Damit ist die kinetische Energie
1
1X
1
1X
1
1
~s
K = m~v 2 +
mi~vsi · (~
ω × ~rsi ) = m~v 2 +
mi ω
~ · (~rsi × ~vsi ) = m~v 2 + ω
~ ·L
2
2
2
2
2
2
i
i
|
{z
}
~
=ω
~ · Ls
18
Ergänzungen zu Physik I
⇒
2
Eigenschaften des Kreisels
1
1
m~v 2 + ω
~ Is ω
~ = Ktrans + Krot
2
2
(31)
In dieser Form der Aufspaltung in Translationsenergie und Rotationsenergie gilt die Gleichung
Gl.(31) nur für Drehungen um den Schwerpunkt. Für die Drehbewegung um einen beliebigen
raumfesten Punkt mit ~vi = ω
~ × ~ri ohne äussere Drehmomente ~τ = 0 hat man die kinetische
Energie
1
~ = 1ω
Kkin = Krot = ω
~ ·L
~ I~
ω ,
(32)
2
2
für welche der Energieerhaltungssatz gilt.
19