Links- und rechtsschiefe Verteilungen

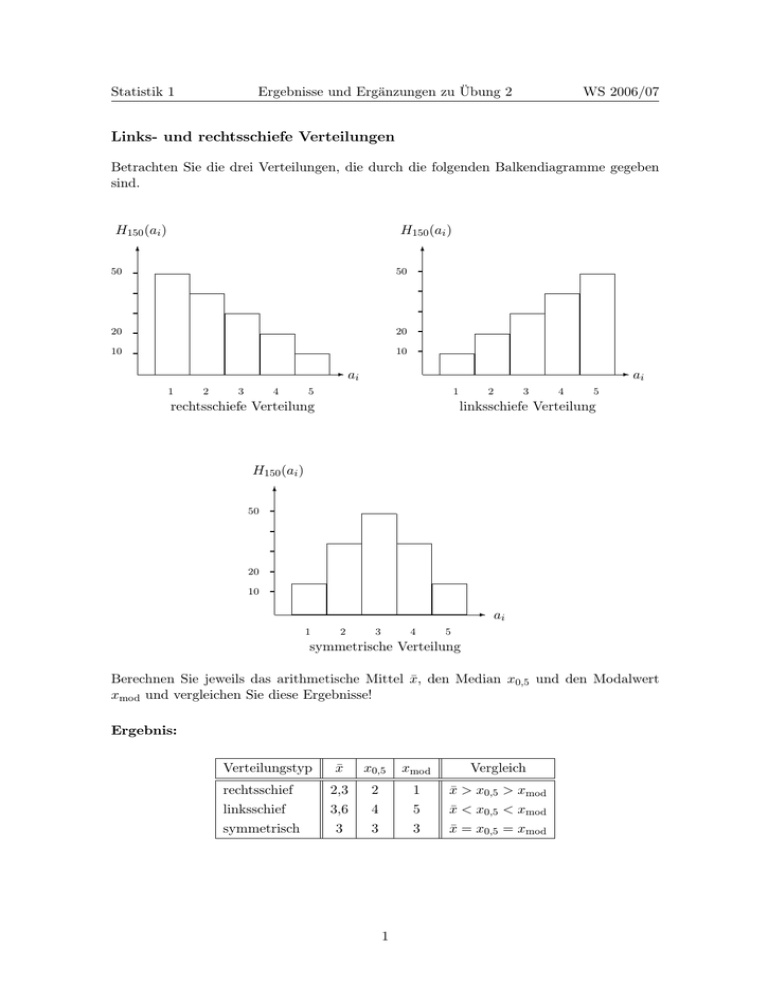
Statistik 1
Ergebnisse und Ergänzungen zu Übung 2
WS 2006/07
Links- und rechtsschiefe Verteilungen
Betrachten Sie die drei Verteilungen, die durch die folgenden Balkendiagramme gegeben
sind.
H150 (ai )
H150 (ai )
6
6
50
-
-
50
-
-
-
-
20
-
20
-
10
-
10
-
-a
i
1
2
3
4
-a
i
5
1
rechtsschiefe Verteilung
2
3
4
5
linksschiefe Verteilung
H150 (ai )
6
50
-
20
-
10
- a
i
1
2
3
4
5
symmetrische Verteilung
Berechnen Sie jeweils das arithmetische Mittel x̄, den Median x0,5 und den Modalwert
xmod und vergleichen Sie diese Ergebnisse!
Ergebnis:
Verteilungstyp
rechtsschief
linksschief
symmetrisch
x̄
x0,5
xmod
Vergleich
2,3
3,6
3
2
4
3
1
5
3
x̄ > x0,5 > xmod
x̄ < x0,5 < xmod
x̄ = x0,5 = xmod
1
Statistik 1
Ergebnisse und Ergänzungen zu Übung 2
WS 2006/07
Hier sind die Ergebnisse der Aufgaben 2 und 4 vom zweiten Übungsblatt.
Fragen zum Lösungsweg können in der Vorlesung geklärt werden.
Aufgabe 2.
Kenngröße
arithmetisches Mittel:
Median:
unteres Quartil:
oberes Quartil:
Modalwert:
Spannweite:
Quartilabstand:
Stichprobenvarianz:
Standardabweichung:
Variationskoeffizient:
a)
x̄
x0,5
x0,25
x0,75
xmod
R
SQ
s2
s
V
b)
4,7
4
4
6
4
6
2
2,70
1,64
0,35
44,045
42,04
24,83
60,74
35
100
35,91
589,81
24,29
0,55
Aufgabe 4.
a)
x̄A = 542
x̄B = 402
s2A ≈ 634, 4
s2B ≈ 584, 4
sA ≈ 25, 2
sB ≈ 24, 2
b) Kosten am Tag: yi = (xi · Stückkosten + Fixkosten), also
yA,i = 26xi + 2010
bzw.
ȳA = 26 · 542 + 2010 = 16102
s2yA
2
= 26 ·
s2A
yB,i = 32xi + 1540 .
ȳB = 32 · 402 + 1540 = 14404
s2yB = 322 · s2B ≈ 598471, 1
≈ 428884, 4
syA ≈ 654, 9
syB ≈ 773, 6
c) Hier war die Aufgabenstellung etwas missverständlich. Man kann zum einen die
durchschnittliche Produktion (bzw. Kosten) pro Tag und Standort berechnen, indem
man die Werte von Standort A und B als eine Stichprobe vom Umfang 20 betrachtet
und hiervon Mittelwert, Varianz und Standardabweichung ermittelt. Das ergibt die
Werte:
Produktion pro Tag und Standort:
10x̄A + 10x̄B
= 472
20
9s2 + 9s2B
10(x̄A − 472)2 + 10(x̄B − 472)2
s2 = A
+
≈ 5735, 3
19
19
s ≈ 75, 7
x̄ =
2
Statistik 1
Ergebnisse und Ergänzungen zu Übung 2
WS 2006/07
Kosten pro Tag und Standort:
10ȳA + 10ȳB
= 15253
20
9s2yA + 9s2yB
10(ȳA − ȳ)2 + 10(ȳB − ȳ)2
s2y =
+
= 1245380
19
19
sy ≈ 1116, 0
ȳ =
Die durchschnittliche Gesamtproduktion und Gesamtkosten pro Tag hingegen ergeben sich, wenn man für jeden Tag die jeweiligen Werte der beiden Standorte addiert,
also folgende Tabelle erstellt
Tag
Gesamtproduktion
Gesamtkosten
Tag
Gesamtproduktion
Gesamtkosten
1
2
3
4
5
960
975
930
930
930
31120
31270
30280
30010
30130
6
7
8
9
10
895
975
935
965
945
29100
31540
30080
30980
30550
und anschließend Mittelwert, Varianz und Standardabweichung errechnet. Man erhält dann:
Gesamtproduktion pro Tag:
x̄ = 944
s2 ≈ 632, 2
s ≈ 25, 1
Gesamtkosten pro Tag:
ȳ = 30506
s2y ≈ 539248, 8
sy ≈ 734, 3
3