physikalische Formelsammlung (Mechanik)

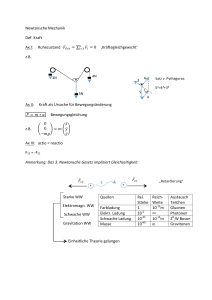
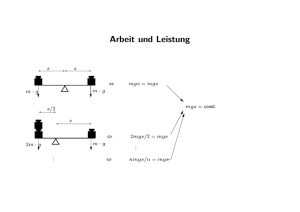
Physikalische Formelsammlung
Gleichförmige Bahnbewegung und Kreisbewegung
Bewegungsgleichung für die
gleichförmige lineare Bewegung:
v=
ds
dt
Winkelgeschwindigkeit bei der
gleichmäßigen Kreisbewegung:
ω=
2π
T
Zusammenhang zwischen der
Bahngeschwindigkeit v und der
Winkelgeschwindigkeit ω:
oder
α
3600
=
4s
4t
(1)
(2)
v =ω∗r
Umrechnung von Gradmaß ins
Bogenmaß :
v=
bzw.
4ϕ
2π
ω=
v
r
(3)
(4)
Die gleichmäßig beschleunigte Bewegung
d2 s
dt2
Definition der Beschleunigung:
a=
Geschwindigkeit-Zeit-Gesetz der
gleichmäßig beschleunigten
Bewegung:
v =a∗t
oder
a=
dv
dt
(5)
(6)
Weg-Zeit-Gesetz der gleichmäßig
beschleunigten Bewegung:
s=
1
2
∗ a ∗ t2
Berechnung des Weges bei
gegebener Geschwindigkeit:
s=
1
2
∗v∗t
(7)
(8)
Die beschleunigte Bewegung mit Anfangsgeschwindigkeit
Geschwindigkeit-Zeit-Gesetz:
v = a ∗ t + v0
Weg-Zeit-Gesetz:
s = v0 ∗ t +
Geschwindigkeit-Zeit-Gesetz
(abgebremste Bewegung)
1
2
(9)
∗ a ∗ t2
v = v0 − a ∗ t
Weg-Zeit-Gesetz
(abgebremste Bewegung)
s = v0 ∗ t −
1
2
(11)
∗ a ∗ t2
Bremszeit beim Abbremsen auf die
Geschwindigkeit Null
tB =
v0
a
(12)
Bremsweg beim Abbremsen auf die
Geschwindigkeit Null
sB =
v02
2a
(13)
sB =
1
2
Bremsweg beim Abbremsen aus der
Geschwindigkeit v0 auf die
Geschwindigkeit v1
1
(10)
∗ t ∗ (v0 + v1 )
(11)
(14)
Freier Fall und Wurfbewegungen
Geschwindigkeit-Zeit-Gesetz
v = g ∗ t mit g = 9.81m/s2
Weg-Zeit-Gesetz für die Fallhöhe
h=
1
2
Fallhöhe in Abhängigkeit
Fallgeschwindigkeit
h=
v2
2g
zur
tw =
Wurfzeit (waagrechter Wurf)
∗ g ∗ t2
(16)
(17)
q
2h
g
(18)
q
2h
g
Wurfweite (waagrechter Wurf)
w = v0 ∗
Wurfzeit (lotrechter Wurf)
tw =
2v0
g
Steigzeit (lotrechter Wurf)
ts =
v0
g
(21)
h=
v02
2g
(22)
Wurfhöhe (lotrechter Wurf)
(15)
(19)
(20)
Geschwindigkeit-Zeit-Gesetz
(lotrechter Wurf)
v = v0 − g ∗ t
Weg-Zeit-Gesetz (lotrechter Wurf)
s = v0 ∗ t −
1
2
(23)
∗ g ∗ t2
(24)
Trägheit, Kraft und Masse
1. Newtonsches Axiom
Ein Körper beharrt im Zustand der
Ruhe oder der gleichförmig gradlinigen
Bewegung, solange keine äußeren
Kräfte auf ihn wirken
2. Newtonsches Axiom
(Grundgleichung der Mechanik)
F =m∗a
(25)
Kräfte und einfache Maschinen
3. Newtonsches Axiom
Übt ein Körper auf einen zweiten
eine Kraft (genannt actio) aus, so übt
auch der zweite Körper auf den ersten eine
Gegenkraft (genannt reactio) aus,
die der ursprünglichen Kraft
entgegengesetzt und gleich groß ist
actio=reactio
Gleitreibung
FR = µ R ∗ FN
Haftreibung
FHa = µHa ∗ FN
Kräftezerlegung bei der schiefen
Ebene
F~G = F~N + F~H
Kräftezerlegung beim Flaschenzug
n ist die Anzahl der Rollen
F =
1
n
∗ FG
(26)
(27)
(28)
(29)
2
Zentipetalkraft
Fr = m ∗ ω 2 ∗ r bzw. Fr = m ∗ vr
Druck
p=
2
F
A
(31)
(30)
Energie und Arbeit
Hubarbeit
WH = G ∗ h
Potentielle Energie
Wpot = G ∗ h = m ∗ g ∗ h
Arbeit(Kraft entlang des Wegs)
W = Fs ∗ s
Arbeit(Kraft in beliebiger Richtung)
W = F ∗ s ∗ cos α
(32)
(33)
(34)
(34)
Kinetische Energie und Energieerhaltung
W = 21 m ∗ v 2
Beschleunigungsarbeit
Beschleunigungsarbeit
von
einer Anfangsgeschwindigkeit v0 auf
eine Endgeschwindigkeit v1
(35)
W = 21 m ∗ (v12 − v02 )
(36)
kinetische Energie
Wkin = 12 m ∗ v 2
mechanische Energieerhaltung
E = Ekin + Epot = const.
(37)
(38)
Spannenergie und Leistung
Hooksches Gesetz
F = D ∗ 4l
Spannenergie
WSpann = 21 D ∗ s2
Reibungsarbeit
WR = F R ∗ s = µ ∗ F N ∗ s
Leistung
P =
Momentanleistung
P = Fs ∗ v
Wirkungsgrad
η=
3
4W
4t
(39)
(40)
(42)
(43)
N utzleistung
Eingangsleistung
(44)
(41)
Impuls und Impulserhaltung
Impuls
p
~ = m ∗ ~v
Gesamtimpuls
p
~=p
~1 + p~2
Impulserhaltung (elastischer Stoß)
p
~1v + p
~2v = p~1n + p~2n
(45)
(46)
(47)
zentraler unelastischer Stoß:
Impulserhaltung
m1 ∗ u1 + m2 ∗ u2 = (m1 + m2 ) ∗ v
Geschwindigkeit nach dem Stoß
v=
kinetische Energie vor dem Stoß
Ekin = 12 m1 ∗ u21 + 12 m2 ∗ u22
kinetische Energie nach dem Stoß
Ekin =
Energiedifferenz
4Ekin =
m1 ∗u1 +m2 ∗u2
m1 +m2
1
2
(49)
∗ (m1 + m2 ) ∗ v 2
1
2
∗
(48)
m1 ∗m2
m1 +m2
(50)
(51)
∗ (u1 − u2 )2
(52)
zentraler elastischer Stoß:
Impulserhaltung
m 1 ∗ u 1 + m 2 ∗ u 2 = m 1 ∗ v1 + m 2 ∗ v2
(53)
Energieerhaltung
1
2 1
2
2 m1 ∗u1 + 2 m2 ∗u2
(54)
Geschwindigkeitsrelation
u 1 + v1 = u 2 + v2
Geschwindigkeit nach dem Stoß
v1 =
2m2
m1 +m2
∗ u2 +
m1 −m2
m1 +m2
∗ u1
(56)
Geschwindigkeit nach dem Stoß
v2 =
2m1
m1 +m2
∗ u1 +
m2 −m1
m1 +m2
∗ u2
(57)
4
= 12 m1 ∗v12 + 12 m2 ∗v22
(55)
Drehmoment und Rotationsenergie
Bahngeschwindigkeit
v=
2∗π∗r
T
Winkelgeschwindigkeit
ω=
4ϕ
4t
Winkelbeschleunigung
α = 4ω
(60)
4t
~ = F~Dreh ∗ ~r = F ∗ r ∗ sin γ
M
Drehmoment
=ω∗r
=
2∗π
T
(58)
(59)
Drehmoment
~ =J ∗α
M
(62)
Trägheitsmoment (Hohlzylinder)
J = m ∗ r2
(63)
Trägheitsmoment (Vollzylinder)
J = 12 m ∗ r 2
Trägheitsmoment (Rechteckplatte)
J=
1
12 m
∗ l2
(65)
Trägheitsmoment eines Stabes
J=
1
12 m
∗ l2
(66)
Trägheitsmoment einer Kugel
J = 52 m ∗ r 2
(67)
Trägheitsmoment eines Kegels
J=
Rotationsenergie
WRot = 21 J ∗ ω 2
Arbeit bei der Rotation
WRot = M ∗ ϕ
Drehimpuls
L=J ∗ω
Drehmoment
~ =
M
Rotationsleistung
P =M ∗ω
5
3
10 m
(64)
∗ r2
~
4L
4t
(68)
(69)
(70)
(71)
(72)
(73)
(61)
Planetenbewegung und Gravitation
1. Keplersches Gesetz:
Die Planeten bewegen sich auf Ellipsen, in
deren einem gemeinsamen Brennpunkt die
Sonne steht.
2. Keplersches Gesetz:
Ein von der Sonne zum Planeten gezogener ’Fahrstrahl’ überstreicht in gleichen
Zeiten gleiche Flächen.
3. Keplersches Gesetz:
T12
r13
Gravitationsgesetz
F =f∗
Fallbeschleunigung des Satelliten
gh = g ∗
=
T22
r23
r
= C = konst
m1 ∗m2
r2
2
rE
2
rS
g∗
2
rE
2
rS
(74)
(75)
(76)
∗ rS =
r
g∗
2
rE
rS
Bahngeschwindigkeit des Satelliten
v=
Hubarbeit
4W = f ∗ m1 ∗ mE ∗ ( r1E −
Hubarbeit
4W1,2 f ∗ m1 ∗ mE ∗ ( r11 −
1. kosmische Geschwindigkeit
v=
2. kosmische Geschwindigkeit
v=
Gravitationspotential
V = −f ∗
Gravitationskonstante
f = 6.67 ∗ 10−11
Sonnenmasse
mS = 1.99 ∗ 1030 kg
(83)
Erdmasse
mE = 5.97 ∗ 1024 kg
(84)
Mondmasse
mM = 7.36 ∗ 1022 kg
(85)
Erdradius
rE = 6.37 ∗ 106 m
Bahnradius (Erde)
0 = 1.50 ∗ 1011 m
rE
(87)
Bahnradius (Mond)
0 = 3.84 ∗ 108 m
rM
(88)
6
q
q
f∗
mE
rE
2∗f ∗
m
r
1
r1 )
= 11.18 ∗ 103
(82)
m3
kg∗s2
(82)
(86)
(78)
1
r2 )
m
s
= 7.91 ∗ 103
mE
rE
(77)
(79)
(80)
m
s
(81)
Gasgesetz und Wärmelehre
Längenausdehnung:
4` = α ∗ `0 ∗ 4T
Längenausdehnung:
4` = α ∗ `1 ∗ (T2 − T1 )
Längenausdehnung:
`T = `0 ∗ (1 + α ∗ T )
(91)
Volumenausdehnung:
VT = V0 ∗ (1 + γ ∗ T )
(92)
Volumenausdehnung (Gas):
VT = V0 ∗ (1 +
Gasgleichung (p,V,T):
p∗V
T
Gasgleichung (p,V,T):
p1 ∗V1
T1
Gasgleichung (p,V,T):
p∗V = n∗R∗T
Gasgleichung (ρ,p,T):
p=
Barometrische Höhenformel:
p = p0 ∗ e
1
273
= konst.
=
R
M
(89)
(90)
∗ 4T )
(93)
(94)
p2 ∗V2
T2
= konst.
∗T ∗ρ
(95)
(n = m/M )
(96)
(97)
ρ
− p0 ∗g∗h
(98)
ρ
− p0
0
(99)
0
∗g∗h
Barometrische Höhenformel:
ρ = ρ0 ∗ e
kin. Gastheorie:
kin =
kin. Gastheorie:
p ∗ Vmol = R ∗ T =
Wärmemenge:
4Q = c ∗ m ∗ 4T
(102)
Innere Energie (1.Hauptsatz):
4U = 4Q + 4W
(103)
Isochore Zustandsänderung:
dQ = dU = CV ∗ dT
Isobare Zustandsänderung:
dQ = dU +p∗dV = Cp ∗dT (Cp = cp ∗m) (105)
Zusammenhang Cp , CV :
Cp = CV + n ∗ R
Isotherme Zustandsänderung:
dQ = p ∗ dV → W = n ∗ R ∗ T ∗ ln( VV12 )
Adiabatische Zustandsänderung:
dU = CV ∗ dT = −p ∗ dV
Adiabatische Zustandsänderung:
T ∗ V κ−1 = const.
Wärmeleistung:
P =
Entropie
Q
t
4S =
7
3
2
∗k∗T
(100)
2
3
∗ NA ∗ kin
(CV = cV ∗ m)
dQrev
T
(104)
(106)
(109)
(110)
R
(101)
(111)
(108)
(107)
Mechanik deformierbarer Medien
Zugspannung:
σ=
F
A
(112)
Dehnung:
=
4`
`
(113)
Elastizitätsmodul E:
σ =E ∗
(114)
Elastizitätsmodul E:
E=
F/A
4`/`
(115)
Scherspannung τ :
τ=
FS
A
Scherung γ:
γ=
4x
`
= tan θ
Torsionsmodul G:
G=
τ
γ
FS /A
4x/`
Kompressionsmodul κ:
κ = − dVdp/V
Kontinuitätsgleichung:
v1
v2
=
8
(116)
=
A2
A1
(117)
(118)
(119)
(120)