E1 V5

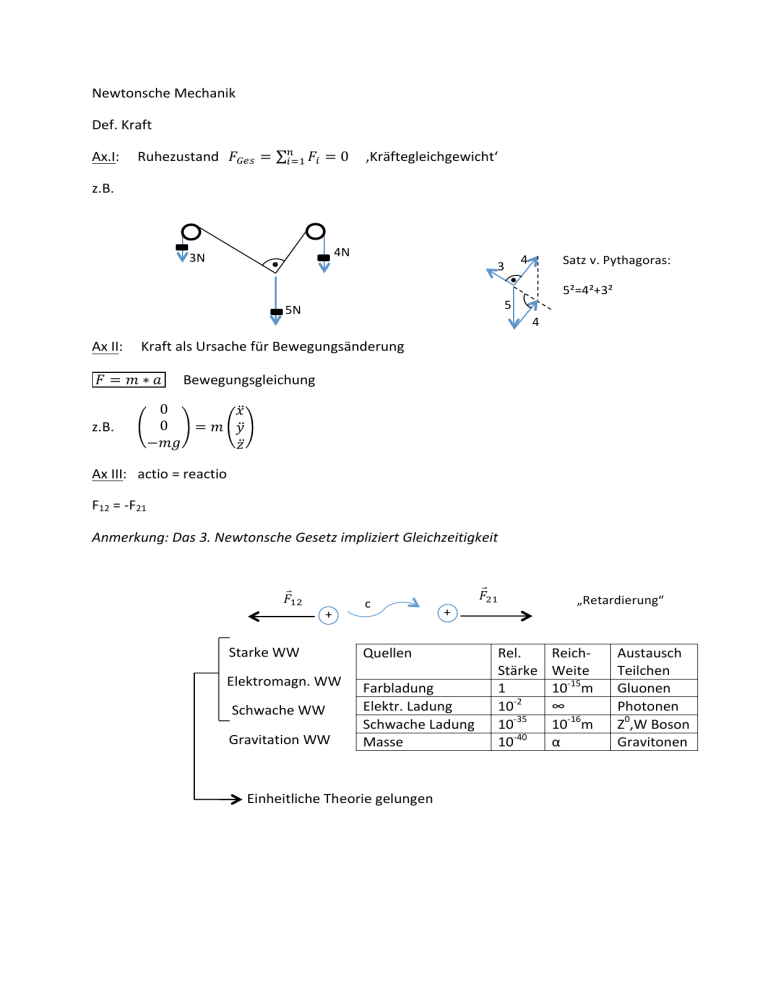
Newtonsche Mechanik Def. Kraft !
!!! 𝐹!
Ax.I: Ruhezustand 𝐹!"# =
= 0 ‚Kräftegleichgewicht‘ z.B. 4N 3N 3 4 Satz v. Pythagoras: 5N 5²=4²+3² 5 4 Ax II: Kraft als Ursache für Bewegungsänderung 𝐹 = 𝑚 ∗ 𝑎 Bewegungsgleichung z.B. 0
𝑥
0
= 𝑚 𝑦 −𝑚𝑔
𝑧
Ax III: actio = reactio F12 = -­‐F21 Anmerkung: Das 3. Newtonsche Gesetz impliziert Gleichzeitigkeit 𝐹⃑ ⃑
𝐹!" + Starke WW Elektromagn. WW Schwache WW Gravitation WW + Quellen Farbladung Elektr. Ladung Schwache Ladung Masse Einheitliche Theorie gelungen c !"
Rel. Stärke 1 10-­‐2 10-­‐35 10-­‐40 „Retardierung“ Reich-­‐ Weite 10-­‐15m ∞ 10-­‐16m α Austausch Teilchen Gluonen Photonen Z0,W Boson Gravitonen Arbeit: !!
𝐹
!!
𝑤=
F
“Wegintegral der Kraft” x 𝑟 𝑑𝑟 Fx *x > 0 “der Körper verrichtet Arbeit” -­‐F * x < 0 „es wird gegen Kraft Arbeit verrichtet“ x F
Pot. E nergie: „Fähigkeit Arbeit zu verrichten“ !!
Δ𝐸!"# 𝑃! 𝑃! = 𝐸!"# 𝑃! − 𝐸!"# 𝑃! = −
𝐹 𝑟 𝑑𝑟 = −𝑊 !!
Kin. Energie: „Beschleunigungsarbeit“ Masse wird durch Kraft beschleunigt 1
𝐹 = 𝑚 ∗ 𝑎 𝑣 = 𝑎 ∗ 𝑡 𝑥 = 𝑎𝑡² 2
Kraft wirkt über Strecke x 𝑤!"#$!!. = 𝐹 ∗ 𝑥 = 𝑚 ∗ 𝑎
1 !
1
𝑎𝑡 = 𝑚 𝑎𝑡
2
2
!
1
= 𝑚𝑣² 2
1
𝐸!"# = 𝑚𝑣² 2
Potentielle Energie und Hubarbeit P2 Epot = m*g*h h P1 Epot = 0 !!
𝑊=
!!
(𝐹! 𝑒! + 𝐹! 𝑒! + 𝐹! 𝑒! ) ∗ 𝑑𝑥𝑒! + 𝑑𝑦𝑒! + 𝑑𝑧𝑒! =
!!
⇒𝑊=
𝐹! 𝑑𝑥 +
!!
Spezialfall Gravitationskraft 𝐹! =
!
−𝑚𝑔 𝑑𝑧
!
!!
0
0 −𝑚𝑔
= −𝑚𝑔ℎ = 𝐸!"# 0 − 𝐸!"# (ℎ) Konvention: 𝐸!"# 𝑧 = 0 = 0 ⇒ 𝐸!"# ℎ = 𝑚 ∗ 𝑔 ∗ ℎ !!
𝐹! 𝑑𝑧 𝐹! 𝑑𝑦 +
!!
!!
Kraftfeld + Potential Änderung der pot. Energie bei virtueller Verschiebung dx dEp,x Δ𝐸! =
!!!
!"
Δ𝑥 +
!!!
!"
Δ𝑦 +
!!!
!"
Δ𝑧 𝑊 = 𝐹! ∗ Δ𝑥 + 𝐹! ∗ Δ𝑦 + 𝐹! ∗ Δ𝑧 Vergleich der Koeffizienten: wegen 𝑊 = −Δ𝐸! 𝐹! = −
Def. !!!
!"
!!!
𝐹! = −
𝑔𝑟𝑎𝑑 =
!
!
!"
𝐹! = −
!
!
!!!
!"
!
!
„Vektoroperator“ „Nabla“ , ,
= 𝑒! !" + 𝑒! !" + 𝑒! !" = ∇ !" !" !"
⇒ 𝐹 = −𝑔𝑟𝑎𝑑 𝐸! (𝑟) Beispiele für pot. Energie 𝐸!"# = 𝑚 ∗ 𝑔 ∗ ℎ Hubarbeit Rückstellkraft 𝐸!"# = ! 𝐷𝑥² Feder F=-­‐Dx 𝐸!"# = 𝑚 ∗ 𝑔 ∗ ℎ Pendel !
𝑤 = ! −𝐷𝑥𝑑𝑥 = 𝑚 ∗ 𝑔 ∗ 𝑙 ∗ (1 − cos 𝛼) l !
≈ 𝑚 ∗ 𝑔 ∗ 𝑙 ∗ ! ∗ 𝛼² !
h ~𝑐𝑜𝑛𝑠𝑡 ! 𝛼² X0 Rückstellkraft 𝐹 = −𝑐𝑜𝑛𝑠𝑡. 𝛼 Epot X0 1 !!
𝐸!"# ≈ 𝐸! + 𝐸!"#
𝑥! ∗ 𝑥 − 𝑥!
2
!
+ ⋯ Nicht-­‐ konservative Kräfte (Dissipation) h 𝐸!"# = 𝐸!"# + 𝐸!"# + Δ𝐸!"## Δ𝐸!"## : Reibungsverlust, Wärmeenergie Reibungskräfte 𝐹! = −𝜇 ∗ 𝑓(v) Μ: Reibungskoeffizient z.B. 𝐹!"#$% = −6𝜋𝜂𝑟 ∗ v Bewegungsgleichung: 𝑚 ∗ 𝑎 = 𝐹!"# + 𝐹! 𝑚 ∗ 𝑎 = 𝐹!"# − 𝜇𝑓(v) Versuch: Ballistisches Pendel m1*v1 h X0 Wie erhalte ich Geschw des Blocks? Ekin (Geschoß) > Ekin (Block) wegen Reibungsverlust! Lösung Impulserhaltung! 𝑚! ∗ 𝑣! = 𝑚!"# ∗ 𝑣! Kinetische (Rest)Energie des Blocks nach Aufprall wird in pot. Energie verwandelt. !
!
!
𝑚!"# ∗ 𝑣!! = 𝑚!"# ∗ 𝑔 ∗ ℎ = ! 𝑚!"# ∗ 𝑔 ∗ 𝑙 ∗ 𝛼 ! ⇒ 𝑣!!" = 𝑔 ∗ 𝑙 ∗ 𝛼 ! =
!
!
𝑙∗𝛼
!
𝑣!! = 𝜔! ∗ 𝑥! 𝜔! =
= (𝜔! ∗ 𝑥! )! !
!
=
!!
!
Impulserhaltung 1 2 actio = reactio 𝐹⃑!" = −𝐹⃑!" è abgeschlossenes System wechselwirkender Teilchen 1 2 𝐹⃑!" + 𝐹⃑!" + 𝐹⃑!" + 𝐹⃑!" + … … . . +𝐹⃑!" = 0 3 4 Keine Kräfte von außen !
𝐹!" = 0 𝑎𝑙𝑙𝑔𝑒𝑚𝑒𝑖𝑛: !,!!!
!!!
2.Newtonsche Gesetz: !!!
!"
!!!
!"
= 𝐹!" + 𝐹!" + ⋯ = 𝐹!" + 𝐹!" + ⋯ ⋮ ___________________ !!!
!!! !"
𝑝!"# =
=
!
!,!!! 𝐹!"
!!!
!
!!! 𝑝!
= 0 = 𝑐𝑜𝑛𝑠𝑡 Impulserhaltungssatz „In einem abgeschlossenem System ist der Gesamtimpuls eine Erhaltungsgröße“ !!
Wenn !" ≠ 0, dann wirken äußere Kräfte !
!
!!! 𝑝!
𝐹!"# = !"
=
!!!"#
!"
„Impulsänderungssatz“ Stoßgesetze (eindimensional) v1 Vorher v2 m1 Nachher m2 v‘1 m
1 m2 v‘2 Zwei Fälle: •
•
Elastischer Stoß: 𝐸!"# = 𝑐𝑜𝑛𝑠𝑡 ; 𝑝!"# = 𝑐𝑜𝑛𝑠𝑡 Unelastischer Stoß: 𝐸!"# ≠ 𝑐𝑜𝑛𝑠𝑡 , 𝑝!"# = 𝑐𝑜𝑛𝑠𝑡 (Energie wird Teilweise in Deformationsenergie (èWärme) umgewandelt) Impulserhaltung: 𝑝! = 𝑚! 𝑣! + 𝑚! 𝑣! 𝑝! = 𝑚! 𝑣′! + 𝑚! 𝑣′! Energieerhaltung: !
𝐸!"#
= ! 𝑚! 𝑣 !! + ! 𝑚! 𝑣 ! ! !
𝐸!"#
= ! 𝑚! 𝑣!!" + ! 𝑚! 𝑣!!" !
!
!
!
𝑣! 𝑚! − 𝑚! + 2𝑚! 𝑣!
𝑚! + 𝑚!
𝑣! 𝑚! − 𝑚! + 2𝑚! 𝑣!
𝑣′! =
𝑚! + 𝑚!
𝑣′! =
Versuch: Luftkissenbahn Spezialfälle: (elastischer Stoß) i)
ii)
iii)
iv)
𝑚! = 𝑚! , 𝑣! = 0 ⇒ 𝑣 !! = 0 , 𝑣 ! ! = 𝑣! 𝑚! = 𝑚! ⇒ 𝑣′! = 𝑣! , 𝑣′! = 𝑣! Geschwindigkeiten vertauscht!!! 𝑚! = ∞ , 𝑣! = 0 ⇒ 𝑣′! = −𝑣! , 𝑣 ! ! = 0 Stoß gegen ruhende Wand (z.B. Gasatome/Gefäß) 𝑚! = 2𝑚! , 𝑣! = 0 ⇒ 𝑣 !! = −
!!
!
, 𝑣 ! ! = ! 𝑣! !
Spezialfall: (in-­‐elastischer Stoß) !
a) 𝑚! = 𝑚! , 𝑣! = 0 ⇒ 𝑣′! = 𝑣′! = ! 𝑣! Ist folgendes möglich? v m v m m m „superelastischer Stoß“ 2v Impulssatz erfüllt!! !
Energiebilanz !
!
!
𝑚𝑣² < ! 𝑚𝑣² + ! 𝑚(2𝑣)² !!!! Nur möglich, wenn innere Energie in kin. Energie umgewandelt wird (z.B. bei chem. Reaktionen) „Explosiver“ Stoß m1 v‘1 m2 m1 m2 v‘2 p!"# = 0 ⇒ 𝑚! 𝑣 !! = −𝑚! 𝑣 ! ! Stoßpendelkette [VERSUCH] 𝑚! = 𝑚! = 𝑚! … … = 𝑚 𝑛! 𝑚𝑣! = 𝑛! 𝑚𝑣! 𝑛! 𝑣! = 𝑛! 𝑣!
𝑛! = 𝑛!
1
1
𝑁𝑢𝑟 𝑓ü𝑟 𝑣 = 𝑣 𝑛! 𝑚𝑣²! = 𝑛! 𝑚𝑣²! 𝑛! 𝑣²! = 𝑛! 𝑣²!
!
!
2
2