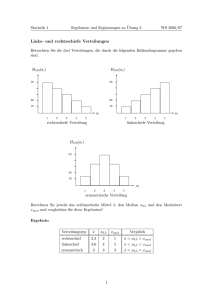
Relativbewegung, Kreisel und Hydordynamik

Ergänzungen zu Physik I
Inhaltsverzeichnis
Ergänzungen zur Physik I
U. Straumann, 2. Dezember 2012
Physik - Institut Universität Zürich
Inhaltsverzeichnis
1 Relativbewegungen
1.1 Relativitätsprinzip der Mechanik . . . . . . . . . . .
1.2 Die Kinematik in einem bewegten Bezugssystem . .
1.3 Die Dynamik in einem bewegten Bezugssystem . . .
1.4 Beispiele und Spezialfälle für bewegte Systeme . . .
1.4.1 Gleichförmig bewegtes System Sr . . . . . . .
1.4.2 Rein translatorisch beschleunigtes System Sr
1.4.3 Gleichförmig rotierendes System Sr . . . . . .
1.5 Trägheitseffekte auf der Erde . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
2
3
6
7
7
7
7
8
2 Eigenschaften des Kreisels
2.1 Trägheitstensor und Eulersche Kreisel-Gleichungen . . . . . .
2.2 Der kräftefreie rotationssymmetrische Kreisel . . . . . . . . .
2.3 Stabilität der Drehachse für Körper ohne Rotationssymmetrie
2.4 Symmetrischer Kreisel im Schwerefeld (Präzession) . . . . . .
2.5 Rotationsenergie und Energiesatz für die allgemeine Drehung
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
11
11
15
17
18
20
3 Dynamik der Fluide
3.1 Kontinuitätsgleichung . . . . . . . .
3.2 Bernoulligleichung . . . . . . . . . .
3.3 Innere Reibung . . . . . . . . . . . .
3.4 Die Navier-Stokes Gleichung . . . . .
3.5 Helmholtzsche Wirbelsätze . . . . .
3.6 Die Anatomie von Wirbeln . . . . .
3.7 Potentialwirbel (Badewannenwirbel)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
22
22
24
24
25
27
28
29
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
Ergänzungen zu Physik I
1
Relativbewegungen
1 Relativbewegungen
Bei der Diskussion der Newtonschen Prinzipien wurde betont, dass diese nur in einem Inertialsystem gültig sind. Nach dem 1. Newtonschen Prinzip ist das ein solches Koordinatensystem,
in dem ein isolierter, also keinen Kräften unterworfener Massenpunkt sich mit konstanter Geschwindigkeit bewegt.1 Als Inertialsystem haben wir meist ein auf der Erdoberfläche verankertes Koordinatensystem benutzt2 . Die mit der Newtonschen Mechanik berechneten Bewegungen
stimmten ausgezeichnet mit den Messungen überein.
Es stellen sich dann die Fragen: Wie kann man verschiedene Inertialsysteme unterscheiden? Wie
lauten die Bewegungsgleichungen in Nicht-Inertialsystemen? Insbesondere die Beantwortung der
zweiten Frage ist von grosser praktischer Bedeutung, da wir sehen werden, dass Rechnungen oft
vereinfacht werden können, wenn man sie in einem beschleunigten Nicht-Inertialsystem ausführt.
1.1 Relativitätsprinzip der Mechanik
Ein Koordinatensystem können wir uns immer durch Vektoren in einem starren Körper realisiert
denken. In einem solchen Körper bleiben per definitionem die Abstände beliebiger Punktepaare
konstant. Wir betrachten zwei Systeme dieser Art, das S-System (z.B. Laborsystem) mit den
xyz-Achsen und das relative Sr -System mit den xr yr zr -Achsen (Abb. Seite 3). Der Ort eines
Massenpunktes m wird durch die Ortsvektoren ~r und ~rr festgelegt.
Dann gilt
~r = ~r◦ + ~rr .
(1)
Wir setzen voraus, dass in beiden Systemen die klassische, nicht-relativistische Mechanik gilt,
d.h. alle Geschwindigkeiten sind klein gegenüber der Lichtgeschwindigkeit (v c). Dann gelten
bis zu einer hohen Genauigkeit die klassischen Vorstellungen von Raum, Zeit und Masse:
a) In beiden Systemen werden die gleichen Massstäbe zur Längenmessung verwendet. Das
impliziert, dass die Standard-Massstäbe von S und Sr verglichen werden können.
b) Beide Systeme benutzen die gleiche Zeit. Wenn in S eine Zeit ∆t zwischen zwei Ereignissen
beobachtet wird, so wird in Sr das gleiche Intevall ∆tr = ∆t gemesen.
c) Der Massenpunkt hat in beiden Systemen die gleiche Masse.
In der Relativitätstheorie sind diese drei Annahmen nicht mehr haltbar, sobald die Geschwindigkeiten der Grösse nach mit c vergleichbar werden.
Wir wollen nun annehmen, durch Versuche habe sich erwiesen, dass S ein Inertialsystem sei.
Dann lässt sich sofort zeigen, dass auch Sr ein Inertialsystem ist, falls es sich gleichförmig geradlinig gegenüber S bewegt, d.h. wenn gilt
d~r◦
= ~v◦ = konst.
dt
1
2
(2)
Vgl. Halliday, Kap. 5-3.
und dabei die Rotation der Erde als kleinen Effekt vernachlässigt. Ein Labor auf der Erde ist bei genauer
Messung jedoch ein beschleunigtes Nicht-Inertialsystem mit den entsprechenden Schein- oder Trägheitskräften.
2
Ergänzungen zu Physik I
1
Relativbewegungen
Denn zweimalige Differenziation von Gl.(1) liefert
d~r
d~r◦ d~rr
= ~v =
+
= ~v◦ + ~vr
dt
dt
dt
und
d2~rr
d2~r
= ~a =
= ~ar .
2
dt
dt2
Aus ~a = ~ar folgt aber, dass die Kräfte F~ = m~a und F~r = m~ar in beiden Systemen die gleichen
sind; demzufolge gilt auch in Sr die Newtonsche Mechanik, Sr ist auch ein Inertialsystem. Alle
Koordinatensysteme, die sich gleichförmig geradlinig gegenüber einem Inertialsystem bewegen,
sind also ebenfalls Inertialsysteme. Sie lassen sich nicht unterscheiden, und es ist daher unmöglich
festzustellen, ob eines dieser Systeme “absolut in Ruhe” ist. Dies ist das Relativitätsprinzip der
Mechanik.
Wenn Gl. (2) gilt, so lässt sich Gl. (1) auch in der Form der Galilei-Transformation
~r = ~rr + ~v◦ t
(3)
schreiben. Wenn diese Transformationsgleichung zwischen den Systemen S und Sr gültig ist, gilt
das Relativitätsprinzip der Mechanik, das man auch in folgenden Worten formulieren kann:
Es ist einem Beobachter unmöglich, mit Hilfe von mechanischen Experimenten
herauszufinden, ob sein Bezugssystem in Ruhe oder in gleichförmiger Bewegung ist.
Mittels anderer Wechselwirkungen wie z.B. elektrodynamischen oder optischen Versuchen ist
eine solche Unterscheidung ebensowenig möglich.
1.2 Die Kinematik in einem bewegten Bezugssystem
Wir behandeln jetzt eine beliebige Bewegung (auch Rotationen und damit beschleunigte Systeme) des Systems Sr gegenüber dem Inertialsystem S (im Folgenden Ruhe- oder Laborsystem
genannt. Ein ausgedehnter Körper mit einer allgemeinen Bewegung hat sechs Freiheitsgrade, 3
der Translation und 3 der Rotation. Es gelte wie oben die klassische Mechanik.
Das bewegte Bezugssystem sei ein starrer Raum Sr (xr , yr , zr ) (Fahrzr 6 ~
m ω
6
zeug), der vom ruhenden System S(x, y, z) aus beschrieben wird mit z
u
Sr
~r
1y
~r◦ , ~v◦ (Ortsvektor und Geschwindigkeit des Ursprungs von Sr ) und
7 r
~r r
ω
~ (Winkelgeschwindigkeit von Sr um eine Achse durch den Ursprung
xr
von Sr ). Im relativen System Sr (xr , yr , zr ) wird eine Masse m mit ~rr ,
~r◦
1
y
~vr und ~ar gekennzeichnet. Im ruhenden System beschreiben ~r, ~v und ~a
S die Masse m. Für eine reine Translation von Sr gilt: ~v = ~v◦ . Für eine
x
reine Rotation von Sr gilt für einen Massenpunkt: ~v = ω
~ × ~rr .
Der Koordinatenursprung von Sr liegt auf der Drehachse. Die Winkelgeschwindigkeit ist (im
~ ◦ und dem Drehmoment ~τ◦ ) unabhängig von der Wahl des BezugsGegensatz zum Drehimpuls L
punktes.
3
Ergänzungen zu Physik I
1
Relativbewegungen
Beweis: P◦ und Ṕ◦ seien zwei beliebige Bezugspunkte mit relativem Verbindungsvektor ~s.
Die Führungsgeschwindigkeit des Fahrzeuges ist
zr
Sr
~
rr
ω
~
m 6
t ´
~
r
I
@
@p~sṔ◦
:
-
P◦
xr
~vF = ~v◦ +~
ω ×~rr
⇒
bzw. ~vF = ~v´◦ +ω
~´ ×~r´r ;
weiter ist ~v´◦ = ~v◦ +~
ω ×~s;
~vF = ~v◦ + ω
~ ×~rr = ~v◦ + ω
~ ×~s + ω
~´ ×~rr − ω
~´ ×~s
~r´r = ~rr −~s
⇒ (~
ω −ω
~´ ) ×~rr = (~
ω −ω
~´ ) ×~s.
Diese Vektorgleichung kann nur dann für alle ~rr erfüllt werden, wenn ω
~ =ω
~´ gilt,
qed.
Für eine allgemeine Bewegung des Fahrzeuges ist die Geschwindigkeit eines beliebigen Punktes
beschrieben durch die Addition3 der beiden oben angegebenen Terme für reine Translation bzw.
Rotation: ~vF = ~v◦ + ω
~ × ~rr . Mit der absoluten Zeit4 t = tr und unter Beachtung der Tatsache,
dass infolge der Drehung dr ~rr 6= d~rr ist5 , gilt in den beiden Systemen für den Ortsvektor, die
dt
dt
Geschwindigkeit und den Beschleunigungsvektor eines Punktes:
S(x, y, z)
Ort:
Geschwindigkeit:
Beschleuigung:
Spezialfall:
Sr (xr , yr , zr )
~r(t) = ~r◦ + ~rr
~v = d~r
dt
2
~a = d~v = d ~2r
dt
dt
Relativbewegung
~rr (tr ) = ~rr (t)
~vr = dr ~rr = dr ~rr
dtr
dt
2
d
~r
d
~
v
~ar = r r = r 2r
dt
dt
nur Führungsgeschwindigkeit
m mit Fahrzeug verbunden
~vF = ~v◦ + ω
~ × ~rr
d~
v
F
~aF =
dt ~vr =0
~rr = konst
~vr = ~ar = 0
Gefragt wird nun nach der Beziehung zwischen den beiden Systemen. Für den allgemeinen Fall
mit der Masse m und ~vr 6= 0 setzt sich die Geschwindigkeit aus der Führungsgeschwindigkeit
des Fahrzeugs ~vF und der vom Fahrzeug aus gesehenen Geschwindigkeit ~vr zusammen:
dr ~rr
dt
:::::::::::::::::
~v = ~vF + ~vr = ~v◦ + ω
~ × ~rr + ~vr = ~v◦ + ω
~ × ~rr +
(4)
Andererseits kann diese gesamte Geschwindigkeit ~v auch durch Ableiten des gesamten Ortsvek-
3
Beachte, dass ~vF , ~v◦ und ω
~ × ~rr alle drei normale polare Vektoren sind, die addiert werden können. Axiale
Vektoren wie ω
~ können nicht so einfach addiert werden.
4
Dies gilt nur für v c; sonst muss die Relativitätstheorie bemüht werden.
5 d~
rr
differenziert im ruhenden und drdt~rr im bewegten System. Wegen der relativen Bewegung und der Drehung
dt
können diese beiden Ableitungen nicht identisch sein – wir müssen eine Beziehung zwischen beiden suchen.
4
Ergänzungen zu Physik I
1
Relativbewegungen
tors im System S berechent werden:
~v =
d
d~rr
(~r◦ + ~rr ) = ~v◦ +
dt
dt
::::::::
(5)
Die beiden Gleichungen sind gleich, die Beziehung für die Transformation der Ableitung vom
System S in das System Sr lautet also
d~rr
dr ~rr
=
+ω
~ × ~rr
dt
dt
(6)
~
Dies gilt nicht nur für ~rr sondern auch für jeden beliebigen Vektor A
~
~
dA
dr A
~
=
+ω
~ ×A
dt
dt
(7)
Für die Beschleunigungen gilt:
• Absolutbeschleunigung: ~a =
d~v
dt
=
d2 ~
r
dt
2
rr
r~
= ddt
2
vF • Führungsbeschleunigung: ~aF = d~dt
dr ~rr
• Relativbeschleunigung: ~ar =
dr ~vr
dt
dt
=~vr =0
Mit den Gleichungen (4) und (7) kann ein Zusammenhang zwischen den Beschleunigungen gefunden werden:
Es ist
d~
ω
dr ω
~
dr ω
~
=
+ω
~ ×ω
~ =
|
{z
}
dt
dt
dt
:::
:::
=0
d~v
d~v◦
d
d
und ~a =
=
+ (~
ω × ~rr ) +
dt
dt
dt
dt
d
dr ~rr
d
Wende den Operator
von Gl.(7) auf
an:
dt
dt
dt
⇒
~a =
dr ~rr
dt
dr
=
dt
dr ~rr
dt
dr ~rr
dt
+ω
~×
.
dr ~rr
dt
d~v◦ d~
ω
d~rr
d2~rr
dr ~rr
+
× ~rr + ω
~×
+ r2 +ω
~×
,
dt
dt
dt
dt
dt
ω
dr ~rr
d2~rr
dr ~rr
~ = ~rr wird ~a = d~v◦ + d~
× ~rr + ω
~×
+ω
~ × (~
ω × ~rr ) + r 2 + ω
~×
mit Gl.(7) für A
dt
dt
dt
dt
dt
~a =
~a =
d~v◦ d~
ω
dr ~rr d2r ~rr
+
× ~rr + ω
~ × (~
ω × ~rr ) + 2 · ω
~×
+ 2
dt
|dt
{z
} |
{z dt } |dt
{z }
~aF
~aC
~ar
+
+
(8)
Wir können also zusammenfassen:
~a = ~aF + ~ar + 2 · ω
~ × ~vr = ~aF + ~ar + ~aC
(9)
5
Ergänzungen zu Physik I
1
Relativbewegungen
Die verschiedenen Beschleunigungsterme bezeichnen wir wie folgt:
~aF
~aT
~aZ
~aω
~aC
~ar
= ~aT + ~aZ + ~aω
Fuehrungsbeschleunigung
d~v◦
=
Beschleunigung des Ursprungs von Sr
dt
= ω
~ × (~
ω × ~rr )
Zentrifugal − Beschleunigung
d~
ω
=
× ~rr
Beschleunigung aufgrund Aenderung von ω
~
dt
= 2·ω
~ × ~vr
Coriolisbeschleunigung
2
dr ~rr
Relativbeschleunigung, gemessen in Sr
=
dt2
(10)
(11)
(12)
(13)
(14)
(15)
Eine Coriolisbeschleunigung ~aC tritt nur dann auf, wenn das bewegte System eine Drehung ω
~
ausführt und der Massenpunkt eine Relativgeschwindigkeit ~vr 6= 0 hat (und ~vr nicht parallel zu
ω
~ liegt).
1.3 Die Dynamik in einem bewegten Bezugssystem
Das Aktionsprinzip der Bewegung eines Körpers mit Masse m im System S ist
m~a =
n
X
F~i = F~
mit F~ gleich den resultierenden äusseren Kräften. Dann gilt auch (mit Gl.(9)):
i=1
m~a = m(~ar + ~aF + ~aC ) = F~ .
Ein in Sr mitbewegter Beobachter registriert nur die Relativbeschleunigung ~ar und findet deshalb
~ sowie −m~aC = −2 · m(~
für das Aktionsprinzip m~ar = F~ − m~aF − m~aC bzw. (mit −m~aF =: Z
ω×
~
~vr ) = 2 · m(~vr × ω
~ ) =: C)
~ +C
~
m~ar = F~ + Z
(Aktionsprinzip im bewegten System).
(16)
~ (die Führungskraft, in der die Zentrifugalkraft −m~
~ (die CoZ
ω × (~
ω × ~rr ) enthalten ist) und C
rioliskraft) haben die Dimension einer Kraft; sie sind jedoch in S keine wahrhaft existierenden
Kräfte, sondern Schein- oder Trägheitskräfte, die ein bewegter Beobachter als Korrektur in die
Newtonsche Bewegungsgleichung einführen muss, wenn er dort an Stelle der Beschleunigung ~a
die Relativbeschleunigung ~ar einsetzt. Sie haben keine Reaktionskräfte. Obwohl sie nur Scheinoder Trägheitskräfte sind, existieren sie als reale Kraft im bewegten System Sr . Ein beschleunigtes Bezugssystem ist kein in sich abgeschlossenes Inertialsystem, es müssen von aussen Kräfte
wirken, um das System mit Massen zu beschleunigen.
6
Ergänzungen zu Physik I
1
Relativbewegungen
1.4 Beispiele und Spezialfälle für bewegte Systeme
1.4.1 Gleichförmig bewegtes System Sr
Es ist ~vF = ~v◦ = konst, folglich ~aF = ~aC = 0 und somit ~ar = ~a. Dann ist auch Sr ein
Inertialsystem, wie wir schon in Abschnitt 1 diskutiert haben.
1.4.2 Rein translatorisch beschleunigtes System Sr
~ = 0 und damit m~ar =
In einem rein translatorisch beschleunigten Bezugssystem gilt ω
~ = 0, C
d~
v◦
~
~
~
F + Z = F − m~aF . Mit ~vF = ~v◦ (t) folgt ~aF = dt = ~a◦ . Damit spürt z.B. der Insasse eines
mit ~a◦ beschleunigten Fahrzeuges die Kraft m~ar = F~ − m~a◦ . Wenn die auf ihn wirkende Kraft
F~ = 0 ist, erfährt er die beschleunigende Trägheitskraft m~ar = −m~a◦ . S und Sr sind nicht mehr
äquivalent, in den beiden Systemen werden unterschiedliche Beschleunigungen gemessen.
Beispiel: Mathematisches Pendel auf einer vertikal beschleunigten Plattform
z
6
a◦
6
~ = −m~a◦ = −ma◦~k und damit die Bewegungsgleichung
Es ist Z
für die Tangentialkomponente
A
A
ϕA `
K
A
AA F ∗
Au
A
?
G
d2r ϕ
= −(mg + ma◦ ) sin ϕ.
dt2
Für kleine Ausschläge ist sin ϕ ' ϕ, also
d2r ϕ
g + a◦
+
ϕ = 0. Mit dem Ansatz
dt2
`
m`
Z
?
x-
r
ϕ(t) = ϕ◦ cos(Ωt − δ)
ist
Ω=
g + a◦
`
die Kreisfrequenz des Pendels.
Fällt die Plattform frei, so ist g = −a◦ , also Ω = 0, d.h. die Schwingungsdauer T =
unendlich. Der freie Fall merkt keine Gravitationskraft.
2π
Ω
ist
1.4.3 Gleichförmig rotierendes System Sr
Die translatorische Bewegung verschwindet ~v◦ = 0. w
~ ist konstant. Wir behandeln zwei Experimente auf dem Drehtisch.
a) Ein Massenpunkt m sei auf einer mit konstanter Winkelgeschwindigkeit ω
~ sich drehenden,
horizontalen Unterlage durch eine Feder mit der Drehachse verbunden. m sei relativ zur
Unterlage in Ruhe. Es herrscht scheinbares Gleichgewicht. Im ruhenden System beschreibt
m eine Kreisbahn. Die wahren Kräfte sind, wenn keine Reibungen vorhanden sind,
7
Ergänzungen zu Physik I
1
v2
= mrr ω 2 .
r
Ein mitbewegter Beobachter muss eine Scheinkraft einzuführen, um sich die relative Ruhe erklären zu können. Es
ist
~ =0
~vF = ω
~ × ~rr , ~vr = 0, also C
G=N
6
ω
~
~rr
~
N
-6
∼∼∼∼∼ u - Z
~
F~F ?
~
G
Relativbewegungen
und
FF = m
ω
sowie ~v˙ ◦ = 0 und d~
= 0. Damit ergibt sich die
dt
Führungskraft aus Gl.(10) zu
~ = −m~aF = −m[~
Z
ω × (~
ω × ~rr )] , der Zentrifugalkraft6 . Ihr Betrag ist gerade Z = mrr ω 2
~ und F~F erfüllen also die Gleichgewichtsbedingung im beschleunigten
(da ω
~ ⊥ ~rr steht). Z
Relativsystem.
b) Vom Ursprung des ruhenden Systems S aus bewegt sich eine Masse m mit konstanter
Geschwindigkeit v◦ , es wirken keine äusseren Kräfte. Der Beobachter in Sr sieht eine
spiralförmig nach aussen bewegte Masse, für welche die Geschwindigkeit direkt angegeben werden kann; in Polarkoordinaten hat sie die Komponenten vrr = drdtrr = v◦ und
vrϕ = rr drdtϕr = −ωrr . Nach einer einfachen Integration erhält man hieraus auch die
Ortskoordinaten rr = v◦ t und ϕr = −ωt. Gemäss Gl.(16) gilt für den Beobachter das
Aktionsprinzip
~ +C
~ = −m~aF − m~aC = −m · ω
m~ar = Z
~ × (~
ω × ~rr ) − 2m · ω
~ × ~vr ,
d.h. er beobachtet eine Zentrifugalkraft und eine Corioliskraft. Letztere sucht die Richtung
der Geschwindigkeit dauernd zu ändern ohne den Betrag zu beeinflussen, wie dies auf der
Erde bei den Monsunen, Passatwinden und dem Golfstrom ebenfalls beobachtet wird.
Versucht der Beobachter in Sr die Masse festzuhalten, so muss er eine Reaktionskraft zu
~ +C
~ aufbringen.
Z
6
Zur Zentrifugalkraft: vgl. Formel (6-35) im Halliday, Kap.6-5.
8
Ergänzungen zu Physik I
1
Relativbewegungen
1.5 Trägheitseffekte auf der Erde
In den vorausgegangenen Beispielen spielte der Hörsaal und damit die Erde die Rolle des ruhenden Systems. Diese Wahl führte zu keinen Widersprüchen mit der Erfahrung, obwohl die
Erde ein bewegtes Bezugssystem ist. Der Grund liegt darin, dass auf der Erde Z und C viel
kleiner als mg sind. Es können aber terrestrische Versuche ausgeführt werden, die eindeutig die
Trägheitseffekte als Folge des Bewegungszustandes der Erde zeigen.
Ein Beispiel: Nachweis der Erdrotation mit dem Foucaultpendel
N
m
→
ω
→
ω
β
S
Ein schwingendes Pendel behält infolge der Trägheit seine
Schwingungsebene im Raum bei. Dieses eigentümliche Verhalten offenbart sich beim Foucault-Versuch7 (1850/51 in Paris).
Ein Ort auf der Erde mit der geographischen Breite β rotiert mit der Winkelgeschwindigkeit ω · sin β um eine zur Erdoberfläche senkrechte Achse; mit dieser Winkelgeschwindigkeit
dreht sich die Erde unter dem schwingenden Pendel hinweg. Die
effektive Umlaufszeit der Horizontalebene relativ zur Schwingungsebene des Pendels in der geographischen Breite β ist
T = 2π/ω sin β mit ω = 2π/24 Stunden. Zur Berechnung wurde hier ω
~ bei der geographischen Breite β in die Komponenten
senkrecht (ω⊥ ) und parallel (ωk ) zur Erdoberfläche zerlegt.8
Die Pendelebene bleibt bei der Drehung im Raum S erhalten, es gilt die Drehimpulserhaltung
~ = 2m(~vr × ω
und die Drehung ist direkt durch ω⊥ gegeben. Es gilt für die Corioliskraft C
~) =
2m(~vr × ω⊥ + ~vr × ωk ), wobei nur der erste Term zu einer Auslenkung führt. Für Zürich mit
β ≈ 47◦ ist T = 34h, am Pol erhalten wir T = 24h und am Äquator T = ∞.
Die Corioliskraft ist auch die Ursache dafür, dass Hochdruckgebiete auf der Nordhalbkugel im
Uhrzeigersinn rotieren, Tiefdruckgebiete in Gegenrichtung. Bei einem Tiefdruckgebiet strömt
die Luft aufgrund des Druckgefälles nach innen. Diese Strömung wird auf der Nordhalbkugel
durch die Corioliskraft nach rechts abgelenkt und es ergibt sich eine gegen den Uhrzeigersinn
gerichtete Rotation.
7
8
Für eine ausführlichere Darlegung siehe Halliday, Kap.16-10.
Dies ist nur deshalb möglich, weil es sich bei ω
~ um einen axialen Vektor handelt.
9
Ergänzungen zu Physik I
1
Relativbewegungen
Schematische Darstellung der athmosphr̈ischen Zirkulation. Temperaturunterschiede führen zu
Fall- und Steigströmungen (rechts dargestellt), die wiederum Hoch- und Tiefdruckgebiete erzeugen. Die Corioliskraft bewirkt, dass rotierende Wirbel entstehen. Tiefdruckwirbel können durch
bei der Kondensation der aufsteigenden Luftfeuchtigkeit freiwerdender Energie weiter angetrieben werden, sodass Wirbelstürme entstehen. Referenz:
http://www.techniklexikon.net/d/atmosphärische zirkulation/atmosphärische zirkulation.htm
10
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
2 Eigenschaften des Kreisels
2.1 Trägheitstensor und Eulersche Kreisel-Gleichungen
Auf Grund der formalen Ähnlichkeit von Impuls- und Drehimpulssatz, also von
~◦
d~
p
dL
= F~
und
= ~τ◦ ,
dt
dt
~
könnte man vermuten, dass der Beziehung p~ = m~v ein ähnlicher Zusammenhang zwischen L
und ω
~ bei der Rotation entspricht. Das ist aber im allgemeinen nicht der Fall. Die Beziehung
L◦z = I◦ ω gilt nur für ebene Bewegungen.9
Wird ein Punkt ◦ eines starren Körpers festgehalten, dann nennt man die Bewegung um ◦ eine
Kreiselung. Sie besitzt drei Rotationsfreiheitsgrade, die jedoch wesentlich komplizierter sind
als drei reine Translationsfreiheitsgrade. Die Schwierigkeiten mehrerer Rotationsfreiheitsgrade
haben folgende Gründe:
1. Es gibt keine Koordinaten, deren Ableitungen direkt Geschwindigkeiten darstellen, wie bei
den Translationen. Drehungen sind Pseudovektoren (axiale Vektoren), deren Reihenfolge
nicht wie bei polaren Vektoren vertauscht werden kann.
2. Die Trägheitsmomente hängen von der Achsenwahl ab. Ändert die Achse mit der Zeit die
Richtung, so wird I = I(t), während in Analogie für Translationen die Masse m konstant
ist.
~ 6= I~
~ im allgemeinen nicht die Richtung von ω
3. Für Drehungen gilt im allgemeinen L
ω , da L
~
hat. Das Trägheitsmoment muss daher durch einen Tensor10 I dargestellt werden, so dass
~ = I~
gilt L
ω.
Im Folgenden wird der Trägheitstensor rein buchhalterisch als Matrix eingeführt11 , wobei die
Rechenregeln in der Matrizendarstellung zwanglos einsichtig sind.
~ =
Ein Beispiel für die Aussage L
6 I~
ω ist die Hantel, deren Mitte mit einer vertikalen Achse
verbunden ist, die mit ω
~ rotiert, und die nicht einer Symmetrieachse entspricht.
→
dL o
m
→
→
Lo
dϕ
α
ω
→
→
→
→
r2
p2
m
.
→
p 1=p
→
r1=r
Die Hantel ist um den Winkel α gegen diese Drehachse geneigt.
~ ◦ der Hantel bezüglich ◦ ist L
~ ◦ = ~r1 × p~1 +
Der Drehimpuls L
~r2 × p~2 , was sich wegen −~r2 = ~r1 =: ~r und −~
p2 = p~1 =: p~ auch
~ ◦ = 2(~r × p~) = 2m(~r ×~v ) schreiben lässt. L
~ ◦ dreht sich mit
als L
der Winkelgeschwindigkeit ω
~ auf einem Kegelmantel um ω
~ mit
~
~
dL◦ /dt = L◦ sin α dϕ/dt = |~
ω × L◦ |; L◦ und ω
~ stehen also nicht
parallel zueinander. Diese Bewegung ist nur möglich mit einem
äusseren (z.B. durch Lagerkräfte aufgebrachten) Drehmoment
~◦
L
~ ◦ ; ohne Lagerkräfte dreht die Hantel, bis
~τ◦ := ddt
= ω
~ ×L
~◦ k ω
L
~ steht und ~τ◦ = 0 wird.
9
Der Kringel im Index steht jeweils um anzugeben, dass die entsprechenden Grössen bezüglich eines raumfesten
Bezugspunktes ◦ betrachtet werden.
10
Tensoren sind physikalische Objekte, die durch ihr Transfomationsverhalten definiert sind. Beispielsweise sind
Skalare Tensoren 0. Stufe; Vektoren sind Tensoren 1. Stufe. Tensoren 2. Stufe wie das Trägheitsmoment können
im einmal gewählten Koordinatensystem durch eine n × n Matrix dargestellt werden.
11
Eine eingehendere Einführung findet sich in den mathematischen Hilfsmitteln zur Physik I.
11
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
~ ◦ und ω
Wir wollen nun einen allgemeinen Zusammenhang zwischen L
~ finden und dann mit Hilfe
des Drehimpulssatzes Bewegungsgleichungen, die Eulerschen Kreiselgleichungen, aufstellen, die
für die Kreiselbewegung gelten, d.h. für Bewegungen eines starren Körpers, von dem ein Punkt
fest gehalten wird.
Wenn bei einer Kreiselung ein Punkt des Körpers im Raume fest bleibt, dann kann dieser Punkt
◦ als raum- (~ri ) und körperfester (~r´i ) Ursprung gewählt werden. Es ist dann ~ri = ~r´i und die
Zeitabhängigkeit steckt im raumfesten System in den Komponenten von ~ri und im körperfesten
System in den Basisvektoren ~´i,~´j,~k´ von ~r´i . Es gilt nach der Definition des Drehimpulses für einen
Massenpunkt ~l◦i = mi ~ri × (~
ω × ~ri ) und damit für n Massenpunkte
~◦ =
L
n
X
i=1
~l◦i =
n
X
mi ~ri × (~
ω × ~ri ) =
i=1
n
X
mi [ri2 ω
~ − (~ri · ω
~ ) ~ri ]
(17)
i=1
wobei im letzten Schritt wird die Vektoridentität
~a × (~b × ~c) = (~a · ~c) ~b − (~a · ~b) ~c
(18)
verwendet wurde.
Für einen ausgedehnten Körper ergibt sich
Z
Z
Z
Z
~ ◦ = ~r ×~v dm = ~r ×(~
L
ω ×~r) dm = [r2 ω
~ −(~r ·~
ω ) ~r ] dm = [r2 ω
~ −(xωx +yωy +zωz ) ~r ] dm.
(19)
Dabei hängt ω
~ in der Summe nicht von i und im Integral nicht von der Massenverteilung ab.
Es besteht jetzt das mathematische Problem, wie man ω
~ aus der Summe herausziehen resp. vor
~ ◦ = I◦ ω
das Integral stellen kann, um so die Beziehung L
~ aufstellen und den Trägheitstensor I◦
bestimmen zu können. Dazu berechnet man die drei Komponenten des Drehimpulses12
Z
Z
Z
2
2
L◦x = ωx (y + z ) dm −ωy yx dm −ωz zx dm
{z
}
| {z }
| {z }
|
Ixx
Cyx
Czx
Z
Z
Z
L◦y = ωy (x2 + z 2 ) dm −ωx xy dm −ωz yz dm
|
| {z }
| {z }
{z
}
Iyy
Cxy
Cyz
Z
Z
Z
L◦z = ωz (x2 + y 2 ) dm −ωx xz dm −ωy yz dm
|
{z
}
| {z }
| {z }
Izz
Cxz
Cyz
Die Trägheitsmomente I in den obigen Gleichungen sind in Analogie zum Trägheitsmoment der
ebenen Bewegung definiert. Die übrigen, nichtdiagonalen Terme C werden als Deviationsmomente
bezeichnet. Für alle drei Komponenten erhält man so in einer buchhalterischen
Anordnung13
:::::::::::::::::::::::::::
12
13
Natürlich erhält man das gleiche Ergebnis, wenn man in Gl.(19) direkt das dreifache Vektorprodukt ausrechnet.
Überprüfe mittels Matrix-Vektor-Multiplikation ( Multipliziere die einzelnen Zeilen-Terme der Matrix mit den
”
Spalten-Termen des Vektors“).
12
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels



L◦x =Ixx ωx −Cxy ωy −Cxz ωz
+Ixx −Cxy −Cxz
ωx
~ ◦ =: I ω
L◦y =Iyy ωy −Cyz ωz −Cyx ωx ⇒ L
~ =  −Cyx +Iyy −Cyz   ωy  ,
L◦z =Izz ωz −Czx ωx −Czy ωy
−Czx −Czy +Izz
ωz
(20)
d.h. man kann den Trägheitstensor I als (3 × 3)-Matrix auffassen. In ausgeschriebener Form
lautet er:
 R
I=
R
R

(y 2R+ z 2 ) dm R − xy dm
− R xz dm
− R yx dm
(x2R+ z 2 ) dm R − yz dm  .
− zx dm
− zy dm
(x2 + y 2 ) dm
(21)
Jede Komponente des Drehimpulses ist eine lineare Funktion von allen Komponenten der Winkelgeschwindigkeit ω
~ . Der Trägheitstensor I ist reell und symmetrisch (Cij = Cji ), und lässt sich
daher14 bezüglich eines geeigneten Koordinatensystems Ś in Diagonalform darstellen. Die Deviationsmomente Cij verschwinden somit allesamt, übrig bleiben nur noch die Trägheitsmomente
Iii der zum Hauptachsensystem Ś gehörigen Hauptachsen. Die Einheitsvektoren entlang dieser
Hauptachsen bezeichnen wir mit ~e1 , ~e2 , ~e3 . Wir haben also (mit den Abkürzungen: Ixx =: I1 ,
Iyy =: I2 , Izz =: I3 ) für ein Hauptachsensystem:


I1 0 0
~ ◦ = I1 ω1~e1 + I2 ω2~e2 + I3 ω3~e3 .
Í =  0 I2 0  und damit L
(22)
0 0 I3
Oft fallen die Hauptachsen mit den (Dreh-)Symmetrieachsen eines Körpers zusammen (Bsp.:
~ ◦ ist auch im Hauptachein Quader und die Achsen des Kartesischen Koordinatensystems). L
sensystem nicht parallel zu ω
~ , da (ausser für eine homogene Kugel) I1 6= I2 6= I3 ist.
Beispiel:
• •
•
Als einfaches Beispiel sei der Trägheitstensor eines zweiatomigen Moleküls (H2 , N2 , O2 ) im
körperfesten Hauptachsensystem berechnet:
r11 = −d,
r21 = +d,
6
2
r12 = 0,
r22 = 0,
r13 = 0,
r23 = 0,
2 + r2 + r2
ri2 = ri1
i2
i3

P
P
2
mP
mi ri1 ri2
−P mi ri1 ri3
i (ri − ri1 ri1 ) P−
2

mP
mi ri2 ri3
I =  − P mi ri2 ri1
i (ri − ri2 ri2 ) P
2
− mi ri3 ri1
− mi ri3 ri2
mi (ri − ri3 ri3 )


0 0 0

I = 2m 0 d2 0  und I1 = 0, I2 = 2md2 , I3 = 2md2 .
0 0 d2
 P
i=1
i=2
u
u
d
3
14
d
-
1
wie in der Linearen Algebra noch gezeigt werden wird
13
Ergänzungen zu Physik I
2
• •
Eigenschaften des Kreisels
•
Bildet man mit Gl.(20), die für ein raumfestes Koordinatensystem hergeleitet wurde, die Be~◦
L
wegungsgleichung (Drallsatz) ~τ◦ = ddt
, dann sind die Komponenten des Trägheitstensors
~ ◦ wird kompliziert – es treten jedoch im raumfesten
zeitabhängig I = I(t) und der Drehimpuls L
System keine Scheinkräfte auf. Im körperfesten und damit bewegten Hauptachsen-System ist der
Trägheitstensor diagonal und der Drehimpuls ist einfach entsprechend Gl.(22); dafür müssen im
rotierenden System Scheinkräfte eingeführt werden. (Das Hauptachsensystem dreht sich mit der
Winkelgeschwindigkeit ω
~ gegenüber dem raumfesten System.) Es war die Idee von Euler15 , die
Vorteile beider Systeme zu kombinieren und die Nachteile zu unterdrücken.
Wir befinden uns also im körperfesten, rotierenden System, und nehmen die Hauptachsen, in
dem der Trägheitstensor diagonal ist, als Bezugssytem. Das ist die entscheidende Annahme für
die Eulergleichungen. Damit müssen wir in diesem beschleunigten Bezugssystem Zentrifugalkräfte Z als Scheinkräfte einführen. Wir lassen im folgenden die Striche bei den Koordinaten
d
weg, r, v und L sowie die Ableitung dt
sind also im rotierenden System gemeint.
Mit der bei gemäss Gleichung (16) definierten Zentrifugalkraft wird
~ = −m(~
Z
ω × (~
ω × ~r))
(23)
Diese Scheinkraft erzeugt ein zusätzliches (scheinbares) Drehmoment τZ wofür wir nach einsetzen
von Z, unter Verwendung der Identität (18) erhalten:
~ = −~
~
τ~Z = ~r × Z
ω×L
(24)
wobei auch verwendet wurde, dass ~v und ~r senkrecht aufeinander stehen und ~v = ω
~ × ~r.
Im rotierenden System gilt also mit einem äusseren, “wirklichen” Drehmoment ~τ :
~τ + τ~Z =
~
dL
dt
(25)
oder umsortiert und eingesetzt:
~
dL
~
+ω
~ ×L
(26)
dt
das ist der Drallsatz im körperfest rotierenden System. Man hätte diese Beziehung auch direkt
~ bekommen
durch Anwendung der Transformationsvorschrift (7) für die Ableitung des Vektors L
können.
~τ =
Befinden wir uns ausserdem im Hauptachsensystem mit den orthonormierten Koordinaten i =
1, 2, 3 ist der Trägheitstensor diagonal und es gilt deshalb
Li = Ii ωi
15
(27)
Leonard Euler (1707-1783), in Basel geboren, der Vater war Pastor in Riehen, studierte in Basel Theologie
und dann Mathematik und Physik. Er war ein Anhänger der Wellentheorie des Lichtes, sein klassisches Werk
populärer Wissenschaft: “Lettres à une Princesse d’Allemagne”.
14
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
was wir koordinatenweise in den Drallsatz (26) einsetzen. Damit sind wir bei den gesuchten
Eulerschen Gleichungen angelangt:
τ1 = I1 dω1 − (I2 − I3 )ω2 ω3
dt
τ2 = I2 dω2 − (I3 − I1 )ω3 ω1
dt
die Eulerschen Gleichungen
im körperfesten
Hauptachsensystem [123]
(28)
τ3 = I3 dω3 − (I1 − I2 )ω1 ω2
dt
Mit diesem Rüstzeug kehren wir zum Kreisel zurück.
2.2 Der kräftefreie rotationssymmetrische Kreisel
Man betrachtet einen rotationssymetrischen starren Körper mit einem Fixpunkt. Rotationssymmetrie bedeutet in unserem Formalisums, dass zwei der drei Trägheitsmomente gleich sind, z.B.
I1 = I2 .
Auf einen kräftefreien Kreisel wirkt kein Drehmoment (~τ◦ = 0). Er kann im Schwerefeld realisiert werden, indem man ihn im Schwerpunkt aufhängt (der raumfeste Punkt ◦ ist dann gleich
dem Schwerpunkt S) oder eine kardanische Aufhängung wählt.16 Bei Rotationssymmetrie ist im
körpereigenen System I1 = I2 =: I und die 3-Achse ist die Figurenachse durch den Schwerpunkt.
3
S=o
2
1
Mit den Eulerschen Gleichungen und dLs = τs = τ◦ = 0
dt
ist
d
0 = I dω1 − (I − I3 )ω2 ω3
| I1 dt
···
dt
dω
0 = I 2 − (I3 − I)ω3 ω1
dt
0 = I3 dω3 − (I − I)ω1 ω2 = I3 dω3 ⇒ ω3 = konst.
dt
dt
3
S
Kombiniert man wie angedeutet die beiden ersten Gleichungen, so erhält man
0=
d2 ω1 I − I3 dω2
(I − I3 )(I3 − I)
ω3 = ω̈1 −
ω1 · ω32 =: ω̈1 + ω1 · ω◦2 .
−
dt2
I
dt
I ·I
(29)
Dies ist eine Schwingungsgleichung mit der konstanten Frequenz
ω◦ =
(I3 − I)
ω3
I
(30)
und den Lösungen
ω1 = c · sin(ω◦ t − δ)
16
(31)
~ am Schwerpunkt angreift.
Ein Diskus fliegt frei von Drehmomenten, da die Schwerkraft G
15
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
. Analog ergibt sich aus der umgekehrten Kombination der beiden Gleichungen ω2 = −c·cos(ω◦ t−
δ).
Beispiel Erde: Die Rotationsachse führt eine Nutationsbewegung aus mit einer Amplitude auf
der Oberfläche der Erde von etwa 6 m. Aus der bekannten Form und unter Annahme einer
konstanten Dichte erhält man eine Period von Tgerechnet = 304 Tage. Der gemessene Wert
beträgt Tgemessen = 433 Tage.
Der Unterschied kommt unter anderem dadurch zustande, dass die Erde kein starrer Körper ist,
sondern einen flüssigen Kern hat und natürlich keine homogene Dichteverteilung besitzt.
Zusätzlich zu dieser freien Nutation kommt noch eine erzwungene Schwingung dazu, die von
den jahreszeitlichen Massenverschiebungen auf der Erdoberfläche (Schnee etc.) und von unregelmässigen Ereignissen (z.B. Erdbeben) erzeugt werden. Die effektiv gemessene Nutationsamplitude schwant deshalb zwischen 2m und 8m.
Figurenachse
→
Gangpolkegel
3
ω
ω→3
ω→
→
ω2
→
ω1
2
1
c
"
korperfestes
System
2 =: c2 . ω und ω
Im körperfesten System ist ω12 + ω22 = ω⊥
1
2
sind die Komponenten eines Vektors ω
~ ⊥ , der in der senkrecht
zur 3-Achse stehenden Ebene mit der Winkelgeschwindigkeit
ω◦ rotiert. Da ω
~ =ω
~ ⊥ + ω3~e3 gilt, ist auch |~
ω | = konst. Somit muss sich ω
~ auf einem Kegel, dem Gangpolkegel, um
die Figurenachse17 drehen. Ist ω1 = ω2 = 0 und damit
ω
~ = ω
~ 3 = konst, dann bleibt der Kreisel in der Figurenachse stehen (ruhender Kreisel). Im raumfesten System ist
~ s = konst. Man wählt daher zweckmässig
der Drehimpuls L
~ s = I1 ω1~e1 + I2 ω2~e2 + I3 ω3~e3 (I hat
die z-Achse ↑↑ L
im körperfesten Hauptachsensystem nur Diagonalelemente). Die 3-Komponente des Drehimpulses ist Ls3 = I3 ω3 =
Ls cos ϑ = konst.
Man beobachtet folgende Bewegungen der einzelnen Axialvektoren:
z
Nutations- →
Ls
kegel
ϑ
3
Ls3
raumfestes System
CO
C
C
~s C
L
CO
C (I3 − I)ω3~e3 C I~
ω
C
17
ω
~ dreht auf dem Gangpolkegel um die Figurenachse 3 im körperfesten
Hauptachsensystem. Die Figurenachse 3 dreht unter dem konstanten
Winkel ϑ um die raumfeste z-Achse (Nutationskegel). Wie bewegt
sich ω
~ in Bezug auf die raumfeste z-Achse?
~ s = 1 ωz Lz =
Aus der Energiebetrachtung Krot = 21 ω
~ Is ω
~ = 12 ω
~ ·L
2
konst (siehe später, Gl.(36)) muss mit Lz = Ls = konst auch
ωz = konst gelten. Damit läuft ω
~ auf einem Kegel um die z-Achse
(Rastpolkegel).
~ s, ω
Wir überzeugen uns, dass dann alle drei Vektoren L
~ und ~e3 (=
ˆ
~
3-Achse) in jedem Moment in einer Ebene liegen. Es ist ja Ls =
I(ω1~e1 + ω2~e2 ) + I3 ω3~e3 = I~
ω⊥ + I3 ω3~e3 = I(~
ω − ω3~e3 ) + I3 ω3~e3 =
~ s liegt also in der durch die
I~
ω + (I3 − I)ω3~e3 . Der Summenvektor L
Komponentenvektoren ω
~ und ~e3 aufgespannten Ebene.
so die Bezeichnung für die Hauptachse mit dem grössten Trägheitsmoment
16
Ergänzungen zu Physik I
Nutationskegel
2
Eigenschaften des Kreisels
Da die relative Lage der drei Vektoren sich nicht ändert,
bleibt als einzig mögliche Bewegung die Drehung dieser Ebene um die raumfeste Ls -Richtung übrig. Da sich aber ω
~
~ sschon um die Figurenachse dreht und sich beide um die L
Achse drehen, haben wir folgendes Resultat für die
z
3
→
→
ω
Bewegung des symmetrischen Kreisels:18
Ls
Rastpolkegel
Gangpolkegel
prolater Kreisel I1 = I2 > I3
a) ω
~ dreht sich um Ls auf dem raumfesten Rastpolkegel.
b) ω
~ dreht sich um die Figurenachse 3 auf dem
körperfesten Gangpolkegel.
z
3
Nutationskegel
Rastpolkegel
~ s auf dem raumd) Die Figurenachse dreht sich um L
festen Nutationskegel.
ω→
Gangpolkegel
c) Beide Kegel rollen aufeinander ab, ω
~ bildet die gemeinsame Mantellinie.
Je nach Anfangsbedingungen ist natürlich auch der Spezialfall möglich, dass die ω
~ -Drehachse und die Figurenachse mit der Richtung des raumfesten Drehimpulses zusammenfallen.
→
Ls
oblater Kreisel I1 = I2 < I3
2.3 Stabilität der Drehachse für Körper ohne Rotationssymmetrie
Die Stabilität eines Systems z.B. im Schwerefeld kann untersucht werden, indem man kleine
Auslenkungen aus der Gleichgewichtslage untersucht und die resultierende Bewegungsgleichung
näherungsweise aufstellt.
Die Bewegungsgleichung ist dann vom Typ
stabil
indifferent
labil
ẍ + a2 x ≈ 0. Mit a2 > 0 erhält man eine Lösung
x(t) ≈ cos(at); x(t) bleibt endlich, ist also stabil.
Mit a2 < 0 ist x(t) ≈ eat und x(t) → ∞, die Lösung ist
labil.
Allgemein ist für eine kräftefreie Bewegung ~τ◦ = 0 und I1 =
6 I2 6= I3 im Hauptachsensystem.
Dreht sich der Körper bei Stabilität praktisch nur um eine Hauptachse, dann ist ω1 ≈ ω2 ≈ 0
18
Die Figuren beschreiben einen prolaten Kreisel (I1 = I2 > I3 ), bei dem der Rastpolkegel ausserhalb auf
dem Gangpolkegel läuft, und einen oblaten Kreisel (I1 = I2 < I3 ), bei dem der Rastpolkegel innerhalb des
Gangpolkegels läuft.
17
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
und ω3 6= 0 und die Eulerschen Gleichungen (Gl.(28)), wenn der quadratisch kleine Term ω1 ω2
vernachlässigt wird, sind
ω̇1 −
I2 − I3
ω2 ω3 = 0,
I1
ω̇2 −
I3 − I1
ω3 ω1 = 0,
I2
ω̇3 −
I1 − I2
ω1 ω2 = 0
I3 | {z }
≈0
⇒ ω3 = konst.
Durch Differenzieren der ersten beiden Gleichungen und Einsetzen erhält man für ω1 und ω2
(analog zu S.15) die Schwingungsgleichungen
ω̈1 −
|
I2 − I3 I3 − I1 2
ω3 ω1 = 0
I1
I
{z 2
}
2
a
und
ω̈2 −
|
I3 − I1 I2 − I3 2
ω3 ω2 = 0
I2
I
{z 1
}
2
a
3 I3 −I1
ã stabil für a2 > 0 ⇒ I2I−I
< 0, es muss dann I3 das grösste oder das kleinste
I2
1
Trägheitsmoment um die Hauptachse 3 sein.
ã instabil für a2 < 0 ⇒ I1 < I3 < I2 führt ω1 exponentiell von einer zunächst reinen
Rotation um die Hauptachse 3 weg ins Torkeln.
Die Hauptachsen mit dem grössten
Trägheitsmoment sind stabile Drehachsen.
und
dem
kleinsten
Anschauliche Betrachtung dieser Stabilitätsbedingungen: Bei gleicher kinetischer Rotationsenergie 21 Iω 2 entspricht die Rotation um die Hauptachse mit dem maximalen (minimalen)
Trägheitsmoment dem minimalen (maximalen) ω, d.h. ω kann bei erhaltener Energie der Rotation nicht mehr in beide Richtungen verändert werden.
Ein anderes Stabilitätsbeispiel ist das Problem des Lassowerfers: Das Lasso klappt beim Drehen
zu einem Stab zusammen, da das Trägheitsmoment für den Stab mit der Länge ` kleiner ist als
1
für einen Kreis mit dem Umfang 2` also IStab = 12
m`2 < IKreis = π12 m`2 . Man muss deshalb
beim Lassowerfen die Anfangsbedingungen besser wählen und das Lasso steifer machen.
2.4 Symmetrischer Kreisel im Schwerefeld (Präzession)
z 6
~◦
~rs k ω
~ kL
@
@ @
@
α ~rs
c
~
G
?
Wir kehren zum symmetrischen Kreisel zurück. Der Kreisel sei jetzt aber
nicht mehr im Schwerpunkt unterstützt, so dass das Gewicht ein Dreh~ ausübt und folglich L
~ ◦ nicht mehr konstant ist. Die
moment ~τ◦ = ~rs × G
daraus resultierende Bewegung der Drehimpulsachse nennt man Präzession.
Zur Vereinfachung nehmen wir an, die Figurenachse, Drehachse und Drehimpulsachse fallen zusammen und ~rs liege in der Figurenachse.
Es ist also
~◦ k ω
L
~ k ~rs .
18
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
Ferner sei ω3 sehr gross.19 Dann sind wir nicht mehr auf die Euler-Gleichungen angewiesen,
sondern können den
~
~ = dL◦
Drehimpulsatz ~τ◦ = ~rs × G
dt
bq
~◦
L
?
~◦
dL
?
~
τ◦
→
benützen.
~ ◦ , aber parallel zu dL
~ ◦ steht, muss dL
~ ◦ senkrecht auf
Da ~τ◦ senkrecht zu L
~
L◦ stehen. Dieser Sachverhalt gilt für jeden Augenblick, also muss sich die
~ ◦ -Vektors auf einem Kreis bewegen, L
~ ◦ selbst präzessiert auf
Spitze des L
~ ◦ ist also ein
einem Kegelmantel, dem Präzessionskegel, um die z-Achse. L
Vektor, der im Relativsystem (Hauptachse) konstant ist und im Absolutsystem nur seine Richtung, nicht aber seinen Betrag ändert. Die Ableitung
des Drehimpulses und somit das Drehmoment stehen deshalb senkrecht auf
L~◦ , man kann somit schreiben (siehe auch Ergänzungsblätter Relativbe”
wegungen“, Gl.(5), S.3.):
→
ωp
dL o
~τ◦ =
~◦
dL
~◦ .
=ω
~p × L
dt
→
Lo
α
ωp nennt man Präzessions-Kreisfrequenz. Der Drehimpulsvektor weicht
~ aus.
also der angreifenden Kraft G
dL
~
◦ ~ = rs G sin α = ω
~ ◦ = ωp L◦ sin α
Da |~τ◦ | = ~p × L
= ~rs × G
dt gilt, folgt
(32)
rs G
rs M g
ωp =
=
L◦
ω3 I3
die Präzessionsfrequenz
des rasch rotierenden
symmetrischen Kreisels
(unabhängig von α).
(33)
Infolge dieser Präzession hat der Kreisel einen kleinen Drehimpuls in der z-Richtung erhalten.
r Mg
Falls jedoch ωp ω3 ist, d.h. für ω32 sI , können wir diesen Drehimpuls vernachlässigen
3
~ ◦ rechnen.
und nur mit L
Eine genaue Rechnung mittels der Euler-Gleichungen zeigt, dass die Kreiselachse nicht eine einfache Präzession um die z-Achse ausführt, sondern dabei noch Schwankungen des Winkels α auftreten (Nutation). Immerhin gibt es immer einen bestimmten Winkel α, bei dem die Präzession
nutationsfrei ist. Insbesondere ist die senkrechte Lage α = 0 nutationsfrei, solange gilt
ω > ωkrit =
19
2p
M grs I1 .
I3
schlafender Kreisel
(34)
Der Grund für diese Annahme wird mit Gl.(33) klar.
19
Ergänzungen zu Physik I
2
Eigenschaften des Kreisels
Sieht man von der Nutation ab, so gelten für den Kreisel die folgenden Regeln:
→
Lo
→
1. Ein äusseres Drehmoment erzeugt bei einem frei beweglichen
~ ◦ , wobei die Änderung von L
~ ◦ die
Kreisel eine Präzession von L
Richtung von ~τ◦ besitzt.
ωp
2. Verhindert man eine Präzession durch Anbringen von
Führungen, so erzeugen die Führungen Kräfte, welche die Kreiselachse senken oder heben.
Wand
→
N
3. Will man eine Präzession der Drehachse erzwingen, so müssen
die Lager die entsprechenden Kräfte und Drehmomente aufbringen.
→
ω
Mg
Beispiel zu 2):
~
~τ = ~r × N
d
H
HH
j
~r Die Führungskraft N erzeugt ein Drehmoment
~
~τ = ~r × N
~ ◦ k ~τ . Die Kreiselachse senkt sich. Wirkt N
~ umund eine Änderung dL
gekehrt, d.h. versucht man die Präzession zu vergrössern, so steigt die
Kreiselachse.
0
→
→
Lo
→
→
F2
ω
F 1 Beispiel zu 3):
Wird die Kreiselachse in der Horizontalebene gedreht, 50
so müssen die Lager die Kräfte F~1 , F~2 ausüben, deren
→
~
Mo Drehmoment parallel zu dL◦ steht.
2.5 Rotationsenergie und Energiesatz für die allgemeine Drehung
Die kinetische Energie K eines Systems von Massenpunkten kann durch die Schwerpunktsgeschwindigkeit ~v und die die Relativgeschwindigkeit ~vsi der DrehungPum den Schwerpunkt
ausgedrückt werden, wobei das Schwerpunktssystem definiert ist durch ni=1 mi~vsi = 0:
1X
1
1X
1X
2
2
mi (~v + ~vsi )2 =
mi (~v 2 + 2~v~vsi + ~vsi
) = m~v 2 +
mi~vsi
.
K=
2
2
2
2
i
i
i
Für einen starren Körper gilt ~vsi = ω
~ × ~rsi mit ~rsi dem Ortsvektor im Schwerpunktssystem.
Damit ist die kinetische Energie
1
1X
1
1X
1
1
~s
K = m~v 2 +
mi~vsi · (~
ω × ~rsi ) = m~v 2 +
mi ω
~ · (~rsi × ~vsi ) = m~v 2 + ω
~ ·L
2
2
2
2
2
2
i
i
|
{z
}
~
=ω
~ · Ls
20
Ergänzungen zu Physik I
⇒
2
Eigenschaften des Kreisels
1
1
m~v 2 + ω
~ Is ω
~ = Ktrans + Krot
2
2
(35)
In dieser Form der Aufspaltung in Translationsenergie und Rotationsenergie gilt die Gleichung
Gl.(35) nur für Drehungen um den Schwerpunkt. Für die Drehbewegung um einen beliebigen
raumfesten Punkt mit ~vi = ω
~ × ~ri ohne äussere Drehmomente ~τ = 0 hat man die kinetische
Energie
1
~ = 1ω
Kkin = Krot = ω
~ ·L
~ I~
ω ,
(36)
2
2
für welche der Energieerhaltungssatz gilt.
21
Ergänzungen zu Physik I
3
Dynamik der Fluide
3 Dynamik der Fluide
3.1 Kontinuitätsgleichung
Fluide sind Zustände von Materie in denen keine (Gase) oder nur sehr kleine Scherkräfte
(Flüssigkeiten) auftreten. Sie besitzen keine starre Form.
Die Bewegung der Massenelemente von Fluiden wird durch deren Geschwindigkeit dargestellt.
An jedem Ort im Raum besitzt das dortige Massenelement eine Geschwindigkeit. Sie hängt vom
Ort und Zeit ab und ist überall definiert, sie stellt also ein Vektorfeld dar, das man die Strömung
nennt:
~v (x, y, z, t)
Stroemung als Vektorfeld
(37)
Die Strömung heisst stationär, wenn es keine explizite Zeitabhängigkeit gibt:
∂~v
=0
stationaere Stroemung
(38)
∂t
Ein Teilchen (Massenelement), das sich mit der Strömung mitbewegt, sieht eine andere Geschwindigkeitsabhängigkeit als ein Beobachter, der an einer festen Stelle (x, y, z) misst. Wenn
sich ein Teilchen um (dx, dy, dz) verschiebt, dann sieht es eine Veränderung
d~v =
∂~v
∂~v
∂~v
∂~v
dx +
dy +
dz +
dt
∂x
∂y
∂z
∂t
(39)
Dividieren wir diese Gleichung durch dt erhalten wir
∂~v
d~v
= (grad ~v ) · ~v +
substantielle Ableitung
dt
∂t
Diese Gleichung ist komponentenweise zu verstehen, es gilt zum Beispiel
dvx
∂vx
= grad vx · ~v +
dt
∂t
Der Gradient ist ja eigentlich für Skalarfelder definiert, und ergibt einen Vektor.
(40)
(41)
Stellen wir uns nun eine Fläche A in der (y,z)-Ebene vor, durch die das Vektorfeld strömt. Aus
den mathematischen Hilfsmitteln (Kap. 8.6., Flächenintegrale) wissen kennen wir schon
Z
~
Φ=
~v · dA
Fluss des Vektorfeldes
(42)
A
22
Ergänzungen zu Physik I
3
Dynamik der Fluide
Mit Massenfluss Q bezeichnen wir die Masse M des Fluides, die pro Zeiteinheit durch die Fläche
A strömt. Diese Masse hat in einem Quader mit Querschnitt A und Länge dx = v · dt Platz. Es
wird also
dM
ρ A dx
Q=
=
= ρ A vx
(43)
dt
dt
Man definiert den Massenfluss pro Fläche
~j = Q = ρ ~v
A
Stromdichte
(44)
Dies geht ganz analog für andere Vektorfelder, wo etwas transportiert wird, zum Beispiel die
elektrische Stromdichte.
Betrachten wir nun einen Quader mit Kantenlängen dx, dy, dz, der mit seinen Kanten also
parallel zu den Koordinatenachsen liegen soll. Wir wollen die gesamte Massenbilanz des Quaders
aufstellen. Dazu müssen wir den Fluss durch alle 6 Seitenflächen des Quaders betrachten. Aus
dem Quader hinausfliessende Masse führt zu einer Abnahme der Masse, hineinfliessende zu einer
Zunahme. Die Summe der 6 Flüsse durch die Seitenwände wird also
Z
X
~
~
~
(45)
Qtot = −
j · A = − ~j · dA
A
Ist der Gesamtfluss verschieden von null, muss die Masse im Quader mit der Zeit entweder zuoder abnehmen, und zwar gerade um den Massenfluss: Qtot = ∂M/∂t. Die Massenbilanz ist
also positiv oder negativ. Wenn die Massenbilanz positiv ist, erwarten wir anschaulich, dass die
Dichte ρ innerhalb des Quaders zunimmt, da das Volumen ja konstant ist. In der Tat:
Z
Z
∂
∂M
∂ρ
=
ρdV =
dV
(46)
∂t
∂t V
V ∂t
Andererseits können wir auf das Volumen den Gauss’schen Satz anwenden (mathematische Hilfsmittel, Kap 9.3 “Divergenz”). Für das Stromdichtefeld ~j(x, y, z, t) gilt demnach für den Fluss
durch die gesamte Oberfläche, also alle 6 Teilflächen
Z
I
~ =
~j · dA
div ~j dV
Satz von Gauss
(47)
V
Durch Kombination der letzten drei Gleichungen ergibt sich sofort
∂ρ
+ div ~j = 0
∂t
Kontinuitaetsgleichung
(48)
Die Kontinuitätsgleichung gilt immer, auch für nicht stationäre Strömungen und solche mit
Reibung. Dei einzige Annahme besteht darin, dass keine Masse verloren gehen darf.
Beispiel: Betrachten wir eine stationäre Strömung durch ein Rohr mit einer Verengung. Dann
ist ∂ρ/∂t = 0 und somit die Divergenz der Stromdichte ebenfalls. Aus dem Gauss’schen Satz
~ = konst. Oder für zwei Querschnitte, die senkrecht zur
folgt für alle Rohrquerschnitte ~j · dA
Strömung sind die Kontinuitätsgleichung in der Form ρ1 v1 A1 = ρ2 v2 A2 .
23
Ergänzungen zu Physik I
3
Dynamik der Fluide
3.2 Bernoulligleichung
Falls keine Reibung oder andere disssipativen Prozesse (solche bei denen Energie in Wärme
verwandelt wird) vorkommen, ist die mechanische Energie erhalten. Die Energieerhaltung pro
Volumeneinheit führt zu der Gleichung
ρ
p + v 2 + ρgz = konst
Bernoulligleichung
(49)
2
für ein Fluid in einem Schwerefeld, das der z-Richtung entgegengesetzt ist. Herleitung und
Anwendungen des Bernoulligleichung werden in der Hauptvorlesung besprochen.
3.3 Innere Reibung
Schon Newton hat festgestellt, dass die Effekte der Strömungsreibung bei kleinen und grossen
Geschwindigkeiten verschieden sind.
a) Für kleine Geschwindigkeiten ist die Viskosität η relevant, die die Reibungskraft aufgrund
von Scherkräften bei laminaren Strömungen beschreibt. Für eine homogene Strömung senkrecht
zur z-Richtung entsteht eine Scherspannung τ (Kraft pro Flächeneinheit)
dv
Newtonsches Reibungsgesetz
(50)
dz
Für eine Kugel vom Radius r, die von einem Fluid laminar umströmt wird, erhält man daraus
die Reibungskraft R
τ =η
R = 6π r η v
Stokesche Reibung an einer Kugel
(51)
Eine weitere Anwendung ist der Massenfluss Q durch ein Rohr mit Radius R, Druckunterschied
∆p über die Rohrlänge l:
Q=
πρ∆p 4
R
8ηl
Hagen − Poiseuille
(52)
b) Für grosse Geschwindigkeiten beobachten wir turbulente Strömungen mit Wirbelbildung. Die
Wirbel enthalten kinetische Energie, die Kraft R auf das umströmte Objekt mit Querschnitt A
muss entsprechende Arbeit leisten. Die kinetische Energie pro Volumeneinheit beträgt ρ2 v 2 , man
macht deshalb den Ansatz
ρ
Reibungskraft bei grossem v
(53)
R = cW v 2 A
2
mit cW einer dimensionslosen Kennzahl, die nur von der Form des Objektes abhängt (z.B. Kugel
cW = 0.22).
24
Ergänzungen zu Physik I
3
Dynamik der Fluide
c) Das Kriterium von Reynold. Bei welchen Geschwindigkeiten liegt die Grenze zwischen “klein”
und “gross”? Das Kriterium von Reynold soll dafür einen Anhaltspunkt geben. Wir betrachten
vorerst eine Kugel, die von einem Fluid umströmt wird. Bei kleinen Geschwindigkeiten dominiert
der lineare Zusammenhang mit v, das Gesetz von Stokes (51), bei grossen Geschwindigkeiten
überwiegt der quadratische Term gemäss (53).
R
v2
Stokes
durch η
bestimmt
durch ρ
bestimmt
vc
v
Der Uebergang von laminar zu turbulent passiert in der Nähe der kritischen Geschwindigkeit
vc , bei dem die beiden Beiträge gleich gross sind:
ρ
cW vc2 A = 6π r η vc
(54)
2
Man definiert die dimensionslose Reynoldszahl Re mit
ρvr
(55)
Re =
η
und stellt durch Umstellen von (54) fest, dass turbulente Strömung für
Re > Rekritisch =
12
cw
(56)
eintritt. Dies nennt man das Reyonldskriterium. Die kritische Reynoldszahl 12/cW ist etwa 60
für eine Kugel. Für Strömungen in einem Rohr mit Radius r und mit glatten Wänden liegt die
kritische Reynoldszahl bei etwa 2300.
Das Aehnlichkeitsgesetz nach Reynold besagt, dass zwei geometrisch ähnliche Anordnungen verschiedener Grösse genau dann die gleichen Strömungsverhältnisse zeigen, wenn sie die gleiche
Reynoldszahl (55) aufweisen. Das ist zum Beispiel bei Messungen mit Modellen in einem Windkanal relevant.
Das Reynoldskrieterium gibt nur einen ungefähren Anhaltspunkt. In Praxis wird die Turbulenz
nicht immer bei der genau gleichen Reynoldszahl eintreten, sondern variieren. Zufällige kleine
Störungen spielen für den Einsatzpunkt der Turbulenz ebenfalls eine Rolle.
3.4 Die Navier-Stokes Gleichung
Wir wollen die allgemeine Bewegungslgleichung eines Massenelementes dm in einer Strömung
eines Fluides mit innerer Reibung kennenlernen. Sei dV = dx · dy · dz wiederum ein Quader der
die Masse dm enthalte. Also dm = ρdV
25
Ergänzungen zu Physik I
3
Dynamik der Fluide
Um die Bewegungsgleichung zu bekommen, müssen wir das II. Newtonsche Prinzip anwenden,
und dafür alle Kräfte kennen.
Es wirken folgende Kräfte auf dm
a) Der Druck. Es gibt nur einen Effekt, wenn der Druck auf der einen Seite von dm verschieden
ist, gegenüber der anderen. Die Kraft auf dm wird dann zum Beispiel auf eine Seitenfläche
dA = dx · dy in z-Richtung Fz = p(z) · dA. Die totale Kraft in z-Richtung setzt sich aus den
beiden gegenüberliegenden Seitenwänden zusammen:
dFz = p(z)dA − p(z + dz)dA
(57)
Machen wir das für alle 3 Koordinatenrichtungen und dividieren durch das Volumen dV = dA·dz
erkennen wir, dass die Druckkraft pro Volumeneinheit f~p = dF~ /dV gerade durch den negativen
Gradienten des Druckes bestimmt wird.
f~p = −grad p
(58)
“Der Druck ist das Potential der Druckkraftdichte”.
b) Die Gewichtskraft. Allgemeiner nennt man eine Kraft, die nur vom Volumen abhängt und
nicht vom dynamischen Zustand des Fluides, eine Volumenkraft. Wir definieren die Volumenkraftdichte zum Beispiel für das Gewicht:
~
G
f~g =
= ρ · ~g
V ol
(59)
c) Die viskose Reibung. Betrachten wir dazu eine laminare Strömung, bei der eine Scheibe der
Fläche dA, der Dicke dx und der Masse dm = ρ dA dx sich in z-Richtung mit der Geschwindigkeit vz bewegt. Die Geschwindigkeit ändere sich in x-Richtung gemäss dem Newtonschen
Reibungsgesetz, was infolge der Viskosität η zu einer Scherkraft FS in z-Richtung führt. Die
Scherspannung ist definiert durch τ = dFS /dA, also die Kraft pro Flächeneinheit (ähnlich wie
Druck). Das Newtonsche Reibungsgesetz (50) lautet hier
τ =η
dvz
dx
(60)
Die Kraft in z-Richtung auf die Scheibe wird
dFz = τ (x + dx) dA − τ (x) dA
Dividieren durch dV = dA · dx ergibt die Kraftdichte
fz =
∂τ
∂x
Wir setzen das Newton’sche Reibungsgesetz ein und erhalten:
fz = η
∂ 2 vz
∂x2
(61)
Macht man die gleiche Ueberlegungen in allen drei Raumrichtungen erhält man in Vektorschreibweise
f~S = η ∆~v
(62)
26
Ergänzungen zu Physik I
3
Dynamik der Fluide
mit der Definition für den Laplaceoperator:
∆vz =
∂ 2 vz
∂ 2 vz
∂ 2 vz
+
+
2
2
∂x
∂y
∂z 2
und
∆~v = (∆vx , ∆vy , ∆vz )
(63)
Nun fassen wir alle drei Kraftdichten zusammen und erhalten die Bewegungsgleichung
d~v
= −grad p + ρ ~g + η ∆~v
(64)
dt
Das ist die Navier-Stokes Gleichung (hier in der Form für inkompressible Flüssigkeiten, andernfalls muss man noch die Volumenviskosität berücksichtigen).
ρ
Man beachte, dass es sich bei der Ableitung d~v /dt um die substantielle Ableitung (40) handelt,
also um die Veränderung, die das mitbewegte Teilchen sieht.
Die Navier-Stokes-Gleichung hat keine nichttrivialen analytischen Lösungen. Man muss numerische Methoden zur Lösung einsetzen.
Falls die innere Reibung vernachlässigt werden kann (η = 0), wird die Navier-Stokes Gleichung
zur Eulergleichung
d~v
ρ
= −grad p + ρ ~g
(65)
dt
Beachte wiederum, dass es sich um die substantielle Ableitung handelt. Wollen wir die Veränderung
der Strömung an einem bestimmten, festen Ort wissen, müssen wir Gleichung (40) einsetzen,
damit wird die Eulergleichung zu
ρ
∂~v
= −ρ(~v · grad ~v ) − grad p + ρ ~g
∂t
(66)
3.5 Helmholtzsche Wirbelsätze
Aus der Eulerschen Gleichung (65) kann man im Prinzip die Helmholtzschen Wirbelsätze ableiten. Sie gelten für reibungsfreie Flüssigkeiten. Unter Wirbelfaden verstehen wir die Linie die die
Zentren der rotierenden Flächen verbindet. Die Helmholtzschen Wirbelsätze lauten:
(1) Im Inneren von Fluiden können Wirbel örtlich weder beginnen noch enden. Das heisst die
Wirbelfäden können nur an Oberflächen enden oder sind geschlossene Kurven.
Flugzeug
(2) Wirbel enthalten zu jeder Zeit die gleichen Teilchen
H
(3) Die Zirkulation um den Wirbelfaden ~v · d~s ist entlang dem Wirbelfaden eine Konstante.
Diese Sätze finden Anwendung bei z.B. in Rauchwirbeln oder bei Ablösewirbeln von startenden
Flugzeugen (ein Teil des Wirbels bleibt am Boden und hebt eventuell Dachziegel ab).
27
Ergänzungen zu Physik I
3
Dynamik der Fluide
3.6 Die Anatomie von Wirbeln
Wir wollen nun die Anatomie von Wirbeln noch etwas genauer studieren:
Ein Wirbel in einem Fluid besteht im allgemeinen aus zwei Teilen, einem Wirbelkern und einem
Zirkulationsgebiet.
Kern
Zirkulationsgebiet
Kern
Zirkulationsgebiet
Zirkulationsgebiet
Im Innern eines Wirbels rotiert das Fluid fast wie ein fester Körper. Das heisst es gilt
v = rω
im Wirbelkern
(67)
Weiter aussen muss die Geschwindigkeit wieder abnehmen, da der Wirbel schon aus Energiegründen örtlich beschränkt sein muss. In erster Näherung gilt
v=
Γ
2πr
im Zirkulationsgebiet
Man definiert allgmein für eine beliebige Strömung die Zirkulation Z durch
I
Z = ~v · d~s
(68)
(69)
also als geschlossenes Linienintegral. Im Zirkulationsgebiet eines Wirbels wird die Zirkulation
auf einem Kreis mit Radius r um das Zentrum des Wirbels also gerade Z = 2πrv = Γ.
Im Wirbelkern beträgt die Zirkulation ZK = 2π r2 ω.
Für eine beliebiges Vektorfeld ~v (x, y, z) definiert man die Rotation durch
rot ~v = (
∂vy ∂vx ∂vz ∂vy
∂vz
∂vx
−
,
−
,
−
)
∂y
∂z ∂z
∂x ∂x
∂y
(70)
Die Rotation erzeugt also aus einem Vektor wieder einen Vektor.
28
Ergänzungen zu Physik I
3
Dynamik der Fluide
Zum Beispiel gilt in einem Wirbelkern ~v = ω (−y~ex + x~ey ), woraus man sofort erhält rot~v =
(0, 0, 2ω). Die Rotation in einem Wirkbelkern ist also überall konstant und zeigt in Richtung
der Drehachse.
Im Vergleich mit der Zirkulation oben findet man für den Wirbelkern den Zusammenhang
ZK = A (rot ~v )z
(71)
In der Tat gilt allgemein der Satz von Stokes (siehe mathematische Hilfsmittel, Kapitel 9.4
“Rotation”)
I
Z
~
rot ~v · dA
(72)
~v · d~s =
A
Falls die Rotation einer Strömung verschwindet, rot ~v = 0, nennt man die Strömung eine
Potentialströmung. Dies ist das Helmholtzkritierium. Es ist motiviert durch die Tatsache, dass
die Rotation eines Gradientenfeldes immer null ist:
rot (grad φ) = 0
φ(x, y, z) = Skalarfeld
(73)
(Beweis durch Einsetzen der Definitionen) Das Strömungsbild einer Potentialströmung lässt sich
also durch den Gradienten eines Potentialfeldes darstellen.
Eine Potentialströmung ist gewissermassen das Gegenteil eines Wirbels. Zum Beispiel besitzt eine
homogene Strömung in x-Richtung mit ~v = (a, 0, 0) ein Potential φ = a · x, sodass ~v = grad φ.
Aber auch der Zirkulationsbereich im äusseren eines Wirbels ist eine Potentialströmung. Für
ein Potential φ = Γ · α/2π (mit α = Azimuthwinkel in der Rotationsebene) erhält man eine
tangentiale Geschwindigkeit ~v = grad φ mit Betrag v = Γ/2πr. (Für die Herleitung rechne den
Gradienten in Polarkoordinaten aus).
Also, merke:
1. Eine Potentialströmung ist durch einen Gradienten darstellbar und ist immer wirbelfrei und
die Zirkulation verschwindet (lokal) Z = 0.
2. Ein Wirbel mit Z 6= 0 besitzt eine nicht verschwindende Rotation und kann nicht durch einen
Gradienten dargestellt werden.
In einer gegebenen Strömung findet
H man die Zirkulation, in dem man um eine kleine Fläche
herum ein gesschlossenes Integral ~v · d~s ausrechnet.
Anschauung für die Zirkulation: Die Zirkulation um eine kleine Fläche gibt an, wie stark die
Fläche im Lauf der Bewegung rotiert. Ist die Zirkulatoin null, behält die Fläche ihre Ausrichtung,
ein kleiner Korkzapfen, der im Wasser schwimmt, ändert seine Orientierung nicht. Wenn die
Zirkulation einen nicht verschwindenden Wert hat, dann rotiert die Flüssigkeit um den Zapfen,
und somit auch der Zapfen selbst. Er ändert seine Ausrichtung (Markierung mit Fähnchen).
3.7 Potentialwirbel (Badewannenwirbel)
Ein spezieller Fall eines Wirbels ist der Badewannenwirbel. Er stellt einen Wirbel dar, bei dem
der Kern fehlt. Im gesamten Wirbelgebiet herrscht also eine Potentialströmung. Die (lokale)
29
Ergänzungen zu Physik I
3
Zirkulation verschwindet
Dynamik der Fluide
I
Z=
~v · d~s = 0
(74)
sofern das Wirbelzentrum durch diesen geschlossenen Weg nicht umschlossen wird.
Im gesamten Innern des Wirbels gilt v = Γ/2πr. Der Druck in der Flüssigkeit muss positiv sein,
dort wo er null ist, befindet sich die Oberfläche. Die Oberfläche am inneren Rand des Wirbels
bildet den “Wirbelstamm”.
Wir wollen die Form dieser Oberfläche berechnen. Wenn wir die innere Reibung vernachlässigen,
können wir das mit dem Gesetz von Bernoulli machen. Sei z die vertikale Achse, mit z0 = 0
an der Oberfläche, wo p0 = 0, und bei grossem Radius r0 , wo v0 = 0. Seien v1 , r1 , z1 die
Grössen an der Oberfläche des Wirbelstammes, nach Definition ist p1 = 0 und v1 = Γ/2πr1 . Die
Bernoulligleichung für den Vergleich von Ort (r0 , z0 ) und Ort (r1 , z1 ) wird:
ρ
0 + 0 + 0 = 0 + v12 − ρgz1
2
(75)
Nach Einsetzen von v1 und Umsortieren erhalten wir die Gleichung für die Form des Wirbelstammes:
Γ2 1
(76)
·
z1 =
8πg r12
v
r
30