4. Selbstrechen ¨ubung -¨Ahnlichkeitstheorie 1

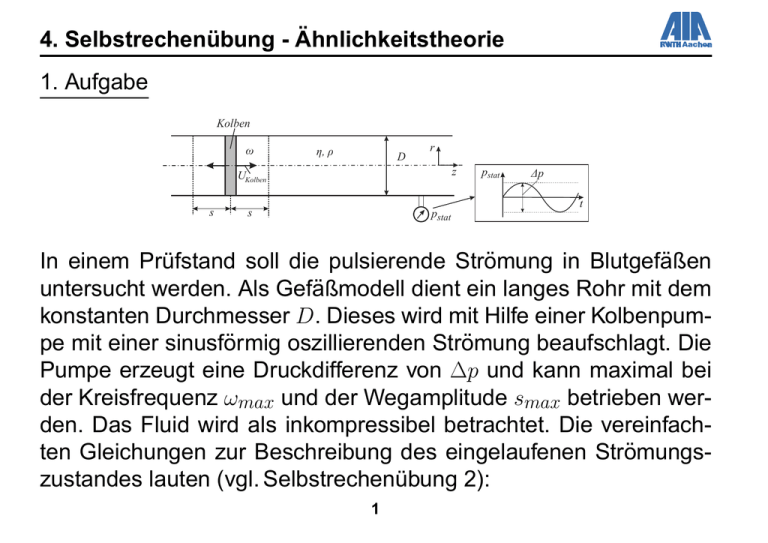
4. Selbstrechenübung - Ähnlichkeitstheorie
1. Aufgabe
Kolben
ω
η, ρ
D
r
z
UKolben
s
pstat
Δp
t
s
pstat
In einem Prüfstand soll die pulsierende Strömung in Blutgefäßen
untersucht werden. Als Gefäßmodell dient ein langes Rohr mit dem
konstanten Durchmesser D. Dieses wird mit Hilfe einer Kolbenpumpe mit einer sinusförmig oszillierenden Strömung beaufschlagt. Die
Pumpe erzeugt eine Druckdifferenz von ∆p und kann maximal bei
der Kreisfrequenz ωmax und der Wegamplitude smax betrieben werden. Das Fluid wird als inkompressibel betrachtet. Die vereinfachten Gleichungen zur Beschreibung des eingelaufenen Strömungszustandes lauten (vgl. Selbstrechenübung 2):
1
4. Selbstrechenübung - Ähnlichkeitstheorie
vr = 0
1 ∂p
−
= 0
ρ ∂r
1 ∂p
1∂
∂
∂vz
= −
+ν
r (vz )
∂t
ρ ∂z
r ∂r ∂r
(1)
(2)
(3)
Bestimmen Sie mit Hilfe der Methode der Differentialgleichungen
die Kennzahlen des vereinfachten Systems und führen Sie diese
auf bekannte Ähnlichkeitsparameter zurück.
Gegeben:
alle nötigen Referenzgrößen
Hinweis:
Bei oszillierenden Strömungsgrößen werden die Kennzahlen mit den
Maximalwerten gebildet.
2
4. Selbstrechenübung - Ähnlichkeitstheorie
2. Aufgabe
Bei der Beschreibung von Mehrphasenströmungen taucht die folgende vereinfachte Differentialgleichung auf:
d2 z
ν
= 18 2
2
dt
dP
dz
1−δ
δ
vz −
+g
1 + αδ
dt
1 + αδ
(4)
Bestimmen Sie mit Hilfe der Methode der Differentialgleichungen die
Kennzahl(en) dieses Problems. Drücken Sie die erhaltene(n) Kennzahl(en) durch eine oder mehrere in der Strömungsmechanik häufig
verwendete Kennzahlen aus.
Gegeben:
νref , dP , g, vref , α = 0, 5, δ = ρF /ρP = const
Hinweis:
Betrachten Sie δ nicht als zu ermittelnde Kennzahl.
3