Klausur im April 2013

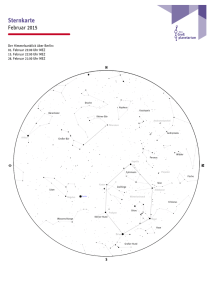
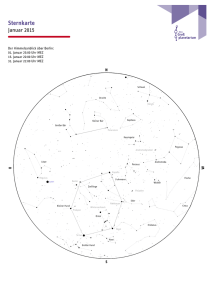
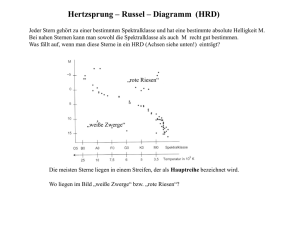
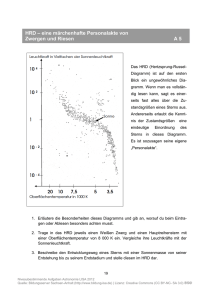
Q12 * Astrophysik * Klausur am 19.04.2013
1. Wega ist der Hauptstern des Sternbildes Leier.
Die jährliche Parallaxe von Wega beträgt 0,130´´ und pro Jahr bewegt sich Wega um ca. 0,350´´
relativ zum weit entfernten Fixsternhimmel.
In ihrem Spektrum ist die H  Linie (o  656, 28nm) etwas verschoben und wird bei
656,23 nm gemessen.
a) Bestimmen Sie die Entfernung von Wega und ihre Tangentialgeschwindigkeit.
b) Bestimmen Sie die Radial- und die Gesamtgeschwindigkeit von Wega.
Nähert sich Wega unserer Sonne oder entfernt sie sich?
2. Prokyon ist der hellste Stern im Sternbild Kleiner Hund.
Seine scheinbare Helligkeit beträgt 0,34 mag.
Für die folgenden Berechnungen sollen weitere
Daten aus dem abgebildeten HRD entnommen werden.
a) Unsere Sonne ist ein G2 Hauptreihenstern.
Zu welcher Spektralklasse etwa gehört Prokyon?
b) Schätzen Sie die absolute Helligkeit von Prokyon
ab! (Ergebnis: M  2,7 Mag )
c) Wie weit etwa ist Prokyon von uns entfernt?
Geben Sie diese Entfernung auch in Lj an.
Welche jährliche Parallaxe sollte man demnach
für Prokyon messen? (Teilergebnis: r = 3,4 pc)
d) Schätzen Sie den Sternradius von Prokyon in
Vielfachen des Sonnenradius ab.
e) Schätzen Sie die Masse von Prokyon in Vielfachen
der Sonnenmasse ab. (Ergebnis: m*  1,9)
f) Prokyon befindet sich seit etwa 1,7 Milliarden Jahren auf der Hauptreihe.
Wie lange etwa wird Prokyon noch ein Hauptreihenstern sein?
Beschreiben Sie in Stichpunkten, welche Entwicklung Prokyon anschließend nehmen wird.
g) Prokyon hat einen leuchtschwachen Begleiter (Prokyon B), der etwa 0,6 Sonnenmassen
besitzt. Die Umlaufperiode des Doppelsternsystems beträgt 41 Jahre.
Bestimmen Sie den Abstand der beiden Sterne voneinander. (Sie dürfen dabei Kreisbahnen
voraussetzen!) Unter welchem maximalen Winkelabstand kann man die beiden Sterne
demnach von der Erde aus beobachten? (Teilergebnis: Abstand d = 2, 4 1012 m )
Daten unserer Sonne:
Längeneinheiten:
Kugeloberfläche:
Aufgabe 1a
Punkte
5
b
5
M  4,8 Mag , Hauptreihen-Verweildauer ca. 1010 Jahre, T = 5800 K
m
1 pc = 3,26 Lj = 3,0861016 m
Lichtgeschwindigkeit: c  3, 0 108
s
3
m
AKugel  4  R 2  
Gravitationskonstante: G  6, 67 10 11
kg  s 2
2a
2
b
4
c
5
d
4
e
3
f
6
g
6
Summe
40
Gutes Gelingen! G.R.
Q12 * Astrophysik * Klausur am 19.04.2013 * Lösung
1. a) r 
1´´
1´´
 pc 
 pc  7, 7 pc  25Lj
p
0,130´´
vt 
r  tan(0,350´´)

1a
0,350o
3600  13 km
365  24  3600s
s
7, 7  3, 086 1016 m  tan

656, 23nm  656, 28nm
m
km
c 
 3, 0 108   23

656, 28nm
s
s
km
km
vges  vr 2  v t 2  232  132
 26
s
s
b) vr 
Wega nähert sich!
2. a) Prokyon ist ein Hauptreihenstern der Spektralklasse F5
(F - Hauptreihenstern als Antwort ausreichend.)
b)
LP
L
 7 (aus HRD) und M P  M   2,5  lg P 
L
L
M P  M  2,5  lg
LP
 4,8  2,5  lg 7  2, 7 Mag
L
c) Mit dem Entfernungsmodul gilt:
mM
mM
0,34  2,7
r
m  M  5  lg
 r  10 pc  10 5  10 pc  10 5  10 pc 10 5  3, 4 pc  11Lj
10 pc
1´´
1´´
1´´
r   pc  p   pc 
 pc  0, 29´´
p
r
3, 4 pc
d) Stefan-Boltzmann:
TP  7500K (aus HRD) und L   A  T mit A  4  R 2   
T 4
LP
  A P  TP 4
R P 2  TP 4
(5800K)4
7



R

R

7


R

7

 1, 6  R
P
L
A T 4
R 2 T 4
TP 4
(7500K) 4
e) Masse-Leuchtkraft-Beziehung für Hauptreihensterne:
L
m3
L m3  7  P  P 3  mP  m  3 7  1,9 m
L
m
f) Verweildauer  auf der Hauptreihe:
m 2
P
1
1
1
1
 m und 


und


 0, 28
3
2
2
L m
m

mP
1,92
P  0, 28    0, 28 1010 a  2,8 Milliarden Jahre ; mit 2,8 1,7 1,1 gilt :
Prokyon wird also noch etwa 1,1Milliarden Jahre auf der Hauptreihe verweilen.
Weitere Entwicklung von Prokyon:
Nach dem Wasserstoffbrennen wird das Heliumbrennen in Prokyon einsetzen, und Prokyon
wird dann zu einem Roten Riesen. Am Ende dieses Stadiums wird Prokyon mehrmals große
Mengen seiner Gasatmosphäre „wegblasen“ (Planetarischer Nebel) und schließlich zu einem
Weißen Zwerg werden. (Falls die Restmasse größer als 1,4 Sonnenmasse ist, wird ein
Neutronenstern entstehen!) Dieser Weißer Zwerg kühlt dann langsam ab und so wird
Prokyon schließlich als Brauner Zwerg enden.
g) Für den Abstand d der beiden Sterne gilt (Zweikörperproblem)
2  G 
m
2
mit 
und m  mP,A  mP,B  (1,9  0, 6)  m  2,5  m 
3
d
T
4 2  r 3
2,5m  2
 d
T G
3
3
2,5m  T 2  G

4 2
2,5 1,989 1030 kg  (41 365  24  3600s) 2  6, 67 1011
4
2
m3
kg  s 2
 2, 4 1012 m
Abstand d = 2, 4 1012 m und Entfernung r = 3,4pc = 1,0 1017 m 
d 2, 4 1012 m

   tan 1 (2, 4 105 )  0, 001375...o  5, 0´´
r 1, 0 1017 m
Der Winkelabstand der beiden Sterne beträgt also 5,0 Bogensekunden.
tan  