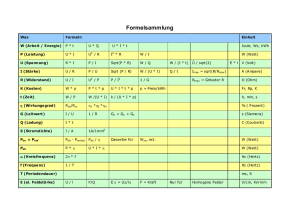
Chaos in Quantensystemen - Website von Andreas Windisch.

Karl-Franzens Universität Graz
Institut für Physik
Chaos in Quantensystemen
Erstellt im Rahmen der Lehrveranstaltung Theoretische Festkörperphysik
(W. Poetz)
von
Andreas Windisch
Graz, am 25. Februar 2010
Inhaltsverzeichnis
1 Chaos
1.1 Flipper-Automat . . . . . . . . . .
1.1.1 Was ist Chaos? . . . . . . .
1.1.2 Symbolische Dynamik . . .
1.1.3 Aufteilung mit periodischen
1.1.4 Escape Rate . . . . . . . .
1.2 Weitere Beispiele . . . . . . . . . .
1.2.1 Logistisches Wachstum . . .
1.2.2 N -Körperproblem . . . . .
.
.
.
.
.
.
.
.
2
2
3
6
6
9
10
10
13
2 Chaos in der Quantenmechanik
2.1 Gibt es ’Quantenchaos’ ? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Mikrowellen Billiards . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
15
22
Appendices
28
A 3-Scheiben Flipper - das Programm
A.1 Kurze Erläuterung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A.2 Der Sourcecode von flipper.f90 . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
28
31
B Feigenbaumdiagramm - das Programm
B.1 Kurze Erläuterung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B.2 Der Sourcecode von feigenbaum.f90 . . . . . . . . . . . . . . . . . . . . . . . . . .
35
35
36
. . . .
. . . .
. . . .
Orbits
. . . .
. . . .
. . . .
. . . .
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
Chaos
Für diesen Einfürungsteil wurde zunächst [2] verwendet. Das Studium von chaotischen, dynamischen Systemen ist keine neue Disziplin, sondern blickt auf eine 200-jährige Zeit der Erforschung
zurück. In dieser Zeit wurden viele Beiträge geleistet. Die Entwicklung folgte dabei nicht einen
einzeigen Weg, vielmehr findet man eine verwobene Struktur vor.
Betrachtet man integrable Systeme der klassischen Mechanik oder der Quantenmechanik, also etwa das Keplerproblem oder den harmonischen Oszillator, so mag man annehmen dass man stets
einfache Lösungen zu einfachen Gleichung vorfindet. Der erste Eindruck bei Betrachtung nichtintegrabler Systeme mag nun sein, dass alle analytischen Methoden versagen und nur statistische
oder numerische Anwendungen zur Lösungsfindung herangezogen werden können. Vielmehr besitzen wir aber bereits eine prädiktive Theorie von deterministischem Chaos, welche von der Qualität
jener einer pertubativen Expansion für beinahe integrable Systeme entspricht [2].
Im traditionellen Zugang werden integrable Bewegungen als 0-te Ordnung Approximationen eines
physikalischen Systemes angesehen, schwache Nichtlinearitäten werden pertubativ hinzugenommen. Für stark nichtlineare, nichtintegrable Systeme versagt dieser Zugang allerdings völlig. Die
reiche Struktur des Phasenraumes wird im Falle der integrablen Approximationen nicht vorgefunden. Versteckt in dem scheinbaren Chaos verbirgt sich jedoch ein starres Skelett, ein Baum von
cycles (periodische Orbits) von steigender Länge und selbstähnlicher Struktur [2].
Was aber ist nun Chaos? Um ein Verständnis dafür zu entwickeln warum und wie instabile cycles
zustandekommen betrachten wir einen Flipper-Automaten.
1.1
Flipper-Automat
Dieser Abschnitt mit dem Flipper-Automaten wurde aus [2] übernommen und übersetzt. Für jeden
der schon einmal eine Partie Pool oder Snooker gespielt hat wird es keine Überraschung sein, dass
eine deterministische Dynamik auf chaotisches Verhalten führt. Ähnlich verhält es sich mit einem
Flipperautomaten, weshalb wir unsere Betrachtung an diesem Beispiel festmachen wollen. Wir
besitzen ein intuitives Gefühl dafür wie sich der Ball verhält wenn er auf der Oberfläche des Automaten rollt. Bereits mit einfacher Geometrie ist man so in der Lage die Trajektorie des Balles zu
beschreiben. Des Physikers Flipper ist ein auf das wesentliche reduziertes Gerät: Drei äquidistant
angeordnete, abstossende Scheiben in einer Ebene (Abbildung 1). Der Flipper ist ideal, also frei
Abbildung 1: Des Physikers Flipper
von Reibung. Punktartige Flipperbälle werden aus verschiedenen Winkeln mit unterschiedlichen
Ausgangspositionen auf die Scheiben geschossen. Sie werden zwischen den Scheiben hin und her
gestossen und verlassen dann den Bereich der Scheiben wieder. Zu Beginn des 18 Jahrhunderts
war Gottfried Wilhelm Leibniz (1646-1716) der Meinung, man könne das Verhalten eines deter2
ministischen Systemes weit in der Zukunft vorhersagen, wenn man nur die Anfangsbedingungen
kenne. Er schrieb [6]:
Von dem Verhängnisse
Daß alles durch ein festgestelltes Verhängniß herfürgebracht werde, ist eben so gewiß,
als daß drey mal drey neun ist. Denn das Verhängniß besteht darin, daß alles an einander hänget wie eine Kette, und eben so unfehlbar geschehen wird, ehe es geschehen,
als unfehlbar es geschehen ist, wenn es geschehen.
Die alten Poeten, als Homerus und andere, haben es die güldene Kette genennet, so
Jupiter vom Himmel herab hängen lasse, so sich nicht zerreißen lässet, man hänge
daran, was man wolle. Und diese Kette besteht in den Verfolg der Ursachen und der
Wirkungen.
Nemlichen jede Ursach hat ihre gewisse Würkung, die von ihr zuwege bracht würde,
wenn sie allein wäre; weilen sie aber nicht allein, so entstehet aus der Zusammenwirkung ein gewisser ohnfelbarer Effect oder Auswurf nach dem Maaß der Kräfte, und das
ist wahr, wenn nicht nur zwey oder 10, oder 1000, sondern gar ohnendlich viele Dinge
zusammen würken, wie dann wahrjaftig in der Welt geschicht.
Die Mathematik oder Meßkunst kann solche Dinge gar schön erläutern, denn alles ist
in der Natur mit Zahl, Maaß und Gewicht oder Kraft gleichsam abgezirkelt. Wenn
zum Exempel eine Kugel auf eine andere Kugel in freier Luft trift, und man weiß ihre
Größe und ihre Linie und Lauf vor dem Zusammentreffen, so kann man vorhersagen
und ausrechnen, wie sie von einander prallen, und was sie vor einen Lauf nach dem
Anstoß nehmen werden. Welches gar schöne Regeln hat; so auch zutreffen, man nehme
gleich der Kugeln so viele als man wolle, oder man nehme gleich andere Figuren, als
Kugeln.
Hieraus sieht man nun, das alles mathematisch, das ist, ohnfehlbar zugehe in der ganzen weiten Welt, so gar, daß wenn einer eine gnugsame Insicht in die innern Theile
der Dinge haben könnte, und dabey Gedächtniß und Verstand gnug hätte, umb alle
Umbstände vorzunehmen und in Rechnung zu bringen, würde er ein Prophet seyn, und
in dem Gegenwärtigen das Zukünftige sehen, gleichsam als in einem Spiegel.
Leibniz zeichnete hier ein Bild welches von eben jener Gestalt ist, als wir es hier als Paradigma für
Chaos heranziehen wollen. Hier irrt Leibniz in tiefer und subtiler Weise: Der Zustand eines physikalischen Systemes kann niemals mit unendlicher Präzision angegeben werden, so hat eine einzelne
Trajektorie keine Bedeutung, allenfalls eine Verteilung von Trajektorien macht physikalisch Sinn.
1.1.1
Was ist Chaos?
Ein deterministisches System ist ein System dessen Momentanzustand zur Gänze durch die Anfangsbedingungen bestimmt ist, ganz im Gegensatz zu einem stochastischen System, für welches
die Anfangsbedingungen den Momentanzustand lediglich zu einem Teil beschreiben, etwa wegen
Rauschen oder anderen externe Umständen die sich unserer Kontrolle entziehen. Für ein stochastisches System spiegelt der Momentanzustand die Anfangsbedingungen und eine Realisierung des
Rauschens wider.
Ein deterministisches System mit hinreichend komplexer Dynamik kann uns veranlassen es fälschlicherweise als ein stochastisches System zu betrachten. Das Entwirren der Deterministik von der
Stochastik ist die Hauptaufgabe in vielen experimentellen Situationen, von der Aktienbörse bis
zum Herzschlag. Was aber ist nun Chaos? Zwei Flipperkugeltrajektorien die sehr nahe aneinander
beginnen entfernen sich exponentiell über die Zeit. Nach einer endlichen (in der Praxis recht geringen) Anzahl an Rückprallprozessen erreicht die Trennung δ~x(t) den Wert L, der charakteristischen
linearen Ausdehnung des Systemes. Die in Abbildung 2 gezeigte Skizze wurde in Anlehnung an
die in [2] gezeigte Graphik erstellt. Nach einer numerischen Simulation (Sourcecode siehe Anhang)
kann dieses Verhalten nun auch belegt werden, soweit eine numerische Rechunung als Legitimation herangezogen werden kann. Während Abbildung 2 nur einen skizzierten, qualitativen Verlauf
3
Abbildung 2: Skizze: Sensibilität auf Anfangsbedingungen, [2]
angibt zeigen die Abbildungen 3 und 4 tatsächlich gerechnete Trajektorien zu (leicht) unterschiedlichen Anfangswerten. Die Eigenschaft der Sensitivität auf Anfangsbedingungen kann wie folgt
geschrieben werden:
|δ~x(t)| ≈ eλt |δ~x(0)|
(1.1)
mit λ Ljapunov-Exponent, welcher die mittlere Rate der Separation der Trajektorien des Systemes
beschreibt. Für eine endliche Genauigkeit des Anfangszustandes δx ist die Dynamik nur bis zu
einer endlichen Ljapunov-Zeit T ≈ − λ1 ln |δx|/L bestimmbar, trotz der Deterministik und der von
Leibniz beschriebenen Einfachheit der Gesetzmäßigkeit der Bewegung.
Ein positiver Ljapunov-Exponent alleine führt nicht auf Chaos. Man könnte etwa ein Ein- oder
Zweischeibenflipperspiel spielen. Die Trajektorien würden auseinanderlaufen und sich nie wieder
begegnen, was das Spiel wohl auch eher langweilig gestaltete. Man benötigt also auch mischen, also
den Umstand dass die Trajektorien wieder und wieder zusammenkommen. Während lokal nahe
Trajektorien auseinanderlaufen ist die interessante Dynamik auf einen global endlichen Bereich
des Phasenraumes beschränkt, weshalb es notwendigerweise zu einer Mischung der Trajektorien
kommen muss. Diese können sich in der Tat beliebig oft beliebig nahe kommen. In unserem Beispiel
gibt es 2n topologisch unterschiedliche n-bounce Trajektorien die von einer gegebenen Scheibe
ausgehen. Allgemeiner kann man sagen, dass die Anzahl unterschiedlicher Trajektorien durch
N (n) ≈ ehn
(1.2)
geschrieben werden kann, wobei die topologische Entropie h, in unserem Beispiel h = ln 2, der
Wachstumsrate der Anzahl von topologisch unterschiedlichen Trajektorien entspricht.
Die Bezeichnung Chaos ist irreführend, da deterministische Dynamik kein Chaos im eigentlichen
Sinne zeigt. Alles geht mathematisch von Statten, dh. im Sinne von Leibniz unfehlbar. Wenn wir
also von Chaos sprechen, dann meinen wir, dass das System zwar unter deterministischen Gesetzen evolviert, der Ausgang aber höchst sensitiv auf kleine Unschärfen der Anfangsbedingungen
ist. Wenn ein deterministisches System lokal instabil ist (positiver Ljapunov-Exponent) und global
mischt (positive Entropie), so sagt man das System ist chaotisch. Obwohl mathematisch korrekt,
sind die Definitionen von Chaos als positiver Ljapunov-Abstand + positive Entropie in der Praxis
unbrauchbar, da eine Messung dieser Quantitäten nur asysmptotisch möglich, und somit außer
Reichweite für in der Natur beobachtete Systeme ist.
Ein mächtigerer Zugang ist dabei jener von Poincaré: Es handelt sich um ein Wechselspiel aus
lokaler Instabilität (instabile periodische Orbits) und globaler Mischung (Verflechtung der stabilen und instabilen Mannigfaltigkeiten). In einem chaotischen System wird jede offene Kugel von
Anfangsbedingungen, ungeachtet wie klein sie auch sei, in endlicher Zeit mit jedem anderen end4
2D - Pinball Game
Trajectories for diff. initial conditions
2
2313231
1.5
3
y-pos
1
2313
0.5
1
2
0
-0.5
Phi = 1.2168 rad
Phi = 1.2158 rad
-1
-1
-0.5
0
0.5
x-pos
1
1.5
2
Abbildung 3: Sensibilität auf Anfangsbedingungen: Unterschiedlicher Startwinkel
2D - Pinball Game
Trajectories for diff. initial conditions
2
2123132
1.5
21231232
3
y-pos
1
0.5
1
2
0
-0.5
r=a/2, phi=PI/4
r=a/2-0.001, phi=PI/4
-1
-1
-0.5
0
0.5
x-pos
1
1.5
2
Abbildung 4: Sensibilität auf Anfangsbedingungen: Unterschiedliche Anfangsorte
lichen Bereich überlappen und sich so über den gesamten asymptotisch zugänglichen Phasenraum
erstrecken. Der Fokus dieser Theorie geht vom Versuch präziser Vorhersagen für einzelne Trajektorien (was Unmöglich ist) bis hin zur Beschreibung der Geometrie des Raumes der möglichen
Ausgänge.
5
Die Analyse eines potentiell chaotischen Systemes erfolgt in drei Schritten:
1. Diagnose: Zuerst muss die intrinsische Dimension des Systems - die minimale Anzahl der
Freiheitsgrade die notwendig ist um die Dynamik des Systems zu bestimmen - festgestellt
werden. Ist das System sehr turbulent, dh. die Beschreibung der Dynamik auf großen Zeitskalen erfordert einen Raum von hoher intrinsischer Dimension, dann sind wir nicht imstande
eine Beschreibung zu liefern. Wir können lediglich die vorrübergehende Ordnung zwischen
regulären Bewegungen und einigen chaotischen Freiheitsgraden beschreiben. Dennoch ist dies
ein leistungsfähiges Konzept: Selbst ein unendlichdimensionales System wie etwa eine brennende Flammenfront kann nur wenige chaotische Freiheitsgrade besitzen. In dieser Ordnung
ist die chaotische Dynamik auf einen Raum von niedriger Dimension beschränkt, die Anzahl
der relevanten Parameter ist gering. Wir gehen nun zum nächsten Schritt.
2. Zählen und Klassifizieren: Wir zählen und klassifizieren alle möglichen, topologisch verschiedenen Trajektorien des Systemes in ein hierarchisches System, dessen sukzessiven Ebenen
erhöhte Präzision erfordern. Ist dies gelungen, so kann man mit Schritt 3 fortfahren.
3. Gewichte: Die Gewichte der unterschiedlichen Systemteile müssen untersucht werden.
1.1.2
Symbolische Dynamik
Mit dem Flipperspiel haben wir Glück. Es handelt sich um das niedrigdimensionale System der
freien Bewegung in der Ebene. Die Bewegung eines Punktteilchens ist so geartet, dass nach einer
Kollision mit einer Scheibe entweder eine andere Scheibe erreicht, oder das System verlassen wird.
Wenn wir nun jede Scheibe mit einer Nummer - etwa 1, 2 und 3 - versehen, so können wir jeder
Trajektorie eine Ablauffolge, also eine Sequenz die die Abfolge der besuchten Scheiben angibt,
zuordnen. In unserer Beispielskizze Abbildung 2 finden wir die Ablauffolgen - englisch itinerary
genannt - 2313 und 23132321 vor. Diese Folgen sind endlich für Trajektorien für welche das
Teilchen vom Unendlichen kommt und nach einer endlichen Anzahl von Streuvorgängen entkommt,
unendlich für geschlossene Trajektorien und unendlich wiederholend für einen periodischen Orbit.
Ein solches ’labeln’, also zuordnen von Nummern, ist die einfachste Form der sogenannten Symbolischen Dynamik. Nachdem das Teilchen niemals zweimal hintereinander an derselben Scheibe
streuen kann müssen zwei aufeunanderfolgende Ziffern in der Abfolge stets unterschiedlich sein.
Dies ist eine Regel des sogenannten pruning. Unter pruning versteht man das Einschränken der
Folge auf erlaubte Subfolgen, dh. bestimmte Abfolgen von Symbolen werden durch Regeln ausgeschlossen. Das Auffinden solcher Regeln ist im Allgemeinen ein sehr schwieriges Unterfangen, aber
für unser Beispiel haben wir Glück: Hier gibt es keine weiteren Regeln.
Die Wahl der Symbole ist in keiner Weise eindeutig. Zum Beispiel kann man nach jedem Streuvorgang entweder zur vorherigen Scheibe zurückkehren oder zur nächsten voranschreiten. Deshalb
kann das Alphabet aus drei Symbolen durch ein binäres Alphabet ersetzt werden: {0, 1}, siehe
Abbildung 3. Eine gute Wahl des Alphabetes beinhaltet wichtige Eigenschaften der Dynamik, wie
etwa deren Symmetrien. Angenommen man wolle einen ’guten’ Durchgang Flipper spielen, dh.
die Kugel soll so oft wie möglich Streuprozesse an den Scheiben erfahren. Was wäre hier die beste
Strategie? Der Einfachste Zugang wäre zu versuchen, die Kugel durch genaues Zielen zwischen
zwei Scheiben streuen zu lassen. Bewegt sich die Kugel gerade auf der Verbindungslinie zwischen
den Mittelpunkten der Scheiben, so verläßt sie diese Linie nicht mehr. Das Spiel wäre im selben
Sinne gut, wenn es denn gelänge die Kugel zwischen drei Scheiben zu halten, bzw. auf jedem periodischen Orbit. Das Problem aber ist, dass jeder dieser Orbits instabil ist, dh. man müsste sehr
genau zielen um eine Weile an der periodischen Bahn zu verweilen. Instabile periodische Orbits
spielen also die zentrale Rolle wenn man daran interessiert ist eine gute Partie zu spielen. Sie
formen das Skelett auf dem Trajektorien für lange Zeit festgehalten werden.
1.1.3
Aufteilung mit periodischen Orbits
Eine Trajektorie ist periodisch, wenn sie zu ihrem Anfangsort und Impuls zurückkehrt. Wir nennen
die Menge der periodischen Punkte die zu einem gegebenen periodischen Orbit gehören einen Zy6
Abbildung 5: Skizze: Binäres Alphabet für 3-Scheiben-Flipper-Trajektorien, [2]
klus (cycle). Diese qualitativen Verläufe von 3-Scheiben Zyklen wurden ebenfalls in Anlehnung an
die in [2] gezeigten Bilder erstellt. Dabei finden wir für die dargestellten Fälle: Im Bild (a) werden
die Zyklen 12123 und 13132 durch eine Rotation um die z-Achse ineinander transformiert (σ23 ).
Dieser Zyklus ist 6-fach entartet unter der C3v Symmetrie, der Symmetriegruppe des gleichseitigen
Dreieckes. Im Falle (b) finden wir für 123 und 132, wie auch in (c) 1213, 1232 und 1323, Entartung
unter C3v vor. Der Fall (d) sind die Fälle 121212313 und 121212323 nicht im Sinne der C3v Symmetrie entartet, sondern unter Zeitumkehr. Die beiden einfachsten Fälle von periodischen Orbits
konnten mittels Modell nachgerechnet werden: Bei der Modellrechnung zeigte sich, dass die periodischen Zyklen eine gute Messbarkeit der numerischen Stabilität des Algorithmus darstellt. Man
kann beobachten wann, also etwa nach wievielen Streuungen der Prozess abweicht. Tatsächlich
hat sich hier gezeigt, dass der entwickelte Algorithmus sehr instabil ist, dh. bereits nach wenigen
Zyklen weicht die Trajektorie erheblich ab. Dies ist zum einen ein wünschenswerter Effekt, belegt
er doch den chaotischen Charakter des Systemes, zum anderen natürlich unerwünscht. Eine kurze Analyse des vorliegenden Algorithmus, der im Prinzip iterativ in kleinen Schritten von einem
Streupunkt zum nächsten wandert, zeigt, dass eine erhebliche Verbesserung erzielt würde, wenn
von jedem Streupunkt aus der nächste Streupunkt in einem Schritt berechnet würde. Da hier aber
ohnehin nur wenige Streuungen von Bedeutung sind und auch numerische Geschwindigkeit keine
große Rolle spielt wurde die Adaption aus Zeitgründen unterlassen.
In unserem Flipperbeispiel betrachten wir Projektionen von 4-dimensionalen Phasenraum-Trajektorien
in den 2-dimensionalen Unterraum, den Ortsraum. Die Trajektorien können sich nicht schneiden,
denn das würde deren deterministische Eindeutigkeit verletzen. Sehrwohl aber können sich die
Projektionen auf Unterräumen schneiden. Ein besseres Bild der Dynamik wird durch PhasenraumPoincaré-Schnitte erhalten.
Die Position der Kugel wird durch ein Zahlenpaar beschrieben (Koordinaten in der Ebene), die
Geschwindigkeiten durch ein weiteres Paar (Komponenten der Geschwindigkeit). Dies ist eine
vollständige Beschreibung im Leibniz’schen Sinne.
Nehmen wir nun an die Kugel wäre gerade von Scheibe 1 abgeprallt. In Abhängigkeit von Position
und Winkel kann sie nun entweder zur Scheibe 2, oder zur Scheibe 3 voranschreiten. Während
die Kugel unterwegs zum nächsten Streupunkt ist, ist ihre Bewegung unverändert. So kann man
anstelle der 4-dimensionalen Beschreibung eine zweidimensionale Abbildung f einführen, die die
Koordinaten der Kugel von einer Scheibe zur nächsten abbildet.
Wir wollen dies noch etwas eingehender betrachten: Die Trajektorie ist nach dem Einschlag durch
die Koordinaten qi (Bogenlängenposition des i-ten Abprallens) und durch pi = sin θi , der Impulskomponente parallel zur Wand, bestimmt. Siehe dazu auch Abbildung 8. So ein Abschnitt in
der Bewegung heißt Poincaré-Schnitt. In Termen der Poincaré-Schnitte ist die Dynamik auf eine
Abbildung f : (pi , qi ) 7→ (pi+1 , qi+1 ) vom Rand einer Scheibe zum Rand der nächsten Scheibe. Wir
markieren nun in den Poincaré-Schnitten jene Anfangsbedingungen welche nicht mit einem Abprallen bereits entkommen. Wir finden zwei Streifen von Überlebenden, nachdem es ja auch zwei
7
Abbildung 6: Skizze: Qualitativer Verlauf von einigen 3-Scheiben Zyklen, [2]
Scheiben gibt die von einer dritten aus erreicht werden können. Wir bezeichnen die zwei Streifen
mit M0 und M1 . Eingebettet in die beiden Streifen finden wir vier Streifen M00 , M10 , M01 , M11
von Anfangsbedingungen welche zweimaliges Abprallen überleben, usf. Im Falle (a) von Abbildung
9 sehen wir, dass die Kugel entweder eine Disk trifft oder aber entkommt. Im Falle (b), wenn zwei
Disks hintereinander getroffen werden sollen, ist ein viel genaueres Zielen notwendig. Sollen mehr
und mehr Scheiben hintereinander getroffen werden, so ist stets ein kleinerer Streifen die Folge.
Gesetzt dem Falle die Disks sind hinreichend weit auseinander, nach n Abprallprozessen sind die
überlebenden Streifen in 2n unterschiedliche Streifen geteilt: Der i-te Streifen besteht aus allen
Punkten mit der Abfolge i = s1 s2 s3 . . . sn , s ∈ {0, 1}. Hier zeigt sich auch das Skelett aus instabilen Zyklen, welches bereits Eingangs erwähnt wurde: Jeder Streifen beinhaltet eine periodische
Struktur s1 s2 s3 . . . sn , deren Basisblock unendlich oft wiederholt wird. Die periodischen Punkte
sind dabei ein Skelett im Sinne dessen, dass, je weiter wir sehen, die Streifen zwar schmäler und
schmäler werden, die periodischen Punkte jedoch invariant bleiben.
Wir sehen nun auch warum es sich bezahlt macht diese symbolische Dynamik einzuführen: Sie
stattet uns mit einem Plan des chaotischen Phasenraumes aus. Für jede gültige, unendlich lange
Abfolge gibt es eine eindeutige Trajektorie, und eine eindeutige Abfolge benennt jede geschlossene
Trajektorie. Etwa ist die einzige Trajektorie die durch 12 dargestellt wird der 2-fache Abprallpro8
2D - Pinball Game
2D - Pinball Game
Periodic trajectory, one cycle evolved
periodic trajectory, one cycle evolved
2
2
3213
32313
1.5
1.5
3
3
1
y-pos
y-pos
1
0.5
1
0.5
2
1
0
0
-0.5
-0.5
-1
-1
-0.5
0
0.5
x-pos
1
1.5
-1
-1
2
-0.5
0
2
0.5
x-pos
1
1.5
2
Abbildung 7: Periodische Orbits
zess entlang der Linie die die Mittelpunkte der Scheiben 1 und 2 verbindet. Jede andere Trajektorie
die mit 12 . . . beginnt trifft entweder die dritte Disk oder entkommt früher oder später.
1.1.4
Escape Rate
Was ist eine gute physikalische Größe für das Flipper-Spiel? Die escape rate ist eine solche wichtige, messbare Größe. Ein Beispiel für so eine Messung wäre etwa ein instabiler Molekül- oder
Atomzustand der durch ein klassisches Potential mit der Möglichkeit in verschiedene Richtungen
zu entkommen, ausgestattet ist. In einem Experiment werden viele Projektile in so ein nichtbegrenzendes Potential injeziert und die mittlere escape rate wird gemessen. Das numerische Experiment könnte etwa so aussehen, dass man die Kugel in eine zufällige Richtung zwischen die
Disks injeziert und fragt wie oft sie abprallt bevor sie den Bereich zwischen den Disks verläßt. Für
den Theoretiker besteht ein gutes Spiel daraus, die asysmptotische Lebenszeit (escape rate) der
Kugel exakt vorherzusagen. Dazu benutzt man die Theorie der periodischen Orbits.
Nach jedem Abprallen dünnen die Anfangsbedingungen aus und liefern zweimal so viele dünne
Streifen wie aus dem vorherigen Prozess resultiert sind. Der gesamte Bereich der zu einer gegebenen Zeit verbleibt ist die Summe der Flächen dieser Streifen, so dass der Anteil der Überlebenden
nach n-maligem Abprallen proportional zu
Γ̂1
=
|M0 | + |M1 |,
(n)
Γ̂n
=
X
i
Γ̂2 = |M00 | + |M10 | + |M01 | + |M11 |,
(1.3)
|Mi |
ist, mit i das Label des i-ten Streifens. Da nach jedem Abprallprozess der selbe Anteil an Trajektorien verloren wird, erwartet man einen exponentiellen Abfall mit n und Grenzverhalten:
Γ̂n+1 /Γ̂n = e−γn → e−γ .
(1.4)
Die Größe γ nennt man die escape rate. Dies beschließt auch unsere Betrachtung dieses Beispieles,
mehr dazu siehe [2].
9
Abbildung 8: Skizze: 3-Scheiben Flipper mit Koordinaten und Poincaré-Schnitten, [2]
1.2
1.2.1
Weitere Beispiele
Logistisches Wachstum
Der erste Teil hiezu wurde aus [1] übernommen, hernach eine kurze numerische Berechnung durchgeführt. Wir wollen eine biologische Population betrachten, deren Zahl Nn+1 in der (n + 1)-ten
Generation proportional zur Zahl Nn in der n-ten Generation sei:
Nn+1 = a · Nn ,
(1.5)
mit a Vermehrungsfaktor. Durch Futtermangel in der n-ten Generation möge der Vermehrungsfaktor a reduziert werden auf a(1 − bNn ), da ja die Futterreduktion proportional zur Zahl Nn der
Futterverbraucher ist. So folgt:
Nn+1 = a · Nn (1 − bNn ).
(1.6)
Ein stationärer Zustand (Fixpunkt) der Bevölkerung wird erreicht für
Nn+1 = Nn = Nst ⇒ b =
a−1
.
a · Nst
(1.7)
Für a < 1 wird Nn+1 < Nn , dh. die Bevölkerung stirbt aus, selbst für b = 0, also wenn kein
Futtermangel vorliegt, während für a > 1 und b = 0 die Bevölkerung wächst. Mit der Normierung
x = b · N ≤ 1 geht (1.6) in die Verhulst-Gleichung über:
xn+1 = axn (1 − xn ) = axn − ax2n .
(1.8)
Mit der angegebenen Normierung (x ≤ 1) werden die möglichen Werte für den Parameter a auf das
Intervall a ∈ [0, 4] beschränkt. Die Lösung dieser Gleichung für die verschiedenen Generationen n
und ihre Abhängigkeit von dem Kontrollparameter a kann graphisch verdeutlicht werden. Dazu
zeichnet man die Parabel y = ax − ax2 und die Gerade y = x auf: Wir betrachten Abbildung
10: Zu jedem Wert xn < 1 findet man den durch (1.8) bestimmten Wert xn+1 als Ordinatenwert
auf der Parabel. Gehen wir von diesem Punkt (xn , yn = xn+1 ) in waagerechter Richtung bis zur
Geraden y = x, so gibt uns der Schnittpunkt den neuen Startwert xn+1 , von dem aus wieder
durch eine Senkrechte der Schnittpunkt (xn+1 , yn+1 = xn+2 ) bestimmt wird, usf. Auf diese Weise
erhält man die Folge xn , n = 0, 1, . . . als Stufenlinie, startend von einem beliebigen Anfangspunkt x0 . Im Falle der Abbildung 10 sieht man nun, dass der Wert rasch gegen den Fixpunkt
10
Abbildung 9: Skizze: Bereiche von Trajektorien für einmaliges und zweimaliges Abprallen, [2]
y
0.5
0.4
0.3
0.2
0.1
x
0.2
0.4
0.6
0.8
1.0
Abbildung 10: Logistische Abbildung, a = 2 mit stabilem Fixpunkt xf = 0.5, x0 = 0.1, [1]
xf = 0.5 konvergiert. Ganz anders verhält es sich für die in Abbildung 11 dargestellte Situation:
Der Startwert x0 ist derselbe, jedoch ist nun a = 3.5. Hier oszilliert die Folge xn zwischen vier
Grenzwerten von Teilfolgen. Es stellt sich heraus, dass für a > 3.57 das Verhalten der Folge ganz
wesentlich vom Kontrollparameter a abhängt, während der Wert der Glieder xn für für große n
nicht vom gewählten Anfangswert x1 abhänt, solange a < 3.57 ist. Trägt man die Grenzwerte
der logistischen Gleichung (1.8) als Funktion des Parameters a auf, so erhält man das sogenannte
Feigenbaum-Diagramm. Aus dem Feigenbaumdiagramm können folgende Eigenschaften abgelesen
werden:
1. Für a ≤ 1 konvergiert die Folge gegen Null, und zwar umso langsamer, je näher a gegen 1
strebt. Der stabile Fixpunkt des Systemes ist xf = 0. Aus der in Abbildung 12 gezeigten
Rechnung ist dies aufgrund des zugunsten einer besseren Auflösung gewählten Bereiches von
a zwar nicht ersichtlich, natürlich leistet das Programm jedoch auch die Berechnung von
a = 0 an.
2. Für 1 < a < 3 ergibt sich ein stabiler Konvergenzpunkt (Fixpunkt) limn→∞ = xF < 1 und
6= 0.
3. Für 3 < a < a∞ oszillieren die Werte xn zwischen 2k Werten hin und her, wobei a∞ ≈ 3.57
ist. Die Punkte im Diagramm, an welchen sich k um 1 erhöht nennt man Bifurkationspunkte.
Am ersten Bifurkationspunkt in Abbildung 12 spaltet die Kurve xf = 1 − 1/a, welche die
stabilen Fixpunkte xf als Funktion von a bis a = 3 angibt, in zwei Kurven auf, welche die
11
y
0.8
0.6
0.4
0.2
x
0.2
0.4
0.6
0.8
1.0
Abbildung 11: Logistische Abbildung, a = 3.5 in oszillierendem Bereich, x0 = 0.1, [1]
Bifurcation Diagram for the Logistic Map
x(n+1)=a*x(n)*(1-x(n))
1
0.8
x
0.6
0.4
0.2
0
2.75
3
3.25
Parameter a
3.5
3.75
4
Abbildung 12: Feigenbaumdiagramm, erstellt mit einem FORTRAN95-Programm, Sourcecode siehe
Anhang
Grenzwerte xf (a) angeben, zwischen denen die Werte xn oszillieren. Diese beiden Kurven
spalten dann am nächsten Bifurkationspunkt a2 jeweils wieder in zwei Kurven auf, usf. Das
System hat also für die Werte ak ≤ a ≤ ak+1 zwischen den Bifurkationspunkten ak und ak+1
2k Attraktoren xi = limn→∞ xq·n+i , mit q = 2k und i = 0, . . . , 2k − 1. Mit wachsendem Wert
von a wird das Intervall zwischen zwei aufeinander folgenden Bifurkationen immer kleiner.
Die Werte ak für die Bifurkationspunkte k-ter Ordnung folgen einer geometrischen Reihe
ak = a∞ − c · δ −k ,
k >> 1.
(1.9)
Für den Abstand ∆k = ak − ak−1 ergibt sich dann:
∆k = c · δ −k (δ − 1).
(1.10)
Die Feigenbaumkonstante δ wird damit zu δ = limk→∞ ∆k /∆k+1 . Sie ergibt sich numerisch
zu δ ≈ 4.669201660910 . . .. Die Folge der Bifurkationspunkte konvergiert gegen einen Grenzwert a∞ = limk→∞ ak = 3.5699456 . . . . Der Ljapunov-Exponent λ ist im Bereich 3 < a < a∞
immer negativ, außer an den Bifurkationspunkten, an denen λ immer Null ist.
12
4. Im Wertebereich a∞ < a < 4 treten ’chaotische’ Bereiche auf, in denen die Werte der
Fixpunkte xf statistisch streuen und der Wert des Ljapunov-Exponenten λ ist größer Null.
Zwischen diesen Bereichen liegen periodische ’Fenster’, in denen stabile Fixpunkte auftreten,
zwischen denen die Folge xn oszilliert. Der Ljapunov-Exponent ist in diesen Fenstern negativ.
Der chaotische Bereich verdrängt mit steigendem Wert von a die Fenster zunehmend.
5. In den chaotischen Bereichen liefern rationale Startwerte Fixpunkte, irrationale Startwerte
ergeben keine Konvergenz. Für a = 4 läßt sich die Gleichung
exakt durch die Funktion
xn+1 = 4xn (1 − xn )
(1.11)
xn = sin2 (2n πx0 )
(1.12)
lösen, mit x0 Startwert.
1.2.2
N -Körperproblem
Zusammenfassend wollen wir festhalten, dass Chaos als Folge von nichtlinearer Dynamik herrührt.
Der Begriff Chaos darf nicht im eigentlichen Sinne verstanden werden, sondern bedeutet Sensibilität auf Anfangsbedingungen. Diese Sensibilität haben wir anhand des Beispieles eines Flipperautomaten diskutiert. Als wichtige Größe haben wir ferner den Ljapunov-Exponenten, sowie die
escape rate kennengelernt. Wir haben auch gesehen, dass man chaotischen Systemen mit symbolischer Dynamik zu Leibe rücken kann. Außerdem haben wir das Konzept der Poicaré-Schnitte
kennengelernt. Es ermöglicht eine leistungsfähige Beschreibung der Dynamik im Phasenraum.
Hernach haben wir ein weiteres System diskutiert, jenes des logistischen Wachstums. Wir finden dort wichtige Begriffe vor, etwa die Bifurkation, den Attraktor oder den Fixpunkt. Weitere
wichtige Systeme wären etwa das N -Körperproblem. Ein ausführlicher Artikel zu diesem Thema
ist unter [7] zu finden, der Vollständigkeit halber wollen wir einen kurzen Blick darauf werfen.
Wieder war es Poincaré der dem chaotischen Charakter unseres Planetensystems auf die Schliche
kam. Mit modernen Computersystemen können immer bessere Simulationen von Planetensystemen vorgenommen werden. Es zeigt sich, dass solche Systeme immer nur eine bestimmte Anzahl
an Planeten aufnehmen können um eine stabile Dynamik zu zeigen. Die Simulationen ergaben,
dass Systeme in der Regel bis an die Grenze ihrer Kapazität aufgefüllt sind. Ging Laplace noch
davon aus dass die Planetenbewegungen stabil wie die Bewegung eines Uhrwerkes erfolgen, so fand
der Astronom Daniel Kirkwood im Jahr 1866 den ersten Beleg für Instabilitäten im Sonnensystem.
Er untersuchte den Asteroidengürtel zwischen Mars und Jupiter. Er fand Lücken in den Zeiten
der Umlaufdauer um die Sonne. Keines der Objekte besaß eine Umlaufdauer von 3.9 Jahren, was
einem Drittel der Umlaufdauer von Jupiter entspricht. Der Grund hierfür ist folgender: Wären die
Umlaufzeiten ein ganzzahliges Vielfaches voneinander, so näherten sich die beiden Körper stets
an der selben Stelle nach stets drei Umläufen des einen und einem Umlauf des anderen Körpers
aneinander an. Dort erführe der Körper aufgrund des massereichen Jupiters stets einen Impuls.
Dies führt mit der Zeit auf einen sogennanten Resonanzeffekt der mittleren Bahnkurve, in diesem
Falle eine 3 : 1 Resonanz. Es gibt weitere Lücken die durch 5 : 2 bzw. 7 : 3 Resonanz entstehen.
Die Bahnexzentrität könnte aufgrund der Resonanzen so weit anwachsen, dass der Asteroid in die
Sonne stürzte. Es kann vorkommen dass ein Asteroid in eine solche Kikwoodlücke gestossen und
dann aus dem Gürtel geschleudert wird.
Mit Computersimulationen werden heute Ensteheungsmodelle des Planetensystems gerechnet.
Man geht davon aus, dass sich das Sonnensystem durch die Kondensation und Ansammlung von
Staub und Gas in einer abgeplatteten Scheibe um einen jungen Stern bildete. Die staubkorngroßen
Partikel verbinden sich zu einer Vielzahl von Asteroiden und Kometen mit wenigen Kilometern
Durchmesser, den Planetesimalen. Diese Objekte stoßen zusammen und bilden so Hunderte von
mond- bis marsgroßen Embryos, die ihre Bahnen inmitten der verbleibenden Planetesimalen ziehen. Ohne weiter auf die folgenden Prozesse einzugehen wollen wir nun einen Blick auf die Sensibilität der Anfangsbedingungen werfen. In Computermodellen können solche Entstehungsprozesse
13
inzwischen simuliert und gerechnet werden, wobei manche von ihnen auf Systeme führen die dem
unseren ähnlich sind. Wenn zu Beginn einer solchen Rechnung nur ein einziger von hundert Embryos um einen Meter verschoben wird kann dies darüber Entscheiden, ob am Ende drei oder fünf
terrestrische Planeten entstehen!
Dieser Sensitivität auf Anfangsbedingungen kann man auch leicht zum Opfer fallen wenn man
etwa ein Dreikörperproblem der Art Sonne-Erde-Mond simulieren möchte: Es erweist sich als kein
leichtes Unterfangen geeignete Anfangsbedingungen zu finden um die drei Körper in eine Stabile,
dem Sonnensystem ähnliche Bahn zu zwingen.
14
2
2.1
Chaos in der Quantenmechanik
Gibt es ’Quantenchaos’ ?
Dieser Abschnitt wurde auf Basis von [8] ausgearbeitet. Die zentrale Frage hier ist zunächst: Gibt
es Quantenchaos? Wie verstehen wir Chaos im quantenmechanischen Sinn? Dem soll hier auf den
Grund gegangen werden. Die Quantenmechanik kann nicht nur klassisch integrable Systeme wie
das Wasserstoffatom bedienen, sondern auch klassisch nichtintegrable Systeme wie etwa das Heliumatom. Man kann nun unsere erste Frage betrachten: Gibt es Quantenchaos? Die SchrödingerGleichung ist eine lineare Gleichung, die keinen Raum für Chaos läßt. Andererseits gibt es das
Korrespondenzprinzip, dh. wenn die Wellenlängen groß im Vergleich zur de Broglie Wellenlänge
sind dann geht das System in Richtung klassische Mechanik. Im Jahre 1989 gab es sogar eine Debatte im Zuge einer Summer School, zu der sich die Akteure dieses Gebietes eingefunden hatten,
darüber, ob der Term Quantenchaos überhaupt verwendet werden sollte. Ein Vorschlag etwa war
quantum chaology, der sich aber nicht durchsetzte.
Heute versteht man unter dem Begriff Quantenchaos alle Probleme die mit dem quantenmechanischen Verhalten klassischer chaotischer Systeme zu tun haben. Für Billiardexperimente muss
ein weiterer Aspekt berücksichtigt werden: die meisten Experimente nutzen die Äquivalenz der
Helmholtz-Gleichung mit der stationären Schrödinger-Gleichung. Deshalb bemüht man hier auch
oft den Begriff wave chaos.
Das Problem der Definition von Quantenchaos rührt daher, dass der Begriff der Trajektorie unter
dem Aspekt der Quantenmechanik jegliche Signifikanz einbüßt. Erst in semiklassichen Modellen
treten Trajektorien auf. Zur Illustration wollen wir ein klassisches System mit N dynamischen Variablen x1 , . . . , xN betrachten, die unter dem Einfluss einer Wechselwirkung stehen. Üblicherweise
nehmen die xn alle Komponenten von Orten und Impulsen an. Die Anzahl der dynamischen Variablen ist dann N = 6M für ein 3-dimensionales M -Teilchensystem. Sei ~x(0) = [x1 (0), . . . , xN (0)]
der Vektor der dynamischen Variablen zur Zeit t = 0. Zu einer späteren Zeit t notieren wir ~x(t)
als eine Funktion der Anfangsbedingungen und der Zeit als
~x(t) = F~ [~x(0), t].
(2.1)
Wenn wir nun die Anfangsbedingung infinitesimal ändern, also
~
~x1 (0) = ~x(0) + ξ(0),
(2.2)
dann entwickeln sich die dynamischen Variablen zur Zeit t wie
~
~x1 (t) = F~ [~x(0) + ξ(0),
t].
(2.3)
~ = ~xn (t) − ~x(t) zwischen den beiden Trajektorien folgt aus den Gleichungen (2.1)
Der Abstand ξ(t)
und (2.3) in linearer Näherung als
~ = (ξ(0)
~ ∇)
~ F~ [~x(0), t],
ξ(t)
(2.4)
~ ist der Gradient von F~ bzgl. den Anfangswerten. In Komponentenschreibweise wird dann
und ∇
(2.4) zu
X ∂Fn
ξn (t) =
ξm (0).
(2.5)
∂xm
m
Die Eigenwerte der Matrix M = (∂Fn /∂xm ) bestimmen die Stabilitätseigenschaften der Trajektorie. Sind die Beträge aller Eigenwerte kleiner als 1, dann ist die Trajektorie stabil und alle Abweichungen von der Trajektorie gehen rasch gegen Null. Ist der Betrag mindestens eines Eigenwertes
größer als 1 so entfernen sich die Trajektorien exponentiell voneinander, selbst für infinitesimale
~
Abweichungen der Anfangsbedingungen ξ(0).
Nun ist in der Quantenmechanik diese Definition
von Chaos obsolet, da die Unschärferelation
∆x∆p ≥
15
1
~
2
(2.6)
einer präzisen Determinierung der Anfangsbedingungen im Wege steht. Dies kann anhand des Beispieles der Propagation eines punktartigen Teilchens in einer Box mit unendlich hohen Wänden
illustriert werden. Solche Systeme nennt man Billiards. Die quantenmechanische Behandlung erfolgt in zwei Schritten: Zunächst muss die Schrödinger-Gleichung
−
∂ψ
~2
∆ψ = i~
2m
∂t
unter der Annahme von Dirichlet Randbedingungen
ψ = 0
(2.7)
(2.8)
S
gelöst werden, wobei S den Rand der Box bezeichnet. Stationäre Lösungen der Gleichung werden
durch Separieren der Zeitabhängigkeit erhalten:
ψn (x, t) = ψn (x)e−iωn t .
(2.9)
(∆ + kn2 )ψn (x) = 0,
(2.10)
Einsetzen in Gleichung (2.7) liefert
wobei ωn und kn über die Dispersionsrelation
ωn =
~ 2
k
2m n
(2.11)
miteinander verknüpft sind. Die Gleichung (2.10) wird ebenfalls erhalten wenn man von einer
Wellengleichung
1 ∂2
(2.12)
(∆ − 2 2 )ψ = 0,
c ∂t
mit c der Wellengeschwindigkeit, ausgeht und den Separationsansatz wie in (2.9) vornimmt. Im
Gegensatz zur quadratischen Dispersionsrelation (2.11) im quantenmechanischen Falle haben wir
nun eine lineare Dispersionsrelation
ωn = ckn
(2.13)
zwischen ωn und kn . Eben dieser Zusammenhang zwischen der stationären Schrödinger-Gleichung
und der stationären Wellengleichung, die man auch Helmholtz-Gleichung nennt, wird in vielen Billiardexperimenten dazu benutzt, um quantenchaotische Systeme unter der Verwendung von ’wellenanalogen’ Systemen zu studieren. Sobald die stationären Lösungen der Schrödinger-Gleichung
bekannt sind kann ein Wellenpaket durch Superposition von Eigenfunktionen konstruiert werden:
X
ψ(x, t) =
an ψn (x)e−iωn t .
(2.14)
n
Für ein Gauß’sches Wellenpaket, welches von Breite ∆k und um k zentriert ist, sind die Koeffizienten an gegeben durch
1 kn − k 2
) ],
(2.15)
an = a exp[− (
2 ∆k
wobei a so gewählt ist, dass die Gesamtwahrscheinlichkeit das Teilchen im Paket zu finden auf
1 normiert ist. Sind die an zur Zeit t = 0 bekannt, etwa durch Messung des Impulses mit einer
Unschärfe ∆p = ~∆k, so kann die quantenmechanische Evolvierung des Paketes für jede beliebige spätere Zeit beliebig genau berechnet werden. Um ein Wellenpaket einer bestimmten Breite
zu erzeugen reduziert sich die Summe in (2.14) auf eine endliche Anzahl an Termen. Abgesehen
von atypischen Ausnahmen ist die resultierende Funktion nicht periodisch, da die ωn im Allgemeinen nicht kommensurabel sind, sondern quasiperiodisch (Vgl dazu: irrationale Rotationszahl:
Der Torus wird immer dichter aufgefüllt). Das Wellenpaket wird sich so immer rekonstruieren.
16
Das exponentielle Auseinanderlaufen benachbarter Trajektorien wie in der klassischen Dynamik
ist komplett verschwunden. Die Welleneigenschaften der Materie bewirken kein Aufweiten der
Wahrscheinlichkeitsdichte.Während es Systeme gibt denen die klassische Wahrscheinlichkeitsdichte mit der Zeit immer mehr aufweitet, wie etwa bei einem Random Walk Prozess, tendiert die
Quantenmechanik dazu diese Aufweitung einzufrieren und die Wellenpakete zu lokalisieren. Dies
wurde in einer Vielzahl von Rechnungen, aber auch experimentell gezeigt. Um zu zeigen wie das
konstruierte Wellenpaket in der Zeit evolviert betrachten wir das einfachste Billiard, ein Teilchen
in einer eindimensionalen Box mit unendlich hohen Wänden. Nimmt man die Wände bei x = 0
und x = l an, so findet man Eigenfunktionen des Systemes der Form
r
2
sin kn x, n = 1, 2, 3, . . .
(2.16)
ψn (x) =
l
mit
kn =
Einsetzen in Gleichung (2.14) liefert
r
ψ(x, t) = a
πn
.
l
(2.17)
∞
1 kn − k 2
2X
) ] sin kn xe−iωn t .
exp[− (
l n=1
2 ∆k
(2.18)
Diese Gleichung gilt sowohl für Teilchenpakete, als auch für gewöhnliche Wellen, vorausgesetzt
die entsprechenden Dispersionsrelationen (2.11), bzw. (2.13) sind erfüllt. Die Berechnung ist für
Wellen einfacher. Deshalb betrachten wir den Fall ωn = ckn . Für Teilchenwellen folgt die Rechnung
genau demselben Schema. Um die Rechnung weiter zu vereinfachen wollen wir annehmen, dass
der mittlere Impuls groß gegen die Breite der Verteilung ist, dh. k >> ∆k. Dann kann die Summe
auf −∞ bis +∞ erweitert und die Poisson-Summenrelation angewandt werden:
∞
X
(2.19)
f (n)e2πinm dn
(2.20)
n=−∞
n=−∞
mit
g(n) =
∞
X
g(n),
f (n) =
Z
∞
−∞
der Fouriertransformierten f (n). Die Anwendung auf (2.18) liefert dann
r
Z
∞
2 X l ∞
1 k−k 2
ψ(x, t) = a
) ] sin kxei(2lm−ct)k dk,
exp[− (
l m=−∞ π −∞
2 ∆k
(2.21)
wobei für die Integrationsvariable n mit k = nπ/l substituiert wurde. Das Gauß’sche Integral kann
mit der bekannten Relation
r
Z ∞
π
b2
exp[−(ak 2 + 2bk + c)]dk =
exp( − c)
(2.22)
a
a
−∞
gelöst werden, die auch für komplexe Werte von a, b, c gilt, sofern ℜe(a) > 0 ist. Das Ergebnis ist
ψ(x, t) =
∞
X
[φ(x − ctm ) − φ(l − x − ctm+1 )],
(2.23)
m=−∞
mit
2l
c
(2.24)
l
1
∆k exp[ikx − (x∆k)2 ].
π
2
(2.25)
tm = t − m
und
φ(x) = 2a
r
17
Die Gleichung (2.23) erlaubt nun eine Interpretation. Sie beschreibt die Propagation eines Gauß’schen
Paketes mit ∆x = 1/∆k und Geschwindigkeit c, welches zwischen den Wänden hin und her läuft
und bei jeder Reflexion das Vorzeichen wechselt. Für die Propagation von Teilchenwellen findet
man qualitativ dieselbe Situation vor, allerdings kommt nun die quadratische Dispersionsrelation
(2.11) zum Tragen, was zu einer Aufweitung des Pulses mit der Zeit führt, die für einen Puls der
Breite ∆x(t) durch
~(∆k)2 t 2 1/4
1
[1 + (
) ]
(2.26)
∆x(t) =
∆k
m
gegeben ist. Für t = 0 erhält man die quantenmechanische Unschärferelation ∆x∆k = 1.
Wir haben durch die Poisson-Summenrelation zwei unterschiedliche Ausdrücke für Ψ(x, t) erhalten. In Term (2.18) haben wir ψ(x, t) durch eine Summe über die Eigenfunktionen des Systemes
ausgedrückt, in (2.23) als einen Puls der mit einer Geschwindihkeit c zwischen den Wänden hin
und her propagiert. Diese Gegensätzlichkeit, also das quantenmechanische Spektrum auf der einen,
die klassischen Trajektorien auf der anderen Seite, ist der Hauptbestandteil der semiklassischen
Theorie, insbesondere jener der Gutzwiller Spur-Formel. In dem speziellen Beispiel, welches hier
präsentiert wurde, funktioniert die angewandte Prozedur besonders gut, da die Menge der Eigenwerte {kn } äquidistant war, was zu einer perfekten Pulsrekonstruktion nach jeder Reflexion führt.
Im Allgemeinen würde der Puls nach wenigen Reflexionen zerstört, aber Pulsrekonstruktionen
wären noch möglich. Die Korrespondenz zwischen klassischer und Quantenmechanik soll anhand
zweier Beispiele verdeutlicht werden.
Abbildung 13 zeigt die Propagation eines Mikrowellenpulses in einer Kavität in Form eines Vier-
Abbildung 13: Propagation eines Mikrowellenpulses in einer Mikrowellenkavität in Form eines
Viertelstadions, aus [4]
telstadions. Eine kreisförmige Welle wird von einer Antenne aus emittiert und propagiert durch
das Billiard, bis sie an der Wand reflektiert wird, wobei ein Vorzeichenwechsel, dh. ein Phasenshift
von π, erfolgt. Dies ist in der Abbildung 13 (d) für die obere und untere Wand ersichtlich. Nach
18
einigen weiteren Reflexionen ist die Pulsamplitude mehr oder weniger gleich verteilt. Nach einiger
Zeit erscheint die Amplitude jedoch plötzlich wieder, siehe dazu 13 (f). Die gleiche Situation wird
auch in der dreidimensionalen Darstellung deutlich, wie sie in Abbildung 14 zu sehen ist.
Sie zeigt Momentaufnahmen die zu der Abbildung 13 (a) und (f) gehören. Die Rekonstruktion
Abbildung 14: Dreidimensionale Ansicht der Pulspropagation aus Abbildung 13 (a) und (f), aus [4]
hat nichts mit der Quantenmechanik zu tun sondern resultiert aus den fokussierenden Eigenschaften der kreisförmigen Grenze. Alle klassischen Pfade die von diesem Teil des Stadions reflektiert
werden später simultan im Bildpunkt der Antennenposition nach der Reflexion am kreisartigen
Spiegel fokussiert. Die Pulsrekonstruktion zeigt, dass Welleneigenschaften und klassische Trajektorien nur ’zwei Seiten derselben Münze’ darstellen.
Das zweite Beispiel stammt vom gestossenen Rotator. Er zählt zu den am besten studierten chaotischen Systemen, sowohl klassisch als auch quantenmechanisch. Der Hamiltonian ist gegeben durch
H (t) =
X
L2
+ k cos Θ
δ(t − nT ).
2I
n
(2.27)
Der erste Term beschreibt die Rotation eines Pendels mit Drehimpuls L und Trägheitsmoment
I. Der zweite Term beschreibt periodische Stöße (kicks) mit einer Periode T durch ein gepulstes, gravitatives Potential der Stärke k = mgh (eine solche Situation ist experimentell schwer
herzustellen und zeigt so den Unterschied zwischen Theorie und Experiment auf). Der gestossene Rotator gehört zu den Hamilton’schen Systemen, dh. Kräfte und Impuls sind invariant. Die
Bewegungsgleichungen folgen aus den kanonischen Gleichungen
Θ̇ =
∂H
,
∂L
L̇ = −
∂H
,
∂Θ
(2.28)
und mit dem Hamilton (2.27) ist
Θ̇ = L,
L̇ = k sin Θ
X
n
19
δ(t − n),
(2.29)
I und T wurden auf 1 normiert. L ändert sich unstetig und die Bewegungsgleichungen definieren
eine Abbildung für die dynamischen Variablen Θ und L. Seien Θn und Ln die Werte der Variablen
unmittelbar vor dem n + 1 Kick. Unmittelbar nach dem Kick nimmt Ln den Wert Ln + sin Θn an,
wobei Θn nicht geändert wird. Zwischen den Kicks bleibt L konstant, aber Θ steigt linear mit der
Zeit t. Unmittelbar vor dem nächsten Kick nehmen die dynamischen Variablen die Werte
Θn+1 = Θn + Ln+1
Ln+1 = Ln + k sin Θn
(2.30)
(2.31)
an. Dies nennt man Chirikov’s Standard Map. Eine solche Abbildung ist eine gebietserhaltende
Abbildung für zwei kanonische, dynamische Variablen. Dabei ist k ein dimensionsloser Parameter,
der den Grad des Chaos beeinflusst. Mit dem Mathematica Notebook von [11] konnten folgende,
interessante Plots produziert werden: Die Standard Map eignet sich besonders gut um den Über0.9716
0.2
0
0
2Π
Π
Π
2Π
2Π 2Π
2Π
Π
0
0
Π
Π
0
0
2Π
Π
2Π
Π
0
0
Π
2Π
5
0
Π
2Π
2Π
2Π
Π
Π
0
0
0
Π
2Π
Abbildung 15: Poincaré-Schnitte für die Standard Map für unterschiedliche Kick-Stärken, generiert
mit dem Mathematica-Notebook von [11]
gang eines Hamilton’schen Systems vom regulären zum chaotischen Verhalten zu untersuchen. Die
Abbildung 15 zeigt Poincaré-Schnitte für unterschiedliche Werte von k. Jeder Punkt entspricht
einem Paar (Θ, L) unmittelbar nach dem Kick. Für einen Wert von k = 0.2 verhält sich der Rotator regulär für die meisten Anfangswerte von Θ und L. Die Bewegung im Phasenraum erfolgt auf
den sogenannten invarianten Tori, wo L nur gering variiert, während Θ alle Werte von 0 bis 2π
mit etwa gleicher Wahrscheinlichkeit annimmt (erstes Bild). Mit steigendem k brechen mehr und
20
mehr Tori auf, bis schließlich beim kritischen Wert von k = 0.9716 . . . der letzte invariante Torus
zerstört wird (zweites Bild). Es gibt noch immer reguläre Bereiche im Phasenraum. Für k ≥ 5 ist
dann bereits beinahe der gesamte Phasenraum chaotisch.
Beim kritischen Wert k = kC wird die Bewegung im Phasenraum diffus. Bei geeingneter Wahl
der Anfangsbedingungen kann der Rotator den nun voll zugägigen Phasenraum besuchen. Die
verbleibenden Tori stellen unüberwindliche Barrieren dar. Auch die Cantori Ketten (chains of
cantori), die im zweiten Bild für Werte von 1 ≤ L ≤ 2.5 und 3.5 ≤ L ≤ 5 zu sehen sind, stellen
dynamische Barrieren dar. Die Cantori sind die Überreste der zerstörten Tori. Überschreitet die
Kopplungsstärke einen kritischen Wert, so zerfällt der Torus in eine Kette von Subtori, die nach
weiterem Erhöhen der Kopplung in Sub-Subtori aufbrechen, usf. Ist der Rotator in der fraktalen
Struktur der Cantori gefangen, so bleibt er dort für eine sehr lange Zeit, bis er eventuell entkommt.
Nachdem der Hamiltonian (2.27) zeitabhängig ist, ist es nicht möglich die Zeitabhängigkeit der
Schrödinger-Gleichung abzuseparieren. Die Energie ist nicht erhalten. In ’gekickten’ Systemen wird
die Zeitentwicklung des quantenmechanischen Zustandsvektors durch
ψn = F n ψ0
(2.32)
erhalten, mit ψ0 , ψn den Zustandsvektoren am Anfang und nach dem n-ten Kick. F heißt der
Floquet-Operator. Für den gekickten Rotator ist er gegeben durch
iT L2
i
),
F = exp(− k cos Θ) exp(
~
~ 2I
(2.33)
∂
wobei L nun als der quantenmechanische Operator −i~ ∂Θ
interpretiert wird. Die Matrixelemente
für F können mit der Eigenbasis von L gefunden werden. Dann reduziert sich die Berechnung der
Zeitentwicklung auf eine Matrixmultiplikation. Auf diese Weise konnten Geisel et al. die quantenmechanische Evolvierung der Drehimpulsverteilung exakt an der kritischen Grenze k = kC
berechnen. Sie begannen mit einem Drehimpulseigenzustand L = 3.2~. Die aus [9] entnommenen
Plots in Abbildung 16 zeigen die asymptotische Verteilung der Drehimpulse. Wir finden keine
Abbildung 16: Asymptotische Drehimpulsverteilung für den gekickten Rotator mit k = kC =
0.9716 . . ., linear (a) und logarithmisch (b) skaliert, aus [9]
Gauß’sche Verteilung wie man für einen solchen diffusen Prozess erwarten könnte, sondern drei
21
scharfe Grenzen, sowohl auf der hohen als auch auf der niedrigen Drehimpulsseite. Die erste Grenze
wird für jene L Werte gefunden für die gerade der letzte Torus aufbricht, siehe Bild 2 in Abbildung 15 für k = kC . Obwohl in der Quantenmechanik keine undurchdringbaren Barrieren so nicht
existieren, da ja die Unschärferelation gilt, ist der Einfluss der klassischen Grenze denoch auch in
der quantenmechanischen Verteilung des Drehimpulses zu erkennen. Die nächsten beiden Grenzen sind sogar noch überraschender: sie gehören zu zwei aufeinanderfolgenden Cantori-Ketten.
In der Quantenmechanik ist deren Rolle als Barriere noch beeindruckender als in der klassischen
Mechanik. Beide Beispiele haben uns gezeigt, dass es eine starke Verbindung zwischen klassischer
Dynamik und Wellenmechanik, bzw. Quantenmechanik gibt. Man sucht deshalb nach Spuren von
klassischem Chaos im korrespondierenden quantenmechanischen System.
2.2
Mikrowellen Billiards
Wir wollen nun einen tieferen Blick auf Mikrowellenbilliards werfen. Ausgangspunkt sind die
Maxwell-Gleichungen
~
~ ×E
~ = − ∂B ,
∇
∂t
~
∂
~ ×H
~ = D,
∇
∂t
~
~
∇D = 0,
~B
~ = 0,
∇
(2.34)
(2.35)
(2.36)
(2.37)
wobei in Vakuum das Displacement D und die Induktion B mit E und H über
~
~ = ǫ0 E,
D
~
~ = µ0 H
B
(2.38)
(2.39)
verknüpft sind. ǫ0 und µ0 sind die dielektrische Konstante, sowie die Permeabilität des Vakuums.
Mit periodischer Zeitabhängigkeit für das elektromagnetische Feld erhalten wir die Helmholtz~ und B
~ (siehe dazu [5]):
Gleichungen für E
~ = 0,
(∆ + k 2 )E
~ = 0,
(∆ + k 2 )B
(2.40)
(2.41)
wobei k = ω/c die Wellenzahl und ω die Kreisfrequenz ist. Zusätzlich müssen Randbedingungen
erfüllt werden:
~ = 0, n̂B
~ = 0,
n̂ × E
(2.42)
wobei n̂ der Einheitsvektor normal auf die Fläche ist. In vielen Experimenten werden Resonatoren
mit zylindrischer Geometrie verwendet. Mit der z-Achse parallel zur Zylinderachse nehmen die
Gleichungen für die Randbedingungen (2.42) eine einfache Form
(2.43)
EZ = 0, ∇⊥ BZ = 0,
S
S
auf der Zylinderoberfläche an, wobei ∇⊥ die ’normale’ Ableitung bedeutet. Für EZ folgt dies
unmittelbar aus Gleichung (2.42), für BZ aus Gleichung (2.42) und der zweiten Maxwell-Gleichung.
Die folgende Rechnung ist nicht ausgeführt, siehe dazu etwa [5], Kapitel 8. Wir betrachten hier nur
die Ergebnisse: Es gibt zwei Möglichkeiten die Randbedingungen (2.43) zu erfüllen. Für sogenannte
transversal magnetische Moden (TM) finden wir
EZ (x, y, z) = E(x, y) cos(
nπz
),
d
22
n = 0, 1, 2, . . .
(2.44)
BZ (x, y, z) = 0,
(2.45)
wobei E(x, y) der zweidimensionalen Helmoltz-Gleichung
[∆ + k 2 − (
nπ 2
) ]E = 0,
d
(2.46)
mit Dirichlet Randbedingung
E(x, y) = 0
(2.47)
S
~ und B
~ können aus E(x, y)
an der Zylinderoberfläche, genügt. Die x und y Komponenten von E
berechnet werden, sind hier aber nicht relevant. Für die transveral elektrischen Moden (TE) finden
wir
nπz
),
BZ (x, y, z) = B(x, y) sin(
d
EZ (x, y, z) = 0,
(2.48)
n = 1, 2, 3, . . . ,
(2.49)
wobei B(x, y) nun der zweidimensionalen Helmholtz-Gleichung
[∆ + k 2 − (
nπ 2
) ]B = 0,
d
(2.50)
mit Neumann Randbedingungen
∇⊥ B(x, y) = 0.
(2.51)
S
Für Frequenzen ν < c/2d korrespondiernd zu Wellenzahlen k < π/d sind nur TM Moden mit
n = 0 möglich, und Gleichung (2.46) reduziert sich auf
(∆ + k 2 )E = 0.
(2.52)
Im Folgenden betrachten wir Billiards dieser Art als zweidimensional. Es gibt eine vollständige
Äquivalenz zur zweidimensionalen Schrödinger-Gleichung für ein Teilchen in einer Box mit unendlich hohen Wänden, inklusive der Randbedingungen. In dieser Analogie entspricht E(x, y) der
Wellenfunktion und k 2 der Eigenenergie. Um die Eigenmoden zu messen werden Mikrowellen über
eine Antenne in den Resonator emittiert. Diese Antenne besteht üblicherweise aus einem Draht
mit einem Durchmesser von etwa 0.1mm, die durch ein Loch in den Resonator eingeführt ist.
Die reflektierten Mikrowellen werden mittels einer Messbrücke (microwave bridge, Impendanzmessung) vermessen, es sind aber auch Transmissionsmessungen zwischen mehreren Antennen möglich.
Schon in den 1950ern wurde die Äquivalenz zwischen Mikrowellen und Schallwellen benutzt um
etwa Raumakustik zu vermessen. Die ersten Mikrowellenexperimente die quantenchaotische Fragestellungen behandelten fanden jedoch nicht vor 1990 statt, vgl. [3]. Man studierte die Eigenmoden
eines Resonators von Viertelstadion-Form durch Messung der reflektierten Mikrowellenleistung.
Abbildung 17 zeigt einen Teil des Reflexionsspektrums. Jedes Minimum in der reflektierten Mikrowellenleistung entspricht einer Eigenmode. Es gibt gute Gründe Systeme ohne Symmetrien
zu studieren. Das vollständige Stadion besitzt zwei Spiegelsymmetrien, woraus eine Superposition von vier unterschiedlichen Spektren entsteht, die zu unterschiedlichen Paritätsklassen gehören.
Dies würde die Analyse der Daten in Termen der Random Matrix Theory unnötig verkomplizieren.
Konfrontiert mit einem chaotisch anmutenden Spektrum, wie in Abbildung 17 gezeigt, könnte man
sich fragen, ob denn überhaupt relevante Information im Spektrum zu finden ist. Wir wollen einen
kurzen, qualitativen Blick darauf werfen wie man so ein Problem angeht. Bereits in den 1960ern
hatte man mit ähnlichen Problemen zu tun als man Spektren komplexer Kerne studierte. Es stellte
sich als nützlich heraus die Verteilungsfunktionen P (s) der Abstände benachbarter Eigenenergien
sn = En − En−1 zu plotten. In Abbildung 18 betrachten wir Verteilungen für unterschiedliche
Mikrowellenbilliards. Der mittlere Abstand hsi muss dabei auf 1 normiert sein. Das erste Bild in
Abbildung 18 zeigt P (s) für ein rechteckiges Billiard. Die entsprechende klassische Dynamik ist
integrabel. In diesem Falle wird eine Poisson-Verteilung
P (s) = exp(−s)
23
(2.53)
Abbildung 17: Teil eines Mikrowellen Reflexionsspektrums einer Kavität in Form eines Viertelstadion (b = 20cm, l = 36cm) und einer Höhe h = 0.8cm. Jedes Minimum in der reflektierten
Mikrowellenleistung entspricht einer Eigenfrequenz, [3]
für die Verteilung des Nächste-Nachbarn-Abstandes erwartet. Das Experiment folgt der theoretischen Kurve, allerdings gibt es einige signifikante Abweichungen. Die experimentell gewonnene
Verteilung zeigt ein ausgeprägtes Loch für kleine Werte von s, wobei hier aber ein Maximum erwartet wird, wie uns Gleichung (2.53) sagt. Der Grund für diese Diskrepanz liegt in der endlichen
Breite der Resonanzkurven. Wenn zwei Resonanzen durch einen Abstand der kleiner als die experimentelle Linienbreite ist, getrennt sind, so werden sie als eine Resonanz registriert. Weitere
Abweichungen finden wir für größere Abstände.
Aufgrund der Existenz der Antenne wird das System pseudointegrabel. Abbildung 18 (b) zeigt
P (s) für dasselbe Rechteck wie (a), aber nun für einen höheren Frequenzbereich. Es gibt keine Ähnlichkeit mit der Poisson-Verteilung (2.53) mehr. Die durchgezogene Linie folgt aus einer
Rechenmethode, die den Einfluss der Antenne explizit berücksichtigt, [12]. Nahezu perfekte Übereinstimmung mit dem Experiment findet man für P (s) für das Viertelstadion-Billiard, dessen
Spektrum wir bereits in Abbildung 17 betrachtet haben. Die durchgezogene Linie entspricht der
Wigner-Verteilung
π
π
P (s) = s exp(− s2 ).
(2.54)
2
4
Diese Verteilung ist in Spektren chaotischer Systeme quasi omnipresent.
Wir wollen nun die Breiten der Resonanzen diskutieren. Die Randbedingungen (2.43) gelten für
ideal leitende Wände. Tatsächlich aber finden wir endliche Leitfähigkeit der Wände. Die Mikrowellen treten teilweise in die Wände ein. Die Eindringtiefe (skin depth) ist gegeben durch
p
(2.55)
δ = 2µ0 ωσ,
(siehe [5], Kapitel 7), wobei σ die Leitfähigkeit der Wand ist. Für einen guten Leiter wie etwa
ω
Messing (brass) mit σ = 2 × 107Ω−1 m−1 und einer Mikrowellenfrequenz ν = 2π
von 10GHz findet
man Eindringtiefen von etwa 1µm.
Die Dissipation der Mikrowellen in der Wand führt auf eine exponentielle Dämpfung der elektromagnetischen Energie im Resonator,
W (t) = W0 exp(−t/τ ),
(2.56)
und einer entsprechenden Dämpfung der elektrischen Felder,
~
~ 0 exp(−t/2τ ) cos(ω0 t).
E(t)
=E
(2.57)
~ Die spektrale Verteilung der Energie, das sogennante power
Eine analoge Relation gilt für B.
spectrum, ist gegeben durch
S(ω) = |Ê(ω)|2 ,
(2.58)
24
Abbildung 18: Nächste-Nachbarn-Abstand Histogramme, gewonnen aus rechteckigen Mikrowellenresonatoren mit Seitenlängen a = 16.5 . . . 51.0cm, b = 20cm, in den zwei Frequenzbereichen
5 − 10GHz (a), und 15 − 18GHz (b), sowie für das Viertelstadion-Billiard aus Abbildung 17
(c), [12], [3]
~
mit Ê(ω) der Fouriertransformierten von E(t),
1
Ê(ω) = √
2π
Man findet schließlich
S(ω) ≈
Z
∞
E(t)eiωt dt.
(2.59)
−∞
1
1 2.
(ω − ω0 )2 + ( 2τ
)
(2.60)
Der Energieverlust in den Wänden führt auf eine Lorentz-Verbreiterte Resonanz mit einer FWHM
(full width at half maximum) von
1
∆ω = .
(2.61)
τ
Die Resonatorgüte (resonator quality) Q = ω0 /∆ω ist mit der Zerfallzeit τ verknüpft:
τ=
Q
.
ω0
25
(2.62)
Typische Güten für normal leitende Kavitäten sind etwa 103 bis 104 . Um die Güte zu berechnen
muss man die endliche Leitfähigkeit der Wände mit einbeziehen. Man erhält
Q=α
V
,
Sδ
(2.63)
mit V Volumen und S Oberfläche des Resonators, und α ein dimensionsloser Faktor abhängig
von der Resonatorgeometrie, siehe [5], Kapitel 8. Abgesehen von einem konstanen Faktor ist die
Güte des Resonantors durch das Verhältnis der im Resonator gespeicherten Energie zu der in den
Wänden gespeicherten Energie gegeben.
Die Güte limitiert die Gesamtzahl der Eigenfrequenzen die experimentell ermittelt werden können.
Der Einfachheit halber wollen wir einen rechteckigen Resonator mit Seitenlängen a, b und c
betrachten. Die Wellenzahlen der entsprechenden Eigenfrequenzen sind dann gegeben durch
r
lπ
mπ 2
nπ
klmn = ( )2 + (
) + ( )2 l, m, n = 0, 1, 2, . . . .
(2.64)
a
b
c
Abgesehen von den Fällen in denen eine der Quantenzahlen Null ist muss jede Resonanz zweimal
gezählt werden, da es transversal elektrische (TE) und transversal magneteische (TM) Moden gibt.
Die Anzahl der Resonanzen im Bereich hk, k + dki ist dann gegeben durch
X
ρ(k)dk = 2
klmn
(2.65)
k<klmn <k+dk
= 2
X Z
l,m,n
k+dk
k
r
(
δ(k −
lπ 2
mπ 2
nπ
) +(
) + ( )2 )dk.
a
b
c
Ersetzt man die Summen durch Integrale, so findet man
ρ(k)dk =
2
V k 2 dk,
π2
(2.66)
mit V = abc dem Volumen des Resonators. Dies ist die Weyl-Formel, die Planck benutzte um die
Formel für Schwarzkörperstrahler abzuleiten. Das Ergebnis gilt grundsätzlich für Resonatoren mit
rechteckiger Struktur, man kann jedoch zeigen, dass sie asymptotisch für Resonatoren beliebiger
Formen gilt. Für die Anzahl an Resonanzen unter einem gegebenen k finden wir mit Gleichung
(2.66)
N (k) =
Z
k
ρ(k)dk
(2.67)
0
=
2
V k3 .
3π 2
Die experimentellen Grenzen der Auflösung liegen bei kmax , bei dem der mittlere Abstand zwischen
benachbarten Resonanzen, dh. die reziproke Zustandsdichte, gerade der Breite ∆k einer Resonanz
entspricht,
2
2
)−1 ,
(2.68)
∆k = ( 2 V kmax
π
woraus für die Güte unter Verwendung von ω = ck folgt:
Q=
kmax
2
ωmax
3
.
=
= 2 V kmax
∆ω
∆k
π
(2.69)
Unter Verwendung von Formel (2.67) kann man schreiben:
Nmax =
26
1
Q,
3
(2.70)
Abbildung 19: Teil eines Spektrums eines Niob-Mikrowellenresonators der Form eines Viertelstadions. Das Spektrum in der oberen Hälfte wurde bei Zimmertemperatur aufgenommen, jenes der
unteren Hälfte bei Supraleitung. Im rechten oberen Eck sehen wir den verwendeten Resonator,
sowie die Positionen der drei gekoppelten Antennen, [10]
wobei Nmax die Maximalanzahl der auflösbaren Resonanzen ist. Für Güten der Größenordnung
1000 ist die Anzahl der Größenordnung 1000 mit dem Experiment in Übereinstimmung.
Die Experimente wurden von Richter und seiner Gruppe [10] auf supraleitende Kavitäten erweitert,
wo Güten von 105 bis sogar 107 auftreten. Daraus resultieren außergewöhnlich scharfe Resonanzlinien. Abbildung 19 zeigt einen Teil des Spektrums eines Stadion-Billiards. Nach Gleichung (2.70)
sollte man in der Lage sein Millionen von Resonanzen zu finden. Solche Messungen wurden jedoch nicht realisiert. Mit einem Q von 106 und einer Maximalfrequenz von 40GHz (dem aktuell
verfügbaren Limit, [8] 1999), lernen wir aus Gleichung (2.69), dass ein Volumen von 104 cm3 nötig
wäre um alle auflösbaren Resonanzen in das technisch erreichbare Gebiet zu bringen. Volumina
dieser Größe wurden bislang nicht untersucht, obwohl sie vermutlich nicht außer Reichweite liegen.
Die extrem geringe Dämpfung erlaubt es nicht nur ein Spektrum mit beispielloser Auflösung aufzunehmen, es ist auch möglich den Zerfall von Resonanzen in einer zeitlichen Tiefe zu studieren,
die anderen Methoden nicht zugänglich ist.
Die Zahl der Untersuchungen von Spektren von Mikrowellen-Billiards sind in den letzten Jahren ( [8] 1999) beträchtlich angestiegen. Die Fragestellungen reichen von Random Matrix über
Periodic Orbit Theory bis hin zu Streumatrix-Zugängen und Spectral Level Dynamics. Billiards
mit Strahlteilung (ray-splitting) wurden ebenfalls untersucht indem man die Mikrowellenkavitäten
mit dielektrischen Materialien lud. Es wurden auch Experimente mit dreidimensionalen Billiards
veröffentlicht, sowohl mit, als auch ohne Supraleitung. Hier geht die Äquivalenz zwischen Elektrodynamik und Quantenmechanik verloren. Eine Auftrennung in TE und TM Moden ist nicht
mehr möglich. Dennoch unterscheiden sich die Spektren nicht Signifikant von jenen welche aus
quasi-zweidimensionalen und quantenmechanischen Systemen gewonnen wurden.
27
Appendices
A
A.1
3-Scheiben Flipper - das Programm
Kurze Erläuterung
Einige kurze Erläuterungen zu dem Programm des 3-Scheiben Flippers will ich nicht schuldig bleiben. Die Aufgabenstellung für sich betrachten wirkt harmlos und einfach. Als Mensch hat man
auch keine weitere Schwierigkeit den Verlauf einer Trajektorie geometrisch zu konstruieren. Ein
wenig anders verhält es sich, wenn man dem Computer beibringen will dieses Problem zu lösen.
Folgende Geometrie wurde für die Berechnung angenommen: Die Parameter a und R werden einmal
Abbildung 20: Geometrie und Wahl des Koordinatensystemes
eingestellt und nicht mehr verändert. Genauso verhält es sich für die Anfangsbedingungen. Man
benötigt vier Anfangsbedingungen, die in Polarkoordinaten ausgedrückt in drei Parametern zusammengefasst sind, da die Geschwindigkeit v ebenfalls konstant gehalten wird: initr1, initp1
und vphi. Das Programm arbeitet iterativ, dh. vom Anfangsort ausgehend macht es einen Schritt
in die durch den Geschwindigkeitswinkel vphi vorgegebene Richtung. Dabei splitten sich die Geschwindigkeiten in x- und y-Richtung auf und liefern so zwei unabhängige Gleichungen. Hierin
liegt auch die Crux: Der gewählte Zugang ist sehr einfach zu realisieren, da man nur die Gleichung hinschreiben muss. Es zeigt sich jedoch, dass aufgrund der vielen unnötigen Iterationen im
’leeren Raum’ zwischen den Scheiben der Fehler enorm anwächst. Der naheliegendere und elegantere Zugang ist also, von jedem Streupunkt ausgehend den nächsten Streupunkt zu berechnen, usf.
Dadurch ließe sich ein viel stabilerer Algorithmus hinschreiben, was allerdings aus Zeitgründen unterlassen wurde. Anhand von periodischen Orbits, deren Anfangsbedingungen aus geometrischen
Überlegungen ausgerechnet werden können, läßt sich die Stabilität des Algorithmus überprüfen.
Nachdem der implementierte Algorithmus eine ausreichende Anzahl von Streuprozessen relativ
genau berechnet, reicht es für den Demonstrationszweck völlig aus. Außerdem weist der Einfluss
des Fehlers selbst wieder auf den chaotischen Charakter des Systemes hin.
Nachdem ein neuer Schritt berechnet wurde, wird geprüft ob eine Scheibe in Reichweite ist. Es ist
wichtig, möglichst genau an der Kreisoberfläche zu streuen. Um zu prüfen, ob eine Streubedingung
vorliegt, werden einfach die Koordinaten des Teilchens in die jeweiligen Kreisgleichungen eingesetzt. Ist eine der Gleichungen erfüllt, wobei wegen des Float-Charakters nicht nur der Rand der
Kresscheibe sondern die gesamte Kreisscheibe als Bedingung herangezogen (≤) wird, so wird der
28
Streuprozess nur anerkannt, wenn die letzte Streuung an einer anderen Scheibe (oder gar nicht)
erfolgt ist. Nun muss der neue Streuwinkel vphi berechnet werden, der uns sagt in welche Richtung
reflektiert wird. Aus geometrischen Überlegungen wurden folgende Fälle hergeleitet:

−π − 2ξ + φ φ > π, P rozess von RE nach LI



−π + 2ξ + φ φ > π, P rozess von LI nach RE
φ′ =
(A.1)

+π − 2ξ + φ φ < π, P rozess von RE nach LI



+π + 2ξ + φ φ < π, P rozess von LI nach RE
mit φ′ der neue Winkel von v, φ der Einfallswinkel und ξ der Winkel zwischen Einfallsrichtung
und Lot (Verbindung Streupunkt Kreismittelpunkt).
In Abbildung 21 sehen wir ein Beispiel eines solchen Streuprozesses, hier ist φ < π und der Prozess
erfolgt von links nach rechts. Die Richtung des Prozesses ist wie folgt festzustellen: Blickt man
vom Streupunkt aus entlang des ’Lotes’ in Richtung des Kreismittelpunktes, so kann entschieden
werden wann ein Prozess von links nach rechts oder umgekehrt abläuft. Das Problem ist nun, ein
Abbildung 21: Beispiel für Geometrie eines Streuprozesses von LI nach RE, φ < π
Kriterium zu finden wann ein Prozess von rechts nach links verläuft und wann umgekehrt. Sie
unterscheiden sich durch ein Vorzeichen, wie in der Gleichung mit Fallunterscheidung für φ′ zu
sehen ist. Um dies festzustellen betrachtet man die Winkeldifferenz zwischen dem Lot und dem
einfallenden Teilchen ΦLOT − ΦT EILCHEN . Ist diese größer als π oder kleiner als Null, so handelt
es sich um einen Prozess von rechts nach links, anderenfalls um einen Prozess von links nach
rechts. Um die Entscheidung treffen zu können muss man den Lotwinkel berechnen, der aus dem
arctan xy gewonnen wird, mit y und x die Komponenten des stets auf dem Kreismittelpunkt der
~ =R
~ −S
~ ist, mit R
~ Ortsvektor des
aktuellen Streuscheibe weisenden Differenzenvektors von LOT
~ Ortsvektor jenes Ortes an dem die Streuung erfolgt.
Scheibenmittelpunktes und S
Da der arctan einen Wertebereich von (− π2 , π2 ) hat, der Lotwinkel aber alle Werte aus [0, 2π)
annehmen kann, muss der entsprechende Winkel mit Hilfsmitteln bestimmt werden. Dazu wurde
die Streuscheibe willkürlich in Quadranten eingeteilt (siehe Abbildung 22). Um den Winkel des
Lotes zu bestimmen wurden folgende Relationen gefunden:

Quadrant I
arctan xy



π + arctan y
Quadrant II
x
φLOT =
(A.2)
y

π + arctan x
Quadrant III



2π + arctan xy Quadrant IV
Damit können alle Streuprozesse berechnet werden.
29
Abbildung 22: Einteilung der Quadranten
Technische Informationen:
• Compiler: gfortran, gcc version 4.3.2 (Debian 4.3.2-1.1)
• OS: Debian GNU/Linux, 2.6.30, x86 64
• Editor: vi
• Graphik: xmgrace, Grace-5.1.22
• Dokumentation: LATEX
30
A.2
Der Sourcecode von flipper.f90
MODULE f u n c t i o n s
IMPLICIT NONE
CONTAINS
FUNCTION l o t w i n k e l ( x , y , x1 , y1 , xx , yy )
! B er ech n et Winkel d es L o t e s
IMPLICIT NONE
REAL(KIND=8) , INTENT( IN ) : : x , y , xx , yy , x1 , y1
REAL(KIND=8) , PARAMETER : : PI = 3 . 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4
REAL(KIND=8) : : l o t w i n k e l
IF ( ( x1 < xx ) .AND. ( y1 < yy ) ) THEN ! I Quadrant , x <0 , y<0
l o t w i n k e l = ATAN( y /x )
ELSE IF ( ( x1 > xx ) .AND. ( y1 < yy ) ) THEN ! I I Quadrant , x >0 , y<0
l o t w i n k e l = PI + ATAN( y/ x )
ELSE IF ( ( x1 > xx ) .AND. ( y1 > yy ) ) THEN ! I I I Quadrant , x >0 , y>0
l o t w i n k e l = PI + ATAN( y/ x )
ELSE
! IV Quadrant , x <0 , y>0
l o t w i n k e l = 2∗ PI + ATAN( y/ x )
END IF
END FUNCTION l o t w i n k e l
END MODULE f u n c t i o n s
PROGRAM main
USE f u n c t i o n s
IMPLICIT NONE
INTEGER, PARAMETER : : TIME = 7000
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
REAL(KIND=8) ,
PARAMETER
PARAMETER
PARAMETER
PARAMETER
PARAMETER
PARAMETER
PARAMETER
PARAMETER
PARAMETER
PARAMETER
REAL(KIND=8)
REAL(KIND=8)
REAL(KIND=8)
REAL(KIND=8)
REAL(KIND=8)
REAL(KIND=8)
REAL(KIND=8)
REAL(KIND=8)
REAL(KIND=8)
::
::
::
::
::
::
::
::
::
::
::
::
::
::
::
::
::
::
::
! Zeitparameter
PI = 3 . 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4
v0=1e−7
! const . Geschwindigkeit
R = 0.5
! Ausdehnung d er D i s c s
a = 1.25
! Sei tenl aenge g l e i c h s e i t . Dreieck
r 1 = 0 . d0
! r−pos e r s t e S c h e i b e
p h i 1 = 0 . d0
! phipos e r s t e Scheibe
r2 = a
! r−pos z w e i t e S c h e i b e
p h i 2 = 0 . d0
! phipos zweite Scheibe
r3 = a
! r−pos d r i t t e S c h e i b e
p h i 3=PI / 3 . d0 ! p h i p o s d r i t t e S c h e i b e
phi
! Winkel Phi ( eb en e P o l a r k o o r d )
x , y , x1 , y1
! k a r t . K o o r d i n a ten
vx1 , vy1
! v−Komponenten
vphi
! Richtung von v
lotphi
! Richtung von Lot
initr1
! Startwert R
initp1
! S t a r t w e r t Phi
xx1 , yy1 , xx2 , yy2 , xx3 , yy3 ! P o s i t i o n e n d er S c h e i b e n
xl , yl
! Lotvektor
INTEGER : : t
INTEGER : : l a s t s t r e u
! Zeitparameter
! l e t z t e S tr eu u n g
i n i t r 1 = R+0.01
i n i t p 1 = ATAN(2 ∗ SIN ( PI/3) −2∗R/ a )
!%
v p h i = ATAN(2 ∗ SIN ( PI /3) −2∗R/ a )
xx1 = r 1 ∗COS( p h i 1 )
! P o s i t i o n umrechnen e r s t e D i s c
31
yy1
xx2
yy2
xx3
yy3
=
=
=
=
=
r 1 ∗SIN ( p h i 1 )
r 2 ∗COS( p h i 2 )
r 2 ∗SIN ( p h i 2 )
r 3 ∗COS( p h i 3 )
r 3 ∗SIN ( p h i 3 )
!
!
!
!
!
Position
Position
Position
Position
Position
umrechnen
umrechnen z w e i t e D i s c
umrechnen
umrechnen d r i t t e D i s c
umrechnen
x1 = i n i t r 1 ∗COS( i n i t p 1 )
y1 = i n i t r 1 ∗SIN ( i n i t p 1 )
vx1 = v0 ∗COS( v p h i )
vy1 = v0 ∗SIN ( v p h i )
!
!
!
!
Startwert
Startwert
Startwert
Startwert
laststreu = 0
PRINT ∗ , ” v p h i : ”
PRINT ∗ , v p h i
! Jede S tr eu u n g m o e g l i c h
! Kontrollausgabe
umrechnen
umrechnen
umrechnen
umrechnen
OPEN (UNIT=10 , FILE=” t r a j e c t o r y . dat ” , ACTION=” w r i t e ” )
100 FORMAT ( F8 . 2 ,XXXXXXXXXX, F8 . 2 )
! Ausgabe v o r b e r e i t e n
! Format angeben
DO t =1 , TIME
! Evolviere Zeit
WRITE ( 1 0 , 1 0 0 ) x1 , y1
x1 = x1 + vx1 ∗ t
y1 = y1 + vy1 ∗ t
! Ausgabe i n D a tei
! B ew eg u n g s g l ei ch u n g
! B ew eg u n g s g l ei ch u n g
IF (SQRT( x1 ∗ x1 + y1 ∗ y1 ) <= R) THEN
IF ( l a s t s t r e u .NE. 1 ) THEN
PRINT ∗ , t
PRINT ∗ , ”STREU1”
laststreu = 1
x l = xx1 − x1
y l = yy1 − y1
! S tr eu b ed i n g u n g d i s c 1
! L e t z t e S tr eu u n g muss u n g l . 1 s e i n
! l e t z t e S tr eu u n g s e t z e n
! Lot b er ech n en
l o t p h i = l o t w i n k e l ( x l , y l , x1 , y1 , xx1 , yy1 )
! L o t w i n k e l b er e ch n en
PRINT ∗ , ” l o t w i n k e l : ”
PRINT ∗ , l o t p h i
IF ( v p h i > PI ) THEN
IF ( ( l o t p h i − v p h i < 0 . d0 ) .OR. ( ( l o t p h i − v p h i ) > PI ) ) THEN
! P r o z e s s von Re nach L i
v p h i = −PI + v p h i − 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
ELSE
v p h i = −PI + v p h i + 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
END IF
ELSE
IF ( ( l o t p h i − v p h i < 0 . d0 ) .OR. ( ( l o t p h i − v p h i ) > PI ) ) THEN
! P r o z e s s von Re nach L i
v p h i = PI + v p h i − 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
ELSE
v p h i = PI + v p h i + 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
END IF
END IF
v p h i = MOD( vphi , 2∗ PI )
vx1 = v0 ∗COS( v p h i )
vy1 = v0 ∗SIN ( v p h i )
! S t a r t w e r t umrechnen
! S t a r t w e r t umrechnen
PRINT ∗ , ” v p h i neu : ”
PRINT ∗ , v p h i
! Kontrollausgabe
END IF
ELSE IF (SQRT( ( x1−xx2 ) ∗ ( x1−xx2)+y1 ∗ y1 ) <= R) THEN
IF ( l a s t s t r e u .NE. 2 ) THEN
PRINT ∗ , t
32
! S tr eu b ed i n g u n g d i s c 2
PRINT ∗ , ”STREU2”
laststreu = 2
x l = xx2 − x1
y l = yy2 − y1
! Lot b er ech n en
l o t p h i = l o t w i n k e l ( x l , y l , x1 , y1 , xx2 , yy2 )
! L o t w i n k e l b er e ch n en
PRINT ∗ , ” l o t w i n k e l : ”
PRINT ∗ , l o t p h i
IF ( v p h i > PI ) THEN
IF ( ( l o t p h i − v p h i < 0 . d0 ) .OR. ( ( l o t p h i − v p h i ) > PI ) ) THEN
! P r o z e s s von Re nach L i
v p h i = −PI + v p h i − 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
ELSE
v p h i = −PI + v p h i + 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
END IF
ELSE
IF ( ( l o t p h i − v p h i < 0 . d0 ) .OR. ( ( l o t p h i − v p h i ) > PI ) ) THEN
! P r o z e s s von Re nach L i
v p h i = PI + v p h i − 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
ELSE
v p h i = PI + v p h i + 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
END IF
END IF
v p h i = MOD( vphi , 2∗ PI )
vx1 = v0 ∗COS( v p h i )
vy1 = v0 ∗SIN ( v p h i )
! S t a r t w e r t umrechnen
! S t a r t w e r t umrechnen
PRINT ∗ , ” v p h i neu : ”
PRINT ∗ , v p h i
! Kontrollausgabe
END IF
ELSE IF (SQRT( ( x1−xx3 ) ∗ ( x1−xx3 )+( y1−yy3 ) ∗ ( y1−yy3 ) ) <= R) THEN ! S tr eu b ed i n g u n g d i s c 3
IF ( l a s t s t r e u .NE. 3 ) THEN
PRINT ∗ , t
PRINT ∗ , ”STREU3”
laststreu = 3
x l = xx3 − x1
! Lot b er ech n en L = R − x
y l = yy3 − y1
l o t p h i = l o t w i n k e l ( x l , y l , x1 , y1 , xx3 , yy3 )
! L o t w i n k e l b er e ch n en
PRINT ∗ , ” l o t w i n k e l : ”
PRINT ∗ , l o t p h i
IF ( v p h i > PI ) THEN
IF ( ( l o t p h i − v p h i < 0 . d0 ) .OR. ( ( l o t p h i − v p h i ) > PI ) ) THEN ! P r o z e s s von Re nach L i
v p h i = −PI + v p h i − 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
ELSE
v p h i = −PI + v p h i + 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
END IF
ELSE
IF ( ( l o t p h i − v p h i < 0 ) .OR. ( ( l o t p h i − v p h i ) > PI ) ) THEN
! P r o z e s s von Re nach L i
v p h i = PI + v p h i − 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
ELSE
v p h i = PI + v p h i + 2∗ACOS( ( vx1 ∗ x l+vy1 ∗ y l )
/ (SQRT( vx1 ∗ vx1+vy1 ∗ vy1 )∗SQRT( x l ∗ x l+y l ∗ y l ) ) )
! Winkel b er ech n en
END IF
END IF
v p h i = MOD( vphi , 2∗ PI )
vx1 = v0 ∗COS( v p h i )
vy1 = v0 ∗SIN ( v p h i )
! S t a r t w e r t umrechnen
! S t a r t w e r t umrechnen
33
PRINT ∗ , ” v p h i neu : ”
PRINT ∗ , v p h i
! Kontrollausgabe
END IF
END IF
v p h i = MOD( vphi , 2∗ PI )
IF ( v p h i < 0 . d0 ) THEN
v p h i = v p h i + 2∗ PI
END IF
END DO
! Hole Winkel zu r u eck
! Hole Winkel zu r u eck
CLOSE (UNIT=10)
END PROGRAM main
34
B
Feigenbaumdiagramm - das Programm
B.1
Kurze Erläuterung
Das Programm zur Erstellung des Feigenbaum-Diagrammes ist denkbar einfach. Hier wurde nur
der relevante Bereich von kurz vor der ersten Bifurkation, die bei a= 3 erfolgt, bis a= 4 gerechnet.
Ferner ist für x ein Startwert vorzugeben.
In einer for-Schleife (in FORTRAN DO Schleife) werden für jedes a 300 Folgeglieder aufsummiert.
Dabei läuft a in einer äußeren Schleife, beginnend bei 2.5. Mit jedem äußeren Druchlauf wird
a um 0.005 erhöht, so dass nach 300 Durchläufen der Wert a= 4 erreicht wird. In der inneren
Schleife werden alle Folgeglieder deren Laufindex größer ist als 199 zusammen mit dem aktuellen
Parameter a auf File geschrieben. So können dann die Daten mit xmgrace, gnuplot, etc zum
Diagramm prozessiert werden.
Technische Informationen:
• Compiler: gfortran, gcc version 4.3.2 (Debian 4.3.2-1.1)
• OS: Debian GNU/Linux, 2.6.30, x86 64
• Editor: vi
• Graphik: xmgrace, Grace-5.1.22
• Dokumentation: LATEX
35
B.2
Der Sourcecode von feigenbaum.f90
PROGRAM main
IMPLICIT NONE
INTEGER, PARAMETER : :
REAL(KIND=8) : : a , x
INTEGER : : i , j
i t = 300
! Parameter f u e r Anzahl d er a u f s u m m i er etn F o l g e g l i e d e r
! Parameter a , Werte f u e r a l t e s und a k t u e l l e s x
! Schleifenparameter
OPEN ( UNIT=10 , FILE=”f ei g en b a u m . dat ” , ACTION=” w r i t e ” )
100 FORMAT ( F8 . 5 , 10X, F8 . 5 )
! Formater a n w ei s en
x = 0.5
a = 2.5
DO i =1 , 300
a = a + 0.005
DO j =1 , i t
x = a ∗x − a ∗x ∗x
IF ( i t .GT. 199 ) THEN
WRITE ( 1 0 , 1 0 0 ) x , a
END IF
END DO
END DO
END PROGRAM main
! Ausgabe v o r b e r e i t e n
! S e t z e n d er Parameter
! a s t a r t e t b e i 2 . 5 , da e r s t b e i 3 d i e e r s t e B i f u r k a t i o n
! a l a e u f t b i s 4 , d a h er 300 0 . 0 0 5 e r S c h r i t t e n o e t i g
! a er h o eh en
! F o l g e aufsummieren
! L o g i s t i s c h e Gl ei ch u n g
! l e t z t e n 100 G l i e d e r mitnehmen
! Ausgabe i n D a tei
36
auftritt
Abbildungsverzeichnis
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Des Physikers Flipper . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Skizze: Sensibilität auf Anfangsbedingungen, [2] . . . . . . . . . . . . . . . . . . . .
Sensibilität auf Anfangsbedingungen: Unterschiedlicher Startwinkel . . . . . . . . .
Sensibilität auf Anfangsbedingungen: Unterschiedliche Anfangsorte . . . . . . . . .
Skizze: Binäres Alphabet für 3-Scheiben-Flipper-Trajektorien, [2] . . . . . . . . . .
Skizze: Qualitativer Verlauf von einigen 3-Scheiben Zyklen, [2] . . . . . . . . . . . .
Periodische Orbits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Skizze: 3-Scheiben Flipper mit Koordinaten und Poincaré-Schnitten, [2] . . . . . .
Skizze: Bereiche von Trajektorien für einmaliges und zweimaliges Abprallen, [2] . .
Logistische Abbildung, a = 2 mit stabilem Fixpunkt xf = 0.5, x0 = 0.1, [1] . . . .
Logistische Abbildung, a = 3.5 in oszillierendem Bereich, x0 = 0.1, [1] . . . . . . .
Feigenbaumdiagramm, erstellt mit einem FORTRAN95-Programm, Sourcecode siehe
Anhang . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Propagation eines Mikrowellenpulses in einer Mikrowellenkavität in Form eines Viertelstadions, aus [4] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dreidimensionale Ansicht der Pulspropagation aus Abbildung 13 (a) und (f), aus [4]
Poincaré-Schnitte für die Standard Map für unterschiedliche Kick-Stärken, generiert
mit dem Mathematica-Notebook von [11] . . . . . . . . . . . . . . . . . . . . . . .
Asymptotische Drehimpulsverteilung für den gekickten Rotator mit k = kC =
0.9716 . . ., linear (a) und logarithmisch (b) skaliert, aus [9] . . . . . . . . . . . . . .
Teil eines Mikrowellen Reflexionsspektrums einer Kavität in Form eines Viertelstadion (b = 20cm, l = 36cm) und einer Höhe h = 0.8cm. Jedes Minimum in der
reflektierten Mikrowellenleistung entspricht einer Eigenfrequenz, [3] . . . . . . . . .
Nächste-Nachbarn-Abstand Histogramme, gewonnen aus rechteckigen Mikrowellenresonatoren mit Seitenlängen a = 16.5 . . . 51.0cm, b = 20cm, in den zwei Frequenzbereichen 5 − 10GHz (a), und 15 − 18GHz (b), sowie für das Viertelstadion-Billiard
aus Abbildung 17 (c), [12], [3] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Teil eines Spektrums eines Niob-Mikrowellenresonators der Form eines Viertelstadions. Das Spektrum in der oberen Hälfte wurde bei Zimmertemperatur aufgenommen, jenes der unteren Hälfte bei Supraleitung. Im rechten oberen Eck sehen wir
den verwendeten Resonator, sowie die Positionen der drei gekoppelten Antennen, [10]
Geometrie und Wahl des Koordinatensystemes . . . . . . . . . . . . . . . . . . . .
Beispiel für Geometrie eines Streuprozesses von LI nach RE, φ < π . . . . . . . . .
Einteilung der Quadranten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
2
4
5
5
7
8
9
10
11
11
12
12
18
19
20
21
24
25
27
28
29
30
Literatur
[1] Wolfgang Demtroeder. Experimentalphysik 1 - Mechanik und Waerme. Springer Berlin,
Heidelberg, New York, Kaiserslautern, 2005.
[2] P. Cvitanovic et al.
Classical and
http://www.nbi.dk/ChaosBook, 2000.
Quantum
Chaos.
Free
download
at:
[3] J. Stein H.-J. Stoeckmann. ’Quantum’ Chaos in Billiards Studied by Microwave Absorption.
PHYSICAL REVIEW LETTERS, Volume 64, 2215, 1990.
[4] U. Stoffregen J. Stein, H.-J. Stoeckmann. Microwave Studies of Billiard Green Functions and
Propagators. PHYSICAL REVIEW LETTERS, Volume 75, 23, 1995.
[5] J.D. Jackson. Classical Electrodynamics. John Wiley & Sons, New York, 1962.
[6] Gottfried Wilhelm Leibniz. Philosophische Werke in vier Baenden. FELIX MEINER Verlag
Hamburg, 1996. Zusammenstellung von Ernst Cassirer, Band 2.
[7] Steven Soter. Am Rande des Chaos. Spektrum der Wissenschaft, Jan. 2008.
[8] H-J Stoeckmann. Quantum Chaos - an introduction. Cambridge University Press, Cambridge,
1999.
[9] J. Rubner T. Geisel, G. Radons. Kolmogorov-Arnol’d-Moser Barriers in the Quantum Dynamics of Chaotic Systems. PHYSICAL REVIEW LETTERS, Volume 57, 2883, 1986.
[10] D. Graef H.L. Harney H. Lengeler C.H. Lewenkopf C. Rangacharyulu A. Richter P.
Schardt H.A. Weidenmueller. Distribution of Eigenmodes in a Superconducting Stadium Billiard with Chaotic Dynamics. PHYSICAL REVIEW LETTERS, Volume 69, 1296, 1992.
[11] Eric Weisstein.
Standard Map.
Mathematica Notebook, download at
http://mathworld.wolfram.com/notebooks/DynamicalSystems/StandardMap.nb, 2006.
[12] F. Haake G. Lenz P. Seba J. Stein J.J. Stoeckmann K. Zyczkowski. Manifestation of wave
chaos in pseudointegrable microwave resonators. PHYSICAL REVIEW A, Volume 44, R6161,
1990.
38