Station 2, Aufgabe 1

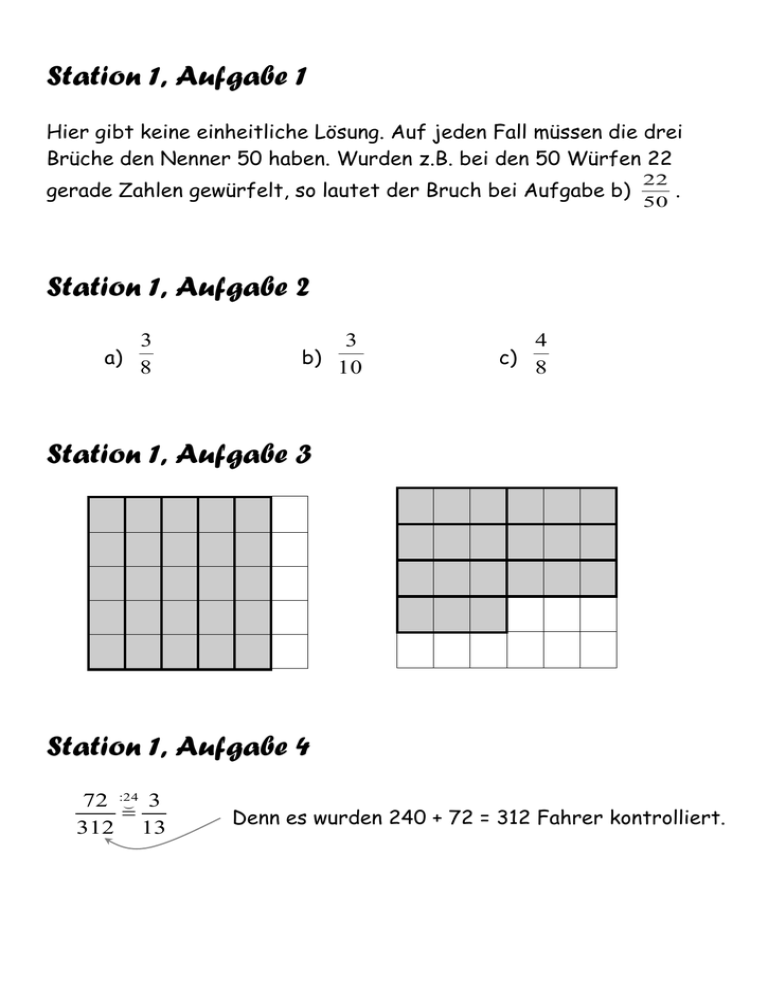
Station 1, Aufgabe 1
Hier gibt keine einheitliche Lösung. Auf jeden Fall müssen die drei
Brüche den Nenner 50 haben. Wurden z.B. bei den 50 Würfen 22
gerade Zahlen gewürfelt, so lautet der Bruch bei Aufgabe b)
22
50
.
Station 1, Aufgabe 2
3
a)
8
3
b)
10
4
c)
8
Station 1, Aufgabe 3
Station 1, Aufgabe 4
72 :24
 3

312 13
Denn es wurden 240 + 72 = 312 Fahrer kontrolliert.
Station 1, Aufgabe 5
Hier kann ich nur Beispiele für die richtige Lösung angeben.
a)
b)
c)
Station 1, Aufgabe 6
76 :4 19

 19%
weißer Anteil:
400 100
100 :4 25

 25%
pinkfarbener Anteil:
400 100
224 :4 56

 56%
blauer Anteil:
400 100
Station 1, Aufgabe 7
Das kleine Stück nach dem ersten Schnitt entspricht ⅓ der Pizza,
denn nur so kann es halb so groß wie das verbleibende Stück ( ⅔ ) sein.
Wenn man das Drittel nochmals in vier Teile zerlegt, muss man (um
identisch große Stückchen zu erhalten) das doppelt so große Gegenstück in 8 Teile zerlegen. Dadurch kommt man auf 12 gleiche Teile.
AWS: Eins so erzeugtes Stück entspricht
1
der Pizza.
12
Station 1, Aufgabe 8
Feld
Bruch
1
2
3
4
5
6
7
1
4
1
4
1
16
1
8
1
16
1
8
1
8
Station 2, Aufgabe 1
Rechenweg:
a)
3
von 560m = 240m
7
c) 20% von 140min =
b)
13
von 3 600kg = 1 170 kg
40
20
2
von 140min =
von 140min = 28 min
100
10
Station 2, Aufgabe 2
2
2
h=
von 60min = 40min
3
3
3
3
b)
g=
von 1000mg = 30mg
100
100
1
9
c) 2 Jahre = von 12 Monaten = 27 Monate
4
4
17
17
d)
km =
von 1000m = 340m
50
50
11
11
e)
€=
von 100 Cent = 44 Cent
25
25
a)
Station 2, Aufgabe 3
Das Ganze sind 3000g Pilze, der Wasser-Anteil betrug offenbar
2400g. Das ist der Bruchteil
2400 :30
 80

 80%.
3000 100
AWS: Der Wasseranteil der Pilze betrug 80%
Station 2, Aufgabe 4
4% von 5600 =
4
von 5600 = 224
100
AWS: Man muss mit etwa 224 Kinder-Unfällen rechnen.
Station 2, Aufgabe 5
Lösungsweg:
a)
7
von 144m sind 84m
12
b)
12
von 3000$ sind 360$
100
Station 2, Aufgabe 6
Übrig sind dann noch
3
von 136€ = 51€.
8
Station 2, Aufgabe 7
Frage: „Wie viele Autos fahren pro Tag durch den Ort?“
Lösung:
6
von
25
AWS:
Täglich fahren 1025 Autos durch Herrn Semmelmanns Dorf.
...............
= 246
Station 2, Aufgabe 8
9
a)
von 20s
12
gekürzt
3
von 20s = 15s
4
gekürzt 1
25
b) 25% von 12kg =
von 12kg 
von 12kg = 3kg
100
4
gekürzt
4
1
c) 4% von 1,25km =
von 1 250m 
von 1 250m = 50m
100
25

Station 2, Aufgabe 9
Die Lösung ist offensichtlich keine eindeutige Zahl, sondern ein
Bereich, der zwischen 2 Zahlen liegt.
1
von ................. = 8m  Gesamthöhe = 64m
8
1
untere Grenze:
von ................. = 8m  Gesamthöhe = 40m
5
obere Grenze:
AWS: Der gesamte Eisberg ist zwischen 40m und 64m hoch.
Station 2, Aufgabe 10
Knifflig an dieser Aufgabe ist, dass die 6 Tage Sonnentage angibt,
3
3
für den Regen steht. Wenn es an der Tage
5
5
2
regnete, war es also an
der Tage sonnig.
5
2
Die Rechnung lautet demzufolge:
von ................. = 6 Tage.
5
aber der Bruch
AWS: Der Urlaub dauerte 15 Tage.
Bruch der
Sonnentage
Anzahl der
Sonnentage
Station 2, Aufgabe 11
1
der Zeitung in 7 gleiche Teile zerlegt, so entspricht ei10
1
5
1
5
nes dieser Teile
der Gesamtzeitung.
von
sind demzufolge
.
7
70
10
70
1
7
Der Sportteil umfasste aber nicht nur
, sondern
der Zeitung.
10
10
Wenn man
5
70
:
35
5 5 5 5 5 5 5 35  1
sein muss. Der Sportteil umfasst also
+ + + + + + = 
70 70 70 70 70 70 70 70 2
Das heißt, dass der Fußball 7mal so groß, wie der berechnete Bruch
der Gesamtzeitung.
Aber nur
2
dieser Zeitungs-Hälfte befassen sich mit der 1.
5
Bundesliga. Zerlegt man diese Hälfte also in 5 gleiche Teile,
so befassen sich 2 davon mit der ersten Bundesliga. Das sind
2 :2 1
 der gesamten Zeitung.
offensichtlich dann
10 5
(Übrigens: Wenn wir dann die Multiplikation und Division von Brüchen kennen gelernt haben, ist diese Aufgabe ziemlich einfach.)
Station 3, Aufgabe 1
3 :3 1

a=
12 4
22 :2 11
5
 1
f=
12 6
6
8 :4 2
b= 
12 3
16 :4 4
1
d=  1
12 3
3
10 :2 5

c=
12 6
27 :3 9
1
 2
g=
12 4
4
31
7
2
h=
12
12
e=
19
7
1
12
12
34 :2 17
5

 2
i=
12 6
6
Station 3, Aufgabe 2
a)
4 20

7 35
b)
6 36

7 42
c)
16
4

12
3
d)
42 6

35 5
e)
1 500

2 1000
Station 3, Aufgabe 3
40 :40
1

200 5
c) 30 :30
1

60 2
27 :9 3

36 4
b) 16 :16 1

32 2
24 8: 3

16 2
a) 120 :40
3

80 2
150 :150
1

300 2
e) 18 :6 3

30 5
60 :20
3

100 5
d) 15 :5 3

50 10
60 :20
3
  3
20 1
f) 125 :125
1

1000 8
Station 3, Aufgabe 4
Lege die Folie auf Deinen Zahlenstrahl und überprüfe, ob er
deckungsgleich mit der Lösung ist!
Station 3, Aufgabe 5
14
6
3
= 1 oder besser 1
8
4
8
134
9
c)
=5
25
25
21 153
e) 3 =
44
44
a)
54
6
1
=2
oder besser 2
24
4
24
2 32
d) 6 =
5
5
12 892
446
f) 44 =
oder besser
20
10
20
b)
Station 3, Aufgabe 6
a)
114 :38
3

152 4
b)
176 :88
2

264 3
c)
198 :22
 9

242 11
d)
156 :39
4

195 5
Station 3, Aufgabe 7
143 11

a)
91 7
8 :4 2 9 18
 
b)
12 3 27
c) Es gibt 5 Möglichkeiten, da die 99 sechs Teiler hat, man aber mit 1 nicht
42 :3 14
126 :9 14
154 :11
462 :33
1386 :99
 14
 14
 14





kürzen kann.
oder
oder
oder
oder
99 33
99 11
99 9
99
3
99
1
Station 3, Aufgabe 8
Die Anzahl der Striche zwischen 0 und 1 muss ein gemeinsames
Vielfaches der Nenner aller 4 einzutragenden Brüche sein. Günstig ist
natürlich das kgV(5, 2, 8, 4 ) = 40.
Station 3, Aufgabe 9
So einen Bruch erhält man, indem man einen nicht weiter kürzbaren
Bruch wie z.B.
2
8
oder
mit einer Zahl erweitert, die genau 6 Teiler
3
11
hat („1“ und 5 andere Zahlen). Das sind z.B. 12, 18, 20, 30, 50, ...
(Zahlen, die 3 Primfaktoren haben, von denen einer doppelt vorkommt – z.B. 12 = 2  2  3)
1 12
 12
Der einfachste mit genau 5 Zahlen kürzbare Bruch ist demnach  .
2 24
Station 3, Aufgabe 10
So einen Bruch erhält man, indem man einen nicht weiter kürzbaren
Bruch wie z.B.
1
2
oder
mit einer Zahl erweitert, die genau 5 Teiler
3
15
hat. Das sind z.B. 16, 81, 625, 1296, ...
(Zahlen, die man als Quadrat einer Quadratzahl berechnen kann, z.B. 81=9²=(3²)² )
1 16
 16
Der einfachste mit genau 4 Zahlen kürzbare Bruch ist demnach  .
2 32
Station 4, Aufgabe 1
a)
1 5
+
2 2
=
=3
6
2
c) 6 -
8
= 12 - 8
5 10
10 10
e)
17 3 85 18
- = 12 10 60 60
g)
1 9 7
+ +
2 4 8
=
=
=
4 :2 2

10 5
1
2
3
5
7
9
13
14
1
4
1
4
7
20
19
36
19
28
4
11
3
22
13
55
41
99
87
154
3
8
1
8
9
40
29
72
31
56
= n.l.
d)
2 2
+
7 5
=
3
=
29
8
Station 4, Aufgabe 2
-
3 7
4 4
10 14 24
+ =
35 35 35
f) 1 2 - 98 =
67
60
4 18 7
+ +
8 8 8
b)
2
7
3
14
11
35
31
63
9
14
h)
67
10
99
165 98 67
- =
99 99 99
- 21 + 11 =
5
2
67 42 55
- +
10 10 10
=
80 :10
8

10 1
=8
Station 4, Aufgabe 3
847
7
7
120
120
95
24
372
120
27
12
8 :2 4

6 3
5
6
1
2
41
24
11
12
19
24
24 :8 3

40 5
5
12
3 :2 1

6 2
1
3
167
120
1
6
3
8
1
4
9
40
1
8
1
10
Es wäre auch möglich, schon in der untersten Zeile alle Brüche auf den
Hauptnenner zu bringen. Das kgV aus 2, 3, 6, 4, 8 und 10 ist 120.
Station 4, Aufgabe 4
1
3
1
8
5
24
7
24
Am besten, man
erweitert alle
Brüche auf den
Hauptnenner 24.
8
24
3
24
4
24
1
24
5
24
9
24
6
24
7
24
2
24
Summe: 15/24
Station 4, Aufgabe 5
2
11
5 18 :9 2
a)




27
27
27 27 3
3
5
1 20 :2 10
b)

 

14
7
2 14 7
c)
4
5
3 58 :2 29

 

9
12
4 36 18
d ) 10  3
e)
2
5
5 22 :2 11




3
6
18 18 9
f ) 14
g) 6
11
3 38 :2 19
 3 

12
4 12 6
h) 7
116
3

17
17
2
1 347
 10 
14
7
2
3
2 79
 3 
7
3 21
Station 4, Aufgabe 6
3
5
x
4
6
9
10
x

12
12
1
 x
12
7
15
x
12
8
62
45
x 

24
24
17
 x 
24
a)
13
5

42 14
13
15

x 
42
43
28 :14
 2

x 
42 3
c) x 
b) 2
Station 4, Aufgabe 7
7
3
a) Welche Zahl muss man von
7
5
x
3
27
63
5
x
27
27

b) Welche Zahl muss man zu
Zahlen
4
3
und
7
4 1
x 

10
3 2
1
2
7
10
subtrahieren, um

x
5
27
zu erhalten?
58
27
addieren, um die Differenz der
zu erhalten?

7
5
 x 
10
6
Station 4, Aufgabe 8

21
25
 x 
30
30

x 
4 :2 2

30 15
Als in der Grundschule erstmals multipliziert wurde, so wurde diese
Rechenoperation als Abkürzung einer Addition eingeführt. Man kann
eine Multiplikation also immer auch als Addition deuten. Zum Beispiel
bedeutet 4  11 nichts Anderes als 11 + 11 + 11 + 11.
a) 4 
3
3
3
3
3
12
bedeutet
+
+
+
=
11
11
11
11
11
11
2
2 2
2
2  2  ...  2
1040 :80
 39

b) 520 
bedeutet
+ +...+
=
=
= 39
80
80
1
80
80 80
80
Station 4, Aufgabe 9
a)
m 7 65
 
6 8 24
b)
m = 11
7 5 11
 
x 12 24
x=8
c)
9 9 3
 
s t 20
s=15 t=20
Station 5, Aufgabe 1
Antwortsatz (AWS):
1 1 1 8 7 3
    
4 2 8 5 2 10
=
Bernd muss 6
11
kg tragen.
40
10 20 5 64 140 12 251
11






6
40 40 40 40 40 40 40
40
Station 5, Aufgabe 2
1 3
1
1
1  1 1
3 4
5
2
4 3 6 3
17
80 45 72 90
  
 

=
=
3 4 5 2
60 60 60 60
60
17
AWS: Am Ende sind noch
t Kies auf dem Lastwagen.
60
=
Station 5, Aufgabe 3
43 + 61 + 12
4
2
=
3
19 13 5
 
4 2 3
=
57 78 20


12 12 12
=
155
11
 12
12
12
AWS: Laura ist dann 12 Jahre und 11 Monate alt.
Station 5, Aufgabe 4
61 + 61 + 82 + 82 4
4
3
3
5
6
25 25 26 25 5
 
 
4
4
3
3 6
75 75 104 104 10 348 :12
 29



 

 29
=
12 12 12 12 12 12
1
=
AWS: Der Zaum ist genau 29m lang.
Station 5, Aufgabe 5
20 1 1 1 8
   
100 3 5 3 15
7
des Leuchtturms aus. Demzufolge sind die 42m die restlichen
der
15
Fundament und Wasserabschnitt machen zusammen
Gesamthöhe.
Rechnung:
7
von
15
............
= 42m 
7
von 90m = 42m
15
AWS: Der Leuchtturm ist insgesamt 90m hoch.
Station 5, Aufgabe 6
Die größte Zuladung ist offenbar nach der 3. Station erreicht. Dann
80
45
72
107
4 3 6
t t t =
t t t =
t Kies geladen und wiegt
3 4 5
60
60
60
60
7 107
212 :4 53
t

t
t t.
insgesamt
=
4
60
60
15
hat er
53
t mit dem zulässigen Höchstgewicht von
15
1
1
t zu viel geladen hat.
3 t , so stellt man fest, dass der Wagen schon
30
2
39 :3 13
4
1
t  t aufladen
Am Anfang hätte der Spediteur also nur t  t =
3 30
30 10
Vergleicht man nun diese
dürfen.
AWS: Er hätte an der ersten Station
13
t aufladen dürfen.
10
Station 5, Aufgabe 7
5
kg
12
5
Traudel:
kg 12
19
Gustel:
kg +
60
Trude:
1
25  6 19
 kg
kg =
60
60
10
6
19  25  24
20 :20
1
5
 kg
kg - kg =
kg =
12
15
60
60 3
5
19
1
25  19  20
64 :4 16
 kg
Zusammen:
kg +
kg + kg =
kg =
60
3
60
60 15
12
AWS: Die Stiefmutter hatte 1
1
kg Linsen ausgekippt.
15
Station 5, Aufgabe 8
Ein Lösungsweg sieht so aus, dass man für die Zeiten von zwei Starterinnen
(am besten für die schnellste und die langsamste) je eine Variable wählt. Alle
anderen Laufzeiten lassen sich dann mit dieser Variable berechnen.
Pia: Mandy - 1
2
5
=
x+1
1
3
2
+
-1
4
5
10
1
4
1
Pauline: y - 1
10
Petra: x + 1
Manuela: Variable x
(kleinste Zahl)
Mareike: Variable y
(größte Zahl)
Mandy: Petra +
3
1
3
=x+1 +
4
10
10
Auswertung:
1
3
2
1
+
- 1 ) + (x + 1 ) + (y
4
5
4
10
1
3
2
1
=x+1 +
-1 +x+1 +y
4
5
4
10
3
7
5
5
= x+x+y+  +
+
5
4
10
4
6
28
25
25
= x+x+y+ 
+
+
20
20
20
 20
Gruppe P benötigte insgesamt (x + 1
Laut Assoziativgesetz darf man
die Klammern einfach weglassen.
Laut Kommutativgesetz darf man
die Zahlen beliebig umordnen.
= x+x+y+
1
)
10
1
-1
10
11 

10 
22 

20 
-1
6
s
20
1
3
+
)
4
10
3
1
=x+y+x+1 +
4
10
5
3
= x+x+y +   
 4 10 
31
= x+x+y +
s
20
Gruppe M benötigte insgesamt x + y + (x + 1
Vergleich : Für beide Gruppen steht nach dem Zusammenzählen der 3 Einzelzeiten
der Ausdruck x+x+y in der Gesamtzeit. Egal, wie groß dieses unbekannte
Zwischenergebnis nun tatsächlich ist, auf jeden Fall ergibt x+x+y in der ersten
Gruppe die gleiche Zeit wie in der zweiten Gruppe. Um herauszufinden, wer
schneller war, kann man diesen Teil weglassen und vergleicht dann nur noch:
Gruppe P: irgendwas +
6
s
20
Gruppe M: irgendwas +
31
s
20
Daran sieht man, dass die Gruppe P eine kürzere Gesamtzeit als Gruppe M hat.
AWS: Die Staffel mit Pia, Petra und Pauline gewinnt das Rennen.
Station 6, Aufgabe 1
3
33
31
31
31
64 :8 8
11

+
=
+
=
+
=
24 3
8
24
8
24
24
24
13
1
25 52 10
5
87 :3 29

b)
+
+ =
+
+
=
60 60 60
60 20
15
6
12
5
5
5
18
3 :3 1
c)
= 
18 18 18 18
18 6
a) 1
Das ist ein Ganzes, also die Zahl 1.
Station 6, Aufgabe 2
3  8 1
  
7  15 6 
a)
3
11

7
30
13
=
210
=

c)   2 
8
5
=
=
=

 
b)  4    
1
 2
41

=
6
43
=
6
3 7 6
11 
    1 
20  10  12 15 
84
7
134
 
20
10
60
42
134
252


60
60
60
:
4
76  19

60 15
3
4
7
7 1
 
3   12 4 
1
3
Station 6, Aufgabe 3
a)
2
3
5
4 - (1 + 2 )
4
12
5
22
21 29
= -( + )
5
12 12
22
25
=
5
6
7
=
30
b) 3
c)
3
3 1
7
- )+( - )
5 2
4
8
15
6
6
5
=(
- )+(
)
8
8
10
10
9
1
=
+
8
10
49
=
40
d) (
(1
4
3 5
- (2 + )
5
10 6
19
5
23
=
- (
+ )
6
5
10
19
94
=
5
30
20 :10
2

=
30 3
7 1
3
1
+ )+( - )
4
5
8 2
19
3
=
+
20
8
53
=
40
Station 6, Aufgabe 4
 15  8 7  1   22 4 
         
 33  9 11  3   33 11 
a) 
 15
=  33 

25
99
53
10

=
99
33
=
23
99
1
10
  
3
33
8  3 3
1 5   9 1 
 1    2      1  
32  16  4
8 2   4 2 
b)
1  3
= 4  116 

1  3
= 4  116 

=
1
1

4
16
3
8
3
8
=
3
16


3

4 
3
4




Station 6, Aufgabe 5
1
9
+
3
8
-
13
36
+
5
24
1
3
=
Station 6, Aufgabe 6
5
 17 7 
  -x=
24
 3 6
5
27
- x=
6
24
108
5
- x=
24
24
103
 x=
24
a) 
b)
11
 7 1
+x=   
10
 4 5
31
11
+x=
10
20
22
31
+x=
20
20
9
 x=
20
76 36
40 :5 8
4 8 8 4








c)
=
=
35 35
35 7
7 5 5 7
Station 6, Aufgabe 7
3
4
+
5 1
8- 2
-
1
8
-
1
12
=
2
3
=
1
3
-
2
9
+
4
3
-
7
9