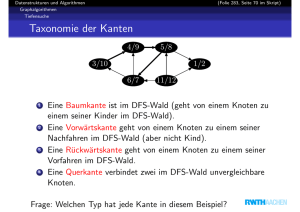
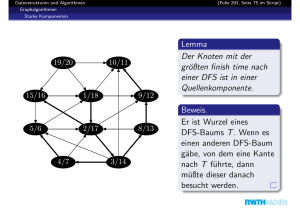
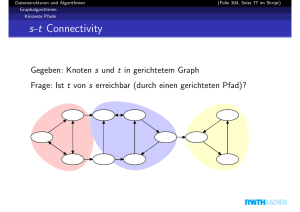
15. Elementare Graphalgorithmen

15. Elementare Graphalgorithmen
Graphen sind eine der wichtigste Modellierungskonzepte
der Informatik
Graphalgorithmen bilden die Grundlage vieler
Algorithmen in der Praxis
Zunächst kurze Wiederholung von Graphen.
Dann Darstellungen von Graphen
Schließlich einfache Graphalgorithmen:
Breiten- und Tiefensuche, Zusammenhangskomponenten,
Minimalspannende Bäume
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
1
Wiederholung Graphen – Gerichtete Graphen
Ein gerichteter Graph G ist ein Paar (V,E), wobei E
eine endliche Menge ist und E ⊆ V × V .
Elemente aus V heissen Knoten, Elemente aus E
heissen Kanten. Entsprechend heisst V Knotenmenge
und E heisst Kantenmenge von G.
Kanten sind geordnete Paare von Knoten. Kanten der
Form (u,u), u ∈ V , sind zugelassen und heissen
Schleifen.
Ist (u, v ) ∈ E , so sagen wir, dass die Kante von u nach
v führt. Sagen auch, dass u und v adjazent sind.
Müssen dann aber noch Richtung berücksichtigen.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
2
Illustration gerichteter Graph
V = {1,2,3,4,5,6}
E = {(1,2), (2,2), (2,4 ), (2,5 ), (4,1), (4,5 ), (5,4 ), (6,3 )}
SS 2006
1
2
3
4
5
6
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
3
Wiederholung Graphen – Ungerichtete Graphen
Ein ungerichteter Graph G ist ein Paar (V,E), wobei V
eine endliche Menge ist und E eine Menge von
2-elementigen Teilmengen von V ist.
Elemente aus V heissen Knoten, Elemente aus E
heissen Kanten. Entsprechend heisst V Knotenmenge
und E heisst Kantenmenge von G.
Formal haben Kanten die Form {u, v} mit u, v ∈ V .
Schreiben aber wir bei gerichteten Graphen Kanten
als Paare (u,v), unterscheiden dabei aber nicht
zwischen (u,v) und (v,u). Kanten der Form (u,u)
sind nicht zugelassen.
Ist (u, v ) ∈ E , so sagen wir, dass u und v adjazent sind.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
4
Illustration ungerichteter Graph
V = {1,2,3,4,5,6}
E = {(1,2), (1,5 ), (2,5 ), (6,3 )}
SS 2006
1
2
3
4
5
6
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
5
Darstellung von Graphen – Adjazenzlisten (1)
Die Adjazenzlisten-Darstellung eines Graphen
G=(V,E) besteht aus einem Array Adj von V Listen.
Pro Knoten u enthält Adj damit genau eine Liste
Adj[u].
Für alle u ∈ V enthält Adj[u] alle Knoten, die zu u
adjazent sind. Äquivalent, Adj[u] enthält alle Knoten
v, so dass (u, v ) ∈ E .
Knoten in Adj[u] sind in beliebiger Reihenfolge
gespeichert.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
6
Darstellung von Graphen – Adjazenzlisten (2)
Ist G gerichtet, so enthalten alle Listen in Adj
zusammen genau E Einträge.
Ist G ungerichete, so enthalten alle Listen in Adj
zusammen genau 2 E Einträge, denn eine Kante
(u,v) führt zu Eintrag v in Adj[u] und zu Eintrag
u in Adj[v ].
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
7
Darstellung von ungerichteten Graphen –
Adjazenzlisten
2
1
3
5
1
2
3
4
5
SS 2006
4
2
1
2
2
4
5
5
4
5
1
/
3
4
/
/
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
3
2
/
/
8
Darstellung von gerichteten Graphen –
Adjazenzlisten
1
2
3
4
5
6
1
2
3
4
5
6
SS 2006
2
5
6
2
4
6
4
/
5
/
/
/
/
/
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
9
Darstellung von Graphen – Adjazenzmatrix
Für die Adjazenzmatrix-Darstellung eines Graphen
nehmen wir an, dass die Knoten in V mit den
Zahlen von 1,K , V nummeriert sind.
Die Adjazenzmatrix von G ist dann eine V × V Matrix
A = (a ij ) mit
 1, falls (i, j ) ∈ E
a ij = 
.
sonst
0,
Ist G ein ungerichteter Graph, so ist die Matrix A
symmetrisch, d.h. für alle (i,j) gilt a ij = a ji .
Adjazenmatrix benötigt immer Speicher Θ ( V ).
SS 2006
2
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
10
Darstellung von ungerichteten Graphen Adjazenzmatrix
2
1
3
5
SS 2006
4
1
2
3
4
5
1
0
1
0
0
1
2
1
0
1
1
1
3
0
1
0
1
0
4
0
1
1
0
1
5
1
1
0
1
0
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
11
Darstellung von gerichteten Graphen - Adjazenzmatrix
SS 2006
1
2
3
4
5
6
1
2
3
4
5
6
1
0
1
0
1
0
0
2
0
0
0
0
1
0
3
0
0
0
0
1
1
4
0
1
0
0
0
0
5
0
0
0
1
0
0
6
0
0
0
0
0
1
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
12
Vergleich der Darstellungen
Die Adjazenzlisten-Darstellung ist besser, wenn E
2
viel kleiner ist als V , also bei dünn besetzten
Graphen.
Die Adjazenzmatrix-Darstellung ist besser, wenn E
2
etwa so groß ist wie V , also bei dicht besetzten
Graphen.
Mit Adjazenzmatrix kann bei je zwei Knoten u,v in
konstanter Zeit überprüft werden, ob (u, v ) ∈ E .
Die meisten Graphenalgorithmen in dieser Vorlesung
benutzen allerdings Adjazenzlisten.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
13
Breitensuche – Überblick (1)
Die Breitensuche ist ein Algorithmus, der die
Grundlage vieler Graphenalgorithmen bildet.
Ziel der Breitensuche ist es, bei einem Graphen
G=(V,E) und einer Quelle s ∈ V alle Knoten v ∈ V
zu finden, die von s aus erreichbar sind. Dabei ist
ein Knoten v von s aus erreichbar, wenn es in G
einen Pfad von s nach v gibt.
Die Breitensuche berechnet auch für alle Knoten v
den Abstand δ(s, v ) von s zu v. Dabei ist der Abstand
von s zu v die minimale Anzahl von Kanten auf einem
Pfad von s nach v.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
14
Breitensuche - Überblick (2)
Die Breitensuche bestimmt alle Knoten mit Abstand
< k vor den Knoten mit Abstand k. Daher der Name
Breitensuche.
Graphensuche funktioniert in gleicher Weise bei
gerichteten und ungerichteten Graphen.
Nehmen an, dass Eingabegraph in AdjazenzlistenDarstellung gegeben ist.
Sagen, dass ein Knoten entdeckt wird, wenn er das
erste Mal bei der Breitensuche angetroffen wird.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
15
Breitensuche - Überblick (3)
Wird v entdeckt, während Adj[u] nach neuen Knoten
durchsucht wird, so heisst u Vorgänger von v.
Knoten sind entweder weiss, grau oder schwarz.
Weiss sind alle noch nicht entdeckten Knoten.
Grau sind alle entdeckten Knoten, deren
Adjazenzliste noch nicht vollständig nach neuen
Knoten durchsucht wurde.
Schwarz sind alle anderen Knoten, d.h., schwarze
Knoten wurden bereits entdeckt und ihre Adjazenzliste wurde vollständig durchsucht.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
16
Pseudocode für Breitensuche
BFS(G, s )
1 for jeden Knoten u in V \ {s}
BFS benutzt Queue für graue Knoten.
do color [u] ← WHITE
2
3
d[u] ← ∞
color [u] := Feld für Farbe von v. Initial
4
π[u] ← NIL
WHITE.
5 color [s] ← GRAY
6 d[s] ← 0
d[u] := Feld für bislang berechneten
7 π[s] ← NIL
Abstand zu s. Initial ∞ .
8 Q←{ }
9 Enqueue (Q, s )
π[u] := Feld für Vorgänger. Initial NIL.
10 while Q ≠ { }
do u ← Dequeue (Q )
11
for v ∈ Adj[u]
12
13
do if color [v ] = WHITE
then color [v ] ← GRAY
14
15
d[v ] ← d[u] + 1
16
π[v ] ← u
17
Enqueue (Q, v )
18
color [u] ← BLACK
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
17
Illustration Breitensuche (1)
r
s
t
u
∞
0
∞
∞
Q
∞
∞
∞
∞
v
w
x
y
r
s
t
u
1
0
∞
∞
Q
∞
1
∞
∞
v
w
x
y
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
s
0
w r
1 1
18
Illustration Breitensuche (2)
SS 2006
r
s
t
u
1
0
∞
∞
∞
1
∞
∞
v
w
x
y
r
s
t
u
1
0
2
∞
∞
1
2
∞
v
w
x
y
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
Q
w r
1 1
Q
r t x
1 2 2
19
Illustration Breitensuche (3)
r
s
t
u
1
0
2
3
Q= ∅
SS 2006
2
1
2
3
v
w
x
y
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
20
Breitensuche – Laufzeitanalyse (1)
Zeilen 2-4 jeweils konstante Zeit. Werden V − 1 mal
durchlaufen. Damit Zeit O ( V ).
Zeilen 5-9 insgesamt konstante Zeit.
Jeder Knoten wird nur einmal in Queue eingefügt
und gelöscht.
Schleife in Zeilen 12 -17 wird für jeden Eintrag v in
Adjazenzlisten nur einmal durchlaufen.
Zeilen 12-17 pro Durchlauf Zeit O (1).
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
21
Breitensuche – Laufzeitanalyse (3)
Gesamtzeit für Durchläufe der Schleife in
Zeilen 11-18 insgesamt O (E ). Denn Gesamtgröße
aller Adjazenzlisten Θ(E ).
Satz 15.1: Bei Eingabe von Graph G=(V,E) und
Quelle s besitzt Algorithmus BFS Laufzeit
O (V + E )
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
22
Pseudocode für Breitensuche
BFS(G, s )
1 for jeden Knoten u in V \ {s}
BFS benutzt Queue für graue Knoten.
do color [u] ← WHITE
2
3
d[u] ← ∞
color [u] := Feld für Farbe von v. Initial
4
π[u] ← NIL
WHITE.
5 color [s] ← GRAY
6 d[s] ← 0
d[u] := Feld für bislang berechneten
7 π[s] ← NIL
Abstand zu s. Initial ∞ .
8 Q←{ }
9 Enqueue (Q, s )
π[u] := Feld für Vorgänger. Initial NIL.
10 while Q ≠ { }
do u ← Dequeue (Q )
11
for v ∈ Adj[u]
12
13
do if color [v ] = WHITE
then color [v ] ← GRAY
14
15
d[v ] ← d[u] + 1
16
π[v ] ← u
17
Enqueue (Q, v )
18
color [u] ← BLACK
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
23
Breitensuche – Erreichbarkeit, Kürzeste Pfade (1)
Lemma 15.2: Sei G= (V,E) ein gerichteter oder
ungerichteter Graph. Sei s ∈ V beliebig. Für
jede Kante (u, v ) ∈ E gilt
δ(s, v ) ≤ δ(s, u) + 1.
Lemma 15.3: Sei G=(V,E) ein gerichteter oder
ungerichteter Graph. Sei s ∈ V beliebig und s,G
Eingabe für BFS. Nach Beendigung von BFS gilt
für jeden Knoten v ∈ V
d[v ] ≥ δ(s, v ).
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
24
Breitensuche – Erreichbarkeit, Kürzeste Pfade (2)
Lemma 15.4: Die Queue Q enthalte zu einem beliebigen
Zeitpunkt des Ablaufs von BFS die Knoten (v 1,K, v r ),
wobei v 1 der Kopf head[Q] und v r das Ende tail[Q]
sei. Dann gilt
d[v r ] ≤ d[v1 ] + 1 und d[v i ] ≤ d[v i+1 ], i = 1,K, r - 1.
Korollar 15.5: Knoten v i werde während des Ablaufs
von BFS vor Knoten v j in die Queue Q eingefügt.
Zum Zeitpunkt, an dem v j in die Queue Q eingefügt
wird, gilt
d[v i ] ≤ d[v j ].
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
25
Breitensuche – Erreichbarkeit, Kürzeste Pfade (3)
Satz 15.6: Sei G=(V,E) ein gerichteter oder
ungerichteter Graph. Sei s ∈ V beliebig und s,G
Eingabe für BFS. Nach Beendigung von BFS gilt
für jeden Knoten v ∈ V
d[v ] = δ(s, v ).
Insbesondere sind die von s aus erreichbaren
Knoten v die Knoten mit d[v ] < ∞ .
Weiter ist für jeden von s aus erreichbaren Knoten
v ≠ s ein kürzester Pfad von s zu v gegeben durch
einen kürzesten Pfad von s zum Vorgänger π[v ]
von v erweitert um die Kante (π[v ], v ).
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
26
Breitensuchbäume
Betrachten nach BFS mit Eingabe G,s den Graphen
Gπ = (Vπ ,E π ) mit
Vπ = {v ∈ V | π[v ] ≠ NIL} ∪ {s}.
und
E π := {(π[v ], v ) | v ∈ Vπ \ {s}}.
Dann gilt
Satz 15.7: Gπ = (Vπ ,E π ) ist ein Baum. Vπ enthält genau
die von s aus erreichbaren Knoten in G. Für jeden
Knoten v ∈ Vπ ist der eindeutige Pfad von s zu v in
Gπ ein kürzester Pfad von s zu v in G.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
27