1 Der Goldene Schnitt

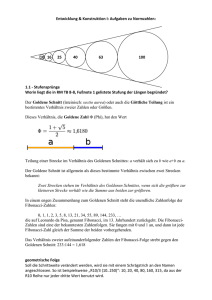
Goldener Schnitt
1
Der Goldene Schnitt
1.1 Das regelmäßige Zehneck
1
1
1.2
1.3
Ein anderer Name für den Goldenen Schnitt
Der Goldene Schnitt in Zahlen
4
6
1.4
1.5
1.6
Die Potenzen von  und 
Drei Beispiele
Quellen
8
10
11
Goldener Schnitt
1
1 Der Goldene Schnitt
Wir beginnen dieses Kapitel mit einigen Überlegungen zum regelmäßigen Zehneck. Wir bieten Ihnen die folgende Aufgabe zur Einstimmung an.
Aufgabe
– Zeichnen Sie in GeoGebra mit dem Werkzeug "Regelmäßiges Vieleck" ein regelmäßiges Zehneck.
– Ermitteln Sie den Mittelpunkt.
– Zeichnen Sie eines der zehn Mittelpunktsdreiecke ein und ermitteln
Sie dessen Winkel.
– Halbieren Sie einen der Basiswinkel und ermitteln Sie die neu entstandenen Winkel.
– Platzieren Sie in Ihrer Zeichnung die Buchstaben r und a für den
Umkreisradius und die Seitenlänge des Zehnecks.
Ein Klick auf das GeoGebra-Logo macht einen Lösungsvorschlag.
1.1 Das regelmäßige Zehneck
Wir haben aus einem regelmäßigen Zehneck eines seiner Mittelpunktsdreiecke herausgelöst und untersuchen im Folgenden dessen
Winkel und Seiten.
Abbildung 1: Ein regelmäßiges Zehneck mit Mittelpunktsdreieck
Abbildung 2: Winkel und Seitenverhältnisse im Mittelpunktsdreieck
Goldener Schnitt
2
Die linke Figur zeigt das Mittelpunktsdreieck und seine Winkel. Der
Winkel  hat den zehnten Teil von 360°, also 36°. Das führt zu
  (180   ) : 2  144 : 2  72 .  ist also gerade doppelt so groß
wie  .
In der mittleren Figur ist die Winkelhalbierende AT des linken Basiswinkels eingezeichnet. Sie zerlegt den Winkel  in zwei Winkel
der Größe  und das Mittelpunktsdreieck in zwei gleichschenklige
Dreiecke, von denen das kleinere zum ursprünglichen Dreieck ähnlich
ist.
In der rechten Figur haben wir den Umkreisradius des regelmäßigen
Zehnecks mit r und seine Seitenlänge mit a bezeichnet. Aus der Ähnlichkeit des gesamten Dreiecks und des blau einfärbten Teildreiecks
ergibt sich folgende Aussage: Der Schnittpunkt T der Winkelhalbierenden teilt den Umkreisradius r so in die Seite a und den Rest r  a ,
dass r : a  a : (r  a) gilt.
Ü
Definition
Wenn eine Strecke durch einen Punkt so geteilt wird, dass sich die
ganze Strecke zum größeren Teil verhält wie der größere Teil zum
kleineren Teil, so sagt man: Der Punkt teilt die Strecke im Goldenen
Schnitt.
Der größere Teil wird Major, der kleinere Teil Minor genannt.1
Die Gültigkeit der obigen Verhältnisgleichung r : a  a : (r  a) lässt
sich dann auch so wiedergeben:
Satz
Die Seite des regelmäßigen Zehnecks ist der Major des Umkreisradius.
Sie können mit Sicherheit ein gleichseitiges Dreieck, ebenso ein
Quadrat und auch ein regelmäßiges Sechseck mit Zirkel und Lineal
konstruieren. Durch Halbieren der Winkel können Sie weitere regelmäßige Vielecke herstellen. Wie aber sieht es mit einem regelmäßigen
Fünfeck aus?
Mit dem obigen Satz können Sie ein regelmäßiges Zehneck und, wenn
Sie jeden zweiten Punkt nehmen, ein regelmäßiges Fünfeck mit Zirkel
und Lineal konstruieren. Sei dazu a  AB eine Seite des Zehnecks.
Dann liefert die folgende Konstruktion eine Strecke AD , zu der die
gegebene Strecke AB der Major ist. Sie stellt also zur Seite a den
Radius r des Zehneckumkreises her.
1
maior (lat) - der größere; minor (lat) - der kleinere
Goldener Schnitt
3
Abbildung 3: Vom Major zur gesamten Strecke
Ein Klick auf das GeoGebra-Logo zeigt die Konstruktion schrittweise.
Ü
Den Nachweis, dass AB der Major zu AD ist, kann man mit dem
2
Tangentensatz2 führen. Mit ihm erhält man AC  AD  AB . Nach
Konstruktion ist CD genauso lang wie BE und mithin genauso lang
2
wie AB . Es folgt AC  AD  CD und hieraus die Verhältnisgleichung AD : CD  CD : AC . Der Punkt C teilt also die Strecke AD im
Goldenen Schnitt, CD ist der Major dieser Teilung und AB ist genauso lang wie CD .
Wenn nicht die Seite des Zehnecks gegeben und der Umkreisradius
gesucht ist, sondern umgekehrt der Radius des Umkreises gegeben ist
und die Seitenlänge zur Konstruktion des Zehnecks fehlt, dann führt
uns dieselbe Konstruktion mit Hilfe der Strahlensätze zum Ergebnis.
Sei hierzu r  AB der Umkreisradius des zu konstruierenden Zehnecks. Dann liefert die um den ersten Strahlensatz bereicherte Konstruktion die gesuchte Seitenlänge a  TB .
Abbildung 4: Von der gesamten Strecke zum Major
Denn die grünen Parallelen übertragen die Teilungsverhältnisse von
der roten auf die blaue Strecke. Der Punkt T teilt also die Strecke AB
im Goldenen Schnitt. Und TB ist als Major der Teilung die gesuchte
Seite des Zehnecks.
2
Für einen Kreis und einen Punkt P außerhalb des Kreises ist das Rechteck aus den
Sekantenabschnitten genauso groß wie das Quadrat über der Tangente. (s. Anhang)
Goldener Schnitt
4
1.2 Ein anderer Name für den Goldenen Schnitt
Wir kehren noch einmal zur Verhältnisgleichung zurück, die den Goldenen Schnitt definiert:
Ganzes : Major  Major : Minor
Umgangssprachlich heißt das: Was der Major für das Ganze ist, ist der
Minor für den Major. Oder mit anderen Worten: Wenn wir das Ganze
nach dem Goldenen Schnitt aufteilen, so ist der größere Teil der Major
und der kleinere der Minor. Wenn wir den Major seinerseits nach dem
Goldenen Schnitt aufteilen, so erhalten wir als größeren Teil den (alten) Minor und als kleineren Teil die Differenz aus (altem) Major und
(altem) Minor. Etwas salopp ausgedrückt heißt das: Der Major vom
Major ist der Minor. Und der Minor vom Major ist der Major verkürzt
um den Minor.
Im Bild sieht das so aus:
Abbildung 5: Stetige Teilung
Ein Klick auf das GeoGebra-Logo lässt diese Abbildung Schritt für
Schritt entstehen.
Der Goldene Schnitt setzt sich also in seinen Teilen fort. Statt vom
Goldenen Schnitt spricht man daher auch von Stetiger Teilung.
Aufgabe
Durchlaufen Sie die Abbildung 5 von unten nach oben und ergänzen
Sie sie um ein Element oberhalb der blauen Strecke. Mit anderen
Worten: Finden Sie die Strecke, aus der die blaue Strecke entstanden
ist.
Goldener Schnitt
5
Abbildung 6: Stetige Teilung - rückwärts
Ein Klick auf das GeoGebra-Logo lässt das oberste Element der Abbildung Schritt für Schritt entstehen.
Wie die Aufgabe und die obige Abbildung zeigen, müsste man nicht
nur von Stetigem Teilen sondern auch von Stetigem Verbinden von
Strecken reden; denn der Prozess entwickelt sich mit gleicher Systematik in beide Richtungen. Wir halten dies als Satz fest.
Satz
Verkürzt man den Major einer stetig geteilten Strecke um den Minor,
so entsteht wieder eine stetig geteilte Strecke.
Verlängert man eine stetig geteilte Strecke um ihren Major, so entsteht
wieder eine stetig geteilte Strecke.
Ü
Am Ende dieses Abschnitts wollen wir zeigen, dass dieser Satz sich
auch algebraisch beweisen lässt. Wir führen das hier für den zweiten
Teil aus. Den ersten haben wir als Übungsaufgabe formuliert.
Sei also M der Major einer im Goldenen Schnitt geteilten Strecke G.
Aus der Definitionsgleichung G : M  M : (G  M ) folgt dann:
Goldener Schnitt
6
G  (G  M )  M 2
G2  GM  M 2
G2  GM  M 2
G 2  (G  M )  M
(G  M ) : G  G : M
■
1.3 Der Goldene Schnitt in Zahlen
In diesem Abschnitt berechnen wir die Streckenverhältnisse beim
Goldenen Schnitt. Seien hierzu M und m der Major und der Minor der
stetig geteilten Strecke M  m .
Abbildung 7: Major und Minor einer stetig geteilten Strecke
Es gelte also
M m
M

M
.
(1)
m
Der Anteil des Majors an der gesamten Strecke wird üblicherweise
mit dem kleinen griechischen Buchstaben  (phi) bezeichnet. Wegen
(1) ist das nichts anderes als der Anteil des Minors am Major.
M
m


(2)
M m M
Das kleine  ist also eine Zahl kleiner als 1. Hingegen bezeichnet das
große  das Verhältnis des Majors zum Minor, was wieder wegen (1)
auch das Verhältnis der gesamten Strecke zum Major ist.
M M m


.
(3)
m
M
Das große  ist mithin größer als 1.
Aus (2) und (3) folgt:  und  sind Kehrwerte voneinander.
1
  oder     1

Aus (1) folgt weiter

M

M m
m
 1
M
m
M
 1
1

(4)
(5)
und hieraus mit (4)
  1  .
 ist also um genau 1 größer als  .
Aus (6) folgt wieder wegen (4)
(6)
Goldener Schnitt
7
1

 1  .
(7)
Aus (7) erhält man zunächst
1   2
und dann
 2    1
(8)
2    1 .
(9)
und aus (5) entsprechend
Die folgende Abbildung zeigt  und  als Schnittstellen der Graphen zu den Funktionen aus den Gleichungen (8) und (9).
Abbildung 8: φ und Φ als Schnittstellen von Funktionsgraphen
Man sieht, was auch (8) und (9) schon aussagen: Die Schnittpunkte
liegen symmetrisch zur y-Achse. Die Lösungen zu den Gleichungen
(8) und (9) unterscheiden sich nur durch das Vorzeichen.
Aus den quadratischen Gleichungen (8) und (9) kann man φ und Φ
berechnen. Man erhält aus (8):
 2   1  0
1
1
 1  0
2
4
4
1
1 5
2  2   
2
4 4
2  2  
2
1
2
1 1


      5 
2 2


1
1
1
1
   5     5
2
2
2
2
1 1
1 1
    5     5
2 2
2 2
Goldener Schnitt
8

2
1
  
Ü
Ü

 
5 1
1
2



5 1
Die negative Lösung entfällt. Mithin gilt
1
   5 1 .
2
Analog erhält man aus (9)
1
   5 1 .
2


(10)


(11)
Man kann jede rationale Zahl und, wie Sie der nebenstehenden Übung
entnehmen können, auch jede Wurzel aus einer natürlichen Zahl mit
Zirkel und Lineal konstruieren. Mithin sind auch  und  konstruierbar.
Abbildung 9 zeigt, wie man  mit wenig Aufwand konstruieren kann.
Abbildung 9: Konstruktion von φ
Ein Klick auf das GeoGebra-Logo zeigt die Konstruktion schrittweise.
Die Konstruktion von  erinnert deutlich an die Konstruktion des
Zehneckradius aus seiner Seite (Abbildung 3). Aber hier ist die Beweislage einfacher. Nach dem Satz des Pythagoras hat die grüne Hypotenuse die Länge
12  ( 12 ) 2 
verkürzt die Hypotenuse um
Ü
1
2
5
4
 12  5 . Der graue Kreisbogen
. Wir erhalten   12  5  12 .
■
Die Konstruktion von Φ verlagern wir in die nebenstehende Übung.
Dort finden Sie auch eine Konstruktion des Goldenen Schnittes, die
auf Euklid zurückgehen soll.
1.4 Die Potenzen von  und 
Die Gleichung (8) lässt sich auch so schreiben
( ) 2  ( )  1 .
(12)
Diese Gleichung hat dieselbe Form wie (9). Aus (9) und (12) entwickeln sich folgende Gleichungen für die Potenzen von  und  :
Goldener Schnitt
9
( ) 2  1  ( )  1
 2  1   1
3   2  
 (  1)  
( )3  2  ( )  1
 2  
  1 
 2   1
  3  
 (2    1)  
4
 2  2  
( ) 4  3  (  )  2
 2  (  1)  
 2  2  
 3   2
5
  3  
 (3    2)  
 3 2  2  
( )5  5  ( )  3
 3  (  1)  2  
 3   3  2  
 5  3
Wenn also  n  p    q mit p, q   gilt, so folgt:
 n 1  ( p    q)  
 p  2  q  
 p  (  1)  q  
 p  p  q
 ( p  q)    p
Entsprechend gilt ( ) n 1  ( p  q)  ( )  p .
Es gilt also für alle n
und
n  f n   f n1
wobei
 f n n
( )n  f n  ( )  f n1 ,
die Fibonacci-Folge ist.
Es folgt
n  ( )n  ( f n   f n1 )  ( f n ( )  f n1 )  f n  (  ( ))
oder
fn 
 n  ( ) n
  ( )
oder wegen (10) und (11)
fn 
 n  ( )n
5
.
Goldener Schnitt
10
1.5 Drei Beispiele
Ü
Wir geben zum Schluss drei geometrische Figuren an, in denen der
Goldene Schnitt auftaucht. Mit dem ersten Beispiel kehren wir an den
Anfang des Kapitels zurück. Wir bieten Ihnen dazu die nebenstehende
Übung an.
Abbildung 10: Das Mittelpunktsdreieck des Zehnecks im Fünfeck
Im regelmäßigen Fünfeck finden Sie das Mittelpunktsdreieck des regelmäßigen Zehnecks mit der Winkelhalbierenden des Basiswinkels
wieder. Die Überlegungen am Anfang des Kapitels besagen hier:
Satz
Die Diagonalen des regelmäßigen Fünfecks teilen einander im Goldenen Schnitt.
Aufgabe
Die nebenstehende GeoGebra-Datei gibt schrittweise einen Beweis
zum obigen Satz wieder, der nicht auf das regelmäßige Zehneck zurückgreift. Versehen Sie den Beweis mit Worten.
Die zweite geometrische Figur sieht so aus.
Abbildung 11: Der Inkreis des im Quadrat stehenden gleichschenkligen Dreiecks
Goldener Schnitt
11
Satz
Der Inkreis des im Quadrat stehenden gleichschenkligen Dreiecks teilt
die Höhe im Goldenen Schnitt.
Aufgabe
Abbildung 12: Eine Skizze zum Beweis
L
Wir bieten Ihnen diese Skizze zum Beweis an. Der kleine griechische
Buchstabe  (sprich: rho) bezeichnet, wie üblich, den Radius des
Inkreises.
Das dritte Beispiel präsentieren wir Ihnen in Form einer GeoGebraAufgabe.
L
Aufgabe
Sie sollen in der nebenstehenden GeoGebra-Datei den roten Punkt so
einrichten, dass aus dem Rechteck nach Augenmaß ein Quadrat wird.
Sie haben genau genug geguckt, wenn bei der Probe der rote Punkt im
grünen Kreis steckt. Erst dann wird Ihre Aufgabe eingeblendet.
1.6 Quellen
Lambacher-Schweizer, Mathematisches Unterrichswerk, Geometrie 1
und 2, Ernst Klett Verlag Stuttgart, 1966
Christian Strutz, Über die Eigenschaften der Zahlen Φ (Phi) und φ (phi)
unter http://www.schulphysik.de/strutz/Phiphineu.pdf
Als pdf-Datei Phi und phi - Christian Strutz.pdf
Paul Adam/Arnold Wyss, Platonische und Archimedische Körper,
ihre Sternformen und polaren Gebilde, Verlag Paul Haupt Bern, Verlag Freies Geistesleben Stuttgart, 1994