4.12 Zentrifugalkraft 4.12 Beobachtung im rotierenden
Werbung

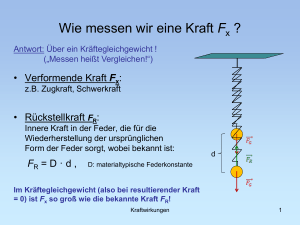
4.12 Zentrifugalkraft Beobachtung aus ruhendem System: Kreisbewegung der Kugel → Es wirkt eine Zentripetalkraft Im rotierenden Bezugsystem ist Kugel in Ruhe ! Im rotierenden Bezugsystem wirkt eine Scheinkraft, die Zentripetalkraft genau kompensiert Scheinkraft, die unabhängig von der Geschwindigkeit des Objektes im rotierenden Bezugssystem ist. 4.12 Beobachtung im rotierenden Bezugssystem Beschreibung eines rotierenden Massenpunktes in ruhendem Inertialsystem x-y-z Geschwindigkeit des Massenpunktes r r r vin = ωin × rin Beschreibung des Massenpunktes im mitrotierenden System x*-y*-z* (gleicher Ursprung, z=z*) Im System r r r r x*-y*-z* ist der Massenpunkt in Ruhe: v rot = 0 = vin − ωin × rin Es gilt allgemein die Transformation: r r r r r ∂ rrot r r − ω × rrot v rot = vin − ω × rin = ∂t Änderung des Ortsvektors bezogen auf statisches Koordinatensystem Änderung des Ortsvektors aufgrund der Variation der Basisvektoren im rotierenden Bezugssystem 1 4.12 Scheinkräfte in rotierendem Bezugssystem r ∂v rot r r r a rot = − ω × v rot ∂t r r r r r r = ain − 2(ω × v rot ) − ω × (ω × rrot ) Für Beschleunigung gilt die gleiche Beziehung Umformen liefert r a rot r r r r r r r r Frot = ma rot = Fin − 2m(ω × v rot ) − mω × (ω × rrot ) Corioliskraft Zentrifugalkraft Geschwindigkeitsabhängig Senkrecht zur Geschwindigkeit Ortsabhängig Parallel zum Ortsvektor 4.13 Foucaultsches Pendel r r Nach der Zeit ∆t: s = v ∆t r r r r v aC d = 12 aC ∆ t 2 r d r s mit Coriolisbeschleunigung: r r r aC = 2 ( v × ω ) = 2vω sin α Breite r d = 12 ( 2vω sin α Breite ) ∆ t 2 Ablenkwinkel: ∆ϕ ≈ d v ω sin α Breite ∆t 2 = s v ∆t Winkelgeschwindigkeit der Pendeldrehung: ωP = ∆ϕ = ω ⋅ sin α Breite ∆t 2 4.12 Corioliskraft und Wetter Luft strömt in ein Tiefdruckgebiet hinein Sicht auf Nordpol Sicht auf Nordpol FC v´ ohne Corioliskraft mit Corioliskraft r r r FC = −2 m (v ′ × ω ) 215 Zusammenfassung 23.11.2004 4. Punktmechanik 4.1 Kinematik eines Massenpunktes 4.2 Dynamik eines Massenpunktes 4.3 Kräfte 4.4 Impuls 4.5 Arbeit, Energie, Potential 4.6 Stöße 4.7 Drehimpuls und Drehmoment 4.8 Bewegung im Zentralpotential 4.9 Gravitation und Planetenbewegung 4.10 Himmelsmechanik 4.11 Wechselwirkungen und Kräfte 4.12 Bezugssysteme und Scheinkräfte Galileitransformation Scheinkräfte Versuch: Tintenpendel, Rotierende Kamera Beobachtung im rotierenden Bezugssystem Scheinkräfte in rotierendem Bezugssystem Zentrifugalkraft und Corioliskraft Corioliskraft und Wetter, „Bad Science“, Flussläufe 3 4.13 Prinzipien der Mechanik “It is increasingly clear that the symmetry group of nature is the deepest thing that we understand about nature today.” Steven Weinberg Erhaltungssätze (abgeschlossenes System ohne äußere Kräfte) Energieerhaltung Impulserhaltung Drehimpulserhaltung ∑ (E + E ) = konstant r ∑ p = konstant r ∑ L = konstant i pot i kin i i i i i Erhaltungssätze sind mit grundlegenden Symmetrien der „Natur“ verknüpft → Symmetrien in der Natur Die Verknüpfung von Erhaltungssätzen und Symmetrien geschieht durch das Noether-Theorem Zur Verknüpfung von Erhaltungssätzen und Symmetrien wird ein Extremalprinzip benötigt → Prinzip der kleinsten Wirkung 4.13 Das Prinzip der kleinsten Wirkung Was ist eine Wirkung ? t2 Definition: S = ∫ (E kin (t ) − E pot (t ))dt t1 Einheit: [S ] = Js Maß der Veränderung engl. action → Hollywood Es gibt eine kleinste Wirkung: Wirkungsquantum h = 1.054 ⋅ 10 −34 Js Wirkung beim freien Fall: Masse 1kg E pot = m g h Das Prinzip der kleinsten Wirkung Die Wirkung wird minimal für die tatsächliche Trajektorie 4 4.13 Impulserhaltung Kräftefreie Bewegung eines Teilchens von 1 nach 3 via 2 Symmetrie: Invarianz gegen Verschiebung a ∆a S = S123 − S1*2*3* ≡ 0 Wirkung: 1 ( x − x1 ) 1 ( x3 − x2 ) S123 = m 2 + m (t2 − t1 ) 2 (t3 − t2 ) 2 2 2 Festhalten von Punkt 1 und 3 Variation von Punkt 2 um dx2 Prinzip der kleinsten Wirkung: ∆a S = ∆S11* + ∆S 22* + ∆S 33* = ∆S11* + ∆S11* = − ∆S 33* ⇒ dS123 dS = − 123 dx1 dx3 dS123 =0 dx 2 dS123 a + ∆S 33* = ∆S11* + ∆S 33* dx2 (x − x1 ) = m (x3 − x2 ) ⇒ m 2 (t3 − t2 ) (t2 − t1 ) Impulserhaltung 4.13 Erhaltungssätze in der Physik Die Erhaltungssätze folgen aus den Symmetrien von Zeit und Raum, also ihrer Homogenität und Isotropie Erhaltungssätze sind Folgen von Invarianzeigenschaften Invarianz bei: Translationen im Raum Drehung im Raum Zeittranslationen → → → Impulserhaltung Drehimpulserhaltung Energieerhaltung Galileotransformation Lorentztransformation → → Schwerpunktsgeschwindigkeit Energie-Impulstensor Eichtransformationen → Ladungserhaltung (elektrisch, stark, schwach) 5 4.14 Zusammenfassung – Ausblick 4. Punktmechanik 4.1 Kinematik eines Massenpunktes 4.2 Dynamik eines Massenpunktes 4.3 Kräfte 4.4 Impuls 4.5 Arbeit, Energie, Potential 4.6 Stöße 4.7 Drehimpuls und Drehmoment 4.8 Bewegung im Zentralpotential 4.9 Gravitation und Planetenbewegung 4.10 Himmelsmechanik 4.11 Wechselwirkungen und Kräfte 4.12 Bezugssysteme und Scheinkräfte 4.13 Prinzipien der Mechanik 5. Spezielle Relativitätstheorie 6. Starre Körper Grenzen der Newtonschen Mechanik 7. Nichtstarre Körper 4.15 Weiterführende Literatur Brownsche Motoren R.D. Astumina, Scientific American July (2001) 57 Satelliten-Gravimetrie „GRACE Measurements of Mass Variability in the Earth System“ B. D. Tapley et al., Science 305 (2004) 503 Dreikörperproblem M.C. Gutzwiler, „Moon-Earth-Sun: The oldest three-body problem“, Rev.Mod. Phys. 70 (1998) 589 P. Hut, J.N. Bahcall, „Binary-single star scattering“ Astrophysical Journal, 268 (1983) 319 van der Waals Kräfte E. Arzt et al., „From micro to nano contacts in biological attachment devices“, Proc. Nat. Acad. Sci. 100 (2003) 10603 Corioliskraft: www.kidsnewsroom.org/elmer/infocentral/frameset/meterology/Bad/BadCoriolis.html www.physics.ohio-state.edu/~dvandom/Edu/index.html 6 4.16 „Reading Assignment“ Feynman Lectures „Das Prinzip der kleinsten Wirkung“ Band II, Kapitel 19, Seite 1 - 11 5 Spezielle Relativitätstheorie War jetz' des gestern oder im 3. Stock? Karl Valentin Zeit und Raum können nicht unabhängig voneinander betrachtet werden ! 7 5.1 Licht im 19. Jahrhundert Beschreibung der elektromagnetischen Felder durch vier Differentialgleichungen Maxwell Gleichungen: im Vakuum r r ∇E = ρ ε0 r r ∇B = 0 r r r ∂B ∇×E = − ∂t r r r r ∂E ∇ × B = µ 0 j + ε 0 ∂t James Clerk Maxwell (1831-1879) Maxwellgleichungen liefern elektromagnetische Wellen als Lösungen Konstante Ausbreitungsgeschwindigkeit c= 1 ε 0 µ0 Maxwells Erklärungshypthese: Der gesamte Raum ist mit Lichtäther gefüllt 5.1 Nachweis des „Äthers“ Messung der Fließgeschwindigkeit des Flusses vB+vF vF Beide Boote bewegen sich mit vB relativ zum Wasser BA = BC Bei A und B drehen die beiden Boote um und kehren nach B zurück Die Boote kommen nicht gleichzeitig in B an ! Zeitdifferenz erlaubt die Bestimmung der Fließgeschwindigkeit. ∆ t ≈ BC v F2 v B3 8 5.1 Michelson Morley Experiment (1887) r v Erde L t2 t1 Lichtquelle L Erwartung nach Äthertheorie ∆t ≈ 2 L v Erde c c2 Halbdurchlässiger Spiegel Interferenz Bei Drehung der Anordnung wurde keine Änderung des Interferenzmusters beobachtet ! 5.1 Einsteins Postulate 1. Konstanz der Lichtgeschwindigkeit Die Lichtgeschwindigkeit ist in allen Inertialsystemen gleich. 2. Relativitätsprinzip Alle Inertialsysteme sind gleichberechtigt für alle physikalischen Gesetze. Albert Einstein (1879-1955) Daraus folgt: Für einen Beobachter gleichzeitige Ereignisse sind nicht unbedingt für einen anderen Beobachter gleichzeitig Zeitdilatation (Schnell bewegte Uhren erscheinen langsamer zu gehen) Längenkontraktion (Schnell bewegte Maßstäbe erscheinen in Bewegungsrichtung verkürzt) 9 5.1 Zeitdilatation Zeitmessung durch die Flugzeit eines Lichtimpulses von Quelle zum Spiegel und wieder zurück Uhr1 und Uhr2 ruhen im Bezugsystem des Beobachter Uhr2 bewegt sich relativ zum Beobachter Lichtimpuls legt in Uhr2 aus Sicht des ruhenden Beobachters längeren → Uhr2 tickt langsamer Weg zurück Aus Sicht des bewegten Beobachters tickt Uhr1 langsamer ! vrel α c ∆ t2 = l = c cos α ∆ t1 v cos arcsin rel c = ∆ t1 1 v2 1 − rel2 c = γ ∆ t1 5.1 Minkowski Raum 1908 erkannte Minkowski, dass sich Raum und Zeit zu einer 4-dimensionalen „Raum-Zeit“ zusammenfassen lassen. Hermann Minkowski (1864-1909) Punkte im Lichtkegel haben einen definierten zeitlichen Bezug zu einem Punktereignis ! 10 5.1 Gleichzeitigkeit Beobachtung in einem Inertialsystem S: t Von einer Signalquelle (B) gehe ein Lichtsignal 0 A mit C0 A0 t0 B c aus, das in den gleichweit von B entfernten Beobachterstationen A, C zum x C Zeitpunkt t0 eintrifft. Jetzt bewegen sich A, B, C mit t t´ ∆x C1´ ∆t t2 Die Signale treffen in S zum Zeitpunkt t1 in A1´ und zu t2 in C1´ ein, also nicht mehr A1´ t1 0 A v = ∆ x / ∆ t. gleichzeitig. B x C In S´ müssen aber wegen der Invarianz von c die Signale gleichzeitig eintreffen. Gleichzeitigkeit ist vom Bezugssystem abhängig 5.2 Lorentztransformation v = vx Geschwindigkeit von S‘ gemessen in S, x = γ ( x ′ + v t ′ ), x ′ = γ ( x − vt ) v x′ t = γ t ′ + 2 , c mit γ (v ) = y′ = y, z′ = z. vx t′ = γ t − 2 c 1 v2 1− 2 c Für v<<c folgen die Galilei-Transformationen. Fazit: Die Newtonsche Mechanik ist der Grenzfall der allgemeineren relativistischen Mechanik für kleine Geschwindigkeiten. 11 Zusammenfassung 25.11.2004 5 Spezielle Relativitätstheorie 5.1 Licht im 19. Jahrhundert Nachweis des „Äthers“ Mitbewegung im Medium Michelson Morley Experiment (1887) 5.1 Einsteins Postulate (1905) Zeitdilatation Experimenteller Nachweis der Zeitdilatation Längenkontraktion Minkowski Raum Gleichzeitigkeit 5.2 Lorentztransformation (1899) 5.2 Addition von Geschwindigkeiten Ein Objekt habe die Geschwindigkeit u‘ in S´. u in S ? dx ′ u′ = dt ′ x = γ ( x ′ + vt ′) ⇒ dx = γ (dx ′ + v dt ′) Wie groß ist ⇒ dx = γ (u ′ + v ) dt ′ v u′ dt = γ 1 + 2 dt ′ c dx u ′ + v = u= dt 1 + v u ′ c2 analog u‘ und v nahe bei c die u niemals größer c sein kann. Man sieht, dass für Geschwindigkeit c: Grenzgeschwindigkeit 12 5.3 Relativistische Masse r Impulserhaltung gilt: u Schwerpunktsystem Bewegtes System (v = −u ) Nach Newton: m0 u ′ = 2 m0 u r −u inelastischer Stoß m(u ) r u′ m(u ) m(u ′) m0 (0) M0 0 Nach Elimination von M (u ) u´= 2u u2 1+ 2 c falsch! Abhilfe durch geschwindigkeitsabhängige Masse: Außerdem Massenerhaltung: r u m (u ′) + m0 = M (u ). M folgt: m (u ) = m0 u2 1− 2 c m (u ′) ⋅ u ′ = M (u ) ⋅ u . = γ ⋅ m0 . 5.3 E=mc2 Relativistische Masse: m0 m (u ) = u2 1− 2 c = γ ⋅ m0 . Entwickeln in Potenzreihe: − 1 2 u 2 2 1 u m(u ) = m0 1 − = m0 + m0 + L c 2 c 1 m(u ) ⋅ c 2 = m0 ⋅ c 2 + m0 u 2 + L 2 oder: Kinetische Energie Gesamtenergie = Ruheenergie + Anteile der Bewegungsenergie Daraus: E ges . = m(u ) ⋅ c0 = γ ⋅ m0 c0 2 2 13 5.4 Beschleunigung und Gravitation Einsteins Äquivalenzprinzip Es ist unmöglich zwischen den Effekten eine beschleunigten Bewegung und den Effekten des Gravitationsfeldes zu unterscheiden. → schwere und träge Masse 5.4 Experimenteller Nachweis Experimenteller Nachweis durch Sir A. Eddington (1919) Messung der Sternposition während und nach einer Sonnenfinsternis → Gravitative Blau- und Rotverschiebung von Licht 14 5.5 Weiterführende Literatur Einführungen Feynman Lectures „Der gekrümmte Raum“ Band II, Kapitel 42 www.theory.caltech.edu/people/patricia/st101.html www.astro.ucla.edu/~wright/relatvty.htm Geschichtliche Entwicklung www-groups.dcs.st-and.ac.uk/~history/HistTopics/General_relativity.html http://www.aip.org/history/einstein/ Nichteuklidische Geometrie "Flächenland" von Edwin A. Abbott, 1884 Franzbecker (Januar 1982) lieferbar bei amazon.de Gesamter Text im Netz: http://www.geom.uiuc.edu/~banchoff/Flatland/ 6 Mechanik starrer Körper Warum gibt es Atome ? 15 6.1 „Starre Körper“ Viele Massenpunkte, deren Relativkoordinaten zeitlich konstant sind. Bei hinreichend großer Zahl von Massenpunkten betrachtet man das Objekt als „starren Körper“ mit kontinuierlicher Massenverteilung. Durch die Festlegung der Relativkoordinaten werden die Freiheitsgrade des starren Körpers auf 6 reduziert: 3 Komponenten der Schwerpunktsgeschwindigkeit 3 Komponenten des Drehimpulses Bewegungen starrer Körper werden zerlegt in Translation und Rotation. 6.1 Schwerpunkt n Erinnerung: Schwerpunkt r rS = r ri ∑m i =1 n i ∑m i =1 massengewichtete Durchschnittskoordinate i Übergang zu kontinuierlicher Massenverteilung dM dV Massendichte ρ= Gesamtmasse r M = ∫ ρ (r ) dV K Schwerpunktsvektor r r r rS = ∫ dM M K Für die Translation des Schwerpunktes gelten die bisher gelernten Gesetze. 16 6.1 Schwerpunktsbewegung Der Schwerpunktsbewegung kann noch eine Rotation überlagert sein, wobei jedoch nur Drehachsen durch den Schwerpunkt möglich sind. Der Schwerpunkt bewegt sich auf einer Parabel (schiefer Wurf) Gleichzeitig wird eine Drehung ausgeführt Hochsprung Schwerpunkt bleibt unter der Latte 6.1 Trägheitsmoment und Rotationsenergie Trägheitsmoment eines Massenpunktes Ursprung in Bewegungsebene ! J = mr 2 Dies gilt für starren Körper nicht mehr ! Drehachse Verallgemeinerung für starren Körper: dM (= EkindM ) = 12 dM v 2 = 12 dM ωr × rr 2 E rot r r r r ω × r = ω r sin α = ω R r ω r dM R = r sin α α r r dM E rot = 12 dM ω 2 R 2 Rotationsenergie E rot = 1 2 2 r 1 ω ∫ R ρ (r ) dV = J ω 2 2 2 K 4243 1 =J Trägheitsmoment r J = ∫ ρ(r ) R 2 dV K 17 Zusammenfassung 26.11.2004 5 Spezielle Relativitätstheorie 5.1 Licht im 19. Jahrhundert 5.1 Einsteins Postulate (1905) 5.2 Lorentztransformation (1899) Addition von Geschwindigkeiten 5.3 Relativistische Masse 5.3 Relativistische Gesamtenergie Beispiel: Compton Streuung 5.4 Allgemeine Relativitätstheorie 6 Mechanik starrer Körper 6.1 „Starre Körper“ Versuch: Luftkissentisch Schwerpunkt Versuch: Bestimmung des Schwerpunktes Schwerpunktsbewegung Erinnerung: Kreisbewegung 6.2 Trägheitsmoment und Rotationsenergie Versuch: Fallmaschine Ein schönes Wochenende 18