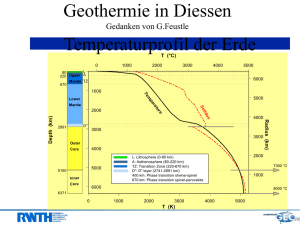
Einzelaufgabe aus der Aufgabensammlung zur Höheren
Werbung

Rolf Haftmann: Aufgabensammlung zur Höheren Mathematik mit ausführlichen Lösungen (Hinweise zu den Quellen für die Aufgaben) Aufgabe 19.4 Ein Produkt wird in unterschiedlichen Qualitäten von 2 Herstellern produziert. Hersteller 1 muss für die Herstellung von einem Stück 4 e, Hersteller 2 muss 5 e aufwenden. Die von den Preisen p1 für ein Stück des Herstellers 1 und p2 für ein Stück des Herstellers 2 abhängige Nachfrage betrage N1 (p1 , p2 ) = 40 000−20 000 p1 +10 000 p2 Stück für das Produkt des Herstellers 1 und N2 (p1 , p2 ) = 60 000+10 000 p1 −10 000 p2 Stück für das Produkt des Herstellers 2. ~ des Preises ~p a) Stellen Sie den Gewinn der beiden Hersteller als vektorwertige Funktion G dar! ~ p) und die Jacobimatrix G ~ ′ (~p) ! b) Berechnen Sie für p1 = 6, p2 = 9 den Gewinn G(~ c) Ermitteln Sie mithilfe der Jacobimatrix näherungsweise, wie sich der Gewinn entwickelt, wenn der Preis p1 von 6,00 auf 6,10 e erhöht und der Preis p2 gleichzeitig von 9,00 auf 8,90 e gesenkt wird! 6,1 ~ d) Geben Sie G exakt an! Vergleichen Sie die tatsächliche Gewinnentwicklung mit 8,9 der mithilfe der Jacobimatrix vorausgesagten! Lösung: a) vgl. Aufgabe 18.8: Gewinn = Umsatz−Kosten = Nachfrage ∗ (Preis−Aufwand): ~ p) = G1 (p1 , p2 ) = 10 000 (4−2p1 +p2 ) (p1 −4) G(~ G2 (p1 , p2 ) (6+ p1 −p2 ) (p2 −5) 6 2 ~ b) G = 10 000 9 12 Bei den angegebene Preisen erzielt der Hersteller 1 einen Gewinn von 20 000 e, während der Hersteller 2 einen Gewinn von 120 000 e erzielt. ~ p) stetig sind, ist die Funktion G(~ ~ p) total differenzierbar, Da alle partiellen Ableitungen von G(~ ihre Ableitung ist die Jacobimatrix, das ist die Matrix der partiellen Ableitungen: G −2(p −4)+(4−2p +p ) p −4 G 1 1 1 2 1 1 p p ′ 1 2 ~ (~p) = G = 10 000 p2 −5 −(p2 −5)+(6+p1 −p2 ) G2 p1 G2 p2 −4p1 +p2 +12 p1 −4 = 10 000 p2 −5 p1 −2p2 +11 −3 2 6 ′ ~ = 10 000 G 4 −1 9 ~ p) total differenzierbar ist, gilt ∆G ~ ≈ dG, ~ dG ~ ist dabei das vollständige Differenzial: c) Da G(~ dG G G dp dp dp +G G 1 1 1 1 2 1 1 1 p p ′ p p 2 1 2 1 ~= ~ (~p) d~p = dG =G = dG2 G2 p1 G2 p2 dp2 G2 p1 dp1 +G2 p2 dp2 (−4p1 +p2 +12) dp1 + (p1 −4) dp2 = 10 000 , (p2 −5) dp1 + (p1 −2p2 +11) dp2 dG 6 −3p +2p 1 1 2 ~= somit dG für ~p = = 10 000 . 9 dG2 4p1 − p2 −5000 −0,3−0,2 ∆p1 0,1 ~ . = ergibt sich schließlich dG=10 000 Für d~p=∆~p= = 5000 0,4+0,1 −0,1 ∆p2 Aufgabe 19.4 2 Der Gewinn des Herstellers 1 sinkt also um ca. 5000 e. Wegen dG1 = 10 000 (−3∆p1 +2∆p2 ) gehen davon 3000 e auf die eigene Preiserhöhung und 2000 e auf die Preissenkung des Konkurrenten zurück. Der Gewinn des Herstellers 2 steigt dagegen um ca. 5000 e, davon sind 1000 e durch die eigene Preissenkung verursacht, während 4000 e der Preiserhöhung des Konkurrenten zu verdanken sind. 14 700 6,1 ~ , nach den Preisänderungen erzielt der Hersteller 1 also nur noch = d) G 124 800 8,9 einen Gewinn von 14 700 e, während sich der des Hersteller 2 einen Gewinn auf 124 800 e erzielt. −5300 0,1 ~ . Das wurde mit dem vollständigen Differenzial re= Folglich ist ∆G 4800 −0,1 −5000 ~ ~ . lativ gut vorausgesagt: ∆G ≈ dG = 5000 Der Vorteil der Verwendung des vollständigen Differenzials liegt daran, dass die Auswirkungen (kleiner) Preisänderungen übersichtlich dargestellt werden. So ist sofort zu sehen, dass Preiserhöhungen des „Billigherstellers“ 1 viel stärker „bestraft“ werden (Multiplikation mit −30 000) als solche des Herstellers 2 (Multiplikation mit −10 000).