Mathematik - 8. Jahrgang: DREIECKSKONSTRUKTIONEN

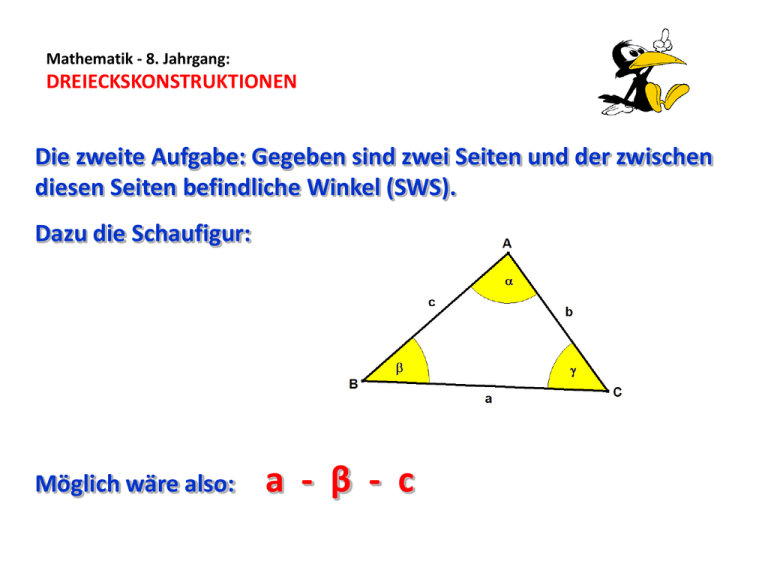
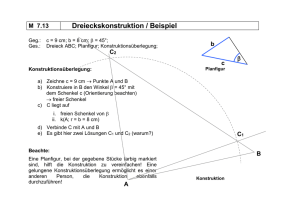
Mathematik - 8. Jahrgang:
DREIECKSKONSTRUKTIONEN
Die zweite Aufgabe: Gegeben sind zwei Seiten und der zwischen
diesen Seiten befindliche Winkel (SWS).
Dazu die Schaufigur:
Möglich wäre also:
a - β - c
Mathematik - 8. Jahrgang:
DREIECKSKONSTRUKTIONEN
Konstruiere ein Dreieck aus den Größen
a = 9,5 cm, β = 67° und c = 6,2 cm.
Die Planfigur zeigt sofort: Du kannst mit der Seite a oder c anfangen. Beide
Seiten haben den Punkt B, in dem dann der Winkel β gezeichnet werden
muss.
Wir fangen einfach mit a an!
Also: Gerade – freier Punkt – Abstand 9,5 mit dem Zirkel auftragen!
Mathematik - 8. Jahrgang:
DREIECKSKONSTRUKTIONEN
Hier kommt Schritt für Schritt die Konstruktion:
1. Gerade mit frei gewähltem Punkt B.
Mathematik - 8. Jahrgang:
DREIECKSKONSTRUKTIONEN
Hier kommt Schritt für Schritt die Konstruktion:
1. Gerade mit frei gewähltem Punkt B.
2. Antragen der Länge von a = 9,5 cm mit dem Zirkel.
Mathematik - 8. Jahrgang:
DREIECKSKONSTRUKTIONEN
Hier kommt Schritt für Schritt die Konstruktion:
1. Gerade mit frei gewähltem Punkt B.
2. Antragen der Länge von a = 9,5 cm mit dem Zirkel.
3. Konstruktion von β = 67° im Punkt B (math. einfach: in B) mit
dem Geo-Dreieck.
Mathematik - 8. Jahrgang:
DREIECKSKONSTRUKTIONEN
Hier kommt Schritt für Schritt die Konstruktion:
1. Gerade mit frei gewähltem Punkt B.
2. Antragen der Länge von a = 9,5 cm mit dem Zirkel.
3. Konstruktion von β = 67° im Punkt B (math. einfach: in B) mit
dem Geo-Dreieck.
4. Auf dem freien Schenkel c = 6,2 cm abtragen (Zirkel). Punkt A.
Mathematik - 8. Jahrgang:
DREIECKSKONSTRUKTIONEN
Hier kommt Schritt für Schritt die Konstruktion:
1. Gerade mit frei gewähltem Punkt B.
2. Antragen der Länge von a = 9,5 cm mit dem Zirkel.
3. Konstruktion von β = 67° im Punkt B (math. einfach: in B) mit
dem Geo-Dreieck.
4. Auf dem freien Schenkel c = 6,2 cm abtragen (Zirkel). Punkt A.
5. Kosmetik, Radieren, Farbe – FERTIG !