jew
Werbung
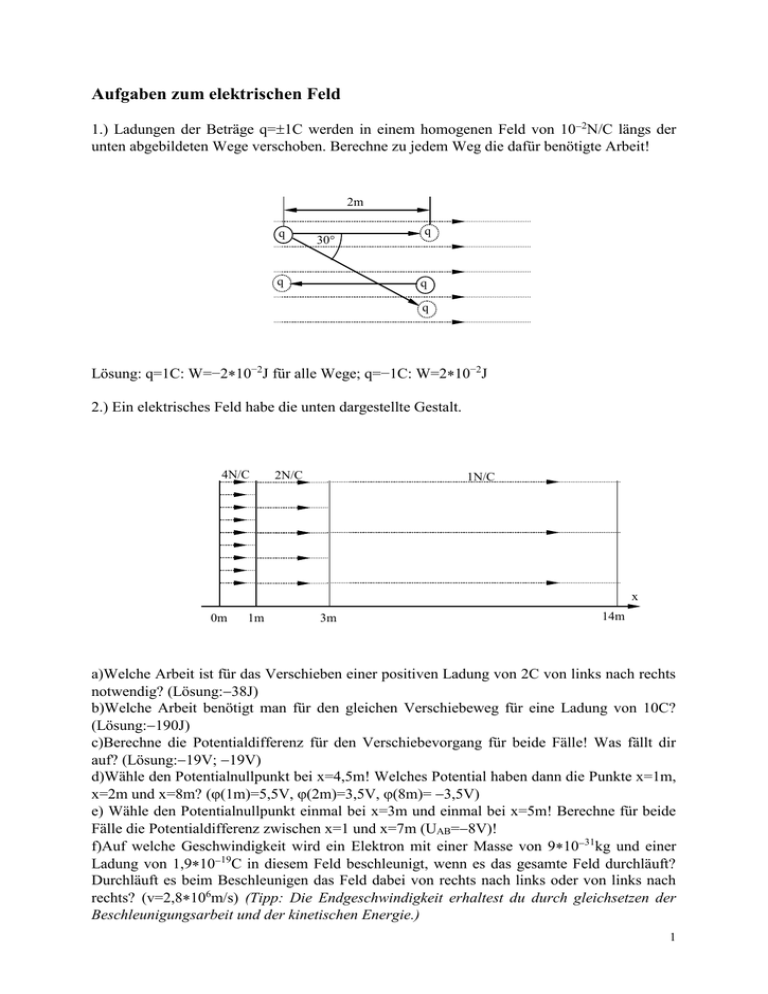
Aufgaben zum elektrischen Feld 1.) Ladungen der Beträge q=1C werden in einem homogenen Feld von 102N/C längs der unten abgebildeten Wege verschoben. Berechne zu jedem Weg die dafür benötigte Arbeit! 2m q 30 q q q q Lösung: q=1C: W=−210−2J für alle Wege; q=−1C: W=210−2J 2.) Ein elektrisches Feld habe die unten dargestellte Gestalt. 4N/C 2N/C 1N/C x 0m 1m 3m 14m a)Welche Arbeit ist für das Verschieben einer positiven Ladung von 2C von links nach rechts notwendig? (Lösung:38J) b)Welche Arbeit benötigt man für den gleichen Verschiebeweg für eine Ladung von 10C? (Lösung:190J) c)Berechne die Potentialdifferenz für den Verschiebevorgang für beide Fälle! Was fällt dir auf? (Lösung:19V; 19V) d)Wähle den Potentialnullpunkt bei x=4,5m! Welches Potential haben dann die Punkte x=1m, x=2m und x=8m? ((1m)=5,5V, (2m)=3,5V, (8m)= 3,5V) e) Wähle den Potentialnullpunkt einmal bei x=3m und einmal bei x=5m! Berechne für beide Fälle die Potentialdifferenz zwischen x=1 und x=7m (UAB=8V)! f)Auf welche Geschwindigkeit wird ein Elektron mit einer Masse von 91031kg und einer Ladung von 1,91019C in diesem Feld beschleunigt, wenn es das gesamte Feld durchläuft? Durchläuft es beim Beschleunigen das Feld dabei von rechts nach links oder von links nach rechts? (v=2,8106m/s) (Tipp: Die Endgeschwindigkeit erhaltest du durch gleichsetzen der Beschleunigungsarbeit und der kinetischen Energie.) 1 3.) Auf welche Geschwindigkeit werden Elektronen in einer Fernsehbildröhre beschleunigt, wenn die Anodenspannung 10kV beträgt? (e=1,61019C, m=9,11031kg) (Lösung: v=6107m/s!!) 4.) Berechne die Formel für den Gesamtwiderstand von 2 in serie und 3 parallel geschaltete Widerstände! R1 R2 R3 (Lösungen: RS=R1+R2; RP ) R1 R2 R1 R3 R2 R3 5.) Um hohe Stromwerte mit Amperemetern messen zu können, baut man sogenannte Messbereichserweiterungsschaltungen. Sehr niederohmige parallel zum eigentlichen Amperemeter geschaltete Widerstände nehmen dann den größten Teil des Stromes auf. Der umgerechnete Wert wird dann vom Amperemeter angezeigt. I IA IN A R Der höchstzulässige Strom durch das Amperemeter soll 3mA betragen. Sein Innenwiderstand sei 20. a) Welcher Nebenwiderstand erlaubt eine Strommessung von 7,5A? (Lösung: R=8,0032m) b) Welchen Messbereich hat das Amperemeter, wenn der Nebenwiderstand R=0,004 beträgt? (Lösung: I=15,003A) 6.) Berechne den Gesamtwiderstand folgender Schaltungen und die Ströme in den einzelnen Zweigen! (Lösungen: (5/3), (11/5), 0,86, (22/15)) 1 10V R2 = 3 10V R2 = 1 1 10V = 1 R2 1 1 1 10V R2 = 1 4 2 7.) Jeder der unten abgebildeten Widerstände hat den Wert 5. Die Eingangsspannung beträgt 10V. Berechne den Gesamtwiderstand und die Teilspannung Ux! (Lösung: Ux=4V, RG=3,125) Ux U 8.) Berechne in den folgenden Schaltungen die gesuchten Bestimmungsstücke! Linke Schaltung: UAB vor und nach dem Schalterschluss. (Lösung: vorher: 5V; nachher: 0V) Rechte Schaltung: Ströme durch die Widerstände (Lösung: I1=0A, I3=3,3333A, I2=5A) A 1 3 R R2 B 10V = 10V 1 = 1 9.) Wie lautet der Zusammenhang zwischen der Einheit der elektrischen Arbeit Ws=J und der Einheit kWh? (Lösung: 1kWh= 3,6106Ws) Berechne für das Beispiel 8.) die Leistungen, die an den Verbrauchern abgeführt werden! (Lösungen Linke Schaltung: vor Schalterschluss: P1=25W; nach Schalterschluss: P1=100W. Rechte Schaltung: P3=33,3333W, P2=50W, P1=0W) 10.) Ein ohmscher Verbraucher hat eine Nennleistung von 250W. Er wird allerdings mit einer Nennspannung von 25 V betrieben. Welchen Widerstand müsste man in serie dazuschalten, damit er mit Netzspannung (230V) betrieben werden kann? (Lösung: R=20,5) 11.) Eine quadratische Platte hat einen Widerstand von 10Ω. a) Die Platte wird nun in der Hälfte auseinandergeschnitten. Für die folgende Aufgabenstellung soll eine Plattenhälfte verwendet werden. i) Lege nun an zwei Seiten der Platte eine Spannung an, so dass der elektrische Widerstand der Plattenhälfte R1=5Ω beträgt! (Skizze) Begründe, warum die Teilplatte den halben Widerstand hat! ii) Lege nun an zwei Seiten der Platte eine Spannung an, so dass der elektrische Widerstand der Plattenhälfte R2=20Ω beträgt! (Skizze) Begründe, warum die Teilplatte den doppelten Widerstand hat! b) Nun werden beide Platten zusammengeschalten. Zeichne Schaltpläne aller 6 Möglichkeiten und berechne die Ersatzwiderstände aller 6 Schaltungsvarianten! 3 c) Die Platten werden nun nicht halbseitig, sondern im Verhältnis x/y geteilt und die Platte der Breite x verwendet. Die Anschlüsse werden nun so gelegt, dass die Länge des Leiters der ursprünglichen Seitenlänge a des Quadrates entspricht. Nun ist das Verhältnis U/I=R, also U/I=10Ω. Zeige über die Überlegung, wie groß die Stromstärke sein muss, wenn die Breitseite nunmehr a x statt a beträgt, dass der elektrische Widerstand R x R sein muss. x d) Berechne die Gesamtwiderstände aller 6 Varianten der Zusammenschaltung der Plattenteile (ähnlich wie in Beispiel b)! Berechne zusätzlich den Spannungsabfall am Widerstand mit der Breitseitenlänge x in der Serienschaltung, wenn die angelegte Spannung 5V beträgt! 12.) Wenn man in einen Leiter eine Kerbe ritzt, dann brennt er bei Überlastung vorwiegend an der Kerbung durch. Erkläre mittels Serienschaltung von Widerständen, warum dies so ist! 13.) Abhandlung über einen Startvorgang Bei einem Auto wurde vergessen, das Licht auszuschalten. Als Konsequenz steigt der sogenannte Innenwiderstand. Die sogenannte Quellenspannung von 12V bleibt erhalten, während an den äußeren Polen die Spannung bei Belastung sinkt. Die Spannung zwischen den äußeren Polen nennt man Klemmenspannung. Im sogenannten Leerlaufbetrieb (unbelasteter Zustand) beträgt die Klemmenspannung nach wie vor 12V. a) Zeichne ein Ersatzschaltbild der Batterie, welches die äußeren Pole, den Innenwiderstand und die Quellenspannungsquelle wiedergibt. b) Bestimme die Stromstärke durch den Starter, wenn der Widerstand des Starters 0,08Ω und der Innenwiderstand der Batterie 0,1Ω beträgt? c) Wie groß ist in der Situation b) die Klemmenspannung? d) Nun wird Starthilfe gegeben. Eine zweite Batterie wird zu Hilfe genommen. Zeichne das Ersatzschaltbild auf und vernachlässige dabei die Kabelwiderstände! e) Die Quellenspannung der helfenden Batterie betrage ebenfalls 12V, der Innenwiderstand sei aber nur 0,01Ω groß. Welcher Strom fließt nun durch den Anlasser? 14.) Unten sind die Kennlinien zweier Glühbirnen abgebildet. Die beiden Glühbirnen sind in Serie geschaltet. An der Glühbirne 1 fällt eine Spannung von 3V ab. Wie groß ist die Quellenspannung und der Widerstand der Glühbirne 2 bei dieser Stromstärke? (Lösung: U=9V, R=35,3) I[A] Glühbirne 1 I[A] Glühbirne 2 I [ A ] 0,2 0,2 U[V] 10 U[V] 20 4 15.) An einem Draht mit dem Durchmesser d liegt eine Spannung U=15V. Als Ergebnis fließt ein Strom von 1A. Nun wird ein Draht aus dem gleichen Material an den anderen Draht gelötet. Dieser hat die gleiche Länge aber den halben Durchmesser. a) Wie groß sind nun die Spannungen, die an den Drahtteilen abfallen? b) Wie groß sind die Leistungen, die an den einzelnen Drahtteilen verbraucht werden? Weitere Erklärungen liefern folgende Links http://www.leifiphysik.de/themenbereiche/komplexere-schaltkreise Weitere Aufgaben findet ihr hier! http://www.leifiphysik.de/themenbereiche/komplexere-schaltkreise/aufgaben# Zweite Lampe im Stromkreis, Leuchtdiode, Schalterstellungen, Messbereichserweiterung beim Spannungsmesser, Tankanzeige. 5











