Aufgabe 5.1: Vorüberlegung: Der Stab 3 ist ein

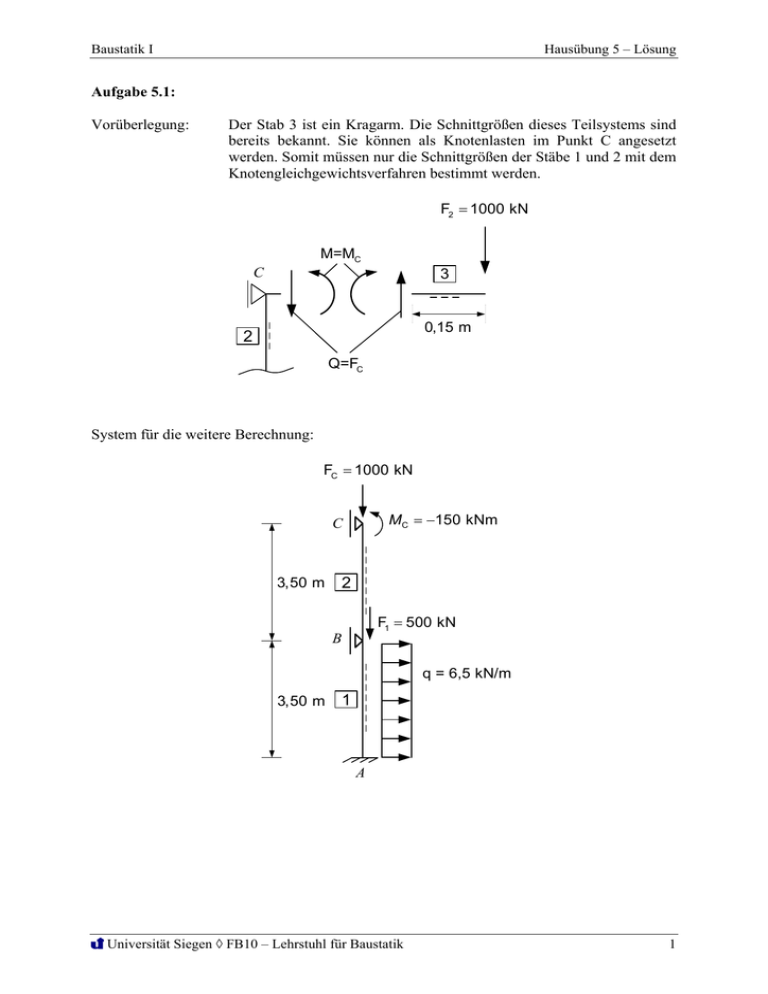
Baustatik I
Hausübung 5 – Lösung
Aufgabe 5.1:
Vorüberlegung:
Der Stab 3 ist ein Kragarm. Die Schnittgrößen dieses Teilsystems sind
bereits bekannt. Sie können als Knotenlasten im Punkt C angesetzt
werden. Somit müssen nur die Schnittgrößen der Stäbe 1 und 2 mit dem
Knotengleichgewichtsverfahren bestimmt werden.
F2  1000 kN
M=MC
C
3
0,15 m
2
Q=FC
System für die weitere Berechnung:
FC  1000 kN
MC  150 kNm
C
3,50 m
2
F1  500 kN
B
q = 6,5 kN/m
3,50 m
1
A
Universität Siegen  FB10 – Lehrstuhl für Baustatik
1
Baustatik I
Hausübung 5 – Lösung
Grad der geometrischen Unbestimmtheit
D2
2
GE I
D1
1
ng = nv  n  0  2  2
GE I
Für Stab 2 kann ebenfalls Grundelement IIa verwendet werden, damit reduziert sich die
Berechnung auf eine unbekannte Verdrehung am Lager B. In diesem Fall muss das
Einzelmoment im Punkt C allerdings als Stablast aufgefasst werden und über die
Stabendkraftgrößen und nicht über die Knotenlast berücksichtigt werden.
Lastzustand (Nullzustand)
Fc  1000 kN
Mc = -150 kNm
K 02
0
0
F1  500 kN
q  l2

12
K10
q = 6,5 kN/m
q  l2
12
Universität Siegen  FB10 – Lehrstuhl für Baustatik
2
Baustatik I
Hausübung 5 – Lösung
Knotengleichgewicht:
Knoten 2:
 M : -K10 -
q  l2
6,5  3,52
= 0  K10 = = -6,64
12
12
Knoten 3:
M :
-K 02 +150 = 0  K 02 = 150
Einheitszustände
EZ1
K
1
2
K
1
1
2 EI2
l2
4 EI2
l2
4 EI1
l1
2 EI1
l1
Knoten 2:
M :
-K11 +
4 EI1
4 EI2
+
=0
l1
l2
 K11 =
4 EIc
4 EIc
16
+
=
EIc
3,5
3,5
7
2 EI2
=0
l2
 K12 =
4
EIc
7
Knoten 2:
M :
-K12 +
Universität Siegen  FB10 – Lehrstuhl für Baustatik
3
Baustatik I
Hausübung 5 – Lösung
EZ2
K 22
4 EI2
l2
2 EI2
l2
K 21
0
0
Knoten 2:
M :
-K12 +
2 EI2
=0
l2
 K12 =
4
EIc
7
4 EI2
=0
l2
 K 22 =
8
EIc
7
Knoten 2:
M :
-K 22 +
Bedingungsgleichung
16
EIc  D1
7
4
EIc  D1
7
4
EIc  D2
7
8
 EIc  D2
7
+
40,818 
1
EIc
 D2 = -151,659 
1
EIc
 D1 =
Universität Siegen  FB10 – Lehrstuhl für Baustatik
= 6,64
= -150
4
Baustatik I
Hausübung 5 – Lösung
Rückrechnung zu den Schnittgrößen
Stab 1
M1i
=
2 EI1
q  l2
 D1
+
12
l1
=6,64 +
2 EIc
1
 40,818 
3,5
EIc
= 29,96 kNm (VK II)  -29,96 kNm (VK I)
M1k
=-
4 EI1
q  l2
 D1
+
12
l1
=-6,64 +
4 EIc
1
 40,818 
3,5
EIc
= 40,01 kNm (VK II = VK I)
Stab 2
M2i
M2k
= 0
+
2 EI2
4 EI1
 D2
 D1 
l2
l1
= 0
+
4 EIc
1
 40,818 
3,5
EIc

2 EIc
1
 (-151,659) 
3,5
EIc
= -40,01 kNm (VK II)
 40,01 kNm (VK I)
2 EI1
4 EI2
= 0 +
 D1 
 D2
l1
l2
= 0 +
4 EIc
1 2 EIc
1
 40,818 

 (-151,659) 
3,5
EIc
3,5
EIc
= -150 kNm (VK II = VK I)
Universität Siegen  FB10 – Lehrstuhl für Baustatik
5
Baustatik I
Hausübung 5 – Lösung
Schnittgrößenverläufe
M [kNm]
Q [kN]
-150

-150


1000
-54,29 

8,62
40,01

-29,96


31,37
N [kN]
-1000
-1500
:
A V = 1500
:
A H = -31,37 kN

kN
MA = -29,96 kNm
:
BH = 8,62 - (-54,29) = 62,91 kN
:
CH = -54,29 kN

Universität Siegen  FB10 – Lehrstuhl für Baustatik
6