4 slides per sheet

Ziele des Kapitels
Kapitel 11:
Binäre Kanäle

Binäre Kanäle und ihre Eigenschaften
Gedächtnisfreie Kanäle
Codierung als Schätzung und Schätzverfahren
Kanalkapazität
Shannon'sches Kanalcodierungstheorem
Kanalcodierung I
Informationstheorie
2
Copyright M. Gross, ETH Zürich 2005, 2006
Grundlegendes

Übertragungsmodell
Reale Übertragungskanäle sind meist
fehlerbehaftet
„Rohe“ Bits oft als analoge Signale
(Spannungspegel) empfangen
Störungen führen zu Fehlklassifikationen
Redundante Codierung ermöglicht eine gewisse
Fehlertoleranz
Quellencodierer versuchen, einen fehlerfreien
Input optimal zu codieren
Kanalcodierer bringen gezielt Redundanz
(Prüfbits) in den Code ein
Kanalcodierung I
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006

Wir betrachten wieder das folgende
Übertragungsmodell
Störung
Quelle X
Quellencodierer
Kanalcodierer
Kanal
Senke Y
3
Kanalcodierung I
Quellendecodierer
Kanaldecodierer
Informationstheorie
4
Copyright M. Gross, ETH Zürich 2005, 2006
1
Grundlegendes

BK Modell
Eine Variante ist, Fehler zu detektieren und das
Zeichen nochmals zu übertragen
Sinnvoll bei kleinen Fehlerwahrscheinlichkeiten
Anspruchsvollere Variante: Fehler detektieren und
beim Empfänger korrigieren
Dazu müssen Fehlerkorrekturverfahren entwickelt
werden
Sehr grosse praktische Bedeutung
(Speichermedien, Netzwerkübertragung etc.)
Grundlegendes Modell: Allgemeiner Binärer Kanal
(BK)
Kanalcodierung I
Informationstheorie
5

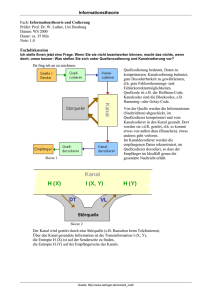
Der binäre Kanal
1-δ
p(x1)
δ
ε
p(x0)
Kanalcodierung I

6
Eigenschaften
Seien p(x0) und p(x1) die Wahrscheinlichkeiten für
die Symbole {0,1} am Kanaleingang
Ebenso seien p(y0) und p(y1) die
Wahrscheinlichkeiten am Kanalausgang
Dann gilt
wobei
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
Eigenschaften

p(y0)
1-ε
Copyright M. Gross, ETH Zürich 2005, 2006

p(y1)
δ ⎞⎛ p ( x0 ) ⎞
⎛ p ( y 0 ) ⎞ ⎛1 − ε
⎜⎜
⎟⎟ = ⎜⎜
⎟
⎟⎜
1 − δ ⎟⎠⎜⎝ p ( x1 ) ⎟⎠
⎝ p ( y1 ) ⎠ ⎝ ε

Definition: Die Transinformation HT ist die pro
Kanalzeichen übertragene Information
Für den binären Kanal ergibt sie sich wie folgt:
mit
H T = I ( X ; Y ) = H (Y ) − H (Y | X )
H (Y ) = −
und
δ ⎞
⎛1 − ε
⎟
p ( y j | xi ) ⇔ ⎜⎜
−
ε
1
δ ⎟⎠
⎝
∑ p( y ) log
j
j∈{0 ,1}
H (Y | X ) = −
2
∑ p( x ) ∑ p( y
i∈{0 ,1}
i
j∈{0 ,1}
p( y j )
j
| xi ) log 2 p ( y j | xi )
die Matrix der Übergangswahrscheinlichkeiten ist
Kanalcodierung I
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
7
Kanalcodierung I
Informationstheorie
8
Copyright M. Gross, ETH Zürich 2005, 2006
2
Binärer Kanal

Spezialfall 1
Gegeben: p(x0)=0.2, p(x1)=0.8, δ=0.1 und ε=0.001
Gesucht HT
⎛ 0.999 0.1 ⎞
⎟⎟
p ( y j | xi ) = ⎜⎜
⎝ 0.001 0.9 ⎠

p ( y0 ) = 0.999 ⋅ 0.2 + 0.1 ⋅ 0.8 = 0.280
Der binäre, symmetrische Kanal (BSK)
1-ε
1
1
p ( y1 ) = 0.001 ⋅ 0.2 + 0.9 ⋅ 0.8 = 0.720
ε
H (Y ) = 0.855 Bit/QZ
H (Y | X ) = −0.2 ⋅ (0.999 ⋅ log 2 0.999 + 0.001 ⋅ log 2 0.001)
ε
− 0.8 ⋅ (0.9 ⋅ log 2 0.9 + 0.1 ⋅ log 2 0.1)
= 0.377 Bit/QZ
0
H T = H (Y ) − H (Y | X ) = 0.478 Bit/QZ
Kanalcodierung I
Informationstheorie
9
Kanalcodierung I
Copyright M. Gross, ETH Zürich 2005, 2006

10
BSK Modell
Jedes Bit wird mit einer Wahrscheinlichkeit ε bei
der Übertragung invertiert (verfälscht)
Bei ε=0 kann 1 bit Information pro Kanalnutzung
zuverlässig übertragen werden
Bei ε=0.5 wird die Ausgabe-Bitfolge gleichverteilt
und statistisch unabhängig von der Eingabe
Es wird keine Information übertragen
Die Kapazität des Kanals ist 1 bit/Nutzung (ε=0 )
und 0 bit/Nutzung (ε=0.5)

H T = H (Y ) + (1 − ε ) log 2 (1 − ε ) + ε log 2 ε
Kanalcodierung I
Informationstheorie
0
Copyright M. Gross, ETH Zürich 2005, 2006
BSK Modell

1-ε
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
11
ε=1 ist gleichwertig zu ε=0
Für 0< ε <0.5 kann eine beliebig zuverlässige
Übertragung erreicht werden, wenn jedes Bit
genügend oft gesendet wird
Mehrheitsentscheidung am Kanalausgang
notwendig
Mit zunehmender Redundanz nimmt hierbei
jedoch die Übertragungsrate ab
Durch geschickte Codierung kann die
Fehlerwahrscheinlichkeit bei gleichbleibender Rate
beliebig verkleinert werden
Kanalcodierung I
Informationstheorie
12
Copyright M. Gross, ETH Zürich 2005, 2006
3
Shannon's Resultate

Gedächtnisfreie Kanäle
Shannon zeigte, dass die Übertragungsrate in
Grenzen unabhängig von der
Übertragungskapazität ist
Jeder Kanal besitzt eine Kapazität
Diese ist die maximale Rate, mit der Information
zuverlässig übertragbar ist
Die dazu nötigen Codes können entsprechend
komplex werden

Dies ist ein zweites, fundamentales Gesetz von Claude
Shannon und in seinem (zweiten)
Kanalcodierungstheorem zusammengefasst
Kanalcodierung I
Informationstheorie
Generell wird ein Kanal durch die
Übergangsmatrix zwischen Eingang und Ausgang
definiert
Eine bedeutende Unterklasse sind sogenannte
gedächtnisfreie Kanäle
Hierbei ist der Output Yi nur vom aktuellen
Input Xi abhängig, nicht von seiner Vorgeschichte
Xi-1… X1
Definition: Ein diskreter, gedächtnisfreier Kanal
(DGK) für ein Inputalphabet χ und ein
Outputalphabet γ ist eine bedingte Verteilung
PY | X : γ × χ → R +
13
Kanalcodierung I
Copyright M. Gross, ETH Zürich 2005, 2006
Spezialfall 2

1-ε
1

1
Definition: Ein Blockcode C mit Blocklänge N für
einen Kanal mit Inputalphabet χ ist eine
Teilmenge C={c1,…,cM } von χN der N-Tupel über
χ. Die Rate R von C ist
R=
ε
A

ε
Kanalcodierung I
14
Blockcodes
Der binäre, Auslöschungskanal (BAK)
Keine Bitinversion, nur Auslöschung
0
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
1-ε
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
log 2 M
.
N
R ist die Anzahl der Bits, die pro Kanalnutzung
gesendet werden können
0
15
Kanalcodierung I
Informationstheorie
16
Copyright M. Gross, ETH Zürich 2005, 2006
4
Decodierung als Schätzung

Bild dazu
Die Decodierung einer fehlerbehafteten
Zeichenfolge, gegeben die Symbolfolge am
Kanalausgang kann als (Parameter)Schätzproblem betrachtet werden
Wir bedienen uns hierzu allgemeiner, statistischer
Schätzmethoden
Es sei U dabei eine Zufallsvariable, die aufgrund
einer Beobachtung V geschätzt werden soll
Die Wahrscheinlichkeitsverteilung PV|U sei bekannt
U

Beobachtung
PV|U
Schätzung f
~
U = f (V )
Der Schätzer ist eine Funktion f, welche jedem
Wert v der Beobachtung den entsprechenden
Schätzwert ũ zuordnet
Wir erinnern uns an das Informationstheorie-Lemma,
welches besagt, dass wir durch Berechnung KEINE
Information hinzufügen können.
Kanalcodierung I
Informationstheorie
17
Kanalcodierung I
Copyright M. Gross, ETH Zürich 2005, 2006
Decodierung als Schätzung

Die Schätzung ist optimal, wenn die
Wahrscheinlichkeit einer korrekten Schätzung
P(U=Ũ) maximiert wird

Wir schreiben

~
P (U = U ) = ∑ PUV ( f (v), v) = ∑ PV |U (v, f (v))PU ( f (v))
v
v
Dieser Ausdruck soll durch Wahl von f maximiert
werden
Kanalcodierung I
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
Fall 1: PU bekannt (prior bekannt): In diesem Fall
muss für jedes v dasjenige ũ für f(v) gewählt
werden, damit
PV |U (v, u~ ) PU (u~ ) → max
v

18
Decodierung als Schätzung
~
~
P(U = U ) = ∑ P (U = U , V = v) → max

Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006

19
Dies wird auch als minimum-error estimation
(ME) bezeichnet
Fall 2: PU nicht bekannt (uniform prior): Man
nimmt an, dass alles Werte von U
gleichwahrscheinlich sind
Da PU(u) für alle u gleich ist, muss es bei der
Maximierung nicht beachtet werden
Kanalcodierung I
Informationstheorie
20
Copyright M. Gross, ETH Zürich 2005, 2006
5
Decodierung als Schätzung

Decodierung als Schätzung
In diesem Fall muss für jedes v dasjenige ũ für
f(v) gewählt werden, damit

PV |U (v, u~ ) → max

Wenn das Codewort cj=[cj1,…,cjN] über einen DGK
mit Übergangsverteilung PY|X gesendet wird, so ist
der Kanaloutput eine Zufallsvariable YN=[Y1,…,YN]
mit Wertmenge γN und Verteilung
Dies wird auch als maximum likelihood estimation
(ML) bezeichnet
N
PY N | X N ( y N , c j ) = ∏ PY | X ( yi , c ji )
i =1

y N = [ y1 ,..., y N ]
Diese beiden Schätzverfahren sind universell und
werden in vielen Anwendungen der Natur- und
Ingenieurwissenschaften ausgiebig eingesetzt.
In der Praxis dominiert oft die ML-Methode, da der Prior
oft nicht bekannt ist.
Kanalcodierung I
Informationstheorie
Im Decoder muss also für ein empfangenes
Kanaloutputwort
die beste Schätzung für das gesendete Codewort
finden
21
Kanalcodierung I
Copyright M. Gross, ETH Zürich 2005, 2006
Decodierung als Schätzung

V =YN
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
Ein Decoder, der für ein gegebenes Empfangswort
yN als Schätzung des gesendeten Codewortes
eines derjenigen cj=[cj1,…,cjN] wählt, welches
PY N | X N ( y N , c j ) PX N (c j ) → max
erhalten wir die folgenden Theoreme
Es sei Ũ die Schätzung des Coders
Kanalcodierung I
22
Minimum Error Decoder
Dieser Schätzvorgang heisst Decodierung
Mit den Entsprechungen
U = XN
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
erreicht die minimale Fehlerwahrscheinlichkeit
23

Nachteil ist hierbei, dass die Verteilung der
Codewörter bekannt sein muss

In der Praxis ist die Quellenstatistik oft nicht
bekannt
Kanalcodierung I
Informationstheorie
24
Copyright M. Gross, ETH Zürich 2005, 2006
6
Maximum Likelihood Decoder

Kanalkapazität
Ein Decoder, der für ein gegebenes Empfangswort
yN als Schätzung des gesendeten Codewortes
eines derjenigen cj=[cj1,…,cjN] wählt, welches

PY N | X N ( y N , c j ) → max

erreicht die minimale Fehlerwahrscheinlichkeit,
wenn alle Codewörter gleichwahrscheinlich sind

Ein DGK ist durch die bedingte
Wahrscheinlichkeitsverteilung PY|X eindeutig
beschrieben
Die Inputverteilung PX ist jedoch frei
Wir wählen sie so, dass maximal viel Information
übertragen wird
Definition: Die Kapazität eines durch PY|X
charakterisierten DGK ist das Maximum über
Inputverteilungen PX von I(X;Y)
C = max I ( X ; Y ) = max[ H (Y ) − H (Y | X )]
PX
Kanalcodierung I
Informationstheorie
25
Kanalcodierung I
Copyright M. Gross, ETH Zürich 2005, 2006

Informationstheorie
26
Copyright M. Gross, ETH Zürich 2005, 2006
Kanalkapazität

PX
Kanalkapazität
Wir werden zeigen, dass die Kapazität eine obere
Grenze für die Rate darstellt, mit der Information
zuverlässig übertragen werden kann
Im Allgemeinen sind Kapazitätsberechnungen
eher schwierig
Wir suchen eine Inputverteilung PX , die H(Y)
maximiert und H(Y|X) minimiert

Die Berechnung vereinfacht sich für folgende
Bedingungen

A) H(Y|X=x) ist für alle x gleich, also

B) Die folgende Summe ist für alle y gleich
H (Y | X = x) = t
∑P
Y|X
( y, x) = s
X

Letzteres bewirkt, dass bei Gleichverteilung am
Kanaleingang auch Gleichverteilung am
Kanalausgang vorliegt
Die Kanalkapazität ist also das Maximum der
Transinformation des Kanals
Kanalcodierung I
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
27
Kanalcodierung I
Informationstheorie
28
Copyright M. Gross, ETH Zürich 2005, 2006
7
Kanalkapazität

Kanalkapazität des BSK
Theorem: Die Kapazität eines Kanals, welcher die
Bedingungen A) und B) erfüllt, ist

ε ⎞⎛ p ( x0 ) ⎞
⎛ p ( y 0 ) ⎞ ⎛1 − ε
⎜⎜
⎟⎟ = ⎜⎜
⎟
⎟⎜
1 − ε ⎟⎠⎜⎝ p ( x1 ) ⎟⎠
⎝ p ( y1 ) ⎠ ⎝ ε
C = log γ − t

Wir betrachten den BSK als Beispiel
Übertragungsmatrix:

Y|X

( y, x) ist gleich für alle y
Inputverteilung:
max H (Y ) = max( p ( y0 ) ⋅ log 2 p ( y0 ) + p( y1 ) ⋅ log 2 p ( y1 )
X
→ Zeilensumme der Übergangsmatrix

erreicht bei p ( y0 ) = p ( y1 ) =
Berechnung der Kapazität:
Transinformation : H T = H (Y ) + ε ⋅ log 2 ε + (1 − ε ) ⋅ log 2 (1 − ε )
Kapazität : C = max H T
(Gleichverteilung)
p ( y1 ) = ε ⋅ p ( x0 ) + (1 − ε ) ⋅ p ( x1 )
→ p ( x0 ) = p ( x1 ) =
gemäss Formel = log 2 γ − t mit t = ε ⋅ log 2 ε + (1 − ε ) ⋅ log 2 (1 − ε )
Kanalcodierung I
1
2
p ( y0 ) = (1 − ε ) ⋅ p ( x0 ) + ε ⋅ p ( x1 )
Es gilt : p ( y0 ) = 1 − p( y1 )
→ eingesetzt
30
Kanalkapazität des BSK
Bedingung B:
∑P
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
1
2
= 1 + ε ⋅ log 2 ε + (1 − ε ) ⋅ log 2 (1 − ε )
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
31
Kanalcodierung I
Informationstheorie
32
Copyright M. Gross, ETH Zürich 2005, 2006
8
Kapazität und Rate

DGK Modell
Die Kapazität ist eine Obergrenze für die Rate, mit
der Information zuverlässig übertragen werden
kann
Je höher die Rate über der Kapazität, umso
grösser die Fehlerwahrscheinlichkeit
Wir betrachten das Modell eines DGK
Es sollen K Informationsbits UK=[U1,…,UK] durch
N Benutzungen übertragen werden
Die Kapazität sei C
Der Codierer übersetzt die Informationsbits in ein
Codewort XN=[X1,…,XN], welches vom Kanal in
YN= [Y1,…,YN] verfälscht wird
Kanalcodierung I
Informationstheorie
33
Diskrete
Quelle
Empfänger

Kanaldecodierer
~
~
U1 KU K
Kanalcodierung I
Y1 KYN
Informationstheorie
34
Kapazität und Rate
Die Rate R ist demnach
bits pro
DGK
Copyright M. Gross, ETH Zürich 2005, 2006
Kapazität und Rate
K
R=
N
Kanalcodierer
Möglicher Feedback
Copyright M. Gross, ETH Zürich 2005, 2006

X1 K X N
U1 KU K

Nutzung
Damit UK durch ŨK bestimmt ist, muss die Anzahl
der Kanalbenutzungen N mindestens sein:
N=
Der Decoder schätzt nun [Ũ1,…, ŨK]
Ein möglicher Feedback kann Information an den
Decoder zurückliefern
Man kann zeigen (Skript), dass
H (U K )
C
~
H (U K | U K ) ≥ H (U K ) − NC

Die Kanalübertragung kann die Unsicherheit beim
Empfänger nicht um mehr als NC reduzieren
Kanalcodierung I
Informationstheorie
Copyright M. Gross, ETH Zürich 2005, 2006
35
Kanalcodierung I
Informationstheorie
36
Copyright M. Gross, ETH Zürich 2005, 2006
9