Die Cheeger-Ungleichung für Graphen

Seminar Geometrie, Sommersemester 2010
bei Prof. Dr. C. Bär
Institut für Mathematik der Universität Potsdam
Die Cheeger-Ungleichung für Graphen
Frank Pfäffle, 26. Mai 2010
Im Folgenden sei G = (V, E) ein endlicher zusammenhängender Graph. Für jeden
Knoten v ∈ V bezeichne dv den Grad von v wie gehabt.
Definition 1. Es sei eine Teilmenge S ⊂ V . Dann ist das Volumen von S gegeben
durch
X
vol(S) =
dv .
v∈S
Das Komplement von S ist S = V \ S. Als Kantenrand von S bezeichnet man die
Menge
∂S = {u, v} ∈ E u ∈ S und v 6∈ S ,
und den Knotenrand von S nennt man die Menge
δS = v ∈ S ∃u ∈ S mit {u, v} ∈ E .
Definition 2. Für Teilmengen A, B ⊂ V setzen wir
E(A, B) = {u, v} ∈ E u ∈ A und v ∈ B .
Bemerkung 1. Für jedes S ⊂ V gilt ∂S = E(S, S).
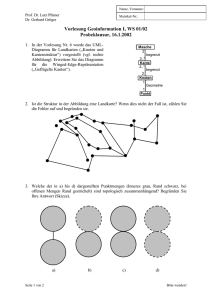
Zwei typische isoperimetrische Probleme sind:
Gegeben sei jeweils eine Zahl m. Finde eine Menge von Knoten S ⊂ V mit m ≤
vol(S) ≤ vol(S), sodass
a) der Kantenrand ∂S möglichst wenige Kanten enthält, oder
b) der Knotenrand δS möglichst wenige Knoten enthält.
Definition 3. (Kanten-Expansion.) Für S ⊂ V mit ∅ =
6 S 6= V setzen wir
hG (S) =
# E(S, S)
,
min vol(S), vol(S)
und die Cheeger-Konstante von G ist gegeben durch
hG = min hG (S).
S⊂V
∅6=S6=V
Bemerkung 2. Hat G mindestens zwei Knoten, so ist hG > 0.
Bemerkung 3. Die Cheeger-Konstante zu berechnen ist äquivalent dazu, dass man
das Problem a) löst, denn es gilt # (∂S) ≥ hg · vol(S).
Definition 4. (Knoten-Expansion.) Für S ⊂ V mit ∅ =
6 S 6= V definieren wir
gG (S) =
vol(δS)
min vol(S), vol(S)
sowie
g G (S) =
# (δS)
,
min # S, # S
und wir setzen
gG = min gG (S)
S⊂V
∅6=S6=V
sowie
g G = min g G (S).
S⊂V
∅6=S6=V
Bemerkung 4. Ist G ein k-regulärer Graph, so gilt gG (S) = g G (S) für alle S ⊂ V
und damit auch gG = g G .
Die Cheeger-Konstante lässt sich gegen den kleinsten positven Laplace-Eigenwert
λG von G abschätzen.
Lemma 1 (Lemma 2.1 in [1]). Für die Cheeger-Konstante gilt folgende untere
Abschätzung:
2 · hG ≥ λ G .
Satz 1 (Cheeger-Ungleichung, Thm. 2.2 in [1]). Die Cheeger-Konstante lässt sich
nach oben abschätzen durch
hG 2
λG >
.
2
Der Beweis von Satz 1 liefert sogar noch etwas mehr, nämlich
p
Satz 2 (Thm. 2.3 in [1]). Es gilt: λG ≥ 1 − 1 − (hg )2 .
Und außerdem liefert der Beweis von Satz 1 auch die folgende untere Eigenwertabschätzung:
Sei f eine harmonische Eigenfunktion zum Eigenwert λG . Wir setzen für jeden
Knoten v ∈ V
Cv = {u, w} ∈ E f (u) ≤ f (v) < f (w) , und
α = min
v
min
#Cv
du ,
P
u
f (u)≤f (v)
P
u
f (u)>f (v)
du
.
Dann gilt:
λG ≥ 1 −
p
1 − α2
Literatur
[1] F. Chung: Spectral Graph Theory, Amer. Math. Soc. 1997
2