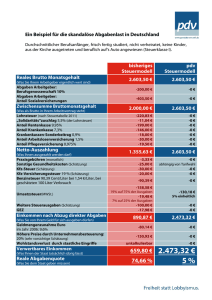
Kapitel 14 - WordPress.com
Werbung
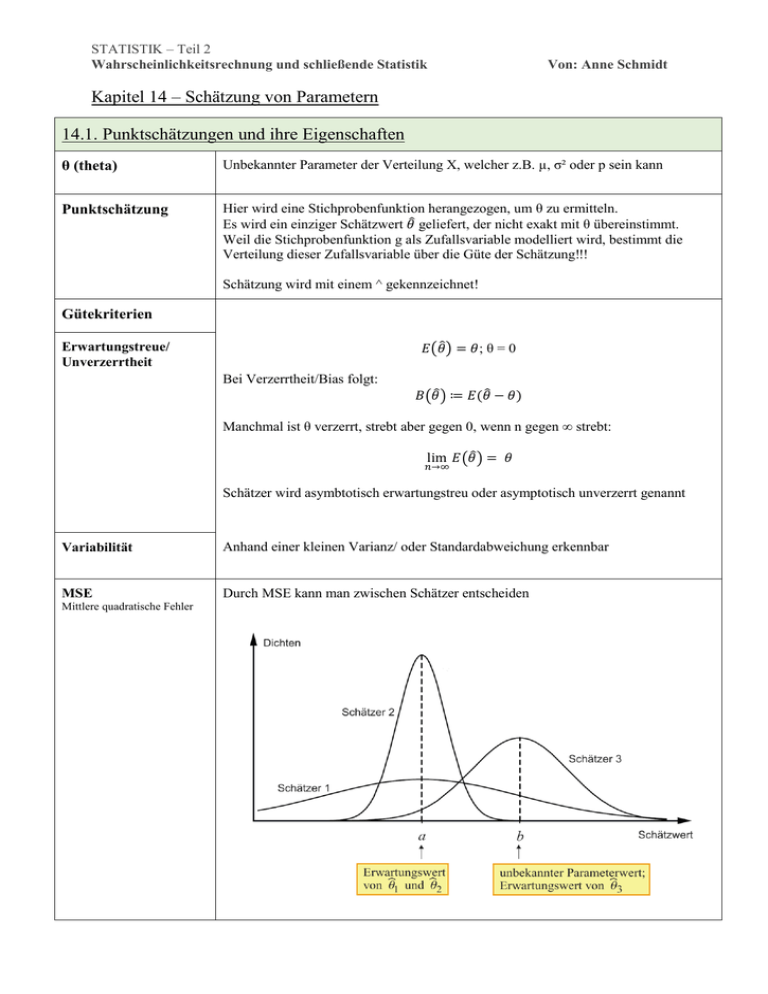
STATISTIK – Teil 2 Wahrscheinlichkeitsrechnung und schließende Statistik Von: Anne Schmidt Kapitel 14 – Schätzung von Parametern 14.1. Punktschätzungen und ihre Eigenschaften θ (theta) Unbekannter Parameter der Verteilung X, welcher z.B. µ, σ² oder p sein kann Punktschätzung Hier wird eine Stichprobenfunktion herangezogen, um θ zu ermitteln. Es wird ein einziger Schätzwert 𝜃̂ geliefert, der nicht exakt mit θ übereinstimmt. Weil die Stichprobenfunktion g als Zufallsvariable modelliert wird, bestimmt die Verteilung dieser Zufallsvariable über die Güte der Schätzung‼! Schätzung wird mit einem ^ gekennzeichnet! Gütekriterien 𝐸(𝜃̂) = 𝜃; θ = 0 Erwartungstreue/ Unverzerrtheit Bei Verzerrtheit/Bias folgt: 𝐵(𝜃̂) ≔ 𝐸(𝜃̂ − 𝜃) Manchmal ist θ verzerrt, strebt aber gegen 0, wenn n gegen ∞ strebt: lim 𝐸(𝜃̂) = 𝜃 𝑛→∞ Schätzer wird asymbtotisch erwartungstreu oder asymptotisch unverzerrt genannt Variabilität Anhand einer kleinen Varianz/ oder Standardabweichung erkennbar MSE Durch MSE kann man zwischen Schätzer entscheiden Mittlere quadratische Fehler STATISTIK – Teil 2 Wahrscheinlichkeitsrechnung und schließende Statistik Von: Anne Schmidt Der MSE repräsentiert eine additive Verknüpfung von Varianz und quadrierter Verzerrung. Man wird von den beiden Schätzern ^θ2 und ^θ3 in der Abbildung denjenigen als „besser“ ansehen, dessen MSE kleiner ausfällt. Bei erwartungstreuen Schätzern sind MSE und Varianz identisch. 14.2. Schätzung von Erwartungswerten, Varianzen und Anteilen Schätzung des Erwartungswerts 𝐸(𝑋̅) = 𝜇 Besagt, dass der Stichprobenmittelwert 𝑋̅ gleich dem Erwartungswert der Grundgesamtheit ist d.h. sie liefert eine unverzerrte Schätzung! Stichprobenvariablen sind unabhängig & feste Varianz σ² (Varianz der Grundgesamtheit), folgt: 𝑉(𝑋̅) = 𝜎² 𝑛 𝑀𝑆𝐸(𝑋̅) = 𝑉(𝑋̅) Qualität von 𝑆𝑐ℎä𝑡𝑧𝑒𝑟 𝑋̅verbessert sich wenn n größer wird Schätzung der Varianz σ² Es wird S²,also der Kennwert der Stichprobe, zu Ermittlung von σ² herangezogen: d.h. S² liefert eine verzerrte Schätzung (asymptotisch erwartungsgetreu) für die Varianz σ²; aber je größer n, desto besser die Schätzung! Um eine unverzerrte Schätzung für σ² zu erhalten, zieht man die korrigierte Stichprobenvarianz heran S*² STATISTIK – Teil 2 Wahrscheinlichkeitsrechnung und schließende Statistik Schätzung von Anteilswerten Von: Anne Schmidt X ist bernoulli-verteilt, charakterisiert zweimögliche Ausgänge 𝑝̂ ≔ 𝑋̅ 14.3. Konfidenzintervalle für Erwartungswerte Intervallschätzung Intervall (möglichst schmal durch viele n d.h. kurz) wird ermittelt, das den zu schätzenden Parameter θ mit einer Wahrscheinlichkeit von mindestens 1-α enthält Schätzung von Erwartungswert Varianz σ² ist bekannt‼ Stichprobenwerte x1,x2 … xn werden als Ausprägungen unabhängiger N(µ,σ²)- verteilter Zufallsvariablen X1 X2 … Xn (aus der Grundgesamtheit) interpretiert 𝑍≔ Standardnormalverteilt Quantile: Intervall [ -z 1-α/2 ; z1-α/2] 𝑋̅ − 𝜇 𝜎𝑋̅ Es gilt die Wahrscheinlichkeitsaussage für den Stichprobenmittelwert Z: Konfidenzintervall zum Konfidenzniveau 1-α für μ Intervallgrenzen sind zufallsabhängig Abnehmender Irrtumswahrscheinlichkeit α nimmt die Länge von KI zu Mit zunehmender n wird das Konfidenzintervall schmaler! STATISTIK – Teil 2 Wahrscheinlichkeitsrechnung und schließende Statistik Von: Anne Schmidt Varianz ist nicht bekannt, man kennt sie nur durch eine Schätzung ! Ausgangspunkt ist nicht mehr aus z standardisierte Stichprobenmittelwert, sondern mit n-1 Freiheitsgraden t-verteilte Zufallsvariable: Länge ist abhängig von n, α und auch von S* (korrigierte Standardabweichung der Stichprobe) – zufallsabhängig Konfidenzintervall ist im Mittel länger