Schulcurriculum Mathematik, Jahrgang 6, gemäß Kerncurriculum

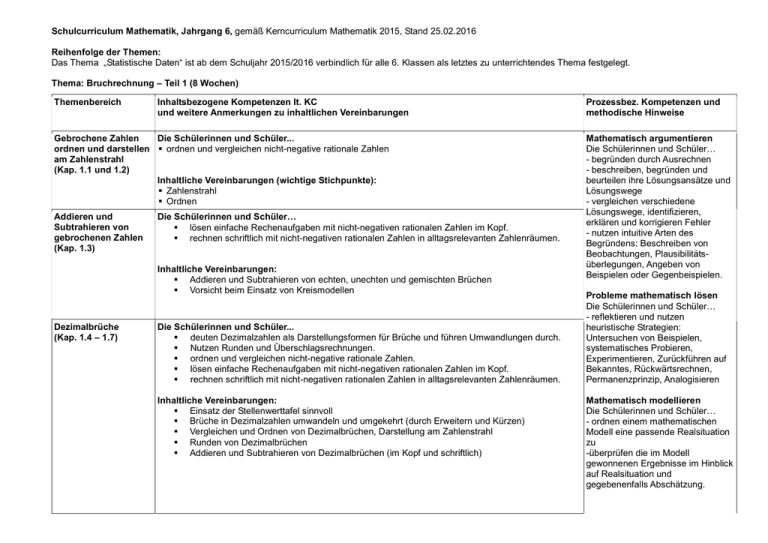
Schulcurriculum Mathematik, Jahrgang 6, gemäß Kerncurriculum Mathematik 2015, Stand 25.02.2016
Reihenfolge der Themen:
Das Thema „Statistische Daten“ ist ab dem Schuljahr 2015/2016 verbindlich für alle 6. Klassen als letztes zu unterrichtendes Thema festgelegt.
Thema: Bruchrechnung – Teil 1 (8 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Gebrochene Zahlen
Die Schülerinnen und Schüler...
ordnen und darstellen  ordnen und vergleichen nicht-negative rationale Zahlen
am Zahlenstrahl
(Kap. 1.1 und 1.2)
Inhaltliche Vereinbarungen (wichtige Stichpunkte):
 Zahlenstrahl
 Ordnen
Addieren und
Subtrahieren von
gebrochenen Zahlen
(Kap. 1.3)
Die Schülerinnen und Schüler…
 lösen einfache Rechenaufgaben mit nicht-negativen rationalen Zahlen im Kopf.
 rechnen schriftlich mit nicht-negativen rationalen Zahlen in alltagsrelevanten Zahlenräumen.
Inhaltliche Vereinbarungen:
 Addieren und Subtrahieren von echten, unechten und gemischten Brüchen
 Vorsicht beim Einsatz von Kreismodellen
Dezimalbrüche
(Kap. 1.4 – 1.7)
Die Schülerinnen und Schüler...
 deuten Dezimalzahlen als Darstellungsformen für Brüche und führen Umwandlungen durch.
 Nutzen Runden und Überschlagsrechnungen.
 ordnen und vergleichen nicht-negative rationale Zahlen.
 lösen einfache Rechenaufgaben mit nicht-negativen rationalen Zahlen im Kopf.
 rechnen schriftlich mit nicht-negativen rationalen Zahlen in alltagsrelevanten Zahlenräumen.
Inhaltliche Vereinbarungen:
 Einsatz der Stellenwerttafel sinnvoll
 Brüche in Dezimalzahlen umwandeln und umgekehrt (durch Erweitern und Kürzen)
 Vergleichen und Ordnen von Dezimalbrüchen, Darstellung am Zahlenstrahl
 Runden von Dezimalbrüchen
 Addieren und Subtrahieren von Dezimalbrüchen (im Kopf und schriftlich)
Prozessbez. Kompetenzen und
methodische Hinweise
Mathematisch argumentieren
Die Schülerinnen und Schüler…
- begründen durch Ausrechnen
- beschreiben, begründen und
beurteilen ihre Lösungsansätze und
Lösungswege
- vergleichen verschiedene
Lösungswege, identifizieren,
erklären und korrigieren Fehler
- nutzen intuitive Arten des
Begründens: Beschreiben von
Beobachtungen, Plausibilitätsüberlegungen, Angeben von
Beispielen oder Gegenbeispielen.
Probleme mathematisch lösen
Die Schülerinnen und Schüler…
- reflektieren und nutzen
heuristische Strategien:
Untersuchen von Beispielen,
systematisches Probieren,
Experimentieren, Zurückführen auf
Bekanntes, Rückwärtsrechnen,
Permanenzprinzip, Analogisieren
Mathematisch modellieren
Die Schülerinnen und Schüler…
- ordnen einem mathematischen
Modell eine passende Realsituation
zu
-überprüfen die im Modell
gewonnenen Ergebnisse im Hinblick
auf Realsituation und
gegebenenfalls Abschätzung.
Mathematische Darstellungen
verwenden
Die Schülerinnen und Schüler…
- nutzen unterschiedliche
Darstellungsformen für positive
rationale Zahlen
- beschreiben Beziehungen
zwischen unterschiedlichen
Darstellungsformen
- verwenden eigene Darstellungen
zur Unterstützung individueller
Überlegungen
Mit symbolischen, formalen und
technischen Elemente der
Mathematik umgehen
Die Schülerinnen und Schüler…
- stellen einfache mathematische
Beziehungen durch Terme, auch mit
Platzhaltern, dar und interpretieren
diese
- berechnen die Werte einfacher
Terme
- verwenden die Relationszeichen
(„=“, „<“, „>“, „≤ “, „≥“ und „≈“)
sachgerecht
- nutzen die Umkehrung der
Grundrechenarten
Thema: Symmetrie (10 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Prozessbez. Kompetenzen und
methodische Hinweise
Kreise und Winkel
(Kap.2.1 und 2.2)
Die Schülerinnen und Schüler…
 schätzen messen und zeichnen Winkel.
 zeichnen Winken und Kreise, um ebene geometrische Figuren zu erstellen oder zu
reproduzieren.
 beschreiben Kreise als Ortslinien.
 beschreiben ebene und räumliche Strukturen mit den Begriffen Winkel und Radius.
Mathematisch argumentieren
Die Schülerinnen und Schüler…
- stellen Fragen und äußern
begründete Vermutungen in
eigener Sprache
- bewerten Informationen für
mathematische Argumentationen.
- begründen durch Konstruieren
- beschreiben, begründen und
beurteilen ihre Lösungsansätze
und Lösungswege
- vergleichen verschiedene
Lösungswege, identifizieren,
erklären und korrigieren Fehler
- erläutern einfache mathematische
Sachverhalte, Begriffe, Regeln,
Verfahren und Zusammenhänge
mit eigenen Worten und
geeigneten Fachbegriffen
Symmetrien,
Drehungen und
Verschiebungen
(Kap. 2.3 – 2.6. )
Inhaltliche Vorgaben:
 Begriff des Winkels
 Winkelarten
 Winkel messen und zeichnen
Die Schülerinnen und Schüler…
 beschreiben Symmetrien.
 verschieben, spiegeln und drehen Figuren in der Ebene und erzeugen damit Muster.
 identifizieren und erzeugen Mittelsenkrechte und Winkelhalbierende als Symmetrieachsen.
 beschreiben ebene und räumliche Strukturen mit dem Begriff Symmetrie.
Inhaltliche Vorgaben:
 Achsensymmetrie und Achsenspiegelung
 Mittelsenkrechte und Winkelhalbierende als Spiegelachse
 Punktsymmetrie und Punktspiegelung
 Drehsymmetrie und Drehungen
 Verschiebungen
Winkelsätze an
Die Schülerinnen und Schüler…
Geradenkreuzungen
 Berechnen Winkelgrößen mithilfe von Neben-, Scheitel- und Stufenwinkelsatz und dem
(Kap.1.2),
Winkelsummensatz für Dreiecke.
Winkel an Vielecken
 Begründen die Winkelsumme und Dreieck und Viereck
und Körpern (Kap.1.3)
 Wenden Neben-, Scheitel- und Stufenwinkelsatz sowie den Winkelsummensatz für Dreiecke bei
Konstruktionen und Begründungen an.
 charakterisieren Dreiecke und Vierecke
Inhaltliche Vorgaben
 Winkel an Geradenkreuzungen
 Winkelsumme im Dreieck und Viereck
 Berechnen von Winkeln mithilfe der Winkelsätze
 symmetrische Dreiecke und Vierecke, Basiswinkelsatz, „Haus der Vierecke“
Probleme mathematisch lösen
Die Schülerinnen und Schüler…
- wenden elementare
mathematische Regeln und
Verfahren wie Messen, Rechnen
und einfaches logisches
Schlussfolgern zur Lösung von
Problemen an
- deuten ihre Ergebnisse in Bezug
auf die ursprüngliche
Problemstellung und beurteilen sie
durch Plausibilitätsüberlegungen,
Überschlagsrechnungen oder
Skizzen
- reflektieren und nutzen
heuristische Strategien:
Untersuchen von Beispielen,
systematisches Probieren,
Experimentieren, Zurückführen auf
Bekanntes, Permanenzprinzip,
Zerlegen und Zusammensetzen
von Figuren, Nutzen von
Invarianzen und Symmetrien,
Analogisieren
Mathematisch modellieren
Die Schülerinnen und Schüler…
- verwenden geometrische Objekte,
Terme zur Ermittlung von
Lösungen im mathematischen
Modell
- nutzen Lineal, Geodreieck und
Zirkel zur Konstruktion und
Messung geometrischer Figuren.
Am Ende dieses Lernbereiches bietet sich der Einsatz des LEMAMOP-Kompetenztrainings „Argumentieren“ an.
Thema: Bruchrechnung – Teil 2 (10 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Prozessbez. Kompetenzen
und methodische Hinweise
Multiplizieren und
Dividieren von
Brüchen und
Dezimalbrüchen
(Kap.3.1 bis 3.6)
Die Schülerinnen und Schüler...
 lösen einfache Rechenaufgaben mit nicht-negativen rationalen Zahlen im Kopf.
 rechnen schriftlich mit nicht-negativen rationalen Zahlen in alltagsrelevanten Zahlenräumen.
Gleiche prozessbezogenen
Kompetenzen wie bei
Bruchrechnung – Teil 1
Abbrechende und
periodische
Dezimalbrüche
(Kap.3.7)
Die Schülerinnen und Schüler...
 Stellen nicht-negative rationale Zahlen auf verschiedene Weisen und situationsangemessen dar.
Terme und
Rechengesetze
(Kap.3.8 – 3.10)
Die Schülerinnen und Schüler…
 beschreiben Sachverhalte durch Zahlterme
 geben zu Zahltermen geeignete Sachsituationen an
 beschreiben die Struktur von Zahltermen
 nutzen Rechenregeln zum vorteilhaften Rechnen
 nutzen die Zusammenhänge zwischen den Grundrechenarten auch bei Sachproblemen
Inhaltliche Vereinbarungen:
 Brüche vervielfachen und teilen
 Multiplizieren und Dividieren von echten, unechten und gemischten Brüchen
 Multiplizieren und Dividieren von Dezimalbrüchen
Inhaltliche Vereinbarungen:
 Abbrechende und periodische Dezimalbrüche
 periodische Dezimalbrüche in Brüche umwandeln und umgekehrt.
Inhaltliche Vereinbarungen:
 Rechnen mit Brüchen und Dezimalbrüchen in den vier Grundrechenarten
 Berechnen von Termen und „Doppelbrüchen“
 Kommutativ-, Assoziativ- und Distributivgesetz
Am Ende dieses Lernbereichs bietet sich der Einsatz des LEMAMOP-Kompetenztrainings „Problemlösen“ an.
Thema: Statistische Daten (4 Wochen)
Themenbereich
Inhaltsbezogene Kompeten
zen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Daten darstellen (Kap. Die Schülerinnen und Schüler...
4.1 – 4.3)
 Stellen Daten in angemessener Form dar, interpretieren Fremddarstellungen und bewerten diese
kritisch.
 lesen aus Säulen- und Kreisdiagrammen Daten ab.
 beschreiben und interpretieren Daten mithilfe von absoluten und relativen Häufigkeiten
Kenngrößen
statistischer Daten
(Kap. 4.4)
Inhaltliche Vereinbarungen:
 Absolute und relative Häufigkeiten
 Säulen-, Kreis- und Streifendiagramm
 Bildliche Darstellungen von Daten und ihre Wirkung
 Einteilen von Daten in Klassen, Histogramm
Die Schülerinnen und Schüler...
 beschreiben und interpretieren Daten mithilfe von absoluten und relativen Häufigkeiten,
arithmetischem Mittelwert, Wert(en) mit der größten Häufigkeit und Spannweite.
Inhaltliche Vereinbarungen:
 Arithmetisches Mittel
 Modalwert
 Spannbreite
Prozessbez. Kompetenzen
und methodische Hinweise
Mathematisch argumentieren
Die Schülerinnen und
Schüler…
- beschreiben, begründen und
beurteilen ihre Lösungsansätze
und Lösungswege
- vergleichen verschiedene
Lösungswege, identifizieren,
erklären und korrigieren Fehler
Probleme mathematisch
lösen
Die Schülerinnen und
Schüler…
- nutzen Darstellungsformen
wie Tabellen, Skizzen oder
Graphen zur Problemlösung.
Mathematisch modellieren
Die Schülerinnen und
Schüler…
- verwenden Diagramme,
Tabellen oder Häufigkeiten zur
Ermittlung von Lösungen im
mathematischen Modell
Mit symbolischen, formalen
und technischen Elementen
der Mathematik umgehen
Die Schülerinnen und
Schüler…
- erstellen Diagramme und
lesen aus ihnen Daten ab.
Der prozessbezogene Kompetenzbereich „Kommunizieren“ wird im Allgemeinen im Unterricht in den unterschiedlichen Arbeitsphasen gefördert. Im Detail sind
folgende Kompetenzen zu fördern:
Die Schülerinnen und Schüler…
- dokumentieren ihre Arbeit, ihre eigenen Lernwege und aus dem Unterricht erwachsene Merksätze und Ergebnisse unter Verwendung geeigneter Medien
- teilen ihre Überlegungen anderen verständlich mit, wobei sie auch die Fachsprache benutzen
- präsentieren Ansätze und Ergebnisse in kurzen Beiträgen, auch unter Verwendung geeigneter Medien
- verstehen Überlegungen von anderen zu mathematischen Inhalten, überprüfen diese auf Richtigkeit und gehen darauf ein
- entnehmen Daten und Informationen aus einfachen Texten und mathematikhaltigen Darstellungen, verstehen und bewerten diese und geben sie wieder
- äußern Kritik konstruktiv und gehen auf Fragen und Kritik sachlich und angemessen ein
- bearbeiten im Team Aufgaben oder Problemstellungen
- nutzen das Schulbuch und im Unterricht erstellte Zusammenfassungen zum Nachschlagen