schulinterner Arbeitsplan Mathematik - Albert-Einstein

ALBERT-EINSTEIN-GYMNASIUM
HAMELN
Schulinterner Lehrplan
MATHEMATIK
Klassen 5 – 10
(mit GTR-Curriculum)
Letzte Fortschreibung:
Fachkonferenz vom 29.05.2013
Lehrbücher: (Stand Sj 13/14)
Klasse 5 u. 6:
Baum u.a.,
Lambacher/Schweizer - neu
Mathematik für Gymnasien, Niedersachsen
Klett Verlag
Klassen 6 - 10:
Baum u.a.,
Lambacher Schweizer
Mathematik für Gymnasien, Niedersachsen
Klett Verlag
Sonstige Unterrichtsmaterialien:
Klasse 5 - 8:
Arbeitshefte (zu Lambacher/Schweizer)
Ab Klasse 7:
Grafikfähiger Taschenrechner (GTR) – Modell: TI- 84 Plus
Ab Klasse 9:
Das große Tafelwerk interaktiv 2.0 - Niedersachsen
Cornelsen Verlag
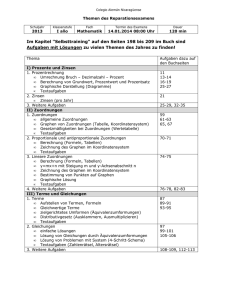
Anzahl der Stunden und Klassenarbeiten:
Klasse
Stundenzahl
Anzahl Klassenarbeiten
5
6
7
8
9
5
4
4
4
4
4
4
4
3
4
10
4
4
Absprachen zur Leistungsbewertung und Zensurengebung

Das Verhältnis schriftlich : mündlich soll innerhalb der Grenzen 50 : 50 bis 60 : 40 gebildet werden.
Dieses kann in Anlehnung an die Anzahl der Klassenarbeiten im Vergleich zu der Anzahl der mündlichen Zensuren erfolgen.

Bei der Bewertung der Klassenarbeiten ist besonders zu beachten (s. Kerncurriculum):
- unter 50% mangelhaft und unter 20% ungenügend;
- Aufteilung der Bereiche für „sehr gut“ bis „ausreichend“ in annähernd gleich große Intervalle.

Sonst siehe die entsprechenden Vorgaben in Kerncurriculum für 5-10
Jg 5 / 6
Prozessbezogene Kompetenzen Jg 5/6 – Tabellarische Übersicht
5/6
Mathematisch
argumentieren
Probleme mathematisch lösen
 Fragen stellen und
Vermutungen äußern
 Problemstellung erfassen, wiedergeben
und Fragen stellen
 Modellannahmen
finden und beschreiben
 Darstellungen für
rationale Zahlen nutzen
 Lösungswege beschreiben und begründen
 Direkt erkennbare
Modelle nutzen
 Tabelle und Graph
 Informationen bewerten
 Erläutern von Sachverhalten und Rechenwegen
 Intuitive Arten des
Begründens
 Einzelschritte in Argumentationsketten
begründen
 Lösungswege beschreiben
 Lösungswege vergleichen, Fehler finden
Mathematisch
modellieren
Mathematische
Darstellungen
verwenden
Mit symbolischen,
formalen, …
 einfache Terme und
Formeln aufstellen,
interpretieren und
auswerten
 Dreisatzschema und
 Schrägbilder und
Operatormodell nut Einem Modell eine
Modelle von Quadern
zen
 Näherungswerte erRealsituation zuord Diagramme in der
mitteln
nen
 Diagramme erstellen
Statistik
und Daten ablesen
 Plausibilitätsüber Ermitteln Lösungen
 Darstellungen analylegungen durchführen
im Modell
sieren und bewerten  Werte berechnen
 Heurismen anwenden  Überprüfen im Modell  Beziehungen zwi In Sprachen übersetgewonnene Ergebzen
 Darstellungen anschen Darstellungsnisse
an
der
Realsiwenden
formen erkennen
 Strategien für Gleituation
chungslösen nutzen
 Mathematische Re Darstellungsformen
geln und Verfahren
auswählen und
 Überprüfung von
anwenden
wechseln
Ergebnissen
 Ergebnisse deuten
 Fehler erkennen und
korrigieren
 Lineal, Geodreieck,
Zirkel
 Nachschlagen in
Schulbuch und Zusammenfassungen
Kommunizieren
 Arbeit, Lernwege und
Ergebnisse dokumentieren
 Überlegungen anderen mitteilen
 Ansätze und Ergebnisse in kurzen Beiträgen präsentieren
 Überlegungen anderer verstehen, überprüfen und darauf
eingehen
 Daten und Informationen entnehmen,
verstehen und wiedergeben
 Umgang mit Kritik
 Aufgaben im Team
bearbeiten
Inhaltsbezogene Kompetenzen (Leitideen) Jg 5/6 – Tabellarische Übersicht
L1
Zahlen und Operationen
5/6
 Zahlbereichserweiterung
von N nach Q begründen
 Rationale Zahlen angemessen darstellen
 Rationale Zahlen ordnen
und vergleichen
 Brüche deuten
 Kürzen und Erweitern




L2
Größen und Messen
 Größen messen
 Winkel schätzen und
messen
 Maßstäbe nutzen
 Einheiten wählen
 Größen vergleichen und
schätzen
L3
Raum und Form
 ebene Figuren und räum-  Zuordnungen erkennen
liche Strukturen charak-  proportionale und antiterisieren und identifizieproportionale Zuordnunren
gen identifizieren, klassi Symmetrien erkennen
fizieren und nutzen
und begründen
 Zuordnungen darstellen
 Winkel, Strecken, Kreise
zeichnen
 Mit Zuordnungen modellieren
Punkte, Strecken und
Figuren im Koordinatensystem
 Grundaufgaben der Prozent- und
Zinsrechnung
Schrägbilder, Netze,
Körpermodelle
 Dreisatz
 Winkelgrößen berechnen 
Dezimalbruch und Prozen-  Umfang und Flächenintangabe als Darstellungshalt von Rechtecken
form
schätzen

Rechnen mit rationalen
 Oberflächeninhalt und
Zahlen
Volumen von Quadern

Rechnen im Kopf
 Formeln begründen
Runden und Überschlagen  Figuren und Körper ab
 Zahlterme
 Sachsituationen zu Zahltermen angeben
 Zahltermstrukturen erkennen und vergleichen
 Variablen in Formeln
 Rechengesetze erläutern,
begründen und anwenden
 Zusammenhänge zwischen Grundrechenarten
kennen und nutzen
schätzen
 Maßangaben entnehmen, maßstäbliche
Zeichnungen, Berechnungen mit gemessenen
Größen
L4
Funktionaler
Zusammenhang
einfache Winkelsätze
anwenden
Figuren spiegeln, drehen
und verschieben und
damit Muster erzeugen
L5
Daten und Zufall
 statistische Erhebungen planen und Daten erheben und
darstellen
 Häufigkeiten darstellen
 Daten bewerten
 einstufige Zufallsexperimente
identifizieren und durchführen
 Ergebnissen Wahrscheinlichkeiten zuordnen
 Additionsregel und Komplementärregel begründen und
anwenden
 Wahrscheinlichkeiten für
Prognosen nutzen
 Simulationen durchführen
und beurteilen
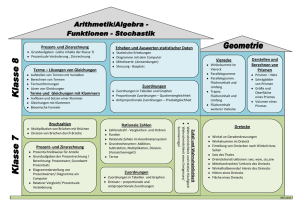
Klasse 5 – Schulinterner Arbeitsplan
Thema









Kreis und
Winkel






Rechnen
Leitideen
LS
5 Nds
Daten sammeln und die Zählergebnisse darstellen (Säulen- und
Balkendiagramme)
rationale Zahlen ordnen und vergleichen und auf verschiedene Arten situationsangemessen darstellen: Wortform, Stellenwerttafel, Zifferndarstellung, Zahlensymbole, Zahlenstrahl
große Zahlen im Zehnersystem, runden
Größen schätzen und vergleichen
Umrechnen von Größen
Größen in Kommaschreibweise
Grundrechenarten wiederholen (Begriffe)
evtl. römische Zahlzeichen
L1
L2
L5
Kapitel
I
senkrechte und parallele Lagen von Strecken und Geraden
Koordinatensystem: Grundlagen, Punkte einzeichnen,
Koordinaten bestimmen
Strecke, Strahl, Gerade, Punkt, Abstand
Kreis mit vorgeg. Radius zeichnen; Radius bestimmen
Kreisteile (Vollwinkel, gestreckter Winkel, rechter Winkel, spitzer,
stumpfer und überstumpfer Winkel)
Winkel schätzen, messen, zeichnen
L2
L3
Kapitel
II
L1
Kapitel
III
L3
Kapitel
IV
Längenmaße ( Wiederholung)  Flächen- und Volumeneinheiten
Flächen- und Rauminhalte messen, schätzen, vergleichen
Umfang und Flächeninhalt eines Rechtecks und daraus abzuleitender Figuren schätzen und berechnen
Oberfläche und Volumen eines Quaders und daraus abzuleitender
gKörper schätzen und berechnen
L1
L2
Kapitel
V
Brüche als Anteile, Begriffe „Zähler“ und „Nenner“
Brüche als Operatoren, Anteile und Verhältnisse
Erweitern und Kürzen (verfeinern und vergröbern der Teilung)
Vergleich von Brüchen; Ordnen; Zahlenstrahl (geeignet)
Brüche in Verbindung mit Längen, Gewichten, Zeiten
Prozentbegriff, „Prozent“ als „Hundertstelbruch“ ;
Umwandeln zwischen den drei Darstellungsformen Bruch, Dezimalbruch, Prozentsatz
Maßstäbe
L1
L2
Kapitel
VI
Unverzichtbare Inhalte

Zahlen und
Größen
(neu ab 2013/2014)





Zahlterme verbalisieren, visualisieren, vergleichen
Rechenbäume ( im Hinblick auf Struktur von Termen )
Vorrangregeln
vorteilhaft rechnen (Kommutativ-/ Assoziativ-/Distributivgesetz)
Schriftliches Addieren, Subtrahieren, Multiplizieren (auch mit Kommazahlen)
Division mit Rest (wichtig: Schreibweise !)
Potenzen
Methoden: * AB „Textaufgaben“, AB „Lernallee“ (Vorbereitung KA)
Figuren und
Körper




Symmetrien (nur kurz) (Faltübungen) (Kongruenzabbildungen in 6)
Eigenschaften von Vierecken wiederholen
Geometrische Körper und Figuren: Netze, Kantenmodelle,
Schrägbilder von Würfel und Quader
Medium: Polydron-Koffer
Flächen- und
Rauminhalte
Bruchzahlen












Klasse 6 – Schulinterner Arbeitsplan
Thema
Unverzichtbare Inhalte

Rechnen mit
Bruchzahlen
Winkelsummen,
Abbildungen
und
Symmetrien
Rationale
Zahlen
Zuordnungen










Daten
Addition und Subtraktion von nennergleichen und von ungleichnamigen Brüchen (dabei Kürzen und gemischte Schreibweise wiederholen)
Multiplikation von Brüchen
Division von Brüchen
Wiederholung des Rechnens mit Dezimalbrüchen
Verknüpfung der vier Grundrechenarten
Anwendungsaufgaben
Besondere Dreiecke
Berechnen von Winkeln mit Hilfe von Neben–, Scheitel–, Stufenwinkelsatz
Winkelsummensatz für Innenwinkel im Dreieck
Winkelsumme im Viereck
Kongruenzabbildungen: Spiegelung, Verschiebung, Drehung,
damit Muster erzeugen








negative Zahl, Gegenzahl, Betrag
Ordnung und Darstellung auf der Zahlengeraden
Erweiterung des Koordinatensystems, Quadrant
Veranschaulichung der Rechenoperationen Addition und Subtr.
Rechenregeln für die Multiplikation u. Division
Potenzen mit einfachen natürlichen Exponenten
Vergleich der Zahlbereiche IN, Z, Q
Permanenzprinzip, Rechengesetze, Minusklammern


Zuordnungen in unserer Umwelt darstellen und interpretieren
Graphen von Zuordnungen
Zuordnungsvorschriften
proportionale und antiproportionale Zuordnungen
Verhältnisgleichheit, Tabelle, Graph
Dreisatz „Rechnen für die Praxis“









Bruchschreibweise Prozentschreibweise
Prozentsatz – Prozentwert – Grundwert
Berechnung des fehlenden Wertes mit Hilfe vom Dreisatz
Heuristische Strategie: Problemlösung
Zinsrechnung
evtl. Zinseszins



Diagramme : Kreisdiagramme, Säulen- u. Balkendiagramme (Wh)
Daten analysieren: Minimum, Maximum, Median, Mittelwert
Diagramme auswerten und vergleichen

Prozente und
Zinsen
(neu ab 2013/2014)
Leitideen
LS
6 Nds
L1
Kapitel
I
L3
Kapitel
II
L1
Kapitel
III
L1
L4
L4
Kapitel
VI
L5
Kapitel
IV
Methode/Medium: * AB „Visualisierung Diagramme“
Excel (ca. 5 Stunden) – AB “Tabellenkalkulation”





Eingeben von Daten
Tabellen in Diagramme umwandeln (Säulen- u. Kreisdiagramme);
auch wenn Spalten nicht direkt nebeneinander liegen
nachträgliche Änderungen vornehmen
Diagramme bewerten
Kapitel
V
Jg 7 / 8
Prozessbezogene Kompetenzen Jg 7/8 – Tabellarische Übersicht
7/8
Mathematisch
argumentieren
Probleme mathematisch lösen
Mathematisch
modellieren
 Vermutungen präzisieren
 Problemstellung erfassen, fehlende Informationen beschaffen
 Einflussfaktoren finden und beschreiben
 Darstellungen für
reelle Zahlen nutzen
 Modelle wählen und
begründen
 Tabelle, Graph und
Term
 Informationen beschaffen und bewerten
Mathematische
Darstellungen
verwenden
 Heurismen anwenden  Ermitteln Lösungen
 Baumdiagramm
 Wissen für
 Darstellungen anim Modell
mehrschrittige Arguwenden
 Interpretieren Ergebmentationen nutzen
 Mathematische Vernisse, reflektieren und
 Argumentationsketten
fahren oder Konstrukvariieren Annahmen
aufbauen und betionen anwenden
gründen
 Lösungsvielfalt
 Heurismen
 Lösungswege vergleichen und bewerten
Mit symbolischen,
formalen, …
 Terme mit Variablen
 Tabellen, Graphen,
Terme und Gleichungen in linearen und
quadratischen Zusammenhängen nutzen


 Ergebnisse beurteilen

 Ursachen für Fehler
erklären

Kommunizieren
 Überlegungen anderen mitteilen
 Lösungsansätze und
Lösungswege präsentieren
 Überlegungen anderer verstehen, auf
Schlüssigkeit überTerme umformen
prüfen und darauf
Verfahren zur Lösung
eingehen
linearer und quadratischer Gleichungen
 Daten und Informationen strukturieren,
Taschenrechner zur
interpretieren, analyKontrolle
sieren und bewerten
dynamische Geomet Teamarbeit selbstriesoftware zur Darständig organisieren
stellung, Erkundung
und Ergebnisermittlung
 nutzen Medien zur
Informationsbeschaffung
Inhaltsbezogene Kompetenzen (Leitideen) Jg 7/8 – Tabellarische Übersicht
L1
Zahlen und Operationen
7/8
 Zahlbereichserweiterung
von Q nach R begründen
L2
Größen und Messen
 Längen durch Konstruktion maßstäblicher Figuren ermitteln
 Unterschiede zwischen
rationalen und reellen Zah-  Zusammengesetzte
len nennen
Größen berechnen und
interpretieren
 Rechnen mit dem Taschenrechner
 Rechnen bei reellen Zahlen
 Sachsituationen durch
Terme und Gleichungen
beschreiben
 Terme veranschaulichen
und interpretieren
 Termstrukturen erkennen
und vergleichen
 Terme und Gleichungen
nutzen
 Terme umformen
 Lineare und quadratische
Gleichungen, LGS lösen
 Fragen der Lösbarkeit und
Lösungsvielfalt
 Probe nutzen
 Parametervariationen
 Winkelgrößen mit Satz
des Thales berechnen
 Streckenlängen mit Satz
des Pythagoras berechnen
 Umfang und Flächeninhalt von gradlinig begrenzter Figuren schätzen
 Oberflächeninhalt und
Volumen von Prismen
 Formeln begründen
 Figuren und Körper abschätzen
 Messungen planen,
durchführen, Maßangaben entnehmen und Ergebnisse und Weg bewerten
L3
Raum und Form
 Kongruenzen erkennen
und begründen
 Konstruktion ebener
Figuren
 Aussagen zur Lösbarkeit
und Lösungsvielfalt bei
Konstruktionen
 Transversalensätze im
Dreieck
 Satz des Thales
 Satz des Pythagoras
L4
Funktionaler
Zusammenhang
 lineare und quadratische
Zuordnungen erkennen,
beschreiben und erläutern
 Streumaße und Boxplots
bestimmen und anwenden
 Zuordnungen darstellen
experimente identifizieren
und durchführen
 Datenpaare darstellen, lineare und quadratische Regres lineare und quadratische
sionen durchführen und nutFunktionen identifizieren,
zen
klassifizieren und nutzen  mehrstufige Zufalls Mit Zuordnungen modellieren
 Parameter deuten und
nutzen
 Kreis, Parallele, Mittel Funktionsgleichungen
senkrechte, Winkelhalaus Graphen bestimmen
bierende und Parabel als
Ortslinie
 Steigung als Änderungsrate
 Symmetrie, Kongruenz,
Lagebeziehungen beschreiben, begründen
und nutzen
L5
Daten und Zufall
 mehrstufige Zufallsexperimente im Baumdiagramm darstellen
 Pfadregeln begründen und
anwenden
Klasse 7 – Schulinterner Arbeitsplan
Thema
Geometrische
Konstruktionen
Unverzichtbare Inhalte
Methode/Medium: Geogebra
 Besondere Linien / Ortslinien (Kreis, Mittelsenkrechte, Winkelhalbierende)
 Entsprechende Konstruktionen mit Zirkel und Lineal
 Satz des Thales mit Beweis und Anwendungen
Leitideen
LS
7 Nds
L2
L3
Kapitel
II
L1
Kapitel
I
(weiter s. Kl. 8 – Kap. III)



Terme

und
Gleichungen 

Mathematische Zusammenhänge, geometrische Sachverhalte, Alltagsprobleme, ... durch Terme beschreiben
Terme umformen (Zusammenfassen, Ausmultiplizieren, Ausklammern)
Gleichungen aufstellen
Lösungsstrategien für einfache lineare Gleichungen (Tabelle, Probieren, Äquivalenzumformungen)
Sonderfälle (allgemeingültig, unlösbar)
ggf. Ungleichungen als Zusatz
(weiter s. unten „Lineare Zuordnungen ....“ und Kl. 8 - Kap I)
GTR *



Kongruenz
Methodentag /std
Grundfunktionen des grafikfähigen Taschenrechners
*(flexibel im Zusammenhang mit einem geeigneten Thema im 1.Hj einführen)


Kongruente Figuren
Dreieckskonstruktionen über gegebene Seiten und Winkel (Kongruenzsätze)
Begründungen mit Kongruenzsätzen
ggf. Konstruktion von Vierecken
L2
L3
Kapitel
IV
L1
L4
Kapitel
III
L5
Kapitel
V
L2
L3
Kapitel
VI
(weiter Körper s. unten)
Lineare
Zuordnungen
und lineare
Gleichungen
Methode/Medium: GTR
 Spezialfall: lineare Zuordnungen; ggf. Funktionsbegriff
 Darstellung: Tabelle, Zuornungsvorschrift (Gleichung), Graph (Gerade)
 Lineare Gleichungen und Gleichungssysteme mit zwei Variablen
(Darstellung und grafische Lösung)
Rechnen mit
Wahrscheinlichkeiten
 Beispiele für mehrstufige Zufallsversuche
 Urnenmodell mit / ohne Zurücklegen
 Darstellung mit Baumdiagrammen
 Reduzierte Baumdiagramme mit den relevanten Pfaden
 Pfadregeln, Gegenereignis
 Simulationen
Methode/Medium: Excel (abs. u. rel. Häufigk., Simulation, ca. 2 Std.)
(weiter s. Kl. 8 – Kap. I/II)




Diagramme, Beschriftung
Summe, Autosumme
Adressierung Konstante/ Variable
Markierung, Bereiche, Kopie

Flächeninhaltsformeln für Dreieck, Parallelogramm Trapez herleiten
und anwenden
Verschiedene Strategien zur Bestimmung von Flächeninhalten
(Näherungsverfahren, zerlegen,.ergänzen...)
Volumen und Oberflächeninhalt von Prismen (und aus ihnen zusammengesetzten Körpern)
Flächeninhal- 
te und Volu
mina
Klasse 8 – Schulinterner Arbeitsplan
Thema
Lineare Funktionen / Gleichungen und Gleichungssysteme
Reelle Zahlen
Unverzichtbare Inhalte
 Begriffe Funktion, Funktionsterm, Funktionswert, Nullstelle
 Schreibweise: f(x) ,
 Darstellung: Tabelle, Gleichung, Graph
Methode/Medium: GTR
 Spezialfall: lineare Funktion
 Parameter : Steigung, Achsenabschnitt
 Allgemeine Form der Geradengleichung y = mx+b bzw. f(x) = ..
 Zeichnung von Geraden ohne Wertetabelle
 Bestimmung der Geradengleichung aus 2 Punkten
 Lineare Regression
 Lineare Gleichungen und Gleichungssysteme mit 2 Variablen
(rechnerische Lösung: Gleichsetzungs-, Einsetzungs- und Additionsverfahren)
 Lösbarkeit von LGS
 ggf. Systeme mit 3 Variablen als Zusatz (GTR)






Quadratische
Funktionen und
Gleichungen










Pythagoras
Besondere
Linien und
Punkte im
Dreieck


Zahlbereichserweiterung von Q nach IR begründen
Unterschiede zwischen rationalen und reellen Zahlen
Näherungsverfahren (Intervallschachtelungen) beschreiben
und anwenden (u.a. Intervallhalbierung, Heron  Excel)
Quadratwurzel
Rechnen mit Quadratwurzeln (Wurzelgesetze)
Multiplizieren von Summen
Binomische Formeln algebraisch und geometrisch herleiten
und anwenden
Quadratische Funktionen (Graphen und Gleichungen)
Normal- und Scheitelform
Parameter quadratischer Funktionen deuten
Quadratische Funktionen identifizieren und klassifizieren
Modellieren mit Parabeln; Optimierungsaufgaben
Leitideen
LS
8 Nds
Kapitel
L1
L4
I
II
Kapitel
L1
IV
Kapitel
L3
V
L1
L4
Quadratische Gleichungen lösen (quadratische Ergänzung,
pq-Formel, Vieta)
Anwendungen, Modellierungen
Quadratische Regression
ggf. Programm zur Lösung einer quadrat. Gl. (GTR)
Satz des Pythagoras, Katheten- und Höhensatz
Anwendungen bei Berechnungen (Abstände in Ebene
und Raum) und ggf. Flächenumwandlungen
Methode/Medium: DGS (Geogebra)
 Besondere Linien im Dreieck (neu: Höhen, Seitenhalbierende)
– Umkreis, Inkreis, Schwerpunkt
 Ortslinien (neu: Parabel)
 Dreieckskonstruktionen über gegebene Seiten, Winkel und
Dreieckstransversalen
L2
L3
Kapitel
VI
Kapitel
L2
L3
III
Jg 9 / 10
Prozessbezogene Kompetenzen Jg 9/10 – Tabellarische Übersicht
Mathematisch
argumentieren
9/10  Erläutern mathematischer Zusammenhänge
 Wissen für
mehrschrittige Argumentationen kombinieren
 Formale und symbolische Elemente nutzen
 Argumentationsketten
aufbauen, analysieren und bewerten
Probleme mathematisch lösen
Mathematisch
modellieren
Mathematische
Darstellungen
verwenden
Mit symbolischen,
formalen, …
Kommunizieren
 Heurismen auswählen und anwenden
 Modelle wählen, variieren und verknüpfen
 Schrägbilder und
Modelle von Körpern
 Überlegungen anderen mitteilen
 Änderungsrate nutzen
 Verwenden Rekursionen
 Vierfeldertafel
 Tabellen, Graphen,
Terme und Gleichungen in funktionalen
Zusammenhängen
nutzen
 Analysieren und bewerten verschiedene
Modelle
 Terme umformen
 Gleichungslöseverfahren auswählen
 Tabellenkalkulation
und CAS zur Darstellung, Erkundung und
Ergebnisermittlung
 Formelsammlung
 Problembearbeitungen präsentieren
 Überlegungen anderer verstehen, auf
Schlüssigkeit und
Vollständigkeit überprüfen und darauf
eingehen
 beurteilen und bewerten Teamarbeit und
entwickeln weiter
Inhaltsbezogene Kompetenzen (Leitideen) Jg 9/10 – Tabellarische Übersicht
L1
Zahlen und Operationen
9/10
L2
Größen und Messen
 Rechengesetze für Poten-  Winkelgrößen und Strezen begründen und anckenlängen berechnen
wenden
 Umfang und Flächenin Gleichungen lösen
halt eines Kreises
 Oberflächeninhalt und
Volumen von Körpern
 Formeln begründen
 Figuren und Körper abschätzen
L3
Raum und Form
 Ähnlichkeiten erkennen
und begründen
 Schrägbilder, Netze,
Körpermodelle
L4
Funktionaler
Zusammenhang
 Funktionale Zusammenhänge erkennen, beschreiben und erläutern
 Funktionen identifizieren,
klassifizieren und nutzen
 Ähnlichkeit erfassen und
nutzen
 Funktionsgleichungen aus
Graphen bestimmen
 Potenz-, Exponential- und
Sinusfunktion
 lineares, potentielles und
exponentielles Wachstum
und deren Überlagerung
 mittlere und lokale Änderungsrate beschreiben und
interpretieren
 Graphen und Ableitungsgraphen auseinander entwickeln, beschreiben und
begründen
 Ableitungsfunktion von
ganzrationalen Funktionen
bis 4. Grades, x 
1:(a∙x+b) und x
sin(a∙x+b)
 Summen- und Faktorregel
anwenden
 Ableitung bei Sachproblemen anwenden
 Funktionen und ihre Graphen untersuchen
L5
Daten und Zufall
 Datenpaare darstellen, Regressionen durchführen und
nutzen
 Kenntnisse nutzen, um statistische Aussagen mit Hilfe
von Baumdiagrammen oder
Vierfeldertafel zu interpretieren
Klasse 9 – Schulinterner Arbeitsplan
Thema
Ähnlichkeit /
Trigonometrie
Stochastik
Funktionen mit
Potenzen
Unverzichtbare Inhalte
-
ähnliche Figuren erkennen
Längenverhältnisse bestimmen und vergleichen
Verhältnisse am rechtwinkligen Dreieck
(Definition von Sinus, Kosinus, Tangens)
Winkelsätze am Dreieck ( Sinussatz; Kosinussatz)
Sinus, Kosinus, Tangens und Zusammenhänge am
Einheitskreis ( > 90°)
Sinus- und Kosinusfunktion   sin bzw. cos
-
Ereignis / Gegenereignis
Verknüpfungen, Schnittmenge, Vereinigungsmenge
abhängige und unabhängige Ereignisse
Additionssatz
Baumdiagramme, Vierfeldertafeln anfertigen und deuten
Baumdiagramme umkehren, doppelte Baumdiagramme
Denkfehler erkennen und aufdecken
-
große und kleine Zahlen, wissenschaftl. Schreibweise
(Zehnerpotenzen, GTR)
Rechengesetze für Potenzen und Wurzeln
Potenzen mit gleicher Basis, gleichem Exponenten
Potenzen mit ganzzahligen und rationalen Exponenten
Schreibweisen: Wurzeln als Potenzen
Potenzgleichungen lösen
Exponentialgleichungen lösen mit Logarithmen
(ggf. Logarithmengesetze)
-
-
Wachstum
Berechnungen
am Kreis
Leitideen
LS
9 Nds
L3
Kapitel
L2
I (1-6)
L4
II (1-6)
Kapitel
L5
III
L1
Kapitel
L4
V
L5
VI
-
Potenzfunktionen: Graphen identifizieren, Eigenschaften
erkennen und zuordnen
Funktionsgleichungen aus Graphen entwickeln
-
lineares Wachstum
exponentielles Wachstum (Verdopplungs- und Halbwertszeit)
rekursive und explizite Formeln
L4
Kapitel
L5
VII
-
Kreis: Flächeninhalt und Umfang; Kreisring
Kreissektor, -bogen, -segment
Berechnungen an zusammengesetzten Kreisfiguren
Bogenmaß
Näherungsverfahren zur Bestimmung von 
L3
Kapitel
L2
IV (1-4)
Klasse 10 – Schulinterner Arbeitsplan
Thema
Unverzichtbare Inhalte
Darstellung und
Berechnung
von Körpern
-
Änderungsrate
und
Ableitung
- (ggf. Basiswissen Funktionen - Wh., s. AH)
- Mittlere Änderungsrate
- Momentane (lokale) Änderungsrate, Tangentensteigung,
Ableitung an einer Stelle (Differenzenquotient,
h-Methode )
- Tangentengleichung berechnen
- Ableitungsfunktion f’ , Graphen von f und f’ auseinander
entwickeln
- Ableitungsregeln für Potenzfunktionen
(Potenz-, Summen- und Faktorregel, incl. x-1, x )
Ganzrationale
Funktionen
-
-
Weitere Funktionen und
Modellierung
-
Darstellen von Körpern
(Projektionen, Schrägbilder, Netze, Körpermodelle)
Zylinder: Volumen, Mantel- und Oberfläche
Pyramiden, Kegel: Volumen, Mantel- und Oberfläche
Kugel: Volumen, Oberfläche
Perspektive (siehe Kunstunterricht Kl. 9)
Untersuchung ganzrationaler Funktionen (Symmetrie,
Monotonie, Extrempunkte, Wendepunkte), rechnerisch
und vor allem mit GTR
Kriterien
Optimierungsaufgaben
-
Exponentialfunktionen (ggf. Logarithmusfunktion als
Umkehrfunktion)
Sinus- und Kosinusfunktion (Einfluss der Parameter,
Funktionsterme deuten und bestimmen)
Ableitung von Sinus- und Kosinusfunktion
Ableitung von sin(ax+b), 1/(ax+b), („Kleine Kettenregel“)
-
Modellierung von Wachstumsprozessen
Modellierung periodischer Prozesse
Regression
-
Leitideen
LS
10 Nds
L3
Kapitel
L2
I
Kapitel
L4
II
Kapitel
L4
III
L4
Kapitel
IV
L5
V
GTR-Curriculum Sek I
(zunächst noch vorläufig)
Verbindlich einzuführende Menüpunkte und Befehle des TI-84 Plus
Die folgende Zusammenstellung enthält die Taschenrechnerbefehle, die alle Schülerinnen und Schüler am Ende der
Sek I mindestens kennen müssen, um den Rechner effektiv einsetzen zu können und später den Abituranforderungen
hinsichtlich des Taschenrechnereinsatzes gerecht zu werden.
Dies ist zugleich ein Beitrag des Faches zum Methodenkonzept der Schule hinsichtlich des Einsatzes von Medien.
Jg
7
Mögl. unterrichtlicher
Kontext
Einführung GTR /
Terme und Gleichungen
TR-Befehl
Erläuterungen/Bemerkungen
+, –, x, 
- (Vorz.) / – (Rechenz.)
( , ) / 
Rechenarten
Unterscheidung !
Klammern / Komma
MODE
FLOAT 0 1 .....
Anzahl der Nachkommastellen
DEL / INS / QUIT
Löschen / Einfügen
ANS / ENTRY
STO> ALPHA A, ...
Speichern
2
x /^
Potenzen
MATH MATH
1: >Frac
2: >Dec
MEM MEMORY
u.a. Reset
Mehrstufige Zufallsversuche
MATH PRB
1: rnd
5: randInt(
Erzeugen von Zufallszahlen –
Simulieren von Zufallsexperimenten
Lineare Funktionen /
LGS mit 2 Variablen
Y= / X, T, , n /
Eingabe von linearen Funktionen
GRAPH / TRACE / TABLE
WINDOW / TABLSET
ZOOM ZOOM
ZOOM MEMORY
CALC
1: value
2: zero
5: intersect
Wahl des richtigen Ausschnitts
Verstellen der Zoomfaktoren (!)
Jg
8
Mögl. unterrichtlicher
Kontext
Parabeln /
Quadratische Gleichungen
TR-Befehl
{ , } und STO> L1 …
2
(im Zshg. mit Y= L1 * x + L2 * x + L3)
CALC
3 : minimum
4 : maximum
Streudiagramme
Erläuterungen/Bemerkungen
Eingabe und Speichern von Listen
zur Parametervariation im Funktions-term
MODE
… PAR …
Parameterdarstellung der Parabel
PRGM
Ggf. Programm zur pq-Formel
STAT EDIT
1: Edit
Eingabe von Listen direkt in Tabellen
oder s.o. mit geschw. Klammern
LIST NAMES
LIST OPS
5:seq(
Regression (linear, quadratisch)
STAT PLOT
ZOOM ZOOM
9: ZoomStat
Darstellung von Diagrammen
STAT CALC
4: LinReg(ax+b)
5: QuadReg
VARS Y-VARS
1: Function …
Reelle Zahlen
Zum direkten Speichern der Regressionsfunktion
Berechnung von n-ten Wurzeln;
Klammern beachten(!)
MATH MATH
5. x
PRGM
Ggf. Programme zum Intervallhalbierungs – und Heronverfahren
Jg
Mögl. unterrichtlicher
Kontext
TR-Befehl
9
Trigonometrie
SIN, COS, TAN sowie SIN
MODE
RADIAN DEGREE
Flächen und Körper

Funktionen mit Potenzen
MODE
....SCI ...
....SEQ ...
Erläuterungen/Bemerkungen
–1
etc.
Berechnungen am rechtwinkligen
Dreieck
(Allgemeine) Sinusfunktion mit Bogenmaß
Wissenschaftliche Schreibweise
Folgenmodus im Zshg. mit exponentiellem Wachstum
EE
Modellierungen / Regressionen
LOG
Logarithmen zur Lösung von Exponentialgleichungen
STAT CALC
6: CubicReg
7: QuartReg
0: ExpReg
A: PwrReg
C: SinReg
s. a. Klasse 8
Erläuterungen/Bemerkungen
Jg
Mögl. unterrichtlicher
Kontext
TR-Befehl
10
Differentialrechnung
MATH MATH
8: nderive(
CALC
3: minimum
4: maximum
.
6: dy/dx
DRAW DRAW
5: Tangent(
MATRIX EDIT
MATRIX MATH
B: rref(
Bei „Steckbriefaufgaben“:
Eingabe der erweiterten Koeffizientenmatrix von LGS
Lösen von LGS