Übung 1 - Institut für Elektrische Energiewandlung

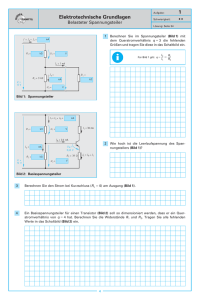
Universität
Stuttgart
Institut für Leistungselektronik
und Elektrische Antriebe
Abt. Elektrische Energiewandlung
Prof. Dr.-Ing. N. Parspour
Übung 1
Komplexe Rechnung
Einschwingvorgänge 1
Aufgabe 1.1
(Komplexe Rechnung)
Im Bild 1.1 ist eine R-L-Reihenschaltung gegeben. Die Schaltung wird an einer sinusförmigen
Wechselspannung betrieben.
Bild 1.1 R-L-Reihenschaltung
Von der Schaltung sind folgende Daten bekannt:
Spannungsquelle
Spannungseffektivwert:
U = 100 V
Frequenz:
f = 50 Hz
Ohmscher Widerstand
R = 150 
Induktivität
L = 550 mH

Fragen
1.
Zeichnen Sie das Ersatzschaltbild erneut auf und tragen Sie Zählpfeile und Bezeichner für den
Strom und sämtliche Spannungen ein.
2.
Berechnen Sie den Strom und die Teilspannungen an R und L nach Betrag und Phase.
3.
Berechnen Sie die komplexe Scheinleistung S, den Wirkleistungs- und Blindleistungsanteil.
Einführung in die Elektrotechnik 2
Übung 1: Komplexe Rechnung, Einschwingvorgänge 1
- 1/4 -
Aufgabe 1.2
(Komplexe Rechnung)
Im Bild 1.2 ist das Ersatzschaltbild eines elektrischen Netzwerks gegeben. Die Schaltung wird an einer
sinusförmigen Wechselspannung betrieben. Nachfolgend sollen sämtliche Ströme, Spannungen sowie die
umgesetzte Wirkleistung und Blindleistung in der Schaltung berechnet werden.
Bild 1.2 Elektrisches Wechselstromnetzwerk
Von der Schaltung sind folgende Daten bekannt:
Spannungsquelle
Spannungseffektivwert:
U = 400 V
Frequenz:
f = 1200 Hz
Ohmsche Widerstände
R1 = 150 
R2 = 200 






R3 = 350 

Induktivitäten
L1 = 10 mH
L2 = 20 mH
Kondensator
C = 1,0 µF
Fragen
1.
Zeichnen Sie das Ersatzschaltbild erneut auf und tragen Sie Zählpfeile und Bezeichner für
sämtliche Ströme und Spannungen ein.
2.
Berechnen Sie für jeden Zweig des Netzwerks die Teilimpedanzen und stellen Sie die Impedanzen
in kartesischer Schreibweise und in exponentieller Schreibweise dar.
Einführung in die Elektrotechnik 2
Übung 1: Komplexe Rechnung, Einschwingvorgänge 1
- 2/4 -
3.
Berechnen Sie den Strom I1.
4.
Berechnen Sie die Ströme I2 und I3.
5.
Berechnen Sie die Teilspannungen an den ohmschen Widerständen, den Induktivitäten und am
Kondensator jeweils nach Betrag und Phase.
6.
Berechnen Sie die komplexe Scheinleistung S, den Wirkleistungsanteil P und den
Blindleistungsanteil Q der gesamten Schaltung.
7.
Prüfen Sie die Ergebnisse aus Frage 6 mithilfe eines alternativen Rechenwegs.
8.
Zeichnen Sie das Ersatzschaltbild aus Bild 1.2 erneut auf und ergänzen Sie dieses durch ein
weiteres Bauelement, so dass der Blindleistungsbedarf der Schaltung aufgehoben wird, d. h. dass
die Spannungsquelle nur noch Wirkleistung liefern muss? Berechnen Sie den Wert des dafür
erforderlichen Bauelementes.
Einführung in die Elektrotechnik 2
Übung 1: Komplexe Rechnung, Einschwingvorgänge 1
- 3/4 -
Aufgabe 1.3
(Einschwingvorgang)
Im nachfolgenden Bild 1.3 ist eine einfache R-C-Reihenschaltung gegeben. Die R-C-Schaltung wird zur
Zeit t = 0 über den Schalter S an die Gleichspannungsquelle mit der Spannung U geschaltet. Der
Kondensator C war vor dem Schließen des Schalters ungeladen. Nachfolgend soll nun der Ladevorgang
des Kondensators untersucht werden.
Bild 1.3 Ladevorgang eines Kondensators
Von der Schaltung sind folgende Daten bekannt:
Spannungsquelle
Spannung
U = 24 V
Ohmscher Widerstand
R1 = 40 

Kondensator
1.
Kapazität
C = 100 µF
Anfangsbedingung
u C (t  0)  0
Zeichnen Sie das Ersatzschaltbild erneut auf und tragen Sie Zählpfeile und Bezeichner für
sämtliche Ströme und Spannungen ein.
2.
Geben Sie die Grundgesetze für die beiden Elemente R und C an und stellen Sie die
Maschengleichung sowie die Differentialgleichung für die energiekennzeichnende Größe auf.
Begründen Sie, welche Größe energiekennzeichnend ist!
3.
Berechnen Sie die zeitlichen Verläufe sämtlicher elektrischer Größen für t  0 und stellen Sie sie
in Diagrammen qualitativ dar.
4.
Welche Energie WC ist am Ende des Ladevorganges im Kondensator gespeichert? Welche Energie
WR wurde im Ohmwiderstand R während des Ladevorganges in Wärme umgesetzt?
Einführung in die Elektrotechnik 2
Übung 1: Komplexe Rechnung, Einschwingvorgänge 1
- 4/4 -