Quelle - JavaPsi
Werbung

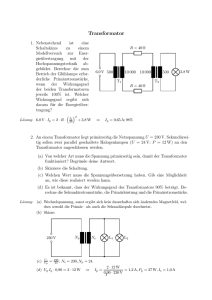
TR – Transformator Blockpraktikum Herbst 2007 Moritz Stoll, Marcel Schmittfull (Gruppe 2b) 25. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 1.1 Unbelasteter Transformator 1.2 Belasteter Transformator . 1.3 Leistungsanpassung . . . . 1.4 Verluste . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 3 3 4 2 Versuchsdurchführung 4 3 Auswertung 3.1 Aufgabe 1 3.2 Aufgabe 2 3.3 Aufgabe 3 3.4 Aufgabe 4 3.5 Aufgabe 5 3.6 Aufgabe 6 5 5 5 6 6 6 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 GRUNDLAGEN 1 TR 2 Grundlagen Ein Transformator dient v.a. dazu, Wechselspannungen in niedrigere oder höhere Wechselspannungen zu transformieren. Der typische Aufbau mit zwei Spulen mit einem gemeinsamen Eisenkern ist in Abb. 1 skizziert. Am Primärstromkreis wird eine Wech- Abbildung 1: Transformator mit Primär- und Sekundärspule, sowie einem gemeinsamen Eisenkern (Quelle: Wikipedia). selspannung Up = U1 angelegt, so dass der magnetische Fluss Φ im Eisenkern abwechselnd auf- und abgebaut wird. Dies induziert eine Wechselspannung US = U2 im Sekundärstromkreis. Die Amplitude von U2 kann dabei durch das Verhältnis der Windungszahlen der Spulen geregelt werden. 1.1 Unbelasteter Transformator Ein Transformator wird unbelastet genannt, wenn kein ohmscher Verbraucher an der Sekundärseite angeschlossen ist. Im Primärkreis kompensiert wegen der Maschenregel die Induktionsspannung U1,ind die angelegte Spannung U1 , d.h. U1 = −U1,ind = n1 Φ̇, wobei n1 die Windungszahl der Primärspule ist. Wegen des gemeinsamen Eisenkerns induziert Φ̇ auf der Sekundärseite die Spannung U2 = U2,ind = −n2 Φ̇. Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull 1 GRUNDLAGEN TR 3 Die Spannungen verhalten sich also wie die Windungszahlen U1 n1 =− . U2 n2 Das Minuszeichen beschreibt dabei die Phasenverschiebung um 180◦ zwischen U1 und U2 . Im Primärkreis sind Strom und Spannung wegen Z1 = U1 /I1 = iωL um ϕ1 = 90◦ phasenverschoben, d.h. der Strom ist ein reiner Blindstrom I1,wirk = I1,max cos ϕ1 = 0, I1,blind = I1,max sin ϕ1 = I1,max und führt zu keiner Leistung im Primärkreis. Da im Sekundärkreis des unbelasteten Transformators kein Strom fließt, ist die Energieerhaltung erfüllt. 1.2 Belasteter Transformator Schließt man an den Sekundärstromkreis einen ohmschen Verbraucher an, so fließt dort ein Strom I2 = U2 /R, der mit der Spannung U2 in Phase ist (ohmscher Widerstand), d.h. ϕ2 = 0◦ . Wegen Energieerhaltung müssen die Wirkleistungen auf Primär- und Sekundärseite gleich groß sein P 1 = P2 U1,eff I1,eff cos ϕ1 = U2,eff I2,eff cos ϕ2 I1,eff U2,eff n2 ⇒ cos ϕ1 · = =− . I2,eff U1,eff n1 Wenn kein ohmscher Widerstand im Primärkreis (ϕ = 0◦ ) wirkt, verhalten sich also die Ströme in Primär- und Sekundärkreis gerade umgekehrt zu den Windungszahlen und Spannungen. 1.3 Leistungsanpassung Spannungsquellen haben in der Regel einen Innenwiderstand Ri . An einem ohmschen Verbraucher Rv fließt deshalb der Strom Iv = U0 , Ri + Rv so dass die Leistung Pv = U0 Iv = Rv Iv2 = Rv U02 (Ri + Rv )2 aufgebracht wird. Diese Leistung wird bzgl. Rv maximal, wenn dPv (Ri + Rv )2 − 2Rv (Ri + Rv ) Rv − Ri = U02 = U02 =0 4 dRv (Ri + Rv ) (Ri + Rv )3 Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull 2 VERSUCHSDURCHFÜHRUNG TR 4 gilt, d.h. für Rv = Ri . Für eine beliebige Spannungsquelle mit Innenwiderstand wird der Spannungsquelle also genau dann die größte Leistung entnommen, wenn die Last gleich dem Innenwiderstand der Spannungsquelle ist. Man erhält als Maximalleistung Pmax = 1.4 U02 . 4Ri Verluste Die Rechnungen gelten nur für ideale Transformatoren. In der Realität haben die Drähte der Spulen ohmsche Widerstände. Wirbelströme im Eisenkern erwärmen diesen und disspieren deshalb ebenfalls Energie. Durch die beim dauernd abwechselnden Magnetisieren des Eisenkerns entstehende Hysterese geht weitere Energie verloren. Man versucht durch geeignete Anordnungen und Geometrien der Spulen, sowie durch geeignete Materialien diese Verluste zu minimieren. 2 Versuchsdurchführung Der Schaltplan des Versuchs ist in Abb. 2 gezeigt. Zunächst werden bei unbelastetem Abbildung 2: Schaltplan zur Versuchsdurchführung (Quelle: Anleitung). Sekundärkreis für unterschiedliche Primärspannungen U2 , UΦ , I1 und ϕ = ϕ1 gemessen. Anschließend werden bei belastetem Sekundärkreis und konstanter Primärspannung U1 für verschiedene Sekundärströme I2 die Größen I1 , U2 , UΦ und ϕ gemessen. Zuletzt wird die Abhängigkeit der Sekundärspannung U2 (I2 ) vom Sekundärstrom I2 gemessen (Primärspannung U1 nicht konstant). Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull 3 AUSWERTUNG 3 3.1 TR 5 Auswertung Aufgabe 1 Aus der ersten Versuchsreihe bekommen wir das Übersetzungsverhältnis ü = 9, 961 ± 0, 013 und die Phasenverschiebung ϕ = 57, 6±1, 7◦ für den unbelasteten Transformator. Ein idealer Transformator hätte eine Phasenverschiebung von 90°. 3.2 Aufgabe 2 In Abb. 3 sind U2 , I1 und ϕ als Funktion vom Sekundärstrom I2 gezeigt. Wie man sieht Abbildung 3: U2 , I1 und ϕ in Abhängigkeit vom Sekundärstrom I2 . sinkt U2 mit zunehmendem Sekundärstrom I2 . Dies lässt sich wie folgt erklären. Die Maschenregel im belasteten Sekundärkreis liefert (U2,ind Induktionsspannung an der Sekundärspule, R2,i Innenwiderstand der Sekundärspule, R2 Sekundärlast) U2,ind = R2,i I2 + R2 I2 = R2,i I2 + U2 ⇒ U2 = U2,ind − R2,i I2 , d.h. U2 (I2 ) ist eine Gerade mit negativer Steigung. Der Betrag der Steigung ist dabei der Innenwiderstand R2,i . Um den Innenwiderstand R2,i zu berechnen, ermittelt man also die Steigung von U2 (I2 ): Aus dem Kurzschlussstrom I2 (U2 = 0) = 1, 79A und der Leerlaufspannung U2 (I2 = 0) = 4, 00V folgt 4, 00V R2,i = = 2, 23Ω. 1, 79A Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull 3 AUSWERTUNG TR 6 Im Leerlauf beträgt der Primärstrom I1 = 5, 33mA, woraus der Magnetisierungsstrom (Blindstromanteil) IM = 2, 86mA und der Verluststrom (Wirkstromanteil) IV = 4, 50mA folgen. 3.3 Aufgabe 3 Für einen unbelasteten Transformator gilt für das Verhältnis von Primär- zu Sekundärstrom (vgl. oben) n2 I1 =− . I2 n1 Für einen Transformator mit ohmscher Belastung erhält man aus den Kirchhoffschen Regeln (vgl. Anleitung) R + iωL2 I1 =− , I2 iωM wobei L2 die Induktivität der Sekundärspule und M die Gegeninduktivität ist. In Abb. 4 sind die dazugehörigen Zeigerdiagramme für Primär- und Sekundärstrom schematisch abgebildet. Abbildung 4: Zeigerdiagramme für Primär- und Sekundärstrom I1 und I2 für einen unbelasteten (links) und einen belasteten Transformator (rechts). Der Fluss Φ ist proportional zu I1 , d.h. Φ = LI1 . In der Schaltung wird die Flussspannung UΦ gemessen, die proportional zum Fluss ist. Den linearen Zusammenhang zwischen Fluss Φ und Primärstrom I1 kann man in Abb. 5 gut erkennen. 3.4 Aufgabe 4 Wirk- und Blindstromanteil des Primärstroms I1 für verschiedene Sekundärströme I2 sind in Abb. 6 gezeigt. 3.5 Aufgabe 5 Der Wirkungsgrad η in Abhängigkeit der Sekundärleistung P2 ist in Abb. 7 gezeigt. Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull 3 AUSWERTUNG TR 7 Abbildung 5: Fluss Φ bzw. Flussspannung UΦ als Funktion vom Primärstrom I1 . Abbildung 6: Wirk- und Blindstromanteil des Primärstroms I1 für verschiedene Sekundärströme I2 . Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull 3 AUSWERTUNG TR 8 Abbildung 7: Wirkungsgrad η als Funktion der Sekundärleistung P2 . 3.6 Aufgabe 6 In Abb. 8 ist die abgegebene Leistung P2 (R2 ) als Funktion des Lastwiderstands R2 aufgetragen. Man kann ein Maximum der Leistung für R2 = 6, 1Ω ablesen. Der gesamte auf der Sekundärseite wirkende Innenwiderstand1 R2,i,ges ergibt sich aus der Steigung der Regressionsgeraden von U2 (I2 ) zu R2,i,ges = 6, 13Ω. Dies bestätigt die obige Rechnung (Leistungsanpassung), nach der einer Spannungsquelle mit Innenwiderstand die maximale Leistung entzogen wird, wenn die Last gleich dem Innenwiderstand der Quelle ist. Der soeben direkt aus Messung 3 bestimmte insgesamt wirkende Innenwiderstand R2,i,ges auf Sekundärseite lässt sich auch aus dem in Messung 2 bestimmten Innenwiderstand R2,i = 2, 23Ω der Wicklungen der Sekundärspule und dem gemessenen Widerstand R1,i = 400Ω auf Primärseite berechnen. Der insgesamt wirkende Innenwiderstand R2,i,ges ist die Summe aus dem Innenwiderstand R2,i der Sekundärspule und dem transformierten Primär-Widerstand R̃1,i , den der Sekundärkreis durch die Kopplung über die Spulen erfährt: R2,i,ges = R2,i + R̃1,i . (1) 1 Auf der Sekundärseite wirkt zum einen der Innenwiderstand R2,i der Wicklungen der Sekundärspulen. Zum anderen beeinflusst der Innenwiderstand R1,i der Primärspule die Spannung an der Primärspule und somit auch die Spannung an der Sekundärspule. Man kann deshalb den auf die Sekundärspule wirkenden Primär-Innenwiderstand als zusätzlichen Innenwiderstand auf der Sekundärseite auffassen. Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull 3 AUSWERTUNG TR 9 Abbildung 8: Leistung P2 (R2 ) (in Watt) als Funktion des Lastwiderstands R2 (in Ω). Zur Berechnung des auf Sekundärseite wirkenden, transformierten Primär-Widerstands betrachte man die Spannungen U10 , U20 und Ströme I1 , I2 an Primär- und Sekundärspule, für welche die Transformationsformeln U10 n1 =− , U20 n2 I1 n2 =− I2 n1 gelten. Für die Widerstände R1,i (Primärspule) und R̃1,i (transformierter Widerstand an Sekundärspule) gilt das ohmsche Gesetz R1,i = U10 , I1 R̃1,i = U20 . I2 Daraus folgt die Widerstandstransformation R1,i n2 = 12 = ü2 n2 R̃1,i ⇒ R̃1,i = R1,i . ü2 Setzen wir diesen auf Sekundärseite wirkenden Widerstand nun in (1) ein, so erhalten wir mit ü = 9, 961, R1,i = 400Ω und R2,i = 2, 23Ω R2,i,ges = R2,i + R1,i 400Ω = + 2, 23Ω = 6, 26Ω. ü2 9, 9612 Dieser Wert ist dem tatsächlich wirkenden Innenwiderstand R2,i,ges von 6, 13Ω und dem Lastwiderstand von 6, 1Ω mit maximaler Leistung sehr nahe und bestätigt somit Leistungsanpassung und Widerstandstransformation. Version: 25. Oktober 2007 Moritz Stoll, Marcel Schmittfull