Elementare Einführung in die Physik II – SS 2013 – ¨Ubungsblatt 7

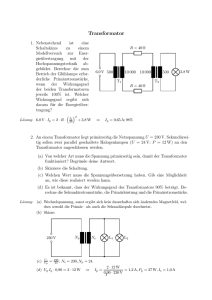
Prof. Dr. Jürgen Eschner
Bau E26 Zi. 3.02
T +49 (681) 302 58016
v +49 (681) 302 58018
k [email protected]
Elementare Einführung in die Physik II
– SS 2013 –
Übungsblatt 7
Aufgabe 1: Der Transformator
Bei einem Transformator werden zwei Spulen auf ein Joch aus Weicheisenkern gewickelt, um damit
Spannungen auf höhere oder niedrige Werte zu transformieren. Der magnetische Fluss φ ist überall
mit der Windungszahl N .
im Eisenkern gleich, und es gilt Uind = −N dφ
dt
a) Beschreiben Sie den Vorgang der Spannungsinduktion in der Sekundärspule über den magnetischen Fluss im Joch.
b) Wie ergibt sich das Spannungsverhältnis aus dem Übersetzungsverhältnis der Windungen am
Transformator?
c) Wie ergibt sich das Stromverhältnis im Leerlaufbetrieb, d.h. wenn keine Ohm’schen Verluste
existieren?
Jetzt habe die Primärspule des Transformators 400 und die Sekundärspule 8 Windungen.
d) Wird die Spannung herauf oder herunter gesetzt?
e) Welche Leerlaufspannung liegt an der Sekundärspule an, wenn die Spannung der Primärspule
220V beträgt?
f) Wie groß ist der Sekundärstrom bei einem Primärstrom von 0,1 A, wenn man Verluste vernachlässigt?
Aufgabe 2: Erzwungene elektromagnetische Schwingungen
Der in der Abbildung zu sehende Reihenschwingkreis wird mit einem Wechselspannungsgenerator
der Spannung U (t) = U0 · cos(ωt) angetrieben.
L
R
C
U~
a) (Wiederholung aus Vorlesung) Stellen Sie die lineare Differentialgleichung 2. Ordnung auf,
indem Sie die Maschenregel für den Schaltkreis anwenden.
b) Zeigen Sie durch Einsetzen, dass I(t) = I0 · sin(ωt − φ) Lösung der in a) aufgestellten Differentialgleichung ist.
c) Mit welcher Frequenz schwingt nun bei dieser erzwungenen Schwingung das System?
d) Wie lautet die Phasenverschiebung zwischen Spannung und Strom im Kreis?
e) Wie lautet die Amplitude des Stroms I0 ? Was passiert, wenn der kapazitive und induktive
Widerstand gleich groß sind? Welche Frequenz muss dazu von außen angelegt werden?
Aufgabe 3: Energien im LC-Schwingkreis
Betrachten Sie einen Kondensator der Kapazität C = 2 µF in einem ungedämpften LC-Schwingkreis,
der zunächst von einer Spannungsquelle auf 20 V geladen werden soll. Danach wird der Schalter S
umgelegt, sodass der Kondensator nur noch mit der Spule mit L = 6 µH verbunden ist.
S
U
C
L
a) Berechnen Sie nach dem Umlegen des Schalters die Frequenz des Schwingkreises.
b) Berechnen Sie die Anfangsladung q0 des Kondensators sowie die maximale Amplitude der
Stromstärke I0 .
c) Berechnen Sie die elektrische Energie We , die magnetische Energie Wm und die Gesamtenergie
Wges zum Zeitpunkt t = 1 s, wenn die Ladung mit q(t) = q0 cos(ωt) oszilliert.
Zusatzaufgabe 1: Dielektrische Eigenschaften der Materie
Welche der folgenden Stoffe zeigen im elektrischen Feld
a) dielektrische Verschiebungspolarisation?
b) dielektrische Orientierungspolarisation?
c) ferroelektrische Eigenschaften?
(1) He; (2) H2 ; (3) H2 O; (4) KNbO3 ; (5) Glycerin; (6) CH4 ; (7) O2 ; (8) NaCL; (9) N2 ; (10) SeignetteSalz; (11) Ar; (12) CO2
Zusatzaufgabe 2: Magnetische Eigenschaften der Materie
Welche der folgenden Stoffe sind bei Raumtemperatur
a) diamagnetisch?
b) paramagnetisch?
c) ferromagnetisch?
(1) Pt; (2) He; (3) H2 O; (4) FeCl3 ; (5) Co; (6) Fe; (7) O2 ; (8) Bi; (9) H2 ; (10) Au; (11) Al; (12) Ar;
(13) Ni; (14) Na; (15) Na+
web: http://www.uni-saarland.de/lehrstuhl/eschner/lehre/ss2013/eep2.html