Naturwissenschaften II (B. Sc. Maschinenbau) - IAP TU

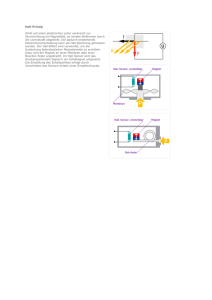
Übungen zur Vorlesung
Naturwissenschaften II
(B. Sc. Maschinenbau)
Sommersemester 2008
Übungsblatt 6
Professor Dr. G. Birkl, Dr. N. Herschbach
Besprechung in der Woche
vom 26.5 - 2.6.08
www.physik.tu-darmstadt/apq/naturwissenschaften
1. Hall-Effekt
Man betrachte einen Leiter, der von einem Strom I durchflossen ist und sich in ei~ befindet. Im Leiter werden die Ladungsträger dabei infolge der
nem Magnetfeld B
Lorentzkraft senkrecht zum Magnetfeld und senkrecht zur Stromrichtung abgelenkt.
Dies bewirkt eine Ladungsträgertrennung, die wiederum den Aufbau eines elektrischen
UHall
ez
ey
n
B
ex
+
vD
h
e
b
-
I
+
U
~ H zur Folge hat. Hierbei erfolgt die Ladungstrennung so weit, bis die von den
Feldes E
~ H die Lorentzkraft, der sie entgegen
Ladungsträgern erfahrene Coulombkraft im Feld E
~ H ruft eine Spannung UHall hervor, die Hall-Spannung
wirkt, kompensiert. Das Feld E
genannt wird. Die Hall-Spannung soll berechnet werden für die in der Abbildung darge~ stehe horizontal
stellte Geometrie. Das Leiterstück habe die Höhe h und die Breite b. B
und zum Leiter orthogonal. Die freien Ladungsträger, die den Stromfluß ermöglichen,
seien Elektronen mit Ladung −e und Ladungsträgerdichte n.
a) Berechnen Sie die Stromdichte ~j, und geben Sie einen Ausdruck für die Driftgeschwindigkeit ~vD der Elektronen an.
~ H her.
b) Leiten Sie einen Ausdruck für das elektrische Feld E
c) Berechnen Sie eine Formel für die Hall-Spannung UHall .
d) Die auf dem Hall-Effekt beruhenden Magnetfeldsensoren sind fast immer aus
Halbleitermaterial aufgebaut. In Halbleitern ist die Ladungsträgerdichte 106 mal
kleiner als in Metallen. Weshalb werden Halbleiter zur Herstellung von Hallsonden
bevorzugt?
1
2. Induktionsgesetz von Faraday
Ein rechteckiger Drahtbügel in der x-y-Ebene mit der Breite b = 1 m liegt senkrecht
~ das in positive z-Richtung (= aus der Bildebene)
zu einem homogenen Magnetfeld B
steht und 0.1 T beträgt. Der Drahtbügel habe einen vernachlässigbar kleinen elektrischen Widerstand. Zieht man einen Stab mit elektrischem Widerstand R = 1 Ω, der
B=(0, 0, B)
R
y
b
v
B
Uind
x
reibungsfrei über den Drahtbügel gleiten kann, mit konstanter Geschwindigkeit ~v in
x-Richtung mit |~v | = v = 1 m/s, wird durch die Änderung des magnetischen Flußes
ein Strom I induziert. Dabei muss man Arbeit gegen die Lorentzkraft leisten, die dieser
Strom hervorruft.
a) Bestimmen Sie die induzierte Spannung Uind .
b) Berechnen Sie den Strom I und die Lorentzkraft F~L .
c) Berechnen Sie die mechanische Leistung Pmech , die erbracht werden muss, um die
Bewegung des Stabes mit Geschwindigkeit ~v zu ermöglichen. Wie verhält sich
diese im Vergleich mit der elektrischen Leistung Pel , die im Widerstand R in
Joule’sche Wärme umgewandelt wird?
d) Wie würden sich die Lorentzkraft F~L und die aufzubringende mechanische Leistung Pmech ändern, wenn für den elektrischen Widerstand R sehr kleine Werte erreicht werden könnten, wie es die Benutzung von Supraleitern ermöglichen
würde?
3. Transformator
Ein Transformator bestehe aus einer Primärspule mit N1 = 500 Windungen und einer
Sekundärspule mit N2 = 25 als Windungszahl. An der Primärspule liege die Netzspannung an, also U1 = 240 V.
a) Welcher Strom fließt in der Primärspule, wenn an der Sekundärseite ein Verbraucher mit einem Widerstand von 200 Ω angeschlossen ist?
b) Wieviele Windungen müsste die Sekundärspule haben, wenn man bei gleicher
Primärspannung U1 , gleichem N1 und gleichem Lastwiderstand auf der Sekundärseite die vierfache Leistung zur Verfügung stellen will?
2