Versuch 004

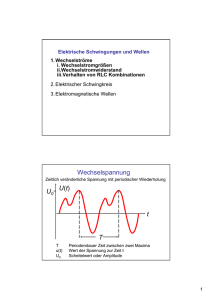
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
Versuch 004
Das Elektronenstrahloszilloskop
Aufgaben
1.
2.
3.
4.
Graphische Darstellung einer Wechselspannung (zwei unterschiedliche Ablenkspannungen) nach dem
Abbild am Oszilloskop. Bestimmung der Frequenz, Amplitude und des Effektivwertes.
Bestimmen einer Frequenz aus Lissajous Figuren.
Messen der Phasenverschiebung eines RC- Tiefpasses.
(Bonusaufgabe:) Untersuchen von Amplitude und Phase an Hoch und Tiefpass in Abhängigkeit von der
Frequenz.
Grundlagen
Wechselspannung
Idealisierte Wechselspannung
Als Wechselspannung bezeichnet man jegliche Spannung, welche sich periodisch ändert. In der Praxis engt man
den Begriff weiter ein, in dem man eine harmonische Schwingung der Spannung der Form
U = U 0 ⋅ sin ϖt
damit bezeichnet. Glücklicher Weise liefern die meisten Generatoren (Wechselspannungsdynamo, z.B.) eine
mathematisch derart beschreibbare Spannung.
Effektivwerte
Da die meisten elektrischen Geräte zu schwerfällig sind, die schnelle zeitliche Änderung der Spannung
respektive des Stromes zu erfassen, stößt man auf die Größe des Effektivwertes der Spannung, bzw. des
Stromes. Herleiten kann man das Ganze über die elektrische Arbeit an einem ohmschen Widerstand, die gleich
der abgegebenen Wärme ist.
U 0 sin 2 (ϖt )dt U 0 2  t sin ϖt ⋅ cosϖt 
U2
∫
Wel = WQ = ∫ Pdt = ∫ dt =
=
⋅ −

R
R
R 2
2ϖ

2
Gibt es eine Effektivspannung, so muss diese bei dem gleichen Widerstand die gleiche Wärme erzeugen:
2
U
Wel = WQ = E ⋅ t
R
Eingesetzt für eine gesamte Periode ergibt sich also:
2
2
U
UE
t
⋅t = 0 ⋅
R
R 2
U0
I
U E :=
, I E := 0
2
2
Verhalten von Widerständen in Wechselspannung
In einem Wechselstromkreis ergibt sich auf Grund der Tatsache, dass die Spannung zeitlich pulsiert, und damit
auch die Stromstärke sich in gleichen zeitlichen Verhältnissen sich ändert, dass neben dem bekannten ohmschen
Widerstand auch noch die Spule (durch ihre Induktivität) und der Kondensator (durch dessen Kapazität) die
Spannung abfallen lassen, so dass sich Widerstände ungleich null Ohm (bei der Spule) und unendlich (beim
Kondensator) ergeben. Es ergibt sich eine Trilogie der Widerstände:
R=
U
1
2Π
, X L = ϖL , X C =
mit ϖ = 2πf =
T
I
ϖC
Verhalten von I(t) zu U(t)
Wie man leicht sehen kann, sind XL und XC von der angelegten Frequenz abhängig. Doch nicht nur ihre
Abhängigkeit von der Spannungsfrequenz unterscheidet sie von dem „einfachen Ohmschen“, sie führen
gegenüber der Stromstärke eine Phasenverschiebung der darüber abfallenden Spannung ein: Die Spule erzeugt
wegen ihrer Selbstinduktion eine Phase ϕ = 90°, der Kondensator wegen des kontinuierlichen Ladens/ Entladens
eine Phase von ϕ = -90°.
Versuchsnummer: 004
Seite 25
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
Der Hochpass, der Tiefpass
Dies nutzt man in der Elektrotechnik u.A. aus, um frequenzabhängige Spannungsteiler und Filter zu
konstruieren. Man könnte z. B. durch Reihenschaltung eines Kondensators mit einem ohmschen Widerstandes
einen solchen Spannungsteiler aufbauen: den RC- Tief- oder Hochpass:
ABB I.1.A & B: Schaltbilder und Phasendiagramme für RC- Tief- und Hochpass
wobei natürlich UR mit der Stromstärke gleichgerichtet ist und UC einen Phasenwinkel von ϕ = -90° erzeugt.
Damit ergeben sich folgende Gleichungen:
&
&
&
UE = U R + UC
&
&
&
U E = U R +UC
U Ex = sin ϕTP ⋅ U E = U R = R ⋅ I
U Ex = cos ϕ HP ⋅ U E = U R = R ⋅ I
U Ey = cos ϕTP ⋅ U E = U C =
1
⋅I
ϖC
U Ey = sin ϕ HP ⋅ U E = U C =
UR
R
= ϖCR
ϖC ⋅ U C = I =
tan ϕTP
ϖC ⋅ U C = I =
tan ϕ HP =
1
⋅I
ϖC
UR
R
1
ϖCR
Weiterhin gilt:
RGes =
UC =
UC =
X C + R2 =
2
UE
I
UE
RGes = X C + R 2 =
2
1
I = XC ⋅
2
ϖC
X C + R2
UE
1+
2
R
2
XC
=
U R = RI = R ⋅
UE
UR =
1 + (ϖRC )
2
UE
2
XC
+1
R2
UE
I
UE
X C + R2
2
=
UE
 1 
1+ 

 ϖRC 
2
Das Elektronenstrahloszilloskop
Aufbau
Das „Oszi“ besteht aus einer Verstärkereinheit, einer Braunschen Röhre und einem Sägezahnspannungsgenerator
mit Trigger. Die eingehenden Spannungen werden entweder auf die x- und y- Ablenkkondensatoren der Röhre
gelegt (x-y- Betrieb) oder zeitlich voneinander getrennt auf die y- Ablenkung gelegt, während die automatisch
modifizierte Sägezahnspannung den Strahl linear in x- Richtung ablenkt (Dualbetrieb).
Schaltbild
ABB I.2: Darstellung eines Elektronenstrahloszilloskops als Schaltbild.
Versuchsnummer: 004
Seite 26
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
Bildschirmanzeige
Der Bildschirm ist in 10x8 Kästchen (Divergenzen, div) eingeteilt, welche wiederum zu einem kartesischen
Koordinatensystem mit vier gleich großen Quadranten angeordnet sind. Die Maßeinheiten erhält man mit
Multiplikation mit dem eingestellten Messbetreich (z.B. 0,1 ms pro div). In diesen Zusammenhang folgt, dass
der Ablesefehler mit ±0,1 div zu beziffern ist.
Lissajous- Figuren
Entstehung
Legt man statt der internen Sägezahnspannung im Singlestrahlbetrieb an die x- Ausrichtung eine zweite
Wechselspannung, so wird der Strahl zeitlich nicht mehr linear abgelenkt, sondern in Form einer Sinusfunktion.
Er ergibt sich also für die Koordinaten der Menge aller am Bildschirm dargestellten Punkte:
(x, y ) = U 0 x ⋅ sin (ϖ xt ),U 0 y ⋅ sin ϖ yt ± ϕ wobei ϕ die Phasenverschiebung bei t=0s ist.
(
))
(
Phasenwinkel
Mittels Lissajous- Figuren kann man ebenso die Phase zwischen zwei anliegenden Spannungen bestimmen,
sofern das Bild stabil ist. Dies wiederum ist nur der Fall, wenn beide Frequenzen fx und fy durch einen rationalen
Faktor voneinander abhängen. Für alle t = k·Txy (Txy ist kgV von Tx und Ty) gilt:
(x , y ) =
Daraus folgt für folgende Nomierung (
(0 , U
⋅ sin (ϕ
Æ siehe: ABB I.2):
0 y
)) = (0 , U )
1y
U1E = U 0 E ⋅ sin ϕ
sin ϕ =
U1E
U0E
ϕ = arcsin
U1E
U0E
wobei aber ϕ nur einen Wert annehmen kann, nämlich
den mathematisch korrekt drehenden.
ABB I.2: Phasendiagramm mit Frequenzverhältnis 1:1
Frequenzmessung
Ausgehend von der Koordinatendarstellung gelangt weiterhin man zu der Einsicht, dass sich theoretisch nur
„stabile“ Figuren ergeben, wenn fy ein rationales Vielfaches von fx ist. Dabei gibt das Verhältnis der Anzahl der
Maxima das Verhältnis der Frequenzen zueinander an.
Natürlich kann man auch die unbekannte Frequenz ein sich ändernden Figur bestimmen, in dem man annimmt,
dass die unbekannte ein rationales Vielfaches sei und sich der Phasenwinkel zeitlich ändert. Man kommt dem
Problem also mit der Erklärung einer Schwebung gut bei. In der Anwendung bedeutet dies: Man bestimmt die
Maxima und die Zeit, die vergeht ist, bis sich das gleiche Figurenbild einstellt.
Diese Methode der Messung ist natürlich eingeschränkt durch die Möglichkeiten des Ablesens, d.h. bei vielen
Maxima wird ein Ablesen unmöglich.
Versuchsdurchführung
Versuchsteil I: Wechselspannung am Oszilloskop
Versuchsobjekt:
Elektronenstrahloszilloskop, Spannungsquelle mit Wechselspannung
Schaltungsskizze:
ABB. II.1: Beschaltung des Oszilloskops mit Wechselspannung
Versuchsnummer: 004
Seite 27
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
Mögliche systematischen Fehler:
Messwerte werden durch Verstärker manipuliert und könnten so zu systematischen Fehlern führen.
Zu erwartendes Ergebnis:
Spannungs-Zeitdiagramm mit einer Sinuskurve.
Versuchsablauf:
• Aufbau der Schaltung
• Ablesen der gesuchten Messwerte (f, U0, und Skizzieren des Kurvenverlaufes bei min. zwei
unterschiedlichen Darstellungen
Fehlerrechnung:
∆U = 0.1div ⋅ Messbereich
∆U
∆U eff =
2
df
1
∆f =
⋅ ∆t = 2 ⋅ ∆f = f 2 ⋅ 0.1div ⋅ Messbereich
dt
T
Versuchsteil II: Bestimmen einer unbekannten Frequenz aus Lissajous- Figuren
Versuchsobjekt:
Elektronenstrahloszilloskop, Spannungsquelle mit unbekannter Wechselspannung (f2, U2), Spannungsquelle mit
bekannter Wechselspannung (f1, U1). Die Referenzfrequenz f1 ist die aus Teilversuch I.
Schaltungsskizze:
ABB. II.2: Zwei schwingende Spannungen mit unterschiedlichen Frequenzen überlagern sich ungestört im
Oszilloskop.
Mögliche systematischen Fehler:
Ungenaue Frequenzlieferung in U1 führt zu einer ungenauen Angabe der bekannten Frequenz (siehe
Fehlerrechnung).
Zu erwartendes Ergebnis:
Stabile Lissajousfiguren, aus denen wir die unbekannte Frequenz der Spannung U2 ermitteln können.
Versuchsablauf:
• Aufbau der Schaltung
• Justieren von f2, so dass das Bild stabil wird
• Ablesen und Skizzieren der Kurvenverläufe.
Fehlerrechnung:
q ⋅ f 2 = p ⋅ f1 ⇒ ∆f 2 =
p
∆f1
q
Versuchsteil III & IV: Charakterisierung von Tief- und Hochpass
Versuchsobjekt:
Elektronenstrahloszilloskop, Spannungsquelle mit variabler Wechselspannung, RC- Tiefpass, RC- Hochpass
Versuchsnummer: 004
Seite 28
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
Schaltungsskizze:
(A)
(B)
ABB. II.3: (A) Ein RC- Tiefpass, bzw. (B) ein RC Hochpass zur Beobachtung am Oszilloskop
Mögliche systematischen Fehler:
Messwerte werden evtl. durch Spannungsverstärkung manipuliert.
Zu erwartendes Ergebnis:
Für den Tiefpass:
ϕTP = arctan(ϖRC )
Für den Hochpass:
 1 
ϕ HP = arctan

 ωRC 
1
UA
=
2
UE
 1 
1+ 

 ϖRC 
UA
1
=
2
UE
1 + (ϖRC )
Versuchsablauf:
• Aufbau der Schaltung
• Ablesen der Verhalten von Phase und Amplitude bei unterschiedlichen Frequenzen im Dualbetrieb
• Ablesen der Achsen und Maximaldifferenzen bei unterschiedlichen Frequenzen der Lissajousfiguren
Fehlerrechnung:
∆
U A ∆U A U A ⋅ ∆U E U A + U E
=
+
=
⋅ 0.1div ⋅ Messbereich
2
UE
UE
UE
UE
 d
U
d
U 
arcsin 1 +
arcsin 1  ⋅ 0.1div ⋅ Messbereich
∆ϕ = 
U 0 dU 0
U0 
 dU1
U1 + U 0
=
⋅ 0.1div ⋅ Messbereich
2
2
U1 + U 0 ⋅ U 0
Messwerte
Versuchsteil I: Wechselspannung am Oszilloskop
(A)
(B)
ABB I.1: Die gleiche Spannung (U: y* 2 V/div) mit unterschiedlichen Ablenkgeschwindigkeiten (A) 0,1 ms/div
und (B) 0,2 ms/div an der x- Achse.
Versuchsteil II: Bestimmen einer unbekannten Frequenz aus Lissajous- Figuren
Folgende Lissajous- Figuren haben wir bei der Referenzfrequenz aus Versuchsteil I erhalten:
Versuchsnummer: 004
Seite 29
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
(Abbildungen im Maßstab 1:2)
(A)
(B)
(C)
ABB II.2: (A) Lissajousfigur zur ersten, (B) zur zweiten und (C) zur dritten Messung.
Versuchsteil III & IV: Charakterisierung von Tief- und Hochpass
Messwerte für den Tiefpass:
UE in div
f in Hz
200
250
500
1000
2500
5000
10000
2,8
2,8
2,7
2,7
2,8
2,7
2,7
Messwerte für den Hochpass:
UE in div
f in Hz
200
250
500
1000
2500
5000
10000
2,8
2,8
2,8
2,8
2,8
2,8
2,8
Ue in div
UA in div
0,4
0,5
0,9
1,5
2,3
2,6
2,7
Ue in div
Ua in div
2,7
2,6
2,5
2,2
1,3
0,8
0,4
UA in div
2,7
2,7
2,6
2,2
1,4
0,8
0,5
0,4
0,5
0,9
1,3
1,1
0,7
0,4
Ua in div
0,5
0,6
1
1,6
2,4
2,7
2,7
0,5
0,5
0,9
1,2
1,1
0,6
0,3
Auswertung
Versuchsteil I: Wechselspannung am Oszilloskop
1
1
1
=1
= 1000 Hz = 1kHz
f1 = =
V
ms
T 10div ⋅ 0.1
ms
U 0 = 2.8div ⋅ 2
= 5.6V
div
div
V
ms
2
∆U 0 = 0.1div ⋅ 2
= 0.2V
1
0
.
1
0
.
1
∆
f
=
f
⋅
∆
t
=
MHz
⋅
div
⋅
= 10 Hz
1
div
div
U
1
U eff = 0
f
=
= 1kHz
2
2
ms
5div ⋅ 0.2
dU eff
div
∆U 0
∆Ueff =
⋅ ∆U 0 =
ms
dU 0
2
∆f 2 = f 2 ⋅ ∆t = 1MHz ⋅ 0.1div ⋅ 0.2
= 20 Hz
div
Versuchsteil II: Bestimmen einer unbekannten Frequenz aus Lissajous- Figuren
Figur (a):
1⋅ fx = 2 ⋅ f y
f x = 2 f y = 2kHz
∆f x = 2∆f y = 0.02kHz
Figur (b):
Figur (c):
3 ⋅ f x = 1⋅ f y
fx =
1fy
2 ⋅ fx = 3 ⋅ fy
= 0.33kHz
3
∆f x = 0.003kHz
Versuchsnummer: 004
Seite 30
3 fy
= 1.5kHz
2
∆f x = 0.015kHz
fx =
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
Versuchsteil III & IV: Charakterisierung von Tief- und Hochpass
UA UA
=
UE UE
∆
U A ∆U A U A
U +U
V
=
+ 2 ∆U E = A 2 E 0.1div ⋅ 2
UE
UE UE
div
UE
ϕ = arcsin
∆ϕ =
U
U1
= arcsin e
U0
UE
U1 + U 0
U 1 + U 0 ⋅U 0
2
2
⋅ 0.1div ⋅ 2
V
div
Ergebnisse
Versuchsteil I: Wechselspannung am Oszilloskop
U0 = 5.6 V ± 0.2 V
Uef f= 3.96 V ± 0.14 V
f = 1 kHz ± 0.01 kHz
Versuchsteil II: Bestimmen einer unbekannten Frequenz aus Lissajous- Figuren
a) f = 2 kHz ± 20 Hz
b) f = 0.33 kHz ± 3 Hz
c) f = 1.5 kHz ± 15 hz
Versuchsteil III & IV: Charakterisierung von Tief- und Hochpass
(a) Tiefpass:
f in Hz
200
250
500
1000
2500
5000
10000
UA/UE
0,96 ± 0,07
0,93 ± 0,07
0,93 ± 0,07
0,81 ± 0,07
0,46 ± 0,05
0,30 ± 0,05
0,15 ± 0,04
3
(b) Hochpass:
f in Hz
-0,15 ± 0,01
-0,19 ± 0,02
-0,37 ± 0,04
-0,63 ± 0,11
-1,01 ± 0,45
-1,07 ± 0,85
-1,57 ± ?
200
250
500
1000
2500
5000
10000
UA/UE
0,18 ± 0,04
0,21 ± 0,04
0,36 ± 0,05
0,57 ± 0,06
0,86 ± 0,07
0,96 ± 0,07
0,96 ± 0,07
3
1,57 ± ?
0,99 ± 0,92
0,85 ± 0,78
0,48 ± 0,24
0,22 ± 0,06
0,22 ± 0,02
0,11 ± 0,01
ABB III.1: Diagramme zur Abhängigkeit von Phasenwinkel und Spannungsverhältnis von der Frequenz beim
Tiefpass. Der theoretische Kurvenverlauf ist blau unter die Messergebnisse gelegt.
Versuchsnummer: 004
Seite 31
Physikalisches Grundpraktikum
Ralf Erlebach
Versuchsprotokolle
ABB. III.2: Diagramme zur Abhängigkeit von Phasenwinkel und Spannungsverhältnis von der Frequenz am
Hochpass. Blau eingelegt ist der theoretische Kurvenverlauf.
Diskussion
In dem konnten wir alle theoretischen Voraussagen in guter Näherung bestätigen. Der Phasenwinkel am
Hochpass wäre einer Nachbetrachtung im Experiment wert, da die Voraussagen nicht mehr innerhalb der selbst
gesteckten Toleranzen sich befindet.
Das Experiment verlief ohne Komplikationen, die abgezeichneten Messwerte sind im Anhang zu finden.
Jena, 25.11.2001
Versuchsnummer: 004
Seite 32